Abstract
Starting from a particle system with short-range interactions, we derive a continuum model for the bending, torsion, and brittle fracture of inextensible rods moving in three-dimensional space. As the number of particles tends to infinity, it is assumed that the rod’s thickness is of the same order as the interatomic distance. For this reason, discrete terms and energy contributions from the ultrathin rod’s lateral surface appear in the limiting functional. Fracture energy in the \(\Gamma \)-limit is expressed by an implicit cell formula, which covers different modes of fracture, including (complete) cracks, folds, and torsional cracks. In special cases, the cell formula can be significantly simplified—we illustrate this by the example of a full crack and also show that the energy of a mere fold is strictly lower for a class of models. Our approach applies e.g. to atomistic systems with Lennard–Jones-type potentials and is motivated by the research of ceramic nanowires.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Ceramic and semiconductor nanowires (composed of Si, SiC, \(\text {Si}_3\text {N}_4\), \(\text {TiO}_2\), or ZnO etc.) under loading exhibit large deflections, but also brittle or ductile fracture. [29] Their mechanical behaviour is often very different from that of bulk materials, size- and structure-dependent, and influenced by surface energy. Laboratory testing at the nanoscale still poses various challenges, so modelling and simulation play an important role in the advancement of nanotechnology. [37]
To set off on a path towards elastic-fractural modelling of nanowires, in this article we derive from three-dimensional atomistic models a continuum theory for ultrathin rods whose elastic energy is of the order corresponding to bending or torsion. After treating the purely elastic case in [71], here we extend our model considerably by adding liability of the material to develop brittle cracks.
Our work stands at the crossroads of three paths of research in applied analysis which are:
-
(DR)
rigorous derivation of elasticity theories for thin structures (often referred to as dimension reduction).
-
(D-C)
discrete-to-continuum limits.
-
(F)
fracture mechanics.
An important tool in all these three branches is \(\Gamma \)-convergence. [19, 20]
In (DR) the aim is to understand the relation between three-dimensional elasticity theory and effective theories for lower-dimensional bodies, such as plates, rods or beams. [9, 30, 62] With the pioneering contributions of L. Euler and D. Bernoulli, the journey started more than two centuries before the first nanowires were manufactured. Yet, most mathematically rigorous derivations of such theories first appeared no sooner than in the 1990s. [1, 10, 58] A decade later, the famous discovery of a quantitative rigidity estimate in [49] brought forth an abundance of works on bending theories. [49, 50, 61]
As for (D-C), ‘establishing the status of elasticity theory with respect to atomistic models’ was listed by Ball among outstanding open problems in elasticity. [13] Research has been devoted to studying the Cauchy–Born rule [35, 51], pointwise limits of interaction energies [17] and their \(\Gamma \)-limits [3, 25, 69], or to finding atomistic deformations approximating a given solution of the equations of elasticity [24, 26, 63]. See also [16] for a survey.
The interest of mathematicians in (F) was particularly ignited after Francfort and Marigo [41] elaborated on the influential model by Griffith, using modern variational methods (see e.g. [18, 40] for further references). In variational models of fracture, be it brittle or cohesive [14], we typically find functionals involving the sum of elastic and fracture energy:
In the above, \(W:{\mathbb {R}}^{3\times 3}\rightarrow [0,\infty )\) stands for the stored energy density of a material body \({\Omega }\subset {\mathbb {R}}^d\), \(d\in \{2,3\}\), \(y^+-y^-\) is the jump of the deformation \(y:{\Omega }\rightarrow {\mathbb {R}}^d\) across the crack set \(J_y\), \(\nu \) denotes the normal vector field to \(J_y\), and \(\kappa :({\mathbb {R}}^d)^2\rightarrow [0,\infty ]\) is the fracture toughness.
Given the myriads of physical situations that emerge in modern materials science, it seems natural that researchers have made efforts to bridge some of the gaps between (DR), (D-C) and (F).
Combining (DR) and (D-C) is motivated by the need of accurate models for thin structures in nanoengineering, such as thin films or nanotubes. [2, 48, 67, 68] Interestingly, when the thickness h of the reference crystalline body is very small (i.e. comparable to the interatomic distance \(\varepsilon \)), the simultaneous \(\Gamma \)-limit as \(\varepsilon \rightarrow 0+\), \(h\rightarrow 0+\) gives rise to new ultrathin plate or rod theories which could not be obtained by (DR) in the purely continuum setting. [27, 66, 71]
Atomistic effects also lie at the core of crack formation and propagation. [15, 28] However, up to now combinations of (D-C) and (F) have only been explored in specific situations such as one-dimensional chains of atoms [21, 55, 65], scalar-valued models [23], or cleavage in crystals [45,46,47].
Similarly, despite the recent progress, theories uniting (DR) and (F) are still under development. In linearized elasticity, models for brittle plates [6, 12, 42, 59], beams [52] or shells [4] have been derived mostly using a weak formulation in SBD or GSBD function spaces [7, 34]. The nonlinear setting of membranes [5, 11, 22], on the other hand, employs the more regular spaces SBV and GSBV. [8] As for nonlinear bending theories, the lack of a piecewise quantitative rigidity estimate in 3D presents an obstacle, so the result of [70] with a dimension reduction from 2D to 1D seems rather isolated; we also refer to [44, 64] for materials with voids.
Fracture of a thin rod composed of atoms
In this article, we treat a problem that falls into all three branches (DR), (D-C) and (F). Our main Theorem 4.1 provides the \(\Gamma \)-limit of atomic interaction energies defined on cubic crystalline lattices in the shape of a slender rod. Unlike in the purely elastic model from [71], we now replace the interaction potentials (expressed by a cell energy function \(W_{\textrm{cell}}\) like in e.g. [31, 51, 66]) with a sequence \((W_{\textrm{cell}}^{(k)})_{k=1}^\infty \) of cell energies to ensure that elastic deformations (bending and torsion) are comparably favourable in terms of energy as cracks (see Fig. 1 for an illustration). This is specifically expressed in condition (W5) for the constants \(({\bar{c}}_1^{(k)})_{k=1}^\infty \), which give a lower bound on the cost of placing atoms far away from each other (see Sect. 2.3). Physically we can interpret this as considering a sequence of materials that are mutually similar but are characterized by different values of material parameters. The limiting strain energy has, just like in (1.1):
-
1.
A bulk part that coincides with its counterpart in [71] and features an ultrathin correction and atomic surface layer terms, neither of which appears in the corresponding rod theory [61] derived by (DR) without (D-C). These traits might make a model better-suited for the description of nanostructures.
-
2.
A fracture part which turns out to be a weighted sum over the singular set of a limiting deformation. The weights are given by an implicit cell formula \(\varphi =\varphi (y^+-y^-,(R^-)^{-1}R^+)\), where \(y^+-y^-\in {\mathbb {R}}^3\) denotes the jump of the deformation mapping at a specified crack point and \((R^-)^{-1}R^+\in \textrm{SO}(3)\) is related to kinks/folds or torsional rupture.
Implicit cell formulas arise in \(\Gamma \)-convergence problems in homogenization [20] or phase transitions [32, 33, 56].
To comment on some important aspects of the proofs, in the liminf inequality we first derive a preliminary cell formula by a blowup technique reminiscent of [8, 39] and then relate it to a more simple asymptotic formula which uses rigid boundary values (cf. [43]). The atomistic setting allows us to circumvent the unavailability of a 3D piecewise rigidity theorem in SBV (in fact, it is enough to work with piecewise Sobolev functions here). The main challenge of our analysis is, however, to provide a matching limsup inequality. Due to the k-dependency of the interaction potential \(W_{\textrm{cell}}^{(k)}\), it is a priori not clear how to construct a global recovery sequence \((y^{(k)})\) that not only works for a specific subsequence. We resolve this difficulty by establishing a localization of cracks on the atomic length scale, which appears to be of some independent interest. More precisely, we argue that an approximative minimizing sequence 
for \(\varphi \) can be chosen with cracks confined to a fixed number of atomic slices (Lemma 6.1), which lets us transfer 
to a lattice with different interatomic distances (Proposition 6.1) and thus define \((y^{(k)})\) for every \(k\in {\mathbb {N}}\). \(\Gamma \)-convergence problems involving brittle fracture often have to deal with pieces of the deformed body escaping to \(\infty \). As our limiting theory is one-dimensional we can sidestep working on GSBV-type spaces and instead obtain a limiting functional on piecewise \(H^2\) functions. By an explicit construction using assumption (W9) in Lemma 6.2 we show that \(L^\infty \) (or weaker) bounds could be imposed energetically so as to ensure matching compactness properties of low-energy sequences.
After describing our discrete model in Sect. 2, we prove a compactness theorem for sequences of bounded energy in Sect. 3. The lower bound in the \(\Gamma \)-convergence result from Sect. 4 is shown in Sect. 5 and then followed in Sect. 6 by an analysis of the cell formula and the construction of recovery sequences for Theorem 4.1(ii). Section 7 provides examples of interatomic potentials to which our approach applies. In Sect. 8, we show that for full cracks and a class of mass-spring models there is an explicit expression for the cell formula. Moreover, it is proved that in such models, the energy needed to produce a full crack is strictly greater than the energy of a mere kink. The last short discussion section gives some hints on possible future research.
1.1 Notation
We write \(\textrm{dist}(B_1,B_2):=\inf \{|x^{(1)}-x^{(2)}|;\;x^{(1)}\in B_1,\; x^{(2)}\in B_2\}\) for \(B_1,B_2\subset {\mathbb {R}}^3\). Whenever the symbol ± appears in an equation, we mean that the equation holds both in the version with \(+\) in all occurrences and in the version with −. The letter C denotes a positive generic constant, whose value may be different in different instances. One-sided limits are written as \(f(\sigma \pm )=\lim _{x\rightarrow \sigma \pm } f(x)\). Further, \({\mathbb {R}}_{\textrm{skew}}^{3\times 3}=\{A\in {\mathbb {R}}^{3\times 3};\;A=-A^\top \}\). The symbol \(A_{\cdot i}\) denotes the i-th column of a matrix A and \({\mathcal {H}}^n\) is the n-dimensional Hausdorff measure. The restriction 
of a measure \(\mu \) to the measurable set K is defined by 
.
2 Model assumptions and preliminaries
2.1 Atomic lattice and discrete gradients
In our particle interaction model, \(\Lambda _k=([0,L]\times \frac{1}{k}{\bar{S}})\cap \frac{1}{k}{\mathbb {Z}}^3\), \(k\in {\mathbb {N}}\), is a cubic atomic lattice—the reference configuration of a thin rod of length \(L>0\). The interatomic distance 1/k is directly proportional to the thickness of the rod.
The rod’s cross section is represented with a bounded domain \(\emptyset \ne S\subset {\mathbb {R}}^2\). We assume that there is a set \({\mathcal {L}}'\subset (\frac{1}{2}+{\mathbb {Z}})^2\) such that
Moreover, should it happen that \(x'+\{-\frac{1}{2},\frac{1}{2}\}^2\subset {\mathcal {L}}:={\bar{S}}\cap {\mathbb {Z}}^2\), it is assumed that \(x'\in {\mathcal {L}}'\). The symbol \(\Lambda _k'\) is used for the lattice of midpoints of open lattice cubes with sidelength 1/k and corners in \(\Lambda _k\).
Our lattice \(\Lambda _k\) undergoes a static deformation \(y^{(k)}:\Lambda _k\rightarrow {\mathbb {R}}^3\). The main aim of this paper is to investigate the asymptotic behaviour as k becomes large and to establish an effective continuum model as \(k\rightarrow +\infty \).
Sometimes it will be advantageous to work with a rescaled lattice that has unit distances between neighbouring atoms. The points of this lattice are written with hats over their coordinates, i.e. if \(x=(x_1, x_2, x_3)\in \Lambda _k\) we introduce \({\hat{x}}_1:=kx_1\), \({\hat{x}}'=({\hat{x}}_2,{\hat{x}}_3):=kx'=k(x_2,x_3)\) and \({\hat{y}}^{(k)}({\hat{x}}_1,{\hat{x}}_2,{\hat{x}}_3):=k y^{(k)}(\frac{1}{k}{\hat{x}}_1,\frac{1}{k}{\hat{x}}')\) so that \({\hat{y}}^{(k)}:k\Lambda _k\rightarrow {\mathbb {R}}^3\). Then \({\hat{\Lambda }}_k\) and \({\hat{\Lambda }}'_k\) denote the sets of all \({\hat{x}}=({\hat{x}}_1,{\hat{x}}_2,{\hat{x}}_3)\) such that the corresponding downscaled points x are elements of the sets \(\Lambda _k\) and \(\Lambda _k'\), respectively. We will frequently use these eight direction vectors \(z^1,\dots ,z^8\):
With these vectors we can describe the deformation of a unit cell \({\hat{x}}+\{-\frac{1}{2},\frac{1}{2}\}^3\) centred at \({\hat{x}}\in {\hat{\Lambda }}'_k\) – let \(\vec {y}^{\,(k)}({\hat{x}})=({\hat{y}}^{(k)}({\hat{x}}+z^1)|\cdots |{\hat{y}}^{(k)}({\hat{x}}+z^8))\in {\mathbb {R}}^{3\times 8}\). Further we introduce \(\langle {\hat{y}}^{(k)}({\hat{x}})\rangle =\frac{1}{8}\sum _{i=1}^8 {\hat{y}}^{(k)}({\hat{x}}+z^i)\) and the discrete gradient \({\bar{\nabla }}{\hat{y}}^{(k)}({\hat{x}})=({\hat{y}}^{(k)}({\hat{x}}+z^1)-\langle {\hat{y}}^{(k)}({\hat{x}})\rangle |\cdots |{\hat{y}}^{(k)}({\hat{x}}+z^8)-\langle {\hat{y}}^{(k)}({\hat{x}})\rangle )\in {\mathbb {R}}^{3\times 8}\). A discrete gradient has the sum of columns equal to 0 and an important special case is the matrix \({\bar{\textrm{Id}}}:=(z^1|\cdots |z^8)\in {\mathbb {R}}^{3\times 8}\), which satisfies \({\bar{\textrm{Id}}}={\bar{\nabla }}\textrm{id}\). Further we define two noteworthy subsets of \({\mathbb {R}}^{3\times 8}\), later used for characterizing rigid motions:
2.2 Rescaling, interpolation and extension of deformations
To handle sequences of deformations defined on a common domain \({\Omega }=(0,L)\times S\), we set \({\tilde{y}}^{(k)}(x_1,x_2,x_3):=y^{(k)}(x_1,\frac{1}{k}x')\) for \((x_1,\frac{1}{k}x')\in \Lambda _k\) and interpolate \({\tilde{y}}^{(k)}\) as follows so that it is defined even outside lattice points.
Write \(\tilde{z}^i:=(\frac{1}{k}z_1^i,z_2^i,z_3^i)\) and \({\tilde{Q}}({\bar{x}})={\bar{x}}+(-\frac{1}{2k},\frac{1}{2k})\times (-\frac{1}{2},\frac{1}{2})^2\) for \({\bar{x}}\in {\tilde{\Lambda }}_k'=\{\xi \in {\Omega };\;(k\xi _1,\xi ')\in {\hat{\Lambda }}_k'\}\). First, we set \({\tilde{y}}^{(k)}({\bar{x}}):=\frac{1}{8}\sum _{i=1}^8{\tilde{y}}^{(k)}({\bar{x}}+\tilde{z}^i)\) and for each face \({\tilde{F}}\) of the block \({\tilde{Q}}({\bar{x}})\) and the corresponding centre \(x_{{\tilde{F}}}\) of the face \({\tilde{F}}\), define \({\tilde{y}}^{(k)}(x_{{\tilde{F}}}):=\frac{1}{4}\sum _j{\tilde{y}}^{(k)}({\bar{x}}+\tilde{z}^j)\), where the sum runs over all j such that \({\bar{x}}+\tilde{z}^j\) is a corner of \({\tilde{F}}\). Now we interpolate \({\tilde{y}}^{(k)}\) in an affine way on every simplex \({\tilde{T}}=\textrm{conv}\{{\bar{x}},{\bar{x}}+\tilde{z}^i,{\bar{x}}+\tilde{z}^j,x_{{\tilde{F}}}\}\), where \(|z^i-z^j|=1\) and \({\bar{x}}+\tilde{z}^i,{\bar{x}}+\tilde{z}^j\in {\tilde{F}}\) (there are 24 simplices within \({\tilde{Q}}({\bar{x}})\)). Like this, \({\tilde{y}}^{(k)}\) is differentiable almost everywhere, so we can define \(\nabla _k{\tilde{y}}^{(k)}:=\bigl (\frac{\partial {\tilde{y}}^{(k)}}{\partial x_1}\,|\,k\frac{\partial {\tilde{y}}^{(k)}}{\partial x_2}\,|\,k\frac{\partial {\tilde{y}}^{(k)}}{\partial x_3}\bigr )\). For any face \({\tilde{F}}\) of \({\tilde{Q}}({\bar{x}})\) with face centre \(x_{{\tilde{F}}}\), the piecewise affine interpolation satisfies
We also set \({\bar{\nabla }}_k{\tilde{y}}^{(k)}({\bar{x}}):=k({\tilde{y}}^{(k)}({\bar{x}}_1+\frac{1}{k}z_1^i,{\bar{x}}'+(z^i)')-\sum _{j=1}^8{\tilde{y}}^{(k)}({\bar{x}}_1+\frac{1}{k}z_1^j,{\bar{x}}'+(z^j)'))_{i=1}^8\).
For the following reasons we now extend deformations to certain auxiliary surface lattices:
-
surface energy needs to be modelled;
-
in part we would like to apply \(\Gamma \)-convergence results from [71];
-
a fixed domain on which the convergence of \(({\tilde{y}}^{(k)})\) is formulated sometimes does not match with its inscribed crystalline lattice (specifically in the \(x_1\)-direction).
We present here the necessary tools, without too much emphasis on this technical issue later, referring to [71, Subsection 2.3] for more details and a proof, adapted from [69]. Consider a portion \((a,b)\times S\subset (0,L)\times S\) of the rod. Let \(a_k=\frac{1}{k}\lceil ka\rceil \), \(b_k=\frac{1}{k}\lfloor kb\rfloor \), and
Lemma 2.1
There are extensions \(y^{(k)}:\Lambda _k^\textrm{ext}\rightarrow {\mathbb {R}}^3\) such that their interpolations \({\tilde{y}}^{(k)}\) satisfy
and
For \(x\in \overline{{\Omega }_k^\textrm{ext}}\), we denote by \({\bar{x}}\) an element of \({\tilde{\Lambda }}_k'^{,\textrm{ext}}\) that is closest to \(x\). In what follows we always understand the symbols \(\Lambda _k^\textrm{ext}\), \(\Lambda _k'^{,\textrm{ext}}\) etc. with \(a:=0\) and \(b:=L\), unless stated otherwise. We also set \(\Omega ^\textrm{ext}:=(0,L)\times S^\textrm{ext}\).
2.3 Energy
Let \(L_k=\frac{1}{k}\lfloor kL\rfloor \), \({\hat{\Lambda }}_k'^{,\textrm{surf}} = \{\frac{1}{2},\ldots ,kL_k-\frac{1}{2}\}\times ({\mathcal {L}}'^{,\mathrm ext} {\setminus } {\mathcal {L}}')\), and \({\hat{\Lambda }}_k'^{,\textrm{end}} = \{-\frac{1}{2},kL_k+\frac{1}{2}\} \times {\mathcal {L}}'^{,\mathrm ext}\). We give this definition of strain energy \(E^{(k)}\):
with \(W_{\textrm{cell}}^{(k)}:{\mathbb {R}}^{3\times 8}\rightarrow [0,\infty ]\), \(W_{\textrm{surf}}^{(k)}:({\mathcal {L}}'^{,\mathrm ext}{\setminus }{\mathcal {L}}')\times {\mathbb {R}}^{3\times 8}\rightarrow [0,\infty ]\) and \(W_{\textrm{end}}^{(k)}:\{-\frac{1}{2k},L_k+\frac{1}{2k}\}\times {\mathcal {L}}'^{,\mathrm ext}\times {\mathbb {R}}^{3\times 8}\rightarrow [0,\infty ]\). The terms with \(W_{\textrm{surf}}^{(k)}\) and \(W_{\textrm{end}}^{(k)}\) are useful for incorporating surface energy (see [71] for further clarification)—while \(W_\textrm{surf}^{(k)}\) models contributions from the rod’s lateral surface, the terms involving \(W_\textrm{end}^{(k)}\) come from the front and rear bases of the rod and vanish as \(k\rightarrow \infty \). For convenience we assume that for every \(\vec {y}\in {\mathbb {R}}^{3\times 8}\), \(W_{\textrm{surf}}^{(k)}(\cdot ,\vec {y})\) is extended to a piecewise constant function on \(S^\textrm{ext}\setminus {\bar{S}}\) which is equal to \(W_{\textrm{surf}}^{(k)}({\hat{x}}',\vec {y})\) on \({\hat{x}}'+(-\frac{1}{2},\frac{1}{2})^2\). Sometimes it will be useful to group the terms, so for \(\vec {y}\in {\mathbb {R}}^{3\times 8}\) we set
In our \(\Gamma \)-convergence statement, we consider the rescaled energy \(\frac{1/k^3}{1/k^4}E^{(k)}=kE^{(k)}\), where \(k^3\) is the order of the number of particles per unit volume in a bulk system and \(1/k^4\) is the appropriate power of a rod’s thickness for studying the bending/torsion energy regime (see e.g. [60] for more context).
Assumptions on the cell energy functions \(W_{\textrm{cell}}^{(k)}\), \(W_{\textrm{surf}}^{(k)}\), and \(W_{\textrm{end}}^{(k)}\).
Hereafter \({{\mathscr {W}}}^{(k)}\) stands for \(W_{\textrm{cell}}^{(k)}\), \(W_{\textrm{surf}}^{(k)}({\hat{x}}',\cdot )\) with \({\hat{x}}'\in {\mathcal {L}}'^{,\mathrm ext} {\setminus } {\mathcal {L}}'\), and for \(W_{\textrm{end}}^{(k)}({\frac{1}{k}{\hat{x}}_1},{\hat{x}}',\cdot )\) with \({\hat{x}}\in {\hat{\Lambda }}_k'^{,\textrm{end}}\).
-
(W1)
Frame-indifference: \({{\mathscr {W}}}^{(k)}(R\vec {y}+(c|\cdots |c))={{\mathscr {W}}}^{(k)}(\vec {y})\) for all \(R\in \textrm{SO}(3)\), \(\vec {y}\in {\mathbb {R}}^{3\times 8}\), \(c\in {\mathbb {R}}^3\), and \(k\in {\mathbb {N}}\).
-
(W2)
Energy well: For every \(k\in {\mathbb {N}}\), \({{\mathscr {W}}}^{(k)}\) attains a minimum (equal to 0) at rigid deformations, i.e. deformations \(\vec {y}=({\hat{y}}_1|\cdots |{\hat{y}}_8)\) with \({\hat{y}}_i=Rz^i+c\) for all \(i\in \{1,\dots ,8\}\) and some \(R\in \textrm{SO}(3)\), \(c\in {\mathbb {R}}^3\).
-
(W3)
Independence of k in the elastic regime: There are parameters \(c_{\textrm{frac}}^{(k)}\searrow 0\) such that \(\lim _{k\rightarrow \infty }k(c_{\textrm{frac}}^{(k)})^2\in (0,\infty )\) and an elastic stored energy function \(W_0:{\mathcal {L}}'^{,\mathrm ext}\times {\mathbb {R}}^{3\times 8}\rightarrow [0,\infty ]\) such that we have \(\forall \, k\in {\mathbb {N}}\;\forall \,\vec {y}\in {\mathbb {R}}^{3\times 8}\;\forall {x'\in {\mathcal {L}}'^{,\mathrm ext}}\):
$$\begin{aligned} W_{\textrm{tot}}^{(k)}(x',\vec {y})=W_0(x',\vec {y})\quad \text {if }\;\textrm{dist}({\bar{\nabla }}{\hat{y}},\bar{\textrm{SO}}(3))\le c_{\textrm{frac}}^{(k)}. \end{aligned}$$Further, there exists a \(C>0\) independent of \(k\in {\mathbb {N}}\) such that
$$\begin{aligned} W_{\textrm{end}}^{(k)}(\tfrac{1}{k}{\hat{x}}_1,{\hat{x}}',\vec {y})\le C\textrm{dist}^2({\bar{\nabla }}{\hat{y}},\bar{\textrm{SO}}(3))\quad \text {for any }{\hat{x}}\in {\hat{\Lambda }}_k'^{,\textrm{end}}, \end{aligned}$$\(\vec {y}=({\hat{y}}_1|\cdots |{\hat{y}}_8)\in {\mathbb {R}}^{3\times 8}\), and \({\bar{\nabla }}{\hat{y}}=\vec {y}-(\sum _{j=1}^8{\hat{y}}_j)(1,\dots ,1)\) with \(\textrm{dist}({\bar{\nabla }}{\hat{y}},\bar{\textrm{SO}}(3))\le c_{\textrm{frac}}^{(k)}\).
-
(W4)
Regularity in k: \(W_{\textrm{tot}}^{(k+1)}(x',\vec {y})\ge \frac{k}{k+1}W_{\textrm{tot}}^{(k)}(x',\vec {y})\) for all \( k\in {\mathbb {N}}\;\forall \,\vec {y}\in {\mathbb {R}}^{3\times 8}\;\forall {x'\in {\mathcal {L}}'^{,\mathrm ext}}.\)
-
(W5)
Non-degeneracy in the elastic and the fracture regime: The function \(W_0|_{{{\mathcal {L}}'\times {\mathbb {R}}^{3\times 8}}}\) is independent of \(x'\) (hence we omit it from the notation in this region) and satisfies
$$\begin{aligned} W_0(\vec {y})\ge c_{\textrm{W}}\textrm{dist}^2({\bar{\nabla }}{\hat{y}},\bar{\textrm{SO}}(3))\quad \forall \,\vec {y}\in {\mathbb {R}}^{3\times 8} \end{aligned}$$for a constant \(c_{\textrm{W}}>0\). Writing \(W_{\textrm{cell}}^{(k)}(\vec {y})={\bar{W}}^{(k)}(\vec {y})\) if \(\textrm{dist}({\bar{\nabla }}{\hat{y}},\bar{\textrm{SO}}(3))> c_{\textrm{frac}}^{(k)}\), we assume that the mappings \({\bar{W}}^{(k)}\) can be chosen such that
$$\begin{aligned} {\bar{W}}^{(k)}(\vec {y}) \ge {\bar{c}}_1^{(k)} \quad \forall \, k\in {\mathbb {N}}\;\forall \,\vec {y}\in {\mathbb {R}}^{3\times 8} \end{aligned}$$for a sequence \(({\bar{c}}_1^{(k)})_{k=1}^\infty \) of positive numbers with \(\lim _{k\rightarrow \infty }k{\bar{c}}_1^{(k)}\in (0,\infty )\).
-
(W6)
\({{\mathscr {W}}}^{(k)}\) is everywhere Borel measurable and \(W_0({\hat{x}}',\cdot )\), \({\hat{x}}'\in {\mathcal {L}}^{',\textrm{ext}}\), is of class \({\mathcal {C}}^2\) in a neighbourhood of \(\bar{\textrm{SO}}(3)\).
-
(W7)
If \(i\in \{1,2,\dots ,8\}\), \({\hat{x}}'\in {\mathcal {L}}'^{,\textrm{ext}}{\setminus }{\mathcal {L}}'\), and \(\vec {y}=({\hat{y}}_1|\cdots |{\hat{y}}_8)\), then \(\vec {y}\mapsto W_{\textrm{surf}}^{(k)}({\hat{x}}',\vec {y})\) may depend on \({\hat{y}}_i\) only if \({\hat{x}}'+(z^i)'\in {\mathcal {L}}\). If \(x_1\in \{-\frac{1}{2k},L_k+\frac{1}{2k}\}\), then \(\vec {y}\mapsto W_{\textrm{end}}^{(k)}(x_1,{\hat{x}}',\vec {y})\) may depend on \({\hat{y}}_i\) only if \((x_1,{\hat{x}}')+\tilde{z}^i\in {\tilde{\Lambda }}_k\).
The quadratic form associated with \(\nabla ^2 W_\textrm{surf}^{(k)}(x',\bar{\textrm{Id}})\) is denoted by \(Q_\textrm{surf}(x',\cdot )\).
Throughout we will assume that Assumptions (W1)–(W7) are satisfied. We also introduce conditions which imply that long-range interactions of atoms are bounded or even are negligible.
-
(W8)
We say that inelastic interactions are bounded if
$$\begin{aligned} {{\mathscr {W}}}^{(k)}(\vec {y}) \le {\bar{C}}_1^{(k)} \quad \forall \, k\in {\mathbb {N}}\;\forall \,\vec {y}\in {\mathbb {R}}^{3\times 8} \end{aligned}$$for a sequence \(({\bar{C}}_1^{(k)})_{k=1}^\infty \) of positive numbers with \(\lim _{k\rightarrow \infty }k{\bar{C}}_1^{(k)}\in (0,\infty )\).
-
(W9)
We say that the cell energies have maximum interaction range scaling with \((M_k)_{k=1}^{\infty }\), where \(M_k\rightarrow 0\), \(M_kk \rightarrow \infty \), if the following holds true: If there is a partition \(\{1,\ldots ,8\}=J_1{\dot{\cup }}J_2{\dot{\cup }}\cdots {\dot{\cup }}J_{n_{\textrm{C}}}\) such that for some \(\vec {y},{\vec {y}}\,'\in {\mathbb {R}}^{3\times 8}\) one has
$$\begin{aligned}{} & {} \min _{1\le \ell<m\le n_{\textrm{C}}}\textrm{dist}(\{{\hat{y}}_{i_\ell }\}_{i_\ell \in J_\ell },\{{\hat{y}}_{i_m}\}_{i_m\in J_m})\ge M_kk \quad \text {and}\\{} & {} \quad \min _{1\le \ell <m\le n_{\textrm{C}}}\textrm{dist}(\{{\hat{y}}'_{i_\ell }\}_{i_\ell \in J_\ell },\{{\hat{y}}'_{i_m}\}_{i_m\in J_m})\ge M_kk \end{aligned}$$and there are rigid motions given by \(R_m\in \textrm{SO}(3)\) and \(c_m\in {\mathbb {R}}^3\) such that
$$\begin{aligned} {\hat{y}}'_{i_m} = R_m{\hat{y}}_{i_m} + c_m \quad \forall \, i_m\in J_m,\; m=1,\ldots , n_{\textrm{C}}, \end{aligned}$$then
$$\begin{aligned} |{{\mathscr {W}}}^{(k)}({\vec {y}}\,') - {{\mathscr {W}}}^{(k)}(\vec {y})| \le \frac{{C_{\textrm{far}}}}{M_k{k^2}} \end{aligned}$$for a uniform constant \(C_{\textrm{far}}>0\).
Remark 2.1
We remark that the assumption in (W4) is a monotonicity assumption only for \(kW_{\textrm{tot}}^{(k)}(x',\cdot )\) but not for \(W_{\textrm{tot}}^{(k)}(x',\cdot )\) itself. It is in line with our assuming that the elastic energy is independent of k in (W3) and the fracture toughness scales with \(\frac{1}{k}\), cf. (W5).
Remark 2.2
By (W2), (W3), and (W6) we have
for a constant \(c_{\textrm{w}}\) and all \(\vec {y}\in {\mathbb {R}}^{3\times 8}\) such that \(\textrm{dist}({\bar{\nabla }}{\hat{y}},\bar{\textrm{SO}}(3))\le c_{\textrm{frac}}^{(k)}\). Moreover, by (W2), (W5) and (W6) the quadratic form \(Q_3\) associated with \(\nabla ^2 W_0({\bar{\textrm{Id}}})\), is positive definite on \(\textrm{span}\{V_0\cup {\mathbb {R}}_{\textrm{skew}}^{3\times 3}{\bar{\textrm{Id}}}\}^\bot \).
2.4 Piecewise Sobolev functions
We work with the linear spaces \(P\text {-}H^m(0,L;{\mathbb {R}}^{\ell })\), \(m=1,2\), \(\ell \in {\mathbb {N}}\), of functions that are piecewise Sobolev in the following sense:
Here we say that \((\sigma ^i)_{i=0}^{n+1}\) is a partition of [0, L] if \(0=\sigma ^0< \sigma ^1<\cdots < \sigma ^{n+1}=L\). Suppose \({\tilde{y}}\in P\text {-}H^m(0,L;{\mathbb {R}}^{\ell })\) and \(\{\sigma ^i\}_{i=0}^{n+1}\) is the minimal set with property (2.3). For \(m=1\) one has
For \(m=2\) we have \(\{\sigma ^i\}_{i=1}^{n} = S_{\tilde{y}} \cup S_{\tilde{y}'}\), which is the set of points at which \(\tilde{y}\) or \(\tilde{y}'\) jumps.
3 Compactness
Theorem 3.1
Suppose the sequence \((y^{(k)})_{k=1}^\infty \) of lattice deformations fulfils
Then after applying the extension scheme from Sect. 2.2 we can find an increasing sequence \((k_j)_{j=1}^\infty \subset {\mathbb {N}}\), functions \({\tilde{y}}\in P\text {-}H^2(0,L;{\mathbb {R}}^3)\), \(d_2,d_3\in P\text {-}H^1(0,L;{\mathbb {R}}^3)\) with \(R=(\partial _{x_1}{\tilde{y}}|d_2|d_3)\in \textrm{SO}(3)\) a.e., and a partition \((\sigma ^i)_{i=0}^{{\bar{n}}_{\textrm{f}}+1}\) of [0, L] such that for any \(\eta \in (0,\frac{1}{2}\min _{0\le i\le {\bar{n}}_f} |\sigma ^{i+1}-\sigma ^i|)\) and every \(0\le i\le {\bar{n}}_{\textrm{f}}\) we have:
-
(i)
\({\tilde{y}}^{(k_j)}\rightarrow {\tilde{y}}\) in \(L^2({\Omega }^\textrm{ext};{\mathbb {R}}^{3\times 3})\);
-
(ii)
\(\nabla _{k_j}{\tilde{y}}^{(k_j)}\rightarrow R=(\partial _{x_1}{\tilde{y}}|d_2|d_3)\) in \(L^2((\sigma ^i+\eta ,\sigma ^{i+1}-\eta )\times S^\textrm{ext};{\mathbb {R}}^{3\times 3})\);
-
(iii)
\({\textrm{dist}({\bar{\nabla }}_{k_j}{\tilde{y}}^{(k_j)},\bar{\textrm{SO}}(3))} \le c_{\textrm{frac}}^{(k)}\) on \((\sigma ^i+\eta ,\sigma ^{i+1}-\eta )\times S^\textrm{ext}\), for j sufficiently large;
-
(iv)
if we define the measures \(\mu _k\) on [0, L] by
$$\begin{aligned} \mu _k(A) = \sum _{\begin{array}{c} {\hat{x}}\in {\hat{\Lambda }}_k'^{,\textrm{ext}},\\ {\hat{x}}_1\in kA \end{array}}kW_{\textrm{tot}}^{(k)}\bigl ({\hat{x}}',\vec {y}^{\,(k)}({\hat{x}})\bigr ), \end{aligned}$$for Borel sets A, then \(\mu _{k_j}\rightharpoonup ^*\mu \) for a Radon measure \(\mu \).
Proof
By properties of the extension scheme from Sect. 2.2 (see [71, Remark 2.1]) there is a constant \({\hat{C}}_{e}\ge 1\) such that for any \(x\in {\tilde{\Lambda }}_k'^{,\textrm{ext}}\), setting \({\mathcal {U}}(x)=\bigl (\{x_1-\frac{1}{k},x_1,x_1+\frac{1}{k}\}\times {\mathcal {L}}'\bigr ) {\cap {\tilde{\Lambda }}_k'}\) we have
Let \(S_k(x_1)\) denote a slice of the rod at the point \(x_1\):
A slice \(S_k(x_1)\) is regarded as broken if there is an \(x'\in S\) such that
Like this, for any x such that the slice \(S_k(x_1)\) and, if existent, the neighbouring slices \(S_k(x_1\pm \frac{1}{k})\) are not broken, \({\bar{\nabla }}_k{\tilde{y}}^{(k)}(x)\) is at most \(c_{\textrm{frac}}^{(k)}\)-far from \(\bar{\textrm{SO}}(3)\) even if \(x\in {\Omega }_k^\textrm{ext}{\setminus } (0,L_k)\times S^\textrm{ext}\). Write \(X_1^{(k)}\) for the set of all midpoints of the \(x_1\)-projections of broken slices:
We have \(\sharp X_1^{(k)}\le C_{\textrm{f}}\) with \(C_{\textrm{f}}>0\) independent of k, since by Assumptions (W3) and (W5)
for a constant \(c > 0\) and so
If we pass to a subsequence \(\{k_j\}_{j=1}^\infty \subset {\mathbb {N}}\), we find \(n_{\textrm{f}}\in {\mathbb {N}}\), \(0\le n_{\textrm{f}}\le C/c\), such that for every \(j\in {\mathbb {N}}\), there are always precisely \(n_{\textrm{f}}\) broken slices, i.e. \(\forall j\in {\mathbb {N}}:\sharp X_1^{(k_j)}=n_{\textrm{f}}\), and
We observe that the location \(s_j^i\) of the i-th broken slice, \(1\le i\le n_{\textrm{f}}\), remains in the compact interval [0, L], so we construct a further subsequence, which we still denote by \((k_j)_{j=1}^\infty \), so that
Naturally it can be that some of the limiting positions of cracks \(s^i\), \(i=1,2,\dots n_{\textrm{f}}\), coincide or appear at the endpoints of the rod, hence we rewrite
where the number \({\bar{n}}_{\textrm{f}}\le n_{\textrm{f}}\). Further, \(\sigma ^0:=0\) and \(\sigma ^{{\bar{n}}_{\textrm{f}}+1}:=L\).
Suppose \(0<\eta <\frac{1}{2}\min _{0\le i\le {\bar{n}}_f} |\sigma ^{i+1}-\sigma ^i|\). If j is large enough, then for all i, \(0\le i\le {\bar{n}}_{\textrm{f}}\),
Thus the regions \([\sigma ^i+\eta ,\sigma ^{i+1}-\eta ]\times S\) are intact, so we can replace \(W_{\textrm{cell}}^{(k)}\) by \(W_0\) and safely apply our results about purely elastic rods here (see [71, Theorem 2.4]). Specifically, \({\tilde{y}}^{(k_j)} \rightarrow {\tilde{y}}\) in \(L^2((\sigma ^i+\eta ,\sigma ^{i+1}-\eta )\times S^\textrm{ext};{\mathbb {R}}^3)\), \(\nabla _{k_j}{\tilde{y}}^{(k_j)}\rightarrow R=(\partial _{x_1}{\tilde{y}}|d_2|d_3)\) in \(L^2((\sigma ^i+\eta ,\sigma ^{i+1}-\eta )\times S^\textrm{ext};{\mathbb {R}}^{3\times 3})\), and the \(x'\)-independent limit satisfies \({\tilde{y}}\in H^2((\sigma ^i+\eta ,\sigma ^{i+1}-\eta );{\mathbb {R}}^3)\), \(d_2,d_3\in H^1((\sigma ^i+\eta ,\sigma ^{i+1}-\eta );{\mathbb {R}}^3)\), and \(R\in \textrm{SO}(3)\) a.e. (We extracted another subsequence without changing the subindices.) By passing to a diagonal sequence we find a single sequence that satisfies convergence properties (i)–(ii) for any choice of \(\eta \). Moreover, the \(L^{\infty }\) bound in (3.1) and the uniform energy bound in (3.4) show that indeed \({\tilde{y}}\in P\text {-}H^2(0,L;{\mathbb {R}}^3)\) and \(R \in P\text {-}H^1(0,L;{\mathbb {R}}^{3\times 3})\). Finally passing to yet another subsequence (not relabelled), we find \(\mu _{k_j}\rightharpoonup ^*\mu \) for some Radon measure \(\mu \) since (3.3) implies \(\sup _k \mu _k([0,L])< \infty \). \(\square \)
4 Main result
Recall the Hessian quadratic forms \(Q_3\) and \(Q_\textrm{surf}(x',\cdot )\) of \(W_0\) and \(W_\textrm{surf}^{(k)}(x',\cdot )\) at \(\bar{\textrm{Id}}\), respectively.
Theorem 4.1
If \(k\rightarrow \infty \), we have \(E^{(k)}{\mathop {\rightarrow }\limits ^{\Gamma }}E_{\textrm{lim}}\), more precisely:
-
(i)
(liminf inequality) Let \((y^{(k)})_{k=1}^\infty \) be a sequence of lattice deformations such that their piecewise affine interpolations and extensions \(({\tilde{y}}^{(k)})_{k=1}^\infty \subset H^1({\Omega }_k^\textrm{ext};{\mathbb {R}}^3)\), defined in Sect. 2.2, converge in \(L^2({\Omega }^\textrm{ext};{\mathbb {R}}^3)\) to \({\tilde{y}}\in L^2((0,L);{\mathbb {R}}^3)\) for which there is a partition \((\varsigma ^i)_{i=0}^{{\tilde{n}}_{\textrm{f}}+1}\) of [0, L] such that \({\tilde{y}}|_{(\varsigma ^i,\varsigma ^{i+1})}\in H^1((\varsigma ^i,\varsigma ^{i+1})\times S^\textrm{ext};{\mathbb {R}}^3)\), \(0\le i\le {\tilde{n}}_{\textrm{f}}\). Assume further that for any \(\eta >0\) sufficiently small, we have \(k\partial _{x_s}{\tilde{y}}^{(k)}\rightarrow d_s\in L^2((0,L);{\mathbb {R}}^3)\) in \(L^2((\varsigma ^i+\eta ,\varsigma ^{i+1}-\eta )\times S^\textrm{ext};{\mathbb {R}}^3)\), \(s=2,3\), \(0\le i\le {\tilde{n}}_{\textrm{f}}\) (\(L_{\textrm{loc}}^2\)-convergence). Then
$$\begin{aligned} E_{\textrm{lim}}({\tilde{y}},d_2,d_3)\le \liminf _{k\rightarrow \infty } kE^{(k)}(y^{(k)}). \end{aligned}$$ -
(ii)
(existence of a recovery sequence) Let \({\tilde{y}}\in L^2((0,L);{\mathbb {R}}^3)\) be such there is a partition \((\varsigma ^i)_{i=0}^{{\tilde{n}}_{\textrm{f}}+1}\) of [0, L] for which \({\tilde{y}}|_{(\varsigma ^i,\varsigma ^{i+1})}\in H^1((\varsigma ^i,\varsigma ^{i+1});{\mathbb {R}}^3)\), and let \(d_2,d_3\in L^2((0,L);{\mathbb {R}}^3)\). Then there exists a sequence of lattice deformations \((y^{(k)})_{k=1}^\infty \) such that their piecewise affine interpolations and extensions \(({\tilde{y}}^{(k)})_{k=1}^\infty \subset H^1({{\Omega }_k^\textrm{ext}};{\mathbb {R}}^3)\) satisfy \({\tilde{y}}^{(k)}\rightarrow {\tilde{y}}\) in \(L^2({{\Omega }^\textrm{ext}};{\mathbb {R}}^3)\), \(k\frac{\partial {\tilde{y}}^{(k)}}{\partial x_s}\rightarrow d_s\) in \(L_{\textrm{loc}}^2((\varsigma ^i,\varsigma ^{i+1})\times S^\textrm{ext};{\mathbb {R}}^3)\) for \(s=2,3\), \(0\le i\le {\tilde{n}}_{\textrm{f}}\), and
$$\begin{aligned} \lim _{k\rightarrow \infty } kE^{(k)}(y^{(k)})=E_{\textrm{lim}}({\tilde{y}},d_2,d_3). \end{aligned}$$Moreover, if \(||{\tilde{y}}||_{{L^\infty ((0,L);{\mathbb {R}}^3)}} \le M\) and the cell energies satisfy the maximum interaction range property (W9), then for any \((\zeta _k)_{k=1}^{\infty }\subset (0,1)\) with \(\zeta _k \searrow 0\) and \(\zeta _k/M_k \rightarrow \infty \) one can choose \(y^{(k)}\) such that \({||y^{(k)}||_{{\ell ^\infty (\Lambda _k;{\mathbb {R}}^3)}}} \le M+\zeta _k\).
The limit energy functional is given by
where \(R:=(\partial _{x_1}{\tilde{y}}|d_2|d_3)\), \(S_R:=S_{{\tilde{y}}'}\cup S_{d_2}\cup S_{d_3}\), and the class of admissible deformations
The relaxed quadratic form \(Q_3^\textrm{rel}:{\mathbb {R}}^{3\times 3}_{\textrm{skew}}\rightarrow [0,+\infty )\) is defined as
with \(Q_{\textrm{tot}}(x',\cdot )=Q_3+Q_{\textrm{surf}}(x',\cdot )\), and \(\varphi :{\mathbb {R}}^3 \times \textrm{SO}(3) \rightarrow [0,\infty ]\) is introduced in (5.3).
Remark 4.1
It follows from the positive semidefiniteness of \(Q_{\textrm{tot}}\) that the minimum in (4.1) is attained. Basic code for approximating a minimizer of (4.1) can be found in [72].
Remark 4.2
The elastic part of our limiting functional includes a matrix expressing what we call an ultrathin correction—it is the first term on the second line of (4.1). The term is responsible for atomic effects that a continuum theory merely based on the Cauchy-Born rule would not capture.
Remark 4.3
Assumptions (W3), (W5) and the compactness result [71, Theorem 2.4] in the elastic case imply that \(\varphi \ge {\bar{c}}_1\) for some constant \({\bar{c}}_1 > 0\) on \({\mathbb {R}}^3 \times \textrm{SO}(3) {\setminus } \{(0,{\textrm{Id}})\}\) (and \(\varphi (0,{\textrm{Id}}) = 0\)). If (W8) holds true, then we also have \(\varphi \le {\bar{C}}_1\) for a constant \({\bar{C}}_1 < \infty \).
Remark 4.4
The universality of the sequence \(\zeta _k\) obtained in (ii) would allow to impose an \(L^{\infty }\) constraint energetically by simply setting \(E^{(k)}(y^{(k)}) = +\infty \) if \(||y^{(k)}||_{\infty } > {M+\zeta _k}\). One then has a directly matching compactness result in Theorem 3.1.
Remark 4.5
The convergence of deformations used in Theorem 4.1 is equivalent to
which shows the limit’s independence of our interpolation scheme.
5 Proof of the lower bound
The proof is divided into four parts.
5.1 First step—elastic part
Since the conclusion is immediate if the liminf is infinite, let us assume the contrary; \({\tilde{y}}^{(k)}\rightarrow {\tilde{y}}\) in \(L^2({\Omega };{\mathbb {R}}^3)\) and after extracting a subsequence,
Let \((\sigma ^i)_{i=0}^{{\bar{n}}_{\textrm{f}}+1}\), \(\nabla _{k_j}{\tilde{y}}^{(k_j)}\), \(\mu _k\), \(\mu \) be as in Theorem 3.1 and fix \(\eta >0\) small. Then by the results about purely elastic rods ( [71, Theorem 3.1]), the bound
\(i=0,1,\dots ,{\bar{n}}_{\textrm{f}},\) holds true. Since this is fulfilled for any \(\eta \), we can let \(\eta \rightarrow 0+\) and use the monotone convergence theorem, as we will see later.
5.2 Second step—\({\varvec{w^*}}\)-limit in measures
For the crack contribution to the strain energy, we use the blow-up method of Fonseca and Müller [39]. We will not make a notational distinction between \(({\tilde{y}}^{(k)})\) and its hitherto constructed subsequence \(({\tilde{y}}^{(k_j)})\) any more, as this is not relevant for our \(\Gamma \)-convergence proof.
Now note that \(S_{{\tilde{y}}}\cup S_R\subset X_1\), where \(X_1=\{\sigma ^i\}_{i=1}^{{\bar{n}}_{\textrm{f}}}\) is from the proof of Theorem 3.1. Write
. Decomposing
\(\mu \) into an absolutely continuous part and a singular part, we have
with \(\mu _{\textrm{s}}\ge 0\). The \(w^*\)-convergence then gives (cf. [36, Th. 1.40])
The goal now is to find the asymptotic minimal energy \(\varphi =\varphi ({\tilde{y}}^+-{\tilde{y}}^-,(R^-)^{-1}R^+)\) necessary to produce a crack or kink and for every \(1\le i\le n_{\textrm{f}}\), show that
Let us expand the definition of the derivative of \(\mu \):
By [38, Prop. 1.15] and [36, Th. 1.40], we can find \(r_n\searrow 0\) such that
5.3 Third step—preliminary cell formula obtained by blowup
First we shall find a preliminary lower bound \(\psi \) for \(\frac{d \mu }{d \tilde{\mathcal {H}}}\) by rescaling \((\sigma ^i-r_n,\sigma ^i+r_n)\) to a fixed interval (cf. [8, proof of Theorem 5.14, Step 3]). There is a sequence \((k_n)_{n=1}^\infty \) such that \(k_n\ge n\), \(r_nk_n\rightarrow \infty \),
as well as
and \(\sigma ^i-\frac{r_n}{2}+\frac{2}{k_n}<s_{k_n}^j<\sigma ^i+\frac{r_n}{2}-\frac{2}{k_n}\) for every \(n\in {\mathbb {N}}\) and each of the (finitely many) sequences \((s_{k_n}^j)_{n=1}^\infty \) of midpoints of broken slices satisfying \(\lim _{n\rightarrow \infty } s_{k_n}^j=\sigma ^i\). Since the restrictions of \({\tilde{y}}\) and R to left and right neighbourhoods of \(\sigma ^i\) are \(H^1\), we get for the rescaled functions
the convergences \(y^{\ddagger ,n}\rightarrow y_{\textrm{PC}}\) in \(L^2([-1,1];{\mathbb {R}}^3)\) and \(R^{\ddagger ,n}\rightarrow R_{\textrm{PC}}\) in \(L^2([-1,1];{\mathbb {R}}^{3\times 3})\) for \(n\rightarrow \infty \), where the piecewise constant functions \(y_{\textrm{PC}}\), \(R_{\textrm{PC}}\) are defined through
We also set, for \(w_1\in [-1,1]\),
where \(\sigma ^i_{k_n}=\frac{1}{k_n}\lfloor {k_n} \sigma ^i \rfloor \). Then using (5.2), we get
in
\(L^2([-1,1]\times S^\textrm{ext};{\mathbb {R}}^3)\) and
in
\(L^2([I_\psi ^-\cup I_\psi ^+]\times S^\textrm{ext}];{\mathbb {R}}^{3\times 3})\), where \(I_\psi ^-=[-1,-\frac{1}{2}]\) and \(I_\psi ^+=[\frac{1}{2},1]\). This gives the preliminary estimate with ‘converging boundary conditions’:
where
and \(\textrm{PAff}(\Lambda _{r_n,k_n})\) denotes the class of piecewise affine mappings 
which are generated by interpolating their values from \(\Lambda _{r_n,k_n}\) by the scheme from Sect. 2.2. The minimum in \({\tilde{\psi }}\) runs over all sequences \(\{r_n\}\subset (0,\infty )\), \(\{k_n\}\subset {\mathbb {N}}\) and 
with the above properties.
It can be shown by a diagonalization argument that the minimum is attained; this is also the case in (5.3). From the translation and rotation invariance of \(W_{\textrm{cell}}^{(k)}\) we see that \({\tilde{\psi }}({\tilde{y}}^-,{\tilde{y}}^+,R^-,R^+)=\psi ({\tilde{y}}^+-{\tilde{y}}^-,(R^-)^{-1}R^+)\) for a function \(\psi :{\mathbb {R}}^3\times \textrm{SO}(3)\rightarrow [0,\infty ]\).
5.4 Fourth step—rigid boundary conditions in the cell formula
At last, we relate the preliminary cell formula \(\psi \) to the final cell formula which uses rigid boundary conditions instead of \(L^2\)-converging ones:
with
\(I^-=[-1,-\frac{3}{4}]\) and \(I^+=[\frac{3}{4},1]\).
Remark 5.1
The particular choice
for given \({\tilde{y}}^+,{\tilde{y}}^-\in {\mathbb {R}}^3\) and \(R^-,R^+\in \textrm{SO}(3)\) shows that, in case (W8) holds true, one has \(\varphi \le {\bar{C}}_1\) for some \({\bar{C}}_1< \infty . \)
We now show that we have \(\psi \ge \varphi \). Suppose \(\varepsilon >0\) and that 
is a sequence \(\textrm{PAff}(\Lambda _{r_n,k_n})\) such that
and
where for any \(I\subset [-1,1]\) we set
and \({{\mathscr {L}}}_n'(I) = (\frac{1}{2r_nk_n}+\frac{1}{r_nk_n} {\mathbb {Z}}) \cap I\). The definition of a rod slice in this section reads
Our goal now is to find a sequence 
which is admissible as a competitor in the definition of \(\varphi \) and has asymptotically lower energy than 
. We provide the construction only for 
, as for 
we could proceed analogously. Writing \(I_{0,n}^-:=\frac{1}{r_nk_n}(\lfloor -\frac{3}{4}r_nk_n\rfloor +1,\lfloor -\frac{1}{2}r_nk_n\rfloor )\) for a discrete approximation of \(I_\psi ^-\setminus I^-\) from inside and \(N_n^-=\lfloor -\frac{1}{2}r_nk_n\rfloor -\lfloor -\frac{3}{4}r_nk_n\rfloor -3 = \sharp {{\mathscr {L}}}'(I_{0,n}^-)-2\) for the number of (interior) slices intersecting \(I_{0,n}^-\times \overline{S^\textrm{ext}}\), we introduce the sets
where 
. The sets \(W_i^{(n)}\), \(i=1,2,3\), are comprised of the midpoints of the \(w_1\)-projections of slices on which, loosely speaking, a certain quantity is below four times its average. By Lemma 5.2 (see p. 19 below) with \(p=4\) we see that for every \(i\in \{1,2,3\}\) and \(n\in {\mathbb {N}}\), the set \(W_i^{(n)}\) contains at least \(\lfloor (3/4)N_n^-\rfloor \) elements. The pigeonhole principle then implies that for every n large enough there is \(w_-^{(n)}\in W_1^{(n)}\cap W_2^{(n)}\cap W_3^{(n)}\). Since \(N_n^-\ge \frac{1}{4}r_nk_n-4\), the inequality in (5.5a) and the finiteness in (5.1) imply an estimate in integral form:
for a constant \(C_{\textrm{e}}>0\). Hence we can employ the growth assumption on the elastic cell energy \(W_0\), properties of the extension scheme (cf. (3.2)), and [49, Theorem 3.1] (in unrescaled variables) to get \(R_-^{(k_n)}\in \textrm{SO}(3)\) such that
for a constant \(C>0\). Combining the previous inequality with (5.6) we deduce that
Setting
we achieve that a Poincaré inequality is satisfied, with a \(C>0\):
Define 
as follows:
We claim that
Concerning (5.9), we notice that for all \(n\in {\mathbb {N}}\),
and that 
since 
on \((-1,w_-^{(n)}-\frac{1}{2r_nk_n})\times S^\textrm{ext}\). Hence it remains to show that the energy on the transition slice \(S_{k_n}(w_-^{(n)})\) vanishes in the limit.
Lemma 5.1
The following is true:
Proof
The proof is divided into several steps. Let \(Q=[w_-^{(n)}-\frac{1}{2r_nk_n},w_-^{(n)}+\frac{1}{2r_nk_n}]\times Q'\), where \(Q'=x'+[-\frac{1}{2},\frac{1}{2}]^2\) for some \(x'\in {\mathcal {L}}'^{,\textrm{ext}}\), be any atomic cell contained in the slice \(\overline{S_{k_n}}(w_-^{(n)})\).
Step 1. Using [69, Lemma 3.5] and (5.7), we can obtain the relation
with a constant \(c>0\).
Step 2. We now compare 
and 
. By construction we have 
for \(i=5,6,7,8\) and from Step 1 we get, for \(i=1,2,3,4\),
Property (2.1) of our piecewise affine interpolation, Hölder’s inequality, (5.8) and (5.7) give
so that 
and, in particular,
since 
and likewise for 
. Together with (5.11) this shows that also 
satisfies
Step 3. Now we use that \(W_{\textrm{tot}}^{(k_n)}\) is independent of \(k_n\) on a tubular neighbourhood of \(\textrm{SO}(3)\) of size \(O(k_n^{-1})\) and, by Taylor expansion, satisfies an estimate of the form \(W_{\textrm{tot}}^{(k_n)} \le C \textrm{dist}^2(\cdot , \textrm{SO}(3))\) there. Thus, (5.11) and (5.12) give
This implies the assertion. \(\square \)
The second convergence in (5.10) is a consequence of (5.5b), (5.4), and (5.7):
The first convergence in (5.10) follows similarly from (5.5c) and (5.4) if we use (5.8) and (5.7) to show that
with a constant \(C>0\).
In the same way, we could construct \((R_+^{(k_n)})_{n=1}^\infty \), \((y_+^{(k_n)})_{n=1}^\infty \), and 
and prove a version of (5.9)–(5.10) on (0, 1]. Thus, as
and \(\varepsilon >0\) was arbitrary, the claim that \(\varphi \le \psi \) is proved.
Lemma 5.2
Let \(c_1\), \(c_2\), \(\dots \), \(c_N\) be nonnegative reals and \(p\ge 1\). Then
Proof
We denote by \({\bar{c}}\) the average \(N^{-1}\sum _j c_j\). If the statement were not true, the number of \(c_j\)’s such that \(c_j>p{\bar{c}}\) would be greater than or equal to N/p. Hence
but that is a contradiction. \(\square \)
Summing up the elastic and crack energy contributions, we get
To obtain the \(\Gamma \)-liminf inequality, we apply the monotone convergence theorem with \(\eta \rightarrow 0+\).
6 Proof of the upper bound
For a construction of recovery sequences it is crucial to first analyze the cell formula more precisely. In particular, we will need to prove that the crack set is essentially localized on the atomic scale.
6.1 Analysis of the cell formula
Lemma 6.1
(localization of crack) Let \({\tilde{y}}^-,{\tilde{y}}^+\in {\mathbb {R}}^3\) and \(R^-,R^+\in \textrm{SO}(3)\). Then for any \(\varepsilon _*>0\), there is an \(N_*\in {\mathbb {N}}\), sequences \(\{k_n\}_{n=1}^\infty \subset {\mathbb {N}}\), \(\{r_n\}\subset (0,\infty )\) and mappings 
, \(n\in {\mathbb {N}}\), with the following properties:
\(r_n\searrow 0\), \(r_nk_n\rightarrow \infty \), and, for suitable \(\smash {\overset{+}{y}}_{\pm }^{(k_n)}\in {\mathbb {R}}^3,\; \smash {\overset{+}{R}}_{\pm }^{(k_n)}\in \textrm{SO}(3)\) with \(\smash {\overset{+}{y}}_{\pm }^{(k_n)}\rightarrow {\tilde{y}}^\pm \), \(\smash {\overset{+}{R}}_{\pm }^{(k_n)}\rightarrow R^\pm \),
where \(I_{\textrm{c}}^{(n)}=\frac{1}{r_nk_n}[-N_*,N_*]\).
Proof
Find \((k_n)_{n=1}^\infty \subset {\mathbb {N}}\), \((r_n)_{n=1}^\infty \subset (0,\infty )\) with \(r_n\searrow 0\) and \(\lim _{n\rightarrow \infty }r_n k_n =\infty \), and 
such that
and, for some \(y_\pm ^{(k_n)}\in {\mathbb {R}}^3\), \(R_\pm ^{(k_n)}\in \textrm{SO}(3)\) with \(y_\pm ^{(k_n)}\rightarrow {\tilde{y}}^\pm \), \(R_\pm ^{(k_n)}\rightarrow R^\pm \),
Recalling assumption (W5) on \(W_{\textrm{cell}}^{(k_n)}\) and passing to a subsequence (without relabelling it), we can assert that there is an \(N_{\textrm{f}}\in {\mathbb {N}}_0\), \(N_{\textrm{f}} \le C\varphi ({\tilde{y}}^+-{\tilde{y}}^-,(R^-)^{-1}R^+)\), such that for every n, only the slices
are broken in the sense from the proof of Theorem 3.1, where \(s_n^1<\cdots <s_n^{N_{\textrm{f}}}\) are the midpoints of the \(w_1\)-projections of the broken slices and \(\lim _{n\rightarrow \infty }s_n^j=s^j\in [-3/4,3/4]\). This means that 
on the remaining ‘intact’ slices is \(c_{\textrm{frac}}^{(k_n)}\)-close to \(\bar{\textrm{SO}}(3)\). Then
are the \(w_1\)-projections of elastically deformed parts of the region surrounding the crack. We fix a number \(N_*' \in {\mathbb {N}}\) (to be determined below) and denote by \(\{{\tilde{I}}_{j_i}^{(n)}\}_{i=1}^{N_{\textrm{U}}}\subset \{{\tilde{I}}_j^{(n)}\}_{j=1}^{N_{\textrm{f}}+1}\) those intervals \({\tilde{I}}_{j_i}^{(n)}\) for which \({r_nk_n|{\tilde{I}}_{j_i}^{(n)}|\ge 2N_*'+4}\). On extracting a further subsequence, \(N_{\textrm{U}}=N_{\textrm{U}}(N_*')\) is independent of n. We assume \(N_{\textrm{U}}>0\), since otherwise the next ‘rigidification’ procedure is redundant and it is enough to construct 
directly from 
later. To shorten notation, we set \({\tilde{I}}_{j_i}^{(n)}=:I_i^{(n)}=[a_i^{(n)}{-\frac{1}{r_nk_n}},b_i^{(n)}{+\frac{1}{r_nk_n}}]\).
As an intermediate step, we now construct mappings 
(illustrated in Fig. 2b) which have the property that middle parts of the segments \(I_i^{(n)}\times \overline{S^\textrm{ext}}\) are only subject to a rigid motion, instead of an elastic deformation. The complements of these middle parts contain no more than \(2N_*'+2\) slices, where \(N_*':=\lfloor 2{N_{\textrm{f}}}C_{\textrm{E}}/\varepsilon _*\rfloor +1\) and \(C_{\textrm{E}}\) is a positive constant (independent of n and \(\varepsilon _*\)) that will be introduced in (6.5). The rigidifying procedure below is presented for an arbitrary but fixed \(i\in \{1,\dots ,N_{\textrm{U}}\}\).
Main steps in the proof of Lemma 6.1. Rigid parts of the rod are drawn in grey. a The original mapping 
. b Rigidification of rod segments to construct 
. c Subsequent shortening of the rigid parts to obtain 
Procedure (R). As in [71, Theorem 2.4] (which is a reformulation of the compactness theorem in [61]), we get piecewise constant mappings \(R^{(k_n)}:I_i^{(n)}\rightarrow \textrm{SO}(3)\) with discontinuity set contained in \(\frac{1}{r_nk_n}{\mathbb {Z}}\), fulfilling
for all \(w_1\in [a_i^{(n)},b_i^{(n)})\) by [49, Theorem 3.1], growth assumptions on \(W_0\), and bounds related to our extension scheme (cf. (3.2)). Moreover, [71, Theorem 2.4] implies
for all \(w_1\in [a_i^{(n)},b_i^{(n)})\).
We now define points that delimit the middle part of \(I_i^{(n)}\times \overline{S^\textrm{ext}}\) (where 
has to be ‘rigidified’) and the sets \(W_-^{(n)}\), \(W_+^{(n)}\) containing the \(w_1\)-coordinates of cell midpoints left of or right of this middle part:
The next few steps, till (6.5), are similar to the proof of the inequality \(\varphi \le \psi \) (cf. Sect. 5.4), so not all computations will be described in full here. We find \(w_-^{(n)}\in W_-^{(n)}\) and \(w_+^{(n)}\in W_+^{(n)}\) such that
Writing \(R_\pm ^{(i,k_n)}\) in place of \(R^{(k_n)}(w_\pm ^{(n)})\) for short and using that all the slices centred in \(W_\pm ^{(n)}\) are intact, from the first inequality in (6.2) we get
Choosing vectors \(c_-^{(n)}\), \(c_+^{(n)}\) as
we get Poincaré inequalities
with a constant \(C>0\).
With the rotated and shifted version of 
, given by
set
so that 
is defined on \(I_i^{(n)}\times \overline{S^\textrm{ext}}\). Besides, to prepare future rigidification on possible next intervals, we redefine 
by 
on \([b_i^{(n)}{+\frac{1}{r_nk_n}},1]\times \overline{S^\textrm{ext}}\).
After some calculations we deduce that on any atomic cell Q such that \(\textrm{Int}\,Q\subset S_{k_n}(w_-^{(k_n)})\),
which implies that for all n sufficiently large, the energetic error occurring on the transition slice \(S_{k_n}(w_-^{(k_n)})\) is controlled by our choice of \(N_*'\):
It should be stressed that the constant \(C_{\textrm{E}}\) above does not depend on n or \(\varepsilon _*\). Due to the definition of 
, an analogous computation reveals that (6.5) also holds if \(w_-^{(n)}\) is replaced with \(w_+^{(n)}\).
Later we will have to check that 
is an admissible competitor of 
in the cell formula. Therefore we now show that the error incurred by the boundary condition due to the previous steps of Procedure (R) tends to zero.
By our interpolation scheme, on any atomic cell Q contained in \(I_i^{(n)}\times \overline{S^\textrm{ext}}\) we have (cf. [69, Lemma 3.5])
since 
. This proves that the mappings 
are Lipschitz with the uniform constant \(Cr_n\). In particular,
Since by iterating (6.3) we derive a ‘pointwise curvature estimate’ (as in [49, 61])
we obtain for 
from (6.4) that 
uniformly.
This finishes Procedure (R) for the chosen i.
We construct 
by letting 
for every \(-1\le w_1\le a_1^{(n)}{-\frac{1}{r_nk_n}}\) and \(x'\in \overline{S^\textrm{ext}}\) and then by successively applying Procedure (R) for \(i=1,2,\dots , N_{\textrm{U}}\) (it should be kept in mind that after each invocation of Procedure (R), 
is redefined on \([b_i^{(n)}{+\frac{1}{r_nk_n}},1]\times \overline{S^\textrm{ext}}\) so that in Step \(i+1\) we get the modified mapping 
from Step i as input).
On \((\frac{1}{r_nk_n}\lfloor \frac{3}{4}r_nk_n\rfloor ,1]\times \overline{S^\textrm{ext}}\), we define 
as 
, where 
is understood as the transformed mapping after the \(N_{\textrm{U}}\)-th step of rigidification.
As we have seen above, the affine transformations given by (6.4) at each step vanish in the limit. Hence, 
.
To summarize, the sequence 
satisfies
Now we proceed to construct the modifications 
of 
which will have more localized non-rigid parts (as depicted in Fig. 2c).
Since no confusion arises, we again use \(R_\pm ^{(k_n)}\) and \(y_\pm ^{(k_n)}\) to denote the rigid deformations near the interval boundaries, i.e.
Now we first extend 
rigidly to a function on \({\mathbb {R}}\times \overline{S^\textrm{ext}}\) by requiring this formula to hold true on \((-\infty ,-\frac{3}{4})\times \overline{S^\textrm{ext}}\) and \((\frac{3}{4},\infty )\times \overline{S^\textrm{ext}}\), with the obvious interpretation of the ± sign.
If \(j=j_i\) for some \(i\in \{1,2,\dots ,N_{\textrm{U}}\}\), then we write \(w_-^{(i,n)}\), \(w_+^{(i,n)}\) in place of \(w_-^{(n)}\), \(w_+^{(n)}\) from Procedure (R), respectively, to stress the dependence on i. We set \(d^{(i,n)}= w_{\mathrm{+}}^{(i,n)}-w_{\mathrm{-}}^{(i,n)}-\frac{1}{r_nk_n}\) and also recall the definition of \(R_-^{(i,k_n)}\) on this interval. Now consecutively do the following steps for \(i\in \{1,2,\dots ,N_{\textrm{U}}\}\), in reverse order starting with \(i=N_{\textrm{U}}\):
This finally results in a configuration with
if \(w_1 \le -\frac{3}{4}\), \(x'\in \overline{S^\textrm{ext}}\), and
where \(d^{(n)}=\sum _{i=1}^{N_{\textrm{U}}}d^{(i,n)}\) and \(c^{(n)}=\sum _{i=1}^{N_{\textrm{U}}} d^{(i,n)} R_-^{(i,k_n)} e_1\), if \(w_1 \ge \frac{3}{4} - d^{(n)}\) and \(x'\in \overline{S^\textrm{ext}}\).
Observe that 
for every \(n\in {\mathbb {N}}\) as we have only shortened the intermediate rigid parts. Also, the length of the non-rigid part now satisfies
Setting \(N_* = (2 N_*{+4})( N_{\textrm{f}}+1)+N_{\textrm{f}}\) and shifting we finally obtain 
as claimed. \(\square \)
Remark 6.1
Lemma 6.1 shows that the choice of \(I^\pm \) in the definition of \(\varphi \) was arbitrary and that a different positive length of \(I^\pm \) which still leaves a nonempty middle interval for fracture would give the same value of \(\varphi \).
Our next task is to prove that the passages to subsequences \((k_n)\) can be avoided when approximating the value of the cell formula.
Proposition 6.1
Suppose that \({\tilde{y}}^-,{\tilde{y}}^+\in {\mathbb {R}}^3\) and \(R^-,R^+\in \textrm{SO}(3)\). Then for any \(\varepsilon _*>0\) and any nonincreasing sequence \(\{\rho _k\}_{k=1}^\infty \subset (0,\infty )\) with \(\lim _{k\rightarrow \infty }\rho _k =0\) and \(\lim _{k\rightarrow \infty }\rho _k k =\infty \) there exist deformations 
such that 
and
Proof
For a given \(\varepsilon _*>0\) we choose \(N_*\in {\mathbb {N}}\), a (without loss of generality nondecreasing) sequence \((k_n)_{n=1}^\infty \), and mappings 
as in Lemma 6.1 so that
and, for suitable \(\smash {\overset{+}{y}}_{\pm }^{(k_{n})}\in {\mathbb {R}}^3,\; \smash {\overset{+}{R}}_{\pm }^{(k_{n})}\in \textrm{SO}(3)\) with \(\smash {\overset{+}{y}}_{\pm }^{(k_{n})}\rightarrow {\tilde{y}}^\pm \), \(\smash {\overset{+}{R}}_{\pm }^{(k_{n})}\rightarrow R^\pm \), after a rigid extension to the left and to the right,
where \(I_{\textrm{c}}^{(n)}=\frac{1}{r_{n}k_{n}}[-N_*,N_*]\).
For each \(k\in {\mathbb {N}}\) find \(n_k\in {\mathbb {N}}\) such that \(k_{n_k}^{-1}\le k^{-1}\le k_{n_k-1}^{-1}\). Set
Like this, 
is well-defined (as far as the boundary condition on \(I^\pm \times \overline{S^\textrm{ext}}\) is concerned), at worst for all k larger than a certain \({\bar{k}}\in {\mathbb {N}}\). If it is the case that \({\bar{k}}>1\), we define 
as we like, e.g. by extending the boundary rigid motions to all of \([-1,1]\times \overline{S^\textrm{ext}}\). Then for \(k\ge {\bar{k}}\),
and
by assumption (W4) on the cell energy. This yields
\(\square \)
The approximating sequence 
around crack points can be chosen to be bounded in \(L^\infty \) in a universal way—this is the content of
Proposition 6.2
Suppose that \({\tilde{y}}^-,{\tilde{y}}^+\in {\mathbb {R}}^3\), \(R^-,R^+\in \textrm{SO}(3)\) and \((r_k)_{k=1}^\infty \subset (0,\infty )\) is a nonincreasing sequence with \(\lim _{k\rightarrow \infty }r_k =0\) and \(\lim _{k\rightarrow \infty }r_k k =\infty \). Assume that 
is such that 
with
for \(R_\pm ^{(k)}\rightarrow R^\pm \), \(y_\pm ^{(k)}\rightarrow {\tilde{y}}^\pm \). If the maximum interaction range property (W9) with rate \((M_k)_{k=1}^{\infty }\) holds true, then there exists a modification 
with 
such that
on \((I^- \cup I^+)\times \overline{S^\textrm{ext}}\) and
Proof
We write \({D}({\bar{x}}) = {\bar{x}} + \{(\frac{1}{r_kk}z^i_1,(z^i)');\; i=1,\ldots ,8\}\) for the corners of the cell with midpoint \({\bar{x}}\in \Lambda _{r_k,k}'\). Our strategy is to move back all pieces of the rod that are too far from \(\{y_-^{(k)},y_+^{(k)}\}\). Fix \(k\in {\mathbb {N}}\) and consider the undirected graph \({\mathfrak {G}}=({\mathfrak {V}},{\mathfrak {E}})\), where \({\mathfrak {V}}=\Lambda _{r_k,k}\) and
Let \({\mathfrak {G}}_1,{\mathfrak {G}}_2,\dots ,{\mathfrak {G}}_{n_{\textrm{G}}}\) be the connected components of \({\mathfrak {G}}\), numbered in such a way that \((I^-\times \overline{S^\textrm{ext}}) \cap \Lambda _{r_k,k} \in {\mathfrak {G}}_1\) and \((I^+\times \overline{S^\textrm{ext}}) \cap \Lambda _{r_k,k} \in {\mathfrak {G}}_{n_{\textrm{G}}}\). Accordingly we partition \(\{z^1,z^2,\dots ,z^8\}=Z_1({\bar{x}}){\dot{\cup }}Z_2({\bar{x}}){\dot{\cup }}\cdots {\dot{\cup }}Z_{n_{{\bar{x}}}}({\bar{x}})\) for every \({\bar{x}}\in \Lambda _{r_k,k}'\), where \(Z_i({\bar{x}})\ne \emptyset \), so that \(z^j,z^m\in Z_\ell ({\bar{x}})\) for some \(\ell \in \{1,2,\dots ,n_{{\bar{x}}}\}\) if and only if there is \(i_{\textrm{V}}\in \{1,2,\dots ,n_{\textrm{G}}\}\) such that \({\bar{x}}+\frac{1}{k}z^j,{\bar{x}}+\frac{1}{k}z^m\in {\mathfrak {V}}_{i_{\textrm{V}}}\), the set of vertices of \({\mathfrak {G}}_{i_{\textrm{V}}}\). Then the induced components of atomic cells are far apart: for any \({\bar{x}}\in \Lambda _{r_k,k}'\) and \(1\le i<j\le n_{{\bar{x}}}\), we have \(\textrm{dist}(y^{(k)}({\bar{x}}+Z_i({\bar{x}})),y^{(k)}({\bar{x}}+Z_j({\bar{x}})))\ge M_k\).
Similarly as before we observe that the number of atomic cells ‘broken’ by 
is controlled by the energy so that the number \(n_{\textrm{G}}\) of connected components of \({\mathfrak {G}}\) satisfies a bound of the form
with a constant \(C_1>0\). The construction further implies that the diameter of each component after deformation is bounded by
with another constant \({C_2}>0\).
For the first and last component we have
If \(n_{\textrm{G}} \ge 3\), we can shift graph components \({\mathfrak {G}}_i\), \(i={2},\ldots ,n_{\textrm{G}}-1\), without considerably changing the total energy, provided we do not put the components at a distance less than \(M_k\). Specifically, for \({\gamma }=2M_k+(C_2+{C_3}) M_k r_kk\le (2+C_2+{C_3}) M_k r_kk\) and \(|e|=1\) with \(e \perp y_+^{(k)}-y_-^{(k)}\) the points \(y_-^{(k)}+{(i-1)}\gamma e\), \(i={2},\ldots ,n_{\textrm{G}}-1\), have a distance \(\ge \gamma \) from each other and from \(\{y_+^{(k)},y_-^{(k)}\}\). We then define 
by shifting \({\mathfrak {G}}_i\) rigidly in such a way that 
, \(i={2},\ldots ,n_{\textrm{G}}-1\).
Then indeed the shifted components have the required minimal distances and moreover
\(i={2},\ldots ,n_{\textrm{G}}-1\). The assertion follows now by noting that 
on \({\mathfrak {V}}_1 \cup {\mathfrak {V}}_{n_{\textrm{G}}}\) and
as only broken cells have been altered. \(\square \)
6.2 Construction of recovery sequences
Proof of Theorem 4.1(ii)
It is known from the theory of \(\Gamma \)-convergence that for any \(\varepsilon >0\) it suffices to find a recovery sequence with \(\limsup _{k\rightarrow \infty } kE^{(k)}(y^{(k)})\le E_{\textrm{lim}}({\tilde{y}},d_2,d_3)+\varepsilon \), which is trivial if \(({\tilde{y}},d_2,d_3)\not \in {\mathcal {A}}\). In the case that \(({\tilde{y}},d_2,d_3)\in {\mathcal {A}}\), let \((\sigma ^i)_{i=0}^{{\bar{n}}_{\textrm{f}}+1}\) be the partition of [0, L] such that \(\{\sigma ^i\}_{i=1}^{{\bar{n}}_{\textrm{f}}}=S_{{\tilde{y}}}\cup S_R\), where \(S_R:=S_{{\tilde{y}}'}\cup S_{d_2}\cup S_{d_3}\). Depending on the assumptions on \({\tilde{y}}\), \(d_2\), \(d_3\), we treat two different cases separately.
First additionally suppose that \({\tilde{y}}|_{(\sigma ^{i-1},\sigma ^i)}\in {\mathcal {C}}^3((\sigma ^{i-1},\sigma ^i);{\mathbb {R}}^3)\), \({d_s}|_{(\sigma ^{i-1},\sigma ^i)}\in {\mathcal {C}}^2((\sigma ^{i-1},\sigma ^i);{\mathbb {R}}^3)\), \(s=2,3\), for all \(i\in \{1,2,\dots ,{\bar{n}}_{\textrm{f}}+1\}\) and that \(R=(\partial _1 {\tilde{y}}| d_2 | d_3)\) is constant on the sets \((\sigma ^0,\sigma ^0+\eta )\), \((\sigma ^i-\eta , \sigma ^i)\), \((\sigma ^i,\sigma ^i+\eta )\), \(i\in \{1,2,\dots ,{\bar{n}}_{\textrm{f}}\}\), and \((\sigma ^{\bar{n}_{\textrm{f}}+1} - \eta , \sigma ^{\bar{n}_{\textrm{f}}+1})\) for some \(\eta >0\). If \(k\in {\mathbb {N}}\), write \(I_0^k:=[-\frac{1}{k},\frac{1}{k}\lfloor k\sigma ^1\rfloor ]\), \(I_i^k:=[\frac{1}{k}\lfloor k\sigma ^i\rfloor +\frac{1}{k},\frac{1}{k}\lfloor k\sigma ^{i+1}\rfloor ]\) for \(i=1,2,\dots ,{\bar{n}}_{\textrm{f}}-1\) and \(I_{{\bar{n}}_{\textrm{f}}}^k:=[\frac{1}{k}\lfloor k\sigma ^{{\bar{n}}_{\textrm{f}}}\rfloor +\frac{1}{k},L_k+\frac{1}{k}]\).
Our analysis of elastic rods in [71, Section 3.4] shows that for a suitable choice of \(\beta (\cdot ,x')\in {\mathcal {C}}^1([0,L];{\mathbb {R}}^3)\) for each \(x'\in {\mathcal {L}}^\textrm{ext}\) and of \(q\in {\mathcal {C}}^2([0,L];{\mathbb {R}}^3)\), by setting
appropriately extended and interpolated on \([-\frac{1}{k},\ldots ,L_k+\tfrac{1}{k}]\times \overline{S^\textrm{ext}}\), one has \({\tilde{y}}^{(k)}\rightarrow {\tilde{y}}\) in \(L^2\) on \((0,L)\times S^\textrm{ext}\) as well as
and
Indeed one can choose \(\beta \equiv 0\) and \(q \equiv 0\) on \((\sigma ^{i},\sigma ^{i}+\frac{\eta }{2})\cup (\sigma ^{i+1}-\frac{\eta }{2},\sigma ^{i+1})\) as R by assumption is constant on a neighbourhood of these sets. So we have
We now update \({\tilde{y}}^{(k)}\) by replacing portions near the jumps \(\sigma ^i\) (and matching all parts by applying suitable rigid motions). Fix a sequence \((r_k)_{k=1}^{\infty }\) such that \(r_k\rightarrow 0\) and \(r_kk\rightarrow \infty \). By Proposition 6.1 for each \(i=1,\ldots ,{\bar{n}}_{\textrm{f}}\) we can choose 
such that 
with
for \(R_\pm ^{(k,i)}\rightarrow R(\sigma ^i\pm )\), \(y_\pm ^{(k,i)}\rightarrow {\tilde{y}}^\pm \) which satisfies the energy estimate
Let \(H_{\sigma ,r}(x):=(\frac{1}{r}(x_1-\sigma ),x')\) for any \(r>0\). Noticing that \({\tilde{y}}^{(k)}\) is rigid near a jump as are the 
near \(\pm 1\), we can now define a modification \({\tilde{y}}^{(k)}_{\textrm{tot}}\) of \({\tilde{y}}^{(k)}\) by setting
where \(O_\pm ^{(k,i)} \in \textrm{SO}(3)\) and \(c_\pm ^{(k,i)} \in {\mathbb {R}}^3\) are such that
for \(i=1,\ldots ,{\bar{n}}_{\textrm{f}}\) (and we have set \(O_+^{(k,0)}:=\textrm{Id}\), \(c_+^{(k,0)}:=0\)). Since \(R_\pm ^{(k,i)}\rightarrow R(\sigma ^i\pm )\), \(y_\pm ^{(k,i)}\rightarrow {\tilde{y}}^\pm \) we get \(O_\pm ^{(k,i)} \rightarrow \textrm{Id}\) and \(c_\pm ^{(k,i)} \rightarrow 0\) as \(k\rightarrow \infty \). Thus we still have \({\tilde{y}}^{(k)}_{\textrm{tot}}\rightarrow {\tilde{y}}\) in \(L^2((0,L)\times S^\textrm{ext})\). By (6.8) and (6.9) the sequence \({\tilde{y}}^{(k)}_{\textrm{tot}}\) satisfies the envisioned energy estimate
It remains to observe that in case (W9) holds true with some sequence of rate functions \((M_k)_{k=1}^{\infty }\) and \(||{\tilde{y}}||_\infty \le M\), then for any \((\zeta _k)_{k=1}^{\infty }\subset (0,1)\) with \(\zeta _k \searrow 0\) and \(\zeta _k{/M_k} \rightarrow \infty \) one can choose \({\tilde{y}}^{(k)}_{\textrm{tot}}\) such that \({||{{\tilde{y}}^{(k)}_{\textrm{tot}}}||_\infty } \le M+\zeta _k\). This is clear by construction for \({\tilde{y}}^{(k)}\) in (6.6) instead of \({\tilde{y}}^{(k)}_{\textrm{tot}}\) since \(\zeta _k \gg \frac{1}{k}\). The bound is indeed preserved by the passage to \({\tilde{y}}^{(k)}_{\textrm{tot}}\) due to Proposition 6.2 once we have \(r_kM_kk \ll \zeta _k\). As Proposition 6.1 allows us to choose \(r_k \searrow 0\) as fast as we wish as long as \(r_kk \rightarrow \infty \), the claim follows.
Now let us assume that \({\tilde{y}}\), \(d_2\), \(d_3\) are general as in Theorem 4.1(ii). Interestingly, a related approximation problem was treated recently by P. Hornung. [54] However, a more elementary construction is sufficient in our case. By a density argument, it is enough to show that there are sequences \(({\tilde{y}}_{\textrm{tot}}^{(j)})_{j=1}^\infty \), \((d_s^{(j)})_{j=1}^\infty \), \(s=2,3\), such that:
-
(i)
for every j and all \(i\in \{1,2,\dots ,{\bar{n}}_{\textrm{f}}+1\}\), the functions satisfy \({\tilde{y}}_{\textrm{tot}}^{(j)}|_{(\sigma ^{i-1},\sigma ^i)}\in {\mathcal {C}}^3((\sigma ^{i-1},\sigma ^i);{\mathbb {R}}^3)\), \(d_2^{(j)}|_{(\sigma ^{i-1},\sigma ^i)},d_3^{(j)}|_{(\sigma ^{i-1},\sigma ^i)}\in {\mathcal {C}}^2((\sigma ^{i-1},\sigma ^i);{\mathbb {R}}^3)\) with \(R_{\textrm{tot}}^{(j)}=(\partial _{x_1}{\tilde{y}}_{\textrm{tot}}^{(j)}|d_2^{(j)}|d_3^{(j)})\) constant on \((\sigma ^i - \eta _j, \sigma ^i)\) for \(i \in \{1,\ldots ,\bar{n}_{\textrm{f}}+1\}\) and on \((\sigma ^i , \sigma ^i + \eta _j)\) for \(i \in \{0,\ldots ,\bar{n}_{\textrm{f}}\}\), and \(({\tilde{y}}_{\textrm{tot}}^{(j)},d_2^{(j)},d_3^{(j)})\in {\mathcal {A}}\);
-
(ii)
\({\tilde{y}}_{\textrm{tot}}^{(j)}\rightarrow {\tilde{y}}\) in \(L^2({(0,L)};{\mathbb {R}}^3)\), \(R_{\textrm{tot}}^{(j)}\rightarrow R=(\partial _{x_1}{\tilde{y}}|d_2|d_3)\) in \(H^1((\sigma ^{i-1},\sigma ^i);{\mathbb {R}}^{3\times 3})\) for any \(i\in \{1,\dots ,{\bar{n}}_{\textrm{f}}+1\}\);
-
(iii)
\(E_{\textrm{lim}}({\tilde{y}}_{\textrm{tot}}^{(j)},d_2^{(j)},d_3^{(j)})\rightarrow E_{\textrm{lim}}({\tilde{y}},d_2,d_3)\), \(j\rightarrow \infty \).
Let \((\eta _j)\) be a positive null sequence. For each \(i\in \{1,2,\dots ,{\bar{n}}_{\textrm{f}}+1\}\) we find an approximating sequence \(({\tilde{R}}^{(j)}|_{(\sigma ^{i-1},\sigma ^i)})\subset {\mathcal {C}}^2([\sigma ^{i-1},\sigma ^i];{\mathbb {R}}^{3\times 3})\), such that \({\tilde{R}}^{(j)}\) is constant on \((\sigma ^{i-1},\sigma ^{i-1}+\eta _j)\) and \((\sigma ^{i}-\eta _j,\sigma ^{i})\) and \({\tilde{R}}^{(j)}\rightarrow R\) in \(H^1((\sigma ^{i-1},\sigma ^i);{\mathbb {R}}^{3\times 3})\) so that \({\tilde{R}}^{(j)}\rightarrow R\) uniformly in \((\sigma ^{i-1},\sigma ^i)\) by the Sobolev embedding theorem. Then we project \({\tilde{R}}^{(j)}(x_1)\) for every \(x_1\in (\sigma ^{i-1},\sigma ^i)\) smoothly onto \(\textrm{SO}(3)\) and get a sequence \(\{R^{(j)}\}\subset {\mathcal {C}}^1([\sigma ^{i-1},\sigma ^i];{\mathbb {R}}^{3\times 3})\) of mappings with values in \(\textrm{SO}(3)\). This implies that \(R^{(j)}\rightarrow R\) in \(H^1((\sigma ^{i-1},\sigma ^i);{\mathbb {R}}^{3\times 3})\) for \(i=1,2,\dots ,{\bar{n}}_{\textrm{f}}+1\).
We write \(R^{(j)}=(\partial _{x_1}{\tilde{y}}^{(j)}|{\bar{d}}_2^{(j)}|{\bar{d}}_3^{(j)})\) for \({\bar{d}}_2^{(j)},{\bar{d}}_3^{(j)}\in {\mathcal {C}}^2([\sigma ^{i-1},\sigma ^i];{\mathbb {R}}^3)\) and \({\tilde{y}}^{(j)}\in {\mathcal {C}}^3([\sigma ^{i-1},\sigma ^i];{\mathbb {R}}^3)\) such that \({\tilde{y}}^{(j)}(\sigma ^{i-1}+)={\tilde{y}}(\sigma ^{i-1}+)\); thus we have \(({\tilde{y}}^{(j)}|{\bar{d}}_2^{(j)}|{\bar{d}}_3^{(j)})\in {\mathcal {A}}\). To avoid issues with crack terms, we rigidly move the pieces of the rod so as to obtain a j-independent contribution from the cracks that is exactly equal to the limiting crack energy. We set
if \(\sigma ^{i-1}< x_1 < \sigma ^i,\ i=1,2,\dots ,{\bar{n}}_{\textrm{f}}+1\), where \(O^{(j,i)} \in \textrm{SO}(3)\) and \(c^{(j,i)}\in {\mathbb {R}}^3\) are defined consecutively by \(O^{(j,0)} = \textrm{Id}\), \(c^{(j,0)}=0\), and requiring that
for \(i=1,\ldots ,{\bar{n}}_{\textrm{f}}\), \(R_{\textrm{tot}}^{(j)}=(\partial _{x_1}{\tilde{y}}_{\textrm{tot}}^{(j)}|d_2^{(j)}|d_3^{(j)}),\; j\in {\mathbb {N}}\). By frame indifference, the elastic energy is not changed by such an operation. Noting that \(O^{(j,i)} \rightarrow \textrm{Id}\) and \(c^{(j,i)}\rightarrow 0\) for \(j\rightarrow \infty \), we see that these mappings are such that (i)-(iii) hold (for (iii) observe that the integral in (6.7) behaves continuously in R with respect to the topologies used here). \(\square \)
7 Examples
Finally, we list a few examples of mass-spring models treatable by our methods: a model with rather general pair interactions, the so-called truncated and shifted Lennard–Jones potential (LJTS), ‘truncated harmonic spring’, and a simplified highly brittle model.
Example 7.1
As general nearest-neighbour (NN) and next-to-nearest-neighbour (NNN) interactions on a cubic lattice, we can consider
where \(y:\Lambda _k\rightarrow {\mathbb {R}}^3\), \({\hat{y}}({\hat{x}})={ky(\frac{1}{k}{\hat{x}})}\), \({\hat{x}}\in {\hat{\Lambda }}_k\), and \(W_{\textrm{NN}}^{(k)}\), \(W_{\textrm{NNN}}^{(k)}\) satisfy the following list of assumptions:
-
(P1)
\(W_{\mathrm{NN(N)}}^{(k)}:[0,\infty )\rightarrow [0,\infty ]\) is continuous and finite on \((0,\infty )\) and \(W_{\mathrm{NN(N)}}^{(k)}(r)=0\) if and only if \(r=1\);
-
(P2)
there is a sequence \((c_{\textrm{f}}^{(k)})_{k=1}^\infty \) with \(c_{\textrm{f}}^{(k)}\searrow 0\) and \(\lim _{k\rightarrow \infty }k[c_{\textrm{f}}^{(k)}]^2\in (0,\infty )\) such that
$$\begin{aligned} W_{\mathrm{NN(N)}}^{(k)}(r)=W_{\mathrm{0NN(N)}}(r) \end{aligned}$$for all \(r\in (1-c_{\textrm{f}}^{(k)},1+c_{\textrm{f}}^{(k)})\), where \(W_{\mathrm{0NN(N)}}\) is of class \({\mathcal {C}}^2\) and \(W_{0NN(N)}''(1)>0\);
-
(P3)
\(W_{\mathrm{NN(N)}}^{(k)}(r)={\bar{W}}_{\mathrm{NN(N)}}^{(k)}(r)\) if \(r\in [0,1-c_{\textrm{f}}^{(k)}]\cup [1+c_{\textrm{f}}^{(k)},\infty )\); the function \({\bar{W}}_{\mathrm{NN(N)}}^{(k)}\) is bounded from below by \({\bar{c}}_{\mathrm{NN(N)}}^{(k)}\) such that \(k{\bar{c}}_{\mathrm{NN(N)}}^{(k)}\rightarrow {\bar{c}}_{\mathrm{NN(N)}}>0\) and \((k+1)W_{\mathrm{NN(N)}}^{(k+1)}\ge kW_{\mathrm{NN(N)}}^{(k)}\) for every \(k\in {\mathbb {N}}\);
-
(P4)
.
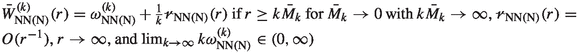.To guarantee preservation of orientation, in (7.1) we have included a nonnegative term \({\mathcal {X}}_k(y)\) that gives rise to \(\chi ^{(k)}\) below. Thus \(E^{(k)}\) can be written in the form (2.2) as a sum of cell energies with
for \(\vec {y}=({\hat{y}}_1|\cdots |{\hat{y}}_8)\in {\mathbb {R}}^{3\times 8}\) and the functions \(W_{\textrm{surf}}^{(k)}\), \(W_{\textrm{end}}^{(k)}\) constructed in a similar manner to account for surface contributions to atomic bonds lying on the rod’s boundary (see [71, Subsection 2.4]). The frame-indifferent term \(\chi ^{(k)}\), \(C/k\ge \chi ^{(k)}\ge 0\), penalizes deformations that are not locally orientation-preserving, i.e. it is greater than or equal to \({\bar{c}}/k\), \({\bar{c}}>0\), on a k-independent neighbourhood of \(\textrm{O}(3){\bar{\textrm{Id}}}{\setminus } \bar{\textrm{SO}}(3)\) and vanishes otherwise (see [46, 66]). An alternative to penalties such as \({\mathcal {X}}_k\) and \(\chi ^{(k)}\) is cell energies with \(\textrm{O}(3)\)-invariance, see [27, Section 2.4].
It can be shown that potentials \(W_{\textrm{NN}}^{(k)}\), \(W_{\textrm{NNN}}^{(k)}\) as above make the corresponding \(W_{\textrm{cell}}^{(k)}\) admissible, i.e. (W1)–(W6), and (W9) hold ((W9) is a consequence of (P4)). In particular, the truncated and splined Lennard–Jones potential from [53] and versions thereof fall under this case, with appropriately chosen parameters.
Example 7.2
Let
where \(r\in (0,\infty )\) and \(d>0\) is a parameter (note that \(\lim _{r\rightarrow \infty }W_{\textrm{LJ}}(r)=d\) and \({{\,\mathrm{\arg \!\min }\,}}_{r>0}W_{\textrm{LJ}}(r)=1\)). Further we set
We again consider pair interactions, so the cell energy function takes the form (7.2) with \(W_{\textrm{LJTS}}^{(k)}\) in place of \(W_{\textrm{NN}}^{(k)}\) and \(W_{\textrm{NNN}}^{(k)}\). The property \((k+1)W_{\textrm{cell}}^{(k+1)}\ge kW_{\textrm{cell}}^{(k)}\) can be proved by discussing for each bond if it is deformed elastically or if the truncation is active. Computing the value of r beyond which truncation applies in \(W_{\textrm{LJTS}}^{(k)}\), we observe that assumptions (W3) and (W5) hold with \(c_{\textrm{frac}}^{(k)}=[\root 6 \of {d+\sqrt{d/k}}-\root 6 \of {d-(1/k)}]/(2\root 6 \of {d-(1/k)})\) and \(W_0\) being the sum of Lennard–Jones interactions with no truncation. By the properties of \(\nabla ^2 W_0({\bar{\textrm{Id}}})\), the estimate \({\hat{C}}W_0(\vec {y})\ge \textrm{dist}^2({\bar{\nabla }}{\hat{y}},\textrm{SO}(3))\) holds with a constant \({\hat{C}}>0\) and the usual symbol \({\bar{\nabla }}{\hat{y}}\) denoting the discrete gradient of \(\vec {y}\in {\mathbb {R}}^{3\times 8}\) (cf. [66, Lemma 3.2 and Section 7]).
Moreover, we claim that if \(\textrm{dist}({\bar{\nabla }}{\hat{y}}, \bar{\textrm{SO}}(3))>c_{\textrm{frac}}^{(k)}\), then \(W_{\textrm{cell}}^{(k)}(\vec {y})\ge \min \{1/(8k),[c_{\textrm{frac}}^{(k)}]^2/{\hat{C}}\}=:{\bar{c}}_1^{(k)}\). Indeed, as long as \(W_{\textrm{cell}}^{(k)}(\vec {y})<{\bar{c}}_1^{(k)}\), the cutoff is not active in any interatomic bond (the arguments of \(W_{\textrm{LJTS}}^{(k)}\) are close enough to 1) and thus \(W_{\textrm{cell}}^{(k)}(\vec {y})=W_0(\vec {y})\) so that \(\textrm{dist}({\bar{\nabla }}{\hat{y}}, \bar{\textrm{SO}}(3))\le c_{\textrm{frac}}^{(k)}\). This shows the second part of assumption (W5).
Example 7.3
For the functions
with positive constants K, \(c_{\textrm{TH}}^-\), \(c_{\textrm{TH}}^-\), one can similarly find \(c_{\textrm{frac}}^{(k)}\) and \({\bar{c}}_1^{(k)}\) so that \(W_{\textrm{cell}}^{(k)}\) defined by (7.2) with \(W_{\textrm{NN}}^{(k)}\) and \(W_{\textrm{NNN}}^{(k)}\) replaced by \(W_{\textrm{TH}}^{(k)}\) is an admissible cell energy.
Example 7.4
Another simplified model can be obtained if we set
and \(c_{\textrm{W}}\), \({\bar{c}}_1^{(k)}\), and frame-indifferent \(W_0\) are as in assumptions (W3), (W5). This corresponds to \({\bar{W}}^{(k)}\equiv {\bar{c}}_1^{(k)}\) and the cell formula then reduces to \(\varphi (u,R)\equiv (\sharp {\mathcal {L}}'){c_{\textrm{W}}}{\bar{c}}_1\), where \({\bar{c}}_1=\lim _{k\rightarrow \infty }k{\bar{c}}_1^{(k)}\), for any \(u\in {\mathbb {R}}^3\) and \(R\in \textrm{SO}(3)\) except \((u,R)=(0,\textrm{Id})\) (specifically, we use sublevel sets of \(W_0\) instead of \(\textrm{dist}^2({\bar{\nabla }}{\hat{y}},\bar{\textrm{SO}}(3))\) to define the threshold distinguishing between \(W_0\) and \({\bar{W}}^{(k)}\), but our findings remain valid in this case as well).
8 Explicit calculation of crack energy
For mass-spring models, it is possible to simplify further (5.3) in specific situations.
Proposition 8.1
If \(E^{(k)}\) is given by (7.1) and assumptions (P1)–(P4) hold, together with
- (P5):
-
\(\lim _{k\rightarrow \infty }k{\bar{W}}_{\mathrm{NN(N)}}^{(k)}(r_k)=\omega _{\mathrm{NN(N)}}\) for any sequence \(r_k\rightarrow \infty \),
for \(W_{\textrm{NN}}^{(k)}\) and \(W_{\textrm{NNN}}^{(k)}\), then
for any \(0\ne u\in {\mathbb {R}}^3\) and \(R\in \textrm{SO}(3)\).
Proof
Step 1. The mapping 
defined as
and interpolated to be piecewise affine (
) has the property that
Thus we find that \(\varphi (u,R)\) is less than or equal to the right-hand side in the above equation.
Step 2. Given \(\varepsilon >0\), we find sequences 
such that
using Proposition 6.1. Set
We show that the nature of our pair interactions causes at least one large gap in the spacing of atoms within each fibre which the rod consists of.
Claim 1: For each \(x'\in {\mathcal {L}}\) and every \(T>1\) there is a \(k_0\in {\mathbb {N}}\) such that whenever \(k\ge k_0\), we can find some \({\bar{w}}_1\in {{\bar{W}}_1^{(k)}}\) satisfying
Proof of claim: If the converse were true, there would be a \({\tilde{T}}>1\) and an increasing sequence \(\{k_n\}_{n=1}^\infty \subset {\mathbb {N}}\) such that for all \({\bar{w}}_1\in {{\bar{W}}_1^{(k_n)}}\):
Then we would get
which is a contradiction.
Step 3. A similar argument applies to NNN bonds (‘diagonal springs’)—if we use zigzag chains of atoms instead of straight atomic fibres. We state the corresponding claim without proof.
Claim \(\sqrt{2}\): For each \((x',x_*')\in {\mathcal {L}}\times {\mathcal {L}}\) with \(|x_*'-x'|=1\) and every \(T>1\) there is a \(k_0\in {\mathbb {N}}\) such that whenever \(k\ge k_0\), we can find a \(j\in {\mathbb {N}}\) and \({\bar{w}}_1={\frac{1}{r_kk}(\lfloor -r_kk\rfloor +\frac{2j+1}{2})\in {\bar{W}}_1^{(k)}}\) such that 
from (8.1) satisfies:
Step 4. Since Claims 1 and \(\sqrt{2}\) hold for every approximating sequence 
fulfilling (8.1), we get
As this is valid for any \(\varepsilon >0\), the desired conclusion follows. \(\square \)
Proposition 8.2
Under the assumptions of Proposition 8.1 and further supposing
- \(({\hbox {P6}})\):
-
\(W_{\textrm{NN}}^{(k)}\), \(W_{\textrm{NNN}}^{(k)}\) are nondecreasing on \([1,\infty )\),
we have
for any \(R,{\tilde{R}}\in \textrm{SO}(3)\), \(R\ne \textrm{Id}\) and \(0\ne u\in {\mathbb {R}}^3\).
Proof
The first inequality was shown in Remark 4.3.
As to the second inequality, Proposition 8.1 implies that for a nonzero u, the crack energy \(\varphi (u,R)\) is independent of R, hence we limit ourselves to the case \({\tilde{R}}=R\) without loss of generality. If \(R\in \textrm{SO}(3)\) and \(u\in {\mathbb {R}}^3\setminus \{0\}\) are fixed, it is enough to find a sequence 
of deformations admissible in the definition of \(\varphi (0,R)\) such that
by Proposition 8.1. Fix \(k\in {\mathbb {N}}\) and let 
, \(R_\pm ^{(k)}\), \(r_k\), and \(y_\pm ^{(k)}\) be as in the proof of Proposition 8.1 with our new definitions of R and u. We define
and observe that \(\textrm{dist}(F^+,F^-) = |y^{(k)}_+-y^{(k)}_-|+O({\frac{1}{k}}) = |u| + {o_{k\rightarrow \infty }(1)}\). Now we choose \(x'_0\in {\mathcal {L}}\) and consider configurations with shifted right parts, given by
where 
, \(t \in [0,1]\). We then define \(t_0^{(k)}\) to be the smallest \(t \in [0,1]\) such that
for some \(x'\in {\mathcal {L}}\), or else, \(x_*',x_{**}'\in {\mathcal {L}}\) with \(|x_*'-x_{**}'| = 1\), respectively. By construction such \(t_0^{(k)} \in (0,1)\) exists if k is large enough and we have \(|c_0^{(k)}({t_0^{(k)}}) - u|{\rightarrow 0}\) as \(k\rightarrow \infty \). Setting 
and recalling \(\mathrm {(P6)}\) we find
We still need to check that the sequence 
thus constructed satisfies the correct boundary conditions for \(\varphi (0,R)\). But this is clear, since \(|y_+^{(k)}-c_0^{(k)}(t_0^{(k)})-y_-^{(k)}|{\rightarrow 0}\). \(\square \)
9 Discussion
Our work makes a contribution to the modelling of elastic-brittle ultrathin structures, but as such, it could be certainly extended in various directions.
We remark that the situation becomes considerably more difficult for plates due to a much richer phenomenology of crack and kink patterns. For bending-dominated configurations also severe geometric obstructions that result from the isometry constraints are encountered. A first step has recently been achieved in [64], where a ‘Blake–Zisserman–Kirchhoff theory’ has been derived for plates with soft inclusions.
From the point of view of applications, it would be interesting to extend our findings to other crystallographic lattices (such as diamond cubic as in [57] or zincblende), heterogeneous nanostructures with several different types of atoms, or to study the influence of lattice defects.
The model could also be studied computationally (e.g. numerical approximations of the cell formula could be implemented).
References
Acerbi, E., Buttazzo, G., Percivale, D.: A variational definition of the strain energy for an elastic string. J. Elast. 25, 137–148 (1991)
Alicandro, R., Braides, A., Cicalese, M.: Continuum limits of discrete thin films with superlinear growth densities. Calc. Var. Partial Differ. Equ. 33(3), 267–297 (2008)
Alicandro, R., Cicalese, M.: A general integral representation result for continuum limits of discrete energies with superlinear growth. SIAM J. Math. Anal. 36, 1–37 (2004)
Almi, S., Belz, S., Micheletti, S., Perotto, S.: A dimension-reduction model for brittle fractures on thin shells with mesh adaptivity. Math. Models Methods Appl. Sci. 31, 37–81 (2021)
Almi, S., Reggiani, D., Solombrino, F.: Brittle membranes in finite elasticity, to appear in Z. Angew. Math. Mech. (2023). arXiv:2204.04171
Almi, S., Tasso, E.: Brittle fracture in linearly elastic plates. Proc. Roy. Soc. Edinburgh Sect. A 153, 68–103 (2023)
Ambrosio, L., Coscia, A., Dal Maso, G.: Fine properties of functions with bounded deformation. Arch. Rational Mech. Anal. 139, 201–238 (1997)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs, Clarendon Press, Oxford (2000)
Antman, S.: Nonlinear Problems of Elasticity, 2nd edn. Springer, New York (2005)
Anzellotti, G., Baldo, S., Percivale, D.: Dimension reduction in variational problems, asymptotic development in \(\Gamma \)-convergence and thin structures in elasticity. Asympt. Anal. 9, 61–100 (1994)
Babadjian, J.-F.: Quasistatic evolution of a brittle thin film. Calc. Var. Partial Differ. Equ. 26, 69–118 (2006)
Babadjian, J.-F., Henao, D.: Reduced models for linearly elastic thin films allowing for fracture, debonding or delamination. Interfaces Free Bound. 18(4), 545–578 (2016)
Ball, J.: Some open problems in elasticity. In: Newton, P., Holmes, P., Weinstein, A. (eds.) Geometry, Mechanics, and Dynamics, pp. 3–59. Springer, New York (2002)
Barenblatt, G.I.: The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. 7, 55–129 (1962)
Bitzek, E., Kermode, J., Gumbsch, P.: Atomistic aspects of fracture. Int. J. Fract. 191, 13–30 (2015)
Blanc, X., Bris, C., Lions, P.: Atomistic to continuum limits for computational materials science. ESAIM Math. Model. Numer. Anal. 41(2), 91–426 (2007)
Blanc, X., Le Bris, C., Lions, P.-L.: From molecular models to continuum mechanics. Arch. Rational Mech. Anal. 164, 341–381 (2002)
Bourdin, B., Francfort, G.A., Marigo, J.-J.: The variational approach to fracture. J. Elast. 91, 5–148 (2008)
Braides, A.: \(\Gamma \)-Convergence for Beginners. Oxford Lecture Series in Mathematics and its Applications, vol. 22. Oxford University Press, Oxford (2002)
Braides, A.: A handbook of \(\Gamma \)-convergence. In: Chipot, M., Quittner, P. (eds.) Handbook of Differential Equations: Stationary Partial Differential Equations, vol. 3, pp. 101–213. Elsevier, Amsterdam (2006)
Braides, A., Cicalese, M.: Surface energies in nonconvex discrete systems. Math. Models Methods Appl. Sci. 17, 985–1037 (2007)
Braides, A., Fonseca, I.: Brittle thin films. Appl. Math. Optim. 44, 299–323 (2001)
Braides, A., Gelli, M.S.: Limits of discrete systems with long-range interactions. J. Convex Anal. 9(2), 363–400 (2002)
Braun, J.: Connecting atomistic and continuous models of elastodynamics. Arch. Ration. Mech. Anal. 224(3), 907–953 (2017)
Braun, J., Schmidt, B.: On the passage from atomistic systems to nonlinear elasticity theory for general multi-body potentials with p-growth. Netw. Heterog. Media 8(4), 879–912 (2013)
Braun, J., Schmidt, B.: Existence and convergence of solutions of the boundary value problem in atomistic and continuum nonlinear elasticity theory. Calc. Var. Partial Differ. Equ. 55(125), 1–36 (2016)
Braun, J., Schmidt, B.: An atomistic derivation of von-Kármán plate theory. Netw. Heterog. Med. (2022)
Buze, M., Hudson, T., Ortner, C.: Analysis of cell size effects in atomistic crack propagation. ESAIM Math. Model. Numer. Anal. 54(6), 1821–1847 (2020)
Chen, Y., Liao, X.: Chapter four—mechanical behaviors of semiconductor nanowires. In Dayeh, S.A., Fontcuberta i Morral, A., Jagadish, C. (eds.) Semiconductor Nanowires II: Properties and Applications, volume 94 of Semiconductors and Semimetals, pp. 109–158. Elsevier, Amsterdam (2016)
Ciarlet, P.: Mathematical Elasticity. Vol. II: Theory of Plates, volume 27 of Studies in Mathematics and Its Applications. Elsevier, Amsterdam (1997)
Conti, S., Dolzmann, G., Kirchheim, B., Müller, S.: Sufficient conditions for the validity of the Cauchy-Born rule close to SO(n). J. Eur. Math. Soc. 8, 515–530 (2006)
Conti, S., Fonseca, I., Leoni, G.: A \(\Gamma \)-convergence result for the two-gradient theory of phase transitions. Comm. Pure Appl. Math. 55(7), 857–936 (2002)
Conti, S., Schweizer, B.: Rigidity and Gamma convergence for solid-solid phase transitions with SO(2) invariance. Comm. Pure Appl. Math. 59, 830–868 (2006)
Dal Maso, G.: Generalised functions of bounded deformation. J. Eur. Math. Soc. 015(5), 1943–1997 (2013)
E, W., Ming, P.: Cauchy-Born rule and the stability of crystalline solids: static problems. Arch. Rational Mech. Anal. 183, 241–297 (2007)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions. Textbooks in mathematics, revised CRC Press, Boca Raton (2015)
Evarestov, R.A.: Theoretical Modeling of Inorganic Nanostructures, 2nd edn. Springer, Cham, Switzerland (2020)
Fonseca, I., Leoni, G.: Modern Methods in the Calculus of Variations: \(L^p\) Spaces. Springer Monographs in Mathematics, Springer, New York (2007)
Fonseca, I., Müller, S.: Quasi-convex integrands and lower semicontinuity in \(L^1\). SIAM J. Math. Anal. 23(5), 1081–1098 (1992)
Francfort, G.A.: Variational fracture: twenty years after. Int. J. Fract., 1–11 (2021)
Francfort, G.A., Marigo, J.-J.: Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 46, 1319–1342 (1998)
Freddi, L., Paroni, R., Zanini, C.: Dimension reduction of a crack evolution problem in a linearly elastic plate. Asymptot. Anal. 70, 101–123 (2010)
Friedrich, M., Kreutz, L., Schmidt, B.: Emergence of rigid polycrystals from atomistic systems with Heitmann–Radin sticky disk energy. Arch. Rational Mech. Anal. 240, 627–698 (2021)
Friedrich, M., Kreutz, L., Zemas, K.: Geometric rigidity in variable domains and derivation of linearized models for elastic materials with free surfaces (2021). arXiv:2107.10808
Friedrich, M., Schmidt, B.: An atomistic-to-continuum analysis of crystal cleavage in a two-dimensional model problem. J. Nonlinear Sci. 24, 145–183 (2014)
Friedrich, M., Schmidt, B.: An analysis of crystal cleavage in the passage from atomistic models to continuum theory. Arch. Ration. Mech. Anal. 217, 263–308 (2015)
Friedrich, M., Schmidt, B.: On a discrete-to-continuum convergence result for a two dimensional brittle material in the small displacement regime. Netw. Heterog. Media 10(2), 321–342 (2015)
Friesecke, G., James, R.D.: A scheme for the passage from atomic to continuum theory for thin films, nanotubes and nanorods. J. Mech. Phys. Solids 48, 1519–1540 (2000)
Friesecke, G., James, R.D., Müller, S.: A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Comm. Pure Appl. Math. 55(11), 1461–1506 (2002)
Friesecke, G., James, R.D., Müller, S.: A hierarchy of plate models derived from nonlinear elasticity by \(\Gamma \)-convergence. Arch. Rational Mech. Anal. 180, 183–236 (2006)
Friesecke, G., Theil, F.: Validity and failure of the Cauchy-Born hypothesis in a two-dimensional mass-spring lattice. J. Nonlinear Sci. 12, 445–478 (2002)
Ginster, J., Gladbach, P.: The Euler–Bernoulli limit of thin brittle linearized elastic beams (2021). arXiv:2111.09706
Holian, B.L., Evans, D.J.: Shear viscosities away from the melting line: a comparison of equilibrium and nonequilibrium molecular dynamics. J. Chem. Phys. 78(8), 5147–5150 (1983)
Hornung, P.: Deformation of framed curves with boundary conditions. Calc. Var. Partial Differ. Equ. 60(3), 87 (2021)
Jansen, S., König, W., Schmidt, B., Theil, F.: Distribution of cracks in a chain of atoms at low temperature. Ann. Henri Poincaré 22, 4131–4172 (2021)
Kitavtsev, G., Luckhaus, S., Rüland, A.: Surface energies emerging in a microscopic, two-dimensional two-well problem. Proc. R. Soc. Edinb. Sect. A 147(5), 1041–1089 (2017)
Lazzaroni, G., Palombaro, M., Schlömerkemper, A.: Rigidity of three-dimensional lattices and dimension reduction in heterogeneous nanowires. Discrete Contin. Dyn. Syst. Ser. S 10(1), 119–139 (2017)
Le Dret, H., Raoult, A.: Le modèle de membrane non linéaire comme limite variationnelle de l’élasticité non linéaire tridimensionnelle. C. R. Acad. Sci. Paris 317, 221–226 (1993)
Léon Baldelli, A., Babadjian, J.-F., Bourdin, B., Henao, D., Maurini, C.: A variational model for fracture and debonding of thin films under in-plane loadings. J. Mech. Phys. Solids 70, 320–348 (2014)
Mora, M.G., Müller, S.: A nonlinear model for inextensible rods as a low energy \(\Gamma \)-limit of three-dimensional nonlinear elasticity. Ann. Inst. Henri Poincaré (C) Anal. Non Linéaire, 21, 71–293 (2004)
Mora, M.G., Müller, S.: Derivation of the nonlinear bending-torsion theory for inextensible rods by \(\Gamma \)-convergence. Calc. Var. Partial Differ. Equ. 18, 287–305 (2003)
O’Reilly, O.M.: Modeling Nonlinear Problems in the Mechanics of Strings and Rods, 1st edn. Springer, Cham (2017)
Ortner, C., Theil, F.: Justification of the Cauchy–Born approximation of elastodynamics. Arch. Rational Mech. Anal. 207(3), 1025–1073 (2013)
Santilli, M., Schmidt, B.: A Blake-Zisserman-Kirchhoff theory for plates with soft inclusions. J. Math. Pures Appl. 175, 143–180 (2023)
Scardia, L., Schlömerkemper, A., Zanini, C.: Boundary layer energies for nonconvex discrete systems. Math. Models Methods Appl. Sci. 21(04), 777–817 (2011)
Schmidt, B.: A derivation of continuum nonlinear plate theory from atomistic models. Multiscale Model. Simul. 5, 664–694 (2006)
Schmidt, B.: On the passage from atomic to continuum theory for thin films. Arch. Rational Mech. Anal. 190(1), 1–55 (2008)
Schmidt, B.: Qualitative properties of a continuum theory for thin films. Ann. Inst. Henri Poincaré (C) Anal. Non Linéaire, 25(1), 43–75 (2008)
Schmidt, B.: On the derivation of linear elasticity from atomistic models. Netw. Heterog. Media 4, 789–812 (2009)
Schmidt, B.: A Griffith-Euler-Bernoulli theory for thin brittle beams derived from nonlinear models in variational fracture mechanics. Math. Models Methods Appl. Sci. 27, 1685–1726 (2017)
Schmidt, B., Zeman, J.: A bending-torsion theory for thin and ultrathin rods as a \(\Gamma \)-limit of atomistic models, to appear in SIAM Multiscale Model. Simul. (2023). arXiv:2208.04199
Zeman, J.: Atomic rods. Github repository. (2023). https://github.com/zeman-j/atomic-rods. Accessed 7 Sept 2023
Acknowledgements
The support of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for project 441138507 within the Priority Programme SPP 2256 ‘Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials’ is gratefully acknowledged by the authors.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest. Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
Additional information
Communicated by Laszlo Szekelyhidi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schmidt, B., Zeman, J. A continuum model for brittle nanowires derived from an atomistic description by \(\Gamma \)-convergence. Calc. Var. 62, 243 (2023). https://doi.org/10.1007/s00526-023-02562-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-023-02562-y
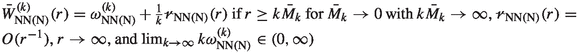