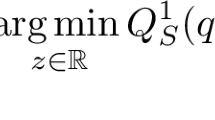Abstract
We derive an effective one-dimensional limit from a three-dimensional Kelvin–Voigt model for viscoelastic thin-walled beams, in which the elastic and the viscous stress tensor comply with a frame-indifference principle. The limiting system of equations comprises stretching, bending, and twisting both in the elastic and the viscous stress. It coincides with the model already identified via Friedrich and Kružík (Arch Ration Mech Anal 238:489–540, 2020) and Friedrich and Machill (Nonlinear Differ Equ Appl NoDEA 29, Article number: 11, 2022) by a successive dimension reduction, first from 3D to a 2D theory for von Kármán plates and then from 2D to a 1D theory for ribbons. In the present paper, we complement the previous analysis by showing that the limit can also be obtained by sending the height and width of the beam to zero simultaneously. Our arguments rely on the static \(\Gamma \)-convergence in Freddi et al. (Math Models Methods Appl Sci 23:743–775, 2013), on the abstract theory of metric gradient flows (Ambrosio et al. in Gradient flows in metric spaces and in the space of probability measures. Lectures mathematics, ETH Zürich, Birkhäuser, Basel, 2005), and on evolutionary \(\Gamma \)-convergence (Sandier and Serfaty in Commun Pure Appl Math 57:1627–1672, 2004).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many three-dimensional models in continuum mechanics are nonlinear and nonconvex, resulting in difficult numerical approximations and high computational costs. The derivation of simplified effective theories still preserving the main features of the original systems plays therefore a significant role in current research. Prominent examples in that direction are variational problems in dimension reduction where a rigorous relationship between the full three-dimensional model and its lower-dimensional counterpart is achieved by means of \(\Gamma \)-convergence [15]. Despite the long history of the subject in elasticity (see [9, 14] for surveys), the theory flourished in the last twenty years triggered by the availability of the rigidity estimate in [27]. In the present paper, we continue the study of [24, 26] and perform a dimension reduction for an evolutionary problem in the setting of viscoelastic materials.
In the purely elastic framework, there exists an extensive literature, among which we only mention the most relevant for our analysis. To this end, suppose that the reference configuration of the material is represented by a thin set \(\Omega _{h,\delta } = (-\frac{l}{2},\frac{l}{2}) \times (-\frac{h}{2},\frac{h}{2})\times (-\frac{\delta }{2},\frac{\delta }{2}) \) with length l, width h, and height \(\delta \), visualized in Fig. 1. After the rigorous justification of bending theory [27], a complete hierarchy of plate models has been derived in [28, 30] in the limit of vanishing height \(\delta \rightarrow 0\), particularly including the von Kármán theory. Starting from the latter, in [22] a further dimension reduction has been performed by sending the width h to zero, identifying an effective one-dimensional model for elastic ribbons. More generally, this theory also appears as \(\Gamma \)-limit from three-dimensional nonlinear elasticity in [20, 21], in which a hierarchy of one-dimensional models was derived by considering the simultaneous limit \(\delta \ll h \rightarrow 0\). These studies differ from effective rod models [5, 35, 36] which are identified under the assumption \(h \sim \delta \rightarrow 0\). We mention that the above \(\Gamma \)-convergence approach can be complemented by convergence of equilibria, i.e., can be obtain effective limits of the three-dimensional momentum balance
see e.g. [37] for \(h \sim 1, \delta \rightarrow 0\) and [17] for \(h \sim \delta \rightarrow 0\). Here, \(f:\Omega _{h,\delta } \rightarrow {\mathbb {R}}\) is a volume density of external forces, \(\nabla w\) denotes the deformation gradient, \(\partial _F W:=\partial W/\partial F\) is the first Piola-Kirchhoff stress tensor, where \(W:{\mathbb {R}}^{3 \times 3} \rightarrow [0,\infty ]\) is a suitable elastic energy density, and \(F \in {\mathbb {R}}^{3 \times 3}\) is the place holder of \(\nabla w\). The density is supposed to satisfy usual assumptions in nonlinear elasticity, in particular frame indifference in the sense \(W(F)=W(QF)\) for \(Q\in \textrm{SO}(3)\) and \(F\in {\mathbb {R}}^{3\times 3}\), which implies that W depends on the right Cauchy-Green strain tensor \(C:=F^\top F\).
The goal of the present paper is to pass to an effective one-dimensional description in a system of PDEs for nonlinear viscoelastic thin-walled beams, corresponding to the limits \(\delta \ll h \rightarrow 0\). This complements the \(\Gamma \)-convergence result by Freddi, Mora, and Paroni [21], and can be considered as the completion of our previous results in [24] and [26], which were the evolutionary analogs of [30] and [22], respectively.
We now describe our setting in more detail. We consider a quasistatic nonlinear model for nonsimple viscoelastic materials in the Kelvin’s–Voigt’s rheology without inertia, which obeys the system of equations
for some \(\zeta _{h,\delta } >0\). In contrast to (1.1), the deformation mapping \(w:[0,T]\times \Omega _{h,\delta }\rightarrow {\mathbb {R}}^3\) additionally depends on the time \(t\in [0,T]\) with \(T>0\). The viscous stress \(\partial _{\dot{F}} R\) can be derived from a (pseudo)potential \(R:{\mathbb {R}}^{3 \times 3} \times {\mathbb {R}}^{3 \times 3} \rightarrow [0,\infty ) \), playing an analogous role to the density W, where \(\dot{F} \in {\mathbb {R}}^{3 \times 3}\) is the placeholder of \(\partial _t \nabla w\). As observed by Antman [8], the viscous stress tensor must comply with a time-continuous frame-indifference principle meaning that \(R(F,\dot{F})={\tilde{R}}(C,\dot{C})\) for a suitable function \({\tilde{R}}\), where \(\dot{C}\) denotes the time derivative of the right Cauchy-Green strain tensor C. In the following, we assume that \(\partial _{\dot{F}}R\) is linear in \(\dot{F}\), implying R to be quadratic in \(\dot{F}\). Note, however, that still a nonlinearity arises in the viscous stress, due to its frame-indifference principle. The system (1.2) is further complemented with appropriate initial and boundary conditions, see (2.8) below.
Eventually, the remaining term, the so-called hyperstress, is induced by an additional term in the mechanical energy given by a convex and frame indifferent density \(P :{\mathbb {R}}^{3\times 3\times 3} \rightarrow [0,+\infty )\) depending on the second gradient of w. In this sense, we treat a model for second-grade materials, originally introduced by Toupin [43, 44] to enhance compactness and regularity properties of problems in mathematical elasticity. In particular, this approach currently seems to be unavoidable to overcome issues in connection with time-continuous frame indifference and to prove the existence of weak solutions in a finite strain setting, see [23, 34]. (We refer, e.g., to [18, 31] for some existence results with other solution concepts not needing second gradients.) In a similar spirit, this idea has been essential in extensions to thermoviscoelasticity [10, 34], and non-interpenetration constraints [29], as well as in the derivation of linearized models [23] and a viscoelastic plate model of von Kármán type [24]. We also refer to [13, 19], where thermodynamical consistency of such models has been shown.
In the present contribution, we consider the limiting passage \(\delta \ll h \rightarrow 0\), extending the purely elastic result in [21] to the viscoelastic setting. More precisely, in Theorem 2.3(iii), we show that weak solutions to (1.2) converge in a suitable sense to a solution of
where \(l>0\) is the length of the beam, and the constants \(C_W^0>0\) and \(C_R^0>0\) as well as the quadratic forms \(Q_W^1\) and \(Q_R^1\) are related to W and R, respectively. Moreover, r is a parameter, specifying the relation of \(\delta \) and the energy scaling, see (2.12) for details. The functions \(\xi _1\) and \(\xi _2\) denote an axial and an orthogonal in-plane displacement, respectively, whereas \(\xi _3\) denotes the out-of-plane displacement. The function \(\theta \) is called twist and is related to warping of the \(x_2\)-\(x_3\)-cross-section in the three-dimensional model, see (2.16) below. Finally, we suppose that f in (1.2) only acts in the \(x_3\)-direction and \(f^{1D}\) is its effective limit.
Our result is directly related to [24, 26], in the sense that in [24], the limit \(\delta \rightarrow 0\) is considered to derive a von Kármán theory for viscoelastic plates, and subsequently in [26], a further dimension reduction \(h \rightarrow 0\) is performed to derive (1.3) for \(r=1\), representing a one-dimensional model for viscoelastic ribbons. The result in the present contribution shows that the same limit can be obtained by a simultaneous instead of a successive limiting passage as \(h,\delta \rightarrow 0\). This is a nontrivial issue as it is well known that there are multiple effective theories for one-dimensional objects such as beams and rods depending on the ratio of the thickness in different directions. Note that we extend the result [21] also in the sense that we prescribe clamped boundary conditions which render the analysis of geometric rigidity properties more delicate.
Both in the three- and one-dimensional setting, weak solutions to (1.2) and (1.3) can be approximated by time-discrete solutions for a fixed time step \(\tau \), and the limiting passage \(h,\delta \rightarrow 0\) can be combined with the time-discrete approximation \(\tau \rightarrow 0\). We obtain a corresponding commutativity result (Theorem 2.3(ii),(iii)) which is illustrated in Fig. 2.
Illustration of the commutativity result, where the columns correspond to the dimension, and the rows indicate the (time-)discretized and continuous problems, respectively. Moreover, \(\tau \) denotes the timestep, and h and \(\delta \) correspond to the width and the height. Whereas the dark arrows are considered in Proposition 2.1 and Theorem 2.3, the dashed arrows have already been addressed in [24,25,26]
We briefly explain the scheme for the three-dimensional problem and highlight the choice of the dissipation. Given an initial value \(w^0\), the first natural idea would consist in solving inductively the minimization problem
for every \(n\in {\mathbb {N}}\), where E is the mechanical energy defined by
and \({\mathcal {R}}\) is the dissipation functional given by \({\mathcal {R}} (w,\partial _t w ) = \int _{\Omega _{h,\delta }} R (\nabla w(x), \partial _t\nabla w(x) ) \, \textrm{d}x\). Then, as \(\tau \rightarrow 0\), limits of suitably defined interpolations of the time-discrete solutions converge to weak solutions of (1.2). Following the discussion in [33, Section 2.2], we propose a slightly modified scheme by considering the minimization problems
where \({\mathcal {D}}\) is a dissipation distance whose square is given by \({\mathcal {D}}^2(w_1,w_2) = \int _\Omega D(\nabla w_1, \nabla w_2)^2\). Assuming that \({\mathcal {D}}\) is connected to R via the relation \(R(F,{\dot{F}}):= \lim _{\varepsilon \rightarrow 0} \frac{1}{2\varepsilon ^2} D^2(F+\varepsilon {\dot{F}},F)\) ensures that both minimization problems only differ from each other by lower order terms effectively leading to the same system (1.2). A main reason why we prefer to consider (1.5) in place of (1.4) is the fact that, due to the separate frame indifference of dissipation distances (see (2.3)(v) below for details), the functional minimized in (1.5) is frame indifferent in contrast (1.4), i.e., this important feature of the model is already satisfied on the time-discrete level.
This approach also allows us to identify time-continuous limits as gradient flows in metric spaces [7], both in the 3D and the 1D setting. Whereas for the one-dimensional system the existence of such solutions, so-called curves of maximal slope, has already been established in [26], the corresponding result for the three-dimensional thin material is new and a byproduct of our analysis, see Proposition 2.1. These curves can be related to weak solutions of the systems (1.2) and (1.3), see [23, Theorem 2.1(iii)] and [26, Theorem 2.2(ii)], respectively, but provide additional information as a certain energy-dissipation-balance is satisfied, see (3.6) below for details. This balance is not just of independent interest but at the core of our approach to relate the 3D to the 1D model by resorting to the theory of convergence of gradient flows introduced in [39, 41, 42]. In using this theory, the challenge is that besides \(\Gamma \)-convergence additional conditions are needed to ensure convergence of gradient flows. We refer to [24, Introduction] for a detailed account of the relevant issues and the main proof strategy in the context of dimension-reduction problems.
Let us highlight again that the approach of nonsimple materials is used due to the presence of viscous effects. Indeed, without second gradients, already the existence of time-discrete solutions (1.5) cannot be guaranteed. This is due to the fact that the structure of \({\mathcal {D}}\) appears to be incompatible with quasiconvexity (see [33] for a detailed discussion), and thus weak lower semicontinuity cannot be expected. Moreover, in a similar spirit to [10, 29, 34], it is essential to show that the topology induced by \({\mathcal {D}}\) is equivalent to the weak \(H^1\)-topology in order to obtain a priori bounds on the strain rate, cf. Lemma 5.2(v). This deeply relies on a generalized Korn inequality (see Theorem 5.3) which requires certain properties of the deformation gradient guaranteed by higher regularity of the spatial gradients.
In the following, we suppose that the material is homogeneous, i.e., neither the elastic stored energy density nor the dissipation depends on the material point. Moreover, for technical reasons, we will essentially restrict our analysis to materials with zero Poisson’s ratio, such as cork, see (H) and (2.21), and also Remark 6.8 for a possible generalization. Such an assumption, also present in other works (see e.g. [11, 24, 26]), simplifies the analysis as it excludes nontrivial relaxation effects in the passage from the 3D to the 1D model.
Let us also mention the related issue of deriving effective theories for problems with inertia but without viscosity. This has been the subject of [3, 4] and [1, 2] in the context of plate and rod models, respectively. Combining inertial and viscosity effects for thin structures, also in connection with temperature [10, 34], will be the subject of future research.
The plan of the paper is as follows. In Sect. 2, we introduce the three- and one-dimensional models in more detail and state our main results. Whereas Sect. 3 is devoted to the collection of results concerning the theory of gradient flows in metric spaces, the abstract theory is adapted to our model in Sects. 4–7. First, in Sect. 4 we adapt the rigidity estimates of [21] to our setting with clamped boundary conditions. Section 5 is devoted to the properties of the three- and one-dimensional system. In Sect. 6, we discuss the main convergence results to apply the abstract theory [41]. In particular, we show the lower semicontinuity of the local slopes (see Theorem 6.5), which is the key difficulty of our paper. Eventually, the proofs of the main results are contained in Sect. 7. Some elementary lemmata about the energies and the dissipations are postponed to Appendix A. We close the introduction with some basic notation.
1.1 Notation
In what follows, we use standard notation for Lebesgue spaces, \(L^p(\Omega )\), which are measurable maps on \(\Omega \subset {\mathbb {R}}^d\), \(d=1,2,3\), integrable with the p-th power (if \(1\le p<+\infty \)) or essentially bounded (if \(p=+\infty \)). Sobolev spaces, written \(W^{k,p}(\Omega )\), denote the linear spaces of maps which, together with their weak derivatives up to the order \(k\in {\mathbb {N}}\), belong to \(L^p(\Omega )\). Moreover, for a function \({\hat{v}} \in W^{k,p}(\Omega )\) the set \(W^{k,p}_{{\hat{v}}}(\Omega )\) contains maps from \(W^{k,p}(\Omega )\) having boundary conditions (in the sense of traces) up to the \((k-1)\)-th order with respect to \({\hat{v}}\). If the target space is a Banach space \(E \ne {\mathbb {R}}\), we use the usual notion of Bochner–Sobolev spaces, written \(W^{k,p}(\Omega ;E)\). For more details on Sobolev spaces and their duals, we refer to [6]. Whereas \(\nabla \) and \(\nabla ^2\) denote the spatial gradient and Hessian, respectively, the symbol \(^\prime \) is used for derivatives of functions depending solely on one spatial variable. Further, \(\partial _t\) indicates a time derivative and \(\delta _{ij}\) denotes the Kronecker delta function. Finally, \(\vert A \vert \) stands for the Frobenius norm of a matrix \(A \in {\mathbb {R}}^{3\times 3}\), and \(\textrm{sym}(A) = \frac{1}{2}(A^\top + A)\) and \(\textrm{skew}(A) = \frac{1}{2}(A - A^\top )\) indicate the symmetric and skew-symmetric part, respectively.
2 The model and main results
2.1 The three-dimensional model
In this subsection, we describe the model and discuss the variational setting. Following the discussion in [33, Section 2.2] and [23, Section 2], we model (1.2) as a metric gradient flow. For this purpose, we need to specify three main ingredients: the state space that contains admissible deformations of the material, the elastic energy that drives the evolution, and the dissipation mechanism represented by a distance. We consider thin-walled beams with rectangular cross-section, i.e., the reference configuration of the material is a cuboid of the form
Here, \((\delta _h)_h\) is an infinitesimal sequence satisfying \(\lim _{h\rightarrow 0} \frac{\delta _h}{h} = 0\), i.e., the width (corresponding to the \(x_2\)-coordinate) tends to zero much slower than the height (described by the \(x_3\)-coordinate).
2.2 Elastic energy
We define the elastic energy per unit cross-section associated with a deformation \(w:\Omega _h \rightarrow {\mathbb {R}}^3\) by
Here, \(W:{\mathbb {R}}^{3 \times 3} \rightarrow [0,\infty ]\) denotes a single well, frame-indifferent stored energy density with the usual assumptions in nonlinear elasticity. More precisely, we suppose that there exists \(c>0\) such that
where \(SO(3) = \lbrace Q\in {\mathbb {R}}^{3 \times 3}: Q^\top Q = \textbf{Id}, \, \det Q=1 \rbrace \). Besides the elastic energy density W depending on the deformation gradient, we also consider a strain gradient energy term P depending on the Hessian \(\nabla ^2 w\), adopting the concept of 2nd-grade nonsimple materials, see [43]. More specifically, for \(p>3\), let \(P:{\mathbb {R}}^{3\times 3 \times 3} \rightarrow [0, +\infty )\) satisfy
for \(0<c_1<c_2\). The contribution to the model of the latter is measured by \((\zeta _h)_h\) indicating an infinitesimal sequence. Finally, \(f^{3D}_h \in L^2(\Omega _h)\) denotes a force acting in the \(x_3\)-direction. For simplicity, we assume \( f^{3D}_{h}\) to be independent of \(x_2\) and \(x_3\) and write \( f^{3D}_{h}:I \rightarrow {\mathbb {R}}\) with a slight abuse of notation. The theory also holds for more general forces which may depend on \(x_2\), see [21, Section 4]. We postpone a more precise definition of \(\zeta _h\) and \(f^{3D}_h\) to (2.13) and (2.14).
2.3 Dissipation mechanism
Consider now time-dependent deformations \(w:[0,T]\times \Omega _h \rightarrow {\mathbb {R}}^3\). In contrast to elasticity, viscosity is not only related to the strain \(\nabla w\) but also to the strain rate \(\partial _t \nabla w\). It can be expressed in terms of \(R(\nabla w, \partial _t \nabla w)\) for the dissipation potential \(R:{\mathbb {R}}^{3 \times 3} \times {\mathbb {R}}^{3 \times 3} \rightarrow [0,\infty )\) given in (1.2). Due to our formulation as a metric gradient flow, we consider a corresponding distance as follows: we introduce \({\mathcal {D}}\), defined by
for \(w_1,w_2:\Omega _h \rightarrow {\mathbb {R}}^3\). Here, for some \(c>0\) we assume that the density \(D:GL_+(3) \times GL_+(3) \rightarrow [0,\infty )\) satisfies for all \(F_1,F_2\in GL_+(3):= \lbrace F \in {\mathbb {R}}^{3 \times 3}: \det F>0 \rbrace \)
We point out that the Hessian of \(D^2\) in direction of \(F_1\) at \((F_1,F_2)\), denoted by \(\partial ^2_{F_1^2} D^2(F_1,F_2)\), is a fourth-order tensor. Note that (i) implies that D is a true distance when restricted to positive definite symmetric matrices. Moreover, (vi) is a natural condition as \({\mathbb {R}}^{3 \times 3}_{\textrm{skew}} = \lbrace A \in {\mathbb {R}}^{3 \times 3}: A=-A^\top \rbrace \) is necessarily contained in the kernel of \(\partial ^2_{F_1^2} D^2(\textbf{Id}, \textbf{Id})\) by (v), see Lemma A.1. The relation of D and the dissipation potential R is given by
for \(F \in GL_+(3)\) and \({\dot{F}} \in {\mathbb {R}}^{3 \times 3}\), whenever \(\partial ^2_{F_1^2} D^2(F,F)\) exists. The second equality follows by a Taylor expansion. In addition, we point out that (v) guarantees that R satisfies frame indifference in the sense
for all \(F \in GL_+(3)\) and \({\dot{F}} \in {\mathbb {R}}^{3 \times 3}\), see [33, Lemma 2.1]. This corresponds to a time-dependent version of frame indifference, and we refer to [8, 33] for a thorough discussion. A further consequence of (v),(vi) is that R depends only the right Cauchy-Green strain tensor \(C:= F^{\top }F\) and its time derivative \(\dot{C}= {\dot{F}}^{\top }F+F^{\top }\dot{F}\), that it is quadratic in \(\dot{C}\), and that
see Lemma A.1. This condition corresponds to [34, assumption (2.30e)] and is essential there in order to derive good compactness properties for establishing solutions in the three-dimensional setting. One possible example of D satisfying (2.3) might be \(D(F_1,F_2)= |F_1^\top F_1-F_2^\top F_2|\). This leads to \(R(F,\dot{F})=| F^\top \dot{F} + \dot{F}^\top F |^2/2\) which is a standard choice. For further examples we refer to [33, Section 2.3].
2.4 Rescaling
For the limiting passage, it is more convenient to work on the rescaled domain \(\Omega := I \times (-1/2,1/2) \times (-1/2, 1/2)\) that does not depend on h. For notational convenience, we denote by \(S:= I\times (-1/2,1/2)\) the scaled \(x_1\)-\(x_2\) cross-section and by \(\omega :=(-1/2,1/2) \times (-1/2,1/2)\) the scaled \(x_2\)-\(x_3\) cross-section. For a deformation \(w:\Omega _h \rightarrow {\mathbb {R}}^3\), we let \(p_h:\Omega \rightarrow \Omega _h\), \(p_h(x_1,x_2,x_3) = (x_1, hx_2,\delta _hx_3)\) be the projection of \(\Omega \) onto \(\Omega _h\) and introduce the scaled deformation mapping \(y:\Omega \rightarrow {\mathbb {R}}^3\) by \(y=w\circ p_h\). For a smooth function \(y:\Omega \rightarrow {\mathbb {R}}^3\), we define the scaled gradient as \(\nabla _h y = ({y,}_1, \frac{{y,}_2}{h}, \frac{{y,}_3}{\delta _h})\), where the subscript indicates the directional derivative along the i-th unit vector. Moreover, \(\nabla _h^2\) denotes the scaled Hessian and is defined by
Let \((\varepsilon _h)_h\) be an infinitesimal sequence representing the energy scaling. Then, by a change of variables, we see that the rescaled energy, defined by \(\phi _h(y) = \frac{1}{\varepsilon _h^2}E(y\circ p_h^{-1})\), satisfies
for all \(y \in W^{2,p}(\Omega ;{\mathbb {R}}^3)\). Concerning the viscosity part of the model, we define the scaled dissipation distance as
for all \(y_0, y_1 \in W^{2,p}(\Omega ;{\mathbb {R}}^3)\).
2.5 Clamped boundary conditions
In contrast to the model studied in [21], we consider a problem with Dirichlet boundary conditions on \( \Gamma :=\{-\frac{l}{2},\frac{l}{2}\} \times \omega \). Given functions \({\hat{\xi }}_1 \in W^{2,p}( I )\), \({\hat{\xi }}_2, {\hat{\xi }}_3 \in W^{3,p}(I)\), \(p>3\), we introduce the set of admissible configurations by
Note that the different components of the boundary conditions are coupled. Such a structure is a typical in dimension-reduction problems to ensure compatibility of the recovery sequence. We refer e.g. to [24, 26, 30].
2.6 Rescaled equations of nonlinear viscoelasticity
As a preparation for the formulation of the rescaled equations of nonlinear viscoelasticity, we introduce the scaled (distributional) divergence. First, for \(g \in L^1(\Omega ;{\mathbb {R}}^3)\) we define \(\textrm{div}_h g\) by \(\textrm{div}_h g = \partial _1 g_1+ \frac{1}{h}\partial _2 g_2 + \frac{1}{\delta _h}\partial _3 g_3\). Then, for \(i,j \in \lbrace 1,2, 3\rbrace \), we denote by \((\partial _ZP(\nabla ^2_h y))_{ij*}\) the vector-valued function \(((\partial _ZP(\nabla ^2_h y))_{ijk})_{k=1,2,3}\), and let
for \(y \in {\mathscr {S}}_h^{3D}\). Rescaling of (1.2) leads to the system of equations
for some initial datum \(y^h_0 \in {\mathscr {S}}_h^{3D}\), where \(\partial _FW(\nabla _h y)-\zeta _h \textrm{div}_h (\partial _ZP(\nabla ^2_h y)) \) denotes the first Piola-Kirchhoff stress tensor and \(\partial _{{\dot{F}}}R(\nabla _h y,\partial _t \nabla _h y)\) the viscous stress with R as introduced in (2.4). Moreover, \(e_3\) indicates the normal vector pointing in the \(x_3\)-direction. We also implicitly assume zero Neumann boundary conditions for the stress and the hyperstress on \(\partial \Omega \setminus \Gamma \), and on the lateral boundary there arise additional Neumann conditions from the second deformation gradient. We do not include the conditions here but refer to [29] for details.
2.7 Existence of solutions to the 3D-model
To guarantee existence of weak solutions to (2.9), we introduce an approximation scheme solving suitable time-incremental minimization problems. We consider a fixed time step \(\tau >0\), and set \(Y^0_{h,\tau } = y_0^h\). Whenever \(Y^0_{h,\tau }, \ldots , Y^{n-1}_{h,\tau }\) are known, \(Y^n_{h,\tau }\) is defined as (if existent)
where \(\phi _h\) and \({\mathcal {D}}_h\) are defined in (2.6) and (2.7). Suppose that, for a choice of \(\tau \), a sequence \((Y^n_{h,\tau })_{n \in {\mathbb {N}}}\) solving (2.10) exists. We define the piecewise constant interpolation by
In the following, \(\tilde{Y}_{h,\tau }\) will be called a time-discrete solution. We often drop the x-dependence and write \( \tilde{Y}_{h,\tau }(t)\) for a time-discrete solution at time t.
Our first result addresses the existence of solutions to the 3D problem. We employ an abstract convergence result concerning metric gradient flows, more precisely for curves of maximal slope and their approximation via the minimizing movement scheme. The relevant notions about curves of maximal slope are recalled in Sect. 3. In particular, the local slopes of \(\phi _h\) with respect to \({\mathcal {D}}_h\) are denoted by \(|\partial {\phi }_h|_{{{\mathcal {D}}}_h}\), see Definition 3.1. For notational convenience, we define the sublevel set \({\mathscr {S}}_{h,M}^{3D}:=\{y\in {\mathscr {S}}_h^{3D}: \phi _h(y)\le M\}\) for \(M>0\), representing deformations with uniformly bounded energy.
Proposition 2.1
(Solutions in the 3D setting) Let \(M>0\), \(y_0^h \in {\mathscr {S}}^{3D}_{h,M}\) and \((\tau _k)_k\) be a sequence converging to zero.
-
(i)
(Time-discrete solutions) Then, there exists a solution of the minimization problems in (2.10).
-
(ii)
(Continuous solutions) Let \((\tilde{Y}_{h,\tau _k})_k\) be a sequence of time-discrete solutions as given in (2.11). Then, for \(h>0\) sufficiently small only depending on M, there exists a subsequence of \((\tau _k)_k\) (not relabeled) and a function \(y^h \in L^\infty ([0,+\infty ); {\mathscr {S}}_{h,M}^{3D} ) \cap W^{1,2}([0,+\infty );H^1(\Omega ;{\mathbb {R}}^3))\) satisfying \(y^h(0) = y_0^h\) such that \(\tilde{Y}_{h,\tau _k}(t) \rightharpoonup y^h(t)\) weakly in \(W^{2,p}(\Omega ;{\mathbb {R}}^3)\) for every \(t\ge 0\) as \(k\rightarrow \infty \), and \(y^h\) is a curve of maximal slope for \({\phi }_h\) with respect to \(|\partial {\phi }_h|_{{{\mathcal {D}}}_h}\).
In particular, in [23, Theorem 2.1] it has been shown that curves of maximal slope are weak solutions of the system (2.9). Let us stress that the existence of weak solutions has already been settled successfully in [29, 34]. Still, our approach sheds light on this issue from a slightly different perspective as our result is formulated in a metric setting, see below (1.5) for the motivation of our scheme. The result is proved in Sect. 7.
2.8 Compactness and limiting variables
As it is customary in dimension-reduction problems, the effective behavior is crucially influenced by the relation between the elastic energy \(\varepsilon _h^2\) and the height \(\delta _h\) of the material. In the purely elastic framework [20, 21], all possible scaling regimes \(\delta _h/\varepsilon _h \) have been addressed. Here, we concentrate on the supercritical regime \( \delta _h/\varepsilon _h \rightarrow +\infty \) and treat the specific case, where
exists. The case \(r=\infty \) also studied in [21] is not covered by our theory and indeed more delicate due to a nonlinear constraint in the limiting model. To perform the passage to the limit, we need to specify the penalization parameter \(\zeta _h\), the force \(f^{3D}_h\) in (2.6), and the topology of the convergence. Fixing \(\alpha < 1\), we suppose that
Whereas the liminf condition will help to derive suitable compactness properties, the limsup condition ensures compatibility with the recovery sequence, see (6.9). Roughly speaking, the scaling parameter \(\zeta _h\) is chosen in such a way that the contribution of the second gradient does not affect the limit, but still contributes in the three-dimensional setting to show quantitative estimates for the deformation gradient, see Lemma 4.1 below. Further, we assume that
for a function \(f^{1D} \in L^2(I)\). Moreover, we define the sequence of displacements \( u^h :\Omega \rightarrow {\mathbb {R}}^3\) by
and define the function \(\theta ^h:I \rightarrow {\mathbb {R}}\) by
where \(I_0:= \int _\omega (x_2^2 + x_3^2) \textrm{d}x_2 \textrm{d}x_3 = \frac{1}{6}\). Whereas \( u_1^h\), \(u_2^h\), and \(u_3^h\) correspond to (scaled) deviations of the deformation from the identity, the function \( \theta ^h\) can be interpreted as a twist. The following proposition identifies limits of \((u^h)_h\) and \((\theta ^h)_h\) by a compactness argument, also defining the topology of the convergence. The limiting variables corresponding to displacements lie in the space of Bernoulli-Navier displacements
where \({\hat{\xi }}_i\), \(i =1,2,3\), were defined in (2.8). On the other hand, the limit of the twists \(\theta ^h\) is a \(W^{1,2}_0(I)\)-function, and we thus introduce the space
Finally, we are in the position to state the compactness result.
Proposition 2.2
(Compactness) Consider a sequence \((y^h)_h\) with \(y^h \in {\mathscr {S}}^{3D}_{h,M}\) for all h. Then, there exists \((u,\theta ) \in {\mathscr {S}}^{1D}\) such that up to subsequences (not relabeled)
-
(i)
\( u^h \rightharpoonup u\) in \(W^{1,2}(\Omega ; {\mathbb {R}}^3)\) and \(u^h_3 \rightarrow u_3\) in \(W^{1,2}(\Omega )\).
-
(ii)
\( \theta ^h \rightharpoonup \theta \) in \(W^{1,2}(I)\).
The proposition will be proved in Sect. 6. Later, we will see that the compactness also holds in an evolutionary setting, see Theorem 2.3(iii).
2.9 Quadratic forms and compatibility conditions
As a preparation for the formulation of the one-dimensional model, we introduce effective quadratic forms related to W and D. We define \(Q^3_W:{\mathbb {R}}^{3\times 3} \rightarrow {\mathbb {R}}\) and \(Q^3_R:{\mathbb {R}}^{3\times 3} \rightarrow {\mathbb {R}}\) by
for \(A \in {\mathbb {R}}^{3 \times 3}\). By Taylor expansion and Polar decomposition in combination with frame indifference (see (2.1) and (2.3)) one can observe that the quadratic forms \(Q^3_W\), \(Q^3_D\) only depend on the symmetric part \(\textrm{sym}(A)\) of \(A \in {\mathbb {R}}^{3\times 3}\) and that they are positive definite on \({\mathbb {R}}^{3\times 3}_\textrm{sym}:= \{A \in {\mathbb {R}}^{3\times 3}: A = A^{\top }\}\). We define reduced quadratic forms by minimizing over stretches in the \(x_2\)- and \(x_3\)-direction. More precisely, we let
The quadratic forms \(Q_S^i\), \(i=1,3\), induce fourth-order and second-order tensors, respectively, denoted by \({{\mathbb {C}}}_W^i\) and \({{\mathbb {C}}}_D^i\) for \(i=1,3\). In a similar spirit to [24, 26], we require some compatibility conditions of the quadratic forms to perform a rigorous evolutionary dimension reduction. This is crucial as we need to construct mutual recovery sequences, compatible with the elastic energy and the viscous dissipation at the same time, see Theorem 6.5 below. We assume that we can decompose \(Q_S^3\) in the following way: there exist quadratic forms \(Q_S^*\) and constants \(C_S^*>0\) such that for all \(A= (a_{ij})_{i,j=1,2,3} \in {\mathbb {R}}^{3\times 3}_\textrm{sym}\) it holds that

where \({\tilde{A}} = ({\tilde{a}}_{ij})_{i,j=1,2,3}\in {\mathbb {R}}^{3\times 3}_\textrm{sym}\) satisfies \({\tilde{a}}_{1j}=0\) for \(j =1,2\), and \( \tilde{a}_{km}= a_{km} \) for \((k,m) \notin \{ (1,1),(1,2), (2,1) \}\). This induces a restriction from a modeling point of view since it essentially corresponds to materials with Poisson ratio zero, such as cork. More precisely, the assumption also covers materials with a nonzero Poisson ratio with respect to the \(x_2\)- and \(x_3\)-direction, e.g. certain orthotropic materials with density (\(\lambda _2,\lambda _3,\mu \ge 0\))
A possible generalization (not included in the following for simplicity) is to assume that \(Q_S^3\) are h-dependent, denoted by \(Q_{S,h}^3\), such that \(Q_{S,h}^3 = Q_S^3 + \textrm{o}(1) \hat{Q}_{S}\) for \(h \rightarrow 0\), where \(Q_S^3\) satisfies (H) and \(\hat{Q}_S\) is any positive definite quadratic form. Another sound option for a compatibility condition consists in vanishing dissipation effects, briefly discussed in Remark 6.8 below.
2.10 The one-dimensional model
To formulate the gradient flow for the one-dimensional theory, we again need to assign a metric and an energy to a suitable space. As the limit variables have already been identified with \({\mathscr {S}}^{1D}\) in Proposition 2.2, it remains to find a metric \({\mathcal {D}}_0\) and an energy \(\phi _0\). Following the abstract theory in [42], the natural candidate for the energy is the \(\Gamma \)-limit of \(\phi _h\) from the static theory, see Theorem 6.2, and thus we define
for \((u,\theta )\in {\mathscr {S}}^{1D}\), where u is identified with \((\xi _1,\xi _2,\xi _3)\) via (2.17) and \(f^{1D}\) is defined in (2.14). Due to the similar structure of the metric \({\mathcal {D}}_h\) and the energy \(\phi _h\), see (2.6) and (2.7), it turns out that the appropriate choice for the metric is
for \((u,\theta ),({\tilde{u}}, {{\tilde{\theta }}})\in {\mathscr {S}}^{1D} \), where \((\xi _1,\xi _2,\xi _3)\) and \(({{\tilde{\xi }}}_1,\tilde{\xi }_2,{{\tilde{\xi }}}_3)\) correspond to u and \({\tilde{u}}\), respectively, see (2.17).
The geometrical interpretation of the variables \((u,\theta ) \in {\mathscr {S}}^{1D}\) is as follows: \(u_2\) and \(u_3\) correspond to orthogonal displacements in the \(x_2\)- and \(x_3\)-direction. The axial displacement \(u_1\) in the \(x_1\)-direction is additionally influenced by linear perturbations of \(u_2'\) and \(u_3'\), see (2.17). Eventually, \(\theta \) corresponds to a twist. Note that in [26] the variable \(\xi _3\) is denoted by w. In [26, Theorem 2.2] it has been shown that curves of maximal slope for \(\phi _0\) with respect to \({\mathcal {D}}_0\) give rise to weak solutions in the sense of [26, (2.13)] of the system given in (1.3). Whereas the cases \(r>0\) considered in [26] lead to the one-dimensional von Kármán theory, \(r=0\) corresponds to a linear system of equations. Note that in that case, \(\phi _0\) and \({\mathcal {D}}_0\) become purely quadratic, and thus convex. Then, existence (and even uniqueness) of weak solutions follow from well-known theory, see e.g. [7, Section 2.4].
2.11 Main convergence result
To relate the three-dimensional with the one-dimensional model, we will use the abstract theory of gradient flows [7] and evolutionary \(\Gamma \)-convergence [32, 41, 42]. In particular, we recall that the local slopes are denoted by \(|\partial {\phi }_h|_{{{\mathcal {D}}}_h}\) and \(|\partial {\phi }_0|_{{{\mathcal {D}}}_0}\), respectively, see Definition 3.1, and we again refer to Sect. 3 for more details. We introduce the topology of convergence as follows: given a deformation \(y^h\in {\mathscr {S}}^{3D}_{h}\), we define mappings \(\pi _h:{\mathscr {S}}^{3D}_{h} \rightarrow {\mathscr {S}}\) by \(\pi _h(y^h) = (u^h,\theta ^h)\) for \({\mathscr {S}} = W^{1,2}(\Omega ;{\mathbb {R}}^3) \times W^{1,2}(I)\), where \(u^h\) and \(\theta ^h\) are defined in (2.15) and (2.16). We write \(y^h {\mathop {\rightarrow }\limits ^{\pi \sigma }} (u,\theta )\) for the convergence found in Proposition 2.2. (The symbol \(\pi \sigma \) is used because of the abstract convergence result, see Sect. 3.) We also write \(y^h {\mathop {\rightarrow }\limits ^{\pi \rho }} (u,\theta )\) if the convergence of \(u_1^h\) and \(u_2^h\) holds with respect to the strong in place of the weak topology. We remark that the limiting variables \((u,\theta )\) are contained in the space \({\mathscr {S}}^{1D} \subset {\mathscr {S}}\) defined in (2.18). Given \((u_0,\theta _0) \in {\mathscr {S}}^{1D}\), we introduce the family of sequences of admissible initial data as \( {\mathcal {B}}(u_0,\theta _0) = \big \{ (y^h_0)_h: \ y^h_0 \in {\mathscr {S}}^{3D}_h, \ y^h_0 {\mathop {\rightarrow }\limits ^{\pi \sigma }} (u_0,\theta _0), \ \phi _h(y^h_0) \rightarrow {\phi }_0(u_0,\theta _0) \big \}\).
Theorem 2.3
(Relation between three-dimensional and one-dimensional system) Let \((u_0,\theta _0) \in {\mathscr {S}}^{1D}\) be an initial datum and suppose that (H) holds.
-
(i)
(Well-posedness of initial datum) There holds \( {\mathcal {B}}(u_0,\theta _0) \ne \emptyset \) for all \((u_0,\theta _0)\in {\mathscr {S}}^{1D}\).
-
(ii)
(Convergence of discrete solutions) Consider a sequence \((y^h_0)_h \in {\mathcal {B}}(u_0,\theta _0)\), an infinitesimal sequence \((\tau _h)_h\), and a sequence of time-discrete solutions \(\tilde{Y}_{h,\tau _h}\) as in (2.11) with \(\tilde{Y}_{h,\tau _h}(0)=y^h_0\). Then, there exists a curve of maximal slope \((u,\theta ):[0,\infty ) \rightarrow {\mathscr {S}}^{1D}\) for \({\phi }_0\) with respect to \(|\partial {\phi }_0|_{{{\mathcal {D}}}_0}\) satisfying \((u(0),\theta (0)) = (u_0,\theta _0)\) such that up to a subsequence (not relabeled) it holds that
$$\begin{aligned} \tilde{Y}_{h,\tau _h}(t) {\mathop {\rightarrow }\limits ^{\pi \rho }} (u(t),\theta (t)) \ \ \ \ \ \text {for all} \ t \in [0,\infty ) \ \ \text { as }h \rightarrow 0. \end{aligned}$$(2.24) -
(iii)
(Convergence of continuous solutions) Consider a sequence \((y^h_0)_h \in {\mathcal {B}}(u_0,\theta _0)\). Let \((y^h)_h\) be a sequence of curves of maximal slope for \(\phi _{h}\) with respect to \(\vert \partial \phi _{h} \vert _{{\mathcal {D}}_{h}}\) satisfying \(y^h(0) = y^h_0\). Then, there exists a curve of maximal slope \((u,\theta ):[0,\infty ) \rightarrow {\mathscr {S}}^{1D}\) for \({\phi }_0\) with respect to \(|\partial {\phi }_0|_{{{\mathcal {D}}}_0}\) satisfying \((u(0),\theta (0)) = (u_0,\theta _0)\) such that up to a subsequence (not relabeled) it holds that
$$\begin{aligned} y^h(t) {\mathop {\rightarrow }\limits ^{\pi \rho }} (u(t),\theta (t)) \ \ \ \ \ \text {for all} \ t \in [0,\infty ) \ \ \text { as }h \rightarrow 0. \end{aligned}$$(2.25)
The result is proved in Sect. 7. Note that Proposition 2.1 provides the existence of discrete solutions, but also the existence of curves of maximal slope in the three-dimensional setting (which are weak solutions of (2.9) due to [23, Theorem 2.1]). Further, we mention once again that in [26] it has been shown that the curves from (ii) and (iii) can be identified as weak solutions to the one-dimensional system (1.3). Moreover, we stress that compared to Proposition 2.2 the convergence of the displacements \(u_1^h\) and \(u_2^h\) also holds in the strong \(W^{1,2}\)-sense. In addition, we point out that the assumpion (H) is only needed in the limiting passage and not for a fixed h in Proposition 2.1. From now on we set \( f_h^{3D} \equiv 0 \) for convenience. The general case indeed follows by minor modifications, which are standard. For details we refer the reader to Lemma A.3.
3 Metric gradient flows
3.1 Definitions
In this section, we recall the relevant definitions about curves of maximal slope and present abstract theorems concerning the convergence of time-discrete solutions and continuous solutions to curves of maximal slope. We consider a complete metric space \(({\mathscr {S}},{\mathcal {D}})\). We say a curve \(y:(a,b) \rightarrow {\mathscr {S}}\) is absolutely continuous with respect to \({\mathcal {D}}\) if there exists \(m \in L^1(a,b)\) such that
The smallest function m with this property, denoted by \(|y'|_{{\mathcal {D}}}\), is called metric derivative of y and satisfies for a.e. \(t \in (a,b)\) (see [7, Theorem 1.1.2] for the existence proof)
We define the notion of a curve of maximal slope. We only give the basic definition here and refer to [7, Section 1.2, 1.3] for motivations and more details. By \(h^+:=\max (h,0)\) we denote the positive part of a function h.
Definition 3.1
(Upper gradients, slopes, curves of maximal slope) We consider a complete metric space \(({\mathscr {S}},{\mathcal {D}})\) with a functional \(\phi :{\mathscr {S}} \rightarrow (-\infty ,+\infty ]\).
(i) A function \(g:{\mathscr {S}} \rightarrow [0,\infty ]\) is called a strong upper gradient for \(\phi \) if for every absolutely continuous curve \( y:(a,b) \rightarrow {\mathscr {S}}\) the function \(g \circ y\) is Borel and
(ii) For each \(y \in {\mathscr {S}}\) the local slope of \(\phi \) at y is defined by
(iii) An absolutely continuous curve \(y:(a,b) \rightarrow {\mathscr {S}}\) is called a curve of maximal slope for \(\phi \) with respect to the strong upper gradient g if for a.e. \(t \in (a,b)\)
3.2 Curves of maximal slope as limits of time-discrete solutions
In the following, we consider a sequence of complete metric spaces \(({\mathscr {S}}_k, {\mathcal {D}}_k)_k\), as well as a limiting complete metric space \(({\mathscr {S}}_0,{\mathcal {D}}_0)\). Moreover, let \((\phi _k)_k\) be a sequence of functionals with \(\phi _k:{\mathscr {S}}_k \rightarrow (-\infty ,\infty ] \) and \(\phi _0:{\mathscr {S}}_0 \rightarrow (-\infty ,\infty ] \).
Fixing \(k\in {\mathbb {N}}\), we now describe the construction of time-discrete solutions for the energy \(\phi _k\) and the metric \({\mathcal {D}}_k\), already mentioned in Sect. 2, but in a general metric setting to give a precise description of the abstract theory. Consider a fixed time step \(\tau >0\) and suppose that an initial datum \(Y^0_{k,\tau }\) is given. Whenever \(Y_{k,\tau }^0, \ldots , Y^{n-1}_{k,\tau }\) are known, \(Y^n_{k,\tau }\) is defined as (if existent)
Then, we define the piecewise constant interpolation by
We call \(\tilde{Y}_{k,\tau }\) a time-discrete solution.
Our goal is to study the limit of time-discrete solutions as \(k \rightarrow \infty \). To this end, we need to introduce a suitable topology for the convergence. We assume that for each \(k \in {\mathbb {N}}\) there exists a map \(\pi _k:{\mathscr {S}}_k \rightarrow {\mathscr {S}}\) for a suitable set \({\mathscr {S}} \supseteq {\mathscr {S}}_0\). Given a sequence \((z_k)_k\), \(z_k \in {\mathscr {S}}_k\), and \(z \in {\mathscr {S}}\), we say
where \(\sigma \) is a topology on \({\mathscr {S}}\) satisfying the following conditions: we suppose that
for all \(z, {{\bar{z}}} \in {\mathscr {S}}_0\). Moreover, we assume that for every sequence \((z_k)_k\), \(z_k \in {\mathscr {S}}_k\), and \(N \in {\mathbb {N}}\) we have
Further, we suppose lower semicontinuity of the energies and the slopes in the following sense: for all \(z \in {\mathscr {S}}_0\) and \((z_k)_k\), \(z_k \in {\mathscr {S}}_k\), we have
For the relation of time-discrete solutions and curves of maximal slope we will use the following result.
Theorem 3.2
Suppose that (3.3)–(3.5) hold. Moreover, assume that \(|\partial \phi _0|_{{\mathcal {D}}_0}\) is a strong upper gradient for \( \phi _0 \). Consider an infinitesimal sequence \((\tau _k)_k\). Let \((Y^0_{k,\tau _k})_k\) with \(Y^0_{k,\tau _k} \in {\mathscr {S}}_k\) and \(z_0 \in {\mathscr {S}}_0\) be initial data satisfying
Then, for each sequence of discrete solutions \((\tilde{Y}_{k,\tau _k})_k\) starting from \((Y^0_{k,\tau _k})_k\) there exists a limiting function \(z:[0,+\infty ) \rightarrow {\mathscr {S}}_0\) such that up to a subsequence (not relabeled)
as \(k \rightarrow \infty \), and z is a curve of maximal slope for \(\phi _0\) with respect to \(|\partial \phi _0|_{{\mathcal {D}}_0}\). In particular, z satisfies the energy-dissipation-balance
The statement is proved in [39, Section 2] for a sequence of functionals and metrics defined on a single space. The generalization for a sequence of spaces is straightforward and follows from standard adaptions. For a more detailed discussion of similar statements, we refer for example to [23, Section 3.3].
3.3 Curves of maximal slope as limits of continuous solutions
As before, \(({\mathscr {S}}_k, {\mathcal {D}}_k)_k\) and \(({\mathscr {S}}_0,{\mathcal {D}}_0)\) denote complete metric spaces, with corresponding functionals \((\phi _k)_k\) and \(\phi _0\). For the relation of the three- and one-dimensional systems, we will use the following result.
Theorem 3.3
Suppose that (3.3)–(3.5) hold. Moreover, assume that \(\vert \partial \phi _n \vert _{{\mathcal {D}}_n}\), \(\vert \partial \phi _0 \vert _{{\mathcal {D}}_0}\) are strong upper gradients for \(\phi _n\), \(\phi _0\) with respect to \({\mathcal {D}}_n\), \({\mathcal {D}}_0\), respectively. Let \( z_0 \in {\mathscr {S}}_0\). For all \(n \in {\mathbb {N}}\), let \(z_n\) be a curve of maximal slope for \(\phi _n\) with respect to \(\vert \partial \phi _n \vert _{{\mathcal {D}}_n}\) such that
Then, there exists a limiting function \( z :[0,\infty ) \rightarrow {\mathscr {S}}_0\) such that up to a subsequence (not relabeled)
as \(n \rightarrow \infty \), and z is a curve of maximal slope for \(\phi _0\) with respect to \(\vert \partial \phi _0 \vert _{{\mathcal {D}}_0}\) and satisfies (3.6).
The result is a variant of [42] and is given in [23, Theorem 3.6]. Once again, we refer to [23, Section 3.3] for a brief discussion.
4 Geometric rigidity
As a preliminary step, we provide the necessary rigidity estimates to adapt the \(\Gamma \)-convergence result of [21] to our setting with clamped boundary conditions. Recall the definitions of Subsection 2.1, especially the definition of \(S = I \times (-1/2,1/2)\) and \({\mathscr {S}}^{3D}_{h,M}\). Due to the frame indifference of W and P and their coercivity properties, see (2.1) and (2.2), one can only expect estimates up to a rigid motion of \((y^h)_h\), see [21]. The crucial point of the following lemma is that the clamped boundary conditions in (2.8) imply rigidity estimates for \((y^h)_h\) itself. To this end, we combine the arguments of [21, Lemma 3.1] and [30, Lemma 13]. Additionally, we derive \(L^\infty \)-estimates for the scaled gradient \(\nabla _h y^h\), as a consequence of the the second-order perturbation in (2.6). (The \(L^\infty \)-bounds will be crucial for validity of Lemma 5.1 and Lemma 5.2 below as any other \(L^q\)-bound would not be sufficient to prove those lemmata.)
Lemma 4.1
(Rigidity estimates on thin domains) Let \(M>0\) and let \((y^h)_h\) be a sequence in \({\mathscr {S}}^{3D}_{h,M}\). Moreover, assume that (2.12)–(2.13) hold. Then, there exists a sequence \((R^h)_h \subset W^{1,2} (S; SO(3))\) such that we have for h small enough
where C only depends on \(\Omega \), \(\Gamma \), M, and p.
Proof
The proof consists of two steps: First, we derive the statement up to a rotation of \(\nabla _h y^h\). This has been essentially proven in [20, Lemma 3.3] and [21, Lemma 3.1]. In our present setting, we derive additional \(L^\infty \)-estimates, see (4.1)(v),(vi). In the second step, we employ the boundary conditions in (2.8) to show that the estimates also hold for the sequence \((y^h)_h\) itself.
Step 1: Due to the coercivity of the energy densitiy W in (2.1)(iii), by [21, Lemma 3.1] we can find a sequence \((R^h)_h \in W^{1,2}(S; SO(3))\) such that (i) and (ii) hold. Note that the sequence is indeed SO(3)-valued by [20, Lemma 3.3] since (2.12) implies \(h^{1/2}\varepsilon _h/\delta _h \rightarrow 0\). The existence of \(R^h\) deeply relies on the rigidity estimate by Friesecke, James, and Müller [27, Theorem 3.1]. We briefly describe the heuristics of the construction, see [20, Lemma 3.3] for the complete proof: working on the original domain \(\Omega _h\), one divides \(\Omega _h\) into cubes with side length \(\delta _h\). On each cube, one uses the rigidity estimate to control the \(L^2\)-norm of the distance between \(\nabla (y^h \circ p_h^{-1}) \) and SO(3) by a positive constant times the \(L^2\)-deviation of gradient from a fixed rotation. Here, \(p_h\) is the projection defined in Subsection 2.1. As the height of \(\Omega _h\) coincides with the side length of a cube, the rotations can be chosen independently of \(x_3\). Then, after defining piecewise-constant interpolations of the rotations, one obtains \(R^h\) by a mollification and a projection onto SO(3). For this argument, the scaling \(h^{1/2}\varepsilon _h/\delta _h \rightarrow 0\) and the smoothness of the manifold SO(3) ensure that the mollification lies in in a tubular neighborhood of SO(3) such that the nearest-point projection onto SO(3), denoted by \(\Pi _{SO(3)}\), is smooth. For later purposes, we recall the precise representation of \(R^h\) from the proof of [20, Lemma 3.3] which is given by
Here, \({\tilde{R}}^h\) is a piecewise-constant function (constant on each cube described above), SO(3)-valued, and successively extended to \({\mathbb {R}}^2\) by reflection, and \((\eta _h)_h\) is a family of standard mollifiers.
Next, we see by [21, Lemma 3.1] that (iii) and (iv) hold for a sequence of rotations \((Q^h)_h\), \(Q^h \in SO(3)\), instead of \(\textbf{Id}\), i.e.,
where the second inequality is an immediate consequence of the first one and (i). We now prove \(Q^h\)-versions of (v) and (vi), inspired by [23, Lemma 4.2]: by the definition of \(\phi _h\) in (2.6) and (2.2)(iii) we get \(\Vert \nabla _h^2 y^h \Vert _{L^p(\Omega )} \le C (\varepsilon _h^2/\zeta _h)^{1/p} \le C \varepsilon _h^\alpha /\delta _h^{\alpha }\), where we used (2.13). Moreover, as \(p>3\), Poincaré’s inequality yields some \(F \in {\mathbb {R}}^{3 \times 3}\) such that \(\Vert \nabla _h y^h - F \Vert _{L^\infty (\Omega )} \le C\varepsilon _h^\alpha /\delta _h^{\alpha }\) for a constant C depending only on \(\Omega \), p, and M. This together the triangle inequality and (4.3) yields
Then, we have
by the triangle inequality. Finally, to derive the \(Q^h\)-version of (vi), recall \({\tilde{R}}^h\) from (4.2), let q be a cube with sidelength \(\delta _h\) on which \({\hat{R}}^h:= {\tilde{R}}^h\circ p_h^{-1}\) is constant, and define \(z^h:= y^h \circ p_h^{-1}\). Since by [27, Theorem 3.1] we can assume that  , (4.4) implies that
, (4.4) implies that
where the constant C does not depend on q. Then recalling the definition of \({{\bar{R}}}^h\) in (4.2) we also get
and eventually we conclude
Step 2: We now prove that the rotations \(Q^h\) are sufficiently close to the identity \(\textbf{Id}\), namely
Then, together with the triangle inequality, (4.3), (4.4), and (4.5) we get that all properties of Lemma 4.1 are satisfied for \(R^h\) and \(y^h\). To show (4.6), we follow the strategy of [30, Lemma 13]. We define the function \({{\bar{u}}}^h\) similar to (2.15) by replacing \(y^h\) with \({{\bar{y}}}^h = ({Q^h})^{\top } y^h - c^h\) for some constant vectors \(c^h \in {\mathbb {R}}^3\). By [21, Lemma 3.7 (ii)] we can choose \(c^h\) in such a way that
for a constant \(C>0\) depending only on \(\Omega \) and M. Moreove, we can calculate
Thus, by passing to the trace in (4.8) we get with (2.8)
which is uniformly bounded by (4.7). In view of \(\Gamma = \lbrace -l/2,l/2\rbrace \times \omega \), we find \( \int _{\Gamma } (x_1, hx_2, \delta _h x_3)\, \textrm{d}{\mathcal {H}}^{2}= 0\). By this and the fact that \(Q^h\) and \(c^h\) are constant, we have by a binomial expansion
Thus, by [16, Lemma 3.3] (note that \(\textrm{aff}(S_0) = {\mathbb {R}}^3\)), we have
where the constant \(C>0\) additionally depends on \(\Gamma \). As \(Q^h\) are rotations, the scaling of each column of \(\textbf{Id}-Q^h\) also holds for the corresponding row. More precisely, as \(\delta _h \le h\), we have
This control is not sufficient yet to get (4.6), and the estimate needs to be refined. For this purpose, it will be convenient to analyze the first momentum in the \(x_3\)-direction, defined by
In a similar fashion, we define the first momentum \(\Psi ^h\) for the non-rotated deformation, simply by replacing \({{\bar{y}}}^h\) with \(y^h\). Analogously to (4.8), we derive
where \(e_3\) denotes the normal vector pointing in the \(x_3\)-direction. Let us define \({{\bar{R}}}^h:= (Q^h)^{\top } R^h\). The relation
implies together with (i) that
Then, a Poincaré inequality with respect to \(x_3\) yields \(\Vert f \Vert _{L^2(\Omega )}\le C \varepsilon _h \), where
for \(x\in \Omega \). By Jensen’s inequality and the definition in (4.9) we thus get
Then, we find by (4.3) that
As \({{\bar{R}}}^h - \textbf{Id}\) is independent of \(x_3\), for \(i=1,2\) it holds that
Then, due to (i) and (4.11), we have
Hereby, we also control the \(L^2\)-trace of \( {\bar{\Psi }}^h\) on \(\Gamma \). Next, note that also the \(L^2\)-trace of \(\Psi ^h\) scales like \(\varepsilon _h\) as the functions \({\hat{\xi }}_2 /h\) and \(\hat{\xi }_3 /\delta _h\) vanish, due to the fact that \(\int _{-1/2}^{1/2} x_3 \textrm{d}x = 0\), see (2.8). Then, by using (4.10), (4.12), and the trace estimate we get
Using that the norm of each column is equal to 1, we see that the remaining entry \(e_2^{\top }(Q^h- \textbf{Id})e_2\) scales like \(\varepsilon _h^2/\delta _h^2\). This along with (2.12) shows (4.6) and concludes the proof. \(\square \)
We close the section by noting that all consequences of the rigidity estimate derived in [21, Lemmata 3.3, 3.4] also hold in our setting for \(Q^h\) replaced by \(\textbf{Id}\).
5 Properties of the three- and the one-dimensional model
Having presented the abstract theory in Sect. 3, let us now apply this approach to our model. More precisely, we need to verify the assumptions of Theorem 3.2 and Theorem 3.3 in our application. In this section, we collect the relevant properties of the three- and the one-dimensional model and postpone the convergence results to the next section.
5.1 Properties of the three-dimensional model
By Lemma 4.1(i) we see that the SO(3)-valued maps \(R^h\) approximate the scaled gradient at the scaling of the energy, see (2.6). Due to frame indifference, the energy is essentially controlled by the distance of \( (R^h)^{\top } \nabla _h y^h\) from \(\textbf{Id}\). Therefore, we introduce the quantity
Recall the definitions of the energies \(\phi _h\) and the distances \({\mathcal {D}}_h\) in (2.6) and (2.7), as well as the quadratic forms in (2.19). As a consequence of Lemma 4.1, we obtain estimates concerning \(\phi _h\) and \({\mathcal {D}}_h\) and their linearized versions.
Lemma 5.1
(Dissipation and energy) Let h be sufficiently small and \(M>0\). Then, there exists \(C=C(M)>0\) such that for all y, \(y_0\), \(y_1 \in {\mathscr {S}}^{3D}_{h,M}\) and all open subsets \(U \subset \Omega \) we have
-
(i)
\(\left| \int _U D^2(\nabla _h y_0, \nabla _h y_1) \,\textrm{d}x - \int _U Q_D^3 (\nabla _h(y_1-y_0)) \,\textrm{d}x \right| \le C \varepsilon _h^\alpha / \delta _h^{\alpha }\),
-
(ii)
\( \left| {\mathcal {D}}_h(y_0,y_1)^2 - \int _\Omega Q_D^3 (G^h(y_0) - G^h(y_1)) \,\textrm{d}x \right| \le C \varepsilon _h^\alpha / \delta _h^{\alpha } \Vert G^h(y_0)-G^h(y_1)\Vert ^2_{L^2(\Omega )} \le C \varepsilon _h^\alpha / \delta _h^{\alpha }\),
-
(iii)
\(\left| \triangle (y) \right| \le C \varepsilon _h^\alpha / \delta _h^{\alpha }\), where \(\triangle (y):= \frac{1}{\varepsilon _h^2} \int _\Omega W(\nabla _hy ) \,\textrm{d}x - \int _\Omega \frac{1}{2} Q_W^3(G^h(y)) \,\textrm{d}x \),
-
(iv)
\(\left| \triangle (y_0) - \triangle (y_1) \right| \le C \varepsilon _h^\alpha / \delta _h^{\alpha } \Vert G^h(y_0) - G^h(y_1) \Vert _{L^2(\Omega )} \le C \varepsilon _h^\alpha / \delta _h^{\alpha }\).
Proof
The lemma is a variant of [24, Lemma 4.3] with the only difference being that suitable scalings are replaced. For the reader’s convenience we included a proof in Appendix A. \(\square \)
The following lemma provides properties about the topology and lower semicontinuity. In addition, the lemma will help to prove lower semicontinuity of the slopes in Lemma 5.4 and Theorem 6.5.
Lemma 5.2
(Properties of (\({\mathscr {S}}^{3D}_{h,M}, {\mathcal {D}}_h\)) and \(\phi _h\)) Let \(M>0\). For \(h>0\) sufficiently small we have
-
(i)
Completeness: \(({\mathscr {S}}^{3D}_{h,M}, {\mathcal {D}}_h)\) is a complete metric space.
-
(ii)
Compactness: If \((y_n)_n \subset {\mathscr {S}}^{3D}_{h,M}\), then \((y_n)_n\) admits a subsequence converging weakly in \(W^{2,p}(\Omega ;{\mathbb {R}}^3)\) and strongly in \(W^{1,\infty }(\Omega ;{\mathbb {R}}^3)\).
-
(iii)
Topologies: The topology on \({\mathscr {S}}^{3D}_{h,M}\) induced by \({\mathcal {D}}_h\) coincides with the weak \(W^{2,p}(\Omega ;{\mathbb {R}}^3)\) topology.
-
(iv)
Lower semicontinuity: Let \((y_n)_n \subset {\mathscr {S}}^{3D}_{h,M}\) be a sequence such that \({\mathcal {D}}_h(y_n,y) \rightarrow 0\) for some \(y\in {\mathscr {S}}^{3D}_{h,M}\). Then, \(\liminf _{n \rightarrow \infty } \phi _h(y_n) \ge \phi _h(y)\).
-
(v)
Local equivalence of metrics: Define \(\overline{{\mathcal {D}}}_h(y_0,y_1) = \Vert \nabla _h y_0 - \nabla _h y_1 \Vert _{L^2(\Omega )}\) for \(y_0,y_1\in {\mathscr {S}}^{3D}_{h,M}\). Then, there exists \( \kappa _h>0\) such that for all \(y_0,y_1\in {\mathscr {S}}^{3D}_{h,M}\) with \(\Vert \nabla _h y_0 - \nabla _h y_1\Vert _{L^{\infty }(\Omega )} \le \kappa _h\) it holds that
$$\begin{aligned} c_h \overline{{\mathcal {D}}}_h(y_0,y_1) \le {\mathcal {D}}_h(y_0,y_1) \le C_h \overline{{\mathcal {D}}}_h(y_0,y_1) , \end{aligned}$$where \(C_h,c_h >0\) and \( \kappa _h\) depend on h and M.
Here, we remark that the positivity of the metric is quite delicate as D is only a true distance when restricted to symmetric and positive definite matrices. A similar problem arises in the proof of (v) due to the nontrivial kernel of the Hessian of \(D^2\), see Lemma A.1. We follow the strategy devised in [34] to circumvent this problem, by using the following version of Korn’s inequality (see [40, Corollary 4.1] and also [34, Theorem 3.3]), which itself is based on [38].
Theorem 5.3
(Generalized Korn’s inequality) Consider an open, bounded, and connected set \(U \subset {\mathbb {R}}^3\) with Lipschitz boundary. Let \(S \subset \partial U\) be a nonempty open subset. Moreover, let \(\mu >0\) be small and \(\gamma \in (0,1]\). Then there exists a constant \(c = c(U,S,\mu ,\gamma ) >0\) such that for all \(\gamma \)-Hölder continuous \(F :{\overline{U}} \rightarrow {\mathbb {R}}^{3 \times 3}\) with \(\inf _{x\in {{\bar{U}}}}\det F(x) \ge \mu \) and \(\Vert F\Vert _{C^\gamma (U)} \le 1/\mu \) we have
Proof of Lemma 5.2
We first show (v). Consider \(y_0,y_1\in {\mathscr {S}}^{3D}_{h,M}\) and recall the projection \(p_h:\Omega \rightarrow \Omega _h\), \(p_h(x_1,x_2,x_3) = (x_1, hx_2, \delta _h x_3)\). We introduce the variables \(z_i = y_i \circ p_h^{-1}\), \(i =0,1\), as it is convenient to formulate the problem for the original (not rescaled) functions \(z_0\) and \(z_1\) defined on \(\Omega _h\). Then, by Lemma 4.1(v) we can fix \(h>0\) such that \(\nabla z_0\) is contained in a small neighborhood of \(\textbf{Id}\), and thus Lemma A.1 is applicable. Further, consider \( \kappa >0\) and let \(Z:= \nabla z_1 - \nabla z_0\) be such that \(\Vert Z \Vert _{L^\infty (\Omega _h)} \le \kappa \). By a Taylor expansion and Lemma A.1 we find constants \(C,c >0\) such that
pointwise in \(\Omega _h\). We now use Theorem 5.3 applied to \(F:= (\nabla z_0)^{\top }\) and \(u:=z_0 - z_1 \in W^{1,2}(\Omega _h;{\mathbb {R}}^3)\), where the \(\gamma \)-Hölder continuity of F with \(\Vert F \Vert _{C^\gamma (\Omega _h)} \le 1/\mu \) for some \(\gamma \in (0,1]\) and \(\mu >0\) follows by a Sobolev embedding as \(p>3\). Moreover, for \(h>0\) sufficiently small, \(\mu >0\) can be chosen such that \(\inf _{x\in {{\bar{U}}}}\det F(x) \ge \mu \) due to Lemma 4.1(v). As the result is applied on \(\Omega _h\) the corresponding constant is h-dependent, denoted by \(C_h\). Recalling (2.7), we get
Thus, taking \( \kappa >0\) suitably small depending on h, we obtain the lower bound. An easier calculation using that \(\nabla z_0\) is uniformly bounded yields the upper bound.
Concerning (i), the positivity follows by an argument similar to [24, Lemma 4.4]. We include the proof in Lemma A.2 for convenience of the reader. The other properties of a metric space follow directly from (2.3). The properties (ii)–(iv) and the completeness of \(({\mathscr {S}}^{3D}_{h,M}, {\mathcal {D}}_h)\) now follow as in [24, Lemma 4.4]. We omit the proof.
\(\square \)
Lemma 5.4
(Properties of \(\vert \partial \phi _h \vert _{{\mathcal {D}}_h}\)) Let \(M>0\) and consider the complete metric space \(({\mathscr {S}}^{3D}_{h,M}, {\mathcal {D}}_h)\). For \(h>0\) sufficiently small, the local slope \(\vert \partial \phi _h \vert _{{\mathcal {D}}_h}\) is
-
(i)
a strong upper gradient for \(\phi _h\),
-
(ii)
lower semicontinuous with respect to the weak topology in \(W^{2,p}(\Omega ;{\mathbb {R}}^3)\).
Proof
(i) As the local slope is a weak upper gradient in the sense of Definition [7, Definition 1.2.2] by [7, Theorem 1.2.5], we only need to show that for an absolutely continuous curve \(z:(a,b) \rightarrow {\mathscr {S}}^{3D}_{h,M}\) (with respect to \({\mathcal {D}}_h\)) satisfying \(\vert \partial \phi _h\vert _{{\mathcal {D}}_h}(z) \vert z '\vert _{{\mathcal {D}}_h} \in L^1(a,b)\) the curve \(\phi _h \circ z\) is absolutely continuous. It is not restrictive to assume that (a, b) is a bounded interval and that z can be extended by continuity to [a, b]. We first show that z is absolutely continuous with respect to \(\overline{{\mathcal {D}}}_h\). Let \( \kappa _h>0\) be the constant from Lemma 5.2(v). As z([a, b]) is compact, there exists \(m\in {\mathbb {N}}\) and \(s_i\in [a,b]\) for \(i=1,...,m\) such that
This is a cover of open sets with respect to \({\mathcal {D}}_h\) as the topologies induced by \(W^{1,\infty }(\Omega )\) and \({\mathcal {D}}_h\) coincide, see Lemma 5.2(iii). Thus, by Lemma 5.2(v), for all \(s,t\in [a,b]\) with \(s<t\) there exists a partition \(s= {\tilde{s}}_0< {\tilde{s}}_1<... < \tilde{s}_m = t\) satisfying \( \overline{{\mathcal {D}}}_h(z(\tilde{s}_i),z({\tilde{s}}_{i-1})) \le C_h {\mathcal {D}}_h(z(\tilde{s}_i),z({\tilde{s}}_{i-1}))\) which yields
In particular, z is absolutely continuous with respect to \(\overline{{\mathcal {D}}}_h\), see (3.1). In view of Definition 3.1(ii) and (3.2), Lemma 5.2(v) also implies that \(\vert \partial \phi _h\vert _{\overline{{\mathcal {D}}}_h}(z) \vert z '\vert _{\overline{{\mathcal {D}}}_h} \in L^1(a,b)\). It now remains to show that the local slope \(\vert \partial \phi _h \vert _{\overline{{\mathcal {D}}}_h}\) is a strong upper gradient and that \(\vert \partial \phi _h \vert _{\overline{{\mathcal {D}}}_h}\circ z\) is Borel, as then \( \phi _h \circ z\) is indeed absolutely continuous by Definition 3.1(i), as desired. To this end, for small \(h>0\), we observe by [34, Proposition 3.2] that \(\phi _h\) is \(\lambda \)-convex with respect to \(\overline{{\mathcal {D}}}_h\) for some \(\lambda < 0\) depending only on M and h. More precisely, given \(y,w \in {\mathscr {S}}^{3D}_{h,M}\), for the convex combination \(y_s:= (1-s) y + sw\), \( s \in [0,1]\), it holds that
Here, we note that this proposition is applicable as Lemma 4.1(v) implies that
Now, (5.2), Lemma 5.2(iii), and [7, Corollary 2.4.10] ensure that the local slope \(\vert \partial \phi _h \vert _{\overline{{\mathcal {D}}}_h}\) is a strong upper gradient and the measurability of \(\vert \partial \phi _h \vert _{\overline{{\mathcal {D}}}_h}\circ z\).
(ii) We first show that there exist constants \(C_h >0\) and \( \kappa _h>0\) depending on h such that for all \(y,w \in {\mathscr {S}}^{3D}_{h,M}\) satisfying \( \Vert y - w\Vert _{W^{1,\infty }(\Omega )} \le \kappa _h\) the functions \(y_s:= (1-s) y + sw\), \( s \in [0,1]\), satisfy
Indeed, due to the uniform bounds on \(\nabla _h w\) and \(\nabla _h y\) in (4.1)(v), we obtain by a Taylor expansion
Similarly, we get
Combination of the two estimates with the lower bound in Lemma 5.2(v) yields (5.3), provided that \( \kappa _h\) is chosen sufficiently small. Whenever \(y \ne w\) and \( \phi _h(y) - \phi _h(w) + \frac{1}{2} \lambda \overline{{\mathcal {D}}}_h(y,w)^2 >0\) we obtain by (5.2)
With (5.3), for \( \Vert y - w\Vert _{W^{1,\infty }(\Omega )} \le \kappa _h\), this implies
Thus, by taking the limit \(s \rightarrow 0 \) and the supremum, we obtain for any \( \kappa ' \le \kappa _h\)
We also get the reverse inequality
where we used Lemma 5.2(v) and the fact that \(w \rightarrow y\) with respect to \({\mathcal {D}}_h\) implies \(\Vert y - w \Vert _{W^{1,\infty }(\Omega )} \rightarrow 0\), see Lemma 5.2(ii),(iii). We are now ready to confirm the lower semicontinuity. Consider a sequence \((y_n)_n\), \(y_n \in {\mathscr {S}}^{3D}_{h,M}\), converging weakly to \(y \in {\mathscr {S}}^{3D}_{h,M}\) in \(W^{2,p}(\Omega )\) (or equivalently with respect to \({\mathcal {D}}_h\), see Lemma 5.2(iii)). For \(w \ne y\) such that \(\Vert w- y \Vert _{W^{ 1,\infty }(\Omega )} \le \kappa _h/2 \), we have \(w\ne y_n\) and \(\Vert w- y_n \Vert _{W^{ 1,\infty }(\Omega )} \le \kappa _h \) for n large enough, and thus
where we used Lemma 5.2(ii)–(iv), and (5.4) for \( \kappa ' = \kappa _h\). By taking the supremum with respect to w, and using (5.5) for \( \kappa ' = \kappa _h/2\), the lower semicontinuity follows.
\(\square \)
5.2 Properties of the one-dimensional model
We now briefly collect some facts of the one-dimensional model. Recall the definitions of \({\mathscr {S}}^{1D}\), \(\phi _0\), and \({\mathcal {D}}_0\) in (2.18), (2.22), and (2.23).
Lemma 5.5
(Properties of \(({\mathscr {S}}^{1D},{\mathcal {D}}_0)\), \(\phi _0\), and \(\vert \partial {\phi }_0\vert _{{\mathcal {D}}_0}\))
Let \(M>0\), \(\Phi ^1(t):= \sqrt{t^2 + C t^3 + C t^4}\) and \(\Phi _{M}^2(t):= C\sqrt{ M} t^2 + C t^3 + Ct^4\) for any \(C>0\) large enough. Then it holds that
-
(i)
Completeness: \(({\mathscr {S}}^{1D},{\mathcal {D}}_0)\) is a complete metric space.
-
(ii)
Generalized convexity: For all \((u_0, \theta _0) \in {\mathscr {S}}^{1D}\) satisfying \(\phi _0(u_0,\theta _0) \le M\) and all \((u_1, \theta _1) \in {\mathscr {S}}^{1D}\) we have
-
(ii’)
\({\mathcal {D}}_0((u_0,\theta _0),(u_s,\theta _s)) \le s \Phi ^1\big ({\mathcal {D}}_0((u_0,\theta _0),(u_1,\theta _1))\big )\)
-
(ii”)
\(\phi _0(u_s,\theta _s) \le (1-s) \phi _0(u_0,\theta _0) + s \phi _0(u_1,\theta _1) + s \Phi _M^2\big ({\mathcal {D}}_0((u_0,\theta _0),(u_1,\theta _1))\big )\)
for \((u_s,\theta _s):= (1-s) (u_0,\theta _0) + s (u_1,\theta _1)\) and \(s \in [0,1]\).
-
(ii’)
-
(iii)
Characterization of the slope: The local slope for the energy \(\phi _0\) admits the representation
$$\begin{aligned} \vert \partial \phi _0 \vert _{{\mathcal {D}}_0}(u,\theta ) := \sup \limits _{(u,\theta )\ne ({\tilde{u}},{{\tilde{\theta }}})\in {\mathscr {S}}^{1D}} \frac{\big (\phi _0(u,\theta ) - \phi _0 (\tilde{u},{{\tilde{\theta }}}) - \Phi _M^2({\mathcal {D}}_0((u,\theta ),(\tilde{u},{{\tilde{\theta }}})) ) \big )^+}{\Phi ^1\big ({\mathcal {D}}_0((u,\theta ),({\tilde{u}},\tilde{\theta }) )\big )} \end{aligned}$$for all \((u,\theta )\in {\mathscr {S}}^{1D}\) satisfying \(\phi _0(u,\theta ) \le M\).
-
(iv)
Strong upper gradient: The local slope \(\vert \partial \phi _0 \vert _{{\mathcal {D}}_0}\) is a strong upper gradient for \(\phi _0\).
-
(v)
Topology: Representing \((u,\theta )\) as \((\xi _1,\xi _2,\xi _3,\theta )\) by (2.17), the topology on \({\mathscr {S}}^{1D}\) induced by \({\mathcal {D}}_0\) coincides with the topology induced by \(W^{1,2}(I) \times W^{2,2}(I) \times W^{2,2}(I) \times W^{1,2}(I)\).
Proof
The proof for the case \(r=1\) is given in [26], and the arguments for general \(r>0\) remain unchanged. For items (i),(v), see [26, Lemma 4.2], where w coincides with \(\xi _3\) and \(y = (\xi _1 - x_2\xi _2',\xi _2)\), and for (ii) we refer to [26, Lemma A.1]. Finally, (iii) and (iv) are addressed in [26, Lemma 4.3]. The case \(r=0\) is even simpler. In fact, \({\mathcal {D}}_0\) becomes a norm and \(\phi _0\) is \(\lambda \)-convex for some \(\lambda \ge 0 \), and the theorem can be replaced by the prototypical theory [7, Section 2.4]. \(\square \)
6 Passage to the one-dimensional limit
In this section, we relate the three-dimensional model to its limit. We first give the proof of the compactness result in Proposition 2.2. Then, we identify the limiting strain in Lemma 6.1 in order to state the \(\Gamma \)-convergence in Theorem 6.2. Eventually, we provide the properties needed in the present evolutionary setting (see the assumptions of Theorem 3.2). Similarly to the \(\Gamma \)-convergence analysis, we derive the lower semicontinuity of the dissipation distances in Theorem 6.3. Afterwards, we show the major part of our contribution: the lower semicontinuity of the local slopes (Theorem 6.5).
Recall the definitions of \(u^h\) and \(\theta ^h\) in (2.15) and (2.16). We now prove the compactness result stated in Proposition 2.2. The key argument is to prove a \(W^{1,2}(\Omega ;{\mathbb {R}}^3)\)-bound on \(u^h\) with a Korn-Poincaré inequality. Whereas in [21] such an inequality is used for functions satisfying \(\int _\Omega \textrm{skew} (\nabla _h y^h) \, \textrm{d}x = 0\) and \(\int _\Omega y^h \, \textrm{d}x = 0\), we use a suitable version for boundary conditions, see [28, Proposition 1].
Proof of Proposition 2.2
By definition we have
Thus, we can write
Recall the boundary conditions (2.8)
Then, by Korn’s inequality (see [28, Proposition 1, equation (81)]) we find
Therefore, we deduce
As part (iii) of [21, Lemma 3.4] ensures that \(\textrm{sym}( \frac{\nabla _h y^h - \textbf{Id}}{\varepsilon _h})\) is bounded in \(L^2(\Omega ;{\mathbb {R}}^{3 \times 3})\), we get by (6.1) that \(\textrm{sym}(\nabla u^h)\) is bounded in \(L^2(\Omega ;{\mathbb {R}}^{3 \times 3})\). Thus, we can extract a subsequence such that \(u^h \rightharpoonup u\) in \(W^{1,2}(\Omega ;{\mathbb {R}}^3)\) for some \(u \in W^{1,2}(\Omega ;{\mathbb {R}}^3)\). To observe that the convergence of \(u_3^h\) is strong, we multiply both sides of (6.1) by \(\delta _h\) and obtain
An analogous observation and the fact that \(\delta _h/h \rightarrow 0\) yield for \(j=2,3\)
Then, as Lemma 4.1(i)–(iii) imply that \(\frac{1}{\varepsilon _h/\delta _h} (\nabla _h y^h - \textbf{Id}) \) converges strongly in \(L^2(\Omega ;{\mathbb {R}}^{3\times 3})\) (see [21, Lemma 3.4(i)] for a detailed calculation), the previous estimates imply the strong convergence of \(u^h_3\).
To conclude the proof of (i), we need to characterize the limit u. As \(\textrm{sym}(\nabla u^h)\) converges weakly in \(L^2(\Omega ;{\mathbb {R}}^{3\times 3})\), we can infer from (6.1) that u satisfies the identities \(u_{i,j} + u_{j,i} = 0\) for all \(i = 1,2,3\) and \(j = 2,3\). Moreover, from (6.2) we deduce \(u_{3,2} = 0\) and thus also \(u_{2,3} = 0\). By arguing analogously to [12, Theorem 4.1], we see that u is a Bernoulli–Navier function, i.e., \(u \in {\mathcal {A}}^{BN}_{{\hat{\xi }}_1, {\hat{\xi }}_2, {\hat{\xi }}_3}\), see (2.17) for the definition. Here, our choice of the boundary values in (2.8) becomes apparent since it guarantees that the limit of the displacements lies in \({\mathcal {A}}^{BN}_{{\hat{\xi }}_1, {\hat{\xi }}_2, \hat{\xi }_3}\). Indeed, we have \(u^h = {\hat{U}}\) on \(\Gamma \), and therefore also the limit satisfies \(u_1 ={\hat{\xi }}_1 - x_2 \hat{\xi }_2' - x_3 {\hat{\xi }}_3'\), \(u_2 = {\hat{\xi }}_2\), and \(u_3 = \hat{\xi }_3\) on \(\Gamma \).
This concludes the proof of (i). The compactness for \(\theta _h\) is a consequence of [21, Lemma 3.7]. One only needs to observe that \(\theta _h\) satisfies zero boundary conditions on \(\Gamma \) due to (2.8). Therefore, \(\theta \in W^{1,2}_0( I )\). \(\square \)
As observed in the discussion above Eq. (5.1), the energy \(\phi _h(y^h)\) is essentially controlled by \(G^h(y^h)\), which converges weakly to some \(G_y \in L^2(\Omega ;{\mathbb {R}}^{3\times 3})\), due to Lemma 4.1(i). As we want to represent the \(\Gamma \)-limit by the variables u and \(\theta \), we therefore need to characterize the limiting strain \(G_y\) in terms of u and \(\theta \). This is addressed in the next lemma, along with an analysis of the limit behavior of the rotations \(R^h\).
Lemma 6.1
(Identification of the scaled limiting strain) Consider a sequence \((y^h)_h\) with \(y^h\in {\mathscr {S}}^{3D}_{h,M}\) for \(M>0\). Let \((u,\theta ) \in {\mathscr {S}}^{1D}\) be the limit given by Proposition 2.2. Then, there exists \(G_y \in L^2(\Omega ;{\mathbb {R}}^{3 \times 3})\) and \(A_{u,\theta } \in W^{1,2}(\Omega ;{\mathbb {R}}^{3 \times 3})\) such that, up to subsequences,
-
(i)
\( G^h(y^h) \rightharpoonup G_y\) in \(L^2(\Omega ;{\mathbb {R}}^{3 \times 3})\) and we have
$$\begin{aligned}{(G_y)}_{11} (x) = \xi _1'(x_1) - x_2 \xi _2''(x_1) - x_3 \xi _3''(x_1) + \frac{r}{2} (\xi _3'(x_1))^2 \quad \text { for a.e. } \ x\in \Omega , \end{aligned}$$as well as
$$\begin{aligned} \frac{1}{2} \big ({(G_y)}_{12} + {(G_y)}_{21}\big )(x) = -x_3 \theta '(x_1) + {\tilde{g}}(x_1,x_2) \quad \text { for a.e. } \ x\in \Omega \end{aligned}$$for a suitable function \({\tilde{g}} \in L^2( S )\), where \((\xi _1,\xi _2,\xi _3)\) are related to u by (2.17).
-
(ii)
\(\frac{R^h - \textbf{Id}}{\varepsilon _h/\delta _h} \rightharpoonup A_{u,\theta }\) in \(W^{1,2}(S;{\mathbb {R}}^{3\times 3}) \quad \) and \( \quad \textrm{sym}\left( \frac{R^h - \textbf{Id}}{\varepsilon _h} \right) \rightarrow \frac{r}{2} A_{u,\theta }^2\) in \(L^2(S;{\mathbb {R}}^{3\times 3}),\)where \(A_{u,\theta } = e_3 \otimes p - p \otimes e_3\) for \(p = (\xi _3',\theta ,0)\).
For later purposes, we note that \(A_{u,\theta }^2\) is given by
Proof
We omit a detailed proof as the statement is essentially proven in [21, Lemma 3.3 and 3.7]. The adaptions are straightforward: the existence of \(G_y\) follows immediately by Lemma 4.1(i). By using the rigidity estimates from Lemma 4.1, one can show part (i) analogously to the proof of [21, Lemma 3.7]. Whereas the convergence of \(\frac{R^h - \textbf{Id}}{\varepsilon _h/\delta _h}\) and \( \textrm{sym}\left( \frac{R^h - \textbf{Id}}{\varepsilon _h} \right) \) is addressed in [21, Lemma 3.3], for a skew-symmetric valued limiting tensor field \(A_{u,\theta }\) (use also (2.12)), the characterization of \(A_{u,\theta }\) is provided in the statement and part ii of the proof of [21, Lemma 3.7]. (Below [21, equation (37)] we find \(A_{12} = 0\) and \(A_{13} = u_{1,3} = - \xi _3'\), where we also use (2.17).) \(\square \)
We now state the \(\Gamma \)-convergence result, based on [21, Theorems 3.11 and 3.14]. To this end, recall the definition of the energies and the metrics in (2.6), (2.7) and (2.22), (2.23), and the topology of convergence in Proposition 2.2, which is denoted with the symbols \(\pi \sigma \) and \(\pi \rho \), see Subsection 2.5.
Theorem 6.2
(\(\Gamma \)-convergence of energies) \(\phi _\varepsilon \) converges to \(\phi _0\) in the sense of \(\Gamma \)-convergence. More precisely:
(i) (Lower bound) For all \((u,\theta ) \in {{\mathscr {S}}^{1D}}\) and all sequences \((y^h)_h\) such that \(y^h {\mathop {\rightarrow }\limits ^{\pi \sigma }} (u,\theta )\) we find
(ii) (Optimality of lower bound) For all \((u,\theta ) \in {{\mathscr {S}}^{1D}}\) there exists a sequence \((y^h)_h\), \(y^h \in {\mathscr {S}}_h^{3D}\) for all \(h > 0\), such that \(y^h {\mathop {\rightarrow }\limits ^{\pi \rho }} (u,\theta )\) and
By minor adaptions to our setting, the proof follows from the one in [21]. The main differences are that the second-order penalization should vanish in the limit, and that the recovery sequence should be compatible with the boundary conditions in (2.8). In our contribution, the proof of (i) is even simpler as the second-order perturbation provides a quantitative estimate concerning the deviation between the nonlinear and linearized energy, see Lemma 5.1(iii). We include the proof of (i) for convenience. For (ii), we refer to its ansatz in (A) and Remark 6.7 as it can be viewed as a corollary of the proof of Theorem 6.5.
Proof of Theorem 6.2 (i) We may suppose that \(\liminf _{h \rightarrow 0 } \phi _h(y^h) < +\infty \) as otherwise there is nothing to prove. Thus, we can assume that \(y^h \in {\mathscr {S}}^{3D}_{h,M}\) for \(M>0\) large enough. By Lemma 5.1(iii) we have
Then, the convexity of the quadratic form \(Q_W^3\), (2.20), and Lemma 6.1(i) imply
for a suitable function \({\tilde{g}} \in L^2( S )\). By a binomial expansion, Fubini’s theorem, and again by (2.20), we derive
The lower bound follows as the second-order perturbation is a nonnegative term, see (2.2). \(\square \)
The force terms in (2.6) and (2.22) represent continuous perturbations of the energies. More precisely, (2.15), strong \(L^2(\Omega )\)-convergence of \(u_3^h\), and weak \(L^2(I)\)-convergence of \(\frac{1}{\varepsilon _h\delta _h} f^{3D}_h\), see (2.14), yield
Before commenting on the ansatz of (ii), we also collect the corresponding result for the dissipation distances.
Theorem 6.3
(Lower semicontinuity of dissipation distances) Let \(M>0\). Then, for sequences \((y^h)_h\) and \(({\tilde{y}}^h)_h\), \(y^h,{\tilde{y}}^h \in {\mathscr {S}}^{3D}_{h,M}\), with \(y^h {\mathop {\rightarrow }\limits ^{\pi \sigma }} (u,\theta )\) and \({\tilde{y}}^h {\mathop {\rightarrow }\limits ^{\pi \sigma }} ({\tilde{u}},{{\tilde{\theta }}})\) we have
Proof
One can follow the lines of the proof of Theorem 6.2(i), with the only difference being that we use the quadratic forms \(Q_D^3\) instead of \(Q_W^3\) and Lemma 5.1(ii) instead of Lemma 5.1(iii). \(\square \)
We now discuss the ansatz for the recovery sequence, based on [21]. By a general approximation argument for \(\Gamma \)-convergence, it suffices to prove the upper bound on a dense subset. To this end, we use the following lemma.
Lemma 6.4
(Density of smooth functions with same boundary conditions) For each \( u \in {\mathcal {A}}^{BN}_{{\hat{\xi }}_1, {\hat{\xi }}_2, {\hat{\xi }}_3} \) represented by \((\xi _1,\xi _2,\xi _3)\) we find sequences \((\xi _{1,\Lambda })_\Lambda \subset W^{2,p}(I)\) and \((\xi _{i,\Lambda })_\Lambda \subset W^{3,p}(I)\), \(i=2,3\), such that
-
(i)
\(\xi _{1,\Lambda } = \hat{\xi }_1,\quad \) \( \xi _{i,\Lambda } = \hat{\xi }_i,\quad \) \(\xi _{i,\Lambda }' = \hat{\xi }_i'\quad \) on \( \partial I\quad \quad \,\) for \( i = 2,3\),
-
(ii)
\(\xi _{1,\Lambda } \rightarrow \xi _1 \) in \(W^{1,2}(I),\quad \) \(\xi _{i,\Lambda } \rightarrow \xi _i \ \ \ \ \) in \(W^{2,2}(I)\) for \(i = 2,3\) as \(\Lambda \rightarrow 0\).
Proof
The proof is standard. We approximate \(\xi _i-\hat{\xi _i}\), \(i =1,2,3\), by smooth functions with compact support in I and add \({\hat{\xi }}_1 \in W^{2,p}(I)\), \({\hat{\xi }}_i \in W^{3,p}(I)\), \(i =2,3\), respectively. \(\square \)
Consider \((u,\theta ) \in {\mathscr {S}}^{1D}\) with \(\theta \in C_c^\infty (I)\) and u having the regularity in Lemma 6.4, i.e., u is represented by \((\xi _1,\xi _2,\xi _3)\) with \(\xi _1 \in W^{2,p}(I)\) and \(\xi _i \in W^{3,p}(I)\), \(i=2,3\). As \(\phi _0\) is continuous with respect to the convergence in Lemma 6.4 and \(W^{1,2}(I)\)-convergence for \(\theta \), by a diagonal argument, it suffices to define recovery sequences for such functions.
We proceed as follows. First, we find approximations \( \xi _{3,h}' \in C_c^\infty (I)\) such that \( \xi _{3,h}' \rightarrow \xi _3'\) in \(L^4(I)\) as \(h \rightarrow 0\). Moreover, by passing to a subsequence we can control the speed of convergence of the derivatives, and thus we find
The ansatz is given by

where
and r is given by (2.12). By construction the function \(\beta ^h\) attains zero boundary values. Therefore, the choice of the sequence is in compliance with the boundary conditions in (2.8) as \(\theta \in C_c^\infty (I)\). Thus we have \(y^h \in {\mathscr {S}}_h^{3D}\). Then, for later purposes, we note that the scaled gradient is given by
where
and
At this point, we remark that the perturbation \(\beta ^h\) is essential to handle the involved relaxation of the quadratic forms, see (2.20).
We will not prove Theorem 6.2(ii) as it can be seen as corollary of the proof of Theorem 6.5, see Remark 6.7. We only show that the second-order perturbation vanishes in the limit. For this purpose, we recall that the scaled Hessian \(\nabla _h^2 y^h\) is defined by \((\nabla _h^2y)_{ijk}:= h^{-\delta _{2j}-\delta _{2k}}\delta _h^{-\delta _{3j} - \delta _{3k}} (\nabla ^2 y_i)_{jk}\) for \(i,j,k \in \{1,2,3\}\). Now, a computation yields that \( \Vert \nabla _h^2 \beta ^h \Vert _{L^p(\Omega )} \le C (\Vert {\xi }_{3,h} \Vert _{W^{3,\infty }(\Omega )} + \Vert \theta \Vert _{W^{2,\infty }(\Omega )})^{2} \). Thus, by (6.6), by the fact that \(\delta _h/h \rightarrow 0\), and a similar computation for the matrix \(M^h\) we see
With (2.2) this implies
and the second-order perturbation converges to zero by (2.13).
The remaining part of the section is dedicated to the proof of the weak lower semicontinuity of the local slopes.
Theorem 6.5
(Lower semicontinuity of slopes) For each sequence \((y^h)_h\) with \(y^h \in {\mathscr {S}}^{3D}_{h,M}\) such that \(y^h {\mathop {\rightarrow }\limits ^{\pi \sigma }} (u,\theta )\) we have
The proof is technical and the main difficulty of this paper. As a first intuition, we observe that it does not suffice to use the \(\Gamma \)-convergence results as in Lemma 5.5(iii) metrics appear in the denominator and energies are subtracted in the enumerator. Therefore, we construct a suitable competitor sequence \((y^h+z_s^h)_h\), perturbing the deformations \((y^h)_h\) with sufficiently small strains \((z_s^h)_h\), such that the difference of the quantities \(G^h(y^h)\) and \(G^h(y^h + z^h_{ s})\) converges strongly in \(L^2(\Omega )\) with linear control in s (weak convergence is already guaranteed). This property is ensured by the following lemma.
Lemma 6.6
(Strong convergence of strain differences) Let \(M>0\). Let \((y^h)_h\) be a sequence with \(y^h \in {\mathscr {S}}^{3D}_{h,M}\) and let \((z^h_s)_{s,h} \subset W^{2,p}(\Omega ;{\mathbb {R}}^3)\), \(h>0\), \(s \in (0,1)\), be functions with \(z^h_s = 0 \) on \(\Gamma \) such that
Then the following holds for a subsequence of \((y^h)_h\) (not relabeled):
(a) For all h sufficiently small, \(w^h_s:= y^h + z^h_s\) lies in \({\mathscr {S}}^{3D}_{h,M'}\) for some \(M' = M'(M)>0\).
(b) Let \((G^h(y^h))_h\), \((G^h(w^h_s))_h\) be the sequences in Lemma 6.1 and let \(G_y\), \(G^s_w\) be their limits. Then, there exist \(C=C(M)>0\) and \(\rho (h)\) with \(\rho (h)\rightarrow 0\) as \(h \rightarrow 0\) such that
(c) Let \(A_{ \hat{u}_s,\hat{\theta }_s } \) and \( A_{u,\theta }\) be the limits as given in Lemma 6.1 (ii), where \((u,\theta )\) and \(( \hat{u}_s,\hat{\theta }_s )\) are the limits in the sense of Proposition 2.2 corresponding to \(y^h\) and \(w^h_s\), respectively. Then, it holds that
Proof
Let \(R(y^h)\) be the SO(3)-valued mappings given by Lemma 4.1. For brevity, we introduce notations for the symmetric and skew-symmetric part of \(\nabla _h z^h_s\) by

The crucial point is to find a suitable SO(3)-valued mapping \(R(w^h_s)\) associated to \(w^h_s = y^h + z^h_s\) depending only on \(x_1\) and \(x_2\) and satisfying the properties stated in Lemma 4.1 (Step 1). Once \(R(w^h_s)\) has been defined, we can prove properties (a)–(c) (Step 2).
Step 1: Definition of \(R(w^h_s)\). We first define

on S. By Lemma 4.1(ii), \(p>2\), and (6.10)(i), we can check that \( \tilde{R}^h \) is in a small tubular neighborhood of SO(3) and satisfies \(\Vert \tilde{R}^h_{,1} \Vert _{L^2(S)} \le C\varepsilon _h/\delta _h\) and \(\Vert \tilde{R}^h_{,2} \Vert _{L^2(S)} \le C\varepsilon _hh/\delta _h\). We let \(R(w^h_s)\) be the map obtained from \(\tilde{R}^h\) by nearest-point projection onto SO(3), see the proof of [20, Theorem 3.2 and Lemma 3.3] and (4.2) for a similar argument. We now check that \(R(w^h_s)\) satisfies the properties stated in Lemma 4.1. By the regularity of the projection, it holds that \(R(w^h_s) \in W^{1,2}(S;SO(3))\). By (6.10)(i) and  for all \((x_1,x_2) \in S\), it follows that
for all \((x_1,x_2) \in S\), it follows that

Indeed, this follows from the fact that \(|((\textbf{Id}+ A -\frac{1}{2}A^\top A)^\top (\textbf{Id}+ A -\frac{1}{2}A^\top A))^{ 1/2 } - \textbf{Id}| \le C|A|^3\) for all \(A \in {\mathbb {R}}^{3 \times 3}_{\textrm{skew}}\) and a Polar decomposition. Along with (6.10)(iii) we thus get
for \(\gamma _h:= \max \{ h^{1/2}, \varepsilon _h^2/\delta _h^3 \} \), which is an infinitesimal sequence due to (2.12). First, \(\Vert {R(w_s^h)}_{,1} \Vert ^2_{L^2(S)} \le C\varepsilon _h/\delta _h\) and \(\Vert {R(w_s^h)}_{,2} \Vert ^2_{L^2(S)} \le C\varepsilon _hh/\delta _h\) by the chain rule as the gradient of the projection is uniformly bounded on a compact neighbourhood of SO(3). Moreover, (6.10)(i), (6.12), and the fact that \(R(y^h)\) satisfies (4.1)(iii) shows that \(\Vert R(w^h_s) -\textbf{Id}\Vert _{L^2(S)}\le C \varepsilon _h/\delta _h\). In a similar fashion, (4.1)(vi) and \(\alpha <1\) yield \(\Vert R(w^h_s) -\textbf{Id}\Vert _{L^\infty (S)}\le C(\varepsilon _h /\delta _h)^{\alpha }\). It thus remains to check (4.1)(i), i.e., that
holds. For notational convenience, we denote by \(\omega ^h_i \in L^2(\Omega ;{\mathbb {R}}^{3 \times 3})\), \(i \in {\mathbb {N}}\), (generic) matrix valued functions whose \(L^2\)-norm is controlled in terms of a constant independent of h and s. By (4.1)(v) (applied for \(y^h\)), (6.10)(i), and (6.12) we find
We now consider the asymptotic expansion of \(R(y^h)^\top (\nabla _h y^h + \nabla _h z^h_s)\) in terms of h: in view of (6.10)(ii), \(\nabla _h z^h_s = E(z^h_s) + F(z^h_s)\), and \(\Vert R(y^h) - \textbf{Id}\Vert _{L^\infty (\Omega )} \le C(\varepsilon _h/\delta _h)^\alpha \) (see (4.1)(vi)) we find
In a similar fashion, by using (4.1)(i),(iii) (for \(y^h\)) and (6.10)(i),(ii), we compute
as well as
By inserting these three estimates into (6.14) and using (6.10)(i) we find
where in the last step we used \( F(z^h_s)^\top + F(z^h_s) = 0\) and (2.12). We now check that (6.13) holds. Indeed, it suffices to use (2.12), (6.15), (6.10)(i),(ii), \(\omega _6^h \in L^2(\Omega ;{\mathbb {R}}^{3\times 3})\), and the fact that (4.1)(i),(iii) hold for \(y^h\). In conclusion, this implies that the mapping \(R(w^h_s)\) satisfies the properties stated in Lemma 4.1.
Step 2: Proof of the statement. We are now in a position to prove the statement.
(a) By (4.1)(v) and (6.10)(i), \(\nabla _h w^h_s\) is in a neighborhood of \(\textbf{Id}\). Thus, by (2.1)(iii) it holds that \(\int _\Omega W(\nabla _h w^h_s) \, \textrm{d}x \le C\int _\Omega {\text {dist}}^2(\nabla _h w^h_s,SO(3)) \, \textrm{d}x \), and then by (6.13) we get \(\int _\Omega W(\nabla _h w^h_s) \, \textrm{d}x \le M' \varepsilon _h^2\) for some \(M'\) sufficiently large (depending on M). Moreover, from (2.2)(iii) and the triangle inequality we get \(P(\nabla ^2_h w^h_s) \le CP(\nabla ^2_h y^h) + CP(\nabla ^2_h z^h_s)\). Therefore, by possibly passing to a larger \(M'\), we obtain \( \zeta _h/\varepsilon _h^{-2} \int _\Omega P(\nabla ^2_h w^h_s) \, \textrm{d}x \le M'\) by (2.13), (2.2)(iii), (6.10)(i), and the fact that \(y^h \in {\mathscr {S}}_{h,M}^{3D}\). Summarizing, since \(z^h_s \in W^{2,p}(\Omega ;{\mathbb {R}}^3)\) with \(z^h_s = 0\) on \(\Gamma \) and thus \(w^h_s\) also satisfies the boundary conditions (2.8), we have shown that \(w^h_s \in {\mathscr {S}}_{h,M'}^{3D}\) for some \(M'=M'(M)>0\) independent of h. In particular, this implies that the statement of Lemma 4.1 holds for \(w^h_s\) with \(R(w^h_s)\) as defined in Step 1.
(b) By \((u,\theta )\) we denote the limit corresponding to \(y^h\) as given in Proposition 2.2. Recalling the definition \(G^h(y^h) = \varepsilon _h^{-1}(R(y^h)^\top \nabla _h y^h -\textbf{Id})\) we find by Lemma 6.1(ii), (6.10)(i),(iv), (2.12), and (6.15) that
where \({\rho }(h) \rightarrow 0\) as \(\rho \rightarrow 0\). By \(G^s_w\) and \(G_y\) we denote the weak \(L^2\)-limits of \(G^h(w^h_s)\) and \(G^h(y^h)\), respectively, which exist by Lemma 6.1. Then (6.16) implies
and the first part of (b) holds. The second part of (b) is a consequence of (4.1) (iii) (for \(y^h\)), (6.10)(i),(ii), (6.15), (2.12), and the fact that \(\omega ^h_6 \in L^2(\Omega ;{\mathbb {R}}^{3 \times 3})\).
(c) By \(( \hat{u}_s,\hat{\theta }_s )\) we denote the limit corresponding to \(w^h_s\), resulting from Proposition 2.2. By Lemma 6.1(ii) (for \(w^h_s\) and \(y^h\), respectively), (6.10)(i),(iv), and (6.12) we observe that pointwise a.e. in \(\Omega \) it holds that
Then by (6.17) and an expansion we get
where in the last step we used that \(A_{u,\theta } \in {\mathbb {R}}^{3 \times 3}_{\textrm{skew}}\) pointwise a.e. in \(\Omega \) and thus \(A_{u,\theta }^\top A_{u,\theta } = -(A_{u,\theta })^2\). \(\square \)
Finally, we are ready to prove Theorem 6.5.
Proof of Theorem 6.5
The proof is divided into several steps. We first define approximations of \((\xi _1,\xi _2,\xi _3,\theta )\) which allow us to work with more regular functions (Step 1). We then construct competitor sequences \((w^h_s)_{h,s}\) for the local slope in the 3D setting satisfying \(w^h_s \rightarrow y^h\) as \(s \rightarrow 0\) (Step 2). Afterwards, we identify the limiting strain of the sequences \((w^h_s)_h\) (Step 3), and we prove the lower semicontinuity (Step 4). Some technical estimates are contained in Steps 5–7.
Step 1: Approximation. By Lemma 6.4, for \(\Lambda >0\) we can fix \(\xi _{1,\Lambda } \in W_{{\hat{\xi }}_1}^{1,2}(I) \cap W^{2,p}(I)\), \(\xi _{2,\Lambda } \in W_{{\hat{\xi }}_2}^{2,2}(I)\cap W^{3,p}(I)\), \(\xi _{3,\Lambda } \in W_{{\hat{\xi }}_3}^{2,2}(I) \cap W^{3,p}(I)\) and \(\theta _\Lambda \in C_c^\infty (I)\) with
This approximation will be necessary to construct sufficiently regular competitor sequences for the local slope of the 3D setting. We denote the approximation by \((u_\Lambda ,\theta _\Lambda )\in {\mathscr {S}}^{1D}\). We further fix \( ({\tilde{u}}, {{\tilde{\theta }}}) \in {\mathscr {S}}^{1D}\), \((\tilde{u},\tilde{\theta })\ne (u,\theta ),(u_\Lambda ,\theta _\Lambda )\), satisfying the same regularity as \((u_\Lambda ,\theta _\Lambda )\). The tuple \((\tilde{u},{{\tilde{\theta }}} )\) will represent the competitor in the local slope of the 1D setting, see Lemma 5.5(iii). Below in (6.33), we will see that by approximation it is enough to work with functions of this regularity. The convex combinations
will be the starting point for the construction of competitor sequences \((w^h_s)_{h,s}\) for the 3D setting. In the following, \(\tilde{C}, C_\Lambda \) denote generic constants which may vary from line to line, where \(\tilde{C}\) may depend on \(\tilde{u},u,{\tilde{\theta }},\theta \), and \(C_\Lambda \) additionally on \(\Lambda \).
Step 2: Construction of competitor sequences \((w^h_s)_{h,s}\). Define \(y^h_\Lambda \) and \(\tilde{y}^h_s\) as in (A) by using the functions \((u_\Lambda ,\theta _\Lambda )\) and \(({\tilde{u}}_s,{{\tilde{\theta }}}_s)\), respectively. In view of (6.6) and (6.19), this can be done in such a way that it holds
where \({\tilde{\xi }}'_{3,s,h}\) and \({\xi }'_{3,\Lambda ,h}\) denote the approximations in (6.6). We observe that \(y^h_\Lambda , \tilde{y}^h_s\) satisfy the boundary conditions, i.e., \({z}^h_s:= \tilde{y}_s^h -y_\Lambda ^h \in W^{2,p}(\Omega ;{\mathbb {R}}^3)\) with \({z}^h_s = 0\) on \(\Gamma \). For \(h>0\) small and \(s \in [0,1]\), we define
By the fact that \((\tilde{u}_s-u_\Lambda , {\tilde{\theta }}_s-\theta _\Lambda )= s(\tilde{u}-u_\Lambda , {\tilde{\theta }}-\theta _\Lambda )\), (6.7)–(6.8), and that \(\delta _h/h \rightarrow 0\), we see
This shows that the assumptions (6.10)(i)–(iii) are satisfied for \((z^h_s)_{s,h}\) (for a constant \(M=M(C_\Lambda )\)). From (6.7) and (6.20) we also get that (6.10)(iv) holds for suitable \(E^s\) and \(F^s\). In particular, by definition we observe \( E^s \, = \lim _{h\rightarrow 0} \frac{1}{\varepsilon _h}\textrm{sym}(\nabla _hz^h_s) \,\)
a.e. in \(\Omega \). Then Lemma 6.6(a) implies \(w^h_s \in {\mathscr {S}}^{3D}_{h,M'}\) for a constant \(M'>0\) sufficiently large depending on \(\Lambda \), but independent of s, h. By Lemma 5.2(ii), there exists a subsequence of \((w^h_s)_s\) converging weakly in \(W^{2,p}(\Omega )\). But by (6.19) and (A) we see that \(z_s^h \rightarrow 0\) strongly in \(L^2(\Omega )\) as \(s \rightarrow 0\) and thus by (6.21) we get that \(w_s^h\rightarrow y^h\) strongly in \(L^2(\Omega )\) as \(s \rightarrow 0\). As the limits are unique, we obtain
Step 3: Identification of limiting strains. Since the ansatz for \((y_\Lambda ^h)_h\) and \((\tilde{y}_s^h)_h\) is compatible with the convergence results in Proposition 2.2 and Lemma 6.1, the scaled displacement fields corresponding to \((y_\Lambda ^h)_h\) and \((\tilde{y}_s^h)_h\) converge to \((u_\Lambda ,\theta _\Lambda )\) and \((\tilde{u}_{s}, {\tilde{\theta }}_{s})\), respectively. Thus, in view of (6.21), the scaled displacement fields corresponding to \(w^h_s\) converge to \( (\hat{u}_{s}^\Lambda , \hat{\theta }_{s}^\Lambda ):= (u - u_\Lambda + \tilde{u}_{s}, \theta - \theta _\Lambda + {\tilde{\theta }}_{s})\). By (6.19), this can be rewritten as
The limits of the mappings \(G^h(y^h)\) and \(G^h(w^h_s)\) given by Lemma 6.1 are denoted by \(G_y\) and \(G^s_w\), i.e, we have (up to a subsequence)
Above we have checked that the assumptions (6.10) hold for \((z^h_s)_{s,h}\). We can therefore use Lemma 6.6(b) and obtain
where \(\rho _\Lambda (h)\) depends on \(\Lambda \) and satisfies \(\rho _\Lambda (h) \rightarrow 0\) as \(h \rightarrow 0\). The representations in (6.23) and (6.11) fully characterize \(\textrm{sym}(G_w^s- G_y)\). Especially, in view of (6.3), (6.19), (6.23), and (6.25), elementary computations lead to
and, after a long and tedious, but elementary computation,
where the variables were identified via (2.17). In similar fashion, we find by (6.3), (6.11), and (6.23)
Moreover, by recalling (6.25) we compute
where the brackets denote the Euclidean scalar product. Thus, we find by Hölder’s inequality, (6.18), and (6.30)
for \(i,j = 2\) and \(i = 3\), \(j=1,2,3\).
Step 4: Lower semicontinuity of slopes. We will show that there exist a continuous function \(\eta _\Lambda :[0,\infty ) \rightarrow [0,\infty )\) with \(\eta _\Lambda (0) = 0\) and a constant \(\tilde{C}\) depending on \(u,\theta ,\tilde{u},{\tilde{\theta }}\) such that for all \(s \in [0,1]\) it holds that
We defer the proof of (6.32) to Steps 5–7 below and now prove the lower semicontinuity. Recall the definition of \(\phi _h\) in (2.6). By combining the three estimates in (6.32) we obtain for all \(s \in [0,1]\)
Recall that \(y^h \in {\mathscr {S}}^{3D}_{h,M}\) and Theorem 6.2(i) imply that \(\phi _0(u,\theta ) \le M\). By applying Lemma 5.5(ii) with \((u_0,\theta _0) = (u,\theta )\) and \((u_1,\theta _1) = \big (\hat{u}_{1}^\Lambda ,\hat{\theta }_{1}^\Lambda )\) we get
Thus, in view of (6.24), Lemma 5.2(iii), and Definition 3.1, we find by letting \(s \rightarrow 0\)
Letting \(h \rightarrow 0\) we then derive
We observe that the limits of \(\hat{u}_{1}^\Lambda \) and \(\hat{\theta }_{1}^\Lambda \) are given by \(\tilde{u}\) and \( {\tilde{\theta }}\), respectively, as \(\Lambda \rightarrow 0\), see (6.18) and (6.25). Thus, letting \(\Lambda \rightarrow 0\) and using the continuity of \(\phi _0\) and \({\mathcal {D}}_0\) with respect to the convergence in (6.18), and then taking the supremum with respect to \((\tilde{u},{\tilde{\theta }})\) we get
where \( {{\mathscr {S}}^{1D}_{\textrm{reg}}} \subset {\mathscr {S}}^{1D}\) denotes the subset consisting of functions \((u,\theta )\) identified with \((\xi _1,\xi _2,\xi _3)\) via (2.17) with regularity \(W^{2,p}(I) \times W^{3,p}(I;{\mathbb {R}}^2) \times C_c^\infty (I)\). Since each \((\tilde{u},{\tilde{\theta }}) \in {\mathscr {S}}^{1D}\) can be approximated in \(W^{1,2}(\Omega ) \times W^{2,2}(I;{\mathbb {R}}^2) \times W^{1,2}(I)\) by a sequence of functions in \({{\mathscr {S}}^{1D}_{\textrm{reg}}}\) (see Lemma 6.4 and (2.17)) and the right-hand side is continuous with respect to that convergence, the previous inequality also holds for \({\mathscr {S}}^{1D}\) instead of \({{\mathscr {S}}^{1D}_{\textrm{reg}}}\). The representation given in Lemma 5.5(iii) then implies
To conclude the proof, it therefore remains to show (6.32).
Step 5: Proof of (6.32)(i). By using Lemma 5.1(ii) and (6.27) we get
Here, the last step follows from the fact that \(Q_D^3(F) = Q_D^3(\textrm{sym}(F))\) for \(F \in {\mathbb {R}}^{3 \times 3}\), see Lemma A.1. Now, the compatibility condition (H) comes into play. It implies together with (6.31) that
In view of (6.28), the representation in (2.17), and quadratic expansions we get (omitting \(\textrm{d}x \) for convenience)
In a similar fashion, (6.29), quadratic expansions, Hölder’s inequality, and (6.18) yield
Then, by (H) and the definition of the metric in (2.23) we get
This combined with (6.34) concludes the proof of (6.32)(i).
Step 6: Proof of (6.32)(ii). In this step, we will frequently use the elementary expansion
for all \(a,b \in {\mathbb {R}}^d\), where \(Q:{\mathbb {R}}^d\rightarrow {\mathbb {R}}\) is a quadratic form with associated bilinear form \({{\mathbb {C}}}\). First, by the first inequality in Lemma 5.1(iv) and (6.27)(ii) we get
Recall the definition of \({{\mathbb {C}}}_W^3\) in Sect. 2.3. Then, the triangle inequality, the weak convergence \(G^h(y^h) \rightharpoonup G_y\) in \(L^2(\Omega ;{\mathbb {R}}^{3 \times 3})\), see (6.26), with \(s^{-1}(G_w^s-G_y)\) as a test function, and (6.27)(i) combined with Hölder’s inequality yield
for some \({\tilde{\rho }}_\Lambda (h)\), satisfying \({\tilde{\rho }}_\Lambda (h) \rightarrow 0\) as \(h \rightarrow 0\). Similarly, (6.35) and (6.27)(i) provide the estimate
Thus, in view of (6.35), (6.37), and (6.38) we get
Using (6.31), (H) and the fact that \(Q_W^3(F) = Q_W^3(\textrm{sym}(F))\) yields
where the last equality follows from (6.35). Moreover, by Lemma 6.1(i), (6.11), (6.28), and (6.29) it holds that
a.e. in \(\Omega \) and
a.e. in \(\Omega \), where we note that \({\tilde{g}} \in L^2( S )\) is the same function as in identity
By expansions similar to Step 5, in particular by exploiting the structure of the quadratic form in (H), we derive the estimates
where for the second estimate we again used (6.18). Eventually, (6.36), (6.39), (6.40), and (6.41) lead to (6.32)(ii).
Step 7: Proof of (6.32)(iii). By convexity of P and the definition \(w^h_s = y^h - y^h_\Lambda + \tilde{y}^h_s\), see (6.21), we find
By Hölder’s inequality and (2.2)(iii) we get
Using \(\phi _h(w^h_s) \le M'\) since \(w^h_s \in {\mathscr {S}}^{M'}_h\) (see Lemma 6.6(a)) and (6.22)(i) we then derive
where \(C_\Lambda \) depends also on \(M'\). By (6.42) and (2.13) we finally get that (6.32)(iii) holds. \(\square \)
Remark 6.7
Step 6 of the proof of Theorem 6.5 ensures the existence of a recovery sequence in Theorem 6.2(ii). Consider \(({\tilde{u}}, {{\tilde{\theta }}}) \in {\mathscr {S}}^{1D}\) and set \(s=1\), \(y^h = y_\Lambda ^h = (x_1,h x_2, \delta _h x_3)^T\), and \((u,\theta ) = 0\) in the proof above, where it suffices that boundary conditions are satisfied for the recovery sequence \((w^h_1)_h\) but not for the other functions. Then, (6.32)(ii),(iii) are even simpler and we obtain
Remark 6.8
(Vanishing dissipation effect) A potential extension for thin materials with general Poisson ratio is to consider a vanishing dissipation effect in the \(x_2\)- and \(x_3\)-direction. A possible modeling choice is the dissipation potential \(R(F,\dot{F}) = \frac{1}{2} \vert A_h (F^{\top } \dot{F} + \dot{F}^{\top } F) \vert ^2\), where \(A_h^2\) a positive definite, symmetric matrix satisfying \(F: A_h^2 F = a_{11} F_{11}^2 + a_{12} F_{12}^2 + o(1) \). Taking (2.4) into account, an associated dissipation distance satisfying (2.3) is given by \(D(F_1,F_2):= \vert A_h(F_1^{\top }F_1) - A_h(F_2^{\top }F_2) \vert \). From a mathematical point of view, this allows us to relax the restrictions for the elastic potential, more precisely, the conditions on \(Q_W^3\) in (H). The crucial part is to ensure that the competitor \(w_s^h\) in the proof Theorem 6.5 still satisfies (6.32). By construction of the quadratic forms in (2.19), there holds \(Q_R^3(F) = \vert A_h \textrm{sym}(F)\vert ^2\) and thus \(\lim _{h \rightarrow 0} Q_R^3(F) = Q_{R}^1(F_{11},F_{12} )\). In particular, it is simpler to verify (6.32)(i). On the other hand, its harder to ensure (6.32)(ii). For this purpose, one would need to employ the (slightly more general) recovery sequence from the purely static setting in [21]. Note that we still need to require the compatibility condition \(\mathop {\textrm{arg min}}_{z \in {\mathbb {R}}} Q_S^1(q_{11},z) = 0 \). We do not provide rigorous proofs for this setting, but refer to [26, Subsection 2.3] where such a model has been discussed in a related two-dimensional setting, and proofs have been provided (see [26, Lemma 5.3, Remark 5.5(b)]).
7 Proof of the main theorems
In this section, we prove the main results.
Proof of Proposition 2.1
(i) is guaranteed by the direct method of the Calculus of Variations. Indeed, let \(Y_{h,\tau _k}^{n-1}\), \(n \ge 1\) be given. Then, the coercivity of \(\Phi _h(\tau _k, Y_{h,\tau _k}^{n-1},\cdot )\) with respect to the weak \(W^{2,p}(\Omega ;{\mathbb {R}}^3)\)-topology is a consequence of (2.2)(iii), Lemma 4.1(v), (2.8), and Poincaré’s inequality. Note that, if forces are included, one needs to employ Lemma A.3. As \(p>3\), the weak lower semicontinuity follows by the compact embedding \(W^{1,\infty }(\Omega )\subset \subset W^{2,p}(\Omega )\), the dominated convergence theorem, and the convexity of P, see (2.2)(ii). To see (ii), we note that the assumptions of Theorem 3.2 (using \(\phi _h\) in place of \(\phi _k\) and \(\phi _0\)) are satisfied for the fixed metric space \(({\mathscr {S}}^{3D}_{h,M},{\mathcal {D}}_h)\), due to Lemma 5.2 and Lemma 5.4, where we use the weak \(W^{2,p}(\Omega ;{\mathbb {R}}^3)\)-topology for the topology of convergence. \(\square \)
Now we give the proof of Theorem 2.3, addressing the relation of the three-dimensional and the one-dimensional model.
Proof of Theorem 2.3
First, (i) corresponds to the construction of a recovery sequence in the static setting and is addressed in Theorem 6.2(ii). To prove (ii) and (iii), we need to check that the assumptions of Theorem 3.2 and Theorem 3.3 are satisfied. The spaces \(({\mathscr {S}}^{3D}_{h,M},{\mathcal {D}}_{h})\) and \(({\mathscr {S}}^{1D},{\mathcal {D}}_{0})\) are complete metric spaces due to Lemma 5.2(i) and Lemma 5.5(i). Moreover, Proposition 2.2 yields (3.4) and Theorems 6.2, 6.3, and 6.5 give (3.3) and (3.5). Furthermore, the slopes are strong upper gradients due to Lemma 5.4(i) and Lemma 5.5(iv). We note that the energies of the curves of maximal slope are uniformly bounded depending only on the initial data, see (3.6). Concluding, we can apply Theorem 3.2 and Theorem 3.3, respectively. This yields the existence of a curve of maximal slope \((u,\theta )\) for \(\phi _0\) with respect to \(\vert \partial \phi _0 \vert _{{\mathcal {D}}_0}\) and the convergence in (2.24) and (2.25) hold for \(t\ge 0\), up to a subsequence.
It remains to show strong convergence. Without restriction, we give the argument for time-continuous evolutions \(u^h(t)\). From now on, we drop the t dependence, for the reader’s convenience. First, we observe that Theorem 3.2 and Theorem 3.3 also guarantee convergence of energies, i.e., \( \phi _h(y^h) \rightarrow {\phi }_0(u,\theta )\). By Lemma 5.1(iii), we obtain \(\int _\Omega \frac{1}{2} Q_W^3(G^h(y^h)) \rightarrow \phi _0(u,\theta )\). As \(G \mapsto \int _\Omega \frac{1}{2}Q_W^3(G)\) is lower semicontinuous with respect to the weak \(L^2(\Omega )\)-topology, we see that \(\int _\Omega \frac{1}{2} Q_W^3(G_y) \le \phi _0(u,\theta )\). The reverse inequality is a consequence of the proof of Theorem 6.2(i), see (6.4)–(6.5). This implies that \(\int _\Omega \frac{1}{2} Q_W^3(G^h(y^h)) \rightarrow \int _\Omega \frac{1}{2} Q_W^3(G_y) \). Integrating the expansion
taking the limits, using the weak \(L^2\)-convergence of \(G^h(y^h)\), and the positive definiteness of \(Q_W^3\) on \({\mathbb {R}}^{3\times 3}_{\textrm{sym}}\) we get that the convergence of \(\big (\textrm{sym}(G^h(y^h))\big )_h\) also holds strongly in \(L^2(\Omega ; {\mathbb {R}}^{3 \times 3} )\). In particular, as \(\Vert R^h - \textbf{Id}\Vert _{L^\infty (S)} \rightarrow 0\) by Lemma 4.1(vi), Lemma 4.1(i) yields that \(\textrm{sym}(R^h G^h(y^h)) \rightarrow \textrm{sym}(G_y)\) in \(L^2(\Omega ;{\mathbb {R}}^{3 \times 3} )\). Moreover, by Korn’s inequality, (6.1), and the structure of u (see (2.17)) we get
where we used the definition of \(\nabla _h\). The right-hand side of the identity \( \textrm{sym}\left( \frac{\nabla _h y^h - \textbf{Id}}{\varepsilon _h}\right) = \textrm{sym}( R^h G^h) + \textrm{sym}\left( \frac{R^h - \textbf{Id}}{\varepsilon _h}\right) \) converges strongly to \(\textrm{sym}(G_y + \frac{r}{2} A_{u,\theta }^2 )\) in \(L^2(\Omega ;{\mathbb {R}}^{3 \times 3} )\), due to Lemma 6.1(ii). Additionally, Lemma 6.1(i) and (6.3) provide the characterization \((G_y + \frac{r}{2} A_{u,\theta }^2)_{11} = \partial _1 u_1\), which concludes the proof. \(\square \)
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Abels, H., Ameismeier, T.: Large times existence for thin vibrating rods. Asymptot. Anal. 131, 471–512 (2023)
Abels, H., Ameismeier, T.: Convergence of thin vibrating rods to a linear beam equation. Z. Angew. Math. Phys. 73, Article number: 166 (2022)
Abels, H., Mora, M.G., Müller, S.: The time-dependent von Kármán plate equation as a limit of 3d nonlinear elasticity. Calc. Var. PDE 41, 241–259 (2011)
Abels, H., Mora, M.G., Müller, S.: Large time existence for thin vibrating plates. Commun. Partial Differ. Equ. 36, 2062–2102 (2011)
Acerbi, E., Buttazzo, G., Percivale, D.: A variational definition for the strain energy of an elastic string. J. Elast. 25, 137–148 (1991)
Adams, R.A., Fournier, J.J.F.: Sobolev Spaces, 2nd edn. Elsevier, Amsterdam (2003)
Ambrosio, L., Gigli, N., Savaré, G.: Gradient Flows in Metric Spaces and in the Space of Probability Measures. Lectures Mathematics, ETH Zürich, Birkhäuser, Basel (2005)
Antman, S.S.: Physically unacceptable viscous stresses. Z. Angew. Math. Phys. 49, 980–988 (1998)
Antman, S.S.: Nonlinear Problems of Elasticity. Springer, New York (2004)
Badal, R., Friedrich, M., Kružík, M.: Nonlinear and linearized models in thermoviscoelasticity. Arch. Ration. Mech. Anal. 247, Article number: 5 (2023)
Bella, P., Kohn, R.V.: Coarsening of folds in hanging drapes. Commun. Pure Appl. Math. 70, 978–1021 (2017)
Bermudez, A., Viaño, J.M.: Une justification des équations de la thermoélasticité des poutres à section variable par des méthodes asymptotiques. RAIRO. Analyse numérique 18, 347–376 (1984)
Capriz, G.: Continua with latent microstructure. Arch. Ration. Mech. Anal. 90, 43–56 (1985)
Ciarlet, P.G.: Mathematical Elasticity. Vol. II: Theory of Plates, volume 27 of Studies in Mathematics and Its Applications, vol. 27. North-Holland Publishing Co., Amsterdam (1997)
Dal Maso, G.: An Introduction to \(\Gamma \)-Convergence. Birkhäuser, Boston (1993)
Dal Maso, G., Negri, M., Percivale, D.: Linearized elasticity as \(\Gamma \)-limit of finite elasticity. Set-Valued Anal. 10, 165–183 (2002)
Davoli, E., Mora, M.G.: Convergence of equilibria of thin elastic rods under physical growth conditions for the energy density. Proc. R. Soc. Edinb., Sect. A, Math. 142, 501–524 (2012)
Demoulini, S.: Weak solutions for a class of nonlinear systems of viscoelasticity. Arch. Ration. Mech. Anal. 155, 299–334 (2000)
Dunn, J.E., Serrin, J.: On the thermomechanics of interstitial working. Arch. Ration. Mech. Anal. 88, 95–133 (1985)
Freddi, L., Mora, M.G., Paroni, R.: Nonlinear thin-walled beams with a rectangular cross-section — Part I. Math. Models Methods Appl. Sci. 22, 1150016 (2012)
Freddi, L., Mora, M.G., Paroni, R.: Nonlinear thin-walled beams with a rectangular cross-section — Part II. Math. Models Methods Appl. Sci. 23, 743–775 (2013)
Freddi, L., Hornung, P., Mora, M.G., Paroni, R.: One-dimensional von Kármán models for elastic ribbons. Meccanica 53, 659–670 (2018)
Friedrich, M., Kružík, M.: On the passage from nonlinear to linearized viscoelasticity. SIAM J. Math. Anal. 50, 4426–4456 (2018)
Friedrich, M., Kružík, M.: Derivation of von Kármán plate theory in the framework of three-dimensional viscoelasticity. Arch. Ration. Mech. Anal. 238, 489–540 (2020)
Friedrich, M., Kružík, M., Valdman, J.: Numerical approximation of von Kármán viscoelastic plates. Discrete Contin. Dyn. Syst. S 14, 299–319 (2021)
Friedrich, M., Machill, L.: Derivation of a one-dimensional von Kármán theory for viscoelastic ribbons. Nonlinear Differ. Equ. Appl. NoDEA 29, Article number: 11 (2022)
Friesecke, G., James, R.D., Müller, S.: A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Commun. Pure Appl. Math. 55, 1461–1506 (2002)
Friesecke, G., James, R.D., Müller, S.: A hierarchy of plate models derived from nonlinear elasticity by Gamma-convergence. Arch. Ration. Mech. Anal. 180, 183–236 (2006)
Krömer, S., Roubíček, T.: Quasistatic viscoelasticity with self-contact at large strains. J. Elast. 142, 433–445 (2020)
Lecumberry, M., Müller, S.: Stability of slender bodies under compression and validity of the von Kármán theory. Arch. Ration. Mech. Anal. 193, 255–310 (2009)
Lewicka, M., Mucha, P.B.: A local existence result for system of viscoelasticity with physical viscosity. Evol. Equ. Control Theory 2, 337–353 (2013)
Mielke, A.: On evolutionary \(\Gamma \)-convergence for gradient systems (ch. 3). In: Muntean, A., Rademacher, J., Zagaris, A. (eds.) Macroscopic and Large Scale Phenomena: Coarse Graining, Mean Field Limits and Ergodicity. Lecture Notes in Applied Mathematics and Mechanics. Springer, 2016. Proceedings of of Summer School in Twente University, vol. 3, pp. 187–249. Springer, Berlin (2012)
Mielke, A., Ortner, C., Şengül, Y.: An approach to nonlinear viscoelasticity via metric gradient flows. SIAM J. Math. Anal. 46, 1317–1347 (2014)
Mielke, A., Roubíček, T.: Thermoviscoelasticity in Kelvin–Voigt rheology at large strains. Arch. Ration. Mech. Anal. 238, 1–45 (2020)
Mora, M.G., Müller, S.: Derivation of the nonlinear bending-torsion theory for inextensible rods by \(\Gamma \)-convergence. Calc. Var. PDE 18, 287–305 (2003)
Mora, M.G., Müller, S.: A nonlinear model for inextensible rods as a low energy \(\Gamma \)-limit of three-dimensional nonlinear elasticity. Ann. Inst. H. Poincaré Anal. Non Linéaire 21, 271–293 (2004)
Mora, M.G., Scardia, L.: Convergence of equilibria of thin elastic plates under physical growth conditions for the energy density. J. Differ. Equ. 252, 35–55 (2012)
Neff, P.: On Korn’s first inequality with non-constant coefficients. Proc. R. Soc. Edinb., Sect. A, Math. 132, 221–243 (2002)
Ortner, C.: Two Variational Techniques for the Approximation of Curves of Maximal Slope. Technical report NA05/10, Oxford University Computing Laboratory, Oxford (2005)
Pompe, W.: Korn’s first Inequality with variable coefficients and its generalization. Comment. Math. Univ. Carolinae 44, 57–70 (2003)
Sandier, E., Serfaty, S.: Gamma-convergence of gradient flows with applications to Ginzburg–Landau. Commun. Pure Appl. Math. 57, 1627–1672 (2004)
Serfaty, S.: Gamma-convergence of gradient flows on Hilbert and metric spaces and applications. Discrete Contin. Dyn. Syst. Ser. A 31, 1427–1451 (2011)
Toupin, R.A.: Elastic materials with couple stresses. Arch. Ration. Mech. Anal. 11, 385–414 (1962)
Toupin, R.A.: Theory of elasticity with couple stress. Arch. Ration. Mech. Anal. 17, 85–112 (1964)
Acknowledgements
This work was funded by the DFG project FR 4083/5-1 and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2044 -390685587, Mathematics Münster: Dynamics–Geometry–Structure.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Laszlo Szekelyhidi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Some elementary lemmata
Appendix A: Some elementary lemmata
In this section we collect elementary lemmata on the energies and the dissipation distances. We also provide a compactness result in the presence of forces. We start with the proof of Lemma 5.1. To this end, we set for shorthand \(H_Y:= \frac{1}{2}\partial ^2_{F_1^2} D^2(Y,Y) = \frac{1}{2}\partial ^2_{F_2^2} D^2(Y,Y)\) for \(Y \in {\mathbb {R}}^{3 \times 3}\) in a neighborhood of SO(3). Given a deformation \(y \in {\mathscr {S}}^{3D}_{h,M}\), we also introduce the mapping \(H_{\nabla _h y}:\Omega \rightarrow {\mathbb {R}}^{3 \times 3 \times 3 \times 3}\) by \(H_{\nabla _h y}(x) = H_{\nabla _h y(x)}\) for \(x \in \Omega \). Note that this is well defined for h sufficiently small by (4.1)(v) and (2.3)(iv). Viewing \(H_Y\) as a bounded operator mapping from \({\mathbb {R}}^{3\times 3} \rightarrow {\mathbb {R}}^{3 \times 3}\) with norm \(\Vert H_Y \Vert _\infty := \sup _{0 \ne A \in {\mathbb {R}}^{3\times 3} } \vert H_Y A\vert / \vert A \vert \), we see that \(Y \rightarrow H_Y\) is Lipschitz near SO(3) satisfying
Proof of Lemma 5.1
As a preparation, we observe that by the uniform bound on \(\nabla _h y_0\), \(\nabla _h y_1\) (see (4.1)(v)) and a Taylor expansion at \((\nabla _h y_0,\nabla _h y_0)\) we obtain for all open subsets \(U \subset \Omega \)
We define \(G(y_i):= \varepsilon _hG^h(y_i) = R(y_i)^\top \nabla _h y_i - \textbf{Id}\), \(i=0,1\), for convenience. Using the separate frame indifference (2.3)(v) we have
Thus, by \(\varepsilon _h^2 {\mathcal {D}}_h(y_0,y_1)^{2} = \int _\Omega D^2(\nabla _h y_0, \nabla _h y_1) \) and again by Taylor expansion we also get
We now show (i). By (A.1) and (4.1)(v) we get \(\Vert H_{\nabla _h y_0} - {{\mathbb {C}}}^3_D \Vert _\infty \le C(\varepsilon _h/\delta _h)^\alpha \), where \({{\mathbb {C}}}^3_D\) is the fourth-order tensor associated to the quadratic form \(Q^3_D \). Therefore, we obtain
for all open \(U \subset \Omega \). By using (A.2) and again (4.1)(v) we get (i).
To see (ii), we observe \(\Vert H_{R(y_0)^\top \nabla _h y_0} - {{\mathbb {C}}}^3_D\Vert _\infty \le C\Vert R(y_0)^\top \nabla _h y_0 - \textbf{Id}\Vert _\infty \le C(\varepsilon _h/\delta _h)^{\alpha }\) by (A.1), (4.1)(vi), and (4.1)(v). Thus, we get
In a similar fashion, (4.1)(vi) and (4.1)(v) also imply \(\Vert G(y_i) \Vert _{L^\infty (\Omega )} \le C(\varepsilon _h/\delta _h)^\alpha \) for \(i=0,1\) and thus
This together with (A.3) and (A.4) (divided by \(\varepsilon _h^2\)), and \(G^h(y_i) = \varepsilon _h^{-1}G(y_i)\) for \(i=0,1\) yields
This shows the first inequality of (ii). To see the second inequality, we use (4.1)(i).
We now show (iii) and (iv). We use the frame indifference of W and [24, Lemma 4.1(iii)] (with \(F_i = R(y_i)^\top \nabla _h y_i = \textbf{Id}+ G(y_i)\) for \(i=0,1\)) to obtain
where \(\Delta (y_0)\) and \(\Delta (y_1)\) are defined in the statement of the lemma. The fact that \(\Vert G(y_i) \Vert _{L^\infty (\Omega )} \le C(\varepsilon _h/\delta _h)^\alpha \) for \(i=0,1\) and Hölder’s inequality yield
Using \(G^h(y_i) = \varepsilon _h^{-1}G(y_i)\) for \(i=0,1\) and (4.1)(i) we obtain the first inequality of (iv). The second inequality follows again by (4.1)(i). Finally, to see (iii), we apply (iv) for \(y_0 = y\) and \(y_1 = \textbf{id}\), where we use \(\Delta (y_1) = 0\). \(\square \)
Lemma A.1
(Hessian of \(D^2\)) For all \(F \in {\mathbb {R}}^{3 \times 3}\) in a neighborhood of SO(3) and all \(G \in {\mathbb {R}}^{3 \times 3}\) it holds that \(\textrm{Ker} (\partial ^2_{F_1^2} D^2(F, F) ) = F^{-\top } {\mathbb {R}}_{\textrm{skew}}^{3 \times 3}\) and
for some universal \(c>0\). In particular, the potential \(R(F,\dot{F})\) introduced in (2.4) depends only on \(C:= F^{\top }F\) and \(\dot{C}= {\dot{F}}^{\top }F+F^{\top }\dot{F}\), it is quadratic in \(\dot{C}\), and satisfies (2.5).
Proof
We choose \(F\in {\mathbb {R}}^{3\times 3}\) near SO(3) and let \(G \in {\mathbb {R}}^{3 \times 3}\). Suppose \(\varepsilon >0\). By Polar decomposition, we can write \(U = QF\) for \(U = \sqrt{F^\top F}\). Then, exploiting the frame indifference (2.3)(v) for \(Q_1 = Q\) and \(Q^\varepsilon _2 = Q \exp (\varepsilon A)\), where \(A = \frac{1}{2}(F^{-\top } G^\top - G F^{-1}) \in {\mathbb {R}}_\textrm{skew}^{3\times 3}\), yields
By using a Taylor expansion, the definition of A, and \(Q = UF^{-1}\) we calculate
Plugging this into (A.6) and using a Taylor expansion we deduce
As \(\partial ^2_{F_1^2} D^2(\textbf{Id},\textbf{Id})\) is positive definite on \({\mathbb {R}}_{\textrm{sym}}^{3\times 3}\) by (2.3)(vi), it follows by a standard continuity argument that also \(U^{-\top } \partial ^2_{F_1^2} D^2(U,U) U^{-1}\) is positive definite on \({\mathbb {R}}_{\textrm{sym}}^{3\times 3}\) for all F sufficiently close to SO(3). By sending \(\varepsilon \rightarrow 0\) this shows (A.5). Using \(G = \dot{F}\) in the above formula, we find that \(R(F,\dot{F})\) depends only on \(U = \sqrt{C}\) and \(\textrm{sym}(F^\top G) = \frac{1}{2}\dot{C}\), and that it is quadratic in \(\dot{C}\). Finally, (2.5) follows from (A.5). \(\square \)
Lemma A.2
(Positivity of \({\mathcal {D}}_h\)) Let \(M>0\) and let h sufficiently small. Let \(y_0, y_1 \in {\mathscr {S}}^{3D}_{h,M}\) with \({\mathcal {D}}_h(y_0,y_1) = 0\). Then \(y_0 = y_1\).
Proof
Instead of working on \(\Omega \), we introduce the rescaled variables \(z_i = y_i \circ p_h^{-1}\), \(i =0,1\) with the projection \(p_h:\Omega \rightarrow \Omega _h\). Consider the family of pairwise disjoint cubes, defined by
for \(i =1,..., N_1^h:= \lfloor l/\delta _h\rfloor \) and \(j = 1,..., N_2^h:= \lfloor h/\delta _h \rfloor \). Then we have \(\Omega _h= \bigcup _{i = 1}^{N_1^h}\bigcup _{j = 1}^{N_2^h} Q_h(i,j) \cup {\tilde{Q}}_h \) for a small set \({\tilde{Q}}_h\). Denote the family of cubes by \( {\mathcal {Q}}_h\). We now first show that \(z_0 = z_1\) on each \(Q_h(1,j)\) for each \(j = 1,..., N_2^h\). To this end, fix j and denote \(Q_h(1,j)\) by Q for convenience. Assuming \(\int _{\Omega _h} D^2(\nabla z_0, \nabla z_1) =0\), we get by a Taylor expansion and (2.4)
Since \(z_1 = z_0\) on \(\partial I \times (-\frac{h}{2}, \frac{h}{2})\times (-\frac{\delta _h}{2}, \frac{\delta _h}{2})\), we get that \(z_1 = z_0\) on at least one face of \(\partial Q\). Then Theorem 5.3 and (2.5) imply
As \(\Vert \nabla z_1- \nabla z_0 \Vert _{L^\infty (Q)} \rightarrow 0\) for \(h \rightarrow 0\) by Lemma 4.1(v), (A.7) and (A.8) show \(\nabla z_1 = \nabla z_0\) a.e. on Q, for h sufficiently small. Since \(z_1 = z_0\) on at least one face of \(\partial Q\), this also gives \(z_1 = z_0\) a.e. on Q, as desired. We now proceed iteratively to show that \(z_1 = z_0\) on each \(Q \in {\mathcal {Q}}_h\): suppose that the property has already been shown for all \(Q \in \bigcup _{i = 1}^{m}\bigcup _{j = 1}^{N_2^h} Q_h(i,j)\). Then \(z_1 = z_0\) on each \(Q \in \bigcup _{j = 1}^{N_2^h} Q_h(m+1,j)\) follows from the above arguments noting that \(z_1 = z_0\) on at least one face of \(\partial Q\) since \(z_1 = z_0\) on all cubes \(Q \in \bigcup _{i = 1}^{m}\bigcup _{j = 1}^{N_2^h} Q_h(i,j)\). This shows \(z_1 = z_0\) on \(\Omega _h {\setminus } {\tilde{Q}}_h\). Our arrangement of cubes ensures that one corner of \(\Omega _h\) is covered. Rearranging the cubes by starting in the remaining corners and repeating the arguments from above yield that \(z_1 = z_0\) on whole \(\Omega _h\). \(\square \)
Finally, for the reader’s convenience, we briefly give the most important adaption if nonzero forces are considered.
Lemma A.3
(Compactness if \(f_h^{3D}\ne 0\)) Suppose that \(f_h^{3D} \ne 0\) satisfies (2.14) and let \((y^h)_h\) be a sequence with \(y^h \in {\mathscr {S}}^{3D}_{h,M}\) for some \(M>0\).
-
(i)
Then, there exists a constant \(C=C(M)\) such that
$$\begin{aligned} I_h(y^h):= \frac{1}{\varepsilon _h^2} \int _\Omega W(\nabla _h y^h(x)) \, \textrm{d}x+\frac{\zeta _h}{\varepsilon _h^2} \int _\Omega P(\nabla ^2_h y^h(x)) \, \textrm{d}x \le C. \end{aligned}$$ -
(ii)
There exists a constant \(c = c(M) \in {\mathbb {R}}\) such that \(\phi _h(y^h)\ge c > -\infty \).
In particular, uniform bounds on \(\phi _h\) imply uniform bounds on \(I_h\), and all proofs concerning compactness properties are applicable.
Proof of Lemma A.3
Let \(M>0\) and let \((y^h)_h\) be a sequence with \(y^h \in {\mathscr {S}}^{3D}_{h,M}\). Note that by Hölder’s inequality we have
Thus, Lemma 4.1(iv) yields
where we also refer to [21, Equation (68)] for the scaling of \(I_h(y^h)\) on the right-hand side. In particular, this estimate and Poincaré’s inequality imply
where we have used that \(y_3^h = \delta _h x_3 + \varepsilon _h/\delta _h \hat{\xi }_3\) on \(\Gamma \), see (2.8). Combining (A.9) and (A.10) yields
Thus, (i) holds as \(\Vert \frac{1}{\varepsilon _h\delta _h}f_h^{3D}\Vert _{L^2(I)}\) is bounded, due to (2.14). Similarly, (ii) follows by using the equality in (A.11) together with (A.9) and (A.10). \(\square \)
Remark A.4
(Horizontal forces) Denoting by \((f^{3D}_{1,h},f^{3D}_{2,h})\) a vector of horizontal forces one would have to assume that \(\Vert \frac{1}{\varepsilon _h\delta _h}f_{i,h}^{3D}\Vert _{L^2(I)}\), \(i=1,2\), are uniformly bounded in order to guarantee compactness, see (A.11) for the analogous computation. However, this implies that \(f_{1,h}^{3D}/ \varepsilon _h\) and \(f_{2,h}^{3D}/ (\varepsilon _h h)\) necessarily converge to 0. In particular, these forces would not affect the \(\Gamma \)-limit, due to (2.15) and Proposition 2.2.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Friedrich, M., Machill, L. One-dimensional viscoelastic von Kármán theories derived from nonlinear thin-walled beams. Calc. Var. 62, 190 (2023). https://doi.org/10.1007/s00526-023-02525-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-023-02525-3