Abstract
We have created a functional framework for a class of non-metric gradient systems. The state space is a space of nonnegative measures, and the class of systems includes the Forward Kolmogorov equations for the laws of Markov jump processes on Polish spaces. This framework comprises a definition of a notion of solutions, a method to prove existence, and an archetype uniqueness result. We do this by using only the structure that is provided directly by the dissipation functional, which need not be homogeneous, and we do not appeal to any metric structure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of dissipative variational evolution equations has seen a tremendous activity in the last two decades. A general class of such systems is that of generalized gradient flows, which formally can be written as
in terms of a driving functional \({{\mathsf {E}}}\) and a dual dissipation potential \({{\mathsf {R}}}^* = {{\mathsf {R}}}^*(\rho ,\upzeta )\), where \({\mathrm {D}}_\upzeta \) and \({\mathrm {D}}_\rho \) denote derivatives with respect to \(\upzeta \) and \(\rho \). The most well-studied of these are classical gradient flows [4], for which \(\upzeta \mapsto {\mathrm {D}}_\upzeta {{\mathsf {R}}}^*(\rho ,\upzeta ) = {\mathbb {K}}(\rho ) \upzeta \) is a linear operator \({\mathbb {K}}(\rho )\), and rate-independent systems [61], for which \(\upzeta \mapsto {\mathrm {D}}_\upzeta {{\mathsf {R}}}^*(\rho ,\upzeta )\) is zero-homogeneous.
However, various models naturally lead to gradient structures that are neither classic nor rate-independent. For these systems, the map \(\upzeta \mapsto {\mathrm {D}}_\upzeta {{\mathsf {R}}}^*(\rho ,\upzeta )\) is neither linear nor zero-homogeneous, and in many cases it is not even homogeneous of any order. Some examples are
-
(1)
Models of chemical reactions, where \({{\mathsf {R}}}^*\) depends exponentially on \(\upzeta \) [6, 32, 38, 46],
-
(2)
The Boltzmann equation, also with exponential \({{\mathsf {R}}}^*\) [38],
-
(3)
Nonlinear viscosity relations such as the Darcy-Forchheimer equation for porous media flow [39, 44],
-
(4)
Effective, upscaled descriptions in materials science, where the effective potential \({{\mathsf {R}}}^*\) arises through a cell problem, and can have many different types of dependence on \(\upzeta \) [16, 28, 46, 55, 65, 72,73,74],
-
(5)
Gradient structures that arise from large-deviation principles for sequences of stochastic processes, in particular jump processes [58, 59].
The last example is the inspiration for this paper.
Regardless whether \({{\mathsf {R}}}^*\) is classic, rate-independent, or otherwise, equation (1.1) typically is only formal, and it is a major mathematical challenge to construct an appropriate functional framework for this equation. Such a functional framework should give the equation a rigorous meaning, and provide the means to prove well-posedness, stability, regularity and approximation results to facilitate the study of the equation.
For classical gradient systems, in which \({\mathrm {D}}_\upzeta {{\mathsf {R}}}^*\) is linear and \({{\mathsf {R}}}^*\) is quadratic in \(\upzeta \) (therefore also called ‘quadratic’ gradient systems) and when \({{\mathsf {R}}}^*\) generates a metric space, a rich framework has been created by Ambrosio, Gigli, and Savaré [4]. For rate-independent systems, in which \({{\mathsf {R}}}^*\) is 1-homogeneous in \(\upzeta \), the complementary concepts of ‘Global Energetic solutions’ and ‘Balanced Viscosity solutions’ give rise to two different frameworks [19, 61, 62, 64, 67].
For the examples (1–5) listed above, however, \({{\mathsf {R}}}^*\) is not homogeneous in \(\upzeta \), and neither the rate-independent frameworks nor the metric-space theory apply. Nonetheless, the existence of such models of real-world systems with a formal variational-evolutionary structure suggests that there may exist a functional framework for such equations that relies on this structure. In this paper we build exactly such a framework for an important class of equations of this type, those that describe Markov jump processes. We expect the approach advanced here to be applicable to a broader range of systems.
1.1 Generalized gradient systems for Markov jump processes
Some generalized gradient-flow structures of evolution equations are generated by the large deviations of an underlying, more microscopic stochastic process [1, 2, 22, 46, 59, 60]. This explains the origin and interpretation of such structures, and it can be used to identify hitherto unknown gradient-flow structures [36, 71].
It is the example of Markov jump processes that inspires the results of this paper, and we describe this example here; nonetheless, the general setup that starts in Sect. 3.1 has wider application. We think of Markov jump processes as jumping from one ‘vertex’ to another ‘vertex’ along an ‘edge’ of a ‘graph’; we place these terms between quotes because the space V of vertices may be finite, countable, or even uncountable, and similarly the space \(E{:}{=} V\times V\) of edges may be finite, countable, or uncountable (see Assumption (\(V\!\pi \kappa \)) below). In this paper, V is a standard Borel space.
The laws of such processes are time-dependent measures \(t\mapsto \rho _t\in {{\mathcal {M}}}^+(V)\) (with \({{\mathcal {M}}}^+(V)\) the space of positive finite Borel measures—see Sect. 2). These laws satisfy the Forward Kolmogorov equation
Here \(Q^*:{{\mathcal {M}}}(V)\rightarrow {{\mathcal {M}}}(V)\) is the dual of the infinitesimal generator \(Q:\mathrm {B}_{\mathrm {b}}(V)\rightarrow \mathrm {B}_{\mathrm {b}}(V)\) of the process, which for an arbitrary bounded Borel function \(\varphi \in \mathrm {B}_{\mathrm {b}}(V)\) is given by
The jump kernel \(\kappa \) in these definitions characterizes the process: \(\kappa (x,\cdot )\in {{\mathcal {M}}}^+(V)\) is the infinitesimal rate of jumps of a particle from the point x to points in V. Here we address the reversible case, which means that the process has an invariant measure \(\pi \in {{\mathcal {M}}}^+(V)\), i.e., \(Q^*\pi =0\), and that the joint measure \(\pi (\mathrm {d}x) \kappa (x,\mathrm {d}y)\) is symmetric in x and y.
In this paper we consider evolution equations of the form (1.2) for the nonnegative measure \(\rho \), as well as various linear and nonlinear generalizations. We will view them as gradient systems of the form (1.1), and use this gradient structure to study their properties.
The gradient structure for equation (1.2) consists of the state space \({{\mathcal {M}}}^+(V)\), a driving functional \({\mathscr {E}}:{{\mathcal {M}}}^+(V)\rightarrow [0,{+\infty }]\), and a dual dissipation potential \({\mathscr {R}}^*:{{\mathcal {M}}}^+(V)\times \mathrm {B}_{\mathrm {b}}(E)\rightarrow [0,{+\infty }]\) (where \(\mathrm {B}_{\mathrm {b}}(E)\) denotes the space of bounded Borel functions on \(E\)). We now describe this structure in formal terms, and making it rigorous is one of the aims of this paper.
The functional that drives the evolution is the relative entropy with respect to the invariant measure \(\pi \), namely
where for the example of Markov jump processes the ‘energy density’ \(\upphi \) is given by
(In the general development below we consider more general functions \(\upphi \), such as those that arise in strongly interacting particle systems; see e.g. [23, 45]).
The dissipation potential \({{\mathsf {R}}}^*\) is best written in terms of an alternative potential \({\mathscr {R}}^*\),
Here the ‘graph gradient’ \({{\overline{\nabla }}}:\mathrm {B}_{\mathrm {b}}(V) \rightarrow \mathrm {B}_{\mathrm {b}}(E)\) and its negative dual, the ‘graph divergence operator’ \( {\overline{\mathrm {div}}}:{{\mathcal {M}}}(E)\rightarrow {{\mathcal {M}}}(V)\), are defined as follows:
and are linked by
The dissipation functional \({\mathscr {R}}^*\) is defined for \(\xi \in \mathrm {B}_{\mathrm {b}}(E)\) by
where the function \(\Psi ^*\) and the ‘edge’ measure \({\varvec{\upnu }}_\rho \) will be fixed in (1.10) below.
With these definitions, the gradient-flow equation (1.1) can be written alternatively as
which can be recognized by observing that
and \({\mathrm {D}}{\mathscr {E}}(\rho ) = \upphi '(u)\) (which corresponds to \( \log u\) for the logarithmic entropy (1.5)). This \(({\overline{\mathrm {div}}},{{\overline{\nabla }}})\)-duality structure is a common feature in both physical and probabilistic models, and has its origin in the distinction between ‘states’ and ‘processes’; see [70, Sec. 3.3] and [69] for discussions.
For this example of Markov jump processes we consider a class of generalized gradient structures of the type above, given by \({\mathscr {E}}\) and \({\mathscr {R}}^*\) (or equivalently by the densities \(\upphi \), \(\Psi ^*\), and the measure \({\varvec{\upnu }}_\rho \)), with the property that equations (1.1) and (1.9) coincide with (1.2). Even for fixed \({\mathscr {E}}\) there exists a range of choices for \(\Psi ^*\) and \({\varvec{\upnu }}_\rho \) that achieve this (see also the discussion in [35, 59]). A simple calculation (see the discussion at the end of Sect. 3.1) shows that, if one chooses for the measure \({\varvec{\upnu }}_\rho \) the form
for a suitable fuction \(\upalpha :[0,\infty )\times [0,\infty )\rightarrow [0,\infty )\), and one introduces the map \({\mathrm {F}}:(0,\infty )\times (0,\infty )\rightarrow {\mathbb {R}}\)
then (1.9) takes the form of the integro-differential equation
in terms of the density \(u_t\) of \(\rho _t\) with respect to \(\pi \). Therefore, a pair \((\Psi ^*,{\varvec{\upnu }}_\rho )\) leads to equation (1.2) whenever \((\Psi ^*,\upphi ,\upalpha )\) satisfy the compatibility property
The classical quadratic-energy, quadratic-dissipation choice
corresponds to the Dirichlet-form approach to (1.2) in \(L^2(V,\pi )\). Here \({\mathscr {R}}^*(\rho ,{{\varvec{j}}})={\mathscr {R}}^*({{\varvec{j}}})\) is in fact independent of \(\rho \): if one introduces the symmetric bilinear form
with \({\varvec{{\varvec{\vartheta }}}}(\mathrm {d}x, \mathrm {d}y) = \pi (\mathrm {d}x ) \kappa (x, \mathrm {d}y)\) (cf. (3.5) ahead), then (1.12) can also be formulated as
Two other choices have received attention in the recent literature. Both of these are based not on the quadratic energy \(\upphi (s)=\tfrac{1}{2}s^2\), but on the Boltzmann entropy functional \(\upphi (s) = s\log s - s + 1\):
-
(1)
The large-deviation characterization [58, 59] leads to the choice
$$\begin{aligned} \Psi ^*(\xi ) {:}{=} 4\bigl (\cosh (\xi /2) - 1\bigr ) \quad \text {and}\quad \upalpha (u,v) {:}{=} \sqrt{uv}. \end{aligned}$$(1.17a)The corresponding primal dissipation potential \(\Psi {:}{=} (\Psi ^*)^*\) is given by
$$\begin{aligned} \Psi (s) {:}{=} 2s\log \left( \frac{s+\sqrt{s^2+4}}{2} \right) - \sqrt{s^2 + 4} + 4. \end{aligned}$$ -
(2)
The ‘quadratic-dissipation’ choice introduced independently by Maas [49], Mielke [52], and Chow, Huang, and Zhou [13] for Markov processes on finite graphs,
$$\begin{aligned} \Psi ^*(\xi ) {:}{=} \tfrac{1}{2} \xi ^2, \quad \Psi (s) = \tfrac{1}{2} s^2 , \quad \text {and}\quad \upalpha (u,v) {:}{=} \frac{ u-v }{ \log (u) - \log (v) }. \end{aligned}$$(1.17b)
Other examples are discussed in Sect. 1.3. With the quadratic choice (1.17b), the gradient system fits into the metric-space structure (see e.g. [4]) and this feature has been used extensively to investigate the properties of general Markov jump processes [25, 29,30,31, 49, 52]. In this paper, however, we focus on functions \(\Psi ^*\) that are not homogeneous, as in (1.17a), and such that the corresponding structure is not covered by the usual metric framework. On the other hand, there are various arguments why this structure nonetheless has a certain ‘naturalness’ (see Sect. 1.4), and these motivate our aim to develop a functional framework based on this structure.
1.2 Challenges
Constructing a ‘functional framework’ for the gradient-flow equation (1.9) with the choices (1.5) and (1.17a) presents a number of independent challenges.
1.2.1 Definition of a solution
As it stands, the formulation of equation (1.9) and of the functional \({\mathcal {R}}^*\) of (1.8) presents many difficulties: the definition of \({\mathcal {R}}^*\) and the measure \({\varvec{\upnu }}_\rho \) when \(\rho \) is not absolutely continuous with respect to \(\pi \), the concept of time differentiability for the curve of measures \(\rho _t\), whether \(\rho _t\) is necessarily absolutely continuous with respect to \(\pi \) along an evolution, what happens if \(\mathrm {d}\rho _t /\mathrm {d}\pi \) vanishes and \(\upphi \) is not differentiable at 0 as in the case of the logarithmic entropy, etcetera. As a result of these difficulties, it is not clear what constitutes a solution of equation (1.9), let alone whether such solutions exist. In addition, a good solution concept should be robust under taking limits, and the formulation (1.9) does not seem to satisfy this requirement either.
For quadratic and rate-independent systems, successful functional frameworks have been constructed on the basis of variational tools such as the Energy-Dissipation balance [4, 42, 61, 63]. Moreover, these functional frameworks have been shown to be stable under various forms of asymptotic limits [46, 54, 66, 79, 80]. This strongly suggests that also the framework proposed here should enjoy this stability with respect to perturbations of \({\mathcal {E}}\) and \({\mathcal {R}}\) which, in particular, would allow one to generalize the more classical notion of solutions developed in Sect. 6. We have chosen not to dwell upon the stability issue to avoid overburdening the exposition; we only provide a ‘partial’ stability result (with \({\mathcal {E}}\) and \({\mathcal {R}}\) fixed) in Theorem 5.10.
In fact, the same large-deviation principle that gives rise to the ‘cosh’ structure (1.17a) above formally yields the ‘EDP’ functional (see Appendix A for a formal derivation)
In this formulation, \({\mathscr {R}}\) is the Legendre dual of \({\mathscr {R}}^*\) with respect to the \(\xi \) variable, which can be written in terms of the Legendre dual \(\Psi {:}{=}\Psi ^{**}\) of \(\Psi ^*\) as
Along smooth curves \(\rho _t=u_t\pi \) with strictly positive densities, the functional \({\mathscr {L}}\) is nonnegative, since
After time integration we find that \({\mathscr {L}}(\rho ,{{\varvec{j}}})\) is nonnegative for any pair \((\rho ,{{\varvec{j}}})\).
The minimum of \({\mathscr {L}}\) is formally achieved at value zero, at pairs \((\rho ,{{\varvec{j}}})\) satisfying
which is an equivalent way of writing the gradient-flow equation (1.9). This can be recognized, as usual for gradient systems, by observing that achieving equality in the inequality (1.21) requires equality in the Legendre duality of \(\Psi \) and \(\Psi ^*\), which reduces to the equations above.
Remark 1.1
It is worth noticing that the joint convexity of the functional \({\mathscr {R}}\) of (1.19) (a crucial property for the development of our analysis) is equivalent to the convexity of \(\Psi \) and concavity of the function \(\upalpha \).
Remark 1.2
Let us add a comment concerning the choice of the factor 1/2 in front of \(\Psi ^*\) in (1.8), and the corresponding factors 1/2 and 2 in (1.19). The cosh-entropy combination (1.17a) satisfies the linear-equation condition \({\mathrm {F}}(u,v) = v-u\) (equation (1.13)) because of the elementary identity
The factor 1/2 inside the \(\sinh \) can be included in different ways. In [59] it was included explicitly, by writing expressions of the form \({\mathrm {D}}{{\mathsf {R}}}^*(\rho ,-\tfrac{1}{2} {\mathrm {D}}{{\mathsf {E}}}(\rho ))\); in this paper we follow [46] and include this factor in the definition of \({\mathscr {R}}^*\).
Remark 1.3
The continuity equation \(\partial _t \rho _t + {\overline{\mathrm {div}}}{{\varvec{j}}}_t = 0 \) is invariant with respect to skew-symmetrization of \({{\varvec{j}}}\), i.e. with respect to the transformation \({{\varvec{j}}}\mapsto {{\varvec{j}}}^\flat \) with \({{\varvec{j}}}^\flat (\mathrm {d}x,\mathrm {d}y){:}{=} \frac{1}{2} \bigl ({{\varvec{j}}}(\mathrm {d}x,\mathrm {d}y)-{{\varvec{j}}}(\mathrm {d}y,\mathrm {d}x)\bigr )\). Therefore we could also write the second integral in (1.20) as
thus replacing \(\Psi \left( 2\frac{\mathrm {d}{{\varvec{j}}}_t}{\mathrm {d}{\varvec{\upnu }}_{\rho _t}}(x,y)\right) \) with the lower term \(\Psi \left( \frac{\mathrm {d}(2 {{\varvec{j}}}^\flat _t)}{\mathrm {d}{\varvec{\upnu }}_{\rho _t}}(x,y)\right) \), cf. Remark 4.12, and obtaining a corresponding equation as (1.22) for \((2{{\varvec{j}}}_t^\flat )\) instead of \(2{{\varvec{j}}}_t\). This would lead to a weaker gradient system, since the choice (1.19) forces \({{\varvec{j}}}_t\) to be skew-symmetric, whereas the choice of a dissipation involving only \({{\varvec{j}}}^\flat \) would not control the symmetric part of \({{\varvec{j}}}\). On the other hand, the evolution equation generated by the gradient system would remain the same.
Since at least formally equation (1.9) is equivalent to the requirement \({\mathscr {L}}(\rho ,{{\varvec{j}}})\le 0\), we adopt this variational point of view to define solutions to the generalized gradient system \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\). This inequality is in fact the basis for the variational Definition 5.4 below. In order to do this in a rigorous manner, however, we will need
-
(1)
A study of the continuity equation
$$\begin{aligned} \partial _t \rho _t + {\overline{\mathrm {div}}}{{\varvec{j}}}_t = 0, \end{aligned}$$(1.23)that appears in the definition of the functional \({\mathscr {L}}\) (Sect. 4.1).
-
(2)
A rigorous definition of the measure \({\varvec{\upnu }}_{\rho _t}\) and of the functional \({\mathscr {R}}\) (Definition 4.9);
-
(3)
A class \({\mathcal {A}}{(0,T)}\) of curves “of finite action” in \({{\mathcal {M}}}^+(V)\) along which the functional \({\mathscr {R}}\) has finite integral (equation (4.81));
-
(4)
An appropriate definition of the Fisher-information functional (see Definition 5.1)
$$\begin{aligned} \rho \mapsto {\mathscr {D}}(\rho ) {:}{=} {\mathscr {R}}^*\bigl (\rho ,- {{\overline{\nabla }}}\upphi '(\mathrm {d}\rho /\mathrm {d}\pi )\bigr ); \end{aligned}$$(1.24) -
(5)
A proof of the lower bound \({\mathscr {L}}\ge 0\) (Theorem 4.16) via a suitable chain-rule inequality.
1.2.2 Existence of solutions
The first test of a new solution concept is whether solutions exist under reasonable conditions. In this paper we provide two existence results that complement each other, one based on dissipative \(L^1\)-theory and the other on the Energy-Dissipation balance. These theories are not completely equivalent, as can be observed for the classical heat equation (cf. [42] for a variational approach), and they reveal different properties of a solution, even when the assumptions for both theories are satisfied.
The first existence proof is based on a reformulation of the equation (1.2) as a differential equation in the Banach space \(L^1(V,\pi )\), driven by a continuous dissipative operator. Under general compatibility conditions on \(\upphi \), \(\Psi \), and \(\upalpha \), we show that the solution provided by this abstract approach is also a solution in the variational sense that we discussed above. The proof is presented in Sect. 6 and is quite robust for initial data whose density takes value in a compact interval \([a,b]\subset (0,\infty )\). In order to deal with a more general class of initial data, we will adopt two different viewpoints. A first possibility is to take advantage of the robust stability properties of the \(({\mathscr {E}},{\mathscr {R}}, {\mathscr {R}}^*)\) Energy-Dissipation balance when the Fisher information \({\mathscr {D}}\) is lower semicontinuous (cf. Theorem 5.10). A second possibility is to exploit the monotonicity properties of (1.12) when the map \({\mathrm {F}}\) in (1.11) exhibits good behaviour at the boundary of \({\mathbb {R}}_+^2\) and at infinity (cf. Theorem 6.5). As mentioned above, neither of these viewpoints are completely contained within the other.
Since we believe that the variational formulation reveals a relevant structure of such systems and we expect that it may also be useful in dealing with more singular cases and their stability issues, we also present a more intrinsic approach by adapting the well-established ‘JKO-Minimizing-Movement’ method to the structure of this equation. This method has been used, e.g., for metric-space gradient flows [4, 42], for rate-independent systems [51], for some non-metric systems with formal metric structure [7, 48], and also for Lagrangian systems with local transport [33].
This approach relies on the Dynamical-Variational Transport cost (DVT) \({\mathscr {W}}(\tau ,\mu ,\nu )\), which is the \(\tau \)-dependent transport cost between two measures \(\mu ,\nu \in {{\mathcal {M}}}^+(V)\) induced by the dissipation potential \({\mathscr {R}}\) via
In the Minimizing-Movement scheme a single increment with time step \(\tau >0\) is defined by the minimization problem
By concatenating such solutions, constructing appropriate interpolations, and proving a compactness result—all steps similar to the procedure in [4, Part I]—we find a curve \((\rho _t,{{\varvec{j}}}_t)_{t\in [0,T]}\) satisfying the continuity equation (1.23) such that
where \({\mathscr {S}}^-:{\mathrm {D}}({\mathscr {E}})\rightarrow [0,{+\infty })\) is a suitable relaxed slope of the energy functional \({\mathscr {E}}\) with respect to the cost \({\mathscr {W}}\) (see (7.29)). Under a lower-semicontinuity condition on \({\mathscr {D}}\) we show that \({\mathscr {S}}^-\ge {\mathscr {D}}\). It then follows that \(\rho \) is a solution as defined above (see Definition 5.4).
Section 7 is devoted to developing the ‘Minimizing-Movement’ approach for general DVTs. This requires establishing
-
(6)
Properties of \({\mathscr {W}}\) that generalize those of the ‘metric version’ \({\mathscr {W}}(\tau ,\mu ,\nu )= \frac{1}{2\tau }d(\mu ,\nu )^2\) (Sect. 7.2);
-
(7)
A generalization of the ‘Moreau-Yosida approximation’ and of the ‘De Giorgi variational interpolant’ to the non-metric case, and a generalization of their properties (Sects. 7.1 and 7.2);
-
(8)
A compactness result as \(\tau \rightarrow 0\), based on the properties of \({\mathscr {W}}\) (Sect. 7.4);
-
(9)
A proof of \({\mathscr {S}}^-\ge {\mathscr {D}}\) (Corollary 7.11).
This procedure leads to our existence result, Theorem 7.4, of solutions in the sense of Definition 5.4.
1.2.3 Uniqueness of solutions
We prove uniqueness of variational solutions under suitable convexity conditions of \({\mathscr {D}}\) and \({\mathscr {E}}\) (Theorem 5.9), following an idea by Gigli [34].
1.3 Examples
We will use the following two guiding examples to illustrate the results of this paper. Precise assumptions are given in Sect. 3.1. In both examples the state space consists of measures \(\rho \) on a standard Borel space \((V,\mathfrak B)\) endowed with a reference Borel measure \(\pi \). The kernel \(x\mapsto \kappa (x,\cdot )\) is a measurable family of nonnegative measures with uniformly bounded mass, such that the pair \((\pi ,\kappa )\) satisfies detailed balance (see Sect. 3.1).
Example 1: Linear equations driven by the Boltzmann entropy. This is the example that we have been using in this introduction. The equation is the linear equation (1.2),
which can also be written in terms of the density \(u =\mathrm {d}\rho /\mathrm {d}\pi \) as
and corresponds to the linear field \({\mathrm {F}}\) of (1.13). Apart from the classical quadratic setting of (1.14), two gradient structures for this equation have recently received attention in the literature, both driven by the Boltzmann entropy (1.5) \(\upphi (s) = s\log s - s + 1\) as described in (1.17):
- (1):
-
The ‘cosh’ structure: \(\Psi ^*(\xi ) = 4\bigl (\cosh (\xi /2) -1\bigr )\) and \(\upalpha (u,v) = \sqrt{uv}\);
- (2):
-
The ‘quadratic’ structure: \(\Psi ^*(\xi ) = \tfrac{1}{2} \xi ^2\) and \(\upalpha (u,v) = (u-v)/\log (u/v)\).
However, the approach of this paper applies to more general combinations \((\upphi ,\Psi ^*,\upalpha )\) that lead to the same equation. Due to the particular structure of (1.11), it is clear that the 1-homogeneity of the linear map \({\mathrm {F}}\) (1.13) and the 0-homogeneity of the term \(\upphi '(v)-\upphi '(u)\) associated with the Boltzmann entropy (1.5) restrict the range of possible \(\upalpha \) to 1-homogenous functions such as the ‘mean functions’ \(\upalpha (u,v) = \sqrt{uv}\) (geometric) and \(\upalpha (u,v) = (u-v)/\log (u/v)\) (logarithmic).
Confining the analysis to concave functions (according to Remark 1.1), we observe that every concave and 1-homogeneous function \(\upalpha \) can be obtained by the concave generating function \({\mathfrak {f}}:(0,{+\infty })\rightarrow (0,{+\infty })\)
The symmetry of \(\upalpha \) corresponds to the property
and shows that the function
The concaveness of \({\mathfrak {f}}\) also shows that \({\mathfrak {g}}\) is increasing, so that we can define
which is convex, even, and superlinear if
A natural class of concave and 1-homogeneous weight functions is provided by the Stolarsky means \({\mathfrak {c}}_{p,q}(u,v)\) with appropriate \(p,q\in {\mathbb {R}}\), and any \(u,v>0\) [12, Chapter VI]:
from which we identify other simpler means, such as the power means \({\mathfrak {m}}_p(u,v) = {\mathfrak {c}}_{p,2p}(u,v)\) with \(p\in [-\infty , 1]\):
and the generalized logarithmic mean \({\mathfrak {l}}_p(u,v)={\mathfrak {c}}_{1,p+1}(u,v)\), \(p\in [-\infty ,-1]\).
The power means are obtained from the concave generating functions
We can thus define
with the obvious changes when \(p=0\) (the case \(\Psi _0^*(\xi )=4(\cosh (\xi /2)-1\))) or \(p=-\infty \) (the case \(\Psi _{-\infty }^*(\xi )= \exp (|\xi |)-1-|\xi |\)).
It is interesting to note that the case \(p=-1\) (harmonic mean) corresponds to
We finally note that the arithmetic mean \(\upalpha (u,v)={\mathfrak {m}}_1(u,v)=(u+v)/2\) would yield \(\Psi _1^*(\xi )=4\log (1/2(1+{\mathrm {e}}^\xi ))-2\xi \), which is not superlinear.
Example 2: Nonlinear equations. We consider a combination of \(\upphi \), \(\Psi ^*\), and \(\upalpha \) such that the function \({\mathrm {F}}\) introduced in (1.11) has a continuous extension up to the boundary of \([0,{+\infty })^2\) and satisfies a suitable growth and monotonicity condition (see Sect. 6). The resulting integro-differential equation is given by (1.12). Here is a list of some interesting cases (we will neglect all the issues concerning growth and regularity).
-
(1)
A field of the form \({\mathrm {F}}(u,v)=f(v)-f(u)\) with \(f:{\mathbb {R}}_+\rightarrow {\mathbb {R}}\) monotone corresponds to the equation
$$\begin{aligned} \partial _t u_t(x) = \int _{y\in V} \bigl (f(u_t(y))-f(u_t(x))\bigr )\, \kappa (x,\mathrm {d}y), \end{aligned}$$and can be classically considered in the framework of the Dirichlet forms, i.e. \(\upalpha \equiv 1\), \(\Psi ^*(r)= r^2/2\), with energy \(\upphi \) satisfying \(\upphi ' = f\).
-
(2)
The case \({\mathrm {F}}(u,v)=g(v-u)\), with \(g:{\mathbb {R}}\rightarrow {\mathbb {R}}\) monotone and odd, yields the equation
$$\begin{aligned} \partial _t u_t(x) = \int _{y\in V} g\bigl (u_t(y)-u_t(x)\bigr )\, \kappa (x,\mathrm {d}y), \end{aligned}$$and can be obtained with the choices \(\upalpha \equiv 1\), \(\upphi (s){:}{=}s^2/2\) and \(\Psi ^*(r){:}{=}\int _0^r g(s)\,\mathrm {d}s\).
-
(3)
Consider now the case when \({\mathrm {F}}\) is positively q-homogeneous, with \(q\in [0,1]\). It is then natural to consider a q-homogeneous \(\upalpha \) and the logarithmic entropy \(\upphi (r)=r\log r-r+1\). If the function \(h:(0,\infty )\rightarrow {\mathbb {R}}\), \(h(r){:}{=}{\mathrm {F}}(r,1)/\upalpha (r,1)\) is increasing, then setting as in (1.35)
$$\begin{aligned} \Psi ^*(\xi ){:}{=}\int _1^{\exp (\xi )}h(r)\,\mathrm {d}r \end{aligned}$$equation (1.12) provides an example of generalized gradient system \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\). Simple examples are \({\mathrm {F}}(u,v)=v^q-u^q\), corresponding to the equation
$$\begin{aligned} \partial _t u_t(x) = \int _{y\in V} \bigl (u^q_t(y)-u^q_t(x)\bigr )\, \kappa (x,\mathrm {d}y), \end{aligned}$$with \(\upalpha (u,v){:}{=} {\mathfrak {m}}_p(u^q,v^q)\) and \(\Psi ^*(\xi ){:}{=}\frac{1}{q}\Psi _p^*(q\xi )\), where \(\Psi ^*_p\) has been defined in (1.35). In the case \(p=0\) we get \(\Psi ^*(\xi )=\frac{4}{q}\big (\cosh (q\xi /2)-1\big )\).
As a last example, we can consider \({\mathrm {F}}(u,v)={\text {sign}} (v-u)|v^m-u^m|^{1/m}\), \(m>0\), and \(\upalpha (u,v)=\min (u, v)\); in this case, the function h given by \(h(r)=(r^m-1)^{1/m}\) when \(r\ge 1\), and \(h(r)=-(r^{-m}-1)^{1/m}\) when \(r<1\), satisfies the required monotonicity property.
1.4 Comments
Rationale for studying this structure. We think that the structure of generalized gradient systems \(({{\mathcal {E}}},{\mathscr {R}},{\mathscr {R}}^*)\) is sufficiently rich and interesting to deserve a careful analysis. It provides a genuine extension of the more familiar quadratic gradient-flow structure of Maas, Mielke, and Chow–Huang–Zhou, which better fits into the metric framework of [4]. In Sect. 6 we will also show its connection with the theory of dissipative evolution equations.
Moreover, the specific non-homogeneous structure based on the \(\cosh \) function (1.17a) has a number of arguments in its favor, which can be summarized in the statement that it is ‘natural’ in various different ways:
-
(1)
It appears in the characterization of large deviations of Markov processes; see Appendix A or [10, 59];
-
(2)
It arises in evolutionary limits of other gradient structures (including quadratic ones) [6, 46, 53, 66];
-
(3)
It ‘responds naturally’ to external forcing [66, Prop. 4.1];
- (4)
We will explore these claims in more detail in a forthcoming paper. Last but not least, the very fact that non-quadratic, generalized gradient flows may arise in the limit of gradient flows suggests that, allowing for a broad class of dissipation mechanisms is crucial in order to (1) fully exploit the flexibility of the gradient-structure formulation, and (2) explore its robustness with respect to \(\Gamma \)-converging energies and dissipation potentials.
Potential for generalization. In this paper we have chosen to concentrate on the consequences of non-homogeneity of the dissipation potential \(\Psi \) for the techniques that are commonly used in gradient-flow theory. Until now, the lack of a sufficiently general rigorous construction of the functional \({\mathscr {R}}\) and its minimal integral over curves \({\mathscr {W}}\) have impeded the use of this variational structure in rigorous proofs, and a main aim of this paper is to provide a way forward by constructing a rigorous framework for these objects, while keeping the setup (in particular, the ambient space V) as general as possible.
In order to restrict the length of this paper, we considered only simple driving functionals \({\mathscr {E}}\), which are of the local variety \({\mathscr {E}}(\rho ) = \int \upphi (\mathrm {d}\rho /\mathrm {d}\pi )\mathrm {d}\pi \). Many gradient systems appearing in the literature are driven by more general functionals, that include interaction and other nonlinearities [25, 26, 40, 78], and we expect that the techniques of this paper will be of use in the study of such systems.
As one specific direction of generalization, we note that the Minimizing-Movement construction on which the proof of Theorem 7.4 is based has a scope wider than that of the generalized gradient structure \(({\mathscr {E}}, {\mathscr {R}}, {\mathscr {R}}^*)\) under consideration. In fact, as we show in Sect. 7, Theorem 7.4 yields the existence of (suitably formulated) gradient flows in a general topological space endowed with a cost fulfilling suitable properties. While we do not develop this discussion in this paper, at places throughout the paper we hint at this prospective generalization: the ‘abstract-level’ properties of the DVT cost are addressed in Sect. 4.7, and the whole proof of Theorem 7.4 is carried out under more general conditions than those required on the ‘concrete’ system set up in Sect. 3.
Challenges for generalization. A well-formed functional framework includes a concept of solutions that behaves well under the taking of limits, and the existence proof is the first test of this. Our existence proof highlights a central challenge here, in the appearance of two slope functionals \({\mathscr {S}}^-\) and \({\mathscr {D}}\) that both represent rigorous versions of the ‘Fisher information’ term \({\mathscr {R}}^*\bigl (\rho ,-{{\overline{\nabla }}}\upphi '(\mathrm {d}\rho /\mathrm {d}\pi )\bigr )\). The chain-rule lower-bound inequality holds under general conditions for \({\mathscr {D}}\) (Theorem 4.16), but the Minimizing-Movement construction leads to the more abstract object \({\mathscr {S}}^-\). Passing to the limit in the minimizing-movement approach requires connecting the two through the inequality \({\mathscr {S}}^-\ge {\mathscr {D}}\). We prove it by first obtaining the inequality \({\mathscr {S}}\ge {\mathscr {D}}\), cf. Proposition 7.10, under the condition that a solution to the \(({\mathscr {E}}, {\mathscr {R}}, {\mathscr {R}}^*)\) system exists (for instance, by the approach developed in Sect. 6). We then deduce the inequality \({\mathscr {S}}^-\ge {\mathscr {D}}\) under the further condition that \({\mathscr {D}}\) be lower semicontinuous, which can be in turn proved under a suitable convexity condition (cf. Prop. 5.3). We hope that more effective ways of dealing with these issues will be found in the future.
Comparison with the Weighted Energy-Dissipation method. It would be interesting to develop the analogous variational approach based on studying the limit behaviour as \(\varepsilon \downarrow 0\) of the minimizers \((\rho _t,{{\varvec{j}}}_t)_{t\ge 0}\) of the Weighted Energy-Dissipation (WED) functional
among the solutions to the continuity equation with initial datum \(\rho _0\), see [76]. Indeed, the intrinsic character of the WED functional, which only features the dissipation potential \({\mathscr {R}}\), makes it suitable to the present non-metric framework.
1.5 Notation
The following table collects the notation used throughout the paper.
- \({{\overline{\nabla }}}\), \({\overline{\mathrm {div}}}\):
-
graph gradient and divergence (1.6)
- \(\upalpha (\cdot ,\cdot )\):
-
multiplier in flux rate \({\varvec{\upnu }}_\rho \) Assumption (\({\mathscr {R}}^*\Psi \upalpha \))
- \(\upalpha ^\infty \), \(\upalpha _*\):
-
recession function, Legendre transform Sect. 2.3
- \(\upalpha {[}\cdot |\cdot {]}\), \({{\hat{\upalpha }}}\):
-
measure map, perspective function Sect. 2.3
- \({\mathcal {A}}{(a,b)}\):
-
set of curves \(\rho \) with finite action (4.33)
- \( \Vert \kappa _V\Vert _\infty \):
-
upper bound on \(\kappa \) Assumption (\(V\!\pi \kappa \))
- \( \mathrm {C}_{\mathrm {b}}\):
-
space of bdd, ct. functions with supremum norm
- \(\mathcal {CE}(a,b)\):
-
set of pairs \((\rho ,{{\varvec{j}}})\) satisfying the continuity equation Def. 4.1
- \({\mathrm {D}}_\upphi (u,v)\), \({\mathrm {D}}^{\pm }_\upphi (u,v)\):
-
integrands defining the Fisher information \({\mathscr {D}}\) (4.53)
- \({\mathscr {D}}\):
-
Fisher-information functional Def. 5.1
- \(E= V\times V\):
-
space of edges Assumption (\(V\!\pi \kappa \))
- \({\mathscr {E}}\), \({\mathrm {D}}({\mathscr {E}})\):
-
driving entropy functional and its domain (1.4) & Assumption (\({\mathscr {E}}\upphi \))
- \({\mathrm {F}}\):
-
vector field (1.11)
- \({\varvec{\vartheta }}_\rho ^{\pm }\):
-
, \(\rho \)-adjusted jump rates (4.18)
- \({\varvec{{\varvec{\vartheta }}}}\):
-
equilibrium jump rate (3.5)
- \(\kappa \):
-
jump kernel (1.3) & Assumption (\(V\!\pi \kappa \))
- \({\varvec{\kappa }}_{\gamma }\):
-
\(\gamma \otimes \kappa \) (2.33)
- \({\mathscr {L}}\):
-
Energy-Dissipation balance functional (1.18)
- \({{\mathcal {M}}}(\Omega ;{\mathbb {R}}^m)\), \({{\mathcal {M}}}^+(\Omega )\):
-
vector (positive) measures on \(\Omega \) Sec. 2
- \({\varvec{\upnu }}_\rho \):
-
edge measure in definition of \({\mathscr {R}}^*\), \({\mathscr {R}}\) (1.8), (1.19), (1.10)
- Q, \(Q^*\):
-
generator and dual generator (1.2)
- \({\mathscr {R}}\), \({\mathscr {R}}^*\):
- \({\mathbb {R}}_+ {:}{=} {[}0,\infty {)}\):
-
[\({{\mathsf {s}}}\)] symmetry map \((x,y) \mapsto (y,x)\) (3.1)
- \({\mathscr {S}}^-\):
-
relaxed slope (7.29)
- \(\Upsilon \):
-
perspective function associated with
- \(\Psi \) and \(\upalpha \):
-
(4.13)
- V:
-
space of states Assumption (\(V\!\pi \kappa \))
- \(\upphi \):
-
density of \({\mathscr {E}}\) (1.4) & Assumption (\({\mathscr {E}}\upphi \))
- \(\Psi \), \(\Psi ^*\):
-
dual pair of dissipation functions Assumption (\({\mathscr {R}}^*\Psi \upalpha \)), Lem. 3.1
- \({\mathscr {W}}\):
- \({\mathbb {W}}\):
-
\({\mathscr {W}}\)- action (4.89)
- \({{\mathsf {x}}},{{\mathsf {y}}}\):
-
coordinate maps \((x,y) \mapsto x\) and \((x,y)\mapsto y\) (3.1)
2 Preliminary results
2.1 Measure theoretic preliminaries
Let \((Y,{\mathfrak {B}})\) be a measurable space. When Y is endowed with a (metrizable and separable) topology \(\tau _Y\) we will often assume that \({\mathfrak {B}}\) coincides with the Borel \(\sigma \)-algebra \({\mathfrak {B}}(Y,\tau _Y)\) induced by \(\tau _Y\). We recall that \((Y,{\mathfrak {B}})\) is called a standard Borel space if it is isomorphic (as a measurable space) to a Borel subset of a complete and separable metric space; equivalently, one can find a Polish topology \(\tau _Y\) on Y such that \({\mathfrak {B}}={\mathfrak {B}}(Y,\tau _Y)\).
We will denote by \({{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) the space of \(\sigma \)-additive measures on \(\mu : {\mathfrak {B}}\rightarrow {\mathbb {R}}^m\) of finite total variation \(\Vert \mu \Vert _{TV}: =|\mu |(Y)<{+\infty }\), where for every \(B\in {\mathfrak {B}}\)
The set function \(|\mu |: {\mathfrak {B}}\rightarrow [0,{+\infty })\) is a positive finite measure on \({\mathfrak {B}}\) [3, Thm. 1.6] and \(({{\mathcal {M}}}(Y;{\mathbb {R}}^m),\Vert \cdot \Vert _{TV})\) is a Banach space.
In the case \(m=1\), we will simply write \({{\mathcal {M}}}(Y)\), and we shall denote the space of positive finite measures on \({\mathfrak {B}}\) by \({{\mathcal {M}}}^+(Y)\). For \(m>1\), we will identify any element \(\mu \in {{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) with a vector \((\mu ^1,\ldots ,\mu ^m)\), with \(\mu ^i \in {{\mathcal {M}}}(Y)\) for all \(i=1,\ldots , m\). If \(\varphi =(\varphi ^1,\ldots ,\varphi ^m)\in \mathrm {B}_{\mathrm {b}}(Y;{\mathbb {R}}^m)\), the set of bounded \({\mathbb {R}}^m\)-valued \({\mathfrak {B}}\)-measurable maps, the duality between \(\mu \in {{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) and \(\varphi \) can be expressed by
For every \(\mu \in {{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) and \(B\in {\mathfrak {B}}\) we will denote by  the restriction of \(\mu \) to B, i.e.
the restriction of \(\mu \) to B, i.e.  for every \(A\in {\mathfrak {B}}\).
for every \(A\in {\mathfrak {B}}\).
Let \((X,{\mathfrak {A}})\) be another measurable space and let \({{\mathsf {p}}}:X\rightarrow Y\) a measurable map. For every \(\mu \in {{\mathcal {M}}}(X;{\mathbb {R}}^m)\) we will denote by \({{\mathsf {p}}}_\sharp \mu \) the push-forward measure obtained by
For every couple \(\mu \in {{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) and \(\gamma \in {{\mathcal {M}}}^+(Y)\) there exist a unique (up to the modification in a \(\gamma \)-negligible set) \(\gamma \)-integrable map \(\frac{\mathrm {d}\mu }{\mathrm {d}\gamma }: Y\rightarrow {\mathbb {R}}^m\), a \(\gamma \)-negligible set \(N\in {\mathfrak {B}}\) and a unique measure \(\mu ^\perp \in {{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) yielding the Lebesgue decomposition

2.2 Convergence of measures
Besides the topology of convergence in total variation (induced by the norm \(\Vert \cdot \Vert _{TV}\)), we will also consider the topology of setwise convergence, i.e. the coarsest topology on \({{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) making all the functions
continuous. For a sequence \((\mu _n)_{n\in {\mathbb {N}}}\) and a candidate limit \(\mu \) in \({{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) we have the following equivalent characterizations of the corresponding convergence [9, §4.7(v)]:
-
(1)
Setwise convergence:
$$\begin{aligned} \lim _{n\rightarrow {+\infty }}\mu _n(B)=\mu (B)\qquad \text {for every set }B\in {\mathfrak {B}}. \end{aligned}$$(2.3) -
(2)
Convergence in duality with \(\mathrm {B}_{\mathrm {b}}(Y;{\mathbb {R}}^m)\):
$$\begin{aligned} \lim _{n\rightarrow {+\infty }}\langle \mu _n,\varphi \rangle = \langle \mu ,\varphi \rangle \qquad \text {for every }\varphi \in \mathrm {B}_{\mathrm {b}}(Y;{\mathbb {R}}^m). \end{aligned}$$(2.4) -
(3)
Weak topology of the Banach space: the sequence \(\mu _n\) converges to \(\mu \) in the weak topology of the Banach space \(({{\mathcal {M}}}(Y;{\mathbb {R}}^m);\Vert \cdot \Vert _{TV})\).
-
(4)
Weak \(L^1\)-convergence of the densities: there exists a common dominating measure \(\gamma \in {{\mathcal {M}}}^+(Y)\) such that \(\mu _n\ll \gamma \), \(\mu \ll \gamma \) and
$$\begin{aligned} \frac{\mathrm {d}\mu _n}{\mathrm {d}\gamma }\rightharpoonup \frac{\mathrm {d}\mu }{\mathrm {d}\gamma } \quad \text {weakly in }L^1(Y,\gamma ;{\mathbb {R}}^m). \end{aligned}$$(2.5) -
(5)
Alternative form of weak \(L^1\)-convergence: (2.5) holds for every common dominating measure \(\gamma \).
We will refer to setwise convergence for sequences satisfying one of the equivalent properties above. The above topologies also share the same notion of compact subsets, as stated in the following useful theorem, cf. [9, Theorem 4.7.25], where we shall denote by \(\sigma ({{\mathcal {M}}}(Y;{\mathbb {R}}^m) ; \mathrm {B}_{\mathrm {b}}(Y;{\mathbb {R}}^m) )\) the weak topology on \({{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) induced by the duality with \(\mathrm {B}_{\mathrm {b}}(Y;{\mathbb {R}}^m)\).
Theorem 2.1
For every set \(\emptyset \ne M\subset {{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) the following properties are equivalent:
-
(1)
M has a compact closure in the topology of setwise convergence.
-
(2)
M has a compact closure in the topology \(\sigma ({{\mathcal {M}}}(Y;{\mathbb {R}}^m) ; \mathrm {B}_{\mathrm {b}}(Y;{\mathbb {R}}^m) )\).
-
(3)
M has a compact closure in the weak topology of \(({{\mathcal {M}}}(Y;{\mathbb {R}}^m);\Vert \cdot \Vert _{TV})\).
-
(4)
Every sequence in M has a subsequence converging on every set of \({\mathfrak {B}}\).
-
(5)
There exists a measure \(\gamma \in {{\mathcal {M}}}^+(Y)\) such that
$$\begin{aligned} \forall \,\varepsilon>0\ \exists \,\delta >0: \quad B\in {\mathfrak {B}},\ \gamma (B)\le \delta \quad \Rightarrow \quad \sup _{\mu \in M}\mu (B)\le \varepsilon . \end{aligned}$$(2.6) -
(6)
There exists a measure \(\gamma \in {{\mathcal {M}}}^+(Y)\) such that \(\mu \ll \gamma \) for every \(\mu \in M\) and the set \(\{\mathrm {d}\mu /\mathrm {d}\gamma :\mu \in M\}\) has compact closure in the weak topology of \(L^1(Y,\gamma ;{\mathbb {R}}^m)\).
We also recall a useful characterization of weak compactness in \(L^1\).
Theorem 2.2
Let \(\gamma \in {{\mathcal {M}}}^+(Y)\) and \(\emptyset \ne F\subset L^1(Y,\gamma ;{\mathbb {R}}^m)\). The following properties are equivalent:
-
(1)
F has compact closure in the weak topology of \(L^1(Y,\gamma ;{\mathbb {R}}^m)\);
-
(2)
F is bounded in \(L^1(Y,\gamma ;{\mathbb {R}}^m)\) and equi-absolutely continuous, i.e.
$$\begin{aligned} \forall \,\varepsilon>0\ \exists \,\delta >0: \quad B\in {\mathfrak {B}},\ \gamma (B)\le \delta \quad \Rightarrow \quad \sup _{f\in F}\int _B |f|\,\mathrm {d}\gamma \le \varepsilon . \end{aligned}$$(2.7) -
(3)
There exists a convex and superlinear function \(\beta :{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) such that
$$\begin{aligned} \sup _{f\in F}\int _Y \beta (|f|)\,\mathrm {d}\gamma <{+\infty }. \end{aligned}$$(2.8)
The name ‘equi-absolute continuity’ above derives from the interpretation that the measure \(f\gamma \) is absolutely continuous with respect to \(\gamma \) in a uniform manner; ‘equi-absolute continuity’ is a shortening of Bogachev’s terminology ‘F has uniformly absolutely continuous integrals’ [9, Def. 4.5.2]. A fourth equivalent property is equi-integrability with respect to \(\gamma \) [9, Th. 4.5.3], a fact that we will not use.
When Y is endowed with a (separable and metrizable) topology \(\tau _Y\), we will use the symbol \(\mathrm {C}_{\mathrm {b}}(Y;{\mathbb {R}}^m) \) to denote the space of bounded \({\mathbb {R}}^m\)-valued continuous functions on \((Y,\tau _Y)\). We will consider the corresponding weak topology \(\sigma ({{\mathcal {M}}}(Y;{\mathbb {R}}^m);\mathrm {C}_{\mathrm {b}}(Y;{\mathbb {R}}^m))\) induced by the duality with \(\mathrm {C}_{\mathrm {b}}(Y;{\mathbb {R}}^m)\). Prokhorov’s Theorem yields that a subset \(M\subset {{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) has compact closure in this topology if it is bounded in the total variation norm and it is equally tight, i.e.
It is obvious that for a sequence \((\mu _n)_{n\in {\mathbb {N}}}\) convergence in total variation implies setwise convergence (or in duality with bounded measurable functions), and setwise convergence implies weak convergence in duality with bounded continuous functions.
2.3 Convex functionals and concave transformations of measures
We will use the following construction several times. Let \(\uppsi :{\mathbb {R}}^m\rightarrow [0,{+\infty }]\) be convex and lower semicontinuous and let us denote by \(\uppsi ^\infty :{\mathbb {R}}^m\rightarrow [0,{+\infty }]\) its recession function
which is a convex, lower semicontinuous, and positively 1-homogeneous map with \(\uppsi ^\infty (0)=0\). We define the functional \({\mathscr {F}}_\uppsi :{{\mathcal {M}}}(Y;{\mathbb {R}}^m) \times {{\mathcal {M}}}^+(Y)\mapsto [0,{+\infty }]\) by
Note that when \(\uppsi \) is superlinear then \(\uppsi ^\infty (x)={+\infty }\) in \({\mathbb {R}}^m\setminus \{0\}\). Equivalently,
We collect in the next Lemma a list of useful properties.
Lemma 2.3
-
(1)
When \(\uppsi \) is also positively 1-homogeneous, then \(\uppsi \equiv \uppsi ^\infty \), \({\mathscr {F}}_\uppsi (\cdot |\nu )\) is independent of \(\nu \) and will also be denoted by \({\mathscr {F}}_\uppsi (\cdot )\): it satisfies
$$\begin{aligned} {\mathscr {F}}_\uppsi (\mu ) =\int _Y \uppsi \left( \frac{\mathrm {d}\mu }{\mathrm {d}\gamma }\right) \,\mathrm {d}\gamma \quad \text {for every }\gamma \in {{\mathcal {M}}}^+(Y)\text { such that } \mu \ll \gamma . \end{aligned}$$(2.13) -
(2)
If \({{\hat{\uppsi }}}:{\mathbb {R}}^{m+1}\rightarrow [0,\infty ]\) denotes the 1-homogeneous, convex, perspective function associated with \(\uppsi \) by
$$\begin{aligned} {{\hat{\uppsi }}}(z,t){:}{=} {\left\{ \begin{array}{ll} \uppsi (z/t)t&{}\text {if }t>0,\\ \uppsi ^\infty (z)&{}\text {if }t=0,\\ {+\infty }&{}\text {if }t<0, \end{array}\right. } \end{aligned}$$(2.14)then
$$\begin{aligned} {\mathscr {F}}_\uppsi (\mu |\nu )={\mathscr {F}}_{{{\hat{\uppsi }}}}(\mu ,\nu )\quad \text {for every } (\mu ,\nu ) \in {{\mathcal {M}}}(Y;{\mathbb {R}}^m)\times {{\mathcal {M}}}^+(Y) \end{aligned}$$(2.15)with \({\mathscr {F}}_{{{\hat{\uppsi }}}}\) defined as in (2.13).
-
(3)
In particular, if \(\gamma \in {{\mathcal {M}}}^+(Y)\) is a common dominating measure such that \(\mu =u\gamma \), \(\nu =v\gamma \), and \(Y'{:}{=}\{x\in Y:v(x)>0\}\) we also have
$$\begin{aligned} {\mathscr {F}}_\uppsi (\mu |\nu )= \int _Y {{\hat{\uppsi }}}(u,v)\,\mathrm {d}\gamma =\int _{Y'} \uppsi (u/v)v\,\mathrm {d}\gamma + \int _{Y\setminus Y'} \uppsi ^\infty (u)\,\mathrm {d}\gamma . \end{aligned}$$(2.16) -
(4)
The functional \({\mathscr {F}}_\uppsi \) is convex; if \(\uppsi \) is also positively 1-homogeneous then
$$\begin{aligned} \begin{aligned} {\mathscr {F}}_\uppsi (\mu +\mu ')&\le {\mathscr {F}}_\uppsi (\mu )+{\mathscr {F}}_\uppsi (\mu ')\\ {\mathscr {F}}_\uppsi (\mu +\mu ')&= {\mathscr {F}}_\uppsi (\mu )+{\mathscr {F}}_\uppsi (\mu ')\quad \text {if }\mu \perp \mu '. \end{aligned} \end{aligned}$$(2.17) -
(5)
Jensen’s inequality:
 (2.18)
(2.18)(with \(\mu = \mu ^a + \mu ^\perp \) the Lebesgue decomposition of \(\mu \) w.r.t. \(\nu \)).
-
(6)
If \(\uppsi (0)=0\) then for every \(\mu \in {{\mathcal {M}}}(Y,{\mathbb {R}}^m)\), \(\nu ,\nu '\in {{\mathcal {M}}}^+(Y)\)
$$\begin{aligned} \nu \le \nu '\quad \Rightarrow \quad {\mathscr {F}}_\uppsi (\mu |\nu )\ge {\mathscr {F}}_\uppsi (\mu |\nu '). \end{aligned}$$(2.19) -
(7)
\({\mathscr {F}}_\uppsi \) is sequentially lower semicontinuous in \({{\mathcal {M}}}(Y;{\mathbb {R}}^m) \times {{\mathcal {M}}}^+(Y)\) with respect to the topology of setwise convergence.
-
(8)
If \({\mathfrak {B}}\) is the Borel family induced by a Polish topology \(\tau _Y\) on Y, \({\mathscr {F}}_\uppsi \) is lower semicontinuous with respect to weak convergence (in duality with continuous bounded functions).
Proof
The above properties are mostly well known; we give a quick sketch of the proofs of the various claims for the ease of the reader.
(1) Let us set \(u{:}{=}\mathrm {d}\mu /\mathrm {d}\nu \), \(u^\perp {:}{=}\mathrm {d}\mu ^\perp /\mathrm {d}|\mu |\) and let \(N\in {\mathfrak {B}}\) \(\nu \)-negligible such that  . We also set \(N'{:}{=}\{y\in Y\setminus N:|u(y)|> 0\}\); notice that
. We also set \(N'{:}{=}\{y\in Y\setminus N:|u(y)|> 0\}\); notice that  . If v is the Lebesgue density of \(|\mu |\) w.r.t. \(\gamma \), since \(\uppsi =\uppsi ^\infty \) is positively 1-homogeneous and \(\uppsi (0)=0\), we have
. If v is the Lebesgue density of \(|\mu |\) w.r.t. \(\gamma \), since \(\uppsi =\uppsi ^\infty \) is positively 1-homogeneous and \(\uppsi (0)=0\), we have
where we also used the fact that \(|\mu |(Y\setminus (N\cup N'))=0\), so that \(\mathrm {d}\mu /\mathrm {d}\gamma =0\) \(\gamma \)-a.e. on \(Y\setminus (N\cup N').\)
(2) Since \({{\hat{\uppsi }}}\) is 1-homogeneous, we can apply the previous claim and evaluate \({\mathscr {F}}_{{{\hat{\uppsi }}}}(\mu ,\nu )\) by choosing the dominating measure \(\gamma {:}{=}\nu +\mu ^\perp \).
(3) It is an immediate consequence of the first two claims.
(4) By (2.15) it is sufficient to consider the 1-homogeneous case. The convexity then follows by the convexity of \(\uppsi \) and by choosing a common dominating measure to represent the integrals. Relations (2.17) are also immediate.
(5) Using (2.15) and selecting a dominating measure \(\gamma \) with \(\gamma (B)=1\), Jensen’s inequality applied to the convex functional \({{\hat{\uppsi }}}\) yields

Applying now the above inequality to the mutally singular couples \((\mu ^a,\nu )\) and \((\mu ^\perp ,0)\) and using the second identity of (2.17) we obtain (2.18).
(6) We apply (2.15) and the first identity of (2.16), observing that if \(\uppsi (0)=0\) then \({{\hat{\uppsi }}}\) is decreasing with respect to its second argument.
(7) By (2.15) it is not restrictive to assume that \(\Psi \) is 1-homogeneous. If \((\mu _n)_n\) is a sequence setwise converging to \(\mu \) in \({{\mathcal {M}}}(Y;{\mathbb {R}}^m)\) we can find a common dominating measure \(\gamma \) such that (2.5) holds. The claimed property is then reduced to the weak lower semicontinuity of the functional
in \(L^1(Y,\gamma ;{\mathbb {R}}^m)\). Since the functional of (2.20) is convex and strongly lower semicontinuous in \(L^1(Y,\gamma ;{\mathbb {R}}^m)\) (thanks to Fatou’s Lemma), it is weakly lower semicontinuous as well.
(8) It follows by the same argument of [3, Theorem 2.34], by using a suitable dual formulation which holds also in Polish spaces, where all the finite Borel measures are Radon (see e.g. [47, Theorem 2.7] for positive measures). \(\square \)
2.3.1 Concave transformation of vector measures
Let us set \({\mathbb {R}}_+{:}{=}[0,{+\infty }[\), \({\mathbb {R}}^m_+{:}{=}({\mathbb {R}}_+)^m\), and let \(\upalpha :{\mathbb {R}}^m_+\rightarrow {\mathbb {R}}_+\) be a continuous and concave function. It is obvious that \(\upalpha \) is non-decreasing with respect to each variable. As for (2.10), the recession function \(\upalpha ^\infty \) is defined by
We define the corresponding map \(\upalpha :{{\mathcal {M}}}(Y;{\mathbb {R}}^m_+)\times {{\mathcal {M}}}^+(Y)\rightarrow {{\mathcal {M}}}^+(Y)\) by
where as usual \(\mu =\frac{\mathrm {d}\mu }{\mathrm {d}\gamma }\gamma +\mu ^\perp \) is the Lebesgue decomposition of \(\mu \) with respect to \(\gamma \); in what follows, we will use the short-hand \(\mu _\gamma {:}{=} \frac{\mathrm {d}\mu }{\mathrm {d}\gamma }\gamma \). We also mention in advance that, for shorter notation we will write \(\upalpha [\mu _1,\mu _2|\gamma ]\) in place of \(\upalpha [(\mu _1,\mu _2)|\gamma ]\).
Like for \({\mathscr {F}}\), it is not difficult to check that \(\upalpha [\mu |\gamma ]\) is independent of \(\gamma \) if \(\upalpha \) is positively 1-homogeneous (and thus coincides with \(\upalpha ^\infty \)). If we define the perspective function \({\hat{\upalpha }}:{\mathbb {R}}_+^{m+1}\rightarrow {\mathbb {R}}_+\)
we also get \(\upalpha [\mu |\gamma ]={{\hat{\upalpha }}}(\mu ,\gamma )\).
We denote by \(\upalpha _*:{\mathbb {R}}^m_+\rightarrow [-\infty ,0]\) the upper semicontinuous concave conjugate of \(\upalpha \)
The function \(\upalpha _*\) provides simple affine upper bounds for \(\upalpha \)
and Fenchel duality yields
We will also use that
Indeed, on the one hand for every \(y \in D(\upalpha _*)\) and \(t>0\) we have that
by the arbitrariness of \(t>0\), we conclude that \(\upalpha ^\infty (z) \le y \cdot z\) for every \(y \in D(\upalpha _*)\). On the other hand, by (2.26) we have
where we have used that \(-\upalpha ^*(y) - \upalpha (0) \ge 0\) since \(\upalpha (0) = \mathrm{inf}_{y\in D(\upalpha ^*) } ({-}\upalpha ^*(y))\).
For every Borel set \(B\subset Y\), Jensen’s inequality yields (recall the notation \(\mu _\gamma = \frac{\mathrm {d}\mu }{\mathrm {d}\gamma }\gamma \))
In fact, for every \(y,y'\in D(\upalpha _*)\),
Taking the infimum with respect to y and \(y'\), and recalling (2.26) and (2.27), we find (2.28). Choosing \(y=y'\) in the previous formula we also obtain the linear upper bound
2.4 Disintegration and kernels
Let \((X,{\mathfrak {A}})\) and \((Y,{\mathfrak {B}})\) be measurable spaces and let \(\big (\kappa (x,\cdot )\big )_{x\in X}\) be a \({\mathfrak {A}}\)-measurable family of measures in \({{\mathcal {M}}}^+(Y)\), i.e.
We will set
and we say that \(\kappa \) is a bounded kernel if \(\Vert \kappa _Y\Vert _\infty \) is finite. If \(\gamma \in {{\mathcal {M}}}^+(X)\) and
then Fubini’s Theorem [18, II, 14] shows that there exists a unique measure \({\varvec{\kappa }}_{\gamma }(\mathrm {d}x,\mathrm {d}y)= \gamma (\mathrm {d}x)\kappa (x,\mathrm {d}y)\) on \((X\times Y,{\mathfrak {A}}\otimes {\mathfrak {B}})\) such that
If \(X=Y\), the measure \(\gamma \) is called invariant if \({\varvec{\kappa }}_{\gamma }\) has the same marginals; equivalently
where \( {{\mathsf {y}}}:E\rightarrow V \) denotes the projection on the second component, cf. (3.1) ahead. We say that \(\gamma \) is reversible if it satisfies the detailed balance condition, i.e. \({\varvec{\kappa }}_{\gamma }\) is symmetric: \({{\mathsf {s}}}_\sharp {\varvec{\kappa }}_{\gamma }={\varvec{\kappa }}_{\gamma }\). The concepts of invariance and detailed balance correspond to the analogous concepts in stochastic-process theory; see Sect. 3.1. It is immediate to check that reversibility implies invariance.
If \(f:X\times Y\rightarrow {\mathbb {R}}\) is a positive or bounded measurable function, then
and
Conversely, if X, Y are standard Borel spaces, \(\varvec{\kappa }\in {{\mathcal {M}}}^+(X\times Y)\) (with the product \(\sigma \)-algebra) and the first marginal \({{\mathsf {p}}}^X_\sharp \varvec{\kappa } \) of \(\varvec{\kappa }\) is absolutely continuous with respect to \(\gamma \in {{\mathcal {M}}}^+(V)\), then we may apply the disintegration Theorem [9, Corollary 10.4.15] to find a \(\gamma \)-integrable kernel \((\kappa (x,\cdot ))_{x\in X}\) such that \({\varvec{\kappa }}={\varvec{\kappa }}_{\gamma }\).
We will often apply the above construction in two cases: when \(X=Y{:}{=}V\), the main domain of our evolution problems (see Assumptions (\(V\!\pi \kappa \)) below), and when \(X{:}{=}I=(a,b)\) is an interval of the real line endowed with the Lebesgue measure \(\lambda \). In this case, we will denote by t the variable in I and by \((\mu _t)_{t\in X}\) a measurable family in \({{\mathcal {M}}}(Y)\) parametrized by \(t\in I\):
Lemma 2.4
If \(\mu _n\in {{\mathcal {M}}}(X)\) is a sequence converging to \(\mu \) setwise and \((\kappa (x,\cdot ))_{x\in X}\) is a bounded measurable kernel in \({{\mathcal {M}}}^+(Y)\), then \({\varvec{\kappa }}_{\mu _n}\rightarrow {\varvec{\kappa }}_{\mu }\) setwise in \({{\mathcal {M}}}(X\times Y,{\mathfrak {A}}\otimes {\mathfrak {B}})\).
If X, Y are Polish spaces and \(\kappa \) also satisfies the weak Feller property, i.e.
(where ‘weak’ means in duality with continuous bounded functions), then for every weakly converging sequence \(\mu _n\rightarrow \mu \) in \({{\mathcal {M}}}(X)\) we have \({\varvec{\kappa }}_{\mu _n}\rightarrow {\varvec{\kappa }}_{\mu }\) weakly as well.
Proof
If \(f:X\times Y\rightarrow {\mathbb {R}}\) is a bounded \({\mathfrak {A}}\otimes {\mathfrak {B}}\)-measurable map, then by (2.35) also the map \(\kappa f\) is bounded and \({\mathfrak {A}}\)-measurable so that
showing the setwise convergence. The other statement follows by a similar argument. \(\square \)
3 Jump processes, large deviations, and their generalized gradient structures
3.1 The systems of this paper
In the Introduction we described jump processes on V with kernel \(\kappa \), and showed that the evolution equation \(\partial _t\rho _t = Q^*\rho _t\) for the law \(\rho _t\) of the process is a generalized gradient flow characterized by a driving functional \({\mathscr {E}}\) and a dissipation potential \({\mathscr {R}}^*\).
The mathematical setup of this paper is slightly different. Instead of starting with an evolution equation and proceeding to the generalized gradient system, our mathematical development starts with the generalized gradient system; we then consider the equation to be defined by this system. In this Section, therefore, we describe assumptions that we make on \({\mathscr {E}}\) and \({\mathscr {R}}^*\) that will allow us to set up the rigorous functional framework for the evolution equation (1.9).
We first state the assumptions about the sets V of ‘vertices’ and \(E{:}{=}V\times V\) of ‘edges’. ‘Edges’ are identified with ordered pairs (x, y) of vertices \(x,y\in V\). We will denote by \({\mathsf {x}},{\mathsf {y}}:E\rightarrow V\) and \({\mathsf {s}}:E\rightarrow E\) the coordinate and the symmetry maps defined by

The measure \(\pi \in {{\mathcal {M}}}^+(V)\) often is referred to as the invariant measure, and it will be stationary under the evolution generated by the generalized gradient system. By Fubini’s Theorem (see Sect. 2.4) we also introduce the measure \({\varvec{{\varvec{\vartheta }}}}\) on \(E\) given by
Note that the invariance of the measure \(\pi \) and the detailed balance condition (3.3) can be rephrased in terms of \({\varvec{{\varvec{\vartheta }}}}\) as
Conversely, if we choose a symmetric measure \({\varvec{{\varvec{\vartheta }}}}\in {{\mathcal {M}}}^+(E)\) such that
then the disintegration Theorem [9, Corollary 10.4.15] shows the existence of a bounded measurable kernel \((\kappa (x,\cdot ))_{x\in X}\) satisfying (3.3) and (3.5).
We next turn to the driving functional, which is given by the construction in (2.11) and (2.12) for a superlinear density \(\uppsi =\upphi \) and for the choice \(\gamma =\pi \).

Under these assumptions the functional \({\mathscr {E}}\) is lower semicontinuous on \({{\mathcal {M}}}^+(V)\) both with respect to the topology of setwise convergence, and any compatible weak topology (see Lemma 2.3). A central example was already mentioned in the introduction, i.e. the Boltzmann-Shannon entropy function
Finally, we state our assumptions on the dissipation.

Note that since \(\upalpha \) is nonnegative, concave, and not trivially 0, it cannot vanish in the interior of \({\mathbb {R}}^2_+\), i.e.
The examples that we gave in the introduction of the cosh-type dissipation (1.17a) and the quadratic dissipation (1.17b) both fit these assumptions; other examples are
In some cases we will use an additional property, namely that \(\upalpha \) is positively 1-homogeneous, i.e. \(\upalpha (\lambda u_1,\lambda u_2) = \lambda \upalpha (u_1,u_2)\) for all \(\lambda \ge 0\). This 1-homogeneity is automatically satisfied under the compatibility condition (1.13), with the Boltzmann entropy function \(\upphi (s) = s\log s - s + 1\).
Concaveness of \(\upalpha \) is a natural assumption in view of the convexity of \({\mathscr {R}}\) (cf. Remark 1.1 and Lemma 4.10 ahead), while 1-homogeneity will make the definition of \({\mathcal {R}}\) independent of the choice of a reference measure. It is interesting to observe that the concavity and symmetry conditions, that one has to naturally assume to ensure the aforementioned properties of \({\mathscr {R}}\), were singled out for the analog of the function \(\upalpha \) in the construction of the distance yielding the quadratic gradient structure of [49].
The choices for \(\Psi ^*\) above generate corresponding properties for the Legendre dual \(\Psi \):
Lemma 3.1
Under Assumption (\({\mathscr {R}}^*\Psi \upalpha \)), the function \(\Psi : {\mathbb {R}}\rightarrow {\mathbb {R}}\) is even and satisfies
Proof
The superlinearity of \(\Psi ^*\) implies that \(\Psi (s)<{+\infty }\) for all \(s\in {\mathbb {R}}\), and similarly the finiteness of \(\Psi ^*\) on \({\mathbb {R}}\) implies that \(\Psi \) is superlinear. Since \(\Psi ^*\) is even, \(\Psi \) is convex and even, and therefore \(\Psi (s) \ge \Psi (0) = \sup _{\xi \in {\mathbb {R}}} [-\Psi ^*(\xi )] = 0.\) Furthermore, since for all \(p\in {\mathbb {R}}\), \(\mathrm{argmin}_{s\in {\mathbb {R}}} (\Psi (s) -p s)= \partial \Psi ^*(p)\) (see e.g. [77, Thm. 11.8]) and \(\Psi ^*\) is differentiable at every p, we conclude that \(\mathrm{argmin}_s (\Psi (s)-ps ) = \{(\Psi ^*)'(p)\}\); therefore each point of the graph of \(\Psi \) is an exposed point. It follows that \(\Psi \) is strictly convex, and \(\Psi (s)>0\) for all \(s\not =0\). \(\square \)
As described in the introduction, we use \(\Psi \), \(\Psi ^*\), and \(\upalpha \) to define the dual pair of dissipation potentials \({\mathscr {R}}\) and \({\mathscr {R}}^*\), which for a couple of measures \(\rho =u\pi \in {{\mathcal {M}}}^+(V)\) and \({{\varvec{j}}}\in {{\mathcal {M}}}(E)\) are formally given by
with
This expression for the edge measure \({\varvec{\upnu }}_\rho \) also is implicitly present in the structure built in [30, 49]. The above definitions are made rigorous in Definition 4.9 and in (4.20) below.
The three sets of conditions above, Assumptions (\(V\!\pi \kappa \)), (\({\mathscr {E}}\upphi \)), and (\({\mathscr {R}}^*\Psi \upalpha \)), are the main assumptions of this paper. Under these assumptions, the evolution equation (1.9) may be linear or nonlinear in \(\rho \). The equation coincides with the Forward Kolmogorov equation (1.2) if and only if condition (1.13) is satisfied, as shown below.
3.1.1 Calculation for (1.13)
Let us call \({\mathscr {Q}}[\rho ]\) the right-hand side of (1.9) and let us compute
for every \( \varphi \in \mathrm {B}_{\mathrm {b}}(V) \) and \(\rho \in {{\mathcal {M}}}^+(V)\) with \(\rho \ll \pi \). With \(u = \frac{\mathrm {d}\rho }{\mathrm {d}\pi } \) we thus obtain
Recalling the definitions (3.17) of \({\varvec{\upnu }}_\rho \) and (1.11) of \({\mathrm {F}}\), (3.18) thus becomes
where for \((*)\) we used the symmetry of \({\varvec{{\varvec{\vartheta }}}}\) (i.e. the detailed-balance condition). This calculation justifies (1.12).
In the linear case of (1.2) it is immediate to see that
Comparing (3.20) and (3.19) we obtain that \({\mathrm {F}}\) has to fulfill (1.13).
4 Curves in \({{\mathcal {M}}}^+(V)\)
A major challenge in any rigorous treatment of an equation such as (1.1) is finding a way to deal with the time derivative. The Ambrosio-Gigli-Savaré framework for metric-space gradient systems, for instance, is organized around absolutely continuous curves. These are a natural choice because on the one hand this class admits a ‘metric velocity’ that generalizes the time derivative, while on the other hand solutions are automatically absolutely continuous by the superlinear growth of the dissipation potential.
For the systems of this paper, a similar role is played by curves such that the ‘action’ \(\int {\mathscr {R}}\,\mathrm {d}t\) is finite; we show below that the superlinearity of \({\mathscr {R}}(\rho ,{{\varvec{j}}})\) in \({{\varvec{j}}}\) leads to similarly beneficial properties. In order to exploit this aspect, however, a number of intermediate steps need to be taken:
-
(a)
We define the class \(\mathcal {CE}(0,T)\) of solutions \((\rho ,{{\varvec{j}}})\) of the continuity equation (1.23) (Definition 4.1).
-
(b)
For such solutions, \(t\mapsto \rho _t\) is continuous in the total variation distance (Corollary 4.3).
-
(c)
We give a rigorous definition of the functional \({\mathscr {R}}\) (Definition 4.9), and describe its behaviour on absolutely continuous and singular parts of \((\rho ,{{\varvec{j}}})\) (Lemma 4.10 and Theorem 4.13).
-
(d)
If the action functional \(\int {\mathscr {R}}\) is finite along a solution \((\rho ,{{\varvec{j}}})\) of the continuity equation in [0, T], then the property that \(\rho _t\) is absolutely continuous with respect to \(\pi \) at some time \(t\in [0,T]\) propagates to all the interval [0, T] (Corollary 4.14).
-
(e)
We prove a chain rule for the derivative of convex entropies along curves of finite \({\mathscr {R}}\)-action (Theorem 4.16) and derive an estimate involving \({\mathscr {R}}\) and a Fisher-information-like term (Corollary 4.20).
-
(f)
If the action \(\int {\mathscr {R}}\) is uniformly bounded along a sequence \((\rho ^n,{{\varvec{j}}}^n)\in \mathcal {CE}(0,T)\), then the sequence is compact in an appropriate sense (Proposition 4.21).
Once properties (a)–(f) have been established, the next step is to consider finite-action curves that also connect two given values \(\mu ,\nu \), leading to the definition of the Dynamical-Variational Transport (DVT) cost
This definition is in the spirit of the celebrated Benamou-Brenier formula for the Wasserstein distance [8], generalized to a broader family of transport distances [20] and to jump processes [30, 49]. However, a major difference with those constructions is that \({\mathscr {W}}\) also depends on the time variable \(\tau \) and that \({\mathscr {W}}(\tau ,\cdot ,\cdot )\) is not a (power of a) distance, since \(\Psi \) is not, in general, positively homogeneous of any order. Indeed, when \({\mathscr {R}}\) is p-homogeneous in \({{\varvec{j}}}\), for \(p\in (1,{+\infty })\), we have (see also the discussion at the beginning of Sec. 7.1)
where \(d_{\mathscr {R}}\) is an extended distance and is a central object in the usual Minimizing-Movement construction. In Sect. 7, the DVT cost \({\mathscr {W}}\) will replace the rescaled p-power of the distance and play a similar role for the Minimizing-Movement approach.
For the rigorous construction of \({\mathscr {W}}\),
- (g)
-
(h)
we establish properties of \({\mathscr {W}}\) that generalize those of the metric-space version (4.2) (Theorem 4.26).
Finally,
-
(i)
we close the loop by showing that from a given functional \({\mathscr {W}}\) integrals of the form \(\int _a^b{\mathscr {R}}\) can be reconstructed (Proposition 4.27).
Throughout this section we adopt Assumptions (\(V\!\pi \kappa \)) and (\({\mathscr {R}}^*\Psi \upalpha \)).
4.1 The continuity equation
We now introduce the formulation of the continuity equation we will work with. Hereafter, for a given function \(\mu :I \rightarrow {{\mathcal {M}}}(V)\), or \(\mu : I \rightarrow {{\mathcal {M}}}(E)\), with \(I=[a,b]\subset {\mathbb {R}}\), we shall often write \(\mu _t\) in place of \(\mu (t)\) for a given \(t\in I\) and denote the time-dependent function \(\mu \) by \((\mu _t)_{t\in I}\). We will write \(\lambda \) for the Lebesgue measure on I. The following definition mimics those given in [4, Sec. 8.1] and [21, Def. 4.2].
Definition 4.1
(Solutions \((\rho ,{{\varvec{j}}})\) of the continuity equation) Let \(I=[a,b]\) be a closed interval of \({\mathbb {R}}\). We denote by \(\mathcal {CE}(I)\) the set of pairs \((\rho ,{{\varvec{j}}})\) given by
-
a family of time-dependent measures \(\rho =(\rho _t)_{t\in I} \subset {{\mathcal {M}}}^+(V)\), and
-
a measurable family \(({{\varvec{j}}}_t)_{t\in I} \subset {{\mathcal {M}}}(E)\) with \(\int _0^T |{{\varvec{j}}}_t|(E)\,\mathrm {d}t <{+\infty }\), satisfying the continuity equation
$$\begin{aligned} {{\dot{\rho }}} + {\overline{\mathrm {div}}}{{\varvec{j}}}=0 \quad \text { in } I\times V, \end{aligned}$$(4.3)in the following sense:
$$\begin{aligned} \int _V \varphi \,\mathrm {d}\rho _{t_2}-\int _V \varphi \,\mathrm {d}\rho _{t_1}= \iint _{J\times E} {{\overline{\nabla }}}\varphi \,\mathrm {d}{{\varvec{j}}}_\lambda \quad \text {for all }\varphi \in \mathrm {B}_{\mathrm {b}}(V),\ J=[t_1,t_2]\subset I. \end{aligned}$$(4.4)where \({{\varvec{j}}}_\lambda (\mathrm {d}t,\mathrm {d}x,\mathrm {d}y){:}{=}\lambda (\mathrm {d}t){{\varvec{j}}}_t(\mathrm {d}x,\mathrm {d}y)\).
Given \(\rho _0,\, \rho _1 \in {{\mathcal {M}}}^+(V)\), we will use the notation
Remark 4.2
The requirement (4.4) shows in particular that \(t\mapsto \rho _t\) is continuous with respect to the total variation metric. Choosing \(\varphi \equiv 1\) in (4.4), one immediately finds that
By the disintegration theorem, it is equivalent to assign the measurable family \(({{\varvec{j}}}_t)_{t\in I}\) in \({{\mathcal {M}}}(E)\) or the measure \({{\varvec{j}}}_\lambda \) in \({{\mathcal {M}}}(I\times E)\).
We can in fact prove a more refined property. The proof of the Corollary below is postponed to Appendix B.
Corollary 4.3
If \((\rho ,{{\varvec{j}}})\in \mathcal {CE}(0,T)\), then there exist a common dominating measure \(\gamma \in {{\mathcal {M}}}^+(V)\) (i.e., \(\rho _t \ll \gamma \) for all \(t\in [a,b]\)), and an absolutely continuous map \({{\tilde{u}}}:[a,b]\rightarrow L^1(V,\gamma )\) such that \(\rho _t=\tilde{u}_t\gamma \ll \gamma \) for every \(t\in [a,b]\).
The interpretation of the continuity equation in Definition 4.1—in duality with all bounded measurable functions—is quite strong, and in particular much stronger than the more common continuity in duality with continuous and bounded functions. However, this continuity equation can be recovered starting from a much weaker formulation. The following result illustrates this; it is a translation of [4, Lemma 8.1.2] (cf. also [21, Lemma 4.1]) to the present setting. The proof adapts the argument for [4, Lemma 8.1.2] and is given in Appendix B.
Lemma 4.4
(Continuous representative) Let \((\rho _t)_{t\in I} \subset {{\mathcal {M}}}^+(V)\) and \(({{\varvec{j}}}_t)_{t\in I}\) be measurable families that are integrable with respect to \(\lambda \) and let \(\tau \) be any separable and metrizable topology inducing \({\mathfrak {B}}\). If
holds for every \(\eta \in \mathrm {C}_\mathrm {c}^\infty ((a,b))\) and \(\zeta \in \mathrm {C}_{\mathrm {b}}(V,\tau )\), then there exists a unique curve \(I \ni t \mapsto {\tilde{\rho }}_t \in {{\mathcal {M}}}^+ (V)\) such that \({\tilde{\rho }}_t = \rho _t\) for \(\lambda \)-a.e. \(t\in I\). The curve \({{\tilde{\rho }}}\) is continuous in the total-variation norm with estimate
and satisfies
for all \(\varphi \in \mathrm {C}^1(I;\mathrm {B}_{\mathrm {b}}(V))\) and \(J=[t_1,t_2]\subset T\).
Remark 4.5
In (4.4) we can always replace \({{\varvec{j}}}\) with the positive measure \({{\varvec{j}}}^+{:}{=}({{\varvec{j}}}-{\mathsf {s}}_\#{{\varvec{j}}})_+ = (2{{\varvec{j}}}^{\flat })_+\), since \({\overline{\mathrm {div}}}{{\varvec{j}}}= {\overline{\mathrm {div}}}{{\varvec{j}}}^+\) (see Lemma B.1); therefore we can assume without loss of generality that \({{\varvec{j}}}\) is a positive measure.
As another immediate consequence of (4.4), the concatenation of two solutions of the continuity equation is again a solution; the result below also contains a statement about time rescaling of the solutions, whose proof follows from trivially adapting that of [4, Lemma 8.1.3] and is thus omitted.
Lemma 4.6
(Concatenation and time rescaling)
-
(1)
Let \((\rho ^i,{{\varvec{j}}}^i) \in \mathcal {CE}(0,T_i)\), \(i=1,2\), with \(\rho _{T_1}^1 = \rho _0^2\). Define \((\rho _t,{{\varvec{j}}}_t)_{t\in [0,T_{1}+T_2]}\) by
$$\begin{aligned} \rho _t: = {\left\{ \begin{array}{ll} \rho _t^1 &{} \text { if } t \in [0,T_1], \\ \rho _{t-T_1}^2 &{} \text { if } t \in [T_1,T_1+T_2], \end{array}\right. } \qquad \qquad {{\varvec{j}}}_t: = {\left\{ \begin{array}{ll} {{\varvec{j}}}_t^1 &{} \text { if } t \in [0,T_1], \\ {{\varvec{j}}}_{t-T_1}^2 &{} \text { if } t \in [T_1,T_1+T_2]\,. \end{array}\right. } \end{aligned}$$Then, \((\rho ,{{\varvec{j}}}) \in \mathcal {CE}(0,T_1+T_2)\).
-
(2)
Let \({\mathsf {t}} : [0,{\hat{T}}] \rightarrow [0,T]\) be strictly increasing and absolutely continuous, with inverse \({\mathsf {s}}: [0,T]\rightarrow [0,{\hat{T}}]\). Then, \((\rho , {{\varvec{j}}}) \in \mathcal {CE}(0,T)\) if and only if \({\hat{\rho }}: = \rho \circ {\mathsf {t}}\) and \({{\hat{{{\varvec{j}}}}}} : = {\mathsf {t}}' ({{\varvec{j}}}{\circ } {\mathsf {t}})\) fulfill \(({{\hat{\rho }}}, {{\hat{{{\varvec{j}}}}}} ) \in \mathcal {CE}(0,{{\hat{T}}})\).
4.2 Definition of the dissipation potential \({\mathscr {R}}\)
In this section we give a rigorous definition of the dissipation potential \({\mathscr {R}}\), following the formal descriptions above. In the special case when \(\rho \) and \({{\varvec{j}}}\) are absolutely continuous, i.e.
we set
and in this case we can define the functional \({\mathscr {R}}\) by the direct formula
Recalling the definition of the perspective function \({{\hat{\Psi }}}\) (2.14), we can also write (4.11) in the equivalent and more compact form
so that it is natural to introduce the function \(\Upsilon : [0,{+\infty })\times [0,{+\infty })\times {\mathbb {R}}\rightarrow [0,{+\infty }] \),
observing that
Lemma 4.7
The function \(\Upsilon :[0,{+\infty })\times [0,{+\infty })\times {\mathbb {R}}\rightarrow [0,{+\infty }]\) defined above is convex and lower semicontinuous, with recession functional
For any \(u,v\in [0,\infty )\) with \(\upalpha ^\infty (u,v)>0\), the map \(w\mapsto \Upsilon (u,v,w)\) is strictly convex.
If \(\upalpha \) is positively 1-homogeneous then \(\Upsilon \) is positively 1-homogeneous as well.
Proof
Note that \(\Upsilon \) may be equivalently represented in the form
The convexity of \(f_\xi \) for each \(\xi \in {\mathbb {R}}\) readily follows from its linearity in w and the convexity of \(-\upalpha \) in (u, v). Therefore, \(\Upsilon \) is convex and lower semicontinuous as the pointwise supremum of a family of convex continuous functions.
The characterization (4.15) of \(\Upsilon ^\infty \) follows from observing that \(\Upsilon (0,0,0)={{\hat{\Psi }}}(0,0)=0\) and using the 1-homogeneity of \({{\hat{\Psi }}}\):
where the last equality follows from the continuity of \(r\mapsto {{\hat{\Psi }}}(w,r)\) for all \(w\in {\mathbb {R}}\).
The strict convexity of \(w\mapsto \Upsilon (u,v,w)\) for any \(u,v\in [0,\infty )\) with \(\upalpha ^\infty (u,v)>0\) follows directly from the strict convexity of \(\Psi \) (cf. Lemma 3.1). \(\square \)
The choice (4.14) provides a rigorous definition of \({\mathscr {R}}\) for couples of measures \((\rho ,{{\varvec{j}}})\) that are absolutely continuous with respect to \(\pi \) and \({\varvec{\vartheta }}\). In order to extend \({\mathscr {R}}\) to pairs \((\rho ,{{\varvec{j}}})\) that are not absolutely continuous, it is useful to interpret the measure
in the integral of (4.11) in terms of a suitable concave transformation as in (2.22) of two couplings generated by \(\rho \). We therefore introduce the measures
observing that
We thus obtain that (4.17), (4.11) and (4.14) can be equivalently written as
where \(\upalpha [{\varvec{\vartheta }}^-_\rho ,{\varvec{\vartheta }}^+_\rho |{\varvec{{\varvec{\vartheta }}}}]\) stands for \(\upalpha [({\varvec{\vartheta }}^-_\rho ,{\varvec{\vartheta }}^+_\rho )|{\varvec{{\varvec{\vartheta }}}}]\), and the functional \( {\mathscr {F}}_\psi (\cdot | \cdot )\) is from (2.11), and also
again writing for shorter notation \({\mathscr {F}}_\Upsilon ({\varvec{\vartheta }}^-_\rho ,{\varvec{\vartheta }}^+_\rho ,2{{\varvec{j}}}|{\varvec{{\varvec{\vartheta }}}})\) in place of \({\mathscr {F}}_\Upsilon (({\varvec{\vartheta }}^-_\rho ,{\varvec{\vartheta }}^+_\rho ,2{{\varvec{j}}}) |{\varvec{{\varvec{\vartheta }}}})\).
Therefore we can use the same expressions (4.20) and (4.21) to extend the functional \({\mathscr {R}}\) to measures \(\rho \) and \({{\varvec{j}}}\) that need not be absolutely continuous with respect to \(\pi \) and \({\varvec{{\varvec{\vartheta }}}}\); the next lemma shows that they provide equivalent characterizations. We introduce the functions \(u^{\pm }:E\rightarrow {\mathbb {R}}\), adopting the notation
(Recall that \({{\mathsf {x}}}\) and \({{\mathsf {y}}}\) denote the coordinate maps from \(E\) to V).
Lemma 4.8
For every \(\rho \in {{\mathcal {M}}}^+(V)\) and \({{\varvec{j}}}\in {{\mathcal {M}}}(E)\) we have
If \(\rho =\rho ^a+\rho ^\perp \) and \({{\varvec{j}}}={{\varvec{j}}}^a+{{\varvec{j}}}^\perp \) are the Lebesgue decompositions of \(\rho \) and \({{\varvec{j}}}\) with respect to \(\pi \) and \({\varvec{{\varvec{\vartheta }}}}\), respectively, we have
Proof
Let us consider the Lebesgue decomposition \(\rho =\rho ^a+\rho ^\perp \), \(\rho ^a=u\pi \), and a corresponding partition of V in two disjoint Borel sets R, P such that  ,
,  and \(\pi (P)=0\), which yields
and \(\pi (P)=0\), which yields

Since \({\varvec{{\varvec{\vartheta }}}}(P\times V)={\varvec{{\varvec{\vartheta }}}}(V\times P) \le \Vert \kappa _V\Vert _\infty \pi (P)=0\), \({\varvec{\vartheta }}^{\pm }_{\rho ^\perp }\) are singular with respect to \({\varvec{{\varvec{\vartheta }}}}\).
Let us also consider the Lebesgue decomposition \({{\varvec{j}}}={{\varvec{j}}}^a+{{\varvec{j}}}^\perp \) of \({{\varvec{j}}}\) with respect to \({\varvec{{\varvec{\vartheta }}}}\). We can select a measure \({\varvec{\varsigma }}\in {{\mathcal {M}}}^+(E)\) such that \({\varvec{\vartheta }}^{\pm }_{\rho ^\perp }=z^{\pm }{\varvec{\varsigma }}\ll {\varvec{\varsigma }}\), \({{\varvec{j}}}^\perp \ll {\varvec{\varsigma }}\) and \({\varvec{\varsigma }}\perp {\varvec{{\varvec{\vartheta }}}}\), obtaining
Since \({{\varvec{j}}}\ll {\varvec{{\varvec{\vartheta }}}}+{\varvec{\varsigma }}\), we can decompose
and by the additivity property (2.17) we obtain
Indeed, identity (*) follows from the fact that, since \({\hat{\Psi }}\) is 1-homogeneous,
for every \(\gamma \in {{\mathcal {M}}}^+(E)\) such that \(w{\varvec{\vartheta }}\ll \gamma \) and \({\varvec{\upnu }}_\rho ^1 \ll \gamma \), cf. (2.13). Then, it suffices to observe that \(w{\varvec{\vartheta }}\ll {\varvec{\vartheta }}\) and \({\varvec{\upnu }}_\rho ^1 \ll {\varvec{\vartheta }}\) with \(\frac{\mathrm {d}{\varvec{\upnu }}_\rho ^1}{\mathrm {d}{\varvec{\vartheta }}} = \upalpha (u^-,u^+)\). The same argument applies to \( {\mathscr {F}}_{{{\hat{\Psi }}}}(w'{\varvec{\varsigma }},{\varvec{\upnu }}_\rho ^2)\), cf. also Lemma 2.3(3). \(\square \)
Definition 4.9
The dissipation potential \({\mathscr {R}}: {{\mathcal {M}}}^+(V)\times {{\mathcal {M}}}(E) \rightarrow [0,{+\infty }]\) is defined by
where \({\varvec{\vartheta }}_{\rho }^{\pm }\) are defined by (4.18). If \(\upalpha \) is 1-homogeneous, then \({\mathscr {R}}(\rho ,{{\varvec{j}}})\) is independent of \({\varvec{{\varvec{\vartheta }}}}\).
Lemma 4.10
Let \(\rho =\rho ^a+\rho ^\perp \in {{\mathcal {M}}}^+(V)\) and \({{\varvec{j}}}={{\varvec{j}}}^a+{{\varvec{j}}}^\perp \in {{\mathcal {M}}}(E)\), with \(\rho ^a=u\pi \), \(2{{\varvec{j}}}^a=w{\varvec{{\varvec{\vartheta }}}}\), and \(\rho ^\perp \), \(j^\perp \) as in Lemma 4.8, satisfy \({\mathscr {R}}(\rho ,{{\varvec{j}}})<{+\infty }\), and let \(P\in {{\mathcal {B}}}(V)\) be a \(\pi \)-negligible set such that  .
.
-
(1)
We have \(|{{\varvec{j}}}|(P\times (V\setminus P))= |{{\varvec{j}}}|((V\setminus P)\times P)=0\),
 , and $$\begin{aligned} {\mathscr {R}}(\rho ,{{\varvec{j}}})= {\mathscr {R}}(\rho ^a,{{\varvec{j}}}^a)+ \frac{1}{2} {\mathscr {F}}_{\Upsilon ^\infty }({\varvec{\vartheta }}^-_{\rho ^\perp },{\varvec{\vartheta }}^+_{\rho ^\perp },2{{\varvec{j}}}^\perp ). \end{aligned}$$(4.30)
, and $$\begin{aligned} {\mathscr {R}}(\rho ,{{\varvec{j}}})= {\mathscr {R}}(\rho ^a,{{\varvec{j}}}^a)+ \frac{1}{2} {\mathscr {F}}_{\Upsilon ^\infty }({\varvec{\vartheta }}^-_{\rho ^\perp },{\varvec{\vartheta }}^+_{\rho ^\perp },2{{\varvec{j}}}^\perp ). \end{aligned}$$(4.30)In particular, if \(\upalpha \) is 1-homogeneous we have the decomposition
$$\begin{aligned} {\mathscr {R}}(\rho ,{{\varvec{j}}})= {\mathscr {R}}(\rho ^a,{{\varvec{j}}}^a)+ {\mathscr {R}}(\rho ^\perp ,{{\varvec{j}}}^\perp ). \end{aligned}$$(4.31) -
(2)
If \(\rho \ll \pi \) or \(\upalpha \) is sub-linear, i.e. \(\upalpha ^\infty \equiv 0\), or \(\kappa (x,\cdot )\ll \pi \) for every \(x\in V\), then \({{\varvec{j}}}\ll {\varvec{{\varvec{\vartheta }}}}\) and \({{\varvec{j}}}^\perp \equiv 0\). In any of these three cases, \({\mathscr {R}}(\rho ,{{\varvec{j}}}) = {\mathscr {R}}(\rho ^a,{{\varvec{j}}})\), and setting \(E'\) as in (4.10) we have \(w=0\) \({\varvec{{\varvec{\vartheta }}}}\)-a.e. on \(E\setminus E'\), and (4.11) holds.
-
(3)
Furthermore, \({\mathscr {R}}\) is convex and lower semicontinuous with respect to setwise convergence in \((\rho ,{{\varvec{j}}})\). If \(\kappa \) satisfies the weak Feller property, then \({\mathscr {R}}\) is also lower semicontinuous with respect to weak convergence in duality with continuous bounded functions.
Proof
(1) Equation (4.30) is an immediate consequence of (4.24).
To prove the properties of \({{\varvec{j}}}\), set \(R = V\setminus P\) for convenience. By using the decompositions \({{\varvec{j}}}=w{\varvec{{\varvec{\vartheta }}}}+w'{\varvec{\varsigma }}\) and \({\varvec{\vartheta }}_{\rho }^{\pm } = {\varvec{\vartheta }}_{\rho ^a}^{\pm } + {\varvec{\vartheta }}_{\rho ^\perp }^ {\pm } = {\varvec{\vartheta }}_{\rho ^a}^{\pm } + z^{\pm } {\varvec{\varsigma }}\) introduced in the proof of the previous Lemma, the definition (4.25) implies that \({\varvec{\vartheta }}^+_{\rho ^\perp }(P\times R)=0\), so that \(z^+=0\) \({\varvec{\varsigma }}\)-a.e. in \(P\times R\); analogously \(z^-=0\) \({\varvec{\varsigma }}\)-a.e. in \(R\times P\). By (3.13) we find that \(\upalpha ^\infty (z^-,z^+)=0\), \({\varvec{\varsigma }}\)-a.e. in \((P\times R)\cup (R\times P)\) and therefore \(w'=0\) as well, since \(\Upsilon ^\infty (z^-,z^+,w')<{+\infty }\) \({\varvec{\varsigma }}\)-a.e (see (4.28)). We eventually deduce that  .
.
(2) When \(\rho \ll \pi \) we can choose \(P=\emptyset \) so that  . When \(\upalpha \) is sub-linear then \({\varvec{\upnu }}_\rho \ll {\varvec{{\varvec{\vartheta }}}}\) so that \({{\varvec{j}}}\ll {\varvec{{\varvec{\vartheta }}}}\) since \(\Psi \) is superlinear.
. When \(\upalpha \) is sub-linear then \({\varvec{\upnu }}_\rho \ll {\varvec{{\varvec{\vartheta }}}}\) so that \({{\varvec{j}}}\ll {\varvec{{\varvec{\vartheta }}}}\) since \(\Psi \) is superlinear.
If \(\kappa (x,\cdot )\ll \pi \) for every \(x\in V\), then \({{\mathsf {y}}}_\sharp {\varvec{\vartheta }}^-_{\rho ^\perp }\ll \pi \) and \({{\mathsf {x}}}_\sharp {\varvec{\vartheta }}^+_{\rho ^\perp }\ll \pi \), so that \({\varvec{\vartheta }}^{\pm }_{\rho ^\perp }(P\times P)=0\), since P is \(\pi \)-negligible. We deduce that \({{\varvec{j}}}^\perp (P\times P)=0\) as well.
(3) The convexity of \({\mathscr {R}}\) follows by the convexity of the functional \({\mathscr {F}}_\Upsilon \). The lower semicontinuity follows by combining Lemma 2.4 with Lemma 2.3. \(\square \)
Corollary 4.11
Let \(\pi _1,\pi _2\in {{\mathcal {M}}}^+(V)\) be mutually singular measures satisfying the detailed balance condition with respect to \(\kappa \), and let \({\varvec{{\varvec{\vartheta }}}}_i=\varvec{\kappa }_{\pi _i}\) be the corresponding symmetric measures in \({{\mathcal {M}}}^+(E)\) (see Sect. 2.4). For every pair \((\rho ,{{\varvec{j}}})\) with \(\rho =\rho _1+\rho _2\), \({{\varvec{j}}}={{\varvec{j}}}_1+{{\varvec{j}}}_2\) for \(\rho _i\ll \pi _i\) and \({{\varvec{j}}}_i\ll {\varvec{{\varvec{\vartheta }}}}_i\), we have
where \({\mathscr {R}}_i\) is the dissipation functional induced by \({\varvec{{\varvec{\vartheta }}}}_i\). When \(\upalpha \) is 1-homogeneous, \({\mathscr {R}}_i={\mathscr {R}}\).
4.3 Curves with finite \({\mathscr {R}}\)-action
In this section, we study the properties of curves with finite \({\mathscr {R}}\)-action, i.e., elements of
The finiteness of the \({\mathscr {R}}\)-action leads to the following remarkable property: A curve \((\rho ,{{\varvec{j}}})\) with finite \({\mathscr {R}}\)-action can be separated into two mutually singular curves \((\rho ^a,{{\varvec{j}}}^a),\ (\rho ^\perp ,{{\varvec{j}}}^\perp )\in {\mathcal {A}}{(a,b)}\) that evolve independently, and contribute independently to \({\mathscr {R}}\). Consequently, finite \({\mathscr {R}}\)-action preserves \(\pi \)-absolute continuity of \(\rho \): if \(\rho _t\ll \pi \) at any t, then \(\rho _t\ll \pi \) at all t. These properties and others are proved in Theorem 4.13 and Corollary 4.14 below.
Remark 4.12
If \((\rho ,{{\varvec{j}}})\in {\mathcal {A}}{(a,b)}\) then the ‘skew-symmetrization’ \( {{\varvec{j}}}^{\flat }=({{\varvec{j}}}-{\mathsf {s}}_\#{{\varvec{j}}})/2\) of \({{\varvec{j}}}\) gives rise to a pair \((\rho ,{{\varvec{j}}}^{\flat })\in {\mathcal {A}}{(a,b)}\) as well, and it has lower \({\mathscr {R}}\)-action:
This follows from the convexity of \(w\mapsto \Upsilon (u_1,u_2,w)\), the symmetry of \((u_1,u_2)\mapsto \Upsilon (u_1,u_2,w)\), and the invariance of the continuity equation (4.3) under the ‘skew-symmetrization’ \({{\varvec{j}}}\mapsto {{\varvec{j}}}^{\flat }\) (cf. also the calculations in the proof of Corollary 4.20).
As a result, we can often assume without loss of generality that a flux \({{\varvec{j}}}\) is skew-symmetric, i.e. that \({\mathsf {s}}_\#{{\varvec{j}}}= -{{\varvec{j}}}\).
Theorem 4.13
Let \((\rho ,{{\varvec{j}}})\in {\mathcal {A}}{(a,b)}\) and let us consider the Lebesgue decompositions \(\rho _t=\rho _t^a+\rho _t^\perp \) and \({{\varvec{j}}}_t ={{\varvec{j}}}_t^a+{{\varvec{j}}}_t^\perp \) of \(\rho _t\) with respect to \(\pi \) and of \({{\varvec{j}}}_t \) with respect to \({\varvec{{\varvec{\vartheta }}}}\).
-
(1)
We have \((\rho ^a,{{\varvec{j}}}^a)\in {\mathcal {A}}{(a,b)}\) with
$$\begin{aligned} \int _a^b {\mathscr {R}}(\rho ^a_t,{{\varvec{j}}}^a_t)\, \mathrm {d}t \le \int _a^b {\mathscr {R}}(\rho _t,{{\varvec{j}}}_t)\, \mathrm {d}t . \end{aligned}$$(4.34)In particular \(t\mapsto \rho _t^a(V)\) and \(t\mapsto \rho _t^\perp (V)\) are constant.
-
(2)
If \(\upalpha \) is 1-homogeneous then also \((\rho ^\perp ,{{\varvec{j}}}^\perp )\in {\mathcal {A}}{(a,b)}\) and
$$\begin{aligned} \int _a^b {\mathscr {R}}(\rho ^a_t,{{\varvec{j}}}^a_t)\, \mathrm {d}t + \int _a^b {\mathscr {R}}(\rho ^\perp _t,{{\varvec{j}}}^\perp _t)\, \mathrm {d}t= \int _a^b {\mathscr {R}}(\rho _t,{{\varvec{j}}}_t)\, \mathrm {d}t . \end{aligned}$$(4.35) -
(3)
If \(\upalpha \) is sub-linear or \(\kappa (x,\cdot )\ll \pi \) for every \(x\in V\), then \(\rho _t^\perp \) is constant in [a, b] and \({{\varvec{j}}}^\perp \equiv 0\).
Proof
(1) Let \(\gamma \in {{\mathcal {M}}}^+(V)\) be a dominating measure for the curve \(\rho \) according to Corollary 4.3 and let us denote by \(\gamma =\gamma ^a+\gamma ^\perp \) the Lebesgue decomposition of \(\gamma \) with respect to \(\pi \); we also denote by \(P\in {{\mathcal {B}}}(V)\) a \(\pi \)-negligible Borel set such that  . Setting \(R{:}{=}V\setminus P\), since \(\rho _t\ll \gamma \) we thus obtain
. Setting \(R{:}{=}V\setminus P\), since \(\rho _t\ll \gamma \) we thus obtain  ,
,  . By Lemma 4.10 for \(\lambda \)-a.e. \(t\in (a,b)\) we obtain
. By Lemma 4.10 for \(\lambda \)-a.e. \(t\in (a,b)\) we obtain  and
and  with \(|{{\varvec{j}}}_t|(R\times P)=|{{\varvec{j}}}_t|(P\times R)=0\). For every function \(\varphi \in \mathrm {B}_{\mathrm {b}}\) we have \({{\overline{\nabla }}}(\varphi \chi _R)\equiv 0\) on \(P\times P\) so that we get
with \(|{{\varvec{j}}}_t|(R\times P)=|{{\varvec{j}}}_t|(P\times R)=0\). For every function \(\varphi \in \mathrm {B}_{\mathrm {b}}\) we have \({{\overline{\nabla }}}(\varphi \chi _R)\equiv 0\) on \(P\times P\) so that we get
showing that \((\rho ^a,{{\varvec{j}}}^a)\) belongs to \(\mathcal {CE}(a,b)\). Estimate (4.34) follows by (4.30). From Lemma 4.4 we deduce that \(\rho _t^a(V)\) and \(\rho _t^\perp (V)\) are constant.
(2) This follows by the linearity of the continuity equation and (4.31).
(3) If \(\upalpha \) is sub-linear or \(\kappa (x,\cdot )\ll \pi \) for every \(x\in V\), then Lemma 4.10 shows that \({{\varvec{j}}}^\perp \equiv 0\). Since by linearity \((\rho ^\perp ,{{\varvec{j}}}^\perp )\in \mathcal {CE}(a,b)\), we deduce that \(\rho ^\perp _t\) is constant. \(\square \)
Corollary 4.14
Let \((\rho ,{{\varvec{j}}})\in {\mathcal {A}}{(a,b)}\). If there exists \(t_0\in [a,b]\) such that \(\rho _{t_0}\ll \pi \), then we have \(\rho _t\ll \pi \) for every \(t\in [a,b]\), \({{\varvec{j}}}^\perp \equiv 0\), and \({\overline{\mathrm {div}}}{{\varvec{j}}}_t\ll \pi \) for \(\lambda \)-a.e. \(t\in (a,b)\). In particular, there exists an absolutely continuous and a.e. differentiable map \(u:[a,b]\rightarrow L^1(V,\pi )\) and a map \(w\in L^1(E,\lambda \otimes {\varvec{{\varvec{\vartheta }}}})\) such that
Moreover there exists a measurable map \(\xi :(a,b)\times E\rightarrow {\mathbb {R}}\) such that \(w=\xi \upalpha (u^-,u^+)\) \(\lambda \otimes {\varvec{{\varvec{\vartheta }}}}\)-a.e. and
If w is skew-symmetric, then \(\xi \) is skew-symmetric as well and (4.36) reads as
Remark 4.15
Relations (4.36) and (4.38) hold both in the sense of a.e. differentiability of maps with values in \(L^1(V,\pi )\) and pointwise a.e. with respect to \(x\in V\): more precisely, there exists a set \(U\subset V\) of full \(\pi \)-measure such that for every \(x\in U\) the map \(t\mapsto u_t(x)\) is absolutely continuous and equations (4.36) and (4.38) hold for every \(x\in U\), a.e. with respect to \(t\in (0,T)\).
Proof
The first part of the statement is an immediate consequence of Theorem 4.13, which yields \(\rho ^\perp _t(V)= 0\) for every \(t\in [a,b]\). We can thus write \(2{{\varvec{j}}}=w(\lambda \otimes {\varvec{{\varvec{\vartheta }}}})\) for some measurable map \(w:(a,b)\times E\rightarrow {\mathbb {R}}\). Moreover \({\overline{\mathrm {div}}}{{\varvec{j}}}\ll \lambda \otimes \pi \), since \({{\mathsf {s}}}_\sharp {{\varvec{j}}}\ll {{\mathsf {s}}}_\sharp (\lambda \otimes {\varvec{{\varvec{\vartheta }}}})= \lambda \otimes {\varvec{{\varvec{\vartheta }}}}\), and therefore
Setting \(z_t=\mathrm {d}({\overline{\mathrm {div}}}{{\varvec{j}}}_t)/\mathrm {d}\pi \) we get for a.e. \(t\in (a,b)\)
The existence of \(\xi \) and formula (4.37) follow from Lemma 4.10(2). \(\square \)
4.4 Chain rule for convex entropies
Let us now consider a continuous convex function \(\upbeta :{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) that is differentiable in \((0,+\infty )\). The main choice for \(\upbeta \) will be the function \(\upphi \) that appears in the definition of the driving functional \({\mathscr {E}}\) (see Assumption (\({\mathscr {E}}\upphi \))), and the example of the Boltzmann-Shannon entropy function (3.10) illustrates why we only assume differentiability away from zero.
By setting \(\upbeta '(0)=\lim _{r\downarrow 0} \upbeta '(r)\in [-\infty ,{+\infty })\), we define the function \({\mathrm {A}}_\upbeta :{\mathbb {R}}_+\times {\mathbb {R}}_+\rightarrow [-\infty ,+\infty ]\) by
Note that \({\mathrm {A}}_\upbeta \) is continuous (with extended real values) in \({\mathbb {R}}_+\times {\mathbb {R}}_+\setminus \{(0,0)\}\) and is finite and continuous whenever \(\upbeta '(0)>-\infty \). When \(\upbeta '(0)=-\infty \) we have \({\mathrm {A}}_\upbeta (0,v)=-{\mathrm {A}}_\upbeta (u,0)={+\infty }\) for every \(u,v>0\).
In the following we will adopt the convention
for every \(a\in [-\infty ,+\infty ]\) and, using this convention, we define the extended valued function \({\mathrm {B}}_\upbeta :{\mathbb {R}}_+\times {\mathbb {R}}_+\times {\mathbb {R}}\rightarrow [-\infty ,+\infty ]\) by
We want to study the differentiability properties of the functional \({\mathscr {F}}_\upbeta (\cdot |\pi )\) along solutions \((\rho ,{{\varvec{j}}})\in \mathcal {CE}(I)\) of the continuity equation. Note that if \(\upbeta \) is superlinear and \({\mathscr {F}}_\upbeta \) is finite at a time \(t_0\in I\), then Corollary 4.14 shows that \(\rho _t\ll \pi \) for every \(t\in I\). If \(\upbeta \) has linear growth then
where we have used that \(t \mapsto \rho _t^\perp (V)\) is constant. Thus, we are reduced to studying \({\mathscr {F}}_\upbeta \) along \((\rho ^a,{{\varvec{j}}}^a)\), which is still a solution of the continuity equation. The absolute continuity property of \(\rho _t\) with respect to \(\pi \) is therefore quite a natural assumption in the next result.
Theorem 4.16
(Chain rule I) Let \((\rho ,{{\varvec{j}}})\in {\mathcal {A}}{(a,b)}\) with \(\rho _t=u_t\pi \ll \pi \) and let \(2{{\varvec{j}}}^\flat ={{\varvec{j}}}-{{\mathsf {s}}}_\sharp {{\varvec{j}}}=w^\flat \lambda \otimes {\varvec{{\varvec{\vartheta }}}}\) as in Corollary 4.14 satisfy
Then the map \(t\mapsto \int _V \upbeta (u_t)\,\mathrm {d}\pi \) is absolutely continuous in [a, b], the map \({\mathrm {B}}_\upbeta (u^-,u^+,w^\flat )\) is \(\lambda \otimes {\varvec{{\varvec{\vartheta }}}}\)-integrable and
Remark 4.17
At first sight condition (4.44) on the positive part of \({\mathrm {B}}_\upbeta \) is remarkable: we only require the positive part of \({\mathrm {B}}_\upbeta \) to be integrable, but in the assertion we obtain integrability of the negative part as well. This integrability arises from the combination of the upper bound on \(\int _V \upbeta (u_a)\,\mathrm {d}\pi \) in (4.44) with the lower bound \(\upbeta \ge 0\).
Proof
Step 1: Chain rule for an approximation. Define for \(k\in {\mathbb {N}}\) an approximation \(\upbeta _k\) of \(\upbeta \) as follows: Let \(\upbeta _k'(\sigma ){:}{=}\max \{-k,\min \{\upbeta '(\sigma ),k\}\}\) be the truncation of \(\upbeta '\) to the interval \([-k,k]\). Due to the assumptions on \(\upbeta \), we may assume that \(\upbeta \) achieves a minimum at the point \(s_0\in [0,{+\infty })\). Now set \(\upbeta _k(s) {:}{=} \upbeta (s_0) + \int _{s_0}^s \upbeta _k'(\sigma )\,\mathrm {d}\sigma \). Note that \(\upbeta _k\) is differentiable and globally Lipschitz, and converges monotonically to \(\upbeta (s)\) for all \(s\ge 0\) as \(k\rightarrow \infty \).
For each \(k\in {\mathbb {N}}\) and \(t\in [a,b]\) we define
By convexity and Lipschitz continuity of \(\upbeta _k\), we have that
Hence, we deduce by Corollary 4.14 that for every \(a\le s<t\le b\)
We conclude that the function \(t\mapsto S_k(t)\) is absolutely continuous. Let us pick a point \(t\in (a,b)\) of differentiability for \(t\mapsto S_k(t)\): it easy to check that
which by integrating over time yields
Step 2: The limit \(k\rightarrow \infty \) Since \(0\le \upbeta _k''\le \upbeta ''\) we have
and
We can thus estimate the right-hand side in (4.46)
where we have used the short-hand notation
Assumption (4.44) implies that the right-hand side in (4.49) is an element of \(L^1([a,b]\times E;\lambda \otimes {\varvec{{\varvec{\vartheta }}}})\), so that in particular \(B_+\in {\mathbb {R}}\) for \((\lambda \otimes {\varvec{{\varvec{\vartheta }}}})\)-a.e. (t, x, y).
Moreover, (4.46) yields
Note that the sequence \(k\mapsto (B_k)_-\) is definitely 0 or is monotonically increasing to \(B_-\). Beppo Levi’s Monotone Convergence Theorem and the uniform estimate (4.51) then yields that \(B_-\in L^1((a,b)\times E,\lambda \otimes {\varvec{{\varvec{\vartheta }}}})\), thus showing that \({\mathrm {B}}_\upbeta (u^-,u^+,w^\flat )\) is \((\lambda \otimes {\varvec{{\varvec{\vartheta }}}})\)-integrable as well.
We can thus pass to the limit in (4.46) as \(k\rightarrow {+\infty }\) and we have
The identity (4.52) is obvious if \(\upbeta '(0)\) is finite, and if \(\upbeta '(0)=-\infty \) then it follows by the upper bound (4.49) and the fact that the right-hand side of (4.49) is finite almost everywhere.
The Dominated Convergence Theorem then implies that
By the monotone convergence theorem \(S(t) = \lim _{k\rightarrow {+\infty }} S_k(t)\in [0,{+\infty }]\) for all \(t\in [a,b]\) and the limit is finite for \(t=0\). For all \(t\in [a,b]\), therefore,
which shows that S is absolutely continuous and (4.45) holds. \(\square \)
We now introduce three functions associated with the (general) continuous convex function \(\upbeta :{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\), differentiable in \((0,+\infty )\), that we have considered so far, and whose main example will be the entropy density \(\upphi \) from (3.9). Recalling the definition (4.40), the convention (4.41), and setting \(\Psi ^*({\pm }\infty ){:}{=}{+\infty }\), let us now introduce the functions \({\mathrm {D}}^+_\upbeta , {\mathrm {D}}^-_\upbeta ,{\mathrm {D}}_\upbeta :{\mathbb {R}}_+^2\rightarrow [0,{+\infty }]\)
The function \({\mathrm {D}}_\upphi \) corresponding to the choice \(\upbeta = \upphi \) shall feature in the (rigorous) definition of the Fisher information functional \({\mathscr {D}}\), cf. (5.1) ahead. Nonetheless, it is significant to introduce the functions \( {\mathrm {D}}^-_\upphi \) and \( {\mathrm {D}}^+_\upphi \) as well, cf. Remarks 5.8 and 7.12 ahead.
Example 4.18
(The functions \({\mathrm {D}}^{\pm }_\upphi \) and \({\mathrm {D}}_\upphi \) in the quadratic and in the \(\cosh \) case) In the two examples of the linear equation (1.2), with Boltzmann entropy function \(\upphi \), and with quadratic and cosh-type potentials \(\Psi ^*\) (see (1.17a) and (1.17b)), the functions \({\mathrm {D}}^{\pm }_\upphi \) and \({\mathrm {D}}_\upphi \) take the following forms:
-
(1)
If \(\Psi ^*(s)=s^2/2\) and, accordingly, \(\upalpha (u,v)=(u-v)/(\log (u)-\log (v))\) for all \(u,v >0\) (with \(\upalpha (u,v)=0\) otherwise), then
$$\begin{aligned} {\mathrm {D}}^-_\upphi (u,v)&= {\left\{ \begin{array}{ll} \frac{1}{2}(\log (u)-\log (v))(u-v) &{} \text {if } u,\, v>0, \\ 0 &{} \text {if }u=0\text { or }v=0, \end{array}\right. }\\ {\mathrm {D}}_\upphi (u,v) = {\mathrm {D}}^+_\upphi (u,v)&= {\left\{ \begin{array}{ll} \frac{1}{2}(\log (u)-\log (v))(u-v) &{} \text {if } u,\, v>0, \\ 0 &{} \text {if } u=v=0, \\ {+\infty }&{} \text {if } u=0 \text { and } v \ne 0, \text { or vice versa}. \end{array}\right. } \end{aligned}$$For this example \({\mathrm {D}}_\upphi ^+\) and \({\mathrm {D}}_\upphi \) are convex, and all three functions are lower semicontinuous.
-
(2)
For the case \(\Psi ^*(s)=4\bigl (\cosh (s/2)-1\bigr )\) and \(\upalpha (u,v)=\sqrt{u v}\) for all \(u,v \ge 0\), one finds
$$\begin{aligned} {\mathrm {D}}^-_\upphi (u,v)&= {\left\{ \begin{array}{ll} 2\Bigl (\sqrt{u}-\sqrt{v}\Bigr )^2 &{} \text {if } u,\, v>0, \\ 0 &{} \text {if }u=0\text { or }v=0, \end{array}\right. }\\ {\mathrm {D}}_\upphi (u,v)&= 2\Bigl (\sqrt{u}-\sqrt{v}\Bigr )^2\qquad {\text {for all }u,v\ge 0,}\\ {\mathrm {D}}^+_\upphi (u,v)&= {\left\{ \begin{array}{ll} 2\Bigl (\sqrt{u}-\sqrt{v}\Bigr )^2 &{} \text {if }u, v>0\text { or }u=v=0, \\ {+\infty }&{} \text {if } u=0 \text { and } v \ne 0, \text { or vice versa}. \end{array}\right. } \end{aligned}$$For this example, \({\mathrm {D}}_\upphi ^+\) and \({\mathrm {D}}_\upphi \) again are convex, but only \({\mathrm {D}}^-_\upphi \) and \({\mathrm {D}}_\upphi \) are lower semicontinuous.
Other examples of functions \({\mathrm {D}}_\upphi \) in the case of power means (1.33) with the Boltzmann entropy function \(\upphi \) are discussed in Appendix E.
We collect a number of general properties of \({\mathrm {D}}_\upbeta \) and \({\mathrm {D}}_\upbeta ^{\pm }\).
Lemma 4.19
-
(1)
\({\mathrm {D}}_\upbeta ^-\le {\mathrm {D}}_\upbeta \le {\mathrm {D}}_\upbeta ^+\);
-
(2)
\({\mathrm {D}}_\upbeta ^-\) and \({\mathrm {D}}_\upbeta \) are lower semicontinuous;
-
(3)
For every \(u,v\in {\mathbb {R}}_+\) and \(w\in {\mathbb {R}}\) we have
$$\begin{aligned} \bigl |{\mathrm {B}}_\upbeta (u,v,w)\bigr | \le \Upsilon (u,v,w)+{\mathrm {D}}^-_\upbeta (u,v). \end{aligned}$$(4.54) -
(4)
Moreover, when the right-hand side of (4.54) is finite, then the equality
$$\begin{aligned} -{\mathrm {B}}_\upbeta (u,v,w) = \Upsilon (u,v,w)+{\mathrm {D}}^-_\upbeta (u,v) \end{aligned}$$(4.55)is equivalent to the condition
$$\begin{aligned} \upalpha (u,v)=w=0\quad \text {or}\quad \biggl [ \upalpha (u,v)>0,\ {\mathrm {A}}_\upbeta (u,v)\in {\mathbb {R}},\ -w=(\Psi ^*)'\big ({\mathrm {A}}_\upbeta (u,v)\big )\upalpha (u,v)\biggr ]. \end{aligned}$$(4.56)
Proof
It is not difficult to check that \({\mathrm {D}}^-_\upbeta \) is lower semicontinuous: such a property is trivial where \(\upalpha \) vanishes, and in all the other cases it is sufficient to use the positivity and the continuity of \(\Psi ^*\) in \([-\infty ,+\infty ]\), the continuity of \({\mathrm {A}}_\upbeta \) in \({\mathbb {R}}_+^2\setminus \{(0,0)\}\), and the continuity and the positivity of \(\upalpha \). It is also obvious that \({\mathrm {D}}^-_\upbeta \le {\mathrm {D}}^+_\upbeta \), and therefore \({\mathrm {D}}^-_\upbeta \le {\mathrm {D}}_\upbeta \le {\mathrm {D}}^+_\upbeta \).
For the inequality (4.54), let us distinguish the various cases:
-
If \(w=0\) or \(u=v=0\), then \({\mathrm {B}}_\beta (u,v,w) =0\) so that (4.54) is trivially satisfied. We can thus assume \(w\ne 0\) and \(u+v>0\).
-
When \(\upalpha (u,v)=0\) then \(\Upsilon (u,v,w) ={+\infty }\) so that (4.54) is trivially satisfied as well. We can thus assume \(\upalpha (u,v)>0\).
-
If \({\mathrm {A}}_\upbeta (u,v)\in \{{\pm }\infty \}\) then \({\mathrm {D}}_\upbeta ^-(u,v)={+\infty }\) and the right-hand side of (4.54) is infinite.
-
It remains to consider the case when \({\mathrm {A}}_\upbeta (u,v)\in {\mathbb {R}}\), \(\upalpha (u,v)>0\) and \(w\ne 0\). In this situation
$$\begin{aligned} \bigl |{\mathrm {B}}(u,v,w)\bigr |&=\bigl |{\mathrm {A}}_\upbeta (u,v)w\bigr |= \bigg |{\mathrm {A}}_\upbeta (u,v)\frac{w}{\upalpha (u,v)}\bigg | \upalpha (u,v) \nonumber \\&\le \Psi \Big (\frac{w}{\upalpha (u,v)}\Big ) \upalpha (u,v)+ \Psi ^*\Big ({\mathrm {A}}_\upbeta (u,v)\Big ) \upalpha (u,v) \nonumber \\&=\Upsilon (u,v,w)+{\mathrm {D}}_\upbeta ^-(u,v). \end{aligned}$$(4.57)This proves (4.54).
It is now easy to study the case of equality in (4.55), when the right-hand side of (4.54) and (4.55) is finite. This in particular implies that \(\upalpha (u,v)>0\) and \({\mathrm {A}}_\upbeta (u,v)\in {\mathbb {R}}\) or \(\upalpha (u,v)=0\) and \(w=0\). In the former case, calculations similar to (4.57) show that \(-w=(\Psi ^*)'\big ({\mathrm {A}}_\upbeta (u,v)\big )\upalpha (u,v)\). In the latter case, \(\alpha (u,v) = w =0\) yields that \( {\mathrm {B}}_\upbeta (u,v,w)=0\), \(\Upsilon (u,v,w) = {\hat{\Psi }}(w,\alpha (u,v)) = {\hat{\Psi }}(0,0) = 0\), and \({\mathrm {D}}_\upbeta (u,v) = \Psi ^*({\mathrm {A}}_\upbeta (u,v)) \alpha (u,v)=0\). \(\square \)
As a consequence of Lemma 4.19, we conclude a chain-rule inequality involving the smallest functional \({\mathrm {D}}_\upbeta ^-\) and thus, a fortiori, the functional \({\mathrm {D}}_\upbeta \) which, for \(\upbeta =\upphi \), shall enter into the definition of the Fisher information \({\mathscr {D}}\).
Corollary 4.20
(Chain rule II) Let \((\rho ,{{\varvec{j}}})\in {\mathcal {A}}{(a,b)}\) with \(\rho _t=u_t\pi \ll \pi \) and \(2{{\varvec{j}}}_\lambda =w (\lambda \otimes {\varvec{{\varvec{\vartheta }}}})\) satisfy
Then the map \(t\mapsto \int _V \upbeta (u_t)\,\mathrm {d}\pi \) is absolutely continuous in [a, b] and
If moreover
then \(2{{\varvec{j}}}={{\varvec{j}}}^\flat \) and
In particular, \( w_t=0\) \({\varvec{{\varvec{\vartheta }}}}\)-a.e. in \(\big \{(x,y)\in E: \upalpha (u_t(x),u_t(y))=0\big \}.\)
Proof
We recall that for \(\lambda \)-a.e. \(t\in (a,b)\)
We can then apply Lemma 4.19 and Theorem 4.16, observing that
since
and the integral of the last term coincides with the right-hand side of (4.61) thanks to the symmetry of \({\varvec{{\varvec{\vartheta }}}}\). \(\square \)
4.5 Compactness properties of curves with uniformly bounded \({\mathscr {R}}\)-action
The next result shows an important compactness property for collections of curves in \({\mathcal {A}}{(a,b)}\) with bounded action. Recalling the discussion and the notation of Sect. 2.4, we will systematically associate with a given \((\rho ,{{\varvec{j}}})\in {\mathcal {A}}{(I)}\), \(I=[a,b]\), a couple of measures \(\rho _\lambda \in {{\mathcal {M}}}^+(I\times V)\), \({{\varvec{j}}}_\lambda \in {{\mathcal {M}}}(I\times E)\) by integrating with respect to the Lebesgue measure \(\lambda \) in I:
Similarly, we define
It is not difficult to check that
Proposition 4.21
(Bounded \(\int {\mathscr {R}}\) implies compactness and lower semicontinuity) Let \((\rho ^n,{{\varvec{j}}}^n)_n \subset {\mathcal {A}}{(a,b)}\) be a sequence such that the initial states \(\rho ^n_a\) are \(\pi \)-absolutely-continuous and relatively compact with respect to setwise convergence. Assume that
Then, there exist a subsequence (not relabelled) and a pair \((\rho ,{{\varvec{j}}})\in {\mathcal {A}}{(a,b)}\) such that, for the measures \({{\varvec{j}}}_\lambda ^n \in {{\mathcal {M}}}([a,b]\times E)\) defined as in (4.62) there holds
where \({{\varvec{j}}}_\lambda \) is induced (in the sense of (4.62)) by a \(\lambda \)-integrable family \(({{\varvec{j}}}_t)_{t\in [a,b]}\subset {{\mathcal {M}}}(E)\). In addition, for any sequence \((\rho ^n,{{\varvec{j}}}^n)\) converging to \((\rho ,{{\varvec{j}}})\) in the sense of (4.66), we have
Proof
Let us first remark that the mass conservation property of the continuity equation yields
for a suitable finite constant \(M_1\) independent of n. We deduce that for every \(t\in [a,b]\) the measures \({\varvec{{\varvec{\vartheta }}}}_{\rho _t^n}^{\pm }\) have total mass bounded by \(M_1 \Vert \kappa _V\Vert _\infty \), so that estimate (2.29) for \(y=(c,c)\in D(\upalpha _*)\) yields
where \(M_2{:}{=}2 c\,M_1 \Vert \kappa _V\Vert _\infty -\upalpha _*(c,c){\varvec{{\varvec{\vartheta }}}}(E)\). Jensen’s inequality (2.18) and the monotonicity property (2.19) yield
with \({{\hat{\Psi }}}\) the perspective function associated with \(\Psi \), cf. (2.14). Since \(\Psi \) has superlinear growth, we deduce that the sequence of functions \(t\mapsto |{{\varvec{j}}}_t^n|(E)\) is equi-integrable.
Since the sequence \((\rho _a^n)_n\), with \(\rho _a^n = u_a^n \pi \ll \pi \), is relatively compact with respect to setwise convergence, by Theorems 2.1(6) and 2.2(3) there exist a convex superlinear function \(\upbeta :{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) and a constant \(M_3<{+\infty }\) such that
Possibly adding \(M_1\) to \(M_3\), it is not restrictive to assume that \(\upbeta '(r)\ge 1\). We can then apply Lemma C.3 and we can find a smooth convex superlinear function \(\upomega :{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) such that (C.10) holds. In particular
By Corollary 4.20 we obtain
By (4.7) we deduce that
Since \(t\mapsto |{{\varvec{j}}}^n_t|(E)\) is equi-integrable we have
We conclude that the sequence of maps \((u_t^n)_{t\in [a,b]}\) satisfies the conditions of the compactness result [4, Prop. 3.3.1], which yields the existence of a (not relabelled) subsequence and of a \(L^1(V,\pi )\)-continuous (thus also weakly-continuous) function \([a,b]\ni t \mapsto u_t\in L^1(V,\pi )\) such that \(u^n_t\rightharpoonup u_t\) weakly in \(L^1(V,\pi )\) for every \(t\in [a,b]\). By (2.5) we also deduce that (4.66a) holds, i.e.
It is also clear that for every \(t\in [a,b]\) we have \({\varvec{{\varvec{\vartheta }}}}_{\rho _t^n}^{\pm }\rightarrow {\varvec{{\varvec{\vartheta }}}}_{\rho _t}^{\pm }\) setwise. The Dominated Convergence Theorem and (2.4), (2.36) imply that the corresponding measures \({\varvec{{\varvec{\vartheta }}}}_{\rho ^n,\lambda }^{\pm }\) converge setwise to \({\varvec{{\varvec{\vartheta }}}}_{\rho ,\lambda }^{\pm }\), and are therefore equi-absolutely continuous with respect to \({\varvec{{\varvec{\vartheta }}}}_\lambda =\lambda \otimes {\varvec{{\varvec{\vartheta }}}}\) (recall (2.7)).
Let us now show that also the sequence \(({{\varvec{j}}}^n_\lambda )_{n}\) is equi-absolutely continuous with respect to \({\varvec{{\varvec{\vartheta }}}}_\lambda \), so that (4.66b) holds up to extracting a further subsequence.
Selecting a constant \(c>0\) sufficiently large so that \(\upalpha (u_1,u_2)\le c(1+u_1+u_2)\), the trivial estimate \({\varvec{\upnu }}_\rho \le c({\varvec{{\varvec{\vartheta }}}}+{\varvec{\vartheta }}_\rho ^-+{\varvec{\vartheta }}_\rho ^+)\) and the monotonicity property (2.19) yield
For every \(B\in {\mathfrak {A}}\otimes {\mathfrak {B}}\), \({\mathfrak {A}}\) being the Borel \(\sigma \)-algebra of [a, b], with \({\varvec{{\varvec{\vartheta }}}}_\lambda (B)>0\), Jensen’s inequality (2.18) yields

Denoting by \(U:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) the inverse function of \(\Psi \), we thus find
Since \(\Psi \) is superlinear, U is sublinear so that
For every \(\varepsilon >0\) there exists \(\delta _0>0\) such that \(\delta U(M/\delta )\le \varepsilon \) for every \(\delta \in (0,\delta _0)\). Since \({\varvec{\varsigma }}^n\) is equi absolutely continuous with respect to \({\varvec{{\varvec{\vartheta }}}}_\lambda \) we can also find \(\delta _1>0\) such that \({\varvec{{\varvec{\vartheta }}}}_\lambda (B)<\delta _1\) yields \({\varvec{\varsigma }}^n(B)\le \delta _0\). By (4.78) we eventually conclude that \({{\varvec{j}}}^n_\lambda (B)\le \varepsilon \).
It is then easy to pass to the limit in the integral formulation (4.4) of the continuity equation. Finally, concerning (4.67), it is sufficient to use the equivalent representation given by (4.64). \(\square \)
4.6 Definition and properties of the cost
We now define the Dynamical-Variational Transport cost \({\mathcal {W}} : (0,{+\infty }) \times {{\mathcal {M}}}^+(V)\times {{\mathcal {M}}}^+(V) \rightarrow [0,{+\infty })\) by
In studying the properties of \({{\mathcal {W}}}\), we will also often use the notation
with \({\mathcal {A}}{(0,\tau )}\) the class from (4.33).
For given \(\tau >0\) and \(\rho _0,\, \rho _1 \in {{\mathcal {M}}}^+(V)\), if the set \({\mathscr {A}}{(0,\tau ;\rho _0,\rho _1)}\) is non-empty, then it contains an exact minimizer for \({\mathscr {W}}(\tau ,\rho _0,\rho _1)\). This is stated by the following result that is a direct consequence of Proposition 4.21.
Corollary 4.22
(Existence of minimizers) If \(\rho _0,\rho _1\in {{\mathcal {M}}}^+(V)\) and \({\mathscr {A}}{(0,\tau ;\rho _0,\rho _1)} \) is not empty, then the infimum in (4.80) is achieved.
Remark 4.23
(Scaling invariance) Let us consider the perspective function \({{\hat{\Psi }}}(r,s)\) associated wih \(\Psi \) as in (2.14), \({{\hat{\Psi }}}(r,s)=s\Psi (r/s)\) if \(s>0\). We call \({\mathscr {R}}_s(\rho ,{{\varvec{j}}})\) the dissipation functional induced by \({\hat{\Psi }}(\cdot , s)\), with induced Dynamic-Transport cost \({\mathscr {W}}_s\). For every \(\tau >0\), \(\rho _0,\rho _1\in {{\mathcal {M}}}^+(V)\) a rescaling argument yields
In particular, choosing \(\sigma =1\) we find
Since \({{\hat{\Psi }}}(\cdot ,\tau )\) is convex, lower semicontinuous, and decreasing with respect to \(\tau \), we find that \(\tau \mapsto {\mathscr {W}}(\tau ,\rho _0, \rho _1) \) is decreasing and convex as well.
Currently, proving that any pair of measures can be connected by a curve with finite action \(\int {\mathscr {R}}\) under general conditions on V, \(\Psi \) and \(\upalpha \) is an open problem: in other words, in the general case we cannot exclude that \({\mathscr {A}}{(0,\tau ;\rho _0,\rho _1)} = \emptyset \), which would make \({\mathscr {W}}(\tau ,\rho _0,\rho _1) = {+\infty }\). Nonetheless, in a more specific situation, Proposition 4.25 below provides sufficient conditions for this connectivity property, between two measures \(\rho _0, \, \rho _1 \in {{\mathcal {M}}}^+(V) \) with the same mass and such that \(\rho _i \ll \pi \) for \(i\in \{0,1\}\). Preliminarily, we give the following
Definition 4.24
Let \(q\in (1,{+\infty })\). We say that the measures \((\pi ,{\varvec{{\varvec{\vartheta }}}}) \) satisfy a q-Poincaré inequality if there exists a constant \(C_P>0\) such that for every \(\xi \in L^q(V;\pi )\) with \(\int _{V}\xi (x) \pi (\mathrm {d}x) =0\) there holds
We are now in a position to state the connectivity result, where we specialize the discussion to dissipation densities with p-growth for some \(p \in (1,{+\infty })\).
Proposition 4.25
Suppose that
and that the measures \((\pi ,{\varvec{{\varvec{\vartheta }}}}) \) satisfy a q-Poincaré inequality for \(q=\tfrac{p}{p-1}\). Let \(\rho _0, \rho _1 \in {{\mathcal {M}}}^+(V) \) with the same mass be given by \(\rho _i = u_i \pi \), with positive \(u_i \in L^1(V; \pi ) \cap L^\infty (V; \pi ) \), for \(i \in \{0,1\}\). Then, for every \(\tau >0\) the set \({\mathscr {A}}{(0,\tau ;\rho _0,\rho _1)} \) is non-empty and thus \({\mathscr {W}}(\tau ,\rho _0,\rho _1)<\infty \).
We postpone the proof of Proposition 4.25 to Appendix D, where some preliminary results, also motivating the role of the q-Poincaré inequality, will be provided.
4.7 Abstract-level properties of \({\mathscr {W}}\)
The main result of this section collects a series of properties of the cost that will play a key role in the study of the Minimizing Movement scheme (1.26). Indeed, as already hinted in the Introduction, the analysis that we will carry out in Sect. 7 ahead might well be extended to a scheme set up in a general topological space, endowed with a cost functional enjoying properties (4.86) below. We will now check them for the cost \({\mathscr {W}}\) associated with generalized gradient structure \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) fulfilling Assumptions (\(V\!\pi \kappa \)) and (\({\mathscr {R}}^*\Psi \upalpha \)). In this section all convergences will be with respect to the setwise topology.
Theorem 4.26
The cost \({\mathscr {W}}\) enjoys the following properties:
-
(1)
For all \(\tau >0,\, \rho _0,\, \rho _1 \in {{\mathcal {M}}}^+(V)\),
$$\begin{aligned} {\mathscr {W}}(\tau ,\rho _0,\rho _1)= 0 \ \Leftrightarrow \ \rho _0=\rho _1. \end{aligned}$$(4.86a) -
(2)
For all \(\rho _1,\, \rho _2,\,\rho _3\in {{\mathcal {M}}}^+(V)\) and \(\tau _1, \tau _2 \in (0,{+\infty })\) with \(\tau =\tau _1 +\tau _2\),
$$\begin{aligned} {\mathscr {W}}(\tau ,\rho _1,\rho _3) \le {\mathscr {W}}(\tau _1,\rho _1,\rho _2) + {\mathscr {W}}(\tau _2,\rho _2,\rho _3). \end{aligned}$$(4.86b) -
(3)
For \(\tau _n\rightarrow \tau >0, \ \rho _0^n \rightarrow \rho , \ \rho _1^n \rightarrow \rho _1\) in \({{\mathcal {M}}}^+(V)\),
$$\begin{aligned} \liminf _{n \rightarrow {+\infty }} {\mathscr {W}}(\tau _n,\rho _0^n, \rho _1^n) \ge {\mathscr {W}}(\tau ,\rho _0,\rho _1). \end{aligned}$$(4.86c) -
(4)
For all \(\tau _n \downarrow 0\) and for all \((\rho _n)_n\), \( \rho \in {{\mathcal {M}}}^+(V)\),
$$\begin{aligned} \sup _{n\in {\mathbb {N}}} {\mathscr {W}}(\tau _n, \rho _n,\rho ) <{+\infty }\quad \Rightarrow \quad \rho _n \rightarrow \rho . \end{aligned}$$(4.86d) -
(5)
For all \(\tau _n \downarrow 0\) and all \((\rho _n)_n\), \( (\nu _n)_n \subset {{\mathcal {M}}}^+(V)\) with \(\rho _n \rightarrow \rho , \ \nu _n \rightarrow \nu \),
$$\begin{aligned} \limsup _{n\rightarrow \infty } {\mathscr {W}}(\tau _n, \rho _n,\nu _n) <{+\infty }\quad \Rightarrow \quad \rho = \nu . \end{aligned}$$(4.86e)
Proof
(1) Since \(\Psi (s)\) is strictly positive for \(s\ne 0\) it is immediate to check that \({\mathscr {R}}(\rho ,{{\varvec{j}}})=0\ \Rightarrow \ {{\varvec{j}}}=0\). For an optimal pair \((\rho ,{{\varvec{j}}}) \) satisfying \( \int _0^\tau {\mathscr {R}}(\rho _t,{{\varvec{j}}}_t)\,\mathrm {d}t =0 \) we deduce that \({{\varvec{j}}}_t=0\) for a.e. \(t\in (0,\tau )\). The continuity equation then implies \(\rho _0=\rho _1\).
(2) This can easily be checked by using the existence of minimizers for \({\mathscr {W}}(\tau ,\rho _0, \rho _1)\).
(3) Assume without loss of generality that \(\liminf _{n\rightarrow +\infty } {\mathscr {W}}(\tau _n,\rho _0^n, \rho _1^n) < \infty \). By (4.83) we use that, for every \(n\in {\mathbb {N}}\) and setting \({{\overline{\tau }}} = \sup _n \tau _n\),
where the identity \((*)\) holds for an optimal pair \((\rho ^n,{{\varvec{j}}}^n) \in \mathcal {CE}(0,1; \rho _0^n,\rho _1^n)\). Applying Proposition 4.21, we obtain the existence of \((\rho , {{\varvec{j}}}) \in \mathcal {CE}(0,1; \rho _0,\rho _1)\) such that, up to a subsequence,
Arguing as in Proposition 4.21 and using the joint lower semicontinuity of \({{\hat{\Psi }}}\), we find that
(4) If we denote by \({\mathscr {R}}_0\) the dissipation associated with \({{\hat{\Psi }}}(\cdot ,0)\), given by \({{\hat{\Psi }}}(w,0) = +\infty \) for \(w\not =0\) and \({{\hat{\Psi }}}(0,0)=0\), we find
By the same argument as for part (3), every subsequence of \(\rho _n\) has a converging subsequence in the setwise topology; the lower semicontinuity result of the proof of part (3) shows that any limit point must coincide with \(\rho \).
(5) The argument combines (4.88) and part (3). \(\square \)
4.8 The action functional \({\mathbb {W}}\) and its properties
The construction of \({\mathscr {R}}\) and \({\mathscr {W}}\) above proceeded in the order \({\mathscr {R}}\rightsquigarrow {\mathscr {W}}\): we first constructed \({\mathscr {R}}\), and then \({\mathscr {W}}\) was defined in terms of \({\mathscr {R}}\). It is a natural question whether one can invert this construction: given \({\mathscr {W}}\), can one reconstruct \({\mathscr {R}}\), or at least integrals of the form \(\int _a^b {\mathscr {R}}\,\mathrm {d}t\)? The answer is positive, as we show in this section.
Given a functional \({\mathscr {W}}\) satisfying the properties (4.86), we define the ‘\({\mathscr {W}}\)-action’ of a curve \(\rho :[a,b]\rightarrow {{\mathcal {M}}}^+(V)\) as
for all \([a,b]\subset [0,T]\) where \({\mathfrak {P}}_f([a,b])\) denotes the set of all partitions of a given interval [a, b].
If \({\mathscr {W}}\) is defined by (4.80), then each term in the sum above is defined as an optimal version of \(\int _{t^{j-1}}^{t^j} {\mathscr {R}}(\rho _t,\cdot )\,\mathrm {d}t\), and we might expect that \({\mathbb {W}}(\rho ;[a,b])\) is an optimal version of \(\int _a^b {\mathscr {R}}(\rho _t,\cdot )\,\mathrm {d}t\). This is indeed the case, as is illustrated by the following analogue of [20, Th. 5.17]:
Proposition 4.27
Let \({\mathscr {W}}\) be given by (4.80), and let \(\rho :[0,T]\rightarrow {{\mathcal {M}}}^+(V)\). Then \({\mathbb {W}}(\rho ;[0,T])<{+\infty }\) if and only if there exists a measurable map \({{\varvec{j}}}:[0,T]\rightarrow {{\mathcal {M}}}(E)\) such that \((\rho ,{{\varvec{j}}})\in \mathcal {CE}(0,T)\) with \(\int _0^T {\mathscr {R}}(\rho _t,{{\varvec{j}}}_t)\mathrm {d}t<{+\infty }\) . In that case,
and there exists a unique \({{\varvec{j}}}_{\mathrm{opt}}\) such that equality is achieved. The optimal \({{\varvec{j}}}_{\mathrm{opt}}\) is skew-symmetric, i.e. \({{\varvec{j}}}_{\mathrm{opt}}= {{\varvec{j}}}^{\flat }_{\mathrm{opt}}\) (cf. Remark 4.12).
Prior to proving Proposition 4.27, we establish the following approximation result.
Lemma 4.28
Let \(\rho :[0,T]\rightarrow {{\mathcal {M}}}^+(V)\) satisfy \({\mathbb {W}}(\rho ;[0,T])<{+\infty }\). For a sequence of partitions \(P_n =(t_n^j)_{j=0}^{M_n}\in {\mathfrak {P}}_f([0,T])\) with fineness \(\tau _n = \max _{j=1,\ldots , M_n} (t_n^j{-}t_n^{j-1})\) converging to zero, let \(\rho ^n :[0,T]\rightarrow {{\mathcal {M}}}^+(V)\) satisfy
Then \(\rho ^n(t) \rightarrow \rho (t)\) setwise for all \(t\in [0,T]\) as \(n\rightarrow \infty \).
Proof
First of all, observe that by the symmetry of \(\Psi \), also the time-reversed curve \({{\check{\rho }}}(t){:}{=} \rho (T-t)\) satisfies \({\mathbb {W}}({\check{\rho }};[0,T])<{+\infty }\). Let \(\overline{{\mathsf {t}}}_{n}\) and \(\underline{{\mathsf {t}}}_{n}\) be the piecewise constant interpolants associated with the partitions \(P_n\), cf. (7.5). Fix \(t\in [0,T]\); we estimate
where (1) follows from property (4.86b) of \({\mathscr {W}}\). Consequently, by property (4.86d) it follows that \(\rho ^n(t) \rightarrow \rho (t)\) setwise in \({{\mathcal {M}}}^+(V)\) for all \(t\in [0,T]\). \(\square \)
We are now in a position to prove Proposition 4.27:
Proof of Proposition 4.27
One implication is straightforward: if a pair \((\rho ,{{\varvec{j}}})\) exists, then
and therefore \({\mathbb {W}}(\rho ;[0,T])<{+\infty }\) and (4.90) holds.
To prove the other implication, assume that \({\mathbb {W}}(\rho ;[0,T])<{+\infty }\). Choose a sequence of partitions \(P_n =(t_n^j)_{j=0}^{M_n}\in {\mathfrak {P}}_f([0,T])\) that becomes dense in the limit \(n\rightarrow \infty \). For each \(n\in {\mathbb {N}}\), construct a pair \((\rho ^n,{{\varvec{j}}}^n)\in \mathcal {CE}(0,T)\) as follows: On each time interval \([t_n^{j-1},t_n^j]\), let \((\rho ^n,{{\varvec{j}}}^n)\) be given by Corollary 4.22 as the minimizer under the constraint \(\rho ^n(t_n^{j-1}) = \rho (t_n^{j-1})\) and \(\rho ^n(t_n^j) = \rho (t_n^j)\), namely
By concatenating the minimizers on each of the intervals a pair \((\rho ^n,{{\varvec{j}}}^n)\in \mathcal {CE}(0,T)\) is obtained, thanks to Lemma 4.6. By construction we have the property
Also by optimality we have
which implies by summing that
By Lemma 4.28 we then find that \(\rho ^n(t)\rightarrow \rho (t)\) setwise as \(n\rightarrow \infty \) for each \(t\in [0,T]\).
Applying Proposition 4.21, we find that \({{\varvec{j}}}^n(\mathrm {d}t\,\mathrm {d}x\,\mathrm {d}y){:}{=} {{\varvec{j}}}_t^n(\mathrm {d}x\,\mathrm {d}y)\,\mathrm {d}t\) setwise converges along a subsequence to a limit \({{\varvec{j}}}\). The limit \( {{\varvec{j}}}\) can be disintegrated as \({{\varvec{j}}}(\mathrm {d}t\,\mathrm {d}x\,\mathrm {d}y) = \lambda (\mathrm {d}t) \, {{\varvec{j}}}_t(\mathrm {d}x\,\mathrm {d}y) \) for a measurable family \(({{\varvec{j}}}_t)_{t\in [0,T]}\), and the pair \((\rho ,{{\varvec{j}}})\) is an element of \(\mathcal {CE}(0,T)\). In addition we have the lower-semicontinuity property
We then have the series of inequalities
which implies that \(\int _0^T {\mathscr {R}}(\rho _t, {{\varvec{j}}}_t) \,\mathrm {d}t = {\mathbb {W}}(\rho ;[0,T])\).
Finally, the uniqueness of \({{\varvec{j}}}\) is a consequence of the strict convexity of \(\Upsilon (u_1,u_2,\cdot )\), cf. Lemma 4.7. Similarly, the skew-symmetry of \({{\varvec{j}}}\) follows from the strict convexity of \(\Upsilon (u_1,u_2,\cdot )\), the symmetry of \(\Upsilon (\cdot ,\cdot ,w)\), and the invariance of the continuity equation (4.3) under the ‘skew-symmetrization’ \({{\varvec{j}}}\mapsto {{\varvec{j}}}^{\flat }\), cf. Remark 4.12. \(\square \)
5 The fisher information \({\mathscr {D}}\) and the definition of solutions
With the definitions and the properties that we established in the previous section we have given a rigorous meaning to the first term in the functional \({\mathscr {L}}\) in (1.18). In this section we continue with the second term in the integral, often called Fisher information, after the canonical version in diffusion problems [68]. Section 5.2 is devoted to
-
(a)
A rigorous definition of the Fisher information \({\mathscr {D}}(\rho )\) (Definition 5.1).
In several practical settings, such as the proof of existence that we give in Sect. 7, it is important to have lower semicontinuity of \({\mathscr {D}}\): this is proved in Proposition 5.3.
We are then in a position to give
-
(b)
a rigorous definition of solutions to the \(({\mathscr {E}}, {\mathscr {R}}, {\mathscr {R}}^*)\) system (Definition 5.4).
In Sect. 1.2.1 we explained that the Energy-Dissipation balance approach to defining solutions is based on the fact that \({\mathscr {L}}(\rho ,{{\varvec{j}}}) \ge 0\) for all \((\rho ,{{\varvec{j}}})\) by the validity of a suitable chain-rule inequality.
-
(c)
A rigorous proof of this chain-rule inequality, involving \({\mathscr {R}}\) and \({\mathscr {D}}\), is given in Corollary 5.6, which is based on Theorem 4.16).
This establishes the inequality \({\mathscr {L}}(\rho ,{{\varvec{j}}}) \ge 0\). Hence, we can rigorously deduce that the opposite inequality \({\mathscr {L}}(\rho ,{{\varvec{j}}}) \le 0\) characterizes the property that \((\rho ,{{\varvec{j}}})\) is a solution to the \(({\mathscr {E}}, {\mathscr {R}}, {\mathscr {R}}^*)\) system. Theorem 5.7 provides an additional characterization of this solution concept.
Finally, in Sects. 5.3 and 5.4,
-
(d)
we prove existence, uniqueness and stability of solutions under suitable convexity/l.s.c. conditions on \({\mathscr {D}}\) (Theorems 5.10 and 5.9). We also discuss their asymptotic behaviour and the role of the invariant measures \(\pi \).
Throughout this section we adopt Assumptions (\(V\!\pi \kappa \)), (\({\mathscr {R}}^*\Psi \upalpha \)), and (\({\mathscr {E}}\upphi \)).
5.1 The fisher information \({\mathscr {D}}\)
Formally, the Fisher information is the second term in (1.18), namely
In order to give a precise meaning to this formulation when \(\upphi \) is not differentiable at 0 (as, for instance, in the case of the Boltzmann entropy function (3.10)), we use the function \({\mathrm {D}}_\upphi \) defined in (4.53c).
Definition 5.1
(The Fisher-information functional \({\mathscr {D}}\)) The Fisher information \({\mathscr {D}}: \mathrm {D}({\mathscr {E}})\rightarrow [0,{+\infty }]\) is defined as
Example 5.2
(The Fisher information in the quadratic and in the \(\cosh \) case) For illustration we recall the two expressions for \({\mathrm {D}}_\upphi \) from Example 4.18 for the linear equation (1.2) with quadratic and cosh-type potentials \(\Psi ^*\) :
-
(1)
If \(\Psi ^*(s)=s^2/2\) , then
$$\begin{aligned} {\mathrm {D}}_\upphi (u,v) = {\left\{ \begin{array}{ll} \frac{1}{2}(\log (u)-\log (v))(u-v) &{} \text {if } u,\, v>0, \\ 0 &{} \text {if } u=v=0, \\ {+\infty }&{} \text {if } u=0 \text { and } v \ne 0, \text { or vice versa}. \end{array}\right. } \end{aligned}$$ -
(2)
If \(\Psi ^*(s)=4\bigl (\cosh (s/2)-1\bigr )\), then
$$\begin{aligned} {\mathrm {D}}_\upphi (u,v) = 2\Bigl (\sqrt{u}-\sqrt{v}\Bigr )^2\qquad \forall \, (u,v) \in [0,{+\infty }) \times [0,{+\infty }). \end{aligned}$$
These two examples of \({\mathrm {D}}_\upphi \) are convex. The convexity of \({\mathrm {D}}_\upphi \) in the case of potentials \(\Psi ^*\) generated by the power means (1.33) is discussed in Appendix E.
Let us discuss the lower-semicontinuity properties of \({\mathscr {D}}\). In accordance with the Minimizing-Movement approach carried out in Sect. 7.1, we will just be interested in lower semicontinuity of \({\mathscr {D}}\) along sequences with bounded energy \({\mathscr {E}}\). Now, since sublevels of the energy \({\mathscr {E}}\) are relatively compact with respect to setwise convergence (by part 2 of Theorem 2.2), there is no difference between narrow and setwise lower semicontinuity of \({\mathscr {D}}\).
Proposition 5.3
(Lower semicontinuity of \({\mathscr {D}}\)) Assume either that \(\pi \) is purely atomic or that the function \({\mathrm {D}}_\upphi \) is convex on \({\mathbb {R}}_+^2\). Then \({\mathscr {D}}\) is (sequentially) lower semicontinuous with respect to setwise convergence, i.e., for all \((\rho ^n)_n,\, \rho \in \mathrm {D}({\mathscr {E}}) \)
Proof
When \(\pi \) is purely atomic, setwise convergence implies pointwise convergence \(\pi \)-a.e. for the sequence of the densities, so that (5.2) follows by Fatou’s Lemma.
A standard argument, still based on Fatou’s Lemma, shows that the functional
is lower semicontinuous with respect to the strong topology in \(L^1(V,\pi )\): it is sufficient to check that \(u_n\rightarrow u\) in \(L^1(V,\pi )\) implies \((u_n^-,u_n^+)\rightarrow (u^-,u^+)\) in \(L^1(E,{\varvec{{\varvec{\vartheta }}}})\). If \({\mathrm {D}}_\upphi \) is convex on \({\mathbb {R}}_+^2\), then the functional (5.3) is also lower semicontinuous with respect to the weak topology in \(L^1(V,\pi )\). On the other hand, since \(\rho _n\) and \(\rho \) are absolutely continuous with respect to \(\pi \), \(\rho _n\rightarrow \rho \) setwise if and only if \(\mathrm {d}\rho _n/\mathrm {d}\pi \rightharpoonup \mathrm {d}\rho /\mathrm {d}\pi \) weakly in \(L^1(V,\pi )\) (see Theorem 2.1). \(\square \)
5.2 The definition of solutions: \({\mathscr {R}}/{\mathscr {R}}^*\) energy-dissipation balance
We are now in a position to formalize the concept of solution.
Definition 5.4
(\(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) Energy-Dissipation balance) We say that a curve \(\rho : [0,T] \rightarrow {{\mathcal {M}}}^+(V)\) is a solution of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) evolution system, if it satisfies the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) Energy-Dissipation balance:
-
(1)
\({\mathscr {E}}(\rho _0)<{+\infty }\);
-
(2)
There exists a measurable family \(({{\varvec{j}}}_t)_{t\in [0,T]} \subset {{\mathcal {M}}}(E)\) such that \((\rho ,j)\in \mathcal {CE}(0,T)\) with
$$\begin{aligned} \int _s^t \left( {\mathscr {R}}(\rho _r, {{\varvec{j}}}_r) + {\mathscr {D}}(\rho _r) \right) \mathrm {d}r+ {\mathscr {E}}(\rho _t) = {\mathscr {E}}(\rho _s) \qquad \text {for all } 0 \le s \le t \le T. \end{aligned}$$(5.4)
Remark 5.5
-
(1)
Since \((\rho ,{{\varvec{j}}})\in \mathcal {CE}(0,T)\), the curve \(\rho \) is absolutely continuous with respect to the total variation distance.
-
(2)
The Energy-Dissipation balance (5.4) written for \(s=0\) and \(t=T\) implies that \((\rho ,{{\varvec{j}}})\in {\mathcal {A}}{(0,T)}\) as well. Moreover, \(t\mapsto {\mathscr {E}}(\rho _t)\) takes finite values and it is absolutely continuous in the interval [0, T].
-
(3)
The chain-rule estimate (4.59) implies the following important corollary:
Corollary 5.6
(Chain-rule estimate III) For any curve \((\rho ,{{\varvec{j}}})\in \mathcal {CE}(0,T)\),
It follows that the Energy-Dissipation balance (5.4) is equivalent to the Energy-Dissipation Inequality
Let us give an equivalent characterization of solutions to the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) evolution system. Recalling the definition (1.11) of the map \({\mathrm {F}}\) in the interior of \({\mathbb {R}}_+^2\) and the definition (4.40) of \({\mathrm {A}}_\upphi \), we first note that \({\mathrm {F}}\) can be extended to a function defined in \({\mathbb {R}}_+^2\) with values in the extended real line \([-\infty ,+\infty ]\) by
where we set \((\Psi ^*)'({\pm }\infty ){:}{=}{\pm }\infty \). The function \(\mathrm {F}_{0}\) is skew-symmetric.
Theorem 5.7
A curve \((\rho _t)_{t\in [0,T]}\) in \({{\mathcal {M}}}^+(V)\) is a solution of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system iff
-
(1)
\(\rho _t=u_t\pi \ll \pi \) for every \(t\in [0,T]\) and \(t\mapsto u_t\) is an absolutely continuous a.e. differentiable map with values in \(L^1(V,\pi )\);
-
(2)
\({\mathscr {E}}(\rho _0)<{+\infty }\);
-
(3)
We have
$$\begin{aligned} \int _0^T \iint _E|\mathrm {F}_{0}(u_t(x),u_t(y))|\,{\varvec{{\varvec{\vartheta }}}}(\mathrm {d}x,\mathrm {d}y)\,\mathrm {d}t<{+\infty }; \end{aligned}$$(5.8)and
$$\begin{aligned} {\mathrm {D}}_\upphi (u_t(x),u_t(y))={\mathrm {D}}^-_\upphi (u_t(x),u_t(y))\quad \text {for }\lambda \otimes {\varvec{{\varvec{\vartheta }}}}\text {-a.e. }(t,x,y)\in [0,T]\times E. \end{aligned}$$(5.9)In particular the complement \(U'\) of the set
$$\begin{aligned} U{:}{=}\{(t,x,y)\in [0,T]\times E: \mathrm {F}_{0}(u_t(x),u_t(y))\in {\mathbb {R}}\} \end{aligned}$$(5.10)is \((\lambda \otimes {\varvec{{\varvec{\vartheta }}}})\)-negligible and \(\mathrm {F}_{0}\) takes finite values \((\lambda \otimes {\varvec{{\varvec{\vartheta }}}})\)-a.e. in \([0,T]\times E\);
-
(4)
Setting
$$\begin{aligned} 2{{\varvec{j}}}_t(\mathrm {d}x,\mathrm {d}y)=-\mathrm {F}_{0}(u_t(x),u_t(y))\,{\varvec{{\varvec{\vartheta }}}}(\mathrm {d}x,\mathrm {d}y), \end{aligned}$$(5.11)we have \((\rho ,{{\varvec{j}}})\in \mathcal {CE}(0,T)\). In particular,
$$\begin{aligned} \dot{u}_t(x)=\int _V \mathrm {F}_{0}(u_t(x),u_t(y))\,\kappa (x,\mathrm {d}y) \quad \text {for }(\lambda \otimes \pi )\text {-a.e. }(t,x,y)\in [0,T]\times E.\nonumber \\ \end{aligned}$$(5.12)
Proof
Let \(\rho _t=u_t\pi \) be a solution of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system with the corresponding flux \({{\varvec{j}}}_t\). By Corollary 4.14 we can find a skew-symmetric measurable map \(\xi :(0,T)\times E\rightarrow {\mathbb {R}}\) such that \({{\varvec{j}}}_\lambda =\xi \upalpha (u^-,u^+)\lambda \otimes {\varvec{{\varvec{\vartheta }}}}\) and (4.36), (4.37) hold. Taking into account that \({\mathrm {D}}^-_\upphi \le {\mathrm {D}}_\upphi \) and applying the equality case of Corollary 4.20, we complete the proof of one implication.
Suppose now that \(\rho _t\) satisfies all the above conditions (1)–(4); we want to apply formula (4.45) of Theorem 4.16 for \(\upbeta =\upphi \). For this we write the shorthand \(u^-,u^+\) for \(u_t(x),u_t(y)\) and set \(w=-\mathrm {F}_{0}(u^-,u^+)\). We verify the equality conditions (4.56) of Lemma 4.19:
-
At (t, x, y) where \(\upalpha (u^-,u^+) = 0\), we have by definition \(w = -{\mathrm {F}}_0(u^-,u^+)=0\);
-
At \((\lambda \otimes {\varvec{\vartheta }})\)–a.e. (t, x, y) where \(\upalpha (u^-,u^+) >0\), \({\mathrm {F}}_0(u^-,u^+)\) is finite by condition (3), and by (5.7) it follows that \((\Psi ^*)'\bigl ({\mathrm {A}}_\upphi (u^-,u^+)\bigr )\) is finite and therefore \({\mathrm {A}}_\upphi (u^-,u^+)\) is finite. The final condition \(-w=(\Psi ^*)'\big ({\mathrm {A}}_\upbeta (u,v)\big )\upalpha (u,v)\) then follows by the definition of w.
By Lemma 4.19 therefore we have at \((\lambda \otimes {\varvec{\vartheta }})\)–a.e. (t, x, y)
In particular \({\mathrm {B}}_\upphi \) is nonpositive, and the integrability condition (4.44) is trivially satisfied. Integrating (4.45) in time we find (5.4). \(\square \)
Remark 5.8
By Theorem 5.7(3), along a solution \(\rho _t = u_t \pi \) of the \(({\mathscr {E}}, {\mathscr {R}}, {\mathscr {R}}^*)\) system, the functions \( {\mathrm {D}}_\upphi \) and \({\mathrm {D}}^-_\upphi \) coincide. Recall that, in general, we only have \( {\mathrm {D}}_\upphi ^- \le {\mathrm {D}}_\upphi \), and the inequality can be strict, as in the examples of the linear equation (1.2) with the Boltzmann entropy and the quadratic and \(\cosh \)-dissipation potentials discussed in Ex. 4.18. There, \( {\mathrm {D}}_\upphi \) and \({\mathrm {D}}^-_\upphi \) differ on the boundary of \({\mathbb {R}}^2\). Therefore, (5.9) encompasses the information that the pair \((u_t(x),u_t(y))\) stays in the interior of \({\mathbb {R}}^2\) \((\lambda {\otimes }{\varvec{{\varvec{\vartheta }}}})\)-a.e. in \([0,T]\times E\).
5.3 Existence and uniqueness of solutions of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system
Let us now collect a few basic structural properties of solutions of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) Energy-Dissipation balance. Recall that we will always adopt Assumptions (\(V\!\pi \kappa \)), (\({\mathscr {R}}^*\Psi \upalpha \)), and (\({\mathscr {E}}\upphi \)).
Following an argument by Gigli [34] we first use convexity of \({\mathscr {D}}\) to deduce uniqueness.
Theorem 5.9
(Uniqueness) Suppose that \({\mathscr {D}}\) is convex and the energy density \(\upphi \) is strictly convex. Suppose that \(\rho ^1,\, \rho ^2\) satisfy the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) Energy-Dissipation balance (5.4) and are identical at time zero. Then \(\rho _t^1 = \rho _t^2\) for every \(t\in [0,T]\).
Proof
Let \({{\varvec{j}}}^i\in {{\mathcal {M}}}((0,T)\times E)\) satisfy \({\mathscr {L}}_t(\rho ^i,{{\varvec{j}}}^i)=0\) and let us set
By the linearity of the continuity equation we have that \((\rho ,{{\varvec{j}}})\in \mathcal {CE}(0,T)\) with \(\rho _0=\rho ^1_0=\rho ^2_0\), so that by convexity
Since \({\mathscr {E}}\) is strictly convex we deduce \(\rho ^1_t=\rho ^2_t\). \(\square \)
Theorem 5.10
(Existence and stability) Let us suppose that the Fisher information functional \({\mathscr {D}}\) is lower semicontinuous with respect to setwise convergence (e.g. if \(\pi \) is purely atomic, or \({\mathrm {D}}_\upphi \) is convex, see Proposition 5.3).
-
(1)
For every \(\rho _0\in {{\mathcal {M}}}^+(V)\) with \({\mathscr {E}}(\rho _0)<{+\infty }\) there exists a solution \(\rho :[0,T]\rightarrow {{\mathcal {M}}}^+(V)\) of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) evolution system starting from \(\rho _0\).
-
(2)
Every sequence \((\rho ^n_t)_{t\in [0,T]}\) of solutions to the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) evolution system such that
$$\begin{aligned} \sup _{n\in {\mathbb {N}}} {\mathscr {E}}(\rho ^n_0)<{+\infty }\end{aligned}$$(5.13)has a subsequence setwise converging to a limit \((\rho _t)_{t\in [0,T]}\) for every \(t\in [0,T]\).
-
(3)
Let \((\rho ^n_t)_{t\in [0,T]}\) is a sequence of solutions, with corresponding fluxes \(({{\varvec{j}}}^n_t)_{t\in [0,T]}\). Let \(\rho ^n_t\) converge setwise to \(\rho _t\) for every \(t\in [0,T]\), and assume that
$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathscr {E}}(\rho ^n_0)={\mathscr {E}}(\rho _0). \end{aligned}$$(5.14)Then \(\rho \) is a solution as well, with flux \({{\varvec{j}}}\), and the following additional convergence properties hold:
$$\begin{aligned} \lim _{n\rightarrow \infty }\int _0^T{\mathscr {R}}(\rho _t^n,{{\varvec{j}}}_t^n)\,\mathrm {d}t&= \lim _{n\rightarrow \infty }\int _0^T{\mathscr {R}}(\rho _t,{{\varvec{j}}}_t)\,\mathrm {d}t, \end{aligned}$$(5.15a)$$\begin{aligned} \lim _{n\rightarrow \infty }\int _0^T{\mathscr {D}}(\rho _t^n)\,\mathrm {d}t&= \lim _{n\rightarrow \infty }\int _0^T{\mathscr {D}}(\rho _t,{{\varvec{j}}}_t)\,\mathrm {d}t, \end{aligned}$$(5.15b)$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathscr {E}}(\rho ^n_t)&={\mathscr {E}}(\rho _t)\quad \text {for every }t\in [0,T]. \end{aligned}$$(5.15c)If moreover \({\mathscr {E}}\) is strictly convex then \(\rho ^n\) converges uniformly in [0, T] with respect to the total variation distance.
Proof
Part (2) follows immediately from Proposition 4.21.
For part (3), the three statements of (5.15) as inequalities \(\le \) follow from earlier results: for (5.15a) this follows again from Proposition 4.21, for (5.15b) from Proposition 5.3, and for (5.15c) from Lemma 2.3. Using these inequalities to pass to the limit in the equation \({\mathscr {L}}_T(\rho ^n,{{\varvec{j}}}^n)=0\) we obtain that \({\mathscr {L}}_T(\rho ,{{\varvec{j}}})\le 0\). On the other hand, since \(\mathscr {L}_T(\rho ,{{\varvec{j}}})\ge 0\) by the chain-rule estimate (5.5), standard arguments yield the equalities in (5.15).
When \({\mathscr {E}}\) is strictly convex, we obtain the convergence in \(L^1(V,\pi )\) of the densities \(u^n_t=\mathrm {d}\rho ^n_t/\mathrm {d}\pi \) for every \(t\in [0,T]\). We then use the equicontinuity estimate (4.75) of Proposition 4.21 to conclude uniform convergence of the sequence \((\rho _n)_n\) with respect to the total variation distance.
For part (1), when the density \(u_0\) of \(\rho _0\) takes value in a compact interval [a, b] with \(0<a<b<\infty \), the existence of a solution follows by Theorem 6.6 below. The general case follows by a standard approximation of \(u_0\) by truncation and applying the stability properties of parts (2) and (3). \(\square \)
5.4 Stationary states and attraction
Let us finally make a few comments on stationary measures and on the asymptotic behaviour of solutions of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system. The definition of invariant measures was already given in Sect. 2.4, and we recall it for convenience.
Definition 5.11
(Invariant and stationary measures) Let \(\rho =u\pi \in D({\mathscr {E}})\) be given.
-
(1)
We say that \(\rho \) is invariant if \({\varvec{\kappa }}_{\rho }(\mathrm {d}x\mathrm {d}y )= \rho (\mathrm {d}x)\kappa (x,\mathrm {d}y)\) has equal marginals, i.e. \({{\mathsf {x}}}_\# {\varvec{\kappa }}_{\rho }= {{\mathsf {y}}}_\# {\varvec{\kappa }}_{\rho }\).
-
(2)
We say that \(\rho \) is stationary if the constant curve \(\rho _t\equiv \rho \) is a solution of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system.
Note that we always assume that \(\pi \) is invariant (see Assumption (\(V\!\pi \kappa \))). It is immediate to check that
If a measure \(\rho \) is invariant, then \(u=\mathrm {d}\rho /\mathrm {d}\pi \) satisfies
which implies (5.16); therefore invariant measures are stationary. Depending on the system, the set of stationary measures might also contain non-invariant measures, as the next example shows.
Example 5.12
Consider the example of the cosh-type dissipation (1.17a),
but combine this with a Boltzmann entropy with an additional multiplicative constant \(0<\gamma \le 1\):
The case \(\gamma =1\) corresponds to the example of (1.17a), and for general \(0<\gamma \le 1\) we find that
resulting in the evolution equation (see (1.12))
When \(0<\gamma <1\), any function of the form \(u(x) = \mathbb {1}\{x\in A\}\) for \(A\subset V\) is a stationary point of this equation, and equivalently any measure  is a stationary solution of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system. For \(0<\gamma <1\) therefore the set of stationary measures is much larger than just invariant measures.
is a stationary solution of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system. For \(0<\gamma <1\) therefore the set of stationary measures is much larger than just invariant measures.
As in the case of linear evolutions, \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) systems behave well with respect to decomposition of \(\pi \) into mutually singular invariant measures.
Theorem 5.13
(Decomposition) Let us suppose that \(\pi =\pi ^1+\pi ^2\) with \(\pi ^1,\pi ^2\in {{\mathcal {M}}}^+(V)\) mutually singular and invariant. Let \(\rho :[0,T]\rightarrow {{\mathcal {M}}}^+(V)\) be a curve with \(\rho _t=u_t\pi \ll \pi \) and let \(\rho ^i_t{:}{=}u_t\pi ^i\) be the decomposition of \(\rho _t\) with respect to \(\pi ^1\) and \(\pi ^2\). Then \(\rho \) is a solution of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system if and only if each curve \(\rho ^i_t\), \(i=1,2\), is a solution of the \(({\mathscr {E}}^i,{\mathscr {R}}^i,({\mathscr {R}}^i)^*)\) system, where \({\mathscr {E}}^i(\mu ){:}{=}{\mathscr {F}}_\upphi (\mu |\pi ^i)\) is the relative entropy with respect to the measures \(\pi ^i\) and and \({\mathscr {R}}^i,({\mathscr {R}}^i)^*\) are induced by \(\pi ^i\).
Remark 5.14
It is worth noting that when \(\upalpha \) is 1-homogeneous then \({\mathscr {R}}^i={\mathscr {R}}\) and \(({\mathscr {R}}^i)^*={\mathscr {R}}^*\) do not depend on \(\pi ^i\), cf. Corollary 4.11. The decomposition is thus driven just by the splitting of the entropy \({\mathscr {E}}\).
Proof of Theorem 5.13
Note that the assumptions of invariance and mutual singularity of \(\pi ^1\) and \(\pi ^2\) imply that \({\varvec{{\varvec{\vartheta }}}}\) has a singular decomposition \({\varvec{\vartheta }}= {\varvec{\vartheta }}^1 + {\varvec{\vartheta }}^2 {:}{=} {\varvec{\kappa }}_{\pi ^1} + {\varvec{\kappa }}_{\pi ^2}\), where the \({\varvec{\kappa }}_{\pi ^i}\) are symmetric. It then follows that \({\mathscr {E}}(\rho _t)={\mathscr {E}}^1(\rho ^1_t)+{\mathscr {E}}^2(\rho ^2_t)\) and \({\mathscr {D}}(\rho _t)={\mathscr {D}}^1(\rho ^1_t)+{\mathscr {D}}^2(\rho ^2_t)\), where
Finally, Corollary 4.11 shows that decomposing \({{\varvec{j}}}\) as the sum \({{\varvec{j}}}^1+{{\varvec{j}}}^2\) where \({{\varvec{j}}}^i\ll {\varvec{{\varvec{\vartheta }}}}^i\), the pairs \((\rho ^i,{{\varvec{j}}}^i)\) belong to \(\mathcal {CE}(0,T)\) and \({\mathscr {R}}(\rho _t,{{\varvec{j}}}_t)= {\mathscr {R}}^1(\rho ^1_t,{{\varvec{j}}}^1_t)+ {\mathscr {R}}^2(\rho ^2_t,{{\varvec{j}}}^2_t)\). \(\square \)
Theorem 5.15
(Asymptotic behaviour) Let us suppose that the only stationary measures are multiples of \(\pi \), and that \({\mathscr {D}}\) is lower semicontinuous with respect to setwise convergence. Then every solution \(\rho :[0,\infty )\rightarrow {{\mathcal {M}}}^+(V)\) of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) evolution system converges setwise to \(c\pi \), where \(c{:}{=}\rho _0(V)/\pi (V)\).
Proof
Let us fix a vanishing sequence \(\tau _n\downarrow 0\) such that \(\sum _n\tau _n={+\infty }\). Let \(\rho _\infty \) be any limit point with respect to setwise convergence of the curve \(\rho _t\) along a diverging sequence of times \(t_n\uparrow {+\infty }\). Such a point exists since the curve \(\rho \) is contained in a sublevel set of \({\mathscr {E}}\). Up to extracting a further subsequence, it is not restrictive to assume that \(t_{n+1}\ge t_n+\tau _n\).
Since
and the series of \(\tau _n\) diverges, we find
Up to extracting a further subsequence, we can suppose that the above \(\liminf \) is a limit and we can select \(t'_n\in [t_n,t_n+\tau _n]\) such that
Recalling the definition (4.80) of the Dynamical-Variational Transport cost and the monotonicity with respect to \(\tau \), we also get \(\lim _{n\rightarrow \infty } \mathscr {W}(\tau _n,\rho _{t_n},\rho _{t_n'})=0\), so that Theorem 4.26(5) and the relative compactness of the sequence \((\rho _{t_n'})_n\) yield \(\rho _{t_n'}\rightarrow \rho _\infty \) setwise.
The lower semicontinuity of \({\mathscr {D}}\) yields \({\mathscr {D}}(\rho _\infty )=0\) so that \(\rho _\infty =c\pi \) thanks to the uniqueness assumption and to the conservation of the total mass. Since we have uniquely identified the limit point, we conclude that the whole curve \(\rho _t\) converges setwise to \(\rho _\infty \) as \(t\rightarrow {+\infty }\). \(\square \)
6 Dissipative evolutions in \(L^1(V,\pi )\)
In this section we construct solutions of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) formulation by studying their equivalent characterization as abstract evolution equations in \(L^1(V,\pi )\). Throughout this section we adopt Assumption (\(V\!\pi \kappa \)).
6.1 Integro-differential equations in \(L^1\)
Let \(J\subset {\mathbb {R}}\) be a closed interval (not necessarily bounded) and let us first consider a map \({\mathrm {G}}:E\times J^2\rightarrow {\mathbb {R}}\) with the following properties:
-
(1)
measurability with respect to \((x,y)\in E\):
$$\begin{aligned} \text {for every }u,v\in J\text { the map } (x,y)\mapsto {\mathrm {G}}(x,y;u,v)\text { is measurable}; \end{aligned}$$(6.1a) -
(2)
continuity with respect to u, v and linear growth: there exists a constant \(M>0\) such that
$$\begin{aligned}&\text {for every }(x,y)\in E\quad (u,v)\mapsto {\mathrm {G}}(x,y;u,v)\text { is continuous and } \nonumber \\&\quad |{\mathrm {G}}(x,y;u,v)|\le M(1+|u|+|v|) \quad \text {for every }u,v\in J, \end{aligned}$$(6.1b) -
(3)
skew-symmetry:
$$\begin{aligned} {\mathrm {G}}(x,y;u,v)=-{\mathrm {G}}(y,x;v,u),\quad \text {for every } (x,y)\in E,\ u,v\in J, \end{aligned}$$(6.1c) -
(4)
\(\ell \)-dissipativity: there exists a constant \(\ell \ge 0\) such that for every \((x,y)\in E\), \(u,u',v\in J\):
$$\begin{aligned} u\le u'\quad \Rightarrow \quad {\mathrm {G}}(x,y;u',v)- {\mathrm {G}}(x,y;u,v)\le \ell (u'-u). \end{aligned}$$(6.1d)
Remark 6.1
Note that (6.1d) is surely satisfied if \({\mathrm {G}}\) is \(\ell \)-Lipschitz in (u, v), uniformly with respect to (x, y). The ‘one-sided Lipschitz condition’ (6.1d) however is weaker than the standard Lipschitz condition; this type of condition is common in the study of ordinary differential equations, since it is still strong enough to guarantee uniqueness and non-blowup of the solutions (see e.g. [41, Ch. IV.12]).
Let us also remark that (6.1c) and (6.1d) imply the reverse monotonicity property of \({\mathrm {G}}\) with respect to v,
and the joint estimate
Let us set \(L^1(V,\pi ;J){:}{=}\{u\in L^1(V,\pi ):u(x)\in J\ \text {for } \pi \text {-a.e. }x\in V\}\).
Lemma 6.2
Let \(u:V\rightarrow J\) be a measurable \(\pi \)-integrable function.
-
(1)
We have
$$\begin{aligned} \int _V\big |{\mathrm {G}}(x,y;u(x),u(y))\big |\,\kappa (x,\mathrm {d}y)<{+\infty }\quad \text {for }\pi \text {-a.e. }x\in V, \end{aligned}$$(6.4)and the formula
$$\begin{aligned} {\varvec{G}}[u](x){:}{=} \int _V {\mathrm {G}}(x,y;u(x),u(y))\,\kappa (x,\mathrm {d}y) \end{aligned}$$(6.5)defines a function \({\varvec{G}}[u]\) in \(L^1(V,\pi )\) that only depends on the Lebesgue equivalence class of u in \(L^1(V,\pi )\).
-
(2)
The map \({\varvec{G}}:L^1(V,\pi ;J)\rightarrow L^1(V,\pi )\) is continuous.
-
(3)
The map \({\varvec{G}}\) is \((\ell \, \Vert \kappa _V\Vert _\infty )\)-dissipative, in the sense that for all \(h>0\),
$$\begin{aligned} \big \Vert (u_1- u_2)-h ({\varvec{G}}[u_1]-{\varvec{G}}[u_2])\big \Vert _{L^1(V,\pi )}\ge (1-2 \ell \Vert \kappa _V|_\infty \,h)\Vert u_1-u_2\Vert _{L^1(V,\pi )}\nonumber \\ \end{aligned}$$(6.6)for every \(u_1,u_2\in L^1(V,\pi ;J)\).
-
(4)
If \(a\in J\) satisfies
$$\begin{aligned} 0={\mathrm {G}}(x,y;a,a)\le {\mathrm {G}}(x,y;a,v)\quad \text {for every }(x,y)\in E,\ v\ge a\,, \end{aligned}$$(6.7)then for every function \(u\in L^1(V,\pi ;J)\) we have
$$\begin{aligned} \begin{aligned} u\ge a\pi \text { -a.e.}\quad&\Rightarrow \quad \lim _{h\downarrow 0}\frac{1}{h} \int _V \Big (a-(u+h{\varvec{G}}[u])\Big )_+\,\mathrm {d}\pi =0\,. \end{aligned} \end{aligned}$$(6.8)If \(b\in J\) satisfies
$$\begin{aligned} 0={\mathrm {G}}(x,y;b,b)\ge {\mathrm {G}}(x,y;b,v)\quad \text {for every }(x,y)\in E,\ v\le b, \end{aligned}$$(6.9)then for every function \(u\in L^1(V,\pi ;J)\) we have
$$\begin{aligned} u\le b\pi \text { -a.e.}\quad \Rightarrow \quad \lim _{h\downarrow 0}\frac{1}{h}\int _V \Big (u+h{\varvec{G}}[u]-b\Big )_+\,\mathrm {d}\pi =0\,. \end{aligned}$$(6.10)
Proof
(1) Since \({\mathrm {G}}\) is a Carathéodory function, for every measurable u and every \((x,y)\in E\) the map \((x,y)\mapsto {\mathrm {G}}(x,y;u(x),u(y))\) is measurable. Since
the first claim follows by Fubini’s Theorem [18, II, 14].
(2) Let \((u_n)_{n\in {\mathbb {N}}}\) be a sequence of functions strongly converging to u in \(L^1(V,\pi ;J)\). Up to extracting a further subsequence, it is not restrictive to assume that \(u_n\) also converges to u pointwise \(\pi \)-a.e. We have
Since the integrand \(g_n\) in (6.12) vanishes \({\varvec{{\varvec{\vartheta }}}}\)-a.e. in \(E\) as \(n\rightarrow \infty \), by the generalized Dominated Convergence Theorem (see for instance [27, Thm. 4, page 21] it is sufficient to show that there exist positive functions \(h_n\) pointwise converging to h such that
We select \(h_n(x,y){:}{=}M(2+|u_n(x)|+|u_n(y)|+|u(x)|+|u(y)|)\) and \( h(x,y){:}{=}2M(1+|u(x)|+|u(y)|)\). This proves the result.
(3) Let us set
and observe that the left-hand side of (6.6) may be estimated from below by
for all \(h>0\). Therefore, estimate (6.6) follows if we prove that
Let us set
and
Since \( \Delta _{\mathrm {G}}(x,y)=-\Delta _{\mathrm {G}}(y,x)\), using (6.1c) we have
Setting \(\Delta (x){:}{=}u_{1}(x)-u_{2}(x)\) we observe that by (6.3)
We deduce that
(4) We will only address the proof of property (6.8), as the argument for (6.10) is completely analogous. Suppose that \(u\ge a\) \(\pi \)-a.e. Let us first observe that if \(u(x)=a\), then from (6.7),
We set \(f_h(x){:}{=}h^{-1}(a-u(x))-{\varvec{G}}[u](x)\), observing that \(f_h(x)\) is monotonically decreasing to \(-\infty \) if \(u(x)>a\) and \(f_h(x)=-{\varvec{G}}[u](x)\le 0\) if \(u(x)=a\), so that \(\lim _{h\downarrow 0}\big (f_h(x)\big )_+=0\). Since \(\big (f_h\big )_+\le \big (\!-\!{\varvec{G}}[u]\big )_+\) we can apply the Dominated Convergence Theorem to obtain
thereby concluding the proof. \(\square \)
In what follows, we shall address the Cauchy problem

Lemma 6.3
(Comparison principles) Let us suppose that the map \({\mathrm {G}}\) satisfies (6.1a,b,c) with \(J={\mathbb {R}}\).
-
(1)
If \({{\bar{u}}}\in {\mathbb {R}}\) satisfies
$$\begin{aligned} 0={\mathrm {G}}(x,y;{{\bar{u}}},{{\bar{u}}})\le {\mathrm {G}}(x,y;{{\bar{u}}},v)\quad \text {for every }(x,y)\in E,\ v\ge {{\bar{u}}}, \end{aligned}$$(6.16)then for every initial datum \(u_0\ge {{\bar{u}}}\) the solution u of (6.15) satisfies \(u_t\ge {{\bar{u}}}\) \(\pi \)-a.e. for every \(t\ge 0\).
-
(2)
If \({{\bar{u}}}\in {\mathbb {R}}\) satisfies
$$\begin{aligned} 0={\mathrm {G}}(x,y;{{\bar{u}}},{{\bar{u}}})\ge {\mathrm {G}}(x,y;{{\bar{u}}},v)\quad \text {for every }(x,y)\in E,\ v\le {{\bar{u}}}, \end{aligned}$$(6.17)then for every initial datum \(u_0\le {{\bar{u}}}\) the solution u of (6.15) satisfies \(u_t\le {{\bar{u}}}\) \(\pi \)-a.e. for every \(t\ge 0\).
Proof
(1) Let us first consider the case \({{\bar{u}}}=0\). We define a new map \({{\overline{{\mathrm {G}}}}}\) by symmetry:
which satisfies the same structural properties (6.1a,b,c), and moreover
We call \({{\overline{{\varvec{G}}}}}\) the operator induced by \({{\overline{{\mathrm {G}}}}}\), and \({{\bar{u}}}\) the solution curve of the corresponding Cauchy problem starting from the same (nonnegative) initial datum \(u_0\). If we prove that \({{\bar{u}}}_t\ge 0\) for every \(t\ge 0\), then \({{\bar{u}}}_t\) is also the unique solution of the original Cauchy problem (6.15) induced by \({\mathrm {G}}\), so that we obtain the positivity of \(u_t\).
Note that (6.19) and property (6.1d) yield
We set \(\upbeta (r){:}{=}r_-=\max (0,-r)\) and \(P_t{:}{=}\{x\in V:\bar{u}_t(x)<0\}\) for each \(t\ge 0\). Due to the Lipschitz continuity of \(\upbeta \), the map \(t\mapsto b(t){:}{=}\int _V \upbeta ({{\bar{u}}}_t)\,\mathrm {d}\pi \) is absolutely continuous. Hence, the chain-rule formula applies, which, together with (6.20) gives
Since b is nonnegative and \(b(0)=0\), we conclude, by Gronwall’s inequality, that \(b(t)=0\) for every \(t\ge 0\) and therefore \({{\bar{u}}}_t\ge 0\). In order to prove the the statement for a general \({{\bar{u}}}\in {\mathbb {R}}\) it is sufficient to consider the new operator \({{\widetilde{{\mathrm {G}}}}}(x,y;u,v){:}{=}{\mathrm {G}}(x,y;u+{{\bar{u}}},v+{{\bar{u}}})\), and to consider the curve \({{\widetilde{u}}}_t{:}{=}u_t-{{\bar{u}}}\) starting from the nonnegative initial datum \({{\widetilde{u}}}_0{:}{=}u_0-{{\bar{u}}}\).
(2) It suffices to apply the transformation \({{\widetilde{{\mathrm {G}}}}}(x,y;u,v){:}{=}-{\mathrm {G}}(x,y;-u,-v)\) and set \(\widetilde{u}_t{:}{=}-u_t\). We then apply the previous claim, yielding the lower bound \(-{{\bar{u}}}\). \(\square \)
We can now state our main result concerning the well-posedness of the Cauchy problem (6.15).
Theorem 6.4
Let \(J\subset {\mathbb {R}}\) be a closed interval of \({\mathbb {R}}\) and let \(G:E\times J^2\rightarrow {\mathbb {R}}\) be a map satisfying conditions (6.1). Let us also suppose that, if \(a=\mathrm{inf}J>-\infty \) then (6.7) holds, and that, if \(b=\sup J<+\infty \) then (6.9) holds.
-
(1)
For every \(u_0\in L^1(V,\pi ;J)\) there exists a unique curve \(u\in {\mathrm {C}}^1([0,\infty );L^1(V,\pi ; J))\) solving the Cauchy problem (6.15).
-
(2)
\(\int _V u_t\,\mathrm {d}\pi =\int _V u_0\,\mathrm {d}\pi \) for every \(t\ge 0\).
-
(3)
If u, v are two solutions with initial data \(u_0,v_0\in L^1(V,\pi ;J)\) respectively, then
$$\begin{aligned} \Vert u_t-v_t\Vert _{L^1(V,\pi )}\le {\mathrm {e}}^{2 \Vert \kappa _V\Vert _\infty \ell \, t}\Vert u_0-v_0\Vert _{L^1(V,\pi )}\quad \text {for every }t\ge 0. \end{aligned}$$(6.21) -
(4)
If \({{\bar{a}}}\in J\) satisfies condition (6.7) and \(u_0\ge {{\bar{a}}}\), then \(u_t\ge {{\bar{a}}}\) for every \(t\ge 0\). Similarly, if \({{\bar{b}}}\in J\) satisfies condition (6.9) and \(u_0\le {{\bar{b}}}\), then \(u_t\le {{\bar{b}}}\) for every \(t\ge 0\).
-
(5)
If \(\ell =0\), then the evolution is order preserving: if u, v are two solutions with initial data \(u_0,v_0\) then
$$\begin{aligned} u_0\le v_0\quad \Rightarrow \quad u_t\le v_t\quad \text {for every }t\ge 0. \end{aligned}$$(6.22)
Proof
Claims (1), (3), (4) follow by the abstract generation result of [50, §6.6, Theorem 6.1] applied to the operator \({\varvec{G}}\) defined in the closed convex subset \(D{:}{=}L^1(V,\pi ;J)\) of the Banach space \(L^1(V,\pi )\). For the theorem to apply, one has to check the continuity of \({\varvec{G}}:D\rightarrow L^1(V,\pi )\) (Lemma 6.2(2)), its dissipativity (6.6), and the property
When \(J={\mathbb {R}}\), the inner infimum always is zero; if J is a bounded interval [a, b] then the property above follows from the estimates of Lemma 6.2(4), since for any \(u\in D\),
When \(J=[a,\infty )\) or \(J = (-\infty ,b]\) a similar reasoning applies.
Claim (2) is an immediate consequence of (6.1c). Finally, when \(\ell =0\), claim (5) follows from the Crandall-Tartar Theorem [14], stating that a non-expansive map in \(L^1\) (cf. (6.21)) that satisfies claim (2) is also order preserving. \(\square \)
6.2 Applications to dissipative evolutions
Let us now consider the map \(\mathrm {F}: (0,+\infty )^2 \rightarrow {\mathbb {R}}\) induced by the system \((\Psi ^*,\upphi ,\upalpha )\), first introduced in (1.11),
with the corresponding integral operator:
Since \(\Psi ^*\), \(\upphi \) are \({\mathrm {C}}^1\) convex functions on \((0,{+\infty })\) and \(\upalpha \) is locally Lipschitz in \((0,{+\infty })^2\) it is easy to check that \(\mathrm {F}\) satisfies properties (6.1a,b,c,d) in every compact subset \(J\subset (0,{+\infty })\) and conditions (6.7), (6.9) at every point \(a,b\in J\). In order to focus on the structural properties of the associated evolution problem, cf. (6.28) below, we will mostly confine our analysis to the regular case, according to the following:

Note that (6.25) is always satisfied if \(\upphi \) is differentiable at 0. Estimate (6.26) is also true if in addition \(\upalpha \) is Lipschitz. However, as we have shown in Sect. 1.3, there are important examples in which \(\upphi '(0)=-\infty \), but (6.25) and (6.26) hold nonetheless. All of the examples given in Sect. 1.3 indeed provide families of maps F that satisfy Assumption (\({\mathrm {F}}\)).
Theorem 6.4 yields the following general result:
Theorem 6.5
Consider the Cauchy problem

for a given nonnegative \(u_0\in L^1(V,\pi )\).
-
(1)
For every \(u_0\in L^1(V,\pi ;J)\) with J a compact subinterval of \((0,{+\infty })\) there exists a unique bounded and nonnegative solution \(u\in {\mathrm {C}}^1([0,\infty );L^1(V,\pi ;J))\) of (6.28). We will denote by \(({{\mathsf {S}}}_t)_{t\ge 0}\) the corresponding \({\mathrm {C}}^1\)-semigroup of nonlinear operators, mapping \(u_0\) to the value \(u_t={{\mathsf {S}}}_t[u_0]\) at time t of the solution u.
-
(2)
\(\int _V u_t\,\mathrm {d}\pi =\int _V u_0\,\mathrm {d}\pi \) for every \(t\ge 0\).
-
(3)
If \(a\le u_0\le b\) \(\pi \)-a.e. in V, then \(a\le u_t\le b\) \(\pi \)-a.e. for every \(t\ge 0\).
-
(4)
The solution satisfies the Lipschitz estimate (6.21) (with \(\ell =\ell _R\)) and the order preserving property if \(\ell _R=0\).
-
(5)
If Assumption (\({\mathrm {F}}\)) holds, then \(({{\mathsf {S}}}_t)_{t\ge 0}\) can be extended to a semigroup defined on every essentially bounded nonnegative \(u_0\in L^1(V,\pi )\) and satisfying the same properties (1)–(4) above.
-
(6)
If additionally \(({\mathrm {F}}_\infty )\) holds, then \(({{\mathsf {S}}}_t)_{t\ge 0}\) can be extended to a semigroup defined on every nonnegative \(u_0\in L^1(V,\pi )\) and satisfying the same properties (1)–(4) above.
We now show that the solution u given by Theorem 6.5 is also a solution in the sense of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) Energy-Dissipation balance.
Theorem 6.6
Assume (\(V\!\pi \kappa \)), (\({\mathscr {R}}^*\Psi \upalpha \)), (\({\mathscr {E}}\upphi \)). Let \(u_0 \in L^1(V;\pi )\) be nonnegative and \(\pi \)-essentially valued in a compact interval J of \((0,\infty )\) and let \(u={{\mathsf {S}}}[u_0] \in \mathrm {C}^1 ([0,{+\infty });L^1(V,\pi ;J))\) be the solution to (6.28) given by Theorem 6.5. Then the pair \((\rho ,{{\varvec{j}}})\) given by
is an element of \(\mathcal {CE}(0,{+\infty })\) and satisfies the \(({\mathscr {E}},{\mathscr {R}}\),\({\mathscr {R}}^*)\) Energy-Dissipation balance (5.4).
If \({\mathrm {F}}\) satisfies the stronger assumption (\({\mathrm {F}}\)), then the same result holds for every essentially bounded and nonnegative initial datum. Finally, if also \(({\mathrm {F}}_\infty )\) holds, the above result is valid for every nonnegative \(u_0\in L^1(V,\pi )\) with \(\rho _0=u_0\pi \in D({\mathscr {E}})\).
Proof
Let us first consider the case when \(u_0\) satisfies \(0<a\le u_0\le b<{+\infty }\) \(\pi \)-a.e.. Then, the solution \(u={{\mathsf {S}}}[u_0]\) satisfies the same bounds, the map \(w_t\) is uniformly bounded and \( \upalpha (u_t(x),u_t(y))\ge \upalpha (a,a)>0\), so that \((\rho ,{{\varvec{j}}})\in {\mathcal {A}}{(0,T)}.\) We can thus apply Theorem 5.7, obtaining the Energy-Dissipation balance
In the case \(0\le u_0\le b\) we can argue by approximation, setting \(u_{0}^a{:}{=}\max \{u_0, a\}\), \(a>0\), and considering the solution \(u_t^a{:}{=}{{\mathsf {S}}}_t[u_0^a]\) with divergence field \(2 {{\varvec{j}}}_t^a(\mathrm {d}x,\mathrm {d}y)=-{\mathrm {F}}(u_t^{a}(x),u_t^{a}(y)){\varvec{{\varvec{\vartheta }}}}(\mathrm {d}x,\mathrm {d}y)\). Theorem 6.5(4) shows that \(u_t^a\rightarrow u_t\) strongly in \(L^1(V,\pi )\) as \(a\downarrow 0\), and consequently also \({{\varvec{j}}}_\lambda ^a\rightarrow {{\varvec{j}}}_\lambda \) setwise. Hence, we can pass to the limit in (6.29) (written for \((\rho ^a,{{\varvec{j}}}^a)\) thanks to Proposition 4.21 and Proposition 5.3), obtaining \({\mathscr {L}}(\rho ,{{\varvec{j}}})\le 0\), which is still sufficient to conclude that \((\rho ,{{\varvec{j}}})\) is a solution thanks to Remark 5.5(3).
Finally, if \(({\mathrm {F}}_\infty )\) holds, we obtain the general result by a completely analogous argument, approximating \(u_0\) by the sequence \(u_0^b{:}{=}\min \{u_0, b\}\) and letting \(b\uparrow {+\infty }\). \(\square \)
7 Existence via minimizing movements
In this section we construct solutions to the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) formulation via the Minimizing Movement approach. The method uses only fairly general properties of \({\mathscr {W}}\), \({\mathscr {E}}\), and the underlying space, and it may well have broader applicability than the measure-space setting that we consider here (see Remark 7.8). Therefore we formulate the results in a slightly more general setup.
We consider a topological space
For consistency with the above definition, in this section we will use use the abstract notation \({\mathop {\rightharpoonup }\limits ^{\sigma }}\) to denote setwise convergence in \(X= {{\mathcal {M}}}^+(V)\). Although throughout this paper we adopt the Assumptions (\(V\!\pi \kappa \)), (\({\mathscr {R}}^*\Psi \upalpha \)), and (\({\mathscr {E}}\upphi \)), in this chapter we will base the discussion only on the following properties:

Assumption (Abs) is implied by Assumptions (\(V\!\pi \kappa \)), (\({\mathscr {R}}^*\Psi \upalpha \)), and (\({\mathscr {E}}\upphi \)). The properties (4.86) are the content of Theorem 4.26; condition (7.2a) follows from Assumption (\({\mathscr {E}}\upphi \)) and Lemma 5.3; condition (7.2b) follows from the superlinearity of \(\upphi \) at infinity and Prokhorov’s characterization of compactness in the space of finite measures [9, Th. 8.6.2].
7.1 The minimizing movement scheme and the convergence result
The classical ‘Minimizing Movement’ scheme for metric-space gradient flows [4, 17] starts by defining approximate solutions through incremental minimization,
In the context of this paper the natural generalization of the expression to be minimized is \({\mathscr {W}}(\tau ,\rho ^{n-1},\rho )+ {\mathscr {E}}(\rho )\). This can be understood by remarking that if \({\mathscr {R}}(\rho ,\cdot )\) is quadratic, then it formally generates a metric
In this section we set up the approximation scheme featuring the cost \({\mathscr {W}}\).
We consider a partition \( \{t_{\tau }^0 =0< t_{\tau }^1< \ldots<t_{\tau }^n< \ldots< t_{\tau }^{N_\tau -1}<T\le t_{\tau }^{N_\tau }\} \), with fineness \(\tau : = \max _{i=n,\ldots , N_\tau } (t_{\tau }^{n} {-} t_{\tau }^{n-1})\), of the time interval [0, T]. The sequence of approximations \((\rho _\tau ^n)_n\) is defined by the following recursive minimization scheme. Fix \(\rho ^\circ \in X\).
Problem 7.1
Given \(\rho _\tau ^0{:}{=}\rho ^\circ ,\) find \(\rho _\tau ^1, \ldots , \rho _\tau ^{N_\tau } \in X \) fulfilling
Lemma 7.2
Under assumption (Abs), for any \(\tau >0\) Problem 7.1 admits a solution \(\{\rho _\tau ^n\}_{n=1}^{{N_\tau }}\subset X\).
We denote by \(\overline{\rho }_{\tau }\) and \(\underline{\rho }_{\tau }\) the left-continuous and right-continuous piecewise constant interpolants of the values \(\{\rho _\tau ^n\}_{n=1}^{{N_\tau }}\) on the nodes of the partition, fulfilling \(\overline{\rho }_{\tau }(t_{\tau }^n)=\underline{\rho }_{\tau }(t_{\tau }^n)=\rho _\tau ^n\) for all \(n=1,\ldots , {N_\tau }\), i.e.,
Likewise, we denote by \(\overline{{\mathsf {t}}}_{\tau }\) and \(\underline{{\mathsf {t}}}_{\tau }\) the piecewise constant interpolants \(\overline{{\mathsf {t}}}_{\tau }(0): = \underline{{\mathsf {t}}}_{\tau }(0): =0\), \( \overline{{\mathsf {t}}}_{\tau }(T): = \underline{{\mathsf {t}}}_{\tau }(T): =T\), and
We also introduce another notion of interpolant of the discrete values \(\{\rho _\tau ^n\}_{n=0}^{N_\tau }\) introduced by De Giorgi, namely the variational interpolant \(\widetilde{\rho }_{\tau }: [0,T]\rightarrow X\), which is defined in the following way: the map \(t\mapsto \widetilde{\rho }_{\tau }(t)\) is Lebesgue measurable in (0, T) and satisfies
The existence of a measurable selection is guaranteed by [15, Cor. III.3, Thm. III.6].
It is natural to introduce the following extension of the notion of (Generalized) Minimizing Movement, which is typically given in a metric setting [4, 5]. For simplicity, we will continue to use the classical terminology.
Definition 7.3
We say that a curve \(\rho : [0,T] \rightarrow X\) is a Generalized Minimizing Movement for the energy functional \({\mathscr {E}}\) starting from the initial datum \(\rho ^\circ \in \mathrm {D}({\mathscr {E}})\), if there exist a sequence of partitions with fineness \((\tau _k)_k\), \(\tau _k\downarrow 0\) as \(k\rightarrow \infty \), and, correspondingly, a sequence of discrete solutions \((\overline{\rho }_{\tau _k})_k\) such that, as \(k\rightarrow \infty \),
We shall denote by \(\mathrm {GMM}({\mathscr {E}},{\mathscr {W}};\rho ^\circ )\) the collection of all Generalized Minimizing Movements for \({\mathscr {E}}\) starting from \(\rho ^\circ \).
We can now state the main result of this section.
Theorem 7.4
Under Assumptions (\(V\!\pi \kappa \)), (\({\mathscr {R}}^*\Psi \upalpha \)), and (\({\mathscr {E}}\upphi \)), let the lower-semicontinuity Property (5.2) be satisfied.
Then \(\mathrm {GMM}({\mathscr {E}},{\mathscr {W}};(0, T),\rho ^\circ ) \ne \emptyset \) and every \(\rho \in \mathrm {GMM}({\mathscr {E}},{\mathscr {W}};(0, T),\rho ^\circ )\) satisfies the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) Energy-Dissipation balance (Definition 5.4).
Throughout Sects. 7.2–7.4 we will first prove an abstract version of this theorem as Theorem 7.7 below, under Assumption (Abs). Indeed, therein we could ‘move away’ from the context of the ‘concrete’ gradient structure for the Markov processes, and carry out our analysis in a general topological setup (cf. Remark 7.8 ahead). In Sect. 7.5 we will ‘return’ to the problem under consideration and deduce the proof of Theorem 7.4 from Theorem 7.7.
7.2 Moreau–Yosida approximation and generalized slope
Preliminarily, let us observe some straightforward consequences of the properties of the transport cost:
-
(1)
the ‘generalized triangle inequality’ from (4.86b) entails that for all \(m \in {\mathbb {N}}\), for all \((m+1)\)-ples \((t, t_1, \ldots , t_m) \in (0,{+\infty })^{m+1}\), and all \((\rho _0, \rho _1, \ldots , \rho _m) \in X^{m+1}\), we have
$$\begin{aligned} {\mathscr {W}}(t,\rho _0,\rho _{m}) \le \sum _{k=1}^{m} {\mathscr {W}}(t_k,\rho _{k-1},\rho _{k}) \qquad \text {if }t=\sum _{k=1}^m t_k. \end{aligned}$$(7.8) -
(2)
Combining (4.86a) and (4.86b) we deduce that
$$\begin{aligned} {\mathscr {W}}(t,\rho ,\mu ) \le {\mathscr {W}}(s,\rho ,\mu ) \quad \text { for all } 0<s<t \text { and for all } \rho , \mu \in X. \end{aligned}$$(7.9)
In the context of metric gradient-flow theory, the ‘Moreau-Yosida approximation’ (see e.g. [11, Ch. 7] or [4, Def. 3.1.1]) provides an approximation of the driving functional that is finite and sub-differentiable everywhere, and can be used to define a generalized slope. We now construct the analogous objects in the situation at hand.
Given \(r>0\) and \(\rho \in X\), we define the subset \(J_r(\rho )\subset X\) by
(by Lemma 7.2, this set is non-empty) and define
In addition, for all \(\rho \in {\mathrm {D}}({\mathscr {E}})\), we define the generalized slope
Recalling the duality formula for the local slope (cf. [4, Lemma 3.15]) and the fact that \({\mathscr {W}}(\tau ,\cdot , \cdot )\) is a proxy for \(\frac{1}{2\tau }d^2(\cdot , \cdot )\), it is immediate to recognize that the generalized slope is a surrogate of the local slope. Furthermore, as we will see that its definition is somehow tailored to the validity of Lemma 7.5 ahead. Heuristically, the generalized slope \({\mathscr {S}}(\rho )\) coincides with the Fisher information \({\mathscr {D}}(\rho ) = {\mathscr {R}}^*(\rho ,-{\mathrm {D}}{\mathscr {E}}(\rho ))\). This can be recognized, again heuristically, by fixing a point \(\rho _0\) and considering curves \(\rho _t {:}{=} \rho _0 -t{\overline{\mathrm {div}}}{{\varvec{j}}}\), for a class of fluxes \({{\varvec{j}}}\). We then calculate
In Theorem 7.9 below we rigorously prove that \({\mathscr {S}}\ge {\mathscr {D}}\) using this approach.
The following result collects some properties of \({\mathscr {E}}_{r}\) and \({\mathscr {S}}\).
Lemma 7.5
For all \(\rho \in {\mathrm {D}}({\mathscr {E}})\) and for every selection \( \rho _r \in J_r(\rho )\)
In particular, for all \(\rho \in {\mathrm {D}}({\mathscr {E}})\)
for every \( r_{0}>0\) and \( \rho _{r_0} \in J_{r_0}(\rho )\).
Proof
Let \(r>0\), \(\rho \in {\mathrm {D}}({\mathscr {E}})\), and \(\rho _r\in J_r(\rho )\). It follows from (7.10) and (4.86a) that
in the same way, one checks that for all \(\rho \in X\) and \(0<r_1<r_2\),
which implies (7.12). Thus, the map \(r \mapsto {\mathscr {E}}_{r}(\rho )\) is non-increasing on \((0,{+\infty })\), and hence almost everywhere differentiable. Let us fix a point of differentiability \(r>0\). For \(h>0\) and \(\rho _r \in J_r (\rho )\) we then have
the latter inequality due to (4.86b), so that
whence (7.14). Finally, (7.17) yields that, for any \(\rho \in {\mathrm {D}}({\mathscr {E}})\) and any selection \(\rho _r \in J_r(\rho )\), one has \( \sup _{r>0} {\mathscr {W}}(r,\rho ,\rho _r) <+ \infty .\) Therefore, (4.86d) entails the first convergence in (7.13). Furthermore, we have
where the first inequality again follows from (7.17), and the last one from the \(\sigma \)-lower semicontinuity of \({\mathscr {E}}\). This implies the second statement of (7.13). \(\square \)
7.3 A priori estimates
Our next result collects the basic estimates on the discrete solutions. In order to properly state it, we need to introduce the ‘density of dissipated energy’ associated with the interpolant \(\overline{\rho }_{\tau }\), namely the piecewise constant function \(\overline{{\mathsf {W}}}_{\tau }:[0,T] \rightarrow [0,{+\infty })\) defined by
Proposition 7.6
(Discrete energy-dissipation inequality and a priori estimates) We have
and there exists a constant \(C>0\) such that for all \(\tau >0\)
Finally, there exists a \(\sigma \)-sequentially compact subset \(K\subset X\) such that
Proof
From (7.16) we directly deduce, for \(t \in (t_{\tau }^{j-1}, t_{\tau }^j]\),
which implies (7.19); in particular, for \(t= t_{\tau }^j\) one has
The estimate (7.20) follows upon summing (7.24) over the index j. Furthermore, applying (7.8)–(7.9) one deduces for all \(1 \le n \le N_\tau \) that
In particular, (7.21) follows, as well as \(\sup _{n=0,\ldots ,N_\tau } {\mathscr {E}}(\rho _\tau ^{n}) \le C\). Then, (7.23) also yields \(\sup _{t\in [0,T]} {\mathscr {E}}(\widetilde{\rho }_{\tau }(t)) \le C\).
Next we show the two estimates
Recall that \(\rho ^*\) is introduced in Assumption (Abs).
To deduce (7.26), we use the triangle inequality for \({\mathscr {W}}\). Preliminarily, we observe that \( {\mathscr {W}}(t, \rho ^*, \rho _0) <{+\infty }\) for all \(t>0\). In particular, let us fix an arbitrary \( m \in \{1,\ldots , N_\tau \}\) and let \(C^*: = {\mathscr {W}}(t_{\tau }^{ m}, \rho ^*, \rho _0) \). We have for any n,
where for (1) we have used that \( {\mathscr {W}}(2T-t_{\tau }^n, \rho ^*, \rho _0) \le {\mathscr {W}}(t_{\tau }^{ m}, \rho ^*, \rho _0) \) since \(2T- t_{\tau }^n \ge t_{\tau }^{ m} \). Thus, in view of (7.25) we we deduce
i.e. the desired (7.26).
Likewise, adding (7.23) and (7.24) one has \( {\mathscr {W}}(t, \rho _0, \widetilde{\rho }_{\tau }(t)) + {\mathscr {E}}(\widetilde{\rho }_{\tau }(t)) \le {\mathscr {E}}(\rho _0) \), whence (7.27) with arguments similar to those in the previous lines. \(\square \)
7.4 Compactness result
The main result of this section, Theorem 7.7 below, states that \(\mathrm {GMM}({\mathscr {E}},{\mathscr {W}};(0, T),\rho ^\circ ) \) is non-empty, and that any curve \(\rho \in \mathrm {GMM}({\mathscr {E}},{\mathscr {W}};(0, T),\rho ^\circ )\) fulfills an ‘abstract’ version (7.31) of the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) Energy-Dissipation estimate (5.6), obtained by passing to the limit in the discrete inequality (7.20).
We recall the \({\mathscr {W}}\)-action of a curve \(\rho :[0,T]\rightarrow X\), defined in (4.89) as
for all \([a,b]\subset [0,T]\), where \({\mathfrak {P}}_f([a,b])\) is the set of all finite partitions of the interval [a, b]. We also introduce the relaxed generalized slope \({\mathscr {S}}^-: {\mathrm {D}}({\mathscr {E}}) \rightarrow [0,{+\infty }]\) of the driving energy functional \({\mathscr {E}}\), namely the relaxation of the generalized slope \({\mathscr {S}}\) along sequences with bounded energy:
We are now in a position to state and prove the ‘abstract version’ of Theorem 7.4.
Theorem 7.7
Under Assumption (Abs), let \(\rho ^\circ \in \mathrm {D}({\mathscr {E}})\). Then, for every vanishing sequence \((\tau _k)_k\) there exist a (not relabeled) subsequence and a \(\sigma \)-continuous curve \(\rho : [0,T]\rightarrow X\) such that \(\rho (0) = \rho ^\circ \), and
and \(\rho \) satisfies the Energy-Dissipation estimate
Remark 7.8
Theorem 7.7 could be extended to a topological space where the cost \({\mathscr {W}}\) and the energy functional \({\mathscr {E}}\) satisfy the properties listed at the beginning of the section.
Proof
Consider a sequence \(\tau _k \downarrow 0\) as \(k\rightarrow \infty \).
Step 1: Construct the limit curve \({\overline{\rho }}\). We first define the limit curve \({\overline{\rho }}\) on the set \(A: = \{0\} \cup N\), with N a countable dense subset of (0, T]. Indeed, in view of (7.22), with a diagonalization procedure we find a function \({{\overline{\rho }}} : A \rightarrow X\) and a (not relabeled) subsequence such that
In particular, \( {{\overline{\rho }}}(0)=\rho ^\circ \).
We next show that \({\overline{\rho }}\) can be uniquely extended to a \(\sigma \)-continuous curve \({\overline{\rho }}:[0,T]\rightarrow X\). Let \(s,t\in A\) with \(s<t\). By the lower-semicontinuity property (4.86c) we have
where (1) follows from (7.20) (using the lower bound on \({\mathscr {E}}\)), and (2) is due to the fact that \(t\mapsto {\mathscr {E}}(\overline{\rho }_{\tau _{k}}(t))\) is nonincreasing.
By the property (4.86e) of \({\mathscr {W}}\), this estimate is a form of uniform continuity of \({\overline{\rho }}\), and we now use this to extend \({\overline{\rho }}\). Fix \(t\in [0,T]\setminus A\), and choose a sequence \(t_m\in A\), \(t_m\rightarrow t\), with the property that \({\overline{\rho }}(t_m)\) \(\sigma \)-converges to some \({{\tilde{\rho }}}\). For any sequence \(s_m\in A\), \(s_m\rightarrow t\), we then have
and since \(|t_m-s_m|\rightarrow 0\), property (4.86e) implies that \({{\overline{\rho }}(s_m)}{\mathop {\rightharpoonup }\limits ^{\sigma }}{{\tilde{\rho }}}\). This implies that along any converging sequence \(t_m\in A\), \(t_m\rightarrow t\) the sequence \({\overline{\rho }}(t_m)\) has the same limit; therefore there is a unique extension of \({\overline{\rho }}\) to [0, T], that we again indicate by \({\overline{\rho }}\). By again applying the lower-semicontinuity property (4.86c) we find that
and therefore the curve \([0,T]\ni t\mapsto {\overline{\rho }}(t)\) is \(\sigma \)-continuous.
Step 2: Show convergence at all \(t\in [0,T]\). Now fix \(t\in [0,T]\); we show that \(\overline{\rho }_{\tau _k}(t)\), \(\underline{\rho }_{\tau _k}(t)\), and \(\widetilde{\rho }_{\tau _k}(t)\) each converge to \({\overline{\rho }}(t)\). Since \(\overline{\rho }_{\tau _k}(t)\in K\), there exists a convergent subsequence \(\overline{\rho }_{\tau _{k_j}}(t){\mathop {\rightharpoonup }\limits ^{\sigma }}{{\tilde{\rho }}}\). Take any \(s\in A\) with \(s\not =t\). Then
by the same argument as above. Taking the limit \(s\rightarrow t\), property (4.86e) and the continuity of \({\overline{\rho }}\) imply \({{\tilde{\rho }}}= {\overline{\rho }}(t)\). Therefore \(\overline{\rho }_{\tau _{k_j}}(t){\mathop {\rightharpoonup }\limits ^{\sigma }}{\overline{\rho }}(t)\) along each subsequence \(\tau _{k_j}\), and consequently also along the whole sequence \(\tau _k\).
Estimates (7.19) & (7.20) also give at each \(t\in (0,T]\)
so that, again using the compactness information provided by (7.22) and property (4.86e) of the cost \({\mathscr {W}}\), it is immediate to conclude (7.30).
Step 3: Derive the energy-dissipation estimate. Finally, let us observe that
Indeed, for any partition \(\{ 0=t^0<\ldots<t^j<\ldots <t^M = t\}\) of [0, t] we find that
with (1) due to (4.86c). Then (7.33) follows by taking the supremum over all partitions. On the other hand, by Fatou’s Lemma we find that
while the lower semicontinuity of \({\mathscr {E}}\) gives
so that (7.31) follows from taking the \(\liminf _{k\rightarrow \infty }\) in (7.20) for \(s=0\). \(\square \)
7.5 Proof of Theorem 7.4
Having established the abstract compactness result of Theorem 7.7, we now apply this to the proof of Theorem 7.4. As described above, under Assumptions (\(V\!\pi \kappa \)), (\({\mathscr {R}}^*\Psi \upalpha \)), and (\({\mathscr {E}}\upphi \)) the conditions of Theorem 7.7 are fulfilled, and Theorem 7.7 provides us with a curve \(\rho :[0,T]\rightarrow {{\mathcal {M}}}^+(V)\) that is continuous with respect to setwise convergence such that
To conclude the proof of Theorem 7.4, we now show that the Energy-Dissipation inequality (5.6) can be derived from (7.34).
We first note that Corollary 4.22 implies the existence of a flux \({{\varvec{j}}}\) such that \((\rho ,{{\varvec{j}}})\in \mathcal {CE}(0,T)\) and \({\mathbb {W}}(\rho ;[0,T]) = \int _0^T {\mathscr {R}}(\rho _t,{{\varvec{j}}}_t)\,\mathrm {d}t\). Then from Corollary 7.11 below, we find that \({\mathscr {S}}^-(\rho (r))\ge {\mathscr {D}}(\rho (r))\) for all \(r \in [0,T]\). Combining these results with (7.34) we find the required estimate (5.6).
It remains to prove the inequality \({\mathscr {S}}^-\ge {\mathscr {D}}\), which follows from the corresponding inequality \( {\mathscr {S}}\ge {\mathscr {D}}\) for the non-relaxed slope (Theorem 7.9) with the lower semicontinuity of \({\mathscr {D}}\) that is assumed in Theorem 7.4. This is the topic of the next section.
7.6 The generalized slope bounds the fisher information
We recall the definition of the generalized slope \({\mathscr {S}}\) from (7.11):
Given the structure of this definition, the proof of the inequality \({\mathscr {S}}\ge {\mathscr {D}}\) naturally proceeds by constructing an admissible curve \((\rho , {{\varvec{j}}})\in \mathcal {CE}(0,T)\) such that  and such that the expression in braces can be related to \({\mathscr {D}}(\rho )\).
and such that the expression in braces can be related to \({\mathscr {D}}(\rho )\).
For the systems of this paper, the construction of such a curve faces three technical difficulties: the first is that \(\rho \) needs to remain nonnegative, the second is that \(\upphi '\) may be unbounded at zero, and the third is that the function \({\mathrm {D}}_\upphi (u,v)\) in (4.53c) that defines \({\mathscr {D}}\) may be infinite when u or v is zero (see Example 5.2).
We first prove a lower bound for the generalized slope \({\mathscr {S}}\) involving \({\mathrm {D}}_\upphi ^-\), under the basic conditions on the \(({\mathscr {E}}, {\mathscr {R}}, {\mathscr {R}}^*)\) system presented in Sect. 3.
Theorem 7.9
Assume (\(V\!\pi \kappa \)), (\({\mathscr {R}}^*\Psi \upalpha \)), and (\({\mathscr {E}}\upphi \)). Then
Proof
Let us fix \(\rho _0=u_0\pi \in {\mathrm {D}}({\mathscr {E}})\), a bounded measurable skew-symmetric map
the Lipschitz functions \(q(r){:}{=}\min (r, 2(r-1/2)_+)\) (approximating the identity far from 0) and \(h(r){:}{=}\max (0,\min (2-r, 1))\) (cutoff for \(r\ge 2\)), and the Lipschitz regularization of \(\upalpha \)
We introduce the field \({\mathrm {G}}_\varepsilon :E\times {\mathbb {R}}_+^2\rightarrow {\mathbb {R}}\)
where
which vanishes if \(\upalpha (u,v)<\varepsilon /2\) or \(\min (u,v)<\varepsilon /2\) or \(\max (u, v)\ge 2/\varepsilon \), and coincides with \(\upalpha \) if \(\upalpha \ge \varepsilon \), \(\min (u,v)\ge \varepsilon \), and \(\max (u, v)\le 1/\varepsilon \). Since \(g_\varepsilon \) is Lipschitz, it is easy to check that \({\mathrm {G}}_\varepsilon \) satisfies all the assumptions (6.1a,b,c,d) and also (6.7) for \(a=0\), since \(0=g_\varepsilon (0,0)\le g_\varepsilon (0,v)\) for every \(v\ge 0\) and every \((x,y)\in E\).
It follows that for every nonnegative \(u_0\in L^1(X,\pi )\) there exists a unique nonnegative solution \(u^\varepsilon \in {\mathrm {C}}^1([0,\infty );L^1(V,\pi ))\) of the Cauchy problem (6.15) induced by \({\mathrm {G}}_\varepsilon \) with initial datum \(u_0\) and the same total mass. Henceforth, we set \(\rho _t^\varepsilon = u_t^\varepsilon \pi \) for all \(t\ge 0\).
Setting \(2 {{\varvec{j}}}_t^\varepsilon (\mathrm {d}x,\mathrm {d}y){:}{=}w_t^\varepsilon (x,y) {\varvec{{\varvec{\vartheta }}}}(\mathrm {d}x,\mathrm {d}y) \), where \(w_t^\varepsilon (x,y){:}{=}{\mathrm {G}}_\varepsilon (x,y;u_t(x),u_t(y))\), it is also easy to check that \((\rho ^\varepsilon ,{{\varvec{j}}}^\varepsilon )\in {\mathcal {A}}{(0,T)}\), since \(g_\varepsilon (u,v)\le \upalpha (u,v)\) and

where \(U_\varepsilon (t){:}{=}\{(x,y)\in E: g_\epsilon (u_t^\varepsilon (x),u_t^\varepsilon (y))>0\}\), thereby yielding
Finally, recalling (4.40) and (4.42), we get
Thus, we can apply Theorem 4.16 obtaining
and consequently
Let us now set \(\Delta _k\) to be the truncation of \(\upphi '(u_0(x))-\upphi '(u_0(y))\) to \([-k,k]\), i.e.
and \(\xi _k(x,y){:}{=} (\Psi ^*)'(\Delta _k(x,y))\) for each \(k\in {\mathbb {N}}\). Notice that \(\xi _k\) is a bounded measurable skew-symmetric map satisfying \(|\xi _k(x,y)|\le k\) for every \((x,y)\in E\) and \(k\in {\mathbb {N}}\). Therefore, inequality (7.38) holds for \(w_0^\varepsilon (x,y) = \xi _k(x,y)\,g_\varepsilon (u_0(x),u_0(y))\), \((x,y)\in E\). We then observe from Lemma 4.19(3) that
and from \(g_\epsilon (u,v)\le \upalpha (u,v)\) that
Substituting these bounds in (7.38) and passing to the limit as \(\varepsilon \downarrow 0\) we obtain
We eventually let \(k\uparrow \infty \) and obtain (7.35). \(\square \)
In the next proposition we finally bound \({\mathscr {S}}\) from below by the Fisher information, by relying on the existence of a solution to the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system, as shown in Sect. 6.
Proposition 7.10
Let us suppose that for \(\rho \in D({\mathscr {E}})\) there exists a solution to the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system. Then the generalized slope bounds the Fisher information from above:
Proof
Let \(\rho _t = u_t \pi \) be a solution to the \(({\mathscr {E}},{\mathscr {R}},{\mathscr {R}}^*)\) system with initial datum \(\rho _0\in {\mathrm {D}}({\mathscr {E}})\). Then, we can find a family \(({{\varvec{j}}}_t)_{t\ge 0}\in {{\mathcal {M}}}(E)\) such that \((\rho ,{{\varvec{j}}})\in \mathcal {CE}(0,{+\infty })\) and
Therefore
Since \(u_t\rightarrow u_0\) in \(L^1(V;\pi )\) as \(t\rightarrow 0\) and since \({\mathscr {D}}\) is lower semicontinuous with respect to \(L^1(V,\pi )\)-convergence (see the proof of Proposition 5.3), with a change of variables we find
\(\square \)
We then easily get the desired lower bound for \({\mathscr {S}}^-\) in terms of \({\mathscr {D}}\), under the condition that the latter functional is lower semicontinuous (recall that Proposition 5.3 provides sufficient conditions for the lower semicontinuity of \({\mathscr {D}}\)):
Corollary 7.11
Let us suppose that Assumptions (\(V\!\pi \kappa \)), (\({\mathscr {R}}^*\Psi \upalpha \)), (\({\mathscr {E}}\upphi \)) hold and that \({\mathscr {D}}\) is lower semicontinuous with respect to setwise convergence. Then
As discussed in Example 4.18, the cosh and the quadratic case provide examples in which the Fisher information functional \({\mathscr {D}}\) is lower semicontinuous. When \(\pi \) is purely atomic, then \({\mathscr {D}}\) is lower semicontinuous for all the examples mentioned in Sect. 1.3. In the case when \(\pi \) is not purely atomic, the lower semicontinuity of \({\mathscr {D}}\) is related to the convexity of the function \({\mathrm {D}}_\upphi \) (4.53). We show in Appendix E that all the power means in (1.34) for \(p\in [-\infty ,-1]\cup [0,1)\), together with \(\Psi ^*\) in (1.35), do lead to \({\mathrm {D}}_\upphi \)’s that are convex and lower semicontinuous, and ultimately to the lower semicontinuity of \({\mathscr {D}}\).
Remark 7.12
The combination of Theorem 7.9, Proposition 7.10, and Corollary 7.11 illustrates why we introduced both \({\mathrm {D}}_\upphi \) and \({\mathrm {D}}^-_\upphi \). For the duration of this remark, consider both the functional \({\mathscr {D}}\) that is defined in (5.1) in terms of \({\mathrm {D}}_\upphi \), and a corresponding functional \({\mathscr {D}}^-\) defined in terms of the function \({\mathrm {D}}_\upphi ^-\):
In the two guiding cases of Example 4.18, \({\mathrm {D}}_\upphi \) is convex and lower semicontinuous, but \({\mathrm {D}}_\upphi ^-\) is only lower semicontinuous. As a result, \({\mathscr {D}}\) is lower semicontinuous with respect to setwise convergence, but \({\mathscr {D}}^-\) is not (indeed, consider e.g. a sequence \(\rho _n\) converging setwise to \(\rho \), with \(\mathrm {d}\rho _n/\mathrm {d}\pi \) given by characteristic functions of some sets \(A_n\), where the sets \(A_n\) are chosen such that for the limit the density \(\mathrm {d}\rho /\mathrm {d}\pi \) is strictly positive and non-constant; then \({\mathscr {D}}^-(\rho _n)=0\) for all n while \({\mathscr {D}}^-(\rho )>0\)). Setwise lower semicontinuity of \({\mathscr {D}}\) is important for two reasons: first, this is required for stability of solutions of the Energy-Dissipation balance under convergence in some parameter (evolutionary \(\Gamma \)-convergence), which is a hallmark of a good variational formulation; and secondly, the proof of existence using the Minimizing-Movement approach requires the bound (7.43), for which \({\mathscr {D}}\) also needs to be lower semicontinuous. This explains the importance of \({\mathrm {D}}_\upphi \), and it also explains why we defined the Fisher information \({\mathscr {D}}\) in terms of \({\mathrm {D}}_\upphi \) and not in terms of \({\mathrm {D}}_\upphi ^-\).
On the other hand, \({\mathrm {D}}_\upphi ^-\) is straightforward to determine, and in addition the weaker control of \({\mathrm {D}}_\upphi ^-\) is still sufficient for the chain rule: it is \({\mathrm {D}}_\upphi ^-\) that appears on the right-hand side of (4.59). Note that if \({\mathrm {D}}_\upphi ^-\) itself is convex, then it coincides with \({\mathrm {D}}_\upphi \).
References
Adams, S., Dirr, N., Peletier, M.A., Zimmer, J.: From a large-deviations principle to the Wasserstein gradient flow: a new micro-macro passage. Commun. Math. Phys. 307, 791–815 (2011)
Adams, S., Dirr, N., Peletier, M.A., Zimmer, J.: Large deviations and gradient flows. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 371(2005), 20120341 (2013)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford University Press, Oxford (2005)
Ambrosio, L., Gigli, N., Savaré, G.: Gradient Flows in Metric Spaces and in the Space of Probability Measures. Lectures in Mathematics ETH Zürich. Birkhäuser, Basel (2008)
Ambrosio, L.: Minimizing movements. Rend. Accad. Naz. Sci. XL Mem. Mat. Appl. 19(5), 1773–1799 (1995)
Arnrich, S., Mielke, A., Peletier, M.A., Savaré, G., Veneroni, M.: Passing to the limit in a Wasserstein gradient flow: from diffusion to reaction. Calc. Var. Partial. Differ. Equ. 44, 419–454 (2012)
Almgren, F., Taylor, J.E., Wang, L.: Curvature-driven flows: a variational approach. SIAM J. Control. Optim. 31, 387–437 (1993)
Benamou, J.-D., Brenier, Y.: A computational fluid mechanics solution to the Monge–Kantorovich mass transfer problem. Numer. Math. 84(3), 375–393 (2000)
Bogachev, V.I.: Measure Theory, vol. I, II. Springer, Berlin (2007)
Bonaschi, G.A., Peletier, M.A.: Quadratic and rate-independent limits for a large-deviations functional. Contin. Mech. Thermodyn. 28, 1191–1219 (2016)
Brezis, H.: Functional Analysis. Sobolev Spaces and Partial Differential Equations. Springer, New York (2011)
Bullen, P.S.: Handbook of Means and their Inequalities. Mathematics and its Applications. Springer, Netherlands (2003)
Chow, S.-N., Huang, W., Li, Y., Zhou, H.: Fokker–Planck equations for a free energy functional or Markov process on a graph. Arch. Ration. Mech. Anal. 203(3), 969–1008 (2012)
Crandall, M.G., Tartar, L.: Some relations between nonexpansive and order preserving mappings. Proc. Am. Math. Soc. 78(3), 385–390 (1980)
Castaing, C., Valadier, M.: Convex Analysis and Measurable Multifunctions. Lectures Notes in Mathematics, vol. 580. Springer, Berlin, New York (1977)
Dondl, P., Frenzel, T., Mielke, A.: A gradient system with a wiggly energy and relaxed EDP-convergence. ESAIM Control Optim. Calc. Var. 25, 68 (2019)
De Giorgi, E., Marino, A., Tosques, M.: Problems of evolution in metric spaces and maximal decreasing curve. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. (8) 68(3), 180–187 (1980)
Dellacherie, C., Meyer, P.-A.: Probabilities and potential, volume 29 of North-Holland Mathematics Studies. North-Holland Publishing Co., Amsterdam-New York; North-Holland Publishing Co., Amsterdam-New York (1978)
Dal Maso, G., DeSimone, A., Mora, M.G.: Quasistatic evolution problems for linearly elastic-perfectly plastic materials. Arch. Ration. Mech. Anal. 180(2), 237–291 (2006)
Dolbeault, J., Nazaret, B., Savaré, G.: A new class of transport distances between measures. Calc. Var. Part. Differ. Equ. 34(2), 193–231 (2009)
Dolbeault, J., Nazaret, B., Savaré, G.: A new class of transport distances between measures. Calc. Var. Part. Differ. Equ. 34(2), 193–231 (2009)
Duong, M.H., Peletier, M.A., Zimmer, J.: GENERIC formalism of a Vlasov–Fokker–Planck equation and connection to large-deviation principles. Nonlinearity 26, 2951–2971 (2013)
Dirr, N., Stamatakis, M., Zimmer, J.: Entropic and gradient flow formulations for nonlinear diffusion. J. Math. Phys. 57(8), 081505 (2016)
Dembo, A., Zeitouni, O.: Large Deviations Techniques and Applications. Springer, New York (1998)
Erbar, M., Fathi, M., Laschos, V., Schlichting, A.: Gradient flow structure for McKean–Vlasov equations on discrete spaces. Disc. Contin. Dyn. Syst. 36(12), 6799–6833 (2016)
Erbar, M., Fathi, M., Schlichting, A.: Entropic curvature and convergence to equilibrium for mean-field dynamics on discrete spaces. arXiv preprint arXiv:1908.03397 (2019)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions. Studies in Advanced Mathematics. CRC Press, Boca Raton, FL (1992)
El Hajj, A., Ibrahim, H., Monneau, R.: Dislocation dynamics: from microscopic models to macroscopic crystal plasticity. Continuum Mech. Thermodyn. 21(2), 109–123 (2009)
Erbar, M., Maas, J.: Gradient flow structures for discrete porous medium equations. Disc. Contin. Dyn. Syst. 34(4), 1355–1374 (2014)
Erbar, M.: Gradient flows of the entropy for jump processes. Ann. Inst. Henri Poincaré Probab. Stat. 50(3), 920–945 (2014)
Erbar, M.: A gradient flow approach to the Boltzmann equation. Arxiv preprint arXiv:01603.00540 (2016)
Feinberg, M.: On chemical kinetics of a certain class. Arch. Ration. Mech. Anal. 46(1), 1–41 (1972)
Figalli, A., Gangbo, W., Yolcu, T.: A variational method for a class of parabolic PDEs. Annali della Scuola Normale Superiore di Pisa-Classe di Scienze 10(1), 207–252 (2011)
Gigli, N.: On the heat flow on metric measure spaces: existence, uniqueness and stability. Calc. Var. Partial. Differ. Equ. 39(1–2), 101–120 (2010)
Glitzky, A., Mielke, A.: A gradient structure for systems coupling reaction-diffusion effects in bulk and interfaces. Z. Angew. Math. Phys. 64(1), 29–52 (2013)
Gavish, N., Nyquist, P., Peletier, M.: Large deviations and gradient flows for the Brownian one-dimensional hard-rod system. arXiv preprint arXiv:1909.02054 (2019). https://doi.org/10.1007/s11118-021-09933-0
Grmela, M.: Particle and bracket formulations of kinetic equations. In: Marsden, J.E. (ed) Proceedings of the AMS–IMS–SIAM Joint Summer Research Conference in the Mathematical Sciences on Fluids and Plasmas: Geometry and Dynamics, pp 125–132 (1984)
Grmela, M.: Multiscale equilibrium and nonequilibrium thermodynamics in chemical engineering. Adv. Chem. Eng. 39, 75–129 (2010)
Girault, V., Wheeler, M.F.: Numerical discretization of a Darcy–Forchheimer model. Numer. Math. 110(2), 161–198 (2008)
Hudson, T., van Meurs, P., Peletier, M.A.: Atomistic origins of continuum dislocation dynamics. Math. Models Methods Appl. Sci. 30(13), 2557–2618 (2020)
Hairer, E., Wanner, G.: Solving ordinary differential equations. II, volume 14 of Springer Series in Computational Mathematics, 2nd edn. Springer, Berlin (1996). Stiff and differential-algebraic problems
Jordan, R., Kinderlehrer, D., Otto, F.: The variational formulation of the Fokker–Planck equation. SIAM J. Math. Anal. 29(1), 1–17 (1998)
Kaiser, M., Jack, R.L., Zimmer, J.: Canonical structure and orthogonality of forces and currents in irreversible Markov chains. J. Stat. Phys. 170(6), 1019–1050 (2018)
Knupp, P.M., Lage, J.L.: Generalization of the Forchheimer-extended Darcy flow model to the tensor permeability case via a variational principle. J. Fluid Mech. 299, 97–104 (1995)
Kipnis, C., Olla, S., Varadhan, S.R.S.: Hydrodynamics and large deviation for simple exclusion processes. Commun. Pure Appl. Math. 42(2), 115–137 (1989)
Liero, M., Mielke, A., Peletier, M.A., Renger, D.R.M.: On microscopic origins of generalized gradient structures. Disc. Cont. Dyn. Syst. Ser. S 10(1), 1 (2017)
Liero, M., Mielke, A., Savaré, G.: Optimal entropy-transport problems and a new Hellinger–Kantorovich distance between positive measures. Invent. Math. 211(3), 969–1117 (2018)
Luckhaus, S., Sturzenhecker, T.: Implicit time discretization for the mean curvature flow equation. Calc. Var. Partial. Differ. Equ. 3(2), 253–271 (1995)
Maas, J.: Gradient flows of the entropy for finite Markov chains. J. Funct. Anal. 261(8), 2250–2292 (2011)
Martin, R.H.: Jr.: Nonlinear operators and differential equations in Banach spaces. Pure and Applied Mathematics. Wiley, New York (1976)
Mielke, A.: Evolution in rate-independent systems. In: Handbook of Differential Equations: Evolutionary Differential Equations, pp 461–559. North-Holland (2005)
Mielke, A.: Geodesic convexity of the relative entropy in reversible Markov chains. Calc. Var. Part. Differ. Equ. 48(1–2), 1–31 (2013)
Mielke, A.: Deriving effective models for multiscale systems via evolutionary \(\Gamma \)-convergence. In: Control of Self-Organizing Nonlinear Systems, pp. 235–251. Springer, New York (2016)
Mielke, A.: On evolutionary \(\varGamma \)-convergence for gradient systems. In: Macroscopic and large scale phenomena: coarse graining, mean field limits and ergodicity, vol 3 of Lecture Notes Applied Mathematics Mechanical, pp 187–249. Springer, New York (2016)
Mielke, A., Montefusco, A., Peletier, M.A.: Exploring families of energy-dissipation landscapes via tilting—three types of EDP convergence. arXiv preprint arXiv:2001.01455 (2020). https://doi.org/10.1007/s00161-020-00932-x
Maes, C., Netočný, K.: Canonical structure of dynamical fluctuations in mesoscopic nonequilibrium steady states. Europhys. Lett. 82(3), 30003 (2008)
Mörters, P.: Introduction to large deviations. Technical report, University of Bath (2010)
Mielke, A., Patterson, R.I.A., Peletier, M.A., Renger, D.R.M.: Non-equilibrium thermodynamical principles for chemical reactions with mass-action kinetics. SIAM J. Appl. Math. 77(4), 1562–1585 (2017)
Mielke, A., Peletier, M.A., Renger, D.R.M.: On the relation between gradient flows and the large-deviation principle, with applications to Markov chains and diffusion. Potential Anal. 41(4), 1293–1327 (2014)
Mielke, A., Peletier, M.A., Renger, D.R.M.: A generalization of Onsagers reciprocity relations to gradient flows with nonlinear mobility. J. Non-Equil. Thermodyn. 41(2), 141–149 (2016)
Mielke, A., Roubíček, T.: Rate-independent systems. Theory and application, volume 193 of Applied Mathematical Sciences. Springer, New York (2015)
Mielke, A., Rossi, R., Savaré, G.: BV solutions and viscosity approximations of rate-independent systems. ESAIM Control Optim. Calc. Variat. 18(01), 36–80 (2012)
Mielke, A., Rossi, R., Savaré, G.: Nonsmooth analysis of doubly nonlinear evolution equations. Calc. Var. Part. Differ. Equ. 46(1–2), 253–310 (2013)
Mielke, A., Rossi, R., Savaré, G.: Balanced viscosity (BV) solutions to infinite-dimensional rate-independent systems. J. Eur. Math. Soc. (JEMS) 18(9), 2107–2165 (2016)
Mirrahimi, S., Souganidis, P.E.: A homogenization approach for the motion of motor proteins. Nonlinear Differ. Equ. Appl. 20(1), 129–147 (2013)
Mielke, A., Stephan, A.: Coarse-graining via EDP-convergence for linear fast-slow reaction systems. Math. Models Methods Appl. Sci. 30(9), 1765–1807 (2020)
Mielke, A., Theil, F., Levitas, V.I.: A variational formulation of rate-independent phase transformations using an extremum principle. Arch. Ration. Mech. Anal. 162(2), 137–177 (2002)
Otto, F.: The geometry of dissipative evolution equations: the porous medium equation. Commun. Part. Differ. Equ. 26, 101–174 (2001)
Öttinger, H.C.: On the combined use of friction matrices and dissipation potentials in thermodynamic modeling. J. Non-Equilib. Thermodyn. 44(3), 295–302 (2019)
Peletier, M.A.: Variational modelling: energies, gradient flows, and large deviations. Arxiv preprint arXiv:1402:1990 (2014)
Peletier, M.A., Redig, F., Vafayi, K.: Large deviations in stochastic heat-conduction processes provide a gradient-flow structure for heat conduction. J. Math. Phys. 55(9), 093301 (2014)
Perthame, B., Souganidis, P.E.: Asymmetric potentials and motor effect: a large deviation approach. Arch. Ration. Mech. Anal. 193(1), 153–169 (2009)
Perthame, B., Souganidis, P.E.: Asymmetric potentials and motor effect: a homogenization approach. Ann. de l’Institut Henri Poincare (C) Non-Linear Anal. 26(6), 2055–2071 (2009)
Peletier, M.A., Schlottke, M.C.: Large-deviation principles of switching Markov processes via Hamilton–Jacobi equations. arXiv preprint arXiv:1901.08478 (2019)
Renger, D.R.M.: Flux large deviations of independent and reacting particle systems, with implications for macroscopic fluctuation theory. J. Stat. Phys. 172(5), 1291–1326 (2018)
Rossi, R., Savaré, G., Segatti, A., Stefanelli, U.: Weighted energy-dissipation principle for gradient flows in metric spaces. J. Math. Pures Appl. 9(127), 1–66 (2019)
Tyrrell Rockafellar, R., Roger, J.-B.: Wets: Variational Analysis. Springer, Berlin (1998)
Renger, M., Zimmer, J.: Orthogonality of fluxes in general nonlinear reaction networks. Disc. Contin. Dyn. Syst. Ser. S (2019)
Serfaty, S.: Gamma-convergence of gradient flows on Hilbert and metric spaces and applications. Disc. Contin. Dyn. Syst. 31(4), 1427–1451 (2011)
Sandier, E., Serfaty, S.: Gamma-convergence of gradient flows with applications to Ginzburg–Landau. Commun. Pure Appl. Math. 57(12), 1627–1672 (2004)
Acknowledgements
M.A.P. acknowledges support from NWO Grant 613.001.552, “Large Deviations and Gradient Flows: Beyond Equilibrium". R.R. and G.S. acknowledge support from the MIUR - PRIN project 2017TEXA3H “Gradient flows, Optimal Transport and Metric Measure Structures". G.S. also acknowledges the support of the Institute of Advanced Study of the Technical University of Munich, of IMATI-CNR, Pavia, and of the Department of Mathematics of the University of Pavia, where this project was partially carried out. O.T. acknowledges support from NWO Vidi grant 016.Vidi.189.102, “Dynamical-Variational Transport Costs and Application to Variational Evolutions". Finally, the authors thank Jasper Hoeksema for insightful and valuable comments during the preparation of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Andrea Malchiodi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Derivation of the cosh-structure from large deviations
We mentioned in the introduction that the choices
arise in the context of large deviations. In this section we describe this context. Throughout this section we work under Assumptions (\(V\!\pi \kappa \)), (\({\mathscr {E}}\upphi \)), and (\({\mathscr {R}}^*\Psi \upalpha \)), and since we are interested in the choices above, we will also assume (A.1), implying that
Consider a sequence of independent and identically distributed stochastic processes \(X^i\), \(i=1, 2, \dots \) on V, each described by the jump kernel \(\kappa \), or equivalently by the generator Q in (1.3). With probability one, a realization of each process has a countable number of jumps in the time interval \([0,{+\infty })\), and we write \(t^i_k\) for the \(k^{\mathrm {th}}\) jump time of \(X^i\). We can assume that \(X^i\) is a càdlàg function of time.
We next define the empirical measure \(\rho ^n\) and the empirical flux \({{\varvec{j}}}^n\) by
where \(t^i_k\) is the \(k^{\mathrm {th}}\) jump time of \(X^i\), and \(X^i_{t-}\) is the left limit (pre-jump state) of \(X^i\) at time t. Equivalently, \({{\varvec{j}}}^n\) is defined by
A standard application of Sanov’s theorem yields a large-deviation characterization of the pair \((\rho ^n,{{\varvec{j}}}^n)\) in terms of two rate functions \(I_0\) and I,
The rate function \(I_0\) describes the large deviations of the initial datum \(\rho ^n_0\); this functional is determined by the choices of the initial data of \(X^i_0\) and is independent of the stochastic process itself, and we therefore disregard it here.
The functional I characterizes the large-deviation properties of the dynamics of the pair \((\rho ^n,{{\varvec{j}}}^n)\) conditional on the initial state, and has the expression
In this expression we write \({\varvec{\vartheta }}_{\rho _t}^-\) for the measure \(\rho _t(\mathrm {d}x)\kappa (x,\mathrm {d}y)\in {{\mathcal {M}}}(E)\) (see also (4.18) ahead). The function \(\upeta \) is the Boltzmann entropy function that we have seen above,
and the functional \({\mathscr {F}}_\upeta :{{\mathcal {M}}}^+(E)\times {{\mathcal {M}}}^+(E) \rightarrow [0,\infty ]\) is given by (2.11). Even though the function \(\upeta \) coincides in this section with \(\upphi \), we choose a different notation to emphasize that the roles of \(\upphi \) and \(\upeta \) are different: the function \(\upphi \) defines the entropy of the system, which is related to the large deviations of the empirical measures \(\rho ^n\) in equilibrium (see [59]); the function \(\upeta \) characterizes the large deviations of the time courses of \(\rho ^n\) and \({{\varvec{j}}}^n\).
Remark A.1
Sanov’s theorem can be found in many references on large deviations (e.g. [24, Sec. 6.2]); the derivation of the expression (A.2) is fairly well known and can be found in e.g. [56, Eq. (8)] or [43, App. A]. Instead of proving (A.2) we give an interpretation of the expression (A.2) and the function \(\upeta \) in terms of exponential clocks. An exponential clock with rate parameter r has large-deviation behaviour given by \(r\eta (\cdot /r)\) (see [24, Exercise 5.2.12] or [57, Th. 1.5]) in the following sense: for each \(t>0\),
The expression (A.2) generalizes this to a field of exponential clocks, one for each edge (x, y). In this case, the rescaled rate parameter r for the clock at edge (x, y) is equal to \(\rho _t(\mathrm {d}x)\kappa (x,\mathrm {d}y)\), since it is proportional to the number of particles \(n\rho _t(\mathrm {d}x)\) at x and to the rate of jump \(\kappa (x,\mathrm {d}y)\) from x to y. The flux \(n{{\varvec{j}}}_t(\mathrm {d}x\,\mathrm {d}y)\) is the observed number of jumps from x to y, corresponding to firings of the clock associated with the edge (x, y). In this way, the functional I in (A.2) can be interpreted as characterizing the large-deviation fluctuations in the clock-firings for each edge \((x,y)\in E\).
The expression (A.2) leads to the functional \({\mathscr {L}}\) in (1.18) after a symmetry reduction, which we now describe (see also [43, App. A]). Assuming that we are more interested in the fluctuation properties of \(\rho \) than those of \({{\varvec{j}}}\), we might decide to minimize \(I(\rho ,{{\varvec{j}}})\) over a class of fluxes \({{\varvec{j}}}\) for a fixed choice of \(\rho \). Here we choose to minimize over the class of fluxes with the same skew-symmetric part,
By the form (1.23) of the continuity equation and the definition (1.6b) of the divergence we have \({\overline{\mathrm {div}}}{{\varvec{j}}}'= {\overline{\mathrm {div}}}{{\varvec{j}}}\) for all \({{\varvec{j}}}'\in A_j\), so that replacing \({{\varvec{j}}}\) by \({{\varvec{j}}}'\) preserves the continuity equation.
Formal Lemma A.2
The minimum of \(I(\rho ,{{\varvec{j}}}'\,)\) over all \({{\varvec{j}}}'\in A_j\) is achieved for the ‘skew-symmetrization’ \({{\varvec{j}}}^\flat = \tfrac{1}{2}({{\varvec{j}}}-{\mathsf {s}}_\#{{\varvec{j}}})\), and for \({{\varvec{j}}}^\flat \) the result equals \(\tfrac{1}{2}{\mathscr {L}}\):
Consequently, for a given curve \(\rho :[0,T]\rightarrow {{\mathcal {M}}}^+(V)\),
and in this final expression the flux can be assumed to be skew-symmetric:
This implies that the two functionals I and \({\mathscr {L}}\) can be considered to be the same, if one is only interested in \(\rho \), not in \({{\varvec{j}}}\). By the Contraction Principle (e.g. [24, Sec. 4.2.1]) the functional \(\rho \mapsto \mathrm{inf}_j I(\rho ,{{\varvec{j}}}) = \mathrm{inf}_j \tfrac{1}{2}{\mathscr {L}}(\rho ,{{\varvec{j}}})\) also can be viewed as the large-deviation rate function of the sequence of empirical measures \(\rho ^n\).
The above lemma is only formal because we have not given a rigorous definition of the functional \({\mathscr {L}}\). While it would be possible to do so, using the construction of Lemma 2.3 and the arguments of the proof below, actually the rest of this paper deals with this question in a more detailed manner. In addition, in the context of this paper, this lemma only serves to explain why we consider this specific class of functionals \({\mathscr {L}}\). Therefore here we only give heuristic arguments.
Proof
We assume throughout this (formal) proof that all measures are absolutely continuous, strictly positive, and finite where necessary. Note that writing \(\rho _t = u_t \pi \) we have \({\varvec{\vartheta }}_{\rho _t}^-(\mathrm {d}x\,\mathrm {d}y) = u_t(x) {\varvec{\vartheta }}(\mathrm {d}x\,\mathrm {d}y)\), and using (A.1) we therefore have
For the length of this proof we write \({{\hat{\upeta }}}\) for the perspective function corresponding to \(\upeta \) (see (2.14) in Lemma 2.3)
We now rewrite \(\mathrm{inf}_{{{\varvec{j}}}'\,\in A_j} I(\rho ,{{\varvec{j}}}'\,)\) as
Since \(\zeta (x,y) - \zeta (y,x) = \mathrm {d}({{\varvec{j}}}'- {\mathsf {s}}_\#{{\varvec{j}}}'\,)/\mathrm {d}{\varvec{{\varvec{\vartheta }}}}\) is constrained in \(A_j\), we follow the expression inside the second integral and set
for which a calculation gives the explicit formula (for \(c,d>0\))
in terms of the function \(\Psi ^*(\xi ) = 4\bigl (\cosh \xi /2 - 1\bigr )\) and its Legendre dual \(\Psi \). This minimization corresponds to minimizing over all fluxes for which the ‘net flux’ \({{\varvec{j}}}- {\mathsf {s}}_\#{{\varvec{j}}}= 2 {{\varvec{j}}}^{\flat }\) is the same; see e.g. [43, 75] for discussions.
Let \(w^{\flat }(x,y) {:}{=} (w(x,y) - w(y,x)) = \frac{\mathrm {d}(2{{\varvec{j}}}^{\flat })}{\mathrm {d}{\varvec{{\varvec{\vartheta }}}}}\) and \(\upalpha _t {:}{=} \upalpha _t(x,y) = \sqrt{u_t(x)u_t(y)}\). We find
In the last identity we used the fact that since \({\overline{\mathrm {div}}}{{\varvec{j}}}^{\flat }_t = -\partial _t \rho _t\), formally we have
The expression on the right-hand side of (A.4) is one half times the functional \({\mathscr {L}}\) defined in (1.18) (see also (1.21)). This proves that
From convexity of \(\Psi \) and symmetry of \({\varvec{\upnu }}_\rho \) we deduce that \({\mathscr {L}}(\rho , {{\varvec{j}}}^{\flat }) \le {\mathscr {L}}(\rho ,{{\varvec{j}}})\) for any \({{\varvec{j}}}\); see Remark 4.12. The identity \(\mathscr {L}\bigl (\rho ,{{\varvec{j}}}^{\flat }\,\bigr ) = \mathrm{inf}_{{{\varvec{j}}}'\,\in A_j} {\mathscr {L}} (\rho ,{{\varvec{j}}}'\,)\) then follows immediately; this proves (A.3).
To prove the second part of the Lemma, we write
This concludes the proof. \(\square \)
Appendix B: Continuity equation
In this Section we complete the analysis of the continuity equation by carrying out the proofs of Lemma 4.4 and Corollary 4.3.
Proof of Lemma 4.4
The distributional identity (4.6) yields that for every \(\zeta \in \mathrm {C}_{\mathrm {b}}(V,\tau )\) the map
with distributional derivative
Hence, setting \({\mathfrak {d}}_t{:}{=}|{\overline{\mathrm {div}}}{{\varvec{j}}}_t|\in {{\mathcal {M}}}^+(V)\), we have
where we used the fact that
which implies
Hence, the set \(L_\zeta \) of the Lebesgue points of \(t\mapsto \rho _t(\zeta )\) has full Lebesgue measure. Choosing \(\zeta \equiv 1\) one immediately recognizes that \(\rho _t(V)\) is (essentially) constant: it is not restrictive to normalize it to 1 for convenience. Let us now consider a countable set \(Z=\{\zeta _k\}_{k\in {\mathbb {N}}}\) of uniformly bounded functions in \(\mathrm {C}_{\mathrm {b}}(V)\) such that
is a distance inducing the weak topology in \( {{\mathcal {M}}}^+(V) \) (see e.g. [4, § 5.1.1]). By introducing the set \(L_Z {:}{=} \bigcap _{\zeta \in Z} L_\zeta \), it follows from (B.2) that
showing that the restriction of \(\rho \) to \(L_Z\) is continuous in \({{\mathcal {M}}}^+(V)\). Estimate (B.2) also shows that for all \(s,t\in L_Z\) with \(s \le t\) we have
Taking the supremum with respect to \(\zeta \) we obtain
which shows that the measures \((\rho _t)_{t\in L_Z}\) are uniformly continuous with respect to the total variation metric in \({{\mathcal {M}}}^+(V)\) and thus can be extended to an absolutely continuous curve \({{\tilde{\rho }}}\in \mathrm {AC}(I;{{\mathcal {M}}}^+(V))\) satisfying (B.5) for every \(s,t\in I\).
When \(\varphi \in \mathrm {C}_{\mathrm {b}}(V)\), (4.4) immediately follows from (B.1). By a standard argument based on the functional monotone class Theorem [9, §2.12] we can extend the validity of (4.4) to every bounded Borel function.
If \(\varphi \in {\mathrm {C}}^1([a,b];\mathrm {B}_{\mathrm {b}}(V))\), combining (B.1) and the fact that the map \(t\mapsto \int _V \varphi (t,x)\,{{\tilde{\rho }}}_t(\mathrm {d}x)\) is absolutely continuous we easily get (4.8). \(\square \)
Proof of Corollary 4.3
Keeping the same notation of the previous proof, if we define
then the estimate (B.2) shows that
thus showing that \(\rho _t={{\tilde{u}}}_t\gamma \) for every \(t\in [0,T]\) and
\(\square \)
We conclude with a result on the decomposition of the measure \( {{\varvec{j}}}-{\mathsf {s}}_\#{{\varvec{j}}}= 2{{\varvec{j}}}^{\flat }\) into its positive and negative part.
Lemma B.1
If \({{\varvec{j}}}\in {{\mathcal {M}}}(E)\) and we set
then we have
When \({{\varvec{j}}}\) is skew-symmetric, we also have
Proof
By definition, we have \({{\varvec{j}}}^+=2{{\varvec{j}}}^{\flat }_+\), \({{\varvec{j}}}^-=2{{\varvec{j}}}^{\flat }_-\). Furthermore, \( {{\varvec{j}}}^{\flat }=-{\mathsf {s}}_\#{{\varvec{j}}}^{\flat }={\mathsf {s}}_\#{{\varvec{j}}}^{\flat }_{-}{-}{\mathsf {s}}_\#{{\varvec{j}}}^{\flat }_+\), where the first equality follows from the fact that \({{\varvec{j}}}^{\flat }\) is skew-symmetric. Since \({\mathsf {s}}_\#{{\varvec{j}}}^{\flat }_-\perp {\mathsf {s}}_\#{{\varvec{j}}}^{\flat }_+\) we deduce that \({\mathsf {s}}_\#{{\varvec{j}}}^{\flat }_+={{\varvec{j}}}^{\flat }_-,\) \({\mathsf {s}}_\#{{\varvec{j}}}^{\flat }_-={{\varvec{j}}}^{\flat }_+\) and \({{\varvec{j}}}^{\flat }={{\varvec{j}}}^{\flat }_+-{\mathsf {s}}_\#{{\varvec{j}}}^{\flat }_+\), so that \({\overline{\mathrm {div}}}{{\varvec{j}}}= {\overline{\mathrm {div}}}{{\varvec{j}}}^{\flat }=2{\overline{\mathrm {div}}}{{\varvec{j}}}^{\flat }_+={\overline{\mathrm {div}}}{{\varvec{j}}}^+\). \(\square \)
Appendix C: Slowly increasing superlinear entropies
The main result of this Section is Lemma C.3 ahead, invoked in the proof of Proposition 4.21. It provides the construction of a smooth function estimating the entropy density \(\upphi \) from below and such that the function \((r,s) \mapsto \Psi ^*(A_\upomega (r,s)) \alpha (r,s)\) fulfills a suitable bound, cf. (C.10) ahead. Prior to that, we prove the preliminary Lemmas C.1 and C.2 below.
Lemma C.1
Let us suppose that \(\upalpha \) satisfies Assumptions (\({\mathscr {R}}^*\Psi \upalpha \)). Then for every \(a\ge 0\)
Proof
Since \(\upalpha \) is symmetric it is sufficient to prove the first limit. Let us first observe that the concavity of \(\upalpha \) yields the existence of the limit since the map \(r\mapsto r^{-1}(\upalpha (r,a)-\upalpha (0,a))\) is decreasing, so that
Let us call \(L(a)\in {\mathbb {R}}_+\) the above quantity. The inequality (following by the concavity of \(\upalpha \) and the fact that \(\upalpha (0,0)\ge 0\))
yields
For every \(b\in (0,a)\) and \(r>0\), setting \(\lambda {:}{=}a/b>1\), we thus obtain
Passing first to the limit as \(b\downarrow 0\) and using the continuity of \(\upalpha \) we get
Eventually, we pass to the limit as \(r\uparrow {+\infty }\) and we get \(L(a)\le \upalpha ^\infty (1,0)=0\) thanks to (3.13). \(\square \)
Lemma C.2
Let \(f:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) be an increasing continuous function and \(f_0\ge 0\) with
Then for every \(g_0\in [0,f_0]\) there exists a \({\mathrm {C}}^\infty \) concave function \(g:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) such that
Proof
By subtracting \(f_0\) and \(g_0\) from f and g, respectively, it is not restrictive to assume \(f_0=g_0=0\). We will use a recursive procedure to construct a concave piecewise-linear function g satisfying (C.5); a standard regularization yields a \({\mathrm {C}}^\infty \) map.
We set
and \(\delta {:}{=}ax_1.\) We consider a strictly increasing sequence \((x_n)_{n\in {\mathbb {N}}}\), \(n\in {\mathbb {N}}\), defined by induction starting from \(x_0=0\) and \(x_1\) as in (C.6), according to
Since \(\lim _{r\rightarrow {+\infty }}f(r)={+\infty }\), the minimizing set in (C.7) is closed and not empty, so that the algorithm is well defined. It yields a sequence \(x_n\) satisfying
so that \((x_n)_{n\in {\mathbb {N}}}\) is strictly increasing and unbounded, and induces a partition \(\{0=x_0<x_1<x_1<\cdots<x_n<\cdots \}\) of \({\mathbb {R}}_+\). We can thus consider the piecewise linear function \(g:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) such that
We observe that g is increasing, \(\lim _{r\rightarrow {+\infty }}g(r)={+\infty }\) and it is concave since
Furthermore, g is also dominated by f: in the interval \([x_0,x_1]\) this follows by (C.6). For \(x\in [x_n,x_n+1]\) and \(n\ge 1\), we observe that (C.7) yields \(f(x_{n+1})\ge f(x_n)+\delta \) so that by induction \(f(x_n)\ge (n+1)\delta \); on the other hand
\(\square \)
Lemma C.3
Let \(\Psi ^*,\upalpha \) be satisfying Assumptions (\({\mathscr {R}}^*\Psi \upalpha \)) and let \(\upbeta :{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) be a convex superlinear function with \(\upbeta '(r)\ge \upbeta _0'>0\) for a.e. \(r\in {\mathbb {R}}_+\). Then, there exists a \({\mathrm {C}}^\infty \) convex superlinear function \(\upomega :{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) such that
Proof
By a standard regularization, we can always approximate \(\upbeta \) by a smooth convex superlinear function \({{\tilde{\upbeta }}}\le \upbeta \) whose derivative is strictly positive, so that it is not restrictive to assume that \(\upbeta \) is of class \({\mathrm {C}}^2\). Let us set \(r_0{:}{=}\mathrm{inf}\{r>0:\Psi ^*(r)>0\}\) and let \(P:(0,{+\infty })\rightarrow (r_0,{+\infty })\) be the inverse map of \(\Psi ^*\): P is continuous, strictly increasing, and of class \({\mathrm {C}}^1\).
Since \(\upalpha \) is concave, the function \(x \mapsto \upalpha (x,1)/x\) is nonincreasing in \((0,{+\infty })\); we can thus define the nondecreasing function \(Q(x){:}{=}P(x/\upalpha (x,1))\) and the function
By construction \(\gamma (1)=2g_0= \min (\upbeta '_0,Q(1))\le \upbeta '(1)\) so that \(\gamma (x)\le \min (\upbeta '(x),Q(x))\) for every \(x\ge 1\). We eventually set
Clearly, we have \(f(0)=2g_0\). Furthermore, we combine the estimate \(\gamma ({\mathrm {e}}^t) \le Q({\mathrm {e}}^t) = P({\mathrm {e}}^t/\upalpha ({\mathrm {e}}^t,1))\) with the facts that \({\mathrm {e}}^t/\upalpha ({\mathrm {e}}^t,1) \rightarrow +\infty \) as \(t\rightarrow +\infty \), thanks to Lemma C.1, and that P has sublinear growth at infinity, being the inverse function of \(\Psi ^*\). All in all, we conclude that
Therefore, we are in a position to apply Lemma C.2, obtaining an increasing concave function \(g:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) such that \(g_0=g(0)\le g(t)\le f(t)\) and \(\lim _{t\rightarrow {+\infty }}g(t)={+\infty }\). Since \(g(0)\ge 0\), the concaveness of g yields \(g(t'')-g(t')\le g(t''-t')\) for every \(0\le t'\le t''\), so that the function \(h(x){:}{=}g(\log (x\vee 1))\) satisfies \(h(x)=g_0\le \upbeta '(x)\) for \(x\in [0,1]\), and
In fact, if \(x\le 1\) we get
and if \(x\ge 1\) we get
Let us now define the convex function \(\upomega (x){:}{=}\int _0^x h(y)\,\mathrm {d}y\) with \(\upomega (0)=0\) and \(\upomega '=h\). In particular \(\upomega (x)\le \upbeta (x)\) for every \(x\ge 0\).
It remains to check the second inequality of (C.10). The case \(r,s\le 1\) is trivial since \(\upomega '(s)-\upomega '(r)=h(r)-h(s)=0\). We can also consider the case \(\upomega '(r)\ne \upomega '(s)\) and \(\upalpha (r,s)>0\); since (C.10) is also symmetric, it is not restrictive to assume \(r\le s\); by continuity, we can assume \(r>0\).
Recalling that \(\upalpha (s,r)\le r\upalpha (s/r,1)\) if \(0<r\le s\), and \((r+s)/r>s/r\), (C.10) is surely satisfied if
Recalling that \(\upomega '(s)-\upomega '(r)\le \upomega '(s/r)\) by (C.11) and \(\Psi ^*\) is nondecreasing, (C.12) is satisfied if
After the substitution \(t{:}{=}r/s\), (C.13) corresponds to
which is a consequence of the first inequality of (C.11). \(\square \)
Appendix D: Connectivity by curves of finite action
Preliminarily, with the reference measure \(\pi \in {{\mathcal {M}}}_+(V)\) and with the ‘jump equilibrium rate’ \({\varvec{{\varvec{\vartheta }}}}\) from (3.5) we associate the ‘graph divergence’ operator \({\overline{\mathrm {div}}}_{\pi ,{\varvec{{\varvec{\vartheta }}}}}: L^p(E;{\varvec{{\varvec{\vartheta }}}}) \rightarrow L^p(V;\pi ) \), \(p\in [1,{+\infty }]\), defined as the transposed of the ‘graph gradient’ \({{\overline{\nabla }}}:L^q(V;\pi ) \rightarrow L^{q}(E;{\varvec{{\varvec{\vartheta }}}})\), with \(q = p'\). Namely
or, equivalently,
(with \({\overline{\mathrm {div}}}\) the divergence operator from (1.6)) in the sense of measures.
We can now first address the connectivity problem in the very specific setup
Then, the action functional \(\int {\mathscr {R}}\) is translation-invariant. Let us consider two measures \(\rho _0, \rho _1 \in {{\mathcal {M}}}_+(V)\) such that for \(i\in \{0,1\}\) there holds \(\rho _i = u_i \pi \) with \(u_i \in L_+^p(V;\pi )\) for some \(p\in (1,{+\infty })\). Thus, we look for curves \(\rho \in {\mathscr {A}}{(0,\tau ;\rho _0,\rho _1)}\), with finite action, such that \(\rho _t \ll \pi \), with density \(u_t\), for almost all \(t\in (0,\tau )\). Consequently, any flux \(({{\varvec{j}}}_t)_{t\in (0,\tau )}\) shall satisfy \({{\varvec{j}}}_t \ll {\varvec{{\varvec{\vartheta }}}}\) for a.a. \(t\in (0,\tau )\) (cf. Lemma 4.10). Taking into account (D.1), the continuity equation reduces to
with \( \zeta _t = \frac{\mathrm {d}{{\varvec{j}}}_t}{\mathrm {d}{\varvec{{\varvec{\vartheta }}}}}\). Furthermore, we look for a connecting curve \(\rho _t = u_t \pi \) with \(u_t = (1{-}t)u_0 +t u_1\), so that (D.3) becomes \( - \overline{\mathrm {div}}_{\pi ,{\varvec{{\varvec{\vartheta }}}}}( \zeta _t ) \equiv u_1 -u_0\). Hence, we can restrict to flux densities that are constant in time, i.e. \(\zeta _t \equiv \zeta \) with \(\zeta \in L^p(E;{\varvec{{\varvec{\vartheta }}}})\). In this specific context, and if we further confine the discussion to the case \(\Psi (r) = \frac{1}{p} |r|^p \) for \(p\in (1,{+\infty })\), the minimal action problem becomes
Now, by a general duality result on linear operators, the operator \({}- {\overline{\mathrm {div}}}_{\pi ,{\varvec{{\varvec{\vartheta }}}}}: L^p(E;{\varvec{{\varvec{\vartheta }}}}) \rightarrow L^p(V;\pi )\) is surjective if and only if the graph gradient \({{\overline{\nabla }}}:L^q(V;\pi ) \rightarrow L^{q}(E;{\varvec{{\varvec{\vartheta }}}})\) fulfills the following property:
namely the q-Poincaré inequality (4.84). We can thus conclude the following result.
Lemma D.1
Suppose that \(\upalpha \equiv 1\), that \(\Psi \) has p-growth (cf. (4.85)), and that the measures \((\pi ,{\varvec{{\varvec{\vartheta }}}}) \) satisfy a q-Poincaré inequality for \(q=\tfrac{p}{p-1}\). Let \(\rho _0, \rho _1 \in {{\mathcal {M}}}^+(V) \) be given by \(\rho _i = u_i \pi \), with positive \(u_i \in L^p(V; \pi )\), for \(i \in \{0,1\}\). Then, for every \(\tau \in (0,1)\) we have \({\mathscr {W}}(\tau ,\rho _0,\rho _1)<{+\infty }\). If \(\Psi (r) = \frac{1}{p} |r|^p\), q-Poincaré inequality is also necessary for having \({\mathscr {W}}(\tau ,\rho _0,\rho _1)<{+\infty }\).
We are now in a position to carry out the
Proof of Proposition 4.25
Assume that \(\rho _0(V) = \int _V u_0 (x) \pi (\mathrm {d}x) = \pi (V)\). Hence, it is sufficient to provide a solution for the connectivity problem between \(u_0\) and \(u_1 \equiv 1\). We may also assume without loss of generality that \(\upalpha (u,v) \ge \upalpha _0(u,v)\) with \(\upalpha _0(u,v) = c_0 \min (u,v,1)\) for some \(c_0>0\), so that
where the first estimate follows from the convexity of \(\Psi \) and the fact that \(\Psi (0)=0\), yielding that \(\lambda \mapsto \lambda \Psi (w/\lambda )\) is non-increasing. It is therefore sufficient to consider the case in which \(c_0=C_p=1\), \(\upalpha _0(u,v) = \min (u,v,1)\), and to solve the connectivity problem for \({{\tilde{\Psi }}}(r) = \frac{1}{p} |r|^p\). By Lemma D.1, we may first find \(w\in L^p(E;{\varvec{{\varvec{\vartheta }}}})\) solving the minimum problem (D.4) in the case \(\upalpha \equiv 1\), so that the flux density \(\zeta _t \equiv \frac{1}{2} w\) is associated with the curve \(u_t = (1{-}t)u_0 +t u_1\), \(t\in [0,\tau ]\). Then, we fix an exponent \(\gamma >0\) and we consider the rescaled curve \({\tilde{u}}_t: = u_{t^\gamma }\), that fulfills \(\partial _t {\tilde{u}}_t = - \overline{\mathrm {div}}_{\pi ,{\varvec{{\varvec{\vartheta }}}}}({\tilde{\zeta }}_t) \) with \({\tilde{\zeta }}_t = \frac{1}{2} {\tilde{w}}_t = \frac{1}{2} \gamma t^{\gamma -1} w\). Moreover,
since \(u_1(x) = u_1(y) =1\). By (D.5) we thus get
Choosing \(\gamma >p-1\) we conclude that
hence \({\mathscr {A}}{(0,\tau ;\rho _0,\rho _1)} \ne \emptyset \). \(\square \)
Appendix E: Convexity of \({\mathrm {D}}_\upphi \) induced by power means
Here, we prove the claim that \({\mathrm {D}}_\upphi \) is convex when \(\upphi \) is the Boltzmann entropy (1.5) and the pair \((\upalpha ,\Psi ^*)\) is induced by the power means \({\mathfrak {m}}_p\) (see Example 1 in Sect. 1.3), for \(p\in [-\infty ,-1]\cup {[}0,1{)}\). More precisely, we consider the case, \(\upalpha (u,v){:}{=}{\mathfrak {m}}_p(u,v) = v {\mathfrak {f}}_p(u/v)\), \(p\in {[}-\infty ,1{)}\), where \({\mathfrak {f}}_p\) is the concave generating function
and
We consider here only the case \(p<1\) since \({\mathfrak {m}}_p\) is not concave for \(p>1\) and \(\Psi _p^*\) is not superlinear for \(p=1\). We have for \(u,v>0\)
so that
\({\mathrm {D}}_{p,\upphi }\) takes a more explicit and remarkable form also in the case of the harmonic mean \(p=-1\):
It is also interesting to note that \({\mathrm {D}}_{p,\upphi }\) has a natural lower semicontinuous extension to the boundary \( \{0\}\times (0,\infty )\cup (0,\infty )\times \{0\}=\partial (0,\infty )^2\setminus \{(0,0)\}\) given by
The main result of this section is summarized in the following lemma (where we just consider the range \(p\in {[}-\infty ,1{)}\)).
Lemma E.1
\({\mathrm {D}}_{p,\upphi }\) is convex on \((0,\infty )^2\) if and only if \(p\in [-\infty ,-1]\cup {[}0,1{)}\).
Proof
The cases \(p=0\) and \(p=-\infty \) can be easily checked, so that we assume \(p\in (-\infty ,1)\setminus \{0\}\). It is not difficult to see that the convexity of \({\mathrm {D}}_{p,\upphi }\) on \((0,\infty )^2\) is determined by the convexity of \(K_p\) on \((0,\infty )\).
Hence, it suffices to check that \(K_p''(\xi )\ge 0\) for \(\xi >0\).
Elementary computations yield
Therefore the assertion holds if and only if \(H_p(\xi )\ge 0\) for \(\xi >0\). Notice that \(H_p(1)=2^{2-1/p}\ge 0\). We now show that if \(p\in {(}-\infty ,-1{]}\cup (0,1)\) then \(H_p\) takes its minimum at \(\xi =1\). Since
we can make a change of variables \(\xi =\exp (\eta )\), \(\eta \in {\mathbb {R}}\), to obtain
Since \({{\tilde{G}}}_p(\eta )\) is an odd function, \(H_p\) takes its minimum at \(\xi =1\) if \({{\tilde{G}}}_p(\eta )\ge 0\) for \(\eta >0\). This property clearly holds if \(p\in (0,1)\). On the other hand, if \(p<0\), \(\tilde{G}_p(\eta )\ge 0\) if and only if \((1+p)\eta \le 0\) for all \(\eta \ge 0\), i.e. the cases \(p\le -1\) apply. Altogether, we conclude that \(H_p(\xi )\ge H_p(1)\ge 0\) and therefore \(K''_p(\xi )\ge 0\) for every \(\xi >0\) if \(p\in {(}-\infty ,-1{]}\cup (0,1)\).
If \(p\in (-1,0)\) then
and
so that
It follows that \(K_p''\) takes strictly negative values in \((0,+\infty )\) and therefore it is not convex. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Peletier, M.A., Rossi, R., Savaré, G. et al. Jump processes as generalized gradient flows. Calc. Var. 61, 33 (2022). https://doi.org/10.1007/s00526-021-02130-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-021-02130-2



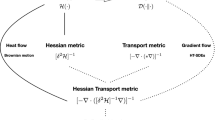

 , and
, and