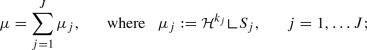A stationary heat conduction problem in low dimensional sets in ${\mathbb {R}}^N$

Abstract

We study a basic linear elliptic equation on a lower dimensional rectifiable set S in ${\mathbb {R}}^N$ with the Neumann boundary data. Set S is a support of a finite Borel measure $\mu$. We will use the measure theoretic tools to interpret the equation and the Neumann boundary condition. For this purpose we recall the Sobolev-type space dependent on the measure $\mu$. We establish existence and uniqueness of weak solutions provided that an appropriate source term is given.

1 Introduction

We study here an old problem of determining the stationary heat distribution in a conductor S in the ambient space $\Omega \subset {\mathbb {R}}^N$, when the conductivity tensor A and the heat sources Q are given. We assume that the conductor S is insulated at the boundary of $\Omega$. Moreover, the set $\Omega \setminus S$ is neither conducting nor it contains any heat source. The main objective of the paper is to investigate the case of “thin” S, i.e., the case when the dimension of S is smaller than N.

In the classical setting, S is a smooth Riemannian manifold. The stationary heat equation takes the following form,

$$\begin{aligned} \begin{array}{ll} \Delta u + Q = 0,&{} x \in S,\\ \frac{\partial u}{\partial \nu }=0,&{} x\in \partial S. \end{array} \end{aligned}$$

(1.1)

Here, $\Delta$ denotes the Laplace-Betrami operator, i.e.,

$$\begin{aligned} \Delta u = {\hbox {div}}\,_S \nabla u, \end{aligned}$$

where ${\hbox {div}}\,_S$ is a surface divergence and $\nabla u$ is the covariant derivative of u. If S is a submanifold of ${\mathbb {R}}^N$, then $\nabla u = P Du$, where P is the projection of ${\mathbb {R}}^N$ onto $T_xS$, the tangent space of S at x. Equation (1.1) is the Euler–Lagrange equation of a variational functional,

$$\begin{aligned} \int _S \left[ \frac{1}{2} |\nabla u|^2 - Q u \right] \,d\sigma ,\qquad u\in W^{1,2}(S), \end{aligned}$$

where $W^{1,2}(S)$ is the Sobolev space on the Riemannian manifold S.

Our main goal is to discuss such variational functionals and to analyze their Euler–Lagrange equations in a more general context, namely when the set S is a lower dimension rectifiable set in ${\mathbb {R}}^N$. To do this we employ the measure theoretic tools and we follow the approach proposed by Bouchitté, Buttazzo and Seppecher in [1]. Namely, we consider a measure $\mu$, supported in S, which is singular with respect to the Lebesgue measure in ${\mathbb {R}}^N$. We assume further that the conductivity tensor A and the heat sources Q are, respectively, a tensor and a scalar valued measure; both measures are absolutely continuous with respect to $\mu$. Applying variational methods, we focus initially on minimizing problem for the functional

$$\begin{aligned} E(u) = \frac{1}{2} \int _\Omega (A(x)\nabla u, \nabla u)\,d \mu - \langle Q, u\rangle , \qquad u \in C^\infty _c({\mathbb {R}}^N). \end{aligned}$$

(1.2)

When , where S is a smooth Riemannian manifold, then the Euler–Lagrange equation for E is of the form

$$\begin{aligned} \begin{array}{ll} {\hbox {div}}\,_S \left( A \nabla u \right) +Q=0&{}\hbox {in } S,\\ \left[ A \nabla u, \nu \right] |_{\partial \Omega } = 0&{}\hbox {on } S\cap \partial \Omega , \end{array} \end{aligned}$$

(1.3)

where $\nu$ is the outward normal unit vector of $\partial \Omega$. However, an effort is required to derive and give meaning to such an equation when $\mu$ is a more general measure.

In this paper we consider a multijunction measure in the sense considered by Bouchitté and Fragalà in [2]. Our precise assumptions, denoted further by [S], are as follows:

• $\Omega$ is a smooth bounded domain in ${\mathbb {R}}^N$;

• a compact set S contained in ${\overline{\Omega }}$ is of the form

  $$\begin{aligned} \mathrm {supp}\, \mu = S = \bigcup _{j=1}^J S_j, \end{aligned}$$

  where each $S_j$ is a compact manifold of class ${\mathcal {C}}^2$ of dimension $k_j<N$;

• the measure $\mu$ is of the form

  

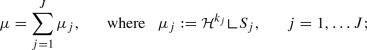
• measures $\mu _j$ are mutually singular, i.e.

  $$\begin{aligned} \mu _j(S_i) = 0 \qquad \text {for all }j \ne i; \end{aligned}$$

• for each $i=1,\ldots ,J$, we assume that the boundary of the manifold $S_i$ is contained in $\partial \Omega \cup \bigcup _{j\ne i} {{\bar{S}}}_j$;

• the relative interior of $S_i$ does not intersect the boundary $\partial \Omega$.

Such measure-oriented point of view proved to be very fruitful when dealing with variational problems considered on low dimensional structures in ${\mathbb {R}}^N$, e.g., see the anisotropic shape optimization problem considered by Bouchitté and Buttazzo in [3]. We refer the reader to [4] for an introduction to this theory.

At this point let us mention the main features of the present work. First of all, let us observe, that contrary to the approach presented in [5] and [2], we do not assume a Poincaré-type inequality to hold globally on S, allowing in particular occurrence of multidimensional junctions. The issue of the Poincaré inequality is addressed further in Sect. 2 and examples are given in Sect. 5. Secondly, we consider the Neumann boundary condition in (1.3), which was not present in aforementioned papers [1, 3, 4]. We stress that the meaning of the boundary condition in (1.3) requires clarification. We shall see in Sect. 4 that the correct interpretation relies on the theory developed by Chen and Frid in [6], and it amounts for the Neumann boundary term to be understood as a normal trace of a measure with bounded divergence. Observe also that the ambient space $\Omega$ is, in fact, a design region restricting the position of set S. Remark 4.1 at the end of Sect. 4 addresses the lack of influence of $\Omega$ on the solutions to (1.3) as long as $\partial \Omega$ is smooth in a neighborhood of $\partial \Omega \cap \partial S$.

And finally, we want to mention the fact that conditions [S] may be relaxed a bit. Namely, we may consider $\mu = \theta {{\bar{\mu }}}$, there ${{\bar{\mu }}}$ satisifes [S] and the density $\theta$ is bounded and strictly positive, see (2.9) and (2.10). In this case the same results hold for such $\mu$ and their proofs do not require any changes. We explain it, while presenting the argument.

The variational approach requires introduction of the appropriate Sobolev-type space and finding the lower semicontinuous envelope of E. To this end we employ the space $H^{1,2}_\mu$ introduced by Bouchitté and Buttazzo, [1]. Its definition and basic properties are discussed in Sect. 2. In particular, we explain there the notion of the tangential gradient operator $\nabla _\mu$ for functions from $H^{1,2}_\mu$ and the notion of the tangent space of $\mu$ at x, denoted by $T_\mu (x)$. The relaxation of E, denoted by $E_\mu$ may be calculated explicitly as in [1]–this is done in Sect. 3, see Proposition 3.1). It is defined as

$$\begin{aligned} E_\mu (u) = \frac{1}{2} \int _\Omega (A_\mu (x)\nabla _\mu u, \nabla _\mu u)\,d \mu - \langle Q, u\rangle , \qquad u \in H^{1,2}_\mu , \end{aligned}$$

(1.4)

where $A_\mu$ is given by (3.4). The Euler–Lagrange equation for $E_\mu$ then takes the form (see Proposition 3.3)

$$\begin{aligned} \int _\Omega (A_\mu \nabla _\mu u, \nabla _\mu \varphi )\,d\mu -\int _\Omega f \varphi \, d\mu =0\qquad \hbox {for all } \varphi \in C^1_0({\mathbb {R}}^N), \end{aligned}$$

(1.5)

where f is the density of the measure Q.

Our main result reads as following:

Theorem 1.1

Let us assume that $\mu$ satisfies the conditions [S], and that Q and A satisfy the conditions (3.1)–(3.3). Suppose also that $\langle Q, h \rangle =0$ for all h in the kernel of $\nabla _\mu$. Then, there exists a unique distributional solution $u\in H^{1,2}_\mu$ to the equation (1.5) which is perpendicular (in the $L^2$ scalar product) to $\mathrm {ker}\, \nabla _\mu$. Moreover, the solution satisfies the boundary condition in the following sense: $[A_\mu \nabla _\mu u, \nu ]|_{\partial \Omega }=0$ as a continuous linear functional on $C^2(\partial \Omega )$.

This Theorem follows from Theorem 3.1, Proposition 3.3, and Theorem 4.1. Uniqueness is addressed in Corollary 3.3. We also make a comment of the boundary conditions in Corollary 4.1. Examples of explicit boundary problems are discussed in Sect. 5.

In the course of proofs, we will explain that Theorem 1.1 is valid also for $\mu$ given by (2.9), where the density $\theta$ satisfies (2.10).

2 Sobolev spaces $H^{1,p}_\mu$

2.1 Definitions

In the problem we study, $\Omega$ is the ambient space, containing S, which is the support of a measure $\mu$. Set S interpreted as the heat conductor. We study an elliptic problem in S, however, we are interested in the Neumann-type boundary conditions on $S\cap \partial \Omega$.

We need properly defined Sobolev spaces to study weak solvability of differential equations like (1.3). We require a definition, which is general, yet easy to use. It seems that the Sobolev space $H^{1,p}_\mu$ introduced for any $p\in [1,\infty )$ by Bouchitté–Buttazzo–Seppecher in [1] is the right tool. We will briefly recall this definition. A recent discussion on other possible definitions of Sobolev space on S is in [7].

We begin with the notion of a tangent space to a measure, there is a number of ways to introduce it. We use the approach proposed in [1] and further exposed in [2, 4, 8, 9] in a more reader friendly way.

We assume that $\mu$ is a positive, Radon measure on ${\mathbb {R}}^N$. If we set

$$\begin{aligned} {\mathcal {N}}_\mu =\{v \in C^\infty _c({\mathbb {R}}^N):\ v = 0\hbox { in }{\hbox {supp}}\,\mu \}, \end{aligned}$$

then we introduce

$$\begin{aligned} {\mathfrak {N}}_\mu := \{ w\in C^\infty _c({\mathbb {R}}^N; {\mathbb {R}}^N):\ \exists v\in {\mathcal {N}}_\mu , \ w =\nabla v \hbox { in }{\hbox {supp}}\,\mu \}. \end{aligned}$$

We define the multifunction $N_\mu : {\mathbb {R}}^N \rightrightarrows {\mathbb {R}}^N$ by

$$\begin{aligned} N_\mu (x):= \{ w(x)\in {\mathbb {R}}^N:\ w\in {\mathfrak {N}}_\mu \}. \end{aligned}$$

The vector subspace of ${\mathbb {R}}^N$ is called the normal space to $\mu$ at x. The vector space $T_\mu (x)\subset {\mathbb {R}}^N$ is defined as the orthogonal complement of $N_\mu (x)$ and it is called the tangent space to $\mu$ at x.

We introduce $\Pi _\mu (x,\cdot )$ as the orthogonal projection of ${\mathbb {R}}^N$ onto $T_\mu (x)$. Due to measurability of $T_\mu (\cdot )$, see [1], the projection is $\mu$-measurable.

For any $u\in {\mathcal {D}}({\mathbb {R}}^n)$, we define, for $\mu$-a.e. $x\in {\mathbb {R}}^n$, the tangential gradient

$$\begin{aligned} \nabla _\mu u(x) = \Pi _\mu (x, \nabla u(x)). \end{aligned}$$

The space $H^{1,p}_\mu$ is defined as a completion of ${\mathcal {D}}({\mathbb {R}}^n)$ in the following norm

$$\begin{aligned} \Vert u \Vert _{1,p,\mu } = \left( \Vert u \Vert ^2_{L^p_\mu (\Omega )} + \Vert \nabla _\mu u \Vert ^2_{L^p_\mu (\Omega )} \right) ^{1/2}. \end{aligned}$$

This space is a reflexive Banach space for $p \in (1, \infty )$. We should stress that we could define the Sobolev space by weak derivatives, this is done in [10]. This space is denoted by $W^{1,p}_\mu$, in general $H^{1,p}_\mu$ is a closed subspace of $W^{1,p}_\mu$, see [10] for details.

The weak convergence on space $H^{1,p}_\mu$ is introduced in a natural way,

$$\begin{aligned} u_k \rightharpoonup u\hbox { weakly in }H^{1,p}_\mu \Leftrightarrow \left\{ \begin{array}{l} u_k\rightharpoonup u\hbox { weakly in }L^p_\mu (\Omega ),\\ \nabla _\mu u_k\rightharpoonup \nabla _\mu u\hbox { weakly in }L^p_\mu (\Omega ). \end{array} \right. \end{aligned}$$

In our situation, i.e., with $\mu$ satisfying the conditions [S], the definitions of the tangent space and the Sobolev space $H^{1,p}_\mu$ are intuitive.

Proposition 2.1

(see [2, Lemma 2.2]) Assume that S is a finite union of $C^2$ compact manifolds, $S = \bigcup _{j=1}^J$, dim$\,S_j =k_j\le N$ and the measures are mutually singular. We set $\mu = \sum _{j=1}^J \mu _j$ and we denote by $T_{S_j}(x)$ the tangent space to $S_j$ at x. Then, we have

$$\begin{aligned} T_\mu (x) = T_{S_j}(x)\qquad \mu _j-a.e. \end{aligned}$$

If $S=\mathrm {supp}\, \mu \subset {\overline{\Omega }}$ and $\Omega$ is an open region in ${\mathbb {R}}^N$ and $\mu ( S \cap \partial \Omega ) = 0$, then

$$\begin{aligned} H^{1,p}_\mu = \{ u \in L^p(S,\mu ):\ u|_{S_j}\in H^{1,p}(S_j),\ j=1, \ldots , J\}. \end{aligned}$$

2.2 On the validity of the Poincaré inequality

An important tool in the analysis of the well posedness of the problem (1.3) is the Poincaré inequality. In case S is a smooth, compact manifold of dimension $k < N$, the global Poincaré inequality holds, i.e. there is $C_P>0$ such that

$$\begin{aligned} \Vert u - u_S\Vert _{L^2(\Omega ,\mu )}^2 \le C_p \Vert \nabla _\mu u\Vert ^2_{L^2(\Omega ,\mu )}\quad \text {for} \quad u\in H^{1,2}_\mu , \quad \text {where} \quad u_S = \frac{1}{\mu (S)} \int _\Omega u \,d\mu .\nonumber \\ \end{aligned}$$

(2.1)

However, we are particularly interested in junctions between several thin structures of possibly different dimension, i.e. when S is a finite union of compact manifolds of possibly different Hausdorff dimensions. In such a case (2.1) may not be true. Further in this section we discuss some positive examples, but let us now concentrate on the problems associated with the lack of (2.1) and the possible remedies.

One of the consequences of the global Poincaré inequality (2.1) is the following property:

$$\begin{aligned} u \in H^{1,2}_\mu (\Omega ), \quad \nabla _\mu u =0\quad \mu -\text {a.e.} \Rightarrow u=\text {const.} \quad \mu -\text {a.e.} \end{aligned}$$

(2.2)

In other words

$$\begin{aligned} \mathrm {dim}\, \mathrm {ker}\, \nabla _\mu = \mathrm {dim}\{ u \in H^{1,2}_\mu (\Omega ) :\nabla _\mu u = 0\}= 1, \end{aligned}$$

so $\mathrm {ker}\, \nabla _\mu$ contains only constant functions. In a general situation of a multijunction measure this is not necessarily true, i.e. it may happen that

$$\begin{aligned} \mathrm {dim}\, \mathrm {ker}\, \nabla _\mu >1. \end{aligned}$$

The important feature is “how big” the junction area is. Every space that supports a global Poincaré inequality is connected. We expect that removing a set of zero capacity from the space should not affect the Poincaré inequality. In particular, removing a set of zero capacity should not disconnect the space. Examples show that our expectation need not be true. We consider the situation presented on Fig. 1. Since the capacity of a point on a plane is equal to zero, the global Poincaré inequality cannot be valid for this set. A similar situation occurs for the set presented on Fig. 6. We do not want to recall the definition of a (Sobolev) capacity here (we refer the interested reader for instance to the book [11], chapter 4). However, in the situation presented on the Fig. 1, the argument is simple and straightforward.

Fig. 1

Set S without Poincaré inequality (2.1)

Consider the unit disk on a plane $D = \{ (x,y) \in {\mathbb {R}}^2 :x^2 + y^2 < 1\}$ and the function

$$\begin{aligned} f(x,y) = -\log \log (1+ (x^2 + y^2)^{-1/2}). \end{aligned}$$

This is an unbounded function which belongs to the Sobolev space $H^{1,2}(D)$. Set

$$\begin{aligned} \zeta (t) = {\left\{ \begin{array}{ll} 0 &{} t<0,\\ t &{} t \in [0,1], \\ 1 &{} t > 1. \end{array}\right. } \end{aligned}$$

Then $\zeta \circ f \in H^{1,2}(D)$ as well. Define a sequence of functions $f_n$ as

$$\begin{aligned} f_n(x,y) = \zeta (f(x,y)-n+1). \end{aligned}$$

Since the $H^{1,2}(D)$ energy of f is finite, the $H^{1,2}(D)$-energy of $f_n$ tends to zero.

Now, we consider a metric space $(S,\mu )$, such that $S= X \cup _P Y$, where

$$\begin{aligned} X = \{ (x,y,z) \in {\mathbb {R}}^3 :z=0;\ x^2 + y^2 \le 1 \} \end{aligned}$$

and is a 2-dimensional Hausdorff measure;

$$\begin{aligned} Y = \{ (x,y,z) \in {\mathbb {R}}^3 :x=y=0; z \in [0,1] \} \end{aligned}$$

and is a 1-dimensional Hausdorff measure and $P=(0,0,0)$.

Proposition 2.2

Let us suppose that S and $\mu$ are defined above. Then, ${\hbox {dim}}\,{\hbox {ker}}\,\nabla _\mu >1$.

Proof

We define a sequence of functions $u_n : S \rightarrow {\mathbb {R}}$ as

$$\begin{aligned} u_n(s) = {\left\{ \begin{array}{ll} \zeta (f(x,y)-n+1) &{} s=(x,y,0) \in X;\\ 1 &{} s=(0,0,z)\in Y \end{array}\right. } \end{aligned}$$

and a function

$$\begin{aligned} u_o(s) = {\left\{ \begin{array}{ll} 0 &{} s=(x,y,0) \in X;\\ 1 &{} s=(0,0,z)\in Y. \end{array}\right. } \end{aligned}$$

Since

$$\begin{aligned} \int _S |u_n(s)| \, d\mu = \int _X |u_n(s)| \, d{\mathcal {H}}^2 + \int _Y |u_n(s)| \, d{\mathcal {H}}^1 \end{aligned}$$

and

$$\begin{aligned} \int _S |\nabla _\mu u_n(s)| \, d\mu = \int _X |\nabla _\mu u_n(s)| \, d{\mathcal {H}}^2 + \underbrace{\int _Y | \nabla _\mu u_n(s)| \, d{\mathcal {H}}^1}_{=0}, \end{aligned}$$

then it follows that $u_n\in H^{1,2}_\mu$. By the construction, we also have

$$\begin{aligned} \Vert u_n -u_o \Vert _{H^{1,2}_\mu } \rightarrow 0, \end{aligned}$$

which implies $u_o \in H^{1,2}_\mu$ which in turn falsifies the Poincaré inequality (2.1) on S and it shows that (2.2) in this situation is not true. As a result, our claim holds. $\square$

Let us denote

$$\begin{aligned} V = {\hbox {ker}}\,\nabla _\mu \subset H^{1,2}_\mu \subset L^2(\Omega , \mu ). \end{aligned}$$

This is a finite dimensional subspace of $L^2(\Omega , \mu )$. We define

$$\begin{aligned} P :H^{1,2}_\mu \rightarrow V \end{aligned}$$

(2.3)

as the orthogonal projection onto V (with respect to $L^2$ scalar product). Set $d={\hbox {dim}}\,V$. We can split the set $\{ 1,\ldots ,J \}$ from the condition [S] into a final family of disjoint sets of indices

$$\begin{aligned} \{ 1,\ldots ,J \} = J_1 \cup \ldots \cup J_d, \quad d\le J, \quad J_l \cap J_m = \emptyset ,\quad l\ne m. \end{aligned}$$

The sets $J_l$, $l=1,\ldots , d$ are defined in the following way. The set

$$\begin{aligned} {\widetilde{S}}_l = \bigcup _{i \in J_l} S_i \end{aligned}$$

is such that

$$\begin{aligned} \chi _{{\widetilde{S}}_l} \in {\hbox {ker}}\,\nabla _\mu , \end{aligned}$$

and $J_l$ are “maximal” in the sense that for any proper subset $K \subset J_l$,

$$\begin{aligned} \text {the characteristic function of } \bigcup _{i \in K } S_i \text { does not belong to }V. \end{aligned}$$

Then the projection P in (2.3) can be expressed as

(2.4)

For a multijunction measure satisfying [S] the following weaker version of the Poincaré inequality holds.

Theorem 2.1

Let us suppose that a multijunction measure satisfies [S]. Then there is $C_l>0$ such that for $u\in H^{1,2}_\mu$

$$\begin{aligned} \sum _{i\in J_l} \int _\Omega | u - P_l u |^2 \, d\mu _i \le C_l \sum _{i\in J_l} \int _\Omega | \nabla _\mu u |^2 \, d \mu _i, \quad \text {for }l=1, \ldots , d, \end{aligned}$$

(2.5)

where $P_l$ is defined in (2.4).

Let us mention in advance that, the regularity of solutions depends in an essential way on whether the set S supports the inequality (2.1) or (2.5). It is known that if a metric measure space (the set S may be treated as such) supports the Poincaré inequality (2.1), one can expect solutions to be continuous. The weaker version (2.5), which is sufficient for the existence result, is not enough to ensure regularity, as shown on examples presented in Sect. 5.

On the other hand, as it is observed in the vast literature concerning analysis on metric-measure spaces, there are many examples of spaces for which validity of Poincaré-type inequality (2.1) can be asserted. It is impossible to discuss this broad topic in all the details within this paper. Various versions of the Poincaré-type inequalities are formulated in different context. However, just to give some justification for our claim that in some examples, one can indeed assert validity of the Poincaré inequality in the form (2.1), we will sketch the framework of metric-measure spaces. An interested reader may find more information and references e.g., in the papers of Semmes [12, Section B], of Hajłasz and Koskela [15], of Heinonen and Koskela [13, Section 6] and in the book [11].

We need to formulate some definitions which are necessary within the framework. Let (X, d) be a connected and complete metric space equipped with a Borel regular measure $\mu$. We say that:

• X is doubling if there exists a constant $C_d \ge 1$ such that

  $$\begin{aligned} \mu (B_{2R}) \le C_d \mu (B_R) \end{aligned}$$

  (2.6)

  for all balls $B_R$ in X of radius $0< R <\mathrm {diam}\, X$.

• X is q-regular if there are constants $C_q \ge 1$ and $q >0$ so that

  $$\begin{aligned} \frac{R^q}{C_q} \le \mu (B_R) \le C_q R^q \end{aligned}$$

  (2.7)

  for all balls $B_R$ in X of radius $0<R < \mathrm {diam}\, X$.

• X is linearly locally contractible if there is a constant C such that every small ball is contractible inside a ball whose radius is C times larger.

Let U be an open set in X and let u be an arbitrary real-valued function in U. We say that a Borel function $g :U \rightarrow [0,\infty ]$ is a very weak gradient of u in U if

$$\begin{aligned} |u(x)-u(y)| \le \int _\gamma g \,d {\mathcal {H}}^1 \end{aligned}$$

whenever $\gamma$ is a rectifiable curve joining x and y in U. In many cases (in particular in the Euclidean setting, when the function u is differentiable) one can take simply $g=|\nabla u|$. Let us observe that this is our case, due to Proposition 2.1.

We say that X admits a local weak (1, p)-Poincaré inequality if

(2.8)

whenever u is a bounded continuous function in a ball $\lambda B$ and g is its very weak gradient. The constants $C_p \ge 1$ and $\lambda \ge 1$ should be independent of B and u. Inequality (2.8) is termed “weak” because we allow a larger ball on the right-hand side than on the left. In many cases this weak estimate can be used to iterate so as to yield an inequality with the same ball on both sides. If the term “weak” is omitted, we assume $\lambda =1$.

With such preparations, we may now state the results due to Semmes (see [12, Section B]):

Theorem 2.2

Assume that $(X,d,\mu )$ is a q-regular metric space which is also locally linearly contractible and a connected orientable topological manifold of dimension q. Then X admits a local (1, p)-Poincaré inequality for all $p \ge 1$.

Theorem 2.3

Suppose that X is a connected, finite simplicial complex of pure dimension $q > 1$ such that the link of each vertex is connected. Then X admits a local (1, q)-Poincaré inequality.

Observe first that both theorems assert validity of the local Poincaré inequality, not just its local weak version. This is a good starting point, but still, local version is not sufficient for our purpose, we want the global version (2.1). Then, even as Theorem 2.3 is much more general, and actually very handy in our situation (our assumptions for the set S actually make it a simplicial complex), we want to avoid introduction of yet another language of simplicial geometry. Therefore to justify passing from the local version (2.8) of the Poincaré inequality to the global one (2.1), we shall start our arguments with the Theorem 2.2.

As observed by Heinonen and Koskela [13], two spaces that support a local (weak) version of the Poincaré inequality may be glued along a sufficiently large common part to produce a new metric space that also supports a Poincaré-type inequality. To make the statement more precise, suppose that X and Y are two locally compact q-regular metric measure spaces. Suppose also that A is a closed subset of X that has an isometric copy inside Y, i.e. there is an isometric embedding $i: A \rightarrow Y$. In the following, we understand this embedding as fixed and think of A as a closed subset of both X and Y. We form a space

$$\begin{aligned} X \cup _A Y \end{aligned}$$

which is the disjoint union of X and Y with points in the two copies of A identified. This space has a natural metric which extends the metrics from X and Y: the distance between $x,y \in X \cup _A Y$ is

$$\begin{aligned} \inf _{a \in A} (d_X(x,a) + d_Y(a,y)). \end{aligned}$$

Furthermore, the measures on X and Y add up to a measure $\mu$ on $X \cup _A Y$ that is obviously q-regular. Recall that the Hausdorff s-content of a set E in a metric space is the number

$$\begin{aligned} {\mathcal {H}}^\infty _s (E) = \inf \sum _i r_i^s, \end{aligned}$$

where the infimum is taken over all countable covers of the set E by ball $B_i$ of radius $r_i$. The Heinonen and Koskela result (see [13, Thm. 6.15]) reads as following:

Theorem 2.4

Let X, Y and A be as above. Suppose that there are numbers $q \ge s > q-p$ and $C \ge 1$ so that for all balls $B_R$ either in X or in Y that are centered at a point in A with $0<R < \min \{ \mathrm {diam}\, X, \mathrm {diam}\, Y \}$ it holds

$$\begin{aligned} {\mathcal {H}}^\infty _s (A \cap B_R) \ge C^{-1} R^s. \end{aligned}$$

If both X and Y admit a local weak (1, p)-Poincaré inequality, then $X \cup _A Y$ admits a local weak (1, p)-Poincaré inequality as well.

Finally, passing from a local weak version of the Poincaré-type inequality (2.8) to the global version (2.1) can be done if the measure $\mu$ is doubling and the space satisfies the so-called chain condition. Roughly speaking, the chain conditions means that each two points of the space can be joint by a sequence of balls with controlled radius and “thick” (in the sense of measure) intersection. An elegant and elementary proof of the fact was given by Hajłasz and Koskela in [14]:

Theorem 2.5

Assume $(X,d,\mu )$ to be a doubling metric measure space which satisfies a chain condition. Assume $\Omega$ to be a bounded domain in X. Assume that a local weak (1, p)-Poincaré inequality holds for functions $u\in L^1_{loc}(\mu )$ and $g\in L^p(\mu )$ for all balls $\lambda B \subset \Omega$. Then there exists $\kappa >1$ which depend on p and the doubling constant only, such that the global Sobolev-Poincaré inequality holds

$$\begin{aligned} \left( \int _\Omega | u - u_\Omega |^{\kappa p} d\mu \right) ^{1/{\kappa p} } \le C \left( \int _\Omega | g |^p d\mu \right) ^{1/p}. \end{aligned}$$

The chain condition is clearly satisfied on a compact smooth manifold or on finite unions of manifolds. The above result allows to give a variety of examples of spaces for which the global Poincaré-type inequality (2.1) holds. In particular, this is the case of sets presented on Figs. 2, 3, and 4. In all these situations one can also expect that the solutions of the Euler–Lagrange Eq. (3.8) are regular.

Fig. 2

Poincaré inequality (2.1) holds on S, condition [S] not satisfied

Fig. 3

Poincaré inequality (2.1) holds on S. Proposition 5.1 yields a continuous solution

Fig. 4

Poincaré inequality (2.1) holds on S

2.3 A more general measure

In the Introduction, we mentioned a possible generalization of our results. Namely, we now assume that ${{\bar{\mu }}}$ satisfies [S] and we consider

$$\begin{aligned} \mu = \theta {{\bar{\mu }}}, \end{aligned}$$

(2.9)

where the density is not only in $L^\infty (S)$, but also $\theta$ is strictly positive. We notice that such measures share the tangent space.

Corollary 2.1

Let us suppose that ${{\bar{\mu }}}$ satisfies [S], $\theta \in L^\infty (S,{{\bar{\mu }}})$ and there exist $0< {\underline{\theta }} , {\bar{\theta }} \in {\mathbb {R}}$ such that

$$\begin{aligned} \theta (x)\in [{\underline{\theta }}, {{\bar{\theta }}}]\qquad \hbox {for } {{\bar{\mu }}} \hbox {-a.e. }x\in S. \end{aligned}$$

(2.10)

We set $\mu = \theta {{\bar{\mu }}}$. Then,

$$\begin{aligned} T_\mu (x) = T_{{{\bar{\mu }}}}(x). \end{aligned}$$

Hence, $H^{1,p}_\mu = H^{1,p}_{{{\bar{\mu }}}}$.

Proof

If we inspect the definition of ${\mathcal {N}}_\mu$, then we notice that ${\mathcal {N}}_\mu$ and ${\mathcal {N}}_{{{\bar{\mu }}}}$ must coincide. As a result, we see that ${\mathfrak {N}}_\mu = {\mathfrak {N}}_{{{\bar{\mu }}}}$ and $N_\mu = N_{{{\bar{\mu }}}}(x)$ for ${{\bar{\mu }}}$ a.e. $x\in S$. Finally,

$$\begin{aligned} \Pi _\mu (x, \cdot ) = \Pi _{{{\bar{\mu }}}} (x, \cdot )\qquad \hbox {for }{{\bar{\mu }}} \hbox { a.e. }x\in S \end{aligned}$$

(2.11)

and our first claim follows.

The second claim follows from (2.11) and the definition of $H^{1,p}_\mu$. $\square$

3 The elliptic problem

We would like to use the calculus of variations to establish existence of solutions to (1.3) in the space $H^{1,2}_\mu$. For this purpose we recall the definition of E(u) for $H^{1,2}_\mu .$ We have to specify the assumptions on A and Q.

In principle, u is an element of $L^2(\Omega ,\mu )$, so we must specify properties of Q appropriately. This is why we make the following assumption,

$$\begin{aligned} \begin{aligned}&Q\text { is a measure of a finite total variation supported in }\Omega ,\\&\text {absolutely continuous with respect to }\mu ,\\&\text {and there is }f\in L^2(\Omega ,\mu )\text { such that } Q = f \mu . \end{aligned} \end{aligned}$$

(3.1)

This assumption in particular makes elements of $H^{1,2}_\mu$ measurable with respect to Q.

Now, we specify our assumptions on A. We consider

$$\begin{aligned} {\left\{ \begin{array}{ll} A\in L^\infty (\Omega ; M(N\times N),\mu ) \quad \text {and}\\ \text {for a.e. }x\text { the matrix }A(x)\text { is symmetric and } T_\mu (x) \subset \hbox {Im}\,A(x). \end{array}\right. } \end{aligned}$$

(3.2)

We have to present the positivity of A in a way suitable for dealing with $\nabla _\mu u$ in the tangent space to $\mu$. We require that at $\mu$-almost every $x\in \Omega$, we have

$$\begin{aligned} (A(x) \xi , \xi ) \ge \lambda |\xi |^2,\qquad \hbox {for all }\xi \in \hbox {Im}\,A(x). \end{aligned}$$

(3.3)

After these preparations, we state our first result.

Proposition 3.1

Let us suppose that A satisfies (3.2) and (3.3). Suppose further that the measure $\mu$ satisfies the assumptions [S]. Moreover, $Q = f\mu$, where $f\in L^2(S,\mu )$. Then, the relaxation of E, defined by (1.2), is given by

$$\begin{aligned} E_\mu (u) = \frac{1}{2} \int _\Omega (A_\mu (x) \nabla _\mu u, \nabla _\mu u)\,d\mu - \int _\Omega fu\, d\mu . \end{aligned}$$

Here, matrix $A_\mu (x)$ is defined by

$$\begin{aligned} A_\mu (x) = A(x) - \sum _{i=1}^l\frac{A (x)e_i(x)\otimes A(x) e_i(x)}{(A(x) e_i(x), e_i(x))} \end{aligned}$$

(3.4)

where vectors $e_i= e_i(x)$, $i=1,\ldots ,l$ are linearly independent, $\mu$-measurable, they span $(T_\mu (x))^\perp \cap \, {\hbox {Im}}\,A(x)$. Moreover we can assume $(A (x)e_i(x), e_j(x))=\delta _{ij}$, for $i,j=1,\ldots ,l$.

Proof

We may assume for the sake of simplicity of notation that $f=0$. Indeed, the term $\int _\Omega f u\,d \mu$ is weakly continuous, hence we have to deal with the lower semicontinuity of the quadratic term.

Step 1. Let us assume first that we are given a matrix $B\in L^\infty (\Omega ,M(N\times N),\mu )$ and for $\mu$-a.e. $x\in \Omega$ matrix B(x) is symmetric and positive definite. Then, for $\mu$-a.e. $x\in \Omega$, the matrix B(x) defines a scalar product in ${\mathbb {R}}^N$:

$$\begin{aligned} (v,w)_B := (B(x)v,w) \quad \text {for }v,w \in {\mathbb {R}}^N. \end{aligned}$$

Let us choose vector fields $e_1,\ldots ,e_{N-k}$ such that for $\mu$-a.e. $x\in \Omega$:

• they are linearly independent,

• they span $(T_\mu (x))^\perp$,

• they are orthonormal with respect to the scalar product defined by the matrix B, i.e. for $\mu$-a.e. $x\in \Omega$

  $$\begin{aligned} (e_i(x), e_j(x))_B = \delta _{ij} \quad i,j=1,\ldots ,N-k. \end{aligned}$$

The $\mu$-measurability of these vector fields is discussed in Step 4.

Observe that for $\mu$-a.e. $x\in \Omega$, the orthogonal projection onto $(T_\mu (x))^\perp$ with respect to the scalar product B(x) is defined as

$$\begin{aligned} P_B v = \sum _{i=1}^{N-k} e_i(x)(e_i(x),v)_B \qquad v\in {\mathbb {R}}^N. \end{aligned}$$

Let us set $F^B(x,p) :=(B(x)p,p)=(p,p)_B$. Then, we define $E^B(u)= \frac{1}{2} \int _\Omega F^B(x,\nabla u)\,d\mu$. By [1], $E^B_\mu$, the relaxation of $E^B$, is given by

$$\begin{aligned} E^B_\mu (u) = \frac{1}{2} \int _\Omega F^B_\mu (x,\nabla _\mu u)\,d\mu , \end{aligned}$$

where

$$\begin{aligned} F^B_\mu (x,p) = \inf \{ F^B(x,p+ \xi ): \quad \xi \in (T_\mu (x))^\perp \}. \end{aligned}$$

The minimization problem in the definition of $F^B_\mu$ may be written as

$$\begin{aligned} \inf \left\{ F^B(x,p + \sum _{i=1}^{N-k}t_i e_i(x)):\ t_i\in {\mathbb {R}}, \ i =1,\ldots , N-k\right\} . \end{aligned}$$

A simple differentiation yields optimality conditions

$$\begin{aligned} t^o_i = -(Bp, e_i)/ (B e_i, e_i)=-(p,e_i)_B, \quad \text {for }i=1,\ldots , {N-k}. \end{aligned}$$

Thus we easily see that

$$\begin{aligned} F^B_\mu (x,p) = (B_\mu (x)p,p), \end{aligned}$$

where $B_\mu (x)$ is given by

$$\begin{aligned} B_\mu (x) = B(x) - \sum _{i=1}^{N-k} B(x) e_i(x)\otimes B(x) e_i(x), \end{aligned}$$

(3.5)

that is

$$\begin{aligned} B_\mu (x)\xi&= B(x)\xi - \sum _{i=1}^{N-k} B(x) e_i(x) (e_i(x), \xi )_B \\&= B(x)\xi - B(x)\left( \sum _{i=1}^{N-k} e_i(x) (e_i(x), \xi )_B \right) \\&= B(x)\xi - B(x) P_B \xi \end{aligned}$$

It is easy to see that for any $\xi \in {\mathbb {R}}^N$ we have $B_\mu \xi \in T_\mu$. Indeed,

$$\begin{aligned} (B_\mu (x) \xi , e_j ) = (B(x) \xi , e_j) - (B(x) e_j, \xi ) = 0 \quad \text {for }j=1,\ldots , N-k. \end{aligned}$$

Moreover, $B_\mu$ is strictly positively definite on $T_\mu (x)$. Indeed, for $\xi \in T_\mu (x)$ we have

$$\begin{aligned} (B_\mu (x) \xi , \xi )&= (\xi ,\xi )_B - (P_B \xi , \xi )_B \\&= (\xi ,\xi )_B - (P_B \xi , P_B \xi )_B > 0 \end{aligned}$$

since $T_\mu \ni \xi \ne P_B \xi$.

Step 2. We assumed that A satisfies (3.3), so if we set $F(x,p)= (A(x)p,p)$, then this integrand need not satisfy the lower estimate

$$\begin{aligned} F(x,p)\ge c_0 |p|^2 \end{aligned}$$

for every $p\in {\mathbb {R}}^N$, which is in the assumption of [1, Theorem 3.1]. For this reason we define the symmetric matrix $B^\epsilon \in L^\infty (\Omega , M(N \times N),\mu )$, as

$$\begin{aligned} B(x) = A(x) + \epsilon P(x), \quad \text {for }\epsilon >0, \end{aligned}$$

(3.6)

where P(x) is the orthogonal (with respect to the euclidean product in ${\mathbb {R}}^N$) projection onto ${\hbox {ker}}\,A$. Hence, for every $\epsilon >0$ and for $\mu$-a.e. $x\in \Omega$ matrix $B^\epsilon (x)$ is symmetric and positive definite and formula (3.5) applies to $B^\epsilon$.

Step 3. We claim that if B is defined by (3.6), then $B^\epsilon _\mu = A_\mu$, where $A_\mu$ is given by (3.4). Indeed, the summation in (3.5) may be split, the first $l\le N-k$ vectors belong to ${\hbox {Im}}\,A\cap (T_\mu )^\perp ,$ while vectors $e_i$, $i=l+1,\ldots , N-k$ span the kernel of A. We note

$$\begin{aligned} (A+ \epsilon P) e_i = A e_i\qquad \hbox {for }i = 1,\ldots , l \end{aligned}$$

and

$$\begin{aligned} (A+ \epsilon P) e_i = \epsilon P e_i = \epsilon e_i \qquad \hbox {for }i = l+1,\ldots , N-k. \end{aligned}$$

Then, $B^\epsilon _\mu$ takes the following form,

$$\begin{aligned} B^\epsilon _\mu&= A + \epsilon P - \sum _{i=1}^l\frac{A e_i\otimes A e_i}{(A e_i, e_i)} - \sum _{i=l+1}^{N-k} \epsilon \frac{ e_i}{ \Vert e_i\Vert } \otimes \frac{ e_i }{\Vert e_i\Vert } \\&= A_\mu , \end{aligned}$$

because $P = \sum _{i=l+1}^{N-k} \frac{ e_i}{ \Vert e_i\Vert } \otimes \frac{ e_i }{\Vert e_i\Vert }$.

Step 4. We claim that the mapping $x\mapsto A_\mu (x)$ is $\mu$-measurable. We know that the multivalued map $x\mapsto T^\perp _\mu (x)$ is $\mu$-measurable, (see [9, page 476]), so is

$$\begin{aligned} x\mapsto T^\perp _\mu (x)\cap \{\xi \in {\mathbb {R}}^N: (A(x)\xi ,\xi ) =1\}=:\Gamma _1(x). \end{aligned}$$

As a result, there is a measurable selection of $\Gamma _1(x)$, which we will call $e_1$.

In the next step we consider a multivalued function

$$\begin{aligned} \Gamma _2 (x) = \Gamma _1(x)\cap \{\xi \in {\mathbb {R}}^N: (A(x)e_1(x),\xi ) =0\}. \end{aligned}$$

Of course it is measurable, we will denotes its selection by $e_2$. After the finite number of steps we will end up with measurable vector fields $e_i(x)$, $i =1,\ldots , l$, which are necessary in the formula for $A_\mu$.

Step 5. We will check that the lower semicontinuous envelope of E is $E_\mu$. By definition we have $E_\mu (u) \le E(u) \le E^B(u)$. Step 3 implies that $E_\mu = E^B_\mu$ and $E^B_\mu$ is semicontinuous. If we denote by bar the lower semicontinuous envelope, then we see,

$$\begin{aligned} E_\mu (u)\le {{\bar{E}}}(u) \le {\bar{E}}^B(u) = E^B_\mu (u) = E^B_\mu (u). \end{aligned}$$

Hence, $E_\mu (u) ={{\bar{E}}}(u)$. $\square$

Interestingly, the conclusion of Proposition 3.1 does not change if we consider $\mu$ of the form (2.9). Here it is:

Corollary 3.1

Let us suppose that all the assumptions of Proposition 3.1 hold, except that $\mu = \theta {{\bar{\mu }}}$, where ${{\bar{\mu }}}$ satisfies [S] and $\theta$ fullfils (2.10). Then, the relaxation of E is given by $E_\mu$ defined in Proposition 3.1, where (3.4) holds.

Proof

Let us notice that (3.4) is well-defined as long as the tangent space $T_\mu (x)$ exists, i.e. also if $\mu$ is of the form (2.9).

Let us now introduce

$$\begin{aligned} {{\bar{A}}} = A \theta ,\quad {{\bar{Q}}} = Q \theta ,\quad {{\bar{f}}} = f \theta . \end{aligned}$$

Due to (2.10) we see that ${{\bar{\mu }}}$, ${{\bar{A}}}$ and ${{\bar{Q}}}$ satisfy the assumptions of Proposition 3.1. Hence, the relaxation of functional E,

$$\begin{aligned} E(u) = \frac{1}{2} \int _\Omega ({{\bar{A}}}(x) \nabla u, \nabla u)\,d{{\bar{\mu }}} - \int _\Omega {{\bar{f}}}u\, d{{\bar{\mu }}}, \qquad u\in C^\infty _c(\Omega ) \end{aligned}$$

is given by $E_{{{\bar{\mu }}}}$, where ${{\bar{A}}}_{{{\bar{\mu }}}}$ is defined in (3.4). We notice that

$$\begin{aligned} E_{{{\bar{\mu }}}}(u) = \frac{1}{2} \int _\Omega ({{\bar{A}}}_{{{\bar{\mu }}}}(x) \nabla _{{{\bar{\mu }}}}u, \nabla _{{{\bar{\mu }}}} u)\,d{{\bar{\mu }}} - \int _\Omega \bar{f}u\, d{{\bar{\mu }}}, \qquad u\in H^{1,2}_{\mu }, \end{aligned}$$

where we use that fact that $H^{1,2}_{\mu } = H^{1,2}_{{{\bar{\mu }}}}$. It is easy to check that the structure of the formula (3.4) implies that

$$\begin{aligned} {{\bar{A}}}_{{{\bar{\mu }}}}(x) = \theta (x) A_{{{\bar{\mu }}}}(x)\quad \mu \hbox {-a.e.} \end{aligned}$$

once we see that vectors in ${\mathbb {R}}^N$ orthogonal with respect to inner product defined by A(x) are orthogonal with respect to inner product defined by ${{\bar{A}}}(x)$. However, this is obvious since both inner products are propotional, with a positive proportionality constant.

Thus, for any $u\in H^{1,2}_{\mu }$ we have,

$$\begin{aligned} E_{{{\bar{\mu }}}}(u)= & {} \frac{1}{2} \int _\Omega (\theta (x) A_{{{\bar{\mu }}}}(x)\nabla _{\mu }u, \nabla _{\mu } u)\,d{{\bar{\mu }}} - \int _\Omega {{\bar{f}}}u\, d{{\bar{\mu }}} \\= & {} \frac{1}{2} \int _\Omega (A_{{{\bar{\mu }}}}(x)\nabla _{\mu }u, \nabla _{\mu } u)\,d\mu - \int _\Omega fu\, d\mu \\= & {} E_{\mu }(u). \end{aligned}$$

$\square$

We have to describe ${\hbox {ker}}\,{\hbox {div}}\,A_\mu \nabla _\mu$, what is necessary, before we can specify Q. Actually, we prove:

Proposition 3.2

${\hbox {ker}}\,{\hbox {div}}\,A_\mu \nabla _\mu = {\hbox {ker}}\,\nabla _\mu$.

Proof

The inclusion $\supset$ is obvious. Let us suppose that $u \in H^{1,2}_\mu$ satisfies

$$\begin{aligned} {\hbox {div}}\,(A_\mu \nabla _\mu u \mu ) = 0\qquad \hbox {in }{\mathcal {D}}'({\mathbb {R}}^N). \end{aligned}$$

In other words,

$$\begin{aligned} \int _\Omega A_\mu \nabla _\mu u \nabla \varphi \,d\mu = 0\qquad \hbox {for all }\varphi \in {\mathcal {D}}({\mathbb {R}}^N). \end{aligned}$$

We notice that $\nabla \varphi (x) = \nabla _\mu \varphi (x) + (Id - \Pi _\mu (x, \nabla \varphi ))$ for $\mu$-a.e. $x\in S$. Since $A_\mu \nabla _\mu u(x) \in T_\mu (x)$ for $\mu$-a.e. $x\in S$, we have

$$\begin{aligned} 0= \int _\Omega A_\mu \nabla _\mu u \nabla \varphi \,d\mu = \int _\Omega A_\mu \nabla _\mu u \nabla _\mu \varphi \,d\mu . \end{aligned}$$

We may take a sequence $\varphi _n\in {\mathcal {D}}({\mathbb {R}}^N)$ such that $\nabla _\mu \varphi _n$ converges to $\nabla _\mu u$. This yields,

$$\begin{aligned} 0= \int _\Omega A_\mu \nabla _\mu u \nabla _\mu u\,d\mu . \end{aligned}$$

Combining this with ellipticity of $A_\mu$, see (3.3), yields the claim. $\square$

Remark 3.1

The same proof works in the case of $\mu$ as in Corollary 2.1.

After these preparations we can state one of our main results.

Theorem 3.1

Let us assume that the conditions: [S] on $\mu$ and (3.1) on Q as well as (3.3) on A hold. In addition, we assume that $\langle Q, h \rangle =0$ for all h in the kernel of $\nabla _\mu$. Then, there exists a minimizer u of the functional $E_\mu$ defined on the linear subspace

$$\begin{aligned} H= \{ u \in H^{1,2}_\mu : \quad Pu =0\}, \end{aligned}$$

where P is the orthogonal projection onto ${\hbox {ker}}\,\nabla _\mu$ described by (2.4).

Proof

We have already computed $E_\mu$, the relaxation of E. Actually, we study minimizers of $E_\mu$. Let us suppose that $\{ u_k\}\subset H$ is a sequence minimizing $E_\mu$, i.e.,

$$\begin{aligned} \lim _{k\rightarrow \infty } E_\mu (u_k) = \inf \{ E_\mu (v):\ v \in H \} =:R. \end{aligned}$$

We may assume that for all $k\in {\mathbb {N}}$ we have,

$$\begin{aligned} R\le \frac{1}{2} \int _\Omega (A_\mu (x)\nabla _\mu u_k, \nabla _\mu u_k)\,d \mu - \int _\Omega fu_k\, d\mu \le R+1. \end{aligned}$$

Due to (3.3), we end up with,

$$\begin{aligned} \frac{\lambda }{2} \int _\Omega | \nabla _\mu u_k|^2 \,d\mu - \int _\Omega fu_k\, d\mu \le R+1. \end{aligned}$$

(3.7)

Now, the Theorem 2.1 and $P u_k =0$ yield that there exists $C>0$ such that

$$\begin{aligned} \int _{\Omega } (u^2_k + | \nabla _\mu u_k|^2) \,d\mu \le C \int _{\Omega } | \nabla _\mu u_k|^2 \,d\mu . \end{aligned}$$

Combining this with (3.7) and Young’s inequality yields,

$$\begin{aligned} (1-\epsilon \frac{C}{2\lambda }) \Vert u_k \Vert ^2_{H^{1,2}_\mu }\le \frac{C}{\lambda 2\epsilon } \Vert f \Vert ^2_{L^2(\Omega , \mu )} +R+1. \end{aligned}$$

In other words the minimizing sequence is bounded in $H^{1,2}_\mu$. Due to the results of [1] we deduce that there is a weakly convergent subsequence (not relabeled), with limit u. Now, we invoke the lower semicontinuity results so that we deduce,

$$\begin{aligned} \varliminf _{k\rightarrow \infty } E_\mu (u_k) \ge \frac{1}{2} \int _\Omega (A_\mu (x)\nabla _\mu u, \nabla _\mu u)\,d \mu - \int _\Omega fu\, d\mu . \end{aligned}$$

Uniqueness of minimizers will be treated separately. $\square$

The claim made in Theorem 3.1 is valid also for $\mu$ as in Corollary 2.1.

Corollary 3.2

Let us assume that the hypotheses of Theorem 3.1 hold except that $\mu = \theta {{\bar{\mu }}}$, where ${{\bar{\mu }}}$ satisfies [S] and (2.9) is valid. Then, the same claim holds.

Proof

We use the notation of Corollary 2.1. Since we may use Corollary 3.1 in place of Proposition 3.1 and $\nabla _\mu = \nabla _{{{\bar{\mu }}}}$, then it remains to check that

$$\begin{aligned} \int _\Omega Q u \,d \mu = \int _\Omega {{\bar{Q}}} u \,d {{\bar{\mu }}}, \end{aligned}$$

but this identity follows from the definition of ${{\bar{Q}}}$ and $\mu$. As a result we may apply Theorem 3.1 to ${{\bar{A}}}$, $\bar{Q}$ and ${{\bar{\mu }}}$. $\square$

Establishing the Euler–Lagrange equations requires further assumptions on $A_\mu$ and $\mu$.

Proposition 3.3

Let us suppose that u is a minimizer of $E_\mu$ on $H^{1,2}_\mu$, then the following weak form of Euler–Lagrange equation holds,

$$\begin{aligned} \int _\Omega (A_\mu \nabla _\mu u, \nabla _\mu \varphi )\,d\mu -\int _\Omega f \varphi \, d\mu =0\qquad \hbox {for all } \varphi \in C^1_0({\mathbb {R}}^N). \end{aligned}$$

(3.8)

Proof

Since u is a minimizer, then for any test function $\varphi \in H^{1,2}_\mu$, (in particular we may take $\varphi \in C^1_0({\mathbb {R}}^N)$), we have

$$\begin{aligned} E_\mu (u) \le E_\mu (u + \varphi ). \end{aligned}$$

Thus,

$$\begin{aligned} 0 \le \int _\Omega (A_\mu \nabla _\mu u, \nabla _\mu \varphi )\,d\mu + \frac{1}{2} \int _\Omega (A_\mu \nabla _\mu \varphi , \nabla _\mu \varphi )\,d\mu - \int _\Omega f \varphi \, d\mu . \end{aligned}$$

After replacing $\varphi$ with $t \varphi$, where t is real, we will deduce that (3.8) holds. $\square$

Corollary 3.3

Let us suppose that the assumptions of the previous theorem hold. If $u_1$ and $u_2$ are two minimizers of $E_\mu$, which are perpendicular to ker$\nabla _\mu$, then $u_1 = u_2$.

Proof

Let us take $u = u_2 - u_1$ and take the difference of (3.8) corresponding to $u_1$ and $u_2$,

$$\begin{aligned} \int _\Omega (A_\mu \nabla _\mu u, \nabla _\mu \varphi )\,d\mu =0. \end{aligned}$$

Since $u = u_2 - u_1$ can be approximated in the $H^{1,2}_\mu$-norm by a sequence of $C^1$ functions, we may take $\varphi = u$ in the identity above,

$$\begin{aligned} 0 = \int _\Omega (A_\mu \nabla _\mu u, \nabla _\mu u)\,d\mu \ge \lambda \Vert \nabla _\mu u\Vert ^2_{L^2_\mu }, \end{aligned}$$

i.e. $u \in {\hbox {ker}}\,\nabla _mu$. Since we assumed that $u \in (\hbox {ker}\,\nabla _\mu )^\perp$, we deduce that $u = 0$, i.e. $u_2 = u_1$. $\square$

We do not specify any boundary conditions so we expect that the solution satisfies the so-called natural boundary condition, however, in a weak form suitable for $H^{1,2}_\mu$.

Remark 3.2

The arguments used in the proofs of Proposition 3.3 and Corollary 3.3 are valid if $\mu$ is as in Corollary 3.1.

Remark 3.3

Let us remark that in the case S is a smooth compact manifold of codimension 1, , and A is the identity matrix, the equation (1.3) takes the familiar form of

$$\begin{aligned} \Delta u +f=0 \quad \text {on }S, \end{aligned}$$

where $\Delta$ is the Laplace–Beltrami operator on S.

4 On the boundary condition

After [6], we introduce the notion of a vector valued measure with bounded divergence.

Definition 4.1

(see [6, Definition 1.1]) Let us suppose that F is a vector-valued Radon measure. We set

$$\begin{aligned} |{\hbox {div}}\,F|(\Omega ) :=\sup \{ \langle F,\nabla \psi \rangle :\ \psi \in C^1_c(\Omega ), |\psi (x)|\le 1\}. \end{aligned}$$

If $|{\hbox {div}}\,F|(\Omega )$ is finite, we say that the divergence of F has a finite total variation.

The advantage of measures whose divergence has a finite total variation is that one can define the trace of their normal component of $\partial \Omega$. We recall, see [6, Theorem 2.2],

Proposition 4.1

We assume that the boundary of $\Omega$ is smooth. If both F and its divergence have a bounded total variation, there exists a continuous linear functional $[F,\nu ]|_{\partial \Omega }$ over $C^2(\partial \Omega )$ such that

$$\begin{aligned} \langle [F,\nu ]|_{\partial \Omega }, \varphi \rangle = \langle {\hbox {div}}\,F, \varphi \rangle + \langle F, \nabla \varphi \rangle \quad \text {for any }\varphi \in C^2({\overline{\Omega }}). \end{aligned}$$

Actually, the original statement of the Proposition is more general, in particular less smoothness of the boundary of $\Omega$ is sufficient. Namely, it suffices if $\partial \Omega$ is Lipschitz deformable, see [6, Definition 2.1]. In addition, $[F,\nu ]|_{\partial \Omega }$ could be defined as a functional on the space ${\hbox {Lip}}\,(\gamma ,\Omega )$, $\gamma >1$, which is larger than $C^2(\partial \Omega )$, see [6]. However, such generality is not necessary here, so we choose the simplicity of exposition.

We want to show that if u is a minimizer of E, then $F:= A_\mu \nabla _\mu u$ has divergence with a finite total variation.

Theorem 4.1

Let us suppose that the structural assumption [S] as well as the condition (3.1) hold. If u is the minimizer of $E_\mu$, then $F:= A_\mu \nabla _\mu u\in {\mathcal {M}}(\Omega , {\mathbb {R}}^N)$ has divergence with finite total variation. As a result, $[A_\mu \nabla _\mu u, \nu ]|_{\partial \Omega } =0$ in the sense of Proposition 4.1.

Proof

We have to reconcile Definition 4.1 with the Euler–Lagrange Eq. (3.8): in (3.8) the inner product of $A_\mu \nabla _\mu u$ with $\nabla _\mu u$ is taken, while in Definition 4.1 $A_\mu \nabla _\mu u$ is multiplied with the full gradient of the test function. The relaxation result, Proposition 3.1, makes this difference apparent. In fact, no matter what the matrix A(x) is, Proposition 3.1 implies that

$$\begin{aligned} A_\mu : T_\mu \rightarrow T_\mu . \end{aligned}$$

(4.1)

Observation (4.1) makes (3.8) coincide with

$$\begin{aligned} \langle F, \nabla \psi \rangle = \langle Q, \psi \rangle \quad \forall \psi \in C^1_c(\Omega ). \end{aligned}$$

Indeed, if $\Pi _\mu (x)$ is the projection onto $T_\mu (x)$ at each $x\in \Omega$, then for $\psi \in C^1_c(\Omega )$ we have $\nabla \psi (x)= \Pi _\mu (x)\nabla \psi (x) + (Id-\Pi _\mu (x) )\nabla \psi (x)$. As a result we notice,

$$\begin{aligned} \langle F, \nabla \psi \rangle= & {} \int _\Omega ( A_\mu \nabla _\mu u, \nabla _\mu \psi + (Id- \Pi _\mu ) \nabla \psi )\,d\mu \\= & {} \int _\Omega (A_\mu \nabla _\mu u, \nabla _\mu \psi ) \, d\mu + 0 \\= & {} \langle Q, \psi \rangle , \end{aligned}$$

where we used (4.1). Now, we can see that $|{\hbox {div}}\,F|(\Omega )$ is finite, because

$$\begin{aligned} \sup \left\{ \langle Q,\psi \rangle :\ \psi \in C^1_c(\Omega ), |\psi (x)|\le 1\right\} = \int _\Omega |f|\,d\mu <\infty . \end{aligned}$$

Thus, we immediately deduce that $[A_\mu \nabla _\mu u,\nu ]|_{\partial \Omega }$ exists in the sense explained in Proposition 4.1. Now, we have to show that it vanishes., i.e.

$$\begin{aligned} \langle {\hbox {div}}\,A_\mu \nabla _\mu u, \varphi \rangle + \langle A_\mu \nabla _\mu u, \nabla \varphi \rangle = 0 \quad \text {for any }\varphi \in C^2({\overline{\Omega }}). \end{aligned}$$

Let us suppose that $\eta _k\in C^\infty _c(\Omega )$ are the cut-off functions such that $\eta _k(x)=0$ for $x\in \Omega$ at a distance smaller than $1/(k+1)$ from $\partial \Omega$ and equal to 1 for x further than 1/k from $\partial \Omega$. Then, since $\eta _k \varphi \in C^1_c (\Omega )$ and by using of the Euler–Lagrange Eq. (3.8) with $(1-\eta _k)\varphi$ as a test function, we obtain

$$\begin{aligned} \langle&{\hbox {div}}\,A_\mu \nabla _\mu u, \varphi \rangle + \langle A_\mu \nabla _\mu u, \nabla \varphi \rangle \\&= \langle {\hbox {div}}\,A_\mu \nabla _\mu u, \eta _k \varphi \rangle +\langle {\hbox {div}}\,A_\mu \nabla _\mu u, (1-\eta _k) \varphi \rangle \\&\quad + \langle A_\mu \nabla _\mu u, \nabla (\eta _k \varphi ) \rangle + \langle A_\mu \nabla _\mu u, \nabla ( (1-\eta _k) \varphi ) \rangle \\&= \langle {\hbox {div}}\,A_\mu \nabla _\mu u, (1-\eta _k) \varphi \rangle + \langle A_\mu \nabla _\mu u, \nabla ( (1-\eta _k) \varphi ) \rangle \\&= \langle {\hbox {div}}\,A_\mu \nabla _\mu u, (1-\eta _k) \varphi \rangle + \int _\Omega f (1-\eta _k) \varphi \, d\mu . \end{aligned}$$

If $\omega$ is a measure with a finite variation, then

$$\begin{aligned} \lim _{k\rightarrow \infty }\int _\Omega (1-\eta _k)\varphi \,d\omega =0, \end{aligned}$$

because of the Lebesgue dominated convergence Theorem. If we apply this remark to $\omega = Q$ and $\omega ={\hbox {div}}\,A_\mu \nabla _\mu u$, then we deduce that

$$\begin{aligned} \langle [ A_\mu \nabla _\mu u, \nu ]_{\partial \Omega },\varphi \rangle =0 \end{aligned}$$

for all $\varphi \in C^2({{\bar{\Omega }}})$. Our claim follows. $\square$

Remark 4.1

Theorem 4.1 tells us about the meaning of $[A_\mu \nabla _\mu u, \nu ]$ only at the boundary of $\Omega$. So, if a part of $\partial S$ does not touch $\partial \Omega$, then we have no information about the boundary behavior of u. This is why we impose the third condition of [S]. On the other hand, the fourth requirement in [S] rules out spurious conditions.

The corollaries discussed in the next section prompt a more general observation on the role of $\Omega$. We notice the lack of dependence of the boundary conditions on $\Omega$, as long as $\partial \Omega$ is smooth in a neighborhood of $\partial \Omega \cap \partial S$. The set $\Omega$ does not enter the problem of minimization of functional $E_\mu$. Moreover, by Corollary 3.3, the solution to the minimization problem is unique. As a result, if $\Omega _i$, $i=1,2$, satisfy [S] and $u_i$, $i=1,2$, are the corresponding minimizers of $E_\mu$, then $u_1= u_2$. However, the boundary conditions

$$\begin{aligned}{}[A_\mu \nabla _\mu u, \nu _1]|_{\partial \Omega _1} = 0 = [A_\mu \nabla _\mu u, \nu _2]|_{\partial \Omega _2} \end{aligned}$$

are a bit different, because $\nu _1$ need not be equal $\nu _2$. We may vary $\Omega$ as long as conditions [S] are satisfied. In particular, at any $x\in S\cap \partial \Omega$ the normal $\nu$ may be any vector perpendicular to $T_{\partial S}(x)$. Hence, we obtain:

Corollary 4.1

If u is a minimizer of $E_\mu$, then $[ A_\mu \nabla _\mu u, \nu ]_{\partial \Omega }=0$ for all $\nu \perp T_{\partial S}$.

Proof

This is so, because for any smooth mapping $S\ni x \mapsto \nu (x)$, where $\nu (x) \perp T_{\partial S}$ we can find such $\Omega$ satisying [S] that $\nu (x) \perp \partial \Omega$ at x. Hence, $[ A_\mu \nabla _\mu u, \nu ]_{\partial \Omega }=0$ holds in the sense of the Chen-Frid, [6]. $\square$

In Sect. 3 we established results corresponding to $\mu$ given by (2.9) with the density $\theta$ satisfying (2.10). We did it by absorbing the density into ${{\bar{A}}}$, ${{\bar{Q}}}$. It can be easily checked that the same techique works here, in this section.

5 Examples of the Neumann boundary problems

We present below several examples of Neumann boundary problems on various sets S. The first two examples deal with situations when the Poincaré inequality (2.1) holds (see Sect. 2.2). We further present an example (see Proposition 5.3) showing that discontinuous solutions actually occur, even for regular data, when the set S supports only the weaker inequality (2.5).

Let us suppose that $\Omega$ is a ball centered at 0 with radius 1, T is an inscribed isosceles triangle and $S_1$, $S_2$, $S_3$ is the set of radii connecting the center of $\Omega$ with the vertices of T (see Fig. 3). We set $S = S_1\cup S_2\cup S_3$. Moreover, . We set $Q = \sum _{i=1}^3 a_i\chi _{S_i}$.

We can state the following fact.

Proposition 5.1

Let us assume that S, $\mu$ and Q are defined above and $a_1 +a_2+ a_3 =0$. If $A = Id$, then the relaxed form of Eq. (1.3) takes the form,

$$\begin{aligned} \frac{d^2 u}{ds^2} = -a_i\qquad \hbox {in the interior of } S_i, \qquad i=1,2,3 \end{aligned}$$

(5.1)

and

$$\begin{aligned} \frac{d u}{ds} = 0\qquad \hbox {on } S_i\cap \partial \Omega , \qquad i=1,2,3. \end{aligned}$$

(5.2)

Here, s is the arc-length parameter counted from the center of $\Omega$.

Finally, the solution of (5.1–5.2) with $\int _S u\,d {\mathcal {H}}^1 =0$ has the following form,

$$\begin{aligned} u = -\sum _{i=1}^3 a_i(\frac{s^2}{2}-s)\chi _{S_i}. \end{aligned}$$

Proof

By Proposition 2.1 $T_\mu (x) = T_{S_i}(x)$, except for x being the center of the ball. Hence, Proposition 3.1 yields ${\hbox {div}}\,A_\mu \nabla _\mu u = \frac{d^2 u}{ds^2}$ in the interior of $S_i$, $i=1,2,3$. Also the form of boundary data (5.2) follows.

The assumption $a_1 +a_2+ a_3 =0$ means that Q is perpendicular to the kernel of $\nabla _\mu$ so that we may apply Theorem 1.1.

The form of any solution to (5.1–5.2) follows from solving the ODE’s (5.1). While doing so, we keep in mind the requirement that the solution must be continuous at $s=0$, i.e. at the center of the ball $\Omega$. The solution is determined up to an additive constant, which can be computed due to the zero average condition, $\int _S u\, d{\mathcal {H}}^1=0$. $\square$

We can also study (1.3) on sums of manifolds of dimension $k\ge 1$. We describe the set S depicted on Fig. 4.

Proposition 5.2

We assume that $A = Id$, $\Omega$ is the unit ball $B(0,1)\subset {\mathbb {R}}^3$ and $S = D_1\cup D_2$ are two great disks of B(0, 1),

$$\begin{aligned} D_1 = \{ (x_1, x_2, x_3)\in B(0,1): x_3 =0\},\qquad D_2 = \{ (x_1, x_2, x_3)\in B(0,1): x_1 =0\}. \end{aligned}$$

Moreover, $Q = Q_1\chi _{D_1} + Q_2\chi _{D_2}$, where $\int _{D_i}dQ_i =0$, $i=1,2$. Then, equation (1.5) takes the form

$$\begin{aligned} \begin{array}{ll} \frac{\partial ^2 u}{\partial x_1^2} + \frac{\partial ^2 u}{\partial x_2^2} + Q_1 = 0&{} \hbox {in } D_1,\\ \frac{\partial u}{\partial \nu _1} = 0&{} \hbox {on } \partial D_1 \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{ll} \frac{\partial ^2 u}{\partial x_2^2} + \frac{\partial ^2 u}{\partial x_3^2} + Q_2 = 0&{} \hbox {in } D_2,\\ \frac{\partial u}{\partial \nu _2} = 0&{} \hbox {on } \partial D_2, \end{array} \end{aligned}$$

where $\nu _i$ are normal to $D_i$ in the plane containing $D_i$, $i=1,2$. The condition of orthogonality to the kernel of $\nabla _\mu$ is $\int _{D_i} u\,d{\mathcal {H}}^2 =0$, $i=1,2$.

Proof

We easily see that, due to Proposition 3.1, we will have

$$\begin{aligned} A_\mu = (e_1\otimes e_1 +e_2\otimes e_2)\chi _{D_1} + (e_3\otimes e_3 +e_2\otimes e_2)\chi _{D_2}. \end{aligned}$$

Hence, the form of relaxed equations follows. The boundary conditions are addressed in Corollary 4.1. $\square$

We notice that $A_\mu$ depends upon $x\in \Omega$ despite A being constant. Moreover, the kernel of $A_\mu$ is two-dimensional.

Due to the generalized Poincaré inequality (2.5), we can study (1.3) on sums of manifolds of different dimensions. We analyze an example of an equation on the domain depicted on Figure 5. We define the design region $\Omega$ to be $B(0,\sqrt{2})\subset {\mathbb {R}}^3$. We set,

$$\begin{aligned}&S_i = \Omega \cap \{(x_1,x_2,x_3)\in {\mathbb {R}}^3:\ x_1 = (-1)^i\}, \quad i =1,2,\\&\qquad S_3 = \{(x_1,0,0)\in {\mathbb {R}}^3:\ |x_1|\le 1\}. \end{aligned}$$

In the case of this domain, we do not expect the global Poincaré inequality (2.1) to hold.

Fig. 5

Poincaré inequality (2.1) does not hold on S. Discontinuous solutions occur in Proposition 5.3

Proposition 5.3

We assume that $A = Id$ and

We assume that $Q = Q_1\chi _{S_1} + Q_2\chi _{S_2}$, i.e. $Q|_{S_3} \equiv 0$. We will require that

$$\begin{aligned} \int _{S_i} Q_i \,d\mu =0,\quad i=1,2. \end{aligned}$$

We set

$$\begin{aligned} Q_1(x_1, x_2,x_3) = q(\sqrt{x_2^2 + x_3^2})\quad \hbox {and} \quad Q_2(x_1, x_2,x_3) = -q(\sqrt{x_2^2 + x_3^2}). \end{aligned}$$

Then, u, the solution to (1.5) in S with $\int _{S_i} u \, d{\mathcal {H}}^2 =0$, $i=1,2$ and $\int _{S_3} u \, d{\mathcal {H}}^2 =0$ is discontinuous.

Proof

We notice that the relaxation of the functional (Proposition 3.1) yields,

$$\begin{aligned} A_\mu = (e_2 \otimes e_2 + e_3 \otimes e_3)\chi _{S_1\cup S_2} + (e_1 \otimes e_1) \chi _{S_3}. \end{aligned}$$

Thus, the equation div$A_\mu \nabla _\mu u + Q=0$ becomes

$$\begin{aligned} \frac{\partial ^2 u}{\partial x_2^2} + \frac{\partial ^2 u}{\partial x_2^3} + q =0 \qquad \hbox {on } S_1, \end{aligned}$$

(5.3)

$$\begin{aligned} \frac{\partial ^2 u}{\partial x_2^2} + \frac{\partial ^2 u}{\partial x_2^3} - q =0 \qquad \hbox {on } S_2 \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 u}{\partial x_1^2} =0 \qquad \hbox {on } S_3. \end{aligned}$$

The radial symmetry of q implies that

$$\begin{aligned} 0 = \int _{\{x_2^2+x_3^2\le 1\}} Q_1 \,d\mu = 2\pi \int _0^R r q(r) \,dr. \end{aligned}$$

(5.4)

The above Eq. (5.3), considered on $S_1$, due to the radial symmetry takes the following form

$$\begin{aligned} u_{rr} + \frac{1}{r} u_r + q =0. \end{aligned}$$

After multiplying by r and integration, we obtain,

$$\begin{aligned} r u_r (r) = a - \int _0^r s q(s)\,ds. \end{aligned}$$

In order to solve it, we have to pay a bit of attention to the boundary conditions. Since $\nu = 2^{-1/2}(-1, x_2,x_3)$ for $(-1, x_2,x_3)\in \partial S_1$, then the Neumann boundary condition

$$\begin{aligned}{}[A_\mu \nabla _\mu u , \nu ]|_{\partial \Omega }= 0 \end{aligned}$$

takes the form

$$\begin{aligned} (0, u_{x_2}, u_{x_3}) \cdot \nu = \nabla _\mu u \cdot \mathbf{n} =0, \end{aligned}$$

where $\mathbf{n}$ is the outer normal to $S_1$ in the plane $x_1 = -1$. We notice that due to (5.4), the above boundary conditions are automatically satisfied, provided that $a=0$. Moreover, $a=0$ is necessary for u to be an element of $H^{1,2}_\mu$. The formula for the solution is as follows,

$$\begin{aligned} u(r) = b - \int _0^r \frac{1}{\rho }\int _0^\rho sq(s)\,dsd\rho . \end{aligned}$$

The zero mean condition imposed on the solution on $S_1$ implies that

$$\begin{aligned} b = \frac{2}{R^2} \int _0^R r \int _0^r \frac{1}{\rho }\int _0^\rho sq(s)\,dsd\rho dr. \end{aligned}$$

We may choose q so that $b>0$. Due to the symmetry of Q, we deduce that $u(-1,x_2,x_3) = -u(1,x_2,x_3)$. Thus, in particular $u(-1,0,0) = b = - u(1,0,0)$.

Since we set $Q|_{S_3} =0$, then we study the problem of minimizing

$$\begin{aligned} \int _{-1}^1 u_{x_1}^2\,dx, \end{aligned}$$

on $S_3$, where $u \in H^{1,2}(-1,1)$ and $\int _{-1}^1 u\, dx_1 =0$. As a result $u|_{S_3} =0$.

We conclude that we constructed a discontinuous solution when the forcing term is continuous. $\square$

The last example, on the domain depicted on Fig. 6, illustrates how the relaxation procedure affects the matrix A.

Fig. 6

Poincaré inequality (2.1) does not hold on S

Proposition 5.4

We take

$$\begin{aligned} \Omega = B(0,\sqrt{2}) \subset {\mathbb {R}}^3, \qquad S_1 = \{ x\in \Omega ; x_3 = -1\}, \quad S_2 = \{ x\in \Omega ; x_1 = 1\}, \end{aligned}$$

and

$$\begin{aligned} A = e_2 \otimes e_2 + \frac{1}{2} (e_1+e_3) \otimes (e_1+e_3) . \end{aligned}$$

Then,

$$\begin{aligned} A_\mu = e_2 \otimes e_2 + \frac{1}{2} e_1 \otimes e_1 \chi _{S_1} + \frac{1}{2} e_3 \otimes e_3 \chi _{S_2} \end{aligned}$$

(5.5)

and the boundary conditions take the following form,

$$\begin{aligned} 0= & {} [A_\nu \nabla _\mu u, \nu _1]|_{\partial \Omega } = 2^{-1/2}( \frac{1}{2} x_1 u_{x_1} + x_2 u_{x_2})\qquad \hbox {on } S_1 \end{aligned}$$

(5.6)

$$\begin{aligned} 0= & {} [A_\nu \nabla _\mu u ,\nu _2]|_{\partial \Omega } = 2^{-1/2}( \frac{1}{2} x_3 u_{x_3} + x_2 u_{x_2})\qquad \hbox {on } S_2. \end{aligned}$$

(5.7)

The condition of orthogonality to the kernel of $\nabla _\mu$ is $\int _{S_i} u \, d{\mathcal {H}}^2 =0$.

Proof

Obviously, ${{\bar{S}}}_1 \cap {{\bar{S}}}_2 = \{(1,0,-1)\}.$ When we take , then we see that an application of Proposition 3.1 yields (5.5).

We shall compute $[A_\mu \nabla _\mu u,\nu ]|_{\partial \Omega }$, where $\nu$ is normal to $\Omega$. We notice that

$$\begin{aligned} \nabla _\mu u = (u_{x_1}, u_{x_2}, 0)\chi _{S_1} + (0, u_{x_2}, u_{x_3})\chi _{S_2}. \end{aligned}$$

Similarly, we see that

$$\begin{aligned} \nu _1 = 2^{-1/2}(x_1,x_2, -1),\qquad x_1^2 +x_2^2 =1 \end{aligned}$$

on $S_1$ and

$$\begin{aligned} \nu _2 = 2^{-1/2}(1,x_2, x_3),\qquad x_3^2 +x_2^2 =1 \end{aligned}$$

on $S_2$.

Thus, $[A_\mu \nabla _\mu u,\nu ]|_{\partial \Omega }$ leads to the conclusion that (5.6) and (5.7) hold. $\square$