Abstract
We consider the intersection of a convex surface \(\Gamma \) with a periodic perforation of \(\mathbb {R}^d\), which looks like a sieve, given by \(T_\varepsilon = \bigcup _{k\in \mathbb {Z}^d}\{\varepsilon k+a_\varepsilon T\}\) where T is a given compact set and \(a_\varepsilon \ll \varepsilon \) is the size of the perforation in the \(\varepsilon \)-cell \((0, \varepsilon )^d\subset \mathbb {R}^d\). When \(\varepsilon \) tends to zero we establish uniform estimates for p-capacity, \(1<p<d\), of the set \(\Gamma \cap T_\varepsilon \). Additionally, we prove that the intersections \(\Gamma \cap \{\varepsilon k+a_\varepsilon T\}_k\) are uniformly distributed over \(\Gamma \) and give estimates for the discrepancy of the distribution. As an application we show that the thin obstacle problem with the obstacle defined on the intersection of \(\Gamma \) and the perforations, in a given bounded domain, is homogenizable when \(p<1+\frac{d}{4}\). This result is new even for the classical Laplace operator.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
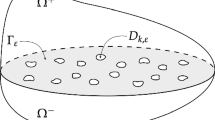
In this paper we study the properties of the intersection of a convex surface \(\Gamma \) with a periodic perforation of \(\mathbb {R}^d\) given by \(T_\varepsilon = \bigcup _{k\in \mathbb {Z}^d}\{\varepsilon k+a_\varepsilon T\}\), where T is a given compact set and \(a_\varepsilon \) is the size of the perforation in the \(\varepsilon \)-cell. Our primary interest is to obtain good control of p-capacity \(1<p<d\) and discrepancy of distributions of the components of the intersection \(\Gamma \cap T_\varepsilon \) in terms of \(\varepsilon \) when the size of perforations tends to zero. As an application of our analysis we get that the thin obstacle problem in periodically perforated domain \(\Omega \subset \mathbb {R}^d\) with given strictly convex and \(C^2\) smooth surface as the obstacle and p-Laplacian as the governing partial differential equation is homgenizable provided that \(p<1+\frac{d}{4}\). Moreover, the limit problem admits a variational formulation with one extra term involving the mean capacity, see Theorem 3. The configuration of \(\Gamma \), \(\Gamma _\varepsilon \), \(T_\varepsilon \) and \(\Omega \) is illustrated in Fig. 1.
This result is new even for the classical case \(p=2\) corresponding to the Laplace operator. Another novelty is contained in the proof of Theorem 2 where we use a version of the method of quasi-uniform continuity developed in [4].
1.1 Statement of the problem
Let
and let
We assume that \(\Gamma \) is a strictly convex surface in \(\mathbb {R}^d\) that locally admits the representation
where \(Q'\subset \mathbb {R}^{d-1}\) is a cube. For example, \(\Gamma \) may be a compact convex surface, or may be defined globally as a graph of a convex function.
Without loss of generality we assume that \(x_d = g(x')\) because the interchanging of coordinates preserves the structure of the periodic lattice in the definition of \(T_\varepsilon \). We will also study homogenization of the thin obstacle problem for the p-Laplacian with an obstacle defined on \(\Gamma _\varepsilon \). Our goal is to determine the asymptotic behaviour, as \(\varepsilon \rightarrow 0\), of the problem
for given \(h\in L^q(\Omega )\), \(1/p+1/q=1\) and \(\phi \in W^{1,p}_0(\Omega )\cap L^\infty (\Omega )\).
We make the following assumptions on \(\Omega \), T, \(\Gamma \), d and p:
-
\((A_1)\) \(\Omega \subset \mathbb {R}^d\) is a Lipschitz domain.
-
\((A_2)\) The compact set T from which the holes are constructed must be sufficiently regular in order for the mapping
$$\begin{aligned} t\mapsto {\text {cap}}(\{\Gamma +t e\}\cap T) \end{aligned}$$to be continuous, where e is any unit vector. This is satisfied if, for example, T has Lipschitz boundary.
-
\((A_3)\) The size of the holes is
$$\begin{aligned} a_\varepsilon =\varepsilon ^{d/(d-p+1)}. \end{aligned}$$This is the critical size that gives rise to an interesting effective equation for (2).
-
\((A_4)\) The exponent p in (2) is in the range
$$\begin{aligned} 1<p<\frac{d+4}{4}. \end{aligned}$$This is to ensure that the holes are large enough that we are able to effectively estimate the intersections between the surface \(\Gamma \) and the holes \(T_\varepsilon \), of size \(a_\varepsilon \). See the discussion following the estimate (15). In particular, if \(p=2\) then \(d>4\).
These are the assumptions required for using the framework from [4], though the \((A_4)\) is stricter here.
1.2 Main results
The following theorems contain the main results of the present paper.
Theorem 1
Suppose \(\Gamma \) is a \(C^2\) convex surface. Let \(I_\varepsilon \subset [0,1)\) be an interval, let \(Q'\subset \mathbb {R}^{d-1}\) be a cube and let
Then
where \(N_\varepsilon = \#\{k'\in \mathbb {Z}^{d-1}\cap \varepsilon ^{-1}Q'\}\).
Next we establish an important approximation result. We use the notation \(T_\varepsilon ^k = \varepsilon k+a_\varepsilon T\) and \(\Gamma _\varepsilon ^k=\Gamma \cap T_\varepsilon ^k\).
Theorem 2
Suppose \(\Gamma \) is a \(C^2\) convex surface and \(P_x\) a support plane of \(\Gamma \) at the point \(x\in \Gamma \). Then
-
\(\mathbf 1^\circ \) the p-capacity of \(P_x^k=P_x\cap T^k_\varepsilon \) approximates \({\text {cap}}_p(\Gamma ^k_\varepsilon )\) as follows
$$\begin{aligned} {\text {cap}}_p(\Gamma _\varepsilon ^k) = {\text {cap}}_p(P_{x}^k\cap \{a_\varepsilon T+\varepsilon k\}) + o(a_\varepsilon ^{d-p}), \end{aligned}$$(3)where \(x\in \Gamma _\varepsilon ^k\).
-
\(\mathbf 2^\circ \) Furthermore, if \(P_1\) and \(P_2\) are two planes that intersect \(\{a_\varepsilon T+\varepsilon k\}\) at a point x, with normals \(\nu _1,\nu _2\) satisfying \(|\nu _1-\nu _2|\le \delta \) for some small \(\delta >0\), then
$$\begin{aligned} |{\text {cap}}_p(P_1\cap \{a_\varepsilon T+\varepsilon k\})-{\text {cap}}_p(P_2\cap \{a_\varepsilon T+\varepsilon k\})|\le c_\delta a_\varepsilon ^{d-p}, \end{aligned}$$(4)where \(\lim _{\delta \rightarrow 0}c_\delta =0\).
As an application of Theorems 1, 2 we have
Theorem 3
Let \(u_\varepsilon \) be the solution of (2). Then \(u_\varepsilon \rightharpoonup u\) in \(W_0^{1,p}(\Omega )\) as \(\varepsilon \rightarrow 0\), where u is the solution to
In (5), \(\nu (x)\) is the normal of \(\Gamma \) at \(x\in \Gamma \) and \({\text {cap}}_{p,\nu (x)}(T)\) is the mean p-capacity of T with respect to the hyperplane \(P_{\nu (x)}=\{y\in \mathbb {R}^ d:\nu (x)\cdot y=0\}\), given by
where \({\text {cap}}_p(E)\) denotes p-capacity of E with respect to \(\mathbb {R}^ d\).
Theorem 3 was proved by the authors in [4] under the assumption that \(\Gamma \) is a hyper plane, which was in turn a generalization of the paper [5]. In a larger context, Theorem 3 contributes to the theory of homogenization in non-periodic perforated domains, in that the support of the obstacle, \(\Gamma _\varepsilon \), is not periodic. Another class of well-studied non-periodic perforated domains, not including that of the present paper, is the random stationary ergodic domains introduced in [1]. In the case of stationary ergodic domains the perforations are situated on lattice points, which is not the case for the set \(\Gamma _\varepsilon \). The perforations, i.e. the components of \(\Gamma _\varepsilon \), have desultory (though deterministic by definition) distribution. For the periodic setting [2] is a standard reference.
The proof of Theorem 3 has two fundamental ingredients. First the structure of the set \(\Gamma _\varepsilon \) is analysed using tools from the theory of uniform distribution, Theorem 1. We prove essentially that the components of \(\Gamma _\varepsilon \) are uniformly distributed over \(\Gamma \) with a good bound on the discrepancy. This is achieved by studying the distribution of the sequence
for g defined by (1) and \(\varepsilon k'\in Q'\). Second, we construct a family of well-behaved correctors based on the result of Theorem 2.
The major difficulty that arises when \(\Gamma \) is a more general surface than a hyperplane is to estimate the discrepancy of the distribution of (the components of) \(\Gamma _\varepsilon \) over \(\Gamma \), which is achieved through studying the discrepancy of \(\{\varepsilon ^{-1}g(\varepsilon k')\}_{k'}\). For a definition of discrepancy, see Sect. 2. In the framework of uniform convexity we can apply a theorem of Erdös and Koksma which gives good control of the discrepancy.
2 Discrepancy and the Erdös–Koksma theorem
In this section we formulate a general result for the uniform distribution of a sequence and derive a decay estimate for the corresponding discrepancy.
Definition 1
The discrepancy of the first N elements of a sequence \(\{s_j\}_{j=1}^\infty \) is given by
where I is an interval, |I| is the length of I and \(A_N\) is the number of \(1\le j\le N\) for which \(s_j\in I\quad (\text {mod}1)\).
We first recall the Erdös–Turán inequality, see Theorem 2.5 in [7], for the discrepancy of the sequence \(\{s_j\}_{j=1}^\infty \)
where n is a parameter to be chosen so that the right hand side has optimal decay as \(N\rightarrow \infty \). Observe that \(s_j\) is the j-th element of the sequence which in our case is \(s_j=f(j)\) for a given function f and \(N=\left[ \frac{1}{\varepsilon }\right] \).
We employ the following estimate of Erdös and Koksma ([7], Theorem 2.7) in order to estimate the second sum in (8): let \(a, b\in \mathbb N\) such that \(0<a<b\) then one has the estimate
where \(F_k(t) = kf(t)\) and \(F_k''(t)\ge \rho >0\) for some positive number \(\rho .\) In order to apply this result to our problem we first need to reduce the dimension of (7) to one. To do so let us assume that the obstacle \(\Gamma \) is given as the graph of a function \(x_d=g(x')\) where g is strictly convex \(C^2\) function such that
for some positive constants \(c_0<C_0\).
Next we rescale the \(\varepsilon \)-cells and consider the normalised problem in the unit cube \([0, 1]^d\). The resulting function is \(f(j)=\frac{g(\varepsilon j)}{\varepsilon }, j\in \mathbb {Z}^{d-1}\).
If \(d=2\) then we can directly apply (9) to the scaled function f above. Otherwise for \(d>2\) we need an estimate for the multidimensional discrepancy in terms of \(D_N\) introduced in Definition 1, a similar idea was used in [4] for the linear obstacle. Suppose for a moment that this is indeed the case. Then we can take \(F_k(t)=kf(t)\) in (9) and noting
one can proceed as follows
for some tame constant \(\lambda >0\) independent of \(\varepsilon , k\). Plugging this into (8) yields
for another tame constant \(\overline{\lambda }>0\). Now to get the optimal decay rate we choose \(\frac{1}{n} =\sqrt{\frac{n}{N}}\) which yields \(N=n^3\) and hence
and we arrive at the estimate
2.1 Proof of Theorem 1
Proof
Suppose \(Q' \) is a cube of size r. Then there is a cube \(Q''\subset \mathbb {R}^{d-2}\) such that \(Q' = [\alpha ,\beta ]\times Q'\), \(\beta -\alpha =r\). We may rewrite \(A_\varepsilon \) as
where \((k_1,k'')=k'\), a, b are the integer parts of \(\varepsilon ^{-1}\alpha \) and \(\varepsilon ^{-1}\beta \) respectively and \(|(b-a)- \varepsilon ^{-1}r|\le 1\). We also note that \(N_\varepsilon = (\varepsilon ^{-1}r)^{d-1}+O(\varepsilon ^{-1}r)^{d-2}\). Consider
Then we have
For each \(k''\) the function \(h:s\rightarrow \varepsilon ^{-1}g(\varepsilon s+\varepsilon k'')\) satisfies \(|h'(s)|\le C_1\) and \(h''(s)\ge \rho \varepsilon \) for \(a\le s\le b\). Thus we may apply the Erdös-Koksma Theorem as described above and conclude that
It follows that the modulus of the left hand side of (13) is bounded by \(C\varepsilon ^{\frac{1}{3}}\), proving the theorem. \(\square \)
3 Correctors
The purpose of this section is to construct a sequence of correctors that satisfy the hypotheses given below. Once we have established the existence of these correctors, the proof of the Theorem 3 is identical to the planar case treated in [4].
-
\(\mathbf H1\) \(0\le w_\varepsilon \le 1\) in \(\mathbb {R}^d\), \(w_\varepsilon =1\) on \(\Gamma _\varepsilon \) and \(w_\varepsilon \rightharpoonup 0\) in \(W^{1,p}_{{\text {loc}}}(\mathbb {R}^d)\),
-
\(\mathbf H2\) \(\int _\Omega |\nabla w_\varepsilon |^pfdx\rightarrow \int \limits _{\Gamma } f(x){\text {cap}}_{p,\nu _x}d\mathcal H^{d-1}\), for any \(f\in W_0^{1,p}(\Omega )\cap L^\infty (\Omega )\),
-
\(\mathbf H3\) (weak continuity) for any \(\phi _\varepsilon \in W_0^{1,p}(\Omega )\cap L^\infty (\Omega )\) such that
$$\begin{aligned} \left\{ \begin{array}{l} \sup \limits _{\varepsilon >0}\Vert \phi _\varepsilon \Vert _{L^\infty (\Omega )}<\infty ,\\ \phi _\varepsilon =0 \text { on } \Gamma _\varepsilon \text { and } \phi _\varepsilon \rightharpoonup \phi \in W_0^{1,p}(\Omega ), \end{array}\right. \end{aligned}$$we have
$$\begin{aligned} \langle -\Delta _p w_\varepsilon , \phi _\varepsilon \rangle \rightarrow \langle \mu , \phi \rangle \end{aligned}$$with
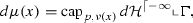 (14)
(14)where \( {\text {cap}}_{p,\nu (x)}\) is given by (6) and
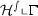 is the restriction of \(s-\)dimensional Hausdorff measure on \(\Gamma \).
is the restriction of \(s-\)dimensional Hausdorff measure on \(\Gamma \).
Setting \(\Gamma _\varepsilon ^k:=\Gamma \cap \{a_\varepsilon T+\varepsilon k\}\ne \emptyset \), we define \(w_\varepsilon ^k\) by
Then it follows from the definition of \({\text {cap}}_p\) [3] that
Indeed, we have
Note that \({\text {cap}}_p(\Gamma _\varepsilon ^k)=O(a_\varepsilon ^{d-p})\) since \(\Gamma _\varepsilon ^k=\Gamma \cap \{\varepsilon k+ a_\varepsilon T\}\) and \({\text {cap}}_p(t E)=t^{d-p}{\text {cap}}_p(E)\) if \(t\in \mathbb {R}_+\) and \(E\subset \mathbb {R}^d\). If \(Q'\) is a cube in \(\mathbb {R}^{d-1}\), the components of \(\Gamma _\varepsilon \cap Q'\times \mathbb {R}\) are of the form \(\Gamma _\varepsilon ^k=\Gamma \cap \{(\varepsilon k',\varepsilon k_d)+a_\varepsilon T\}\) for \(\varepsilon k'\in Q'\). In particular, \(\Gamma _\varepsilon ^ k\ne \emptyset \) if and only if \(\varepsilon ^{-1} g(\varepsilon k')\in I_\varepsilon \quad (\text {mod}1)\) where \(|I_\varepsilon |=O(a_\varepsilon /\varepsilon )\). Thus Theorem 1 tells us that the number of components of \(\Gamma _\varepsilon \cap Q'\times \mathbb {R}\) equals \(A_\varepsilon = |I_\varepsilon |N_\varepsilon +N_\varepsilon O(\varepsilon ^{\frac{1}{3}})\), or explicitly
Here we need to have \(\varepsilon ^{1/3}=o(|I_\varepsilon |)\), which is equivalent to \((A_4)\). Since
we get
Thus \(\int _K|\nabla w_\varepsilon |^p\) is uniformly bounded on compact sets K. Since \(w_\varepsilon (x)\rightarrow 0\) pointwise for \(x\not \in \Gamma \), \(\mathbf H1\) follows.
When verifying \(\mathbf H_2\) and \(\mathbf H_3\) we will only prove that
Once this has been established the rest of the proof is identical to that given in [4].
4 Proof of Theorem 2
Proof
\(\mathbf 1^\circ \) Set \(R_\varepsilon =\frac{\varepsilon }{2a_\varepsilon }\rightarrow \infty \), then after scaling we have to prove that
uniformly in \(\varepsilon \) where
and \(S_1=\frac{1}{a_\varepsilon }\Gamma ^k_\varepsilon , S_2=\frac{1}{a_\varepsilon }P_{x}\).
We approximate \(v_i\) in the domain \(B_{R_\varepsilon }{\setminus } D^t_i\) with \(D^t_i\) being a bounded domain with smooth boundary and \(D^t_i\rightarrow S_i \) as \(t\rightarrow 0\) in Hausdorff distance. Consider
Observe that \(\int _{B_{R_\varepsilon }{\setminus } D_i^t}|\nabla v_i^t|^{p}, i=1, 2\) remain bounded as \(t\rightarrow 0\) thanks to Caccioppoli’s inequality. Indeed, \(w=(1-v_i^t)\eta \in W^{1, p}_0(B_5{\setminus } D_i^t)\) where \(\eta \in C_0^\infty (B_5)\) such that \(0\le \eta \le 1\) and \(\eta \equiv 1\) in \(B_3\). Using w as a test function we conclude that
Since \(\eta \equiv 1\) in \(B_3\) then applying Hölder inequality we infer that \(\int _{B_3{\setminus } D_i^t}|\nabla v_i^t|^p\le C\int _{B_5}(1-v_i^t)^p\). In \(B_{R_\varepsilon }{\setminus } B_2\) the \(L^p\) we compare \(W(x)=|x/2|^{\frac{p-d}{p-1}}\) with \(v_i\). Note that our assumption \(A_4\) implies that \(p<d\). Moreover, since W is p-harmonic in \(B_{R_\varepsilon }{\setminus } B_2\) then the comparison principle yields \(v_i\le W\) in \(B_{R_\varepsilon }{\setminus } B_2\). From the proof of Caccioppoli’s inequality above choosing non-negative \(\eta \in C^\infty (\mathbb {R}^d)\) such that \(\eta \equiv 0\) in \(B_2\), \(\frac{1}{2}\le \eta \le 1\) in \(B_{R_\varepsilon }{\setminus } B_3\), and \(\eta =1\) in \(\mathbb {R}^d{\setminus } B_{R_\varepsilon }\) and using \(\eta v_i\in W_0^{1, p}(B_{R_\varepsilon }{\setminus } B_2)\) as a test function we infer
where the last bound follows from the estimate \(v_i\le W\). Combining these estimates we infer
for some tame constant K independent of t and \(\varepsilon \). Thus, by construction \(v^t_i\rightharpoonup v_i\) weakly in \(W^{1, p}_0(B_{R_\varepsilon })\).
Let \(\psi \in C^\infty (\mathbb {R}^d)\) such that \({\text {supp}}\psi \supset D_1^t\cup D_2^t\) and \(\psi \equiv 1\) in \(\mathbb {R}^d{\setminus } B_2\). Then the function \(\psi (v_1^t-v_2^t)\in W^{1,p}_0(B_{R_\varepsilon })\) and it vanishes on \({\text {supp}}\psi \supset D_1^t\cup D_2^t\). Thus we have
Note that \(v_1^t-v_2^t=0\) on \(D^t_1\cap D_2^t\). Choosing a sequence \(\psi _n\) such that \(1-\psi _m\) converges to the characteristic function \(\chi _{D_1^t\cup D_2^t}\) of the set \(D_1^t\cup D_2^t\) we conclude
where
Notice that on \(\partial D^t_i\) we have that \(\nu =-\frac{\nabla \psi _m}{|\nabla \psi _m|}\) is the unit normal pointing inside \(D^t_i\). We denote \(n=-\nu \) and then we have that
and similarly
Setting
and returning to (19) we infer
But on \(\partial D_i^t\) we have \(\partial _\nu v_i^t\ge 0\) (\(\nu \) points inside \(D_i^t\)) because \(v_i^t\) attains its maximum on \(\partial D_i^t\). Thus we can omit the absolute values of the normal derivatives and obtain
Recall that by Lemma 5.7 [6] there is a generic constant \(M>0\) such that
for all \(\xi , \eta \in \mathbb {R}^d\).
First suppose that \(p>2\) then applying inequality (21) to (20) yields
As for the case \(1<p\le 2\) then from (21) we have
But, from Hölder’s inequality and (18) we get
Therefore, there is a tame constant \(M_0\) such that for any \(p>1\) we have
Letting \(t\rightarrow 0\) we get
with some tame constant \(M_1\).
Since \(1-v_i^t\) are nonnegative p-subsolutions in \(B_{R_\varepsilon }\), from the weak maximum principle, Theorem 3.9 [6] we obtain

Take a finite covering of \(D^t_i\) with balls \(B_r(z_k^i), z_k^i\in S_i, r=3a_\varepsilon , k=1, \dots , N\). Choose t small enough such that \(D^t_j\subset \bigcup _{k=1}^N B_r(z_k^i)\) and applying (24) we obtain for \( i,j\in \{1, 2\}\) with \(i\not =j\)

Since \(\Vert v_i^t\Vert _{W^{1,p}(B_3)}\le C\) uniformly for all \(t>0\) it follows that \(v_i^t\rightarrow v_1\) strongly in \(L^p(B_3)\) and \(v_i\) is quasi-continuous. In other words, for any positive number \(\theta \) there is a set \(E_{\theta }\) such that \({\text {cap}}_p E_\theta <\theta \) and \(v_i\) is continuous in \(B_2{\setminus } E_\theta \). Notice that \(E_\theta \subset S_1\cup S_2\) and hence \(\mathcal H^d(E_\theta )=0\).
This yields

where \(\omega _i(\cdot )\) is the modulus of continuity of \(v_i\) on \(B_{3}\) modulo the set \(E_\theta \). Thus
Hence (17) is established. Rescaling back and noting that \(a_\varepsilon ^{d-p}\omega _i(a_\varepsilon )=o(a_\varepsilon ^{d-p})\) the result follows. Observe that \(L^p\) norm of \(\nabla v_i^t\) remains uniformly bounded in \(B_{R_\varepsilon }\) by (18) and hence the moduli of quasi-continuity in, say, \(B_3\) do not depend on the particular choice of \(\Gamma _\varepsilon ^k\) or the tangent plane \(P_{x}^k\).
\(\mathbf{2^\circ }\) We recast the argument above but now for \(S_1=\frac{1}{a_\varepsilon }P_1, S_2=\frac{1}{a_\varepsilon }P_{2}\). Squaring the inequality \(|\nu _1-\nu _2|\le \delta \) we get that \(2\sin \frac{\beta }{2}\le \delta \) where \(\beta \) is the angle between \(P_1\) and \(P_2\). Since \(\delta \) now measures the deviation of \(v_1^t\) from 1 on \(D_2^t\), (resp. \(v_2^t\) on \(D_1^t\)) we conclude that the corresponding moduli of continuity of the limits \(v_1, v_2\) (as \(t\rightarrow 0\)) modulo a set \(E_\theta \subset S_1\cup S_2\) with small \(p-\)capacity depend on \(\delta \), i.e.

where \(B_r(z_k^i)\) provide a covering of \(D_i^t\) as above but now, say, \(r=6\delta \). Hence we can take \(c_\delta =C(\omega _1(12\delta )+\omega _2(12\delta )).\) \(\square \)
5 Proof of Theorem 3
We now formulate our result on the local approximation of total capacity (say in \(Q'\)) by tangent planes of \(\Gamma \) and prove (16).
Lemma 1
Fix a cube \(Q'\subset \mathbb {R}^{d-1}\) such that if \(x=(x',x_d)\) and \(y=(y',y_d)\) belong to \(\Gamma \) and \(x',y'\in Q'\), then the normals \(\nu _x,\nu _y\) of \(\Gamma \) at x and y satisfy \(|\nu _x-\nu _y|\le \delta \). Then for any \(x=(x',x_d)\in \Gamma \) with \(x'\in Q'\), there holds
where \(\lim _{\delta \rightarrow 0}C_\delta =0\) and \(\Gamma _{Q'}=\{x\in \Gamma :x'\in Q'\}\).
Proof
Fix \(x\in \Gamma _{Q'}\) and let P be the plane \(\{y:y\cdot \nu _x=0\}\), where \(\nu _x\) is the normal of \(\Gamma \) at x. Suppose \(k=(k',k_d)\in \mathbb {Z}^d\), \(\varepsilon k'\in Q'\) and let \(P_{x^k}\) be the tangent plane to \(\Gamma \) at \(x^k=(\varepsilon k',g(\varepsilon k'))\). Then Theorem 2 \(\mathbf 1^\circ \) tells us that
If we set \(P^k_\varepsilon = P+(-\varepsilon k',g(\varepsilon k'))\), then \(P^k_\varepsilon \) will intersect the point \((\varepsilon k',g(\varepsilon k'))\). By assumption, \(|\nu _x-\nu _{x^k}|\le \delta \), so
by Theorem 2 \(\mathbf 2^\circ \). This gives \({\text {cap}}_p(\Gamma _\varepsilon ^k)={\text {cap}}_p(P^k_\varepsilon \cap T_\varepsilon ^k)+O(c_\delta a_\varepsilon ^{d-p})\). Since, by Theorem 1, the sequence \(\{\varepsilon ^{-1}g(\varepsilon k')\}_{k'\in \varepsilon ^{-1}Q'}\) is uniformly distributed mod 1 with discrepancy of order \(\varepsilon ^{1/3}\), the rescaled planes \(\varepsilon ^{-1}P^k_\varepsilon \) have the same distribution mod 1, i.e. they are translates of P and the translates have the same distribution. Using the proof of Lemma 4 of [4], we conclude that
where \(P_{Q'}= \{x\in P:x'\in Q'\}\). Since we know that \(\int _{B_\varepsilon ^k}|\nabla w_\varepsilon ^k|^pdx= {\text {cap}}_p(\Gamma _\varepsilon ^k)+o(a_\varepsilon ^{d-p})\), the result follows from the fact that \(\mathcal {H}^{d-1}(\Gamma _{Q'})=(1+O(c_\delta ))\mathcal {H}^{d-1}(P_{Q'})\). \(\square \)
Lemma 2
Proof
The claim follows by decomposing the set \(\{x'\in \mathbb {R}^{d-1}:(x',g(x'))\in \Gamma \cap Q\}\) into disjoint cubes \(\{Q_j'\}\) that satisfy the hypothesis of Lemma 1. Since \(\Gamma \) is \(C^2\), we can find a finite number of disjoint cubes \(\{Q_j\}_{j=1}^{N(\delta )}\), such that \(\mathcal {H}^{d-1}(\Gamma \cap Q{\setminus } \cup _j Q_j\cap \Gamma )=0\) and \(Q_j'\) is as in Lemma 1. For all \(x\in \Gamma \cap Q_j\) we have \(x=(x',g(x))\) for \(x'\in Q_j'\), after interchanging coordinate axes if necessary. Thus
where in the last step we used that \({\text {cap}}_{p,\nu (x)}(T)={\text {cap}}_{p,\nu _{x^j}}(T)+O(C_\delta )\) for all \(x\in \Gamma _{Q_j'}\), by Lemma 1. Sending \(\delta \rightarrow 0\) proves the lemma. \(\square \)
Having established Lemma 2, the rest of the proof of \(\mathbf {H_2}\) and \(\mathbf {H_3}\) is carried out precisely as in [4], with Lemma 2 above replacing Lemma 4 in [4]. The proof of Theorem 3 from H \(_\mathbf 1 \)–H \(_\mathbf 3 \) is given in section 4 of [4] when \(\Gamma \) is a hyper plane, and remains the same for the present case when \(\Gamma \) is a convex surface.
References
Caffarelli, L.A., Mellet, A.: Random homogenization of an obstacle problem. Annales de l’Institut Henri Poincaré. Analyse Non Linéaire 26, 375–395 (2009)
Cioranescu, D., Murat, F.: A strange term coming from nowhere. In: Topics in the Mathematical Modelling of Composite Materials. Progr. Nonlinear Differential Equations Appl., no. 31, 45–93 (1997)
Frehse, J.: Capacity methods in the theory of partial differential equations. Jahresbericht der Deutschen Math.-Ver. 84, 1–44 (1982)
Karakhanyan, A., Strömqvist, M.: Application of uniform distribution to homogenization of a thin obstacle problem with p-Laplacian. Commun. Partial Differ. Equ. 39(10), 1870–1897 (2014)
Lee, K., Strömqvist, M., Yoo, M.: Highly oscillating thin obstacles. Adv. Math. 237(1), 286–315 (2013)
Maly, J., Ziemer, W.P.: Fine Regularity of Solutions of Elliptic Partial Differential Equations. Mathematical Surveys and Monographs. AMS, Providence, RI (1997)
Kuipers, L., Niederreiter, H.: Uniform Distribution of Sequences. Dover Publications, Mineola, NY (2002)
Acknowledgments
Part of the work was carried out at the Mittag-Leffler Institute during the programme in homogenisation and randomness, Winter 2014. The research of the first author was partially supported by EPSRC Grant EP/K024566/1.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by F. H. Lin.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Karakhanyan, A.L., Strömqvist, M. Estimates for capacity and discrepancy of convex surfaces in sieve-like domains with an application to homogenization. Calc. Var. 55, 138 (2016). https://doi.org/10.1007/s00526-016-1088-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-016-1088-2



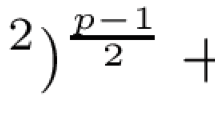

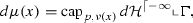
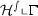 is the restriction of
is the restriction of