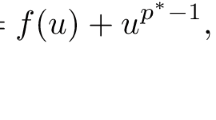Abstract
Let Ω be a bounded, smooth domain in \({\mathbb{R}^2}\). We consider the functional
in the supercritical Trudinger-Moser regime, i.e. for \({\int_\Omega |\nabla u|^2dx > 4\pi}\). More precisely, we are looking for critical points of I(u) in the class of functions \({u \in H_0^1 (\Omega )}\) such that \({\int_\Omega |\nabla u|^2 \, dx = 4\, \pi \, k\, (1+\alpha)}\), for small α > 0. In particular, we prove the existence of 1-peak critical points of I(u) with \({\int_\Omega |\nabla u|^2dx = 4\pi(1 + \alpha)}\) for any bounded domain Ω, 2-peak critical points with \({\int_\Omega |\nabla u|^2dx = 8\pi(1 + \alpha)}\) for non-simply connected domains Ω, and k-peak critical points with \({\int_\Omega |\nabla u|^2 dx = 4k \pi(1 + \alpha)}\) if Ω is an annulus.
Similar content being viewed by others
References
Adimurthi.: Existence of positive solutions of the semilinear Dirichlet problem with critical growth for the n-laplacian. Ann. Sc. Norm. Sup. Pisa, Ser. IV 17, 393-413 (1990)
Adimurthi , Prashanth S.: Failure of Palais-Smale condition and blow-up analysis for the critical exponent problem in \({\mathbb{R}^2}\). Proc. Indian. Acad. Sci. Math. Sci. 107, 283-317 (1997)
Adimurthi, Srikanth, P.N., Yadava, S.L.: Phenomena of critical exponent in \({\mathbb{R}^2}\). Proc. Roy. Soc. Edinburgh 199 A 19-25 (1991)
Adimurthi , Druet O.: Blow-up analysis in dimension 2 and a sharp form of Trudinger-Moser inequality. Comm. Partial Differ. Equ. 29, 295-322 (2004)
Adimurthi , Struwe M.: Global compactness properties of semilinear elliptic equations with critical exponential growth. J. Funct. Anal. 175, 125-167 (2000)
Bahri A., Coron J.M.: On a nonlinear elliptic equation involving the critical Sobolev exponent: the effect of the topology of the domain. Commun. Pure Appl. Math. 41, 255-294 (1988)
Bahri A., Li Y.-Y., Rey O.: On a variational problem with lack of compactness: the topological effect of the critical points at infinity. Calc. Var. 3, 67-93 (1995)
Baraket S., Pacard F.: Construction of singular limits for a semilinear elliptic equation in dimension 2. Calc. Var. Partial Differ. Equ. 6(1), 1-38 (1998)
Brezis H., Nirenberg L.: Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Commun. Pure Appl. Math. 36, 437-447 (1983)
Carleson L., Chang S.-Y.A.: On the existence of an extremal function for an inequality of J. Moser. Bull. Sci. Math. (2) 110, 113-127 (1986)
Coron J.M.: Topologie et cas limite des injections de Sobolev. C. R. Acad. Sci. Paris 299(Series I), 209-212 (1984)
de Figueiredo D.G., do Ó J.M., Ruf B.: On an inequality by N. Trudinger and J. Moser and related elliptic equations. Commun. Pure Appl. Math. 55, 135-152 (2002)
de Figueiredo D.G., Miyagaki O., Ruf B.: Elliptic equations in \({\mathbb{R}^2}\) with nonlinearities in the critical growth range. Calc. Var. Partial Differ. Equ. 3, 139-153 (1995)
de Figueiredo D.G., Ruf B.: Existence and non-existnce of radial solutions for elliptic equations with critical exponent in \({\mathbb{R}^2}\). Commun. Pure Appl. Math. 48, 1-17 (1995)
del Pino M., Kowalczyk M., Musso M.: Singular limits in Liouville-type equations. Calc. Var. Partial Differ. Equ. 24, 47-81 (2005)
del Pino M., Musso M.: Bubbling in Nonlinear Elliptic Problems Near Criticality. In: Chipot, M. (eds) Handbook of Differential Equations, Stationary Partial Differential Equations, vol. 3, pp. 215-316. Elsevier, Amsterdam (2006)
del Pino M., Musso M., Ruf B.: New solutions for Trudinger-Moser critical equations in \({\mathbb{R}^2}\). J. Funct. Anal. 258, 421-457 (2010)
Druet O.: Multibump analysis in dimension 2: quantification of blow-up levels. Duke Math. J. 132(2), 217-269 (2006)
Esposito O., Grossi M., Pistoia A.: On the existence of blowing-up solutions for a mean field equation. Ann. Inst. H. Poincaré Anal. Non Linéaire 22(2), 227-257 (2005)
Flucher M.: Extremal functions for the Trudinger-Moser inequality in 2 dimensions. Comment. Math. Helv. 67, 471-497 (1992)
Han Z.-C.: Asymptotic approach to singular solutions for nonlinear elliptic equations involving critical Sobolev exponent. Ann. Inst. H. Poincaré Anal. Non Linéaire 8(2), 159-174 (1991)
Lamm T., Robert F., Struwe M.: The heat flow with a critical exponential nonlinearity. J. Funct. Anal. 257(9), 2951-2998 (2009)
Lin K.C.: Extremal functions for Moser’s inequality. Trans. Am. Math. Soc. 348(7), 2663-2671 (1996)
Lions P.L.: The concentration-compactness principle in the calculus of variations. The limit case, part 1. Riv. Mat. Iberoamericana 1, 145-201 (1985)
Monahan, J.P.: Numerical solutions of a non-linear boundary value problem, thesis, Princetion Univ., 1971
Moser J.: A sharp form of an inequality by N. Trudinger. Indiana Univ. Math. J. 20, 1077-1092 (1970)
Pohozhaev, S.I.: The Sobolev embedding in the case pl = n, Proc. Tech. Sci. Conf. on Adv. Sci. Research 1964-1965, Mathematics Section, 158-170, Moskov. Ènerget. Inst. Moscow (1965)
Rey O.: The role of the Green’s function in a nonlinear elliptic equation involving the critical Sobolev exponent. J. Funct. Anal. 89(1), 1-52 (1990)
Struwe M.: Critical points of embeddings of \({H_0^{1,n}}\) into Orlicz spaces. Ann. Inst. Henri Poincaré 5(5), 425-464 (1988)
Struwe M.: A global compactness result for elliptic boundary value problems involving limiting nonlinearities. Math. Z. 187, 511-517 (1984)
Struwe M.: Positive solutions of critical semilinear elliptic equations on non-contractible planar domains. J. Eur. Math. Soc. 2, 329-388 (2000)
Trudinger N.S.: On embedding into Orlicz spaces and some applications. J. Math. Mech. 17, 473-483 (1967)
Yudovich, V.I.: Some estimates connected with integral operators and with solutions of elliptic equations, Dokl. Akad. Nauk SSRR 138, 805-808 (1961) (Russian); English transl., Soviet Math. Dokl. 2, 746-749 (1961)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Malchiodi.
Rights and permissions
About this article
Cite this article
del Pino, M., Musso, M. & Ruf, B. Beyond the Trudinger-Moser supremum. Calc. Var. 44, 543–576 (2012). https://doi.org/10.1007/s00526-011-0444-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00526-011-0444-5