1 Introduction

Most practical dynamic systems have uncertain effects such as parameter uncertainties, external disturbances, model nonlinearities and structure uncertainties. These challenging problems cannot be covered using linear and conventional controllers. Subsequently, it is essential to develop robust control schemes for solving such problems and to obtain certain performance requirements [1,2,3]. In recent years, robust adaptive schemes based on trajectory tracking have attracted great attention for nonlinear systems such as adaptive probabilistic Takagi–Sugeno–Kang (TSK) fuzzy controller [4], adaptive interval type-2 TSK fuzzy controller [5], adaptive sliding mode control (SMC) [6] and SMC based on proportional-integral-derivative (PID) and proportional-integral (PI) sliding surface, respectively [7, 8].

SMC approach is a class of the variable structure control schemes, which is a nonlinear robust controller that is able to respond insensitivity to structure uncertainties, rejection of an external disturbance, fast and good transient response, and stable control system [9]. SMC contains a switching control law that moves the states of the plant from any initial value on the sliding surface, which is set by the user in the switching surface and to preserve the system states on a desired sliding surface [10, 11]. However, the SMC includes the following problems: (1) it is necessary to obtain the precise mathematical model for the controlled process to design the SMC [9]. This problem decreases the performance of the controller in some control applications. (2) chattering phenomenon, which is an inherent problem in the design of SMC [10]. This problem also decreases the SMC performance. (3) uncertainty bounds, which are required for designing the switching control law of SMC [11]. To avoid such problems, several researchers proposed several approaches for solving the chattering problems such as approximating the discontinuous switching control law by using saturation function [12], using low pass filter [13], using variable structure adaptive control [14] and using adaptive intelligent technique [15]. On the other hand, some researchers used the adaptive control schemes using Lyapunov theory such as genetic algorithm [16], event-triggering dissipative control [17] and other schemes for complex industrial systems [18] to handle the problem of knowing the perfect mathematical model of the controlled process. In [19], SMC with a bound estimation was introduced for controlling robot manipulator to solve the problem of the uncertainty bounds.

In recent years, several researchers have integrated the SMC with intelligent techniques such as fuzzy logic systems (FLSs) [20] and neural networks (NNs) [9, 11, 21,22,23,24,25,26,27,28,29]. In [10], the fuzzy SMC with PI sliding surface for linear system was introduced. SMC law requires a precise knowledge about the controlled process. Moreover, the FLS was proposed to compensate the chattering phenomenon. In [9], an adaptive radial basis function NN (RBFNN)-based SMC for nonlinear plants was introduced. RBFNN was performed to approximate the unknown parameters of the controlled process. Also, the problem of chattering is solved based on a smooth continuous control action. In [11], a NN-based SMC for rotating stall and surge in axial compressors was introduced. The adaptive NN was used to avoid the problem of obtaining a precise mathematical model for the controlled process. In [25], a recurrent NN (RNN) based fuzzy SMC was introduced for 4-degree freedom remotely operated vehicle. The model uncertainties were compensated and estimated using RNN. On the other hand, the chattering phenomenon was handled using FLS as a switching term. In [29], NN was proposed to approximate the unknown continuous uncertainties and disturbance for an autonomous surface vehicle where the uncertainty bounds for the sliding surface was compensated using Lyapunov theory.

1.1 Motivation

In this paper, SMC based on diagonal RNN (DRNN) is introduced for uncertain nonlinear systems. The developed controller is motivated from the previous published works in [9,10,11, 21,22,23,24,25,26,27,28,29] to cover the disadvantages of the work in [10]. First, the SMC in [10], which was designed to linear systems is developed to uncertain nonlinear system (coupled tank system as a benchmark in this paper). Second, the NN in [9, 11, 21,22,23,24,25,26,27,28,29], which was used to approximate the unknown controlled system is developed to DRNN as the first time that used with SMC based on the authors’ best knowledge. DRNN is a type of NN, which belongs to the partially connected RNNs [30]. DRNN was introduced to identify nonlinear systems, which have a superior modeling accuracy compared with other NN techniques [31].

In this paper, the SMC is designed based on the DRNN. The SMC law consists of two terms; the first one is the equivalent control law, which is performed based on the DRNN. The nonlinear controlled system is approximated using DRNN. The second part is the switching control signal, which is dependent on the sliding surface. The sliding surface is performed based on DRNN. For the proposed controller, the discontinuous signum function is used to compensate the chattering problem. The updating weights of DRNN are obtained using Lyapunov function to guarantee the controlled system stability. The proposed scheme is designed for controlling uncertain nonlinear coupled tank system. The simulation results indicate that the developed controller can respond to the effects of system uncertainties and external disturbances compared to other existing schemes.

1.2 Novelties and contributions

The main contributions of this study are summarized as:

  1. 1.

    Design a novel SMC based on the DRNN for nonlinear systems that is motivated from previous works.

  2. 2.

    Developing the sliding surface based on DRNN.

  3. 3.

    Updating the DRNN weights using Lyapunov function to achieve the controlled system stability.

  4. 4.

    The problem of the knowledge of the controlled system and chattering phenomenon are compensated.

The remainder of this paper is organized as: Sect. 2 presents the problem formulation. The second order SMC for nonlinear coupled tank system is introduced in Sect. 2. The proposed SMC based on the DRNN is presented in Sect. 3. The updating algorithm for the DRNN parameters using Lyapunov function is presented in Sect. 4. Simulation results for the coupled tank system is presented in Sect. 5. Finally, conclusions are given in Sect. 6.

2 Problem formulation

Figure 1 shows the coupled tank system, which is used in this paper as a benchmark. It is considered as one of the hydraulic control systems in industrial applications [32, 33]. The function of the controller is controlling the destination tank level (\({L}_{1}\)) by varying the pump (\(P\)) flow using valve 1 or by valve 2, which is considered as a disturbance.

Fig. 1
figure 1

Coupled tank system [32]

Full size image

The relation between the pump supply voltage (\(u\)) and the input flow (Q) is given as [32]:

$$\left\{\begin{array}{*{20}l}Q= {K}_{g}u\\ {Q}_{2}= {C}_{2}{D}_{2}\sqrt{2g ({L}_{1}-{L}_{2})}\\ {Q}_{3}= {C}_{3}{D}_{3}\sqrt{2g{L}_{2}}\end{array}\right.$$
(1)

The destination tank can be filled from the source tank by opening the valve 1 placed after the pump, which changes the incoming flow. The output flow (\({Q}_{2}\)) can change using valve 2, which inserted below the destination tank. Consider \({Q}_{1}=Q\) for the level control case, we obtain the following using the flow equilibrium equation [32]:

$$\left\{\begin{array}{*{20}l}{\dot{L}}_{1}= \frac{1}{{A}_{d}} ({Q}_{1}- {Q}_{2})\\ {\dot{L}}_{2}= \frac{1}{{A}_{s}} ({Q}_{2}- {Q}_{3})\end{array}\right.$$
(2)

Finally, the mathematical model of the coupled tank system is given as [32]:

$$\left\{\begin{array}{*{20}l}{\dot{L}}_{1}= \frac{1}{{A}_{d}} ({K}_{g}u- {C}_{2}{D}_{2}\sqrt{2g ({L}_{1}-{L}_{2})})\\ {\dot{L}}_{2}= \frac{1}{{A}_{s}}{(C}_{2}{D}_{2}\sqrt{2g ({L}_{1}-{L}_{2})}-{C}_{3}{D}_{3}\sqrt{2g {L}_{2}}\\ y={K}_{t}{L}_{1}\end{array}\right.$$
(3)

The above equation can be rewritten as the following considering \({x}_{a}=\left(\frac{}{}{0pt}{}{{x}_{a1}}{{x}_{a2}}\right)\), \({x}_{a1}= {L}_{1}\) and \({x}_{a2}= {L}_{2}\)

$$\left\{\begin{array}{*{20}l}{\dot{x}}_{a1}= \frac{1}{{A}_{d}} ({K}_{g}u- {C}_{2}{D}_{2}\sqrt{2g ({x}_{a1}-{x}_{a2})})\\ {\dot{x}}_{a2}= \frac{1}{{A}_{s}}{(C}_{2}{D}_{2}\sqrt{2g ({x}_{a1}-{x}_{a2})}-{C}_{3}{D}_{3}\sqrt{2g {x}_{a2}}\\ y={K}_{t}{x}_{a1}\end{array}\right.$$
(4)

Using the above equation, the nonlinear model of the coupled tank system is obtained as:

$$\left\{\begin{array}{*{20}l}{\dot{x}}_{a1}= {f}_{1}\left({x}_{a}\right)+Bu\\ {\dot{x}}_{a2}= {f}_{2}\left({x}_{a}\right)\\ y=C{x}_{a1}\end{array}\right.$$
(5)

where

\({f}_{1}\left({x}_{a}\right)=\frac{{- C}_{2}{D}_{2}}{{A}_{d}}\sqrt{2g \left({x}_{a1}-{x}_{a2}\right)}\), \(C= {K}_{t}\), \({f}_{2}\left({x}_{a}\right)=\frac{{C}_{2}{D}_{2}}{{A}_{s}}\sqrt{2g \left({x}_{a1}-{x}_{a2}\right)}- \frac{{C}_{3}{D}_{3}}{{A}_{s}}\sqrt{2g{x}_{a2}}\) and \(B= \frac{{K}_{g}}{{A}_{d}}\).

The nonlinear model, which is described in Eq. (5), can be modified by considering parameter uncertainties. Therefore, the nonlinear model is given as:

$$\left\{\begin{array}{*{20}l}{\dot{x}}_{a1}= {f}_{1n}\left({x}_{a}\right)+\Delta {f}_{1}\left({x}_{a}\right)+Bu +{E}_{1}(t)\\ {\dot{x}}_{a2}= {f}_{2n}\left({x}_{a}\right)+\Delta {f}_{2}\left({x}_{a}\right)+{E}_{2}(t)\\ y=C{x}_{a1}\end{array}\right.$$
(6)

where \({f}_{1n}\left({x}_{a}\right)\), \({f}_{2n}\left({x}_{a}\right)\) represent the nominal values of the nonlinear functions; \({f}_{1}\left({x}_{a}\right)\) and\({f}_{2}\left({x}_{a}\right)\), respectively. \(\Delta {f}_{1}\left({x}_{a}\right)\) and \(\Delta {f}_{2}\left({x}_{a}\right)\) represent the parameter uncertainties of the nonlinear functions \({f}_{1}\left({x}_{a}\right)\) and\({f}_{2}\left({x}_{a}\right)\), respectively. \({E}_{1}(t)\) and \({E}_{2}(t)\) represent the unknown external perturbations. It is assumed that all the uncertainties can be given as:

$$\left\{\begin{array}{*{20}l}{\rho}_{1}(t)=\Delta {f}_{1}\left({x}_{a}\right)+{E}_{1}(t)\\ {\rho }_{2}(t)=\Delta {f}_{2}\left({x}_{a}\right)+{E}_{2}(t)\end{array}\right.$$
(7)

Therefore, Eq. (6) can be rewritten as:

$$\left\{\begin{array}{*{20}l}{\dot{x}}_{a1}= {f}_{1n}\left({x}_{a}\right)+Bu +{\rho }_{1}(t)\\ {\dot{x}}_{a2}= {f}_{2n}\left({x}_{a}\right)+{\rho }_{2}(t)\\ y=C{x}_{a1}\end{array}\right.$$
(8)

3 Second order sliding mode control

In this section, the second order SMC (SOSMC), which is applied previously [8, 10], is developed to applied to uncertain nonlinear coupled tank system as described in Eq. (8). The PI sliding surface is chosen as [10]:

$$S\left(t\right)= {k}_{1} e\left(t\right)+ {k}_{2}{\int }_{0}^{t}e\left(\tau \right)d\tau $$
(9)

where \(e\left(t\right)= {x}_{d1}- {x}_{a1}\) is the tracking error, \({x}_{d1}\) is the desired level and \({x}_{a1}\) is the actual level of the coupled tank system defined by Eq. (8). The parameters; \({k}_{1}\) and \({k}_{2}\) are the proportional and integral positive gains, respectively for the PI sliding surface.

The main goal of the SOSMC is to make the output of the system; \({x}_{a1}\) to successfully track a given desired signal; \({x}_{d1}\) under the effect of system uncertainties. Therefore, the sliding surface; \(S\left(t\right)\) and the time derivative of the sliding surface; \(\dot{S}\left(t\right)\) should equal zero to make the tracking error kept on the sliding surface [10]. The total control law of the SOSMC consists of two parts, which is given in Eq. (10); the first is the equivalent control term; \({u}_{eq}\left(t\right)\) and the other is the switching control term; \({u}_{sw}\left(t\right)\).

$${u\left(t\right)=u}_{eq}\left(t\right)+ {u}_{sw}(t)$$
(10)

The equivalent control term; \({u}_{eq}\left(t\right)\) is obtained as the solution of \(\dot{S}\left(t\right)=0\) under nominal system dynamic model (\({\rho }_{1}\left(t\right)={\rho }_{2}(t)=0\)). The time derivative of sliding surface, which is described in Eq. (9) is obtained as:

$$\dot{S}\left(t\right)={k}_{1}\dot{e}\left(t\right)+{k}_{2}e\left(t\right)$$
(11)

Putting \(e\left(t\right)= {x}_{d1}- {x}_{a1}\) and \(\dot{e}\left(t\right)= {\dot{x}}_{d1}- {\dot{x}}_{a1}\), Eq. (11) can be rewritten as:

$$\dot{S}\left(t\right)= {k}_{1}{\dot{x}}_{d1}-{k}_{1}{\dot{x}}_{a1}+{k}_{2}{x}_{d1}-{k}_{2} {x}_{a1}$$
(12)

Substitute \({\dot{x}}_{a1}\) from Eq. (8) into Eq. (12), we get the following:

$$\dot{S}\left(t\right)= {k}_{1}{\dot{x}}_{d1}+{k}_{2}{x}_{d1}-{k}_{2} {x}_{a1}-{k}_{1}{f}_{1n}\left({x}_{a}\right)-{k}_{1}Bu-{k}_{1}{\rho }_{1}(t)$$
(13)

Putting \(\dot{S}\left(t\right)=0\) and \({\rho }_{1}(t)=0\), the equivalent control term; \({u}_{eq}(t)\) is obtained as:

$${u}_{eq}\left(t\right)=\frac{1}{{k}_{1}B}[{k}_{1}{\dot{x}}_{d1}+{k}_{2}e(t)-{k}_{1}{f}_{1n}\left({x}_{a}\right)]$$
(14)

The above equation shows \({u}_{eq}\left(t\right)\), which provides the desired performance for the controlled system. The switching control term; \({u}_{sw}\left(t\right)\) should be obtained to compensate the effect of the system uncertainties such as external disturbances and parameters variations. Lyapunov function; \(V\left(t\right)\) is chosen to design the switching control term; \({u}_{sw}\left(t\right)\) as follow:

$$V\left(t\right)= \frac{1}{2}{S}^{2}\left(t\right)$$
(15)

The time derivative \(\dot{V}\left(t\right)\) is obtained as:

$$\dot{V}\left(t\right)= S\left(t\right)\dot{S}\left(t\right)$$
(16)

By Substituting Eqs. (10 and 13) into Eq. (16), we get the following:

$$\dot{V}\left(t\right)= S\left(t\right)[{k}_{1}{\dot{x}}_{d1}+{k}_{2}{x}_{d1}-{k}_{2} {x}_{a1}-{k}_{1}{f}_{1n}\left({x}_{a}\right)-{k}_{1}B({u}_{eq}+{u}_{sw})-{k}_{1}{\rho }_{1}(t)]$$
(17)

By Substituting Eq. (14) into Eq. (17), we get the following:

$$ \begin{aligned} \dot{V}\left( t \right) & = ~S\left( t \right)\left[ {k_{1} \dot{x}_{{d1}} + k_{2} x_{{d1}} - k_{2} ~x_{{a1}} - k_{1} f_{{1n}} \left( {x_{a} } \right) - k_{1} B\left( {\frac{1}{{k_{1} B}}(k_{1} \dot{x}_{{d1}} + k_{2} e\left( t \right)} \right.} \right. \\ & \quad \left. {\left. { - ~k_{1} f_{{1n}} \left( {x_{a} } \right)} \right) - k_{1} Bu_{{sw}} - k_{1} \rho _{1} \left( t \right)} \right] \\ \end{aligned} $$
(18)

The above equation can be rearranged as:

$$\dot{V}\left(t\right)= S\left(t\right)\left[{k}_{1}{\dot{x}}_{d1}+{k}_{2}e\left(t\right)-{k}_{1}{f}_{1n}\left({x}_{a}\right)-{k}_{1}{\dot{x}}_{d1}-{k}_{2}e\left(t\right)+{k}_{1}{f}_{1n}\left({x}_{a}\right)-{k}_{1}B{u}_{sw}-{ k}_{1}{\rho }_{1}\left(t\right)\right]=S\left(t\right)[-{k}_{1}B{u}_{sw}-{k}_{1}{\rho }_{1}(t)]$$
(19)

The switching control signal; \({u}_{sw}(t)\) can be selected as:

$${u}_{sw}\left(t\right)=\frac{-{k}_{r}}{{k}_{1}B} sign\left(S\left(t\right)\right) $$
(20)

where \({k}_{r}\) is the switching control gain and \(sign(\cdot )\) denotes sign function that defined as [10]:

$$sign\left(S\left(t\right)\right)=\left\{\begin{array}{l}1, S(t)>0\\ 0, S\left(t\right)=0\\ -1, S\left(t\right)<0\end{array}\right.$$
(21)

By Substituting Eq. (20) into Eq. (19), we get the following:

$$\dot{V}\left(t\right)={k}_{r} S\left(t\right)sign\left(S\left(t\right)\right)-{k}_{1 }S\left(t\right) {\rho }_{1}(t)$$
(22)

By using \(\left|S(t)\right|=S\left(t\right)sign(S\left(t\right))\), the above equation is rewritten as:

$$\dot{V}\left(t\right)={k}_{r} \left|S(t)\right|-{k}_{1 }S\left(t\right) {\rho }_{1}(t)$$
(23)
$$\dot{V}\left(t\right)\le -\left|S\left(t\right)\right|(-{k}_{r}+{k}_{1 } {\rho }_{max}\left(t\right))$$
(24)

To achieve controlled system stability using SOSMC and the reaching condition \(\dot{V}\left(t\right)\) < 0 is satisfied, the switching control gain; \({k}_{r}\) must be selected as:

$${k}_{r}< {k}_{1 } {\rho }_{max}\left(t\right)$$
(25)

Therefore, the total control law of the SOSMC is given as:

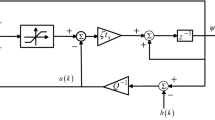
$$u\left(t\right)=\frac{1}{{k}_{1}B}\left[{k}_{1}{\dot{x}}_{d1}+{k}_{2}e\left(t\right)-{k}_{1}{f}_{1n}\left({x}_{a}\right)-{k}_{r} sign\left(S\left(t\right)\right)\right]$$
(26)

The block diagram of the SOSMC scheme is shown in Fig. 2. The SOSMC law that is given in Eq. (26) can compensate the chattering problem where the switching control part contains the discontinuous signum function. Moreover, the witching control gain; \({k}_{r}\) is concerned with the boundaries of unknown uncertainties (as indicated by the stability condition in Eq. (25)), and it is required to know the precise mathematical model of the controlled uncertain system as it appears in the control signal.

Fig. 2
figure 2

Block diagram of SOSMC for coupled tank system

Full size image

4 SMC based on diagonal recurrent NN

In this section, the structure of DRNN is presented. Then, the development of SMC based on DRNN is introduced.

4.1 Structure of DRNN

The structure of the DRNN is shown in Fig. 3. It consists of three layers; input layer, hidden layer, and output layer [30]. The input vector for the DRNN is \({\varvec{Z}}\left(t\right)={\left[{z}_{1}\left(t\right) {z}_{2}\left(t\right) \cdots {z}_{P}(t)\right]}^{T}\), the hidden weight matrix for the hidden layer is represented by Eq. (27) and the diagonal weight vector for the hidden nodes is represented as \({{\varvec{W}}}^{{\varvec{D}}}={\left[{w}_{1}^{D} {w}_{2}^{D} \cdots {w}_{R}^{D}\right]}^{T}\). The output weight vector for the output layer is represented as \({{\varvec{W}}}^{{\varvec{O}}}={\left[{w}_{1}^{O} {w}_{2}^{O} \cdots {w}_{R}^{O}\right]}^{T}\). \(P\) and \(R\) denote the number of inputs and the number of nodes in hidden layer, respectively.

Fig. 3
figure 3

Structure of DRNN

Full size image
$${W}^{I}=\left[\begin{array}{ccc}{w}_{11}^{I}& \cdots & {w}_{1P}^{I}\\ \vdots & \ddots & \vdots \\ {w}_{R1}^{I}& \cdots & {w}_{RP}^{I}\end{array}\right]$$
(27)

For any recurrent neuron, the output \({m}_{r}(t)\) at any \(t\) time and sampling period \(T\) is obtained as follows:

$${g}_{r}\left(t\right)=\sum_{p=1}^{P}{w}_{rp}^{I} {z}_{p}\left(t\right)+{w}_{r}^{D}\left(t\right){m}_{r}\left(t-T\right), r=\mathrm{1,2}, \ldots R\,{\text{and}}\,P=\mathrm{1,2}, \ldots P$$
(28)
$${m}_{r}\left(t\right)=f\left({g}_{r}\left(t\right)\right)=\frac{2}{1+{e}^{-\sigma {g}_{r}(t)}}-1, , r=\mathrm{1,2}, \ldots R$$
(29)

where \(\sigma \) is constant. The DRNN output; \({O}_{DRNN}(t)\) is given as:

$${O}_{DRNN}\left(t\right)=\sum_{r=1}^{R}{w}_{r}^{O}\left(t\right) {m}_{r}(t)={{\varvec{W}}}^{O}\left(t\right) {\varvec{M}}(t)$$
(30)

where \(\left(t\right)={\left[{m}_{1}\left(t\right) {m}_{2}\left(t\right) \cdots {m}_{R}(t)\right]}^{T}\).

4.2 Proposed structure

The approximation ability of the DRNN is used to propose the SMC based on DRNN (SMC-DRNN), where the equivalent control term of SMC law, which depends on the dynamic model of a controlled system, is approximated using DRNN. Equation (13) can be rearranged as follows:

$$\dot{S}\left(t\right)= {k}_{1}{\dot{x}}_{d1}+{k}_{2}e(t)-{k}_{1}{f}_{1n}\left({x}_{a}\right)-{k}_{1}Bu(t)-{k}_{1}{\rho }_{1}\left(t\right)$$
(31)
$$\dot{S}\left(t\right)= -{k}_{1}Bu-{k}_{1}{\rho }_{1}\left(t\right)+{f}_{d}\left({{\varvec{x}}}_{A}\right)$$
(32)

where \({f}_{d}\left({{\varvec{x}}}_{A}\right)\) represents an unknown uncertain nonlinear function and is defined as:

$${f}_{d}\left({{\varvec{x}}}_{A}\right)={k}_{1}{\dot{x}}_{d1}+{k}_{2}e(t)-{k}_{1}{f}_{1n}\left({x}_{a}\right)$$
(33)

where \({{\varvec{x}}}_{A}={[ e\left(t\right) {\dot{x}}_{d1}\left(t\right) {x}_{a1}(t) {x}_{a2}\left(t\right)]}^{T}\). The function; \({f}_{d}\left({{\varvec{x}}}_{A}\right)\) can be universally approximated using the DRNN as:

$${f}_{d}\left({{\varvec{x}}}_{A}\right)={{\varvec{W}}}_{d}^{O}(t) {{\varvec{M}}}_{d}(t)$$
(34)

where \({{\varvec{W}}}_{d}^{O}(t)={\left[{w}_{d1}^{O}(t) {w}_{d2}^{O}(t) \cdots {w}_{dR}^{O}(t)\right]}^{T}\) is the output weight vector of the DRNN, which approximate the function; \({f}_{d}\left({{\varvec{x}}}_{A}\right)\) and \({{\varvec{M}}}_{{\varvec{d}}}(t)={\left[{m}_{d1}\left(t\right) {m}_{d2}\left(t\right) \cdots {m}_{dR}(t)\right]}^{T}\) is the input vector for the output layer and it is obtained as the following where \(R\) is the number of nodes in hidden layer of DRNN, which approximate the function; \({f}_{d}({{\varvec{x}}}_{A})\):

$${{\varvec{M}}}_{d}\left(t\right)=f[{{\varvec{G}}}_{d}\left(t\right)]$$
(35)
$${{\varvec{G}}}_{d}\left(t\right)= {{\varvec{W}}}_{d}^{D}(t) {{\varvec{M}}}_{d}\left(t-T\right)+ {{\varvec{W}}}_{d}^{I}(t){{\varvec{x}}}_{A}$$
(36)

where \({{\varvec{W}}}_{d}^{D}(t)={\left[{w}_{d1}^{D} {w}_{d2}^{D} \cdots {w}_{dR}^{D}\right]}^{T}\) is the diagonal weight vector for the hidden layer of DRNN, which approximate the function; \({f}_{d}\left({{\varvec{x}}}_{A}\right)\) and \({{\varvec{W}}}_{d}^{I}\) is the weight matrix for the hidden layer of DRNN, which is given as:

$${{\varvec{W}}}_{d}^{I}(t)=\left[\begin{array}{c}{w}_{d11}^{I}\\ \vdots \\ {w}_{dR1}^{I} \end{array}\begin{array}{c}{w}_{d12}^{I}\\ \vdots \\ {w}_{dR2}^{I} \end{array}\begin{array}{c}{w}_{d13}^{I}\\ \vdots \\ {w}_{dR3}^{I} \end{array}\begin{array}{c}{w}_{d14}^{I}\\ \vdots \\ {w}_{dR4}^{I}\end{array}\right]$$
(37)

Therefore, the equivalent control part; \({u}_{eq-DRNN}\left(t\right)\) for the proposed SMC-DRNN is obtained as the following by substituting Eqs. (34–36) into Eq. (14):

$${u}_{eq-DRNN}\left(t\right)=\frac{1}{{k}_{1}B}\left[{f}_{d}\left({{\varvec{x}}}_{A}\right)\right]=\frac{1}{{k}_{1}B}\left[{{\varvec{W}}}_{d}^{O}\left(t\right){{\varvec{M}}}_{d}\left(t\right)\right]$$
(38)
$${u}_{eq-DRNN}\left(t\right)=\frac{1}{{k}_{1}B}\left[{{\varvec{W}}}_{d}^{O}\left(t\right)f\left[{{\varvec{W}}}_{d}^{D}\left(t\right){{\varvec{M}}}_{d}\left(t-T\right)+ {{\varvec{W}}}_{d}^{I}\left(t\right){{\varvec{x}}}_{A}\right]\right]$$
(39)

On the other hand, the switching control part for the proposed SMC-DRNN is developed, where the function of the sliding surface; \(S(t)\) is designed based on DRNN. Therefore, the proposed sliding surface; \({S}_{DRNN}(t)\) is obtained as follows:

$${S}_{DRNN}\left(t\right)={{\varvec{W}}}_{s}^{O}(t) f[{{\varvec{W}}}_{s}^{D}(t) {{\varvec{M}}}_{s}\left(t-T\right)+ {{\varvec{W}}}_{s}^{I}(t){{\varvec{x}}}_{s}]$$
(40)

where \({{\varvec{W}}}_{s}^{O}(t)={\left[{w}_{s1}^{O}(t) {w}_{s2}^{O}(t) \cdots {w}_{sM}^{O}(t)\right]}^{T}\) is the output weight vector of the DRNN, which approximate the sliding surface; \({S}_{DRNN}\left(t\right)\) and \({{\varvec{M}}}_{{\varvec{s}}}(t)={\left[{m}_{s1}\left(t\right) {m}_{s2}\left(t\right) \cdots {m}_{sD}(t)\right]}^{T}\) is the input vector for the output layer where \(D\) is the number of nodes in hidden layer of DRNN, which approximate the sliding surface; \({S}_{DRNN}\left(t\right)\). \({{\varvec{x}}}_{s}=\) \({[ e\left(t\right) \int e\left(t\right)]}^{T}\) is the input vector, \({{\varvec{W}}}_{s}^{D}(t)={\left[{w}_{s1}^{D} {w}_{s2}^{D} \cdots {w}_{sD}^{D}\right]}^{T}\) is the diagonal weight vector for the hidden layer of DRNN, which approximate the sliding surface; \({S}_{DRNN}\left(t\right)\) and \({{\varvec{W}}}_{s}^{I}\) is the weight matrix for the hidden layer of DRNN, which is given as:

$${{\varvec{W}}}_{d}^{I}(t)=\left[\begin{array}{c}{w}_{s11}^{I}\\ \vdots \\ {w}_{sD1}^{I} \end{array}\begin{array}{c}{w}_{s12}^{I}\\ \vdots \\ {w}_{sD2}^{I}\end{array}\right]$$
(41)

Therefore, the switching control term for the proposed SMC-DRNN; \({u}_{sw-DRNN}\left(t\right)\) is obtained as follows:

$${u}_{sw-DRNN}\left(t\right)=\frac{-{k}_{r}}{{k}_{1}B} sign\left( {S}_{DRNN}\left(t\right)\right)$$
(42)
$${u}_{sw-DRNN}\left(t\right)=\frac{-{k}_{r}}{{k}_{1}B} sign\left( {{\varvec{W}}}_{s}^{O}\left(t\right)f\left[{{\varvec{W}}}_{s}^{D}\left(t\right){{\varvec{M}}}_{s}\left(t-T\right)+ {{\varvec{W}}}_{s}^{I}\left(t\right){{\varvec{x}}}_{s}\right]\right)$$
(43)

Therefore, the total control law of the proposed SMC-DRNN is given as:

$${u}_{DRNN}\left(t\right)=\frac{1}{{k}_{1}B}\left[{{\varvec{W}}}_{d}^{O}\left(t\right)f\left[{{\varvec{W}}}_{d}^{D}\left(t\right){{\varvec{M}}}_{d}\left(t-T\right)+ {{\varvec{W}}}_{d}^{I}\left(t\right){{\varvec{x}}}_{A}\right]-{k}_{r}\left(sign\left( {{\varvec{W}}}_{s}^{O}\left(t\right)f\left[{{\varvec{W}}}_{s}^{D}\left(t\right){{\varvec{M}}}_{s}\left(t-T\right)+ {{\varvec{W}}}_{s}^{I}\left(t\right){{\varvec{x}}}_{s}\right]\right)\right) \right] $$
(44)

Figure 4 indicates the block diagram of the developed SMC-DRNN. The total control law of the proposed scheme; \({u}_{DRNN}\left(t\right)\) consists of two terms; the first term is the equivalent control term; \({u}_{eq-DRNN}\left(t\right)\), which performed using the DRNN to approximate the dynamics of the controlled system to compensate the problem of the precise knowledge of the mathematical model for the controlled process. The other part is the switching control term; \({u}_{sw-DRNN}\left(t\right)\), which depends on the sliding surface that designed based on the DRNN to compensate the problem of chattering. The weights of the DRNNs are tuned using the Lyapunov function to achieve the controlled system stability. In the next section, the updating algorithm is introduced in detail.

Fig. 4
figure 4

Block diagram of the proposed SMC-DRNN for coupled tank system

Full size image

5 Updating algorithm based on Lyapunov function

In this section, the weights of the DRNN are updated online using Lyapunov function to achieve the coupled tank system stability. The weight vectors; \({{\varvec{W}}}_{d}^{I}\), \({{\varvec{W}}}_{d}^{D}\) and \({{\varvec{W}}}_{d}^{O}\) for the DRNN, which approximate the equivalent control term and the weight vectors; \({{\varvec{W}}}_{s}^{I}\), \({{\varvec{W}}}_{s}^{D}\) and \({{\varvec{W}}}_{s}^{O}\) for the DRNN, which approximate the sliding surface are updated online. The weight adjustment rule is derived using the Lyapunov stability criterion. The error at the \(\varrho \) th instant between the plant output; \({x}_{a1}(\varrho )\) and the reference input; \({x}_{d1}(\varrho )\) is referred to as \(e\left(\varrho \right)= {x}_{d1}(\varrho )- {x}_{a1}(\varrho )\), which is utilized to adjust the weight vectors of the DRNN. The following is the derivation of the weight adjustment rule using the Lyapunov stability criteria:

First, a scalar function; \({V}_{L}(X)\) should be selected, where \(X\) represents an argument vector, and \({V}_{L}(X)\) is positive definite for all initial conditions of its arguments, except when they are all simultaneously equal to zero [31]. A system is considered asymptotically stable if it satisfies both conditions described by Eqs. (45) and (46).

$${V}_{L}\left(X\right)>0for\,all\,X\,except\, X=0$$
(45)
$$\frac{{dV}_{L}}{dt}=negative\,definite\,for\,all\, X$$
(46)

The controlled system is asymptotically stable if both conditions are satisfied. To establish the basis for the weight learning algorithm, we can express the generalized form of the weight update equation as follows:

$${\mathbb{N}}\left(\varrho +1\right)={\mathbb{N}}\left(\varrho \right)- \eta\Delta {\mathbb{N}}\left(\varrho \right)$$
(47)

where \({\mathbb{N}}\left(\varrho \right)\) represents a generalized weight vector, which denotes (\({{\varvec{W}}}_{d}^{I}\),\({{\varvec{W}}}_{d}^{D}\), \({{\varvec{W}}}_{d}^{O}{{\varvec{W}}}_{s}^{I}\), \({{\varvec{W}}}_{s}^{D}\) and\({{\varvec{W}}}_{s}^{O}\)). Here, \(\Delta {\mathbb{N}}\left(\varrho \right)\) represents the necessary weight adjustment to be made and \(\eta \) represents the learning rate. Let \(\varepsilon (\varrho )\) be the cost function, which is a function of the error; \((\varrho )\). It is defined as:

$$\varepsilon (\varrho )=\frac{1}{2}({e(\varrho ))}^{2}$$
(48)

The positive definite Lyapunov function is chosen as:

$${V}_{L}\left(\varrho \right)=\frac{1}{2}{[(e(\varrho ))}^{2}+{({\mathbb{N}}\left(\varrho \right))}^{2}]$$
(49)

The time derivative of \({V}_{L}\left(\varrho \right)\) in discrete form is determined as:

$${\Delta V}_{L}\left(\varrho \right)={V}_{L}\left(\varrho +1\right)-{V}_{L}\left(\varrho \right)\le 0$$
(50)

Theorem:

For Lyapunov function, \({V}_{L}\left(\varrho \right)=\frac{1}{2}{[(e(\varrho ))}^{2}+{({\mathbb{N}}\left(\varrho \right))}^{2}]>0,\) condition \({\Delta V}_{L}\left(\varrho \right)={V}_{L}\left(\varrho +1\right)-{V}_{L}\left(\varrho \right)\le 0\) is satisfied if and only if

$$\Delta {\mathbb{N}}\left(\varrho \right)= - \frac{\left\{{\mathbb{N}}\left(\varrho \right)+e\left(\varrho \right)\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]\right\}}{1+{\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]}^{2}}$$
(51)

Proof

By substituting Eq. (49) into Eq. (50), we get the following:

$${\Delta V}_{L}\left(\varrho \right)=\frac{1}{2}{\{[(e(\varrho +1))}^{2}+{({\mathbb{N}}\left(\varrho +1\right))}^{2}]-{[(e(\varrho ))}^{2}+{\left({\mathbb{N}}\left(\varrho \right)\right)}^{2}]\}$$
(52)

The above equation can be rearranged as:

$${\Delta V}_{L}\left(\varrho \right)=\frac{1}{2}{[(e(\varrho +1))}^{2}-{(e(\varrho ))}^{2}]+\frac{1}{2}[{({\mathbb{N}}\left(\varrho +1\right))}^{2}-{\left({\mathbb{N}}\left(\varrho \right)\right)}^{2}]$$
(53)
$${\Delta V}_{L}\left(\varrho \right)=\frac{1}{2}[ e\left(\varrho +1\right)+e(\varrho )][ e(\varrho +1)-e(\varrho )]+\frac{1}{2}[{\mathbb{N}}\left(\varrho +1\right)+{\mathbb{N}}\left(\varrho \right)][{\mathbb{N}}\left(\varrho +1\right)-{\mathbb{N}}\left(\varrho \right)]$$
(54)

Let \(\Delta e\left(\varrho \right)=e(\varrho +1)-e(\varrho )\) and \(\Delta {\mathbb{N}}\left(\varrho \right)={\mathbb{N}}\left(\varrho +1\right)-{\mathbb{N}}\left(\varrho \right)\) and putting them in Eq. (54), we get the following:

$${\Delta V}_{L}\left(\varrho \right)=\frac{1}{2}\left\{\Delta e\left(\varrho \right) \left[\Delta e\left(\varrho \right)+2e\left(\varrho \right)\right]+\Delta {\mathbb{N}}\left(\varrho \right) \left[\Delta {\mathbb{N}}\left(\varrho \right)+2{\mathbb{N}}\left(\varrho \right)\right]\right\}$$
(55)

The above equation can be written as:

$${\Delta V}_{L}\left(\varrho \right)=\frac{1}{2}{\left[\Delta {\mathbb{N}}\left(\varrho \right) \right]}^{2} \left[ 1+{\left[\frac{\Delta e\left(\varrho \right)}{\Delta {\mathbb{N}}\left(\varrho \right)}\right]}^{2}\right]+\Delta {\mathbb{N}}\left(\varrho \right) \left[{\mathbb{N}}\left(\varrho \right)+e\left(\varrho \right)\left[\frac{\Delta e\left(\varrho \right)}{\Delta {\mathbb{N}}\left(\varrho \right)}\right]\right]$$
(56)

For a very small change, Eq. (56) can be written as:

$${\Delta V}_{L}\left(\varrho \right)=\frac{1}{2}{\left[\Delta {\mathbb{N}}\left(\varrho \right) \right]}^{2} \left[ 1+{\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]}^{2}\right]+\Delta {\mathbb{N}}\left(\varrho \right) \left[{\mathbb{N}}\left(\varrho \right)+e\left(\varrho \right)\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]\right]$$
(57)

From the above equation, let the following:

$${\Delta V}_{L}\left(\varrho \right)=\frac{1}{2}{\left[\Delta {\mathbb{N}}\left(\varrho \right) \right]}^{2} \left[ 1+{\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]}^{2}\right]+\Delta {\mathbb{N}}\left(\varrho \right) \left[{\mathbb{N}}\left(\varrho \right)+e\left(\varrho \right)\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]\right]=-\frac{\delta }{2}$$
(58)

where \(\delta \ge 0\) in order to make \({\Delta V}_{L}\left(\varrho \right)\le 0\). Therefore, the above equation becomes as:

$${\Delta V}_{L}\left(\varrho \right)=\frac{1}{2}{\left[\Delta {\mathbb{N}}\left(\varrho \right) \right]}^{2} \left[ 1+{\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]}^{2}\right]+\Delta {\mathbb{N}}\left(\varrho \right) \left[{\mathbb{N}}\left(\varrho \right)+e\left(\varrho \right)\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]\right]+\frac{\delta }{2}=0$$
(59)

Consider a general quadratic equation: \(a{z}^{2}+bz+c=0\), then the roots of it are given by

$${r}_{1}=\frac{-b+\sqrt{{b}^{2}-4ac}}{2a} {\text{and}} {r}_{1}=\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$$
(60)

Comparing the general quadratic equation and Eq. (59), it can be seen that \(\Delta {\mathbb{N}}\left(\varrho \right)\) acts as \(z\) in the general quadratic equation and values \(a\), \(b\) and \(c\) in Eq. (59) are obtained as:

$$a=\frac{1}{2}\left[1+{\left[\frac{\partial e(\varrho )}{\partial {\mathbb{N}}(\varrho )}\right]}^{2}\right], b=\left[{\mathbb{N}}(\varrho )+e(\varrho )\left[\frac{\partial e(\varrho )}{\partial {\mathbb{N}}(\varrho )}\right]\right] {\text{and}}\, c=\frac{\delta }{2}$$
(61)

To have a single unique of quadratic equation, term \(\sqrt{{b}^{2}-4ac}\) must be equal zero, so, putting values of \(a\), \(b\) and \(c\) in \(\sqrt{{b}^{2}-4ac}=0\), we get the value of \(\delta \) as:

$$\delta = \frac{{\left[{\mathbb{N}}\left(\varrho \right)+e\left(\varrho \right)\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]\right]}^{2}}{1+{\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]}^{2}}$$
(62)

Since \(\delta \ge 0\), which means

$$\frac{{\left[{\mathbb{N}}\left(\varrho \right)+e\left(\varrho \right)\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]\right]}^{2}}{1+{\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]}^{2}}\ge 0$$
(63)

Therefore, the unique root of Eq. (59) will be given as:

$$\Delta {\mathbb{N}}\left(\varrho \right)= -\frac{b}{2a}=- \frac{\left\{{\mathbb{N}}\left(\varrho \right)+e\left(\varrho \right)\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]\right\}}{1+{\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]}^{2}}$$
(64)

So, Eq. (51) is proved. By substituting Eq. (64) to Eq. (47), we get the following generalized form of the weight update equation:

$${\mathbb{N}}\left(\varrho +1\right)={\mathbb{N}}\left(\varrho \right)+\eta \frac{\left\{{\mathbb{N}}\left(\varrho \right)+e\left(\varrho \right)\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]\right\}}{1+{\left[\frac{\partial e\left(\varrho \right)}{\partial {\mathbb{N}}\left(\varrho \right)}\right]}^{2}}$$
(65)

The following algorithm shows the pseudo-code for the proposed controller.

Algorithm 1
figure a

The proposed SMC-DRNN Pseudo Code

Full size image

6 Simulation results

The developed SMC-DRNN is applied to the nonlinear coupled tank system in this section. To show the robustness of the developed SMC-DRNN, the simulation results of the proposed scheme are compared with other existing schemes such as an adaptive radial basis function neural network estimator-based SMC (ARBFNNE-SMC) [9], which used RBFNN to estimate the dynamics of the controlled system and a PID sliding mode control (PID-SMC), which is designed previously for a coupled tank system [32]. The comparisons are done by measuring some performance indices for all controller such as the mean absolute error (MAE) and the root mean square error (RMSE), which are defined as [34, 35]:

$$MAE=\frac{1}{N}\sum_{\varrho =1}^{N}\left|e(\varrho )\right|$$
(66)
$$RMSE=\sqrt{\frac{1}{N}\sum_{\varrho =1}^{N}{e(\varrho )}^{2}}$$
(67)

where \(N\) is the total number of iterations.

6.1 Task 1: Normal case

In this task, the performance of the coupled-tank system under three different set-points, namely 0.5 m, 0.3 m, and 0.55 m is presented. Figure 5 indicates the output response for the proposed SMC-DRNN, ARBFNNE-SMC and PID-SMC. The performance of the developed SMC-DRNN is better than other schemes in which it has less settling time and overshoot than other controllers. Figure 6 indicates the MAE for all schemes. The MAE for the developed SMC-DRNN is less than those obtained for other schemes. So, the developed SMC-DRNN scheme can track the change of desired output with good performance compared with other schemes.

Fig. 5
figure 5

Response of the coupled-tank system for task 1

Full size image
Fig. 6
figure 6

MAE for task 1

Full size image

6.2 Task 2: Uncertainty due to an external disturbance

This task aims to demonstrate how the uncertainty resulting from external disturbance in the water level of the destination tank affects the coupled-tank system. Figure 7 depicts the response of the system with adding external disturbance; \(\Delta {L}_{1}=0.02 {\text{m}}\) after at \(\varrho =150\) of simulation. The results indicate that the developed SMC-DRNN has a better performance with less settling time and an overshoot after adding the disturbance value compared with other schemes. Additionally, Fig. 8 displays that the MAE for the developed SMC-DRNN is less than those obtained with other controllers. Therefore, the developed SMC-DRNN can handle the effect of uncertainties due to an external disturbance.

Fig. 7
figure 7

Response of the coupled-tank system for task 2

Full size image
Fig. 8
figure 8

MAE for task 2

Full size image

6.3 Task 3: Uncertainty in the system parameters

This task demonstrates how introducing uncertainty in the system parameters; \({A}_{d}\) and \({C}_{2}\) affects the performance of the system. Figure 9 shows the output of the coupled-tank system when the uncertainty values; \({A}_{d}=0.01\) and \({C}_{2}=0.15\) are added at \(\varrho =150\) of simulation. Figure 10 shows the MAE for the developed SMC-DRNN and other schemes. It is seen from the results that the developed SMC-DRNN can handle the effect of the uncertainties due to the variations in system parameters compared to other controllers.

Fig. 9
figure 9

Response of the coupled-tank system for task 3

Full size image
Fig. 10
figure 10

MAE for task 3

Full size image

6.4 Task 4: Uncertainty due to external disturbance and parameters variations

This task demonstrates the impact of introducing uncertainty in the system parameters; \({A}_{d}\) and \({C}_{2}\), as well as the uncertainty resulting from adding external disturbance in the destination tank level. Figure 11 indicates the response of the system after adding uncertainties values; \({A}_{d}=0.01\), \({C}_{2}=0.15\) and \(\Delta {L}_{1}=0.02 {\text{m}}\) at \(\varrho =150\) of simulation. The results indicate that the performance of the developed SMC-DRNN after adding the uncertainty values is better than other controllers in which the settling time and the overshoot for the developed controller are less than those obtained for other schemes. On the other hand, the MAE for the developed SMC-DRNN is less than other schemes as shown in Fig. 12. So, the developed SMC-DRNN can reduce the effect of uncertainties due to the variations in system parameters and external disturbance compared with other controllers.

Fig. 11
figure 11

Response of the coupled-tank system for task 4

Full size image
Fig. 12
figure 12

MAE for task 4

Full size image

6.5 Task 5: Uncertainty due to external noise

This task demonstrates the performance of the proposed SMC-DRNN under the effect of uncertainty due to applying random external noise on the system output. Figure 13 shows the system output for the proposed SMC-DRNN and other controllers. Figure 14 shows the MAE for all controllers. The MAE for the proposed SMC-DRNN is less than other controllers. Therefore, the proposed SMC-DRNN can reduce the effect of external random noise.

Fig. 13
figure 13

Response of the coupled-tank system for task 5

Full size image
Fig. 14
figure 14

MAE for task 5

Full size image

Tables 2 and 3 present the MAE and RMSE values, respectively, for the proposed SMC-DRNN and other existing schemes; ARBFNNE-SMC [9] and PID-SMC [32]. It is clear that the MAE and RMSE values for the developed SMC-DRNN are less than those obtained for ARBFNNE-SMC [9] and PID-SMC [32] for all simulation tasks. Therefore, the robustness of the developed SMC-DRNN is better than ARBFNNE-SMC [9] and PID-SMC [32] to handle the effect of system uncertainties due to variations of the system parameters, external disturbance and external random noise.

Table 1 Parameters of coupled tank system [32]
Full size table
Table 2 MAE values for all controllers
Full size table
Table 3 RMSE values for all controllers
Full size table

Table 4 lists the computation time and space complexity of the proposed SMC-DRNN algorithm and other compared algorithms in terms of sliding surface, equivalent control part and sliding surface parameters. It is clear that the computation time for the proposed SMC-DRNN controller is approximately equals the computation time for the ARBFNNE-SMC [9]. The proposed SMC-DRNN uses nonlinear sliding surface, which is designed based on DRNN while the other controllers use linear sliding surface. The proposed SMC-DRNN uses the DRNN to represent the equivalent control part. On the other hand, the ARBFNNE-SMC [9] uses an ARBFNN to represent the equivalent control.

Table 4 The time and space complexity of all algorithms
Full size table

7 Conclusions

In this paper, SMC based-DRNN is introduced for uncertain nonlinear coupled tank system. The control law for the developed scheme consists of two items; the first item is the equivalent control term, which is performed using the DRNN to approximate the dynamics of the coupled tank system. So, the problem of obtaining the precise mathematical model for the controlled process to design the SMC is compensated. The other part of the control law for the developed scheme is the switching control term, in which the sliding surface is performed using the DRNN. The discontinuous signum function is used for the switching control term. Therefore, the problem of chattering is compensated. The updating weights of the DRNN are obtained using Lyapunov function to guarantee the controlled system stability. The simulation results including the system uncertainties due to the effect of variations of system parameters and an external disturbance for the proposed controller are compared with other existing schemes to show the robustness of the developed scheme. The compressions are done by measuring the MAE and RMSE for the developed SMC-DRNN and other schemes. The simulation results indicate that the proposed controller can handle the effects of system uncertainties and external disturbances compared to other existing schemes.

Finaly, the proposed SMC-DRNN improved the performance of the controlled system, and it can handle the problem of knowing the perfect mathematical model of the controlled process by using DRNN, which is used to represent the equivalent control part. Also, the proposed controller handles the problem of the chattering by using DRNN to represent the sliding surface and discontinuous signum function. On the other hand, the author uses a constant number of neurons in the hidden layer of DRNN. The performance of the DRNN depends on the number of neurons in the hidden layer and the structure of the network. Therefore, in the future work, the author will develop the structure of the DRNN by using self-organizing algorithms to learn or update the structure of the DRNN.