1 Introduction

Speed control of electric motors is a significant requirement in several industry applications such as CNC, electric and hybrid vehicles, traction motors, servo systems, pumps and similar systems that need operation under constant speed. In line with the technological improvements, the needs for higher efficiency and lower size have been growing day-by-day and brushless DC (BLDC) motors have gained incontrovertible popularity in this direction, replacing the induction motor (IM) motor and brushed DC motor in several systems. Further, compared with its sinusoidal counterpart termed as permanent magnet synchronous motor (PMSM), the BLDC motor permits some important system and operational simplifications while generating relatively higher power density [1]. However, the major disadvantage of BLDC motor comes from its nonlinear model, which makes the controller design task complicated.

The above-described shortcoming of BLDC motor has inspired many researches reporting advanced control techniques based on sliding modes [2], fuzzy logic [3], adaptive neuro-fuzzy inference system [4], fuzzy neural network PID controller structure [5], nonlinear feedback controller [6], fractional order concept [7], model predictive control [8], etc. Although these controllers are shown to yield satisfactory performance, they are based on complex control laws and heavy computational operations, often resulting in an impractical solution for engineering commissioning. As a result, proposing new control schemes that not only provide a practical solution for the electric drive community but also offer a good controlling effort is always welcome.

Our rigorous literature survey points out that with structural variations and modifications on the classical PID controller, a good option for effective closed-loop control can be achieved, though they are recognized as obsolete. In this regard, two-degree-of-freedom (2DOF) control is successfully applied to speed control in permanent magnet brushed DC motor [9] and PMSM [10], which has a nonlinear model. A PI controller is used in [11] to accomplish speed regulation in PMSMs. The controller parameters are adaptive and adjusted by a fuzzy logic controller (FLC) with respect to the speed error and its time derivative. Similarly, a hybrid method is proposed to achieve an effective control of the speed of the BLDC motor [12]. In the method, PID controller is employed to control the speed of the motor, whose best gain parameters are tuned by student psychology optimization algorithm-based radial basis function neural network. [13] applied particle swarm optimization (PSO) algorithm to search for optimal parameters of PID controller in BLDC speed control system. Experimental results based on TI TMS320F2812 revealed that PSO optimized PID controller could perform better than conventional PID controller in augmenting the step speed response and load impact. A self-tuning PID control scheme is introduced in [14] to deal with the auto-tuning of PID controller for deriving optimal performance under wide speed range. It is shown that the proposed controller is more effective than the classical one with fixed parameter gains. On the other hand, gray wolf optimization [15]/hybrid firefly algorithm-pattern search [16]/quasi-oppositional differential search algorithm [17] optimized PI/PID, jaya algorithm-invasive weed optimization [18]/optics inspired optimization [19]/improved stochastic fractal search algorithm [20]/symbiotic organisms search (SOS) [21] optimized PID, SOS optimized PIDN [22], hybrid invasive weed optimization-pattern search optimized 2DOF-PID [23], biogeography based optimization-based three-degree-of-freedom-PID (3DOF-PID) [24], sine–cosine algorithm optimized proportional derivative-proportional integral derivative with double derivative filter (PDPID + DDF) [25] and dragonfly search algorithm (DSA) tuned (1 + PD)-PI [26] controllers have also appeared to resolve load frequency control (LFC) problem in diverse power systems. Good controlling effort is achieved by the above controllers although the systems tested are governed by several nonlinearities. As a result, by the simple and successful idea of combining the advantages of different P/I/D combinations, it is possible to obtain increased dynamic performance. This is the main intention and contribution of the current article.

It is noticeable from the above discussion that the mechanism of evolutionary computation has been employed to design effective control techniques using metaheuristic algorithms, which have been of interest to researchers in different fields, particularly for the last two decades. The reason behind such a great attention is that the classical deterministic and gradient-based methods are not capable of handling cost functions that are non-convex and contain multiple local optimum solutions. The severity further increases when the complexity of the system under control grows. These concerns give rise to stagnation in the solutions and it is likely to obtain sub-optimal results while more promising solutions are missed out. Nonetheless, thanks to the continuous progress made on metaheuristic algorithms in line with the no-free-lunch theorem [27], new avenues in solution quality, convergence behavior and implementation time have been incorporated to mitigate such issues efficiently. Indeed, the literature has been witnessing numerous metaheuristic algorithms based on inspiration from different concepts and the researchers are found very keen on applying them to acquire unknown controller parameters of their control system design. Apart from the references above, the application of genetic algorithm (GA) to tune all the parameters of FLC was addressed in [28, 29] to enhance speed response profile of PMSM under speed reference and load torque variations. Parameters of a PI controller in a DSP-based DC servo drive were effectively derived by the SOS algorithm [30]. For the same system, PI + DF technique, as a new control scheme, was also suggested and its parameters were tuned by stochastic fractal search algorithm [31]. Optimal design of a robust parallel Fuzzy P + Fuzzy I + Fuzzy D controller based on a GA hybridized by PSO approach was introduced for an automatic voltage regulator system [32]. More recently, a novel imperialist competitive algorithm optimized cascade fuzzy-proportional integral derivative incorporating filter (PIDN)-fractional order PIDN (FPIDN-FOPIDN) controller [33], DSA optimized FOPI-FOPD controller [34] and salp swarm algorithm optimized fuzzy 1 + proportional derivative-tilt integral (F1PD-TI) controller [35] have been also appeared in the literature to better address LFC issue. To our best knowledge, it seems there is no prior research taking advantages of a cascade one proportional derivative with filter (1PDf)-proportional integral (PI) (c-1PDf-PI) controller in any control system. As such, we apply this controller to speed control system of BLDC motor where the snake optimizer (SO) along with a suitable cost function is employed to help in finding the optimal controller parameters.

SO is one of the nature-inspired metaheuristic algorithms that have been recently proposed to handle different optimization problems in a better way [36]. As the name implies, the algorithm mimics the special mating concept of snakes. Each snake (male or female) endeavors to engage with the best partner if the available food is sufficient and the ambient temperature is low enough. By modeling such forage and reproduction strategies mathematically with simple and straightforward operations, SO could achieve a good capacity in exploration–exploitation balance and convergence speed on various search spaces. This has been supported by the numerical results and statistical comparisons obtained in several problems such as LFC problem [37], thermal error forecast model of motorized spindle [38], power-aware task scheduler [39], feature selection [40], etc.

In the present research, a new c-1PDf-PI controller is applied to speed control in BLDC motor and we show the interesting features of this controller with respect to speed reference change and external torque disturbances. In lieu of trial-and-error approach, SO, as the recent and potent optimization algorithm, has been adopted to find out the best combination of controller parameters. It is believed that the improved performance and simplicity of the c-1PDf-PI controller render it attractive for research community and commercial BLDC motor drives. Eventually, results of simulation based on C +  + IDE and real-time experiments using DSP of TI TMS320F28335 are demonstrated to verify the performance of the proposed control scheme. Moreover, comparisons with PI and 1PDf speed controllers are also presented.

The workflow of this article is as follows: Sect. 2 presents the drive system and mathematical modeling of BLDC motor. The c-1PDf-PI controller structure, review of the SO mechanism and SO-based controller design are introduced in Sect. 3. Section 4 is devoted to various comparative results as to reveal the performance of our proposal. Finally, some concluding marks and future work are given in Sect. 5.

2 Brushless DC motor model and its drive system

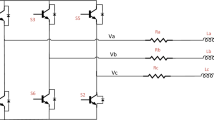
In a BLDC motor drive system, one way is to regulate motor currents individually. This needs three current sensors to be placed in the ac-link to sense each of the phase currents. Given the structure of this kind of drive system in Fig. 1a, rectangular current references shown in Fig. 1b with 120° duration are generated as a function of rotor electrical position θe and current reference I*, which is obtained from the output of the c-1PDf-PI controller. Based on the comparison between current references \({i}_{{\text{a}},{\text{b}},{\text{c}}}^{*}\) and measured currents \({i}_{{\text{a}},{\text{b}},{\text{c}}}\), hysteresis current controllers generate the switch signals directly. So, stator currents are regulated so that they can strictly track their references within a predetermined hysteresis band.

Fig. 1
figure 1

Typical schematics for BLDC motor a drive system b current and emf waveforms

Full size image

The stator voltage equation of a BLDC motor can be written as:

$$\left[\begin{array}{c}{v}_{{\text{a}}}\\ {v}_{{\text{b}}}\\ {v}_{{\text{c}}}\end{array}\right]=\left[\begin{array}{ccc}{R}_{{\text{a}}}& 0& 0\\ 0& {R}_{{\text{a}}}& 0\\ 0& 0& {R}_{{\text{a}}}\end{array}\right]\left[\begin{array}{c}{i}_{{\text{a}}}\\ {i}_{{\text{b}}}\\ {i}_{{\text{c}}}\end{array}\right]+\left[\begin{array}{ccc}{L}_{{\text{s}}}& 0& 0\\ 0& {L}_{{\text{s}}}& 0\\ 0& 0& {L}_{{\text{s}}}\end{array}\right]\frac{{\text{d}}}{{\text{d}}t}\left[\begin{array}{c}{i}_{{\text{a}}}\\ {i}_{{\text{b}}}\\ {i}_{{\text{c}}}\end{array}\right]+\left[\begin{array}{c}{e}_{{\text{a}}}\\ {e}_{{\text{b}}}\\ {e}_{{\text{c}}}\end{array}\right]$$
(1)

where va, vb, vc are phase voltages, ia, ib, ic are phase currents, ea, ea, ec are induced emfs, Ra is stator winding resistance, and Ls is synchronous inductance.

For the electromagnetic torque Te, we have:

$${T}_{e}=\frac{p}{2}\frac{{e}_{{\text{a}}}{i}_{{\text{a}}}+{e}_{{\text{b}}}{i}_{{\text{b}}}+{e}_{{\text{c}}}{i}_{{\text{c}}}}{{\omega }_{e}}$$
(2)

where p is the number of poles and ωe is the electrical rotor speed in rad s−1. Finally, we can arrive the rotor speed equation in state-space form as:

$$\frac{{\text{d}}}{{\text{d}}t}{\omega }_{r}=\frac{p}{2}\left({T}_{e}-{T}_{L}-B\left(\frac{2}{p}\right){\omega }_{r}\right)/J$$
(3)

where J > 0 and B > 0 are inertia and viscous friction coefficient of the whole rotating system, whereas TL is the applied load torque.

In BLDC motor, only two phases are conducted and the remaining phase is kept open at any instant. Considering the emf and corresponding phase current are in phase, the total electromagnetic torque becomes equal to combination of those obtained from the two phases. Let E and I be the magnitude of emf and phase current, respectively, Eq. (2) is simplified and rewritten as:

$${T}_{e}=p\frac{EI}{{\omega }_{e}}$$
(4)

It is noticeable from Eq. (4) that as long as E and I are constant, i.e., free of harmonics, the electromagnetic torque Te maintains constant inherently.

3 Proposed speed control system

3.1 c-1PDf-PI controller

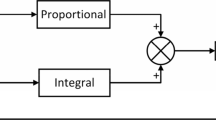
Although PID controller is perceived as outdated, it constitutes a good alternative for effective control system when improved by some structural variations and modifications. In this respect, the literature has witnessed enormous volume of research work to fulfill challenges in different systems, as discussed previously. However, to our best knowledge, c-1PDf-PI controller has not been observed yet in the literature. Thereby, in the present study, it is recommended to regulate velocity in BLDC motor as an effective, vigorous and simple controller. The configuration of this controller is depicted in Fig. 2. As seen, the controller is composed of a 1PDf and PI controller connected in cascade. That is, the output of 1PDf controller is y, which is the input of PI controller. After acting on the speed error eω, the controller produces control input or current reference I*, which is mathematically given by

$$I^{*} = \left( {\overbrace {{e_{\omega } + e_{\omega } K_{{{\text{p}}1}} + \frac{{e_{\omega } K_{{\text{d}}} sf}}{s + f}}}^{y\left( s \right)}} \right) \times \left( {K_{{{\text{p}}2}} + \frac{{K_{{\text{i}}} }}{s}} \right)$$
(5)

where Kp1 and Kp2 are proportional gains, Ki is integral gain, Kd is derivative gain, and f is the filter coefficient.

Fig. 2
figure 2

The configuration of the c-1PDf-PI speed controller

Full size image

Interestingly, this controller has superb performance, but it has some implementational problems, such as chattering due to the noise and integral windup due to the iterated accumulation overflow. The former issue can be resolved by putting a first-order filter on the derivative part and tuning the respective gains, i.e., Kd and f, such in a way that high-frequency noise is damped. The practical solution to the latter problem is to alter the form of the integral term and use the equivalent expression instead. For this, PI control law in s-domain is written first using PI block diagram in Fig. 2:

$${I}^{*}\left(s\right)={K}_{{\text{p}}2}y\left(s\right)+{K}_{{\text{i}}}\frac{y\left(s\right)}{s}$$
(6)

where \(y\left(s\right)={e}_{\omega }\left(s\right)+{{e}_{\omega }\left(s\right)K}_{{\text{p}}1}+\frac{{{e}_{\omega }\left(s\right)K}_{{\text{d}}}sf}{s+f}\) as derived via 1PDf block diagram in Fig. 2. Substituting y(s) in Eq. (6), we can easily arrive at Eq. (5), which relates I* to eω. The time-domain form of Eq. (6) is also written as:

$${I}^{*}\left(t\right)={K}_{{\text{p}}2}y\left(t\right)+{K}_{{\text{i}}}{\int }_{0}^{t}y\left(t\right)dt$$
(7)

Taking the time derivative of both sides of Eq. (7) gives the following equation:

$${I}^{*}\left(k\right)-{I}^{*}\left(k-1\right)={K}_{{\text{p}}2}\left[y\left(k\right)-y\left(k-1\right)\right]+{{\text{K}}}_{{\text{i}}}Ty\left(k\right)$$
(8)

where (k) and (k − 1) are, respectively, the current and previous samples for the given variable, and T is the sampling time greater than zero. Equation (8) can be rewritten as:

$${\Delta I}^{*}\left(k\right)={K}_{{\text{p}}2}\Delta y\left(k\right)+{K}_{{\text{i}}}Ty\left(k\right)$$
(9)

Notice that Eq. (9) results in the change in current reference and it does no longer have integration term, eliminating the risk of excessive accumulation and unwanted problem of windup. Eventually, to calculate the actual current reference I*(k), ∆I*(k) needs to be added to the previous current reference ∆I*(k − 1) as:

$${I}^{*}\left(k\right)={\Delta I}^{*}\left(k\right)+{I}^{*}\left(k-1\right)$$
(10)

The parameters to be tuned for the proposed c-1PDf-PI controller are 5, which are Kp1, Kp2, Ki, Kd and f. To ensure the best performance for the controller, its parameters are optimized using SO through a more appropriate cost function.

3.2 Snake optimizer

As the name implies, SO is an optimizer recently proposed to deal with optimization challenges alternatively [36]. The main inspiration source is special mating concept of snakes. Mating between males and females occurs under some conditions. For example, the temperature should be low enough. Moreover, availability of food also affects the mating process. If the conditions are satisfied, opponent males will fight each other to be a king and accordingly impress females. If the female decides to mate, mating takes place and the female begins to lay its eggs in a nest or burrow. Once the eggs come out, the female leaves the location. Fighting of snakes, their mating and egg-laying are shown in Fig. 3.

Fig. 3
figure 3

Snakes in nature a snake fight b mating process c egg-laying

Full size image

The mathematical modeling of the identified behavior of snakes is described next.

3.2.1 Initialization

SO begins its search by generating a random population from uniform distribution, similar to other metaheuristic algorithms. The random initialization is done by:

$$S_{i} = S_{{{\text{min}}}} + rand \cdot \left( {S_{{{\text{max}}}} - S_{{{\text{min}}}} } \right)$$
(11)

where Si is the position of the ith snake, \(rand\) is a random number in the range [0, 1], Smin and Smax are the problem constraints, standing for the minimum and maximum limits of decision variables, respectively.

3.2.2 Splitting the population into two equal groups: males and females

In original SO, it is assumed that the population of snakes is equally split into two groups: male group and female group. To do this, Eq. (12) is used.

$$\begin{array}{c}{N}_{m}\approx N/2\\ {N}_{f}=N-{N}_{m}\end{array}$$
(12)

where N is the total number of solutions, Nm and Nf denote the number of male and female individuals, respectively.

3.2.3 Evaluation of each group based on temperature and food quantity

The best individual in each group is evaluated and assigned as fbest,m for the best male and fbest,f for the best female. The food position ffood is also gained.

Using the iteration index t and maximal iteration number T, the temperature is altered in an exponentially decreasing trend in the algorithm as:

$$Temp={\text{exp}}\left(\frac{-t}{T}\right)$$
(13)

As concerned to food quantity, it is calculated by:

$$Q={c}_{1}\cdot {\text{exp}}\left(\frac{t-T}{T}\right)$$
(14)

where c1 is a constant equal to 0.5.

3.2.4 Exploration phase with no food

If \(Q\) is smaller than a threshold value, i.e., 0.25, SO emphasizes on exploration where the snakes look for food source by choosing a random solution from the population and updating their position relative to it. This is governed by:

$${S}_{i,m}\left(t+1\right)={S}_{rand,m}\left(t\right)\pm {c}_{2}\cdot {A}_{{\text{m}}}\cdot \left({S}_{{\text{min}}}+rand\cdot \left({S}_{{\text{max}}}-{S}_{{\text{min}}}\right)\right)$$
(15)

where Si,m is the ith male position, Srand,m is the position of random male, c2 is a constant equal to 0.05 and Am is the male ability to discover food, which is calculated as:

$${A}_{{\text{m}}}={\text{exp}}\left(\frac{-{f}_{rand,m}}{{f}_{i,m}}\right)$$
(16)

where frand,m indicates the fitness of Srand,m, whereas the fitness of Si,m is given by fi,m.

Similarly, Eqs. (15) and (16) are also applied to the group of females as in Eqs. (17) and (18).

$${S}_{i,f}\left(t+1\right)={S}_{rand,f}\left(t\right)\pm {c}_{2}\cdot {A}_{{\text{f}}}\cdot \left({S}_{{\text{min}}}+rand\cdot \left({S}_{{\text{max}}}-{S}_{{\text{min}}}\right)\right)$$
(17)
$${A}_{{\text{f}}}={\text{exp}}\left(\frac{-{f}_{rand,f}}{{f}_{i,f}}\right)$$
(18)

where Si,f is the \(i\)th female position, Srand,f is the position of random female, Af is the female ability to discover food, frand,f is the fitness of Srand,f, and fi,f is the fitness of Si,f.

3.2.5 Exploitation phase with food

If Q is greater than the threshold value and Temp is higher than a threshold value (0.6 treated as hot), snakes will locate themselves around the food using Eq. (19).

$${S}_{i,j}\left(t+1\right)={S}_{food}\pm {c}_{3}\cdot Temp\cdot rand\cdot \left({S}_{food}-{S}_{i,j}\left(t\right)\right)$$
(19)

where Si,j is the position of the \(i\)th snake in the jth dimension (either male of female), Sfood is the position of the best individual, and c3 is a constant whose value is tuned to 2.

If Temp falls below 0.6 (treated as cold), snakes will fight or mate. In case they fight, the following position update rules are governed:

$${S}_{i,m}\left(t+1\right)={S}_{i,m}\left(t\right)+{c}_{3}\cdot FM\cdot rand\cdot \left({Q\cdot S}_{best,f}-{S}_{i,m}\left(t\right)\right)$$
(20)

where Si,m is the ith male position, Sbest,f is the best position in female group, and FM is the fighting ability of the male individual. It is assumed that similar fight also takes place among the female snakes and Eq. (20) is modified as in Eq. (21) for the individuals in female group.

$${S}_{i,f}\left(t+1\right)={S}_{i,f}\left(t\right)+{c}_{3}\cdot FF\cdot rand\cdot \left({Q\cdot S}_{best,m}-{S}_{i,f}\left(t\right)\right)$$
(21)

where Si,f is the ith female position, Sbest,m is the best position in male group, and FF is the fighting ability of the female individual. FM and FF are calculated as:

$$FM={\text{exp}}\left(\frac{-{f}_{best,f}}{{f}_{i}}\right)$$
(22)
$$FF={\text{exp}}\left(\frac{-{f}_{best,m}}{{f}_{i}}\right)$$
(23)

where fbest,f and fbest,m refer to the fitness of Sbest,f and Sbest,m, respectively.

In case the snakes are mating, the following position update rules are used:

$${S}_{i,m}\left(t+1\right)={S}_{i,m}\left(t\right)+{c}_{3}\cdot {M}_{m}\cdot rand\cdot \left({Q\cdot S}_{i,f}\left(t\right)-{S}_{i,m}\left(t\right)\right)$$
(24)
$${S}_{i,f}\left(t+1\right)={S}_{i,f}\left(t\right)+{c}_{3}\cdot {M}_{f}\cdot rand\cdot \left({Q\cdot S}_{i,m}\left(t\right)-{S}_{i,f}\left(t\right)\right)$$
(25)

where Si,m is the ith male position, Si,f is the \(i\)th female position, Mm and Mf are the mating ability of male and female, respectively. They are calculated by:

$${M}_{m}={\text{exp}}\left(\frac{-{f}_{i,f}}{{f}_{i,m}}\right)$$
(26)
$${M}_{f}={\text{exp}}\left(\frac{-{f}_{i,m}}{{f}_{i,f}}\right)$$
(27)

If egg hatches, then the worst male and female individuals are replaced as follows:

$${S}_{worst,m}={S}_{{\text{min}}}+rand\cdot \left({S}_{{\text{max}}}-{S}_{{\text{min}}}\right)$$
(28)
$${S}_{{\text{worst}},f}={S}_{{\text{min}}}+rand\cdot \left({S}_{{\text{max}}}-{S}_{{\text{min}}}\right)$$
(29)

where Sworst,m and Sworst,f refer to the position of individuals in male group and female group, respectively. The operator ± used in the above equations is named as flag direction operator or diversity factor, which adds to or subtracts from solutions’ positions to alter the direction of search agents so that the given search space is sampled and scanned thoroughly in different directions. To better understand the concept of SO, its pseudocode description is provided in Algorithm 1.

Algorithm 1
figure a

Pseudocode of SO

Full size image

In the original paper [36], SO has been benchmarked against several popular and newly developed algorithms such as L-SHADE, LSHADE-EpSin, coyote optimization algorithm, moth-flame optimization, Harris hawks optimizer, grasshopper optimization algorithm and whale optimization algorithm on 29 CEC 2017 benchmark functions and four practical engineering problems. The comparison results affirm the performance of SO in terms of solution accuracy and convergence rate—the interested readers are recommended to kindly refer to reference [36]. As such, replicating already reported results would not only be redundant but also repetitive within the context of this article.

3.3 SO-based controller design

In the present research, the BLDC motor, equivalent drive system and c-1PDf-PI controller are modeled in a MATLAB/m-file script. The differential equations are solved by fourth-order Runge–Kutta technique and trapezoidal method is used to numerically calculate the integral operations needed in the controller. The source codes of SO are also written in another MATLAB/m-file script and the two scripts are linked with each other in order to solve our problem for acquiring optimal parameters of the c-1PDf-PI controller.

There are five parameters required for the design of c-1PDf-PI controller, which are Kp1, Kp2, Ki, Kd and f. At the beginning of the algorithm, a number of snakes (search agents) are generated randomly, each of which has therefore different controller parameters. The search agents are sent to the drive system script to simulate and obtain speed response from the controller. Then, a fitness value is computed for each search agent by employing a more appropriate cost function as:

$$J=\alpha \cdot {\int }_{0}^{{t}_{s}}{e}_{s}^{2}dt+\beta \cdot {\int }_{0}^{{t}_{s}}\left|{e}_{s}\right|{\text{d}}t+\gamma \cdot {I}_{rt}$$
(30)

where es is speed error between the reference and actual speed, ts is simulation time in sec, α&β&γ are the weight factors deciding the significance of each term in Eq. (30). To find a suitable set of these weight factors, we first calculate each term in Eq. (30), revealing that the first term has a value far greater than those of the second and the third term in order. This allows the algorithm to pay more attention to minimizing the squared error (first term) rather than the others. To have a balanced optimization process wherein every contribution in Eq. (30) is influential and considered sufficiently by the algorithm, coefficient of the term with high value should be small, whereas that with small value needs to be increased. Given this, setting α = 0.01, β = 1 and γ = 5 results in good results considering the minimization of both es and Irt simultaneously. Here, Irt is the ripple rate in current reference and calculated by:

$${I}_{rt}=\frac{{I}_{{\text{max}}}-{I}_{{\text{min}}}}{{I}_{{\text{avg}}}}$$
(31)

where Imax, Imin and Iavg are the maximum, minimum and average current reference measured over a time period. Notice that the first two terms in Eq. (30) measure and aim at reducing the speed error in order to have an augmented speed response profile. As concerned to the third term, it helps increase the controller robustness to noise come up with the derivative term in the controller. It is worth explaining that during the cost function evaluation, the speed reference \({\omega }^{*}\) and motor load torque TL are assumed to change from 0 to 3500 rpm and from 0 to 3 Nm in steps of 500 rpm and 0.5 Nm, respectively (the maximum limits are selected based on the motor nameplate). So, there are 54 different combinations of these two variables and the final fitness pertaining to one search agent is calculated as the mean of these 54 costs using:

$$FOD=\left(\sum_{i=1}^{NC}{J}_{i}\right)/NC$$
(32)

where NC denotes the number of different cases equal to 54 and FOD is the final fitness, termed as figure of demerit. After the overall performance of the search agents that are evaluated by Eq. (32), they are fed back to the optimization script to evolve based on the SO concept for the next iterations. This process of switching between the drive system script and the optimization script continues unless t > T.

In order to avoid the impact of stochasticity and show that the improvements do not take place by chance, SO is run 20 times and the results obtained over 20 independent runs are analyzed statistically. In this analysis, the best, worst, average and standard deviation of FOD values calculated for c-1PDf-PI, PI and 1PDf controllers are obtained and tabulated in Table 1. Note that all these results are found when T = 100 and N = 30 in the algorithm. As seen in Table 1, the best FOD value is attained with c-1PDf-PI controller (FOD = 148.2831) compared to PI (FOD = 148.5584) and 1PDf (FOD = 51.1239) controllers. Of course, the smaller the value of FOD, the better the performance we achieve. Table 1 also states that c-1PDf-PI is better than its cousins in terms of other statistical metrics. Overall, considering the standard deviation values which are all closer to zero, one can conclude that SO yields robust performance for the studied controllers in speed regulation of BLDC motor.

Table 1 Statistical minimization results of SO for different controllers
Full size table

The best c-1PDf-PI, PI and 1PDf controller parameters offered by SO and the associated FOD values are given in Table 2. Critical observation of Table 2 points out that Kp2 is far smaller than Kp1 because it is multiplied by ∆y in Eq. (9). To ensure ∆I* in Eq. (9) to accommodate new speed reference hastily, Kp2 should be small. Kd and f are also seen to be small so that the derivative will not amplify the high-frequency noise, but smooths it out sufficiently. As concerned to other controller parameters, they are optimized simultaneously by SO in a way that the FOD value is minimized.

Table 2 Controller parameters and their \(FOD\) values offered by SO
Full size table

Twenty convergence profiles of SO during the optimization of the c-1PDf-PI controller parameters, i.e., when minimizing FOD, are depicted in Fig. 4. As seen, at the start of the optimization, the value of FOD is large and SO tries to minimize it by a set number of iterations using the search concept of its own. It is noticeable from Fig. 4 that each curve stars from a different point because SO is initialized randomly at the beginning of each run. After a dramatic decrease, SO stabilizes and converges around the global optimum, which takes between 20 and 40 iterations only. Thus, this justifies our selection of maximum iteration number as T = 100. When the algorithm stops at T = 100, the c-1PDf-PI controller parameters yielding the minimum value of FOD, i.e., 148.2831 are assumed as optimal and used in simulation and experiments.

Fig. 4
figure 4

Some convergence curves of SO during the minimization of FOD

Full size image

4 Simulation and experimental results

In this section, the performance of the speed control scheme presented in this work is assessed. A comparison study is also established with respect to a PI and 1PDf controller to see whether the cascade connection of them has better performance. The brushless AC motor model Sanyo Denki P50B08100D is the motor to be controlled. A hysteresis brake from Magtrol is coupled to BLDC motor shaft to apply external step torque disturbances. The written motor control algorithm is implemented in DSP of TI TMS320F28335. In the system shown in Fig. 5, there is also a built-in tachogenerator with a voltage constant of 7 V/krpm, which is used to display speed responses in Tektronix DPO 2024B oscilloscope.

Fig. 5
figure 5

Experimental system

Full size image

The brushless AC motor has the nominal parameters as in Table 3.

Table 3 Nominal parameters of the motor model Sanyo Denki P50B08100D
Full size table

In order to evaluate the credibility of the c-1PDf-PI controller, the BLDC motor was tested using three conditions such as speed regulation, torque disturbance rejection and parameter uncertainty. Note that all the results were acquired by keeping the controller parameters same as in Table 2. Simulations performed for this research were conducted in Dev-C +  + IDE and the results were plotted using MATLAB R2017b, running on AMD Ryzen 9 5900HX 3.3 Ghz CPU and 32 GB RAM.

4.1 Speed regulation performance

In this test, firstly speed regulation was realized when the load torque is 1Nm and the speed reference signal is step set to ω* = 2000 rpm. The resulting responses are presented in Fig. 6. In the experimental results, the red and turquoise traces indicate the desired speed and measured speed, ω*, ω, respectively, with a speed scaling factor of 714.3 rpm/div. It is clear that the c-1PDf-PI controller responds better because after a mild overshoot, the speed settles to its reference hastily without unwanted oscillations. Response obtained with the 1PDf speed controller does not have any overshoot, but it yields significant speed error and speed ripple sustained in steady state. It is also seen that the simulated responses are comparable with the experimental results.

Fig. 6
figure 6

Simulated and experimental responses to a step speed reference a comparison in simulation b c-1PDf-PI c PI d 1PDf

Full size image

Secondly, the c-1PDf-PI controller is utilized to track a reference trajectory. The reference trajectory selected for this exercise is ω* = 1700 × (sin(t) + cos(0.5t))rpm. The load torque is in its rated value. Figure 7 depicts the trajectory tracking for the reference trajectory for all the controllers. As it can be seen in Fig. 7, all the controllers are able to give more or less the same responses, where the actual speed tracks the desired trajectory well. Nonetheless, some steady state error and notable speed ripple are observed in the case of the 1PDf controller.

Fig. 7
figure 7

Simulated and experimental tracking performance of controllers for the given reference trajectory a comparison in simulation b c-1PDf-PI c PI d 1PDf

Full size image

In the last exercise for the speed regulation test, the system is run under random step speed references. The speed reference signal is configured as increasing up to 2 s. Each increment occurs after every 0.4 s of time duration with a step change of 500 rpm in speed reference. The simulation and experimental responses under such a case are portrayed in Fig. 8. It is evident from this figure that when the system is controlled by the c-1PDf-PI controller, better controlling effort is achieved where the motor speed is able to track its reference with less overshoot and no steady state error. It is also noted that important speed ripple and steady state error still persist with the 1PDf controller.

Fig. 8
figure 8

Simulated and experimental responses to random step speed references a comparison in simulation b c-1PDf-PI c PI d 1PDf

Full size image

4.2 Torque disturbance rejection

This test aims to check disturbance rejection capabilities of the controllers. For this, the load torque is assumed zero initially while the motor rotates at 2500 rpm. Then, step load torque disturbance of 3.185Nm (rated torque) is applied at t = 0.75 s and removed from the BLDC motor shaft at t = 1.5 s. For clarity, these instants are, respectively, indicated by the marks ↓ and ↑ on the experimental responses. When observing the resulting responses in Fig. 9, one can notice that although torque disturbances seem to be rejected fast by the 1PDf controller, it is not capable to offer acceptable steady state response, where the actual speed could not settle to the reference again after the load application. The PI controller eliminates the steady state error effectively, but it causes large deviations and longer settling time for the response to recover. On the other hand, response with the c-1PDf-PI controller does not have steady state error and is recovered quickly following torque disturbances. Here, it is noteworthy to emphasize that some speed error and considerable speed ripple occur in the experimental response with 1PDf controller.

Fig. 9
figure 9

Simulated and experimental disturbance rejection capacity under sudden load variation a comparison in simulation b c-1PDf-PI c PI d 1PDf

Full size image

4.3 Robustness to variation in motor parameters

Finally, robustness of the c-1PDf-PI controller is tested when there is a change in the induced voltage constant (ke), phase armature resistance (Rϕ) and mechanical time constant (tm) in the presence of load torque disturbances. Carrying out experimental work for this test is impossible because there is no any direct methodology to alter these parameters in practice. However, we believe that the considered motor parameters tend to change by temperature increase during operation in above experimentations, thus already proving the robustness of our proposal experimentally. Here, ke, which is related to the motor torque constant also, is assumed to change in the range of ± 40% and Rϕ in the range of ± 75%. To obtain different mechanical time constants, we consider the friction coefficient \(B\) very close to zero, and change of inertia \(J\) three times greater/lower than the nominal inertia. Setting the step speed command to ω* = 2000 rpm and introducing some torque disturbances of +/− 2Nm, the resulting step responses under parameter changes and torque disturbance are depicted in Fig. 10. Critical observation of Fig. 10 points out that speed regulation is preserved in each condition and load changes are rejected satisfactorily. It is also found that phase resistance is the parameter that has the least impact on the time-domain characteristics of the response comparing with the others. As the result of this test, it is affirmed that c-1PDf-PI controller performs robustly to uncertainty in the motor parameters.

Fig. 10
figure 10

Step response and load disturbance rejection of the c-1PDf-PI controller under a change in a \({k}_{e}\) b \({R}_{\phi }\) c \({t}_{m}\)

Full size image

Our simulation and experimental results in previous sections clearly revealed that c-1PDf-PI controller could provide better system performance by combining the distinct features and advantages of the compared approaches. While it provides performance betterment, its time complexity is unknown, which is important from the view point of practical implementation. To address this aspect, time consumption of each control scheme is measured in DSP and visualized in Fig. 11. Expectedly, minimum time is required by the PI controller, which is followed by the 1PDf and c-1PDf-PI controller, respectively. It may be noted that the time consumption increases notably in the 1PDf implementation, attributable to the calculation of derivative. Further, although the c-1PDf-PI controller combines the two controllers in cascade, its time requirement differs only by a slight increase comparing with that of 1PDf controller. As a result of this analysis, it is elucidated that that our proposal is capable of offering improved system performance without compromising on time complexity much.

Fig. 11
figure 11

Time-consuming of DSP implementation for each control scheme

Full size image

5 Conclusion

In this assessment, a c-1PDf-PI controller was presented to handle the speed regulation issue of BLDC motors effectively. The proposed controller brings together and involves the distinct features of 1PDf controller and PI controller by connecting them in cascade. To attain the best performance from this controller, SO was adopted and the controller parameters were optimized through a reasonable cost function. Performance acquired was tested via simulation and experimental work where a comparison with the 1PDf and PI controllers was also presented. The results witnessed that the c-1PDf-PI controller was able to offer eminent reference tracking performance and torque disturbance rejection with a superb robustness to parameter changes. In the following, the technical features and effectiveness of our proposal were elaborated.

  • The resulting controller provides a simple and efficient control technique for adjustable speed in BLDC motor drives.

  • 1PDf controller allows to have a fast response and has the ability to mitigate high-frequency noise that is normally amplified by the derivative.

  • PI controller plays an important role in eliminating speed error in steady state. Thanks to the integration, which accumulates the speed errors, we have zero or negligible steady error in the speed response profile.

  • The equivalent form of PI control law used in this research does not present integral windup problem owing to excessive integral accumulation.

  • The cascade connection of 1PDf and PI controllers enhances the rejection capacity to disturbance before it propagates to other parts of the control system.

  • There are only five controller parameters whose values are acquired effectively by SO without the need for human knowledge/interpretation.

  • In all conditions tested, satisfactory and robust speed regulation performance is attained wherein the acquired controller parameters need not be reset. This is attributed to the way the optimization process is implemented in which various motor working conditions are taken into account.

Several search avenues could be recommended as future research. Other metaheuristic algorithms instead of SO may be tried out to minimize the cost function further and accordingly escalate the system performance. It is also interesting to apply the c-1PDf-PI controller to other control applications in lieu of speed servo system.