1 Introduction and literature review

Time series data are recorded in diverse application areas ranging from earth sciences to healthcare, finance, traffic, etc. Time series often have missing values (gaps) due to, for example, sensor failures, collection errors, or lack of resources [1,2,3,4]. However, often complete time series datasets are required for analysis or when these data are used as inputs to numerical models. For environmental science applications, such time series gaps could coincide with crucial times where hydrological or biogeochemical fluxes or rates are high. As an example, high stream stage conditions or fluctuations in temperature can promote carbon and nutrient cycling in hyporheic zone environments [5, 6]. Thus, it becomes crucial to impute missing time series values with highly accurate estimates. There are two categories of time series missing value imputation methods, namely multivariate and univariate methods [7, 8]. The first class estimates missing values by exploiting relationships between variables. The second class solely relies on available observations of the time series whose gaps must be filled. In this paper, we study a special case where a large number of consecutive values are missing in a single variable of a multivariate time series.

Many different methods have been used to deal with different characteristics of missing values. For example, for small gaps in univariate time series (individual missing values), the last observation before the gap can be carried forward or the next observation after the gap backward to estimate missing values. Other approaches, which are implemented in ImputeTS [9] provide linear, spline interpolation, or Kalman smoothing methods. Machine learning-based algorithms have also been studied for gap filling purposes. For example, [10] estimated missing values in univariate CO\(_2\) concentrations and air temperature data. This approach, however, is not able to take advantage of multidimensional data.

For the imputation of missing values in the multivariate case, the K-nearest neighbor method has been successfully applied for imputing data in the field of medical science [11]. However, this and other such applications have been limited to imputation problems where values are missing only at random. Recently, recurrent neural networks [12, 13] and generative adversarial networks [14, 15] have been used for imputing values in health-care and public air quality datasets. These studies focused exclusively on the performance and accuracy of the proposed approaches for filling individual randomly missing values.

MLPs have also been successfully used for imputing missing time series values across areas of differing complexity and applications. For example, [16, 17] showed that time delayed deep neural network models can impute missing values in univariate hourly traffic volumes. The referenced works focus on filling relatively short gaps (up to 168 data points) and a genetic algorithm was employed for optimizing the hyperparameters of the used gap filling methods. [18] used an MLP to fill missing values in 16 meteorological drivers and three key ecosystem fluxes in the regional Australian and New Zealand flux tower network. The authors analyzed the performance of gap filling methods by manually changing the lags (the number of historical time steps used for making the next time step prediction). To estimate the missing flux values, they used multiple meteorological drivers such as air temperature, wind speed, soil water content, ground heat flux, and net radiation. The architecture of their MLP was determined by using a grid search method provided in scikit-learn [19]. In another study, [20] focused on filling the gaps in methane flux measurements using multiple input variables including net ecosystem exchange (NEE) of CO\(_2\), latent heat flux, sensible heat flux, global radiation, outgoing long wave radiation, air temperature, soil temperature, relative humidity, vapor pressure deficit, friction velocity, air pressure, and water table height. They used an MLP with two hidden layers and determined the number of nodes by using a three-fold cross-validation method.

Unlike the referenced studies, the main contribution of our work is a method for filling a long continuous gap (e.g., multiple continuous months of missing daily observations) in a single variable of a multivariate time series dataset. Another key difference between the previous studies and our research is the size of the datasets used. Our focus is on smaller datasets that have fewer variables than the cited works. Usually, these types of datasets are hard to use and tend to be discarded in analysis and modeling efforts. Our approach would enable greater use of time series datasets that have multi-year gaps in a variable, which are common in many long-term environmental monitoring observations. In contrast to prior approaches using MLPs, our proposed gap filling method optimizes the MLP model architecture and the length of the lag with an efficient method that is based on surrogate models. Our method requires fewer resources because it is automated and uses adaptive sampling rather than evolutionary or trial-and-error approaches.

In this paper, we present a gap filling approach that is based on the concept of Time-Delayed Deep Neural Networks (TDNN) [21] with the goal of filling a long continuous gap in one variable of a multivariate time series. The concept of TDNN is suitable for handling temporal time series that are a characteristic feature of environmental datasets. This research extends our previous work [22] in which we used deep neural networks to predict groundwater levels for multiple years into the future using supporting variables such as temperature, precipitation, and river flux data. In the cited work, we optimized the network architectures with an automated hyperparameter tuning method, which we adopt and modify in the present work to enable gap filling. We assume that the target time series variable has one large gap and that the supporting variables that explain the target variable are fully observed. Our previous work showed that MLPs are successful in making accurate predictions, and therefore, we use an MLP for gap filling in the present study. Our research will have an impact on application areas where gap-free long-term observations are particularly useful.

The remainder of this paper is organized as follows. Section 2 provides a brief description of MLP models and hyperparameter optimization (HPO) used for gap filling. Section 3 presents the results of our numerical study in which we compare the performance of our proposed method with ImputeTS [9] and mtsdi [23] for filling gaps of various lengths (three months to three years) of three different environmental datasets. Finally, Sect. 4 concludes the paper and provides future research directions.

2 Multilayer perceptrons and hyperparameter optimization for gap filling

In this section, we provide brief descriptions of MLPs and the hyperparameter optimization method used to determine its architecture.

2.1 Multilayer perceptron (MLP)

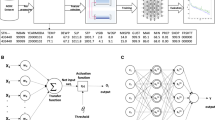
Deep neural networks are known to have the ability to approximate nonlinear functions well. In this paper, we use MLPs with nonlinear activation functions for regression purposes to map input to output features. An MLP is a feed-forward artificial neural network. A generic MLP consists of an input layer, at least one hidden layer, and an output layer with each layer containing multiple nodes. Each node in the input and output layers corresponds to an input feature and target variable, respectively. In order to construct an input layer that encodes temporal information, we structure each input such that it contains multiple time steps. We define the amount of historical information in an input as lag l. Thus, with T time periods, an input is defined as \(\{x_{t-l},\ldots , x_{t-1}, x_t\}\), where \(t=l+1,\ldots , T\). Our goal is to predict the value at the next time step, and thus the output layer has only a single node, which corresponds to the target variable Y that needs to be gap-filled. With this architecture, the MLP is trained by minimizing over a set of weights and biases using a predefined loss function, such as a root-mean-squared error or other metric that reflects how well the MLP approximates the data. The root-mean-squared error is the square root of the average difference between the actual (ground truth) and predicted values. In the first step of this training, linear combinations of input nodes with initial weights are constructed. Each linear combination is passed to all nodes in the first hidden layer. An activation function in the nodes receives this value and returns a transformed value. The transformed values from all nodes in the first hidden layer are given to the nodes in the second hidden layer for further transformation. This process repeats until the output layer returns the final transformed value. The loss function to be minimized reflects the error between the transformed output values and the true values. By iteratively adjusting the weights and biases associated with each node, the loss function is minimized. We use the Rectified Linear Unit (ReLU) activation function, \(f(\cdot )=\max (0,\cdot )\) [24], which allows us to approximate nonlinear functions. Our training objective function (loss) is the mean squared error (MSE). The iterative optimization of the weights and biases is performed with the Adam optimizer [25], which is a type of backpropagation algorithm based on gradient descent and the chain rule [26].

Other essential hyperparameters that influence the performance of the MLP, such as the batch size (size of batched samples in the gradient update), the number of epochs (number of iterations used in training), the dropout rate [27], the number of hidden layers and nodes in each layer, and the lag value l, are determined by the automated optimization method described in the next section. We assume that the learning and decay rates of the stochastic gradient descent method used for training the MLP are known and fixed. For further details about MLPs, we refer the reader to [28].

2.2 Optimization of MLP architectures for gap filling

In order to improve the predictive performance of MLPs (and deep learning models in general), the hyperparameters (model architecture) should be carefully chosen [29]. Different hyperparameter optimization (HPO) methods have been developed and used in the literature, including random search [30], a combination of grid search and trial and error [31], Bayesian optimization [32], and genetic algorithms [33].

In this work, we adapt the HPO method proposed in [22], which interprets the training of a given architecture as an expensive black-box function evaluation of the architecture’s performance. Thus, the goal is to find the best hyperparameters within as few trials as possible by employing computationally efficient methods. To this end, surrogate models (in particular radial basis functions and Gaussian process models) are used to map the hyperparameters to their respective performance. An initial experimental design with \(n_0\) different hyperparameter sets is created for which the performance is evaluated by training the respective models. This initial design is used to create the computationally cheap surrogate models. In each iteration of the optimization, an auxiliary optimization problem is solved on the computationally fast to evaluate surrogate model to determine the next hyperparameters to be tried. The surrogate model is updated each time a new hyperparameter set has been evaluated (see Fig. 1 and Reference [22] for more algorithmic details).

Fig. 1
figure 1

Steps of the surrogate model algorithm used to tune the MLP hyperparameters. For further details, see [22]

Full size image

In order to adapt the HPO algorithm described in [22] for our gap filling purposes, we only have to change the way we split the training and validation datasets by taking into account the fact that some data are missing. Since we include the lag (the number of historical time steps for predicting the value at the next time step) in our list of MLP hyperparameters to be optimized, we have to create a lagged table of the data for each set of hyperparameters we want to evaluate.

We denote the observation matrix with N variables and time length S as \( X = (x_1, x_2, \ldots , x_S)^T \in \mathbb {R}^{S\times N}\), where \(x_s = (x_s^1,x_s^2,\ldots , x_s^N) \in \mathbb {R}^N\) is an observation vector at time \(s, 1\le s\le S\). Each \(x_s^d\) is an observation of the \(d^{th}\) variable, where \(d=1,\ldots , N\). We assume that the first column in the matrix X corresponds to the target vector Y that contains missing values, and the remaining columns are the supporting variables. In the following, we denote \(x^d_s = \text {NaN}\) if the value is missing. For example, assume we have nine observations (\(S=9\)), one target variable, and two supporting variables (\(N=3\)), then the observation matrix and target value vector are, respectively,

figure a

Here, the values for \(x^1_5\) and \(x^1_6\) are missing and the goal is to estimate their values using an optimized MLP. Then, the lagged table for, e.g., lag \(l=1\) becomes

figure b

After the lagged tables have been constructed, we determine if they contain any missing values (NaN). Any row that contains at least one NaN entry in the input or output can be removed because the rows in the lagged table are independent. Thus, for the above example, we obtain the following reduced inputs and outputs

figure c

Once the reduced lagged input and output are obtained, they are divided into training and validation datasets. For any architecture, the reduced lagged training dataset is used to train the corresponding neural network model. Since this training is done by stochastic gradient descent (and thus the final trained model can be interpreted as the realization of a stochastic process), we train the model M times, each with a different random number seed. Each of the M trained models is validated against the reduced lagged validation dataset, and the architecture’s performance is calculated as the sample average over all M values.

Finally, we impute the missing values sequentially starting from the first missing value to the last missing value, using the previous estimated missing value to impute the next missing value. In the small example above, we impute the first missing value \(x^1_5\) and denote it as \(\hat{x}^1_5\) by using \((x^1_3, x^2_3, x^3_3, x^1_4, x^2_4, x^3_4)\). Then, the next missing value (\(x_6^1\)) is estimated based on \(\hat{x}^1_5\), i.e., \((x^1_4, x^2_4, x^3_4, \hat{x}^1_5, x^2_5, x^3_5)\). In this way, all missing values are estimated.

3 Numerical experiments

In this section, we demonstrate that our proposed method for gap filling of multivariate time series data is general enough to be used in different applications that have varying observation frequencies and data characteristics. We describe three time series datasets for which we assume that the target variable has one large gap that must be filled. These time series include observed groundwater levels, simulated soil moisture, and derived net ecosystem exchange from flux tower measurements. Below, we provide details of the setup of the numerical experiments and alternative gap filling algorithms that we use for comparison.

3.1 Description of the datasets

3.1.1 Measured groundwater levels

Our first dataset contained groundwater level time series measured in a groundwater monitoring well in Butte County in California (CA), United States. The monitoring wellFootnote 1 is 200 m deep from the surface, and provides the groundwater elevation above the mean sea level at daily time resolution. We obtained the data from the California Natural Resources Agency. Our goal was to gap fill the time series of groundwater levels using measurements of the supporting variables - temperature, precipitation and river discharge. The nearest discharge monitoring station (Butte Creek Durham) measures the daily discharge rate at the Butte Creek about 8 km from the wellFootnote 2. Temperature and precipitation data were obtained from the Chico weather station located 7 km from the well siteFootnote 3. The dataset used in the study consisted of approximately eight years (2010-2018) of daily observations. For a more detailed description of the dataset and the data sources, we refer the reader to [22, 34]. Figure 2 shows the time series plots for all variables.

Fig. 2
figure 2

Time series plots for the groundwater level imputation test case. Shown are (top to bottom) the daily groundwater levels (GW), temperature (Temp), precipitation (Rain), and log-transformed riverflux

Full size image

3.1.2 Simulated soil moisture

Our second dataset was created with the HYDRUS-1D model [35, 36], a soil hydrologic simulation model. The HYDRUS-1D model is a modular, freely-available, state-of-the-art, and widely used soil hydrologic model with many advanced and coupled water and reactive chemical transport features including equivalent continuum and dual permeability modeling approaches for preferential flow and transport. In particular, the model simulates water, heat and solute transport in variably saturated and saturated porous media. The model has been extensively applied for modeling across scales—from laboratory cores to watersheds [37, 38].

Here, we used the HYDRUS-1D model to simulate a representative soil column in the Butte County in California to determine the changes in soil moisture profiles over approximately seven years (2011-2018). As a result, our target variable was the daily total water content (TWC) in the upper 80 cm of the simulated soil column. The net amount of water entering the soil column from the top (vTop) and the groundwater recharge were used as the supporting variables for calculations. Figure 3 shows the time series plots for all variables. Because simulation models usually do not lead to missing values, we use it here as an ideal case study to investigate the general applicability of our MLP-based gap filling approach.

Fig. 3
figure 3

Time series plots for the soil moisture imputation test case. Shown are (top to bottom) the daily total water content (TWC), the net amount of water entering the soil column from the top (vTop), and the groundwater recharge

Full size image

3.1.3 Net ecosystem exchange data

Our third example application was the most recently produced FLUXNET dataset, that is FLUXNET2015 dataset. It includes data on CO\(_2\), water, energy exchange, and other meteorological and biological measurements [39, 40]. The eddy-covariance method is used to allow for the non-destructive estimation of fluxes between atmosphere and biosphere for a single site to global scale. FLUXNET datasets have been used in a wide range of research areas ranging from soil microbiology to validation of large-scale earth system models.

The target and supporting variables for the Morgan Monroe State Forest site, Indiana, United States for 16 years (1999-2014) [41] are described in Table 1 and the time series are illustrated in Fig. 4. Note that none of the variables in the studied date range have missing values.

Table 1 Target and supporting variables with description of FLUXNET2015 dataset
Full size table
Fig. 4
figure 4

Time series plots for the net ecosystem exchange test case. Shown are (top to bottom) the hourly Net Ecosystem Exchange (NEE_VUT_USTAR50), Air Temperature (TA_F), Vapor Pressure Deficit (VPD_F), and incoming shortwave radiation (SW_IN_F)

Full size image

In all three case studies, the supporting variables had been identified with the help of domain science experts, but filter methods, recursive feature elimination, or sensitivity analyses [34] may prove useful to further downselect the most important features. For all test cases, temporal information such as the time of day, the day, and the month of the year the measurements were taken were also included as additional supporting variables. Also, all values of each feature were rescaled with the min-max normalization, i.e., for each variable \(x^i\), to transform all variables to have the same scale. We found the minimum value \(x^i_{\text {min}}\) and the maximum value \(x^i_{\text {max}}\), and we rescaled the values according to \(\tilde{x}^i = \frac{x^i -x^i_{\text {min}}}{x^i_{\text {max}}-x^i_{\text {min}}}\).

3.2 Setup of numerical experiments

3.2.1 HPO details

We implemented the HPO algorithm for gap filling described in Sect. 2.2 in python (version 3.7) using PyTorch (version 1.4.0) [42]. All experiments were run on Ubuntu 16.04 with Intel\(^\circledR \) Xeon(R) CPU E3-1245 v6 @ 3.70GHz \(\times \) 8, and 31.2 GB memory. We used the same parameter settings as in [22] and we optimized over the following hyperparameters and their ranges:

  • Batch size \(\in \{10,15,\ldots ,195, 200\}\),

  • Epochs \(\in \{50,100,\ldots ,450,500\}\),

  • Layers \(\in \{1,2,\ldots ,5,6\}\),

  • Number of hidden nodes \(\in \{5,10,\ldots ,45,50\}\),

  • Dropout rate \(\in \{0.0,0.1,\ldots ,0.4,0.5\}\),

  • Lags \(\in \{30,35,\ldots ,360,365\}\).

The optimization hyperparameters and their possible values were the same for all three test cases. Note that all parameters were mapped to consecutive integers for the optimization, and there is a finite number of possible combinations (architectures). With the provided options, there are 7,588,800 possible MLP architectures, and it is computationally intractable to train that many networks, thus motivating the use of automated HPO.

We assumed that each hidden network layer has the same number of hidden nodes and the same dropout rate. We use the MSE as performance measure in tuning the hyperparameters and we split the data into 85% training data and 15% validation data.

In the HPO algorithm, we set \(n_0=10\) as the initial experimental design size (we used 10 different hyperparameter sets and we trained the models for each to obtain the model performance, which we use to initialize the surrogate model). We stopped the algorithm after \(n = 50\) hyperparameter sets had been tried. In order to take into account the stochasticity that arises from using the stochastic gradient descent method for training the models, we computed the hyperparameter performance as the sample average over multiple training trials. For example, for the daily groundwater level application and the HYDRUS-1D application, we trained the model for each hyperparameter set five times using the same training dataset, and the performance was defined as the average MSE over those trials. Due to the computational expense associated with training the MLP models for the FLUXNET data (because of the large amount of training data), we computed the performance only over one training trial for each hyperparameter set.

3.2.2 Description of gaps in time series data

In order to test our developed gap filling method, we created an artificial continuous gap in the target time series. We studied different instances in which the gaps have varying lengths and are located at different times of the year. By using artificial gaps, we have the ability to compare the gap-filled values to the true held-out observations as well as analyze and compare the performance of different gap filling methods. In all three test cases, the supporting variables did not have gaps.

For the groundwater application, we created gaps of three, six and twelve months of daily observations. For each case, we used 12 different problem instances in which we removed the data of different months of the year, which allowed us to analyze a possible dependence of the performance of the gap filling methods on the trend characteristics of the missing data. For example, for the three month gap, we assumed that groundwater levels were missing (i) from January through March 2012, (ii) from February through April 2012, (iii) from March through May 2012, etc. For the HYDRUS-1D application, we assumed that the total water content values were missing for 12 and 15 months, respectively. For the 12-month gap, we assumed that the total water content values were missing (i) from January 2013 through December 2013, (ii) from February 2013 through January 2014, and (iii) from March 2013 through February 2014. For the 15 months gap, we considered 9 cases where the missing values were staring from the months of April, May, till December. Finally, for the hourly FLUXNET data, we considered between 2,159 hours (3 months) and 35,063 hours (36 months) of missing values in the Net Ecosystem Exchange data (NEE_VUT_USTAR50).

3.2.3 Gap filling algorithms used in the numerical comparison

We compared our proposed gap filling method with state-of-the-art imputation packages, including ImputeTS [9] and mtsdi [23]. ImputeTS is a univariate time series missing value imputation package implemented in R. We used the na.seadec function with an interpolation algorithm. The na.seadec function imputes missing values with deseasonalized time series data and adds the seasonality again. It has the option to identify the number of observations before the seasonal pattern repeats. However, in our applications, this feature did not yield satisfactory results, and thus we manually set the daily time series frequency, i.e., the frequency of 365. mtsdi is an expectation-maximization algorithm-based multivariate time series missing value imputation package in R. We used the default settings, i.e., the mnimput function with the spline method, and we set the spline smooth control to 7. With mtsdi, we included indicator variables such as the month, week, and day.

3.3 Results and discussion

In this section we provide a description of the outcomes of our numerical experiments for all three use cases. We present results in the form of tables and illustrations of the gap filled time series.

3.3.1 Groundwater level predictions

Tables 2, 3, and 4 present a comparison of the root-mean-squared error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) computed between the predicted values and the true (held-out) values for the groundwater use cases with three, six, and twelve months of missing daily data values, respectively. Shown are the three metrics for our proposed MLP-based gap filling method, ImputeTS, and mtsdi. The RMSE and MAE are given in meters (m), and the MAPE is given in percentage. The lower tables show the optimal hyperparameters that were identified with HPO and led to the MLP outcomes.

Table 2 (a) RMSE, MAE, and MAPE values for the different gap filling methods for three months of missing values in daily groundwater levels. (b) Optimal hyperparameters ([batch size, # epochs, # layers, # nodes per layer, dropout rate, # lags]) for both RBF- and GP-based HPO
Full size table

For three months of missing daily observations (top section of Table 2), our results show that the best results were achieved by different methods depending on the date range for which the data are missing. For example, for the three months that span November 2012-January 2013 (see also Fig. 5), the groundwater levels show a linear growth.

Fig. 5
figure 5

Daily groundwater level imputation for three months of missing daily measurement data (November 2012 - January 2013). The top figure shows the missing time series in the context of available data, and the bottom figure shows a zoom onto the missing period. The missing data have a linear trend which is captured by imputeTS and the MLP-based methods

Full size image

All gap filling methods captured this increasing trend and ImputeTS yielded the best performance in terms of the three comparison metrics. This is due to the fact that ImputeTS uses na.seadec with an interpolation algorithm. In other words, ImputeTS performed seasonally decomposed missing value imputation by linear interpolation which yielded excellent agreement with the held-out data for the missing data segment that had linear behavior. Also the MLP-based gap filling methods were able to capture the linear trend, but the predictions were not as accurate. mtsdi introduced strong oscillations around the overall growing trend. Moreover, mtsdi performed overall the worst for all date ranges for the three month test case.

In contrast, Figs. 6 and 7 show scenarios where the data are behaving nonlinearly. In Fig. 6, the interpolation used by imputeTS failed to capture the trend and produced an almost flat prediction. Both MLP-based methods captured the nonlinear trend in the missing data better, yet the deviation over the last \(\sim \) 3 weeks was larger. mtsdi made again predictions with large oscillations around the true data, and for the last 6 weeks of missing data, it deviated significantly from the truth. In Fig. 7, mtsdi shows again an oscillating pattern, whereas imputeTS underestimated the groundwater level. The MLP solutions are closest to reality. Regarding the optimal MLP architectures that correspond to the best solutions, Table 2 shows that there are only few differences. Most optimal architectures have only 1 layer and 40-45 nodes in that layer, often with a relatively large number of training epochs and no dropout. Similarly, the number of lags used to make predictions are 240 days or more, indicating the importance of at least 8 months worth of data points to make accurate predictions for the gap filling. We can also see that there are a few architectures that are more complex with more layers but that achieve a somewhat similar solution quality as the smaller architectures (e.g., missing date range 2012-01-01 to 2012-03-31). This indicates that different architectures may lead to similar results. In this case, choosing the smaller architecture may be beneficial because they tend to train faster.

Fig. 6
figure 6

Daily Groundwater level imputation for three months of missing daily measurement data (February 2012–April 2012). The top figure shows the missing time series in context of available data, and the bottom figure shows a zoom onto the missing period. The missing data have a nonlinear trend and non-interpolating methods like our MLP approach perform better for these instances

Full size image
Fig. 7
figure 7

Daily Groundwater level imputation for three months of missing daily measurement data (March 2012–May 2012). The top figure shows the missing time series in context of available data, and the bottom figure shows a zoom onto the missing period. The missing data have a nonlinear trend and non-interpolating methods like our MLP approach perform better for these instances

Full size image

The results for the case where six months of daily observations were missing are summarized in Table 3. Except for two cases (missing values from July 2012 to December 2012 and from August 2012 to January 2013), our proposed approach with either RBF or GP made more accurate predictions than imputeTS and mtsdi in terms of the comparison metrics. Similarly to the three-month missing data case, architectures of different complexities can lead to similar performance, e.g., missing date range 2012-03-01 to 2012-08-31. The optimal values for the number of lags shows again that more than 200 days are needed to make good gap-filling predictions. This indicates that information about the ups and downs of groundwater levels over the course of several months are needed for good gap filling performance.

Table 3 (a) RMSE, MAE, and MAPE values for the different gap filling methods for six months of missing values in daily groundwater levels. (b) Optimal hyperparameters ([batch size, # epochs, # layers, # nodes per layer, dropout rate, # lags]) for both RBF- and GP-based HPO
Full size table

Figure 8 shows a comparison between all methods with missing values ranging from November 2012 to April 2013.

Fig. 8
figure 8

Daily Groundwater level imputation for six months of missing daily measurement data (November 2012–April 2013). The top figure shows the missing time series in context of available data, and the bottom figure shows a zoom onto the missing period

Full size image

We can see that our proposed method captured the high peak better than the other methods and imputeTS made again a fairly flat prediction. Similarly to the cases of three months of continuous gaps, mtsdi provided the lowest accuracy. Note that the increased size of the continuous gap allowed for a larger probability that seasonality effects will be included in the missing value ranges.

The results for the case where 12 months of daily observations were missing are summarized in Table 4. For all test cases, the MLP was able to fill the gaps better than ImputeTS and mtsdi. For most cases, the performance of ImputeTS and mtsdi does not come close to MLP. From the optimal architectures (lower table) we can see again that different model complexities can lead to similar results, e.g. missing values from 2012-10-01 to 2013-09-30. Whether the possibility of small improvements is worth a significantly larger amount of training time depends in the end on the user and their insights on how these small differences will effect follow-on analyses. Similarly to the previous cases, the lag should comprise at least several months worth of data for achieving good MLP performance.

Table 4 (a) RMSE, MAE, and MAPE values for the different gap filling methods for twelve months of missing values in daily groundwater levels. (b) Optimal hyperparameters ([batch size, # epochs, # layers, # nodes per layer, dropout rate, # lags]) for both RBF- and GP-based HPO
Full size table

Figure 9 shows that the MLP-based gap filling method captured the nonlinearities in the missing data significantly better than mtsdi (which introduced strong oscillations and did not capture the extrema of the missing values) and imputeTS (which failed to capture the winter data (November 2012-April 2013) and appeared like a piece-wise linear approximation of the missing data). The MLP-based imputation method showed stronger deviations from the true data for the last \(\sim \)1.5 months of gap filling, which is possibly due to the fact that our method estimates the missing values sequentially based on the previously estimated values, and thus it is possible that errors started to accumulate.

Fig. 9
figure 9

Daily Groundwater level imputation for twelve months of missing daily measurement data (June 2012–May 2013). The top figure shows the missing time series in context of available data, and the bottom figure shows a zoom onto the missing period. Although all imputation methods try to capture the nonlinearities, the MLP-based imputation agrees best with the true values

Full size image

Comparing the optimal architectures across Tables 2, 3, and 4 shows that the optimal hyperparameters for the MLP depended on the date range for which the data were missing, and thus the same hyperparameters may not be optimal for all date ranges making tuning necessary. Some “preferences” toward architectures with only one layer and lags larger than 200 exist, indicating that the search range over these hyperparameter could potentially be decreased. However, a detailed sensitivity analysis of the MLP performance with respect to the hyperparameters and their search ranges is beyond the scope of this paper. The MLP performance in terms of RMSE, MAE, and MAPE for a specific architecture was impacted by the data that were missing. For example, in Table 2, we see that the same optimal hyperparameters were obtained for the date ranges June 2012-August 2012, July 2012-September 2012, August 2012-October 2012, October 2012-December 2012, and November 2012-January 2013 when using either the RBF or the GP during hyperparameter tuning, respectively. However, the corresponding RMSE metrics ranged between 0.26 and 0.8 for RBF, and between 0.33 and 0.93 for the GP. We observe a similar behavior for the cases of six and twelve months of missing data.

3.3.2 Total water content predictions

Tables 5 and 6 show the results of our data imputation for the TWC simulated with HYDRUS-1D. Shown are the RMSE, MAE, amd MAPE values between the true and estimated values obtained with the different gap filling methods for the 12- and 15-month cases. The optimal hyperparameters for the MLP-based approaches are also shown. Our MLP-based gap filling method achieved better performance than ImputeTS for all three of the tested 12-month date ranges, but it was outperformed by mtsdi for two of the test cases. Notably, for the two cases where mtsdi outperformed the MLP, the largest indicator for MLP performance is the number of lags, which were significantly larger for the two outperformed cases. This may indicate that a too large lag may be detrimental to predictive performance. Compared to the groundwater level time series, the TWC time series has several pronounced small scale features (peaks and troughs) in addition to larger scale trends. Basing predictions on a larger amount of data may not be the best course of action for TWC. In fact, we observe the same pattern (small lags lead to good performance, large lags lead to bad performance) also in the 15-month missing data case in Table 6. Again, the MLP-based gap filling method outperformed imputeTS for all instances, but it was outperformed by mtsdi for most cases. The two instances for which the MLP performed better than mtsdi had a small lag (30 and 120, respectively).

Table 5 (a) RMSE, MAE, and MAPE for the different gap filling methods for 12 months of missing values in daily TWC. (b) Optimal hyperparameters ([batch size, # epochs, # layers, # nodes per layer, dropout rate, # lags]) for both RBF- and GP-based HPO
Full size table
Table 6 (a) RMSE, MAE, and MAPE for the different gap filling methods for 15 months of missing values in daily TWC. (b) Optimal hyperparameters ([batch size, # epochs, # layers, # nodes per layer, dropout rate, # lags]) for both RBF- and GP-based HPO
Full size table

Figure 10 shows the true simulated TWC values and the values as estimated by the gap filling methods for a 12-month case.

Fig. 10
figure 10

Comparison of gap filling methods for daily TWC with missing values between March 2013 and February 2014. The top figure shows the missing time series in context of available data, and the bottom figure shows a zoom onto the missing period

Full size image

We can see that all methods had difficulties capturing the true data, and our proposed method and imputeTS did a better job than mtsdi at capturing the first seven months of missing data, but then both methods generated larger errors during the remaining five months. In contrast, mtsdi did not capture the trend in the data of the first seven months well, but the resulting RMSE is smaller overall regardless.

Figure 11 shows the results for the gap September 2013-November 2014 (a case in which the MLP-based method performed better than the other methods).

Fig. 11
figure 11

Comparison of gap filling methods for daily TWC with missing values between September 2013 and November 2014. The top figure shows the missing time series in context of available data, and the bottom figure shows a zoom onto the missing period

Full size image

We can see that the MLP that used the RBF in the HPO led to predictions that almost perfectly matched the true data. mtsdi appeared to be able to capture some of the trends in the data, in particular the large peaks with higher frequency oscillations, but it failed to approximate the “less rugged” and lower values well. We can also observe from Fig. 11 how important the choice of hyperparameters is for the MLP. The MLP using the GP during HPO did not perform nearly as well as the MLP that used the RBF during HPO. The main differences between both architectures were in the batch size (50 vs. 70), the number of nodes per layer (50 vs. 25), and the number of lags (30 vs. 345). On the other hand, in Fig. 10, the GP-based and RBF-based MLP predictions were approximately equal, and for this case the optimal architectures differed only with respect to the number of nodes per layer (45 vs. 25), with the larger architecture (RBF solution) being marginally better than the GP-based solution. Thus, we can recognize the importance of HPO when using DL models and the sensitivity of the MLP’s performance with regard to the architecture.

3.3.3 FLUXNET predictions

Table 7 shows the results for the FLUXNET2015 dataset. Note that we show the symmetric mean absolute percentage error (SMAPE) rather than MAPE because the true target variable, NEE VUT USTAR50, includes values close to zero. Because the number of available observations was large, we stress-tested the performance of the gap filling methods for very large continuous data gaps, using between 2,159 (3 months) and 35,063 (36 months) missing observations. The results show that the MLP-based gap filling method attained generally better performance than imputeTS and mtsdi. Unlike the previous two case studies, the optimal hyperparameters do not show a pattern in terms of the best MLP performance. In fact, the three metrics (RMSE, MAE, and SMAPE) are fairly similar for MLP RBF and MLP GP, but the corresponding architectures differ a lot. For example, for the case where 2,159 observations were missing, the difference in RMSEs was only 0.02, but the MLP GP used an additional hidden layer and a significantly larger number of lags than the MLP RBF. Thus, for the FLUXNET use case, there may be nonlinear interactions between hyperparameters present, and thus multiple different architectures are able to achieve similar performance. A detailed study of these hyperparameter interactions and performance sensitivities is, however, out of the scope of this paper.

Table 7 (a) RMSE, MAE, and SMAPE for different gap filling methods for hourly FLUXNET dataset. (b) Optimal hyperparameters ([batch size, # epochs, # layers, # nodes per layer, dropout rate, # lags]) for both RBF- and GP-based HPO
Full size table

Figure 12 shows the results for filling the 8,759 missing value gap of NEE_VUT_USTAR50 with the different methods. The top panel shows the true and the estimated values of NEE_VUT_USTAR50 in the context of the longer time series, the middle panel zooms in on the filled gap, and the lower panels show scatter plots of the true values versus the predicted values. If the methods were able to exactly repredict the missing values, all points would lie on the diagonal. The bottom panel of Fig. 12 clearly shows that imputeTS completely failed to capture the variability in the data and it’s predictions are almost a constant value. The MLP-based methods on the other hand made predictions that were close to the true values (points lie close to the diagonal). The point cloud obtained with mtsdi shows a larger variability around the diagonal, and for this use case mtsdi made less reliable predictions.

Fig. 12
figure 12

Hourly NEE_VUT_USTAR50 (FLUXNET) imputation comparison: missing value range is January 1, 2007 to December 31, 2007. The top panel shows the true and the predicted values in the context of the longer time series. The middle panel shows a zoom onto the filled gap. The bottom panels show scatter plots for each method (ideally, prediction and true data are identical and points would lie on the diagonal)

Full size image

Figure 13 plots the results for the case when 17,543 observations are missing. Again, imputeTS failed to capture the trend in the data completely. mtsdi captured the seasonal trend but it failed to accurately predict the large and small values. Our proposed MLP-based imputation methods estimated the high and low values significantly better. This is also reflected in the scatter plots which show that the point clouds of our proposed method lie closer to the diagonal than those of imputeTS and mtsdi.

Fig. 13
figure 13

Hourly NEE_VUT_USTAR50 imputation comparison: missing value range is January 1, 2007 to December 31, 2008. The top panel shows the true and the predicted values in the context of the longer time series. The middle panel shows a zoom onto the filled gap. The bottom panels show scatter plots for each method (ideally, prediction and true data are identical and points would lie on the diagonal)

Full size image

3.3.4 Discussion

The three gap filling case studies showed that there was no one single method that performed best for all problems and all instances. We found that for the two examples with real observation data (as opposed to simulation-created data), our proposed gap filling method tended to outperform both ImputeTS and mtsdi in terms of RMSE, MAE and MAPE (or SMAPE) in particular when the gaps were large. As described in the previous subsections, ImputeTS performed well when the missing data can be approximated by a somewhat (piecewise) linear function. However, for the FLUXNET2015 data, ImputeTS failed, which may be due to the amount of missing data, or perhaps due to the high frequency oscillations in the data. mtsdi performed better than our method for the simulated total water content data in terms of our metrics, although it did not seem to capture much of the details of the lowest values or the dynamics in the data. Figure 11 shows that mtsdi seemed to capture the large faster oscillating peaks quite well, but for the slower changes of TWC, it appeared to use a mean value instead of capturing the slower variabilities in the data.

Although our proposed imputation approach performed generally well and often outperformed the other methods, its computing time requirement was significantly larger than that of imputeTS and mtsdi. This is due to the hyperparameter optimization trying many different sets of hyperparameters and each training is computationally nontrivial. On the other hand, if the values to be gap filled behave nonlinearly, and if high prediction accuracy is desired, we recommend using the DL-based approach due to the limitations of the other methods in these cases. In practice, one would not conduct a detailed study as presented here with artificially created gaps, but rather optimize and train the MLP once for the time series to be gap filled. One way to speed up the DL approach is to either parallelize the repetitions of the training if compute resources are available or to reduce the number of repetitions. However, the latter option may lead to models that are less reliable in terms of predictive performance. In the FLUXNET test cases, we used only one training repetition (instead of five as done with the two other use cases). The MLP-based gap filling method always performed significantly better than the other two methods, indicating that it was not simply a “lucky” draw. At the same time, we saw that different architectures were able to perform similarly well for this case, indicating that there could be regions in the hyperparameter search space where the objective function is flat and thus finding good hyperparameters and well-performing MLPs may be easier.

Many environmental datasets contain functional relationships between data features. However, many time series imputation methods (including the methods ImputeTS and mtsdi discussed in this paper) do not take advantage of this additional information and they use only statistical information contained in the time series data. In other words, they are purely data-driven approaches. Unlike these approaches, our proposed DL method can be extended to include any known physical relationships and constraints in addition to the statistical information. For example, in the HYDRUS-1D case, we know that there is a mass conservation constraint present between the features and it is possible to include this constraint, e.g., by adding a penalty term to the objective function.

In our study, we compared the different methods based on their RMSE, MAE, and MAPE (or SMAPE) performance. Although these measures are widely used, they do not reflect the individual errors well. For example, in the daily TWC imputation comparison shown in Fig. 10, one could argue that the proposed MLP-based methods produce fairly accurate and better predictions than mtsdi for 50% of the missing values, but they accumulate larger errors for the remaining values. On the other hand, mtsdi does not match most of the data well, but its almost flat prediction accrues overall a lower error. Thus, it is possible that optimizing for another performance measure may lead to better outcomes for the MLP methods.

4 Summary and conclusions

In this paper, we proposed a time series missing value imputation method that uses DL models. Our focus was on time series imputation problems where a long continuous gap was present in one variable, and where all other supporting variables are fully observed. Our proposed method uses an MLP whose architecture is tuned with a derivative-free surrogate model based optimization approach. To this end, we modified the hyperparameter optimization approach proposed in [22] in order to facilitate the imputation of missing values in time series.

After training the MLP, we imputed the missing values sequentially from the first missing value to the last missing value, basing predictions on previous predictions as we go along. Our sequential estimation of missing values allowed us to fill long-term gaps. We chose MLPs as DL models because they have previously shown good performance for time series data and because the time needed to optimize the model is significantly shorter than for other types of DL models (see [22]). Generally, however, any feedforward artificial neural network can be used within our proposed method such as convolutional neural networks [43,44,45].

We performed numerical experiments with three different test cases in which we created artificial gaps which allowed us to assess the quality of the gap filled values. We used two test cases with observed values and one test case with simulated data. The numerical results showed that for many problem instances, our proposed approach was able to fill the gaps with highly accurate values and it was able to capture trends and dynamics in the data better than other data-driven methods such as ImputeTS and mtsdi. Using the RBF as surrogate model during HPO appeared to yield more stable performance than using the GP. Therefore, we recommend using our proposed approach with the RBF surrogate during HPO.

The numerical results also showed that the optimal MLP hyperparameters depended on which data were missing (gap size and location in the time series). Therefore, hyperparameter optimization is essential before using any ML model to impute the missing values.

The results of this paper can lay the foundation for studying new approaches for filling long gaps in time series. Although the proposed method was able to fill large gaps with seasonal trends well, including capturing large and small values, it sometimes failed to correctly estimate the missing values toward the end of the data gap, indicating a potential for accumulation of errors as we inform predictions with previously predicted values. A “backward imputation approach” might be helpful to alleviate this drawback. In this approach, we could modify the MLP inputs such that we start imputing data from the end of the gap backwards in time. Combining both forward and backward imputation may allow us to reap the benefits of both.

Our study focused on time series that have one large gap. However, we expect the method to perform reasonably well when we have multiple large gaps in the time series. Since the inputs to the MLP are designed such that they are independent and the HPO is general, we expect that filling multiple gaps with this method is straight-forward. For time series with a mix of large and small gaps, a combination of our DL model-based method and other methods that are aimed at filling small gaps can be used. Incorporation of physics constraints in the DL model predictions has the potential to improve prediction accuracy. Moreover, if values are missing in several variables of the multivariate time series, it may be possible to modify the proposed approach for this scenario. This is a future research topic.

This paper studied the time-series imputation with the MLP which is the most basic feedforward neural network. It would also be interesting to study the proposed time-series imputation approach with other advanced feedforward neural networks such as convolutional neural network [45] and AR-NET [46] as well as recently developed forecasting software such as NeuralProphet [47].