Abstract
In this paper, an online optimization approach of a fractional-order PID controller based on a fractional-order actor-critic algorithm (FOPID-FOAC) is proposed. The proposed FOPID-FOAC scheme exploits the advantages of the FOPID controller and FOAC approaches to improve the performance of nonlinear systems. The proposed FOAC is built by developing a FO-based learning approach for the actor-critic neural network with adaptive learning rates. Moreover, a FO rectified linear unit (RLU) is introduced to enable the AC neural network to define and optimize its own activation function. By the means of the Lyapunov theorem, the convergence and the stability analysis of the proposed algorithm are investigated. The FO operators for the FOAC learning algorithm are obtained using the gray wolf optimization (GWO) algorithm. The effectiveness of the proposed approach is proven by extensive simulations based on the tracking problem of the two degrees of freedom (2-DOF) helicopter system and the stabilization issue of the inverted pendulum (IP) system. Moreover, the performance of the proposed algorithm is compared against optimized FOPID control approaches in different system conditions, namely when the system is subjected to parameter uncertainties and external disturbances. The performance comparison is conducted in terms of two types of performance indices, the error performance indices, and the time response performance indices. The first one includes the integral absolute error (IAE), and the integral squared error (ISE), whereas the second type involves the rising time, the maximum overshoot (Max. OS), and the settling time. The simulation results explicitly indicate the high effectiveness of the proposed FOPID-FOAC controller in terms of the two types of performance measurements under different scenarios compared with the other control algorithms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nowadays, fractional calculus has been proven to be efficient in both theoretical and practical engineering problems. The limitations of conventional differential equations which only use integer operator powers can be alleviated using fractional calculus [65]. System modeling which takes into account fractional-order phenomena like self-resemblance and system state history dependence has been emerged [59]. Due to the complexity of today’s control systems, they are most likely to exhibit such phenomena [42].
In recent years, researchers have shown an increased interest in FOPID controller, which is the upgraded version of PID controller [55]. The extra parameters of the FOPID controllers (i.e., fractional-order in the derivative and integral terms) give it more flexibility and a higher degree of freedom. Hence, the FOPID controller takes the place of the PID controller due to its numerous advantages including its improved set-point tracking, high disturbance rejection, and superior processing capacity to tolerate model uncertainties in nonlinear and real-time applications [66, 73]. However, choosing FOPID controller parameters is a major source of concern, i.e., they must be appropriately tuned to provide the desired performance and stability. In literature, schemes for tuning FOPID controllers are classified into two classes: model-based tuning methods and model-free tuning methods. Numerous studies have been done in order to establish efficient model-based tuning rules and methodologies for FOPID controllers [5, 15]. State feedback-based fractional integral control scheme was used to evaluate the performance of a rotary flexible-joint system’s trajectory tracking [3]. Two degrees of freedom FOPID controller was implemented for a rotary inverted pendulum [12]. Tuning the FO controllers for industrial applications was studied in [67]. However, these methods require an exact dynamic model which is not available for complex nonlinear systems [7, 19, 20, 45]. On the other side, in the model-free tuning methods, there is no existence of a model or process identification [19]. Consequently, the model-free tuning method for FOPID controllers was investigated in [73]. In [75], a model-free adaptive FOPID tuning method was used when the system’s parameters were time-varying. Among model-free tuning methods, machine learning approaches can be a proper solution in tuning the FOPID controller parameters without prior system dynamics information [23, 41, 45]. Tuning of FOPID parameters based on the metaheuristic optimization algorithms was investigated in several papers [30, 38, 43, 44, 53, 79]. In fact, these tuning methods are off-line schemes. Based on its ability to tune more practical controller parameters without a deep knowledge of the system, neural networks (NN) were developed to tune the FOPID controller for many applications [45]. However, the neural networks-based method needs an offline database based on the system’s output for the specific input to obtain the optimal parameters [51]. Hence, developing of a machine learning-based online tuning approach for FOPID controller parameters is the first concern of this study.
As an advancement of machine learning, reinforcement learning (RL) is based on the concept of learning from experience in response to reward or punishment from environment [64]. Reinforcement learning-based control has constituted a significant aspect since it has achieved significant progress for uncertain nonlinear systems [6]. RL provides a direct link between adaptive and optimum control approaches [32]. More specifically, RL is a type of method that provides the development of adaptive controllers that learn the solutions to an optimal control problem. The idea behind RL is that the controller interacts with a system by defining three signals: the state signal which characterizes the state of the system, the action signal which allows the controller to influence the system and the scalar reward signal which provides the controller with feedback on its immediate performance. In literature, the RL algorithms can be classified into three groups; value function iteration, policy iteration and actor-critic (AC) [9]. In the value function algorithm, the RL approach finds the ideal value function in an iterative learning manner. In this aspect, the most prominent and representable algorithm is the Q-learning method [24]. Policy iteration method seeks the optimal control policy by assessing and upgrading its control policies. The AC reinforcement learning aims to combine the advantages of value function iteration and policy iteration methods. In the AC one, the learning agent has been split into two separate entities; the actor and the critic. The actor is used to carry out control actions, and the critic is used to evaluate the actions and feedback the evaluation to the actor such that control performance can be improved [71]. The AC paradigm could be seen as a step forward in auto-tuning methods, in which the agent learns to adapt the parameters of its internal controller without the need for human interaction. A complete overview of RL methods is provided in [32].
Actor-critic learning algorithms have been a research hotspot in recent years because of their ability to learn and adapt to improve the performance of the controller [22, 61]. To realize the critic and the actor, artificial neural networks (ANNs) were developed [17, 54, 74]. In [17], one ANN was used for the critic and another one for the actor. On the other hand, only one ANN was used to implement both the critic and the actor [54, 74]. The latter manner can decrease the demand for storage space and avoid the repeated computation for the outputs of the hidden units. The kernel function of the hidden unit of the AC neural network can be represented by a sophisticated activation function, i.e., Gaussian and RLU [27, 29, 54]. The RLU function is the simplest nonlinear activation function for faster training processing in large network development [29, 47]. It has the advantage that it does not activate all the neurons at the same time and solve the problem of dead neurons.
Several AC learning algorithms were used to tune control parameters in an adaptive way by taking advantage of the model-free and on-line learning properties of reinforcement learning [16, 31]. The AC algorithm-based adaptive PID controller was designed in [2]. However, this method is subjected to high variance and a slow convergence rate. Adaptive PID based on asynchronous advantage AC algorithm was used to enhance the learning rate to train an agent in the parallel threads [63]. Although the learning rate was enhanced compared with [2], their study did not include the whole interaction scenarios into consideration. Besides, it still suffers from complex computation due to the high variance of gradient estimating and sophisticated back propagation. The deep reinforcement learning technique was used to develop a model-free based algorithm for self-tuning of PID [10]. Q-learning technique was used to tune fuzzy PI and fuzzy PD controllers for single-input/single-output and two-input/two-output systems [8]. FOPID based deep-deterministic policy gradient method (FOPID-DDPG) was developed for the tracking problem of a mobile robot [16].
The gradient descent method is commonly used to implement the back-propagation algorithm to train AC neural networks. Other methods are available to train AC neural networks such as conjugate gradient, Gauss-Newton, and Levenberg-Marquardt [14]. Basically, these algorithms are mainly concentrated on integer-order gradient-based AC neural networks. On the other side, the fractional calculus was efficiently incorporated into the field of neural networks. For instant, FO-neural networks have been conducted for time series prediction [77], nonlinear system modeling and control [1, 13, 36]. Besides, a new fractional derivative operator with sigmoid function as the kernel was proposed in [33]. As the fractional derivative can take several values, the FO learning algorithm was accurate than the IO one. More specifically, there are infinitely many degrees of freedom for the FO parameter that can improve the convergence of the learning process [40, 69, 70]. Hence, the second concern of this study is to enhance the convergence of the learning process of the AC learning algorithm using a developed fractional-order learning algorithm.
Motivated by the aforementioned discussion, the main objective of this manuscript is to develop an online optimal control approach based on the fractional-order calculus framework. This controller approach could address important considerations such as reducing error and enhancing performance regardless of parameter uncertainty and disturbances. This objective can be carried out in terms of the following contributions:
-
1.
Developing a FOAC learning algorithm with adaptive learning rates as an improvement to the regular integer AC (IAC) algorithm. Besides, a fractional-order RLU activation function is introduced to enable the AC neural network to define and optimize its own activation function.
-
2.
Using the proposed FOAC algorithm, an online optimization approach for the FOPID controller parameters is developed.
-
3.
Since the efficient of the FOAC approach relies upon its extra embedded FO parameters, the GWO algorithm [39] is utilized for the optimal setting of the FO parameters.
-
4.
The strict proof concerning the boundedness of the proposed FOAC learning algorithm is given based on Lyapunov’s stability theory.
-
5.
Verifying the effectiveness of the developed FOPID-FOAC controller via applying the FOPID-FOAC controller to two uncertain nonlinear systems; the first one is the 2-DOF helicopter system for tracking and regularization issues and the second one is the IP system for the stabilizing issues. Moreover, the performance of the proposed FOPID-FOAC controller scheme is compared with four controller schemes; they are the FOPID controller [66], the FOPID-GWO [30], the FOPID based on the regular IAC (FOPID-IAC), and the FOPID-DDPG [16].
To the best knowledge of the authors, the extension of fractional-order calculus to the regular AC learning algorithm for online optimization of the FOPID controller with adaptive learning rates is not addressed in the literature.
This paper is prepared as follows. In Sect. (2), some necessary definitions of FO calculus and preliminaries of FOPID controller are given. The controller design strategy and the convergence analysis are presented in Sect. (3). The simulation results are presented in Sect. (4) to verify the effectiveness of the proposed control strategy. Finally, this paper is ended with concluding remarks in Sect. (5) followed by the relevant references.
2 Preliminaries
2.1 Fractional-order operator
The general representation of the FO differ-integral operator is as follows [49]:
where \({}_{t_0}D^{\alpha }_{t}\) denotes the fractional calculus operator; \(\alpha \in {\mathbb {R}}\) is the FO; \(t_0\) and t indicate the lower and upper limits of the operator, respectively.
The most frequently used definitions for the fractional calculus are the Caputo, Grunwald-Letnikov (GL), and Riemann-Liouville (RL) definitions.
Definition 1
The GL fractional derivative of order \(\alpha\) for a given function f(t) is defined as [49]:
where the fractional-order \(\alpha\) satisfies \(n-1< \alpha <n\) (i.e. n is the first integer greater than \(\alpha\)); \(\left[ .\right]\) represents the rounding operation; h denotes the step size of the numerical calculation; \(c_q^{(\alpha )}\) is the binomial coefficient that can be defined as:
Definition 2
The RL integral of order \(\alpha\) for a given function f(t) is defined as [49]:
where \(\varGamma (.)\) represents the gamma function.
Property 1
For the fractional-orders \(\alpha _1\) and \(\alpha _2\), the following equality holds for the fractional derivative [49].
Property 2
For fractional derivative with order \(\alpha\), one may write [49].
2.2 Fractional-order PID
The control law formulation for the discrete-time FOPID controller is given by [58].
where u(k) is the controller output; \(K_p\), \(K_I\) , \(K_D\), \(\xi\), and \(\lambda\) are the proportional gain, integral gain, derivative gain, FO integral value, and FO derivative value respectively; T is sampling period; \(e(k-q)\) is error at the previous sampling time. The coefficient \(c_q\) can be calculated more simply by the following recurrence formula:
It is worth mentioning that the classical PID controller is actually a special case of the FOPID controller with \(\xi =1\) and \(\lambda =1\) [30]. Accordingly, the performance of the FOPID controller can be greatly promoted via the tuning of the two extra fractional orders \(\xi\) and \(\lambda\) of the generalized FOPID controller.
In real-time applications, all systems have some degree of nonlinearity and time-varying characteristics which cause significant changes in the dynamic parameters of the system. These issues should be considered for a well-tuned FOPID controller. Hence, the necessity for sophisticated tuning algorithm for the FOPID controller parameters becomes crucial. A proposed approach based on a developed FOAC algorithm with adaptive learning rates to optimize the FOPID parameters online is introduced in the next section.
3 Controller design strategy and convergence analysis
A general uncertain nonlinear system is described as:
where \(y(k+1)\) denotes the system output and f(.) denotes the unknown nonlinear function. Moreover, \(\varPhi (k)\) is the data vector, which is given by:
where u(k) is the system input at the sampling instant k. \(n_y\), and \(n_u\) are the orders of the output and the input, respectively. Assume the given system is controlled using the FOPID controller defined by Eq. (7). Let the vector \(K(k)=[K_P(k),K_I(k),K_D(k),\xi (k),\lambda (k)]\) denotes to the parameters of FOPID controller at time step k. This section aims to design an online tuning algorithm for the FOPID controller parameters based on a developed FOAC algorithm. The significance of the proposed FOAC algorithm is that it is a generalization of the regular IAC theory, which can lead to a more accurate result.
3.1 The proposed FOPID-FOAC algorithm
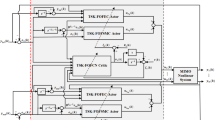
A block diagram of the proposed FOPID-FOAC algorithm is shown in Fig. (1). There are three essential components in the proposed FOPID-FOAC architecture, including a FOAC neural network, a stochastic action modifier (SAM) unit, and a FOPID controller.
The schematic diagram of the proposed FOPID-FOAC algorithm
The FO actor is used to learn the state-to-action mapping that generates the recommended FOPID controller parameters \({\overline{K}}(k)=[{\overline{K}}_P(k),{\overline{K}}_I(k),{\overline{K}}_D(k),{\overline{\xi }}(k),{\overline{\lambda }}(k)]\). The SAM unit is used to generate stochastically the actual FOPID controller parameters according to the recommended parameters suggested by the FO actor [54, 74]. The FO critic receives the system state and external reinforcement signal (i.e., immediate reward r(k)) and produces a temporal difference (TD) error (i.e., \(\delta _{TD}(k)\)) and an estimated value function V(k) of the policy followed by the FO actor. \(\delta _{TD}(k)\) is viewed as an important basis for updating the parameters of the FOAC neural network. V(k) is sent to the SAM unit to modify the output of the FO actor.
3.1.1 Fractional-order actor-critic neural network
The proposed FOAC network is a three layers feed forward network as shown in Fig. (2). It is developed to simultaneously implement the policy function learning of the FO actor and the value function learning of the FO critic. Thus, the FO actor and the FO critic share the input and the hidden layers of the network. The definite meaning of each layer is described as follows.
The input layer receives the state vector x(k) that is \(\left[ e(k), \triangle e(k), \triangle ^2 e(k)\right]\), where e(k) and \(\triangle e(k)\) are the tracking error and its rate of change, respectively.
Fractional-order actor-critic neural network
The proposed FOAC neural network has \(N_{H1}\) neurons on the hidden layer \(H_{1}\). The weighted sum of the n-dimensional input variables to each neuron p on the hidden layer \(H_{1}\) is given by:
where \(w^{(1)}_{p,j}\) is the weighting vector from the input layer to the neuron on the \(H_1\) layer.
The RLU activation function is defined as:
Proposition 1
The RLU activation function given by Eq. (13) can be generalized based on the concept of FO derivative to best fit the input data as:
such that:
where \(\alpha _1\) is the FO derivative parameter of the generalized RLU activation function.
Proof
Let \(f(t)=t^s\), then using Definition 2:
Assumption 1
It should be assumed that t must be greater than 0 to avoid the singularity that can be occurred.
Let
Then
Using the integral bounds 0 and 1, Eq. (16) can be rewritten as:
As the term \(\int _{0}^{1}\left( 1-\hslash \right) ^{(\alpha _1)-1}(\hslash )^{(s+1)-1}d\hslash\) is the Beta function, we have:
By using the properties of Beta function [28], then:
By shifting \(\alpha _1\rightarrow -\alpha _1\) and then using Property 2, the FO derivative of \(t^s\) is:
Let \(s=1\), yields:
\(\varGamma (2)=1!=1\), then:
By applying the FO derivative expressed in Eq. (24), the generalized RLU activation function is obtained as:
It is worth remarking that, the generalized activation function \(\eth (k)\) can change its shape; it can be going from RLU (i.e., \(\alpha _1=0\)) to multi-quadratic (i.e., \(\alpha _1=0.5\)), or to step function for (i.e., \(\alpha _1=1\)) as shown in Fig. (3). This completes the proof of Proposition 1.
The fractional derivative of RLU with order \(\alpha _1\) in the range of [0, 1]
In the proposed FOAC, the output layer is divided into two streams \(\left( H_{2-1},\ H_{2-2}\right)\). There is one neuron in the first stream \(H_{2-1}\) which represents the value function V(k). The second stream \(H_{2-2}\) contains \(N_{H3}\) neurons which derives the control vector \({\overline{K}}(k)\).
The neuron on the \(H_{2-1}\) layer derives the value function V(k) as:
where \(w^{(2)}_{v,p}\) is the weighting vector between \(H_1\) and \(H_{2-1}\) layers.
In the second stream \(H_{2-2}\), the m-dimensional control vector \({\overline{K}}_{i}(k)\) is derived as:
where \(w^{(2)}_{i,p}\) is the weighting vector from the \(H_1\) layer to the output neuron i.
Finally, the SAM unit is presented to expand the search area of the action to generate the actual control parameters. A Gaussian noise term \(n_k(0,\sigma _v(k))\) is added to the recommended control parameters \({{\overline{K}}}(k)\) coming from the FO actor to solve the dilemma of “exploration” and “exploitation”. Consequently, the actual control parameters K(k) is modified as:
where
The magnitude of the Gaussian noise depends on V(k) (i.e., if V(k) is a small value, \(n_k\) will be a large value, and vice versa).
3.1.2 Fractional-order learning rule
In order to obtain the fractional-order adaptive learning rules for the proposed FOAC network, the following quadratic cost function is defined:
where
where \(\varPhi\), \(\psi\), \(\varrho\) and \(\varOmega\) are general positive coefficients.
Here, the temporal difference error of the FO critic \(\delta _{TD}(k)\) is given as:
The reinforcement reward signal r(k) is obtained by:
where
e(k) is the error between the set-point and the output of the system; \(\varepsilon\) is a small constant value( i.e., 0.001).
Essentially, the reinforcement reward signal is the evaluation of the control action , which can take the form of a “zero” or “negative value” corresponding to “adequate” or “insufficiency,” respectively.
Theorem 1
By defining \(\varTheta (k)=\left[ w_{v,p}^{(2)}(k),w_{i,p}^{(2)}(k),w_{p,j}^{(1)}(k)\right] ^T\) and the fractional-order operators \((\alpha _{i},\ i=1:4)\), the learning rules of the proposed FOAC neural network parameters can be defined as:
where \(\kappa _1\textit{, }\kappa _2\text { and }\kappa _3\) are the learning rate parameters.
Proof
The learning procedure is to adapt the parameters \(\varTheta (k)\) of the proposed FOAC by minimizing the criterion \(Q(\varTheta (k))\) defined in Eq. (30). Mainly, it is necessary to solve the following equation:
Thus:
This yields:
Using Definition 1, the general numerical solution of the fractional differential equation can be written as follows [49]:
By substituting from Eq. (42) into Eq. (43), we have:
The TD error difference can be represented using the fractional-order Taylor series expansion as below.
Hence:
where:
As \(\frac{\partial \delta _{TD}(k)}{\partial r(k)}=-1\), the above equation can be set as:
Therefore:
Let \(\kappa _1=\left( \frac{\varPhi }{\varrho }\right)\) , \(\kappa _2=\left( \frac{\psi }{\varrho }\right)\) and \(\kappa _3=\left( \frac{\varOmega }{\varrho }\right)\), hence:
Then, Eq. (44) can be reformulated as:
According to Eqs. (50) and (51), we can write:
Based on the chain rule, the adaptation of the FO critic weights can be obtained by the following equation:
where
Similarly, the adaptation of the FO actor weights can be obtained by :
where
Since there is no gradient information between the actor’s action function and the value function of the critic, the gradient \(\frac{\partial V(k)}{\partial {{\overline{K}}}_{i}(k)}\) can only be estimated by the SAM unit as:
Finally, the adaptation of the FOAC hidden layer weights is obtained by the following equation:
where
This completes the proof of Theorem 1.
The extra FO learning parameters \((\alpha _{i},\ i=1:4)\) play an important role to achieve a desired efficiency of the FOAC approach. In this paper, the FO learning parameters are optimally chosen by employing the GWO algorithm.
3.1.3 Gray wolf optimization
The GWO algorithm mimics the hierarchy of leadership and the mechanism of gray wolf hunting in social life [26, 39]. In decreasing order of dominance, there are four categories of these wolves: \(\mathbbm{k} , \beta , \varLambda \text { and }\omega\). In order to identify the global solution, the optimizer considers three leader wolves \(\mathbbm{k} , \beta \text { and }\varLambda\) as the best solutions for leading the rest of the \(\omega\) wolves toward promising locations. The \(\mathbbm{k} , \beta \text { and }\varLambda\) wolves update their position with respect to the position of the prey in every iteration. This updating will continue until the prey and predator wolf’s distance reaches zero or a satisfactory result is achieved.
In modeling of these wolves, \(\mathbbm{k}\) is the best solution and the other wolves will follow in order of leadership. The hunting is predominantly guided by \(\mathbbm{k} \text { and }\beta\) and then guided by \(\varLambda\) which is followed by \(\omega\).
The GWO algorithm solves the objective function \(J_{obj}\) which includes IAE and ISE as:
where \(\alpha ^*=\left[ \alpha ^*_1,\alpha ^*_2,\alpha ^*_3,\alpha ^*_4\right]\) stands for the optimal solution for the FO parameter of the proposed FOAC learning algorithm, \(\varPsi _\alpha\) is the constrain set of \(\alpha\) which can be formulated as:
where \(\alpha _i^{min}\), \(\alpha _i^{max}\) are the minimum and maximum values of the FO learning parameters, respectively.
According to [68], the GWO algorithm consists of the following steps:
Step 1. The gray wolf population is initially generated. The generated population represented by \(n_{pop}\) dimensional search space for \(M_{ag}\) agent positions. For the iterations, it is initialized from \(h=0\) to maximum iterations \(h_{max}\). The maximum iteration and agent positions in this paper are set to 30 and 100, respectively.
where \(X_{\mathbbm{k} }(h)\), \(X_{\beta }(h)\) and \(X_{\varLambda }(h)\) are the vector solutions.
Step 2. On simulation, the performance of each population member is assessed using Eq. (61). The assessment of member performance yields an objective function value, which is employed in GWO-based optimization using \(X_R(h) = \alpha ,\ \ R = 1\ldots M_{ag}\)
Step 3. The best three solutions acquired by the population members i.e., \(X_{\mathbbm{k} }(h)\), \(X_{\beta }(h)\), \(X_{\varLambda }(h)\) using:
The result of the above equation must satisfy the following condition:
Step 4. The coefficients of the search vector are calculated as below:
with
where \(\varsigma ^f\) is uniformly random number distribution in the range of \(0 \le \varsigma ^f \le 1\), \(f=1\ldots n_{pop}\), and vector coefficient \(a^f(h)\) decreases from 2 to 0 in searching process.
Step 5. The search coefficient agents are permitted to locate their new position \(X_{i}(h+1)\) by using the following equation:
By taking notation \(X^{j}(h)\) for \(\lbrace {\mathbbm{k} , \beta , \varLambda \rbrace }\), update solution
and
The updated \(X_R(h+1)\) vector solution will obtained by:
Step 6. The updated solution from above equation is validated for the proposed FOAC algorithm optimizing parameter \(\alpha =X_R(h+1)\).
Step 7. Go to step 2, until maximum iteration.
Step 8. After the algorithm is stopped, the best solution is obtained as:
The GWO optimization with four variables \(\left( n_{pop}=4\right)\) that belong to the proposed FOAC algorithm parameter vector is:
The pseudo code of GWO is presented in Algorithm 1.
3.2 Convergence analysis
In this subsection , the convergence of the proposed approach has been investigated with the aid of Lyapunov theory according to the following theorem.
Theorem 2
To guarantee the convergence of the update rules depicted in Eqns. (37)-(39), the learning rates should have the following constraints:
Proof
Four Lyapunov candidate functions are proposed. The first candidate Lyapunov function is given as:
For the Lyapunov function \(L_1(k)>0\), the stability condition is satisfied if and only if \(\vartriangle L_1(k)\le 0\). The change of the Lyapunov function can be given by:
The term \(0.5\delta _{TD}^2(k+1)\) can be represented using the fractional-order Taylor series expansion as:
Also,
By substituting from Eq. (79) and Eq. (80) into Eq. (78), we have:
According to Eq. (50), Eq. (81) can be rewritten as:
The stability condition \(\vartriangle L_1(k)\le 0\) is satisfied if
Then, we have:
Define a second candidate Lyapunov function as:
\(\vartriangle L_2(k)\) is as follows:
Substituting from Eq. (50) into Eq. (86),results:
Then \(\vartriangle L_2(k)\le 0\) if
According to Eq. (88) and (84), the first stability condition is given as:
The third candidate Lyapunov function is defined as:
\(\vartriangle L_3(k)\) is as follows:
By substituting from Eq. (50) into Eq. (91), yields:
Let
Then, the second stability condition is given as:
The fourth candidate Lyapunov function is defined as:
\(\vartriangle L_4(k)\) is as follows:
Substituting from Eq. (50) into Eq. (96), the above equation can be reformulated as:
Let
Hence, the third stability condition is given as:
This completes the proof of Theorem 2.
In summary, the pseudo code of the proposed FOAC scheme is presented in Algorithm 2.
4 Results and discussion
In this section , the effectiveness of the developed FOPID-FOAC controller is verified via applying the FOPID-FOAC controller to two uncertain nonlinear systems. The first one is the 2-DOF helicopter system for tracking and regularization issues. The 2-DOF helicopter system provides a nonlinear and complex helicopter flight control test platform to simulate several flight modes such as hovering and taking off. In fact, flight control problems involve serious complications, due to the complex mechanisms of nonlinear and changes in flight conditions depending on payload and climate change [60]. So, controlling the 2-DOF helicopter system involves some difficulties due to the mutual interaction between the two axes, and the non-linearity in motion of mechanisms [34, 78]. The second one is to tackle the stabilizing issue of an inverted pendulum system. In fact, the inverted pendulum is a typical nonlinear, multivariable, and unstable dynamic system that is applied in many applications such as robotics [25] and general industrial processes [35]. Stabilizing issue of the inverted pendulum is used to verify that a new control method has a strong ability to address nonlinear and instability problems [62]. Further, this control method provides a bridge between the theory of control theory and its practice in engineering science.
Since the proposed algorithm is an online optimization approach of a fractional-order PID controller based on a fractional-order actor-critic algorithm, two points of view for the comparisons are conducted. In the first one, the proposed FOPID-FOAC algorithm is compared to two approaches for tuning the FOPID parameters, which are FOPID [66] and FOPID-GWO [30]. From the second point of view, the proposed FOPID-FOAC algorithm is compared with FOPID-IAC, and FOPID-DDPG [16] controllers to reflect the effect of the fractional-order actor-critic reinforcement learning algorithms to optimize the FOPID parameters compared to the IAC algorithm and DDPG algorithm. In order to carry out a comprehensive evaluation of the quantitative results, five performance indices are considered that include the IAE, ISE defined in Eq. (62), rising time, Max.OS and settling time. All simulations are performed by MATLAB 9.2 and implemented using an Intel Core i3, 2.4 GHz CPU, with 4 GB RAM running on Windows 10 (64 bit) operating system.
4.1 2-DOF helicopter system
The 2-DOF helicopter consists of two propellers (pitch and yaw) driven by two motors. Let us define \(V_{mp}\) is the voltage signal applied to the pitch motor; \(V_{my}\) is the voltage signal applied to the yaw motor; \(\phi\) is the pitch angle; \(\vartheta\) is the yaw angle. The generated voltage signal magnitude is bounded to \(\pm 5\ V\) to simulate the saturation of electrical and mechanical components of the 2-DOF helicopter system and the sample time is 10ms. When a sufficient voltage signal is applied to the pitch motor, the helicopter not only pitches up but it also starts to rotate at the same time (i.e., the input \(V_{mp}\) affects both outputs \(\phi\) and \(\vartheta\)). Similarly, when sufficient voltage is applied to the yaw motor, the helicopter rotates in the anti-clockwise direction and changes its pitch a little (i.e., the input \(V_{my}\) affects both outputs \(\phi\) and \(\vartheta\)). Thus, the process is a cross-coupled, MIMO and highly complex nonlinear system. The effect of \(V_{mp}\) on \(\vartheta\) is very strong denoted by strong cross-coupling, while the effect of \(V_{my}\) on \(\phi\) is weak denoted by weak cross-coupling. The 2-DOF helicopter model is described by the following nonlinear equations [48, 57]:
The parameters of the 2-DOF helicopter system with the description is listed in Table 1 [57]. Figure 4 shows the block diagram of a 2-DOF helicopter system controlled by the proposed FOPID-FOAC controller. Here, the 2-DOF helicopter is controlled by two FOPID loops in an uncertain environment. The first controller aims to force the helicopter system to track the pitch angle while the second controller makes the system track the yaw angle. The input of the FOAC network is the utility function that is given as \(x(k)=\left[ e_{1}(k), \triangle e_{1}(k), \triangle ^2 e_{1}(k), e_{2}(k), \triangle e_{2}(k), \triangle ^2 e_{2}(k)\right],\) where \(e_{1}(k)=e_{Pitch}(k)\) and \(e_{2}(k)=e_{Yaw}(k)\). Three scenarios are performed to check the performance of the developed FOPID-FOAC in controlling the 2-DOF helicopter system. In scenario 1, a square reference trajectory is given to the pitch and the yaw axes. In scenario 2, the performance of FOPID-FOAC is evaluated under external voltage disturbance. Scenario 3 is a repetition of scenario 1 but with \(20\%\) increase in \(m_{heli}\) and \(20\%\) decrease in \(l_{cm}\). The system is initialized with \(-45\) degree pitch angle and 20 degree yaw angle in all scenarios. The parameters settings of the FOPID and FOPID-GWO, are listed in Table 2. The hyper-parameters of the proposed FOPID-FOAC are depicted in Table (3).
The 2-DOF helicopter controlled by the proposed FOPID-FOAC controller
4.1.1 Scenario 1: Effect due to variation of the desired output
In this scenario, a square-wave shaped trajectory is applied to the pitch and the yaw axes at \(t=15\ sec\) and at \(t=50\ sec\) respectively. The comparative profiles for the trajectory tracking in pitch and yaw axes for the FOPID, FOPID-GWO, FOPID-IAC, FOPID-DDPG and the proposed FOPID-FOAC controllers are presented in Fig. 5. It is observed that, all controllers can track the desired output in the presence of the mentioned trajectories. However, the system response under the proposed FOPID-FOAC controller is significantly better than the responses under the FOPID, FOPID-GWO, FOPID-IAC, and FOPID-DDPG controllers. Compared to these controllers, two affirmative observations can be recorded: (i) under FOPID-FOAC, the pitch and yaw angles tracks the square wave reference with fewer oscillations and smaller steady-state error, (ii) the FOPID-FOAC controller produces smoother and less fluctuating pitch and yaw angles.
The response of the 2-DOF helicopter system for the proposed FOPID-FOAC under squared trajectory tracking (2-DOF helicopter system, Scenario1)
4.1.2 Scenario 2: Disturbance rejection
In order to verify the robustness of the designed controller, the FOPID, FOPID-GWO, FOPID-IAC, FOPID-DDPG and the proposed FOPID-FOAC controllers are subjected to a \(15\ V\) and \(-15\ V\) external input disturbance. This disturbance is equivalent to \(300\%\) of the maximum input signal to the pitch and yaw motors respectively. The disturbance is simulated by a pulse of \(10\ ms\) duration and applied at \(t=15\ sec\) and at \(t=45\ sec\) to the pitch and yaw motors respectively. Figure 6 illustrates the pitch and yaw angles under the external disturbance of the FOPID, FOPID-GWO, FOPID-IAC, FOPID-DDPG and the proposed FOPID-FOAC controllers. From Figure 6, it is clear that the pitch and yaw angles using the proposed FOPID-FOAC controller are stabilized much faster rather than the FOPID, FOPID-GWO, FOPID-IAC, and FOPID-DDPG. Compared to these controllers, the proposed FOPID-FOAC shows less and shorter fluctuation in the pitch and the yaw angles. Thus, the results confirmed that the proposed control scheme is superior to other compared controllers under external disturbance.
The response of the 2-DOF helicopter system for the proposed FOPID-FOAC under external disturbance (2-DOF helicopter system, Scenario2)
4.1.3 Scenario 3: Uncertainty suppression
In order to examine the uncertainty suppression capability of the proposed FOPID-FOAC controller, this scenario is introduced. In this scenario, the system is subjected to uncertainty in form of \(20\%\) increase in \(m_{heli}\) and \(20\%\) decrease in \(l_{cm}\) for the entire time. The obtained results are depicted in Fig. 7. It is clear that, the system response under the proposed FOPID-FOAC controller is significantly better compared to FOPID, FOPID-GWO, FOPID-IAC and FOPID-DDPG controllers. The FOPID-FOAC controller is still able to force the system to track the desired pitch and yaw trajectories with fewer oscillations and smaller steady-state error while keeping smoother and less fluctuating. As can be seen from this figure, even with system uncertainties, the proposed FOPID-FOAC is superior to all other controllers in the comparative study and is capable of controlling the system with a satisfactory performance.
The response of the 2-DOF helicopter system for the proposed FOPID-FOAC under uncertainty (2-DOF helicopter system, Scenario3)
To demonstrate how effectively the proposed FOPID-FOAC control performs, Tables 4 and 5 show control performance indices for different controllers in the comparative study. The control performance indices include IAE, ISE, the rising time \(t_r(Sec)\), Max.OS and settling time \(t_{s}(Sec)\) criterion. The values of these performance indices are given in Tables 4, 5 for both pitch and yaw angles. The bar chart representation of the variation in performance indices for all scenarios for the FOPID, FOPID-GWO, FOPID-IAC, FOPID-DDPG and the proposed FOPID-FOAC controllers are depicted in Figs. 8, 9. Due to the small oscillations and the trivial steady-state error of pitch angle, as well as the less fluctuating yaw angle, the proposed FOPID-FOAC has the smallest values of both IAE and ISE indices under all test-scenarios. Noted that, the proposed FOPID-FOAC controller has achieved faster settling time and rising time for the pitch and yaw angle for all Scenarios. Also, the proposed FOPID-FOAC controller produced less than Max.OS in most of Scenarios. Nevertheless, the Max.OS difference is too small and not significant.
In order to quantitatively show the improvement of the performance indices by employing the proposed FOPID-FOAC algorithm compared to the other control methods, the quantified results as a percentage reduction regarding the error and time response performance indices are given in Tables 6 and 9. Hence, imposing fractional-order learning parameters in the proposed FOPID-FOAC improves the adaptation capabilities. This ensures that the proposed FOPID-FOAC is more reliable and performs much better. Thus, it is strongly recommended for the control of the 2-DOF helicopter system.
In addition to evaluating the performance using IAE, ISE, \(t_r(Sec)\), Max.OS and \(t_{s}(Sec)\), the computation time for different controllers in the comparative study are computed in Table 10. It’s clear that the proposed FOPID-FOAC controller has larger computation time, however it’s still acceptable for the 2-DOF helicopter system with a sampling period of \(10\ ms\).
Remark
It is worth noting that, the proposed FOPID-FOAC algorithm is basically designed in the fractional-order calculus framework. The fractional-order derivative has a memory represented by the sum in Definition 1. or by the integral in Definition 2. which is neglected in the integer-order derivative (IOD) [37, 52]. This memory is the main reason for the sluggishness and the weakness in the time complexity of FO-based algorithm. However, the sluggishness and weakness in time complexity would be acceptable for the following reasons: i) The rapid development of implementing a very speed CPUs for data processing could be used in implementing FO-based algorithms for numerous applications [18, 21, 46]; ii) Many applications have a sample time that is adequate with algorithms depending on FO calculus, for example the power systems [4], the temperature control systems [50, 76], and electro-mechanical systems [56]. Moreover, to simplify the computation complexity of the proposed FOPID-FOAC algorithm, the numerical solution of the fractional order differential equation in Eq. (43) can be reformulated based on the short memory principle as :
The short memory principle can be used for reducing the memory length such that \(v=1\) for \(k<=L_m\) and \(v=k-L_m\) for \(k>L_m\), where \(L_m\) is the memory length.
Due to the proposed control scheme having been conducted several times, the statistical analysis of the error and the time response performance measurements in terms of the mean value and the standard deviation was performed. Hence, this analysis of the performance indices with 50 runs regarding scenario 1 was calculated and reported in Table 11.
Variation of performance indices values for pitch angle (2-DOF helicopter system)
Variation of performance indices values for yaw angle (2-DOF helicopter system)
4.2 Inverted pendulum system
The inverted pendulum is considered as the second nonlinear system which is modeled by the following differential equations [11, 72]:
where the model parameters are as follows [56]: \(m_p=0.2\ kg\) is the mass of the pendulum rod; \(m_c=0.5\ kg\) is the mass of the moving cart, \(\varUpsilon =\frac{1}{m_p+m_c }\); u is force to be applied on the cart to maintain the pendulum in vertical position in N; \(g=9.81\ m/s^2\) is the acceleration due to gravity; \(\varphi\) is the angle of the IP measured from the vertical y-axis in rad; \(l_p=0.4\ m\) is the length of the pendulum; the sample time is \(10\ ms\). Figure 10 shows the block diagram of inverted pendulum system controlled by the proposed FOPID-FOAC controller. It is noticed that, the IP system is controlled by two FOPID loops. The two controllers aim to stabilize the IP system in the uncertain environment(i.e., to regulate the pendulum around the equilibrium point (0,0)). In this system, the net control signal applied to the IP is the summation of the two control signals generated from the two FOPID controllers. Also for this system, the input of the FOAC network is defined as \(x(k)=\left[ e_{1}(k), \triangle e_{1}(k), \triangle ^2 e_{1}(k), e_{2}(k), \triangle e_{2}(k), \triangle ^2 e_{2}(k)\right],\) where \(e_{1}(k)=e_{angle}(k)\) and \(e_{2}(k)=e_{velocity}(k)\). The simulated results are divided into two scenarios. In scenario 1, the performance of the proposed FOPID-FOAC controller is evaluated under external disturbance, while in scenario 2, the performance of the proposed FOPID-FOAC controller is evaluated when subjected to pendulum-mass uncertainty. The IP system is initialized with \(-30\) degree pendulum angle in the two scenarios. The generated control signal magnitude is bounded to \(\pm 10N\) to simulate the saturation of electrical and mechanical components of the IP system. The parameters settings of the FOPID and FOPID-GWO, are listed in Table 12. The hyper-parameters of the proposed FOPID-FOAC are given in Table (13).
The inverted pendulum controlled by the proposed FOPID-FOAC controller
4.2.1 Scenario 1: Disturbance rejection
In order to verify the robustness of the proposed FOPID-FOAC controller, various levels of external disturbances are applied to the control signal in the studied IP system. Figure 11 illustrates the IP system response under \(15\ N\) external disturbance simulated by a pulse of \(10\ ms\) duration at \(t=10\ sec\) for the FOPID, FOPID-GWO, FOPID-IAC, FOPID-DDPG and the proposed FOPID-FOAC controllers. As depicted in Fig. 11, the pendulum angle is stabilized much faster with less angle-overshoot using the proposed FOPID-FOAC compared to the four selected controllers. Tables 14 and 15 show the error and time response performance indices values for various disturbances that have been imposed on the output of the controller at \(t=10\ sec\). Figures 12 and 13 show the bar chart representation of the variation in performance indices for disturbances for the FOPID, FOPID-GWO, FOPID-IAC, FOPID-DDPG and the proposed FOPID-FOAC controllers. Moreover, Tables 16, 17, 18 and 19) show the quantified results as a percentage reduction regarding the error and time response performance indices. From Tables (11)-(13) and Figures 11, 12 and 13), it is explicitly found that the proposed FOPID-FOAC has better disturbance rejection performance than the other controllers.
The response of the IP system for the proposed FOPID-FOAC under 15N external disturbance (Inverted pendulum system, Scenario1)
Variation of performance indices values with disturbances for pendulum angle (Inverted pendulum system, Scenario1)
Variation of performance indices values with disturbances for pendulum velocity (Inverted pendulum system, Scenario1)
4.2.2 Scenario 2: Uncertainty suppression
In this scenario, the performance of the FOPID, FOPID-GWO, FOPID-IAC, FOPID-DDPG and the proposed FOPID-FOAC controllers is discussed when various levels of uncertainties are considered. Figure 14 illustrates the IP system response under \(30\%\) increase in the pendulum-mass for the entire time under external disturbance \(15\ N\) at \(t=10\ \rm{s}\). The obtained results for this scenario depicted that the proposed FOPID-FOAC gives less and shorter fluctuation in pendulum angle and pendulum velocity. Furthermore, the system exerts less control action, as shown in Fig. 14. Moreover, Tables 20, 21 show the error and time response performance indices values for various levels of uncertainties for both pendulum angle and pendulum velocity, respectively. The uncertainty levels are defined as \(10\%\), \(20\%\), \(30\%\) and \(40\%\) increase in pendulum-mass for the entire time under external disturbance \(15\ N\) at \(t=10\ \rm{S}\). Besides, Figures 15 and 16 show the bar chart representation of the variation in performance indices for the FOPID, FOPID-GWO, FOPID-IAC, FOPID-DDPG and the proposed FOPID-FOAC controllers. Based on the obtained results, the proposed FOPID-FOAC has the lowest IAE and ISE values and it has achieved faster settling time and rising time for pendulum angle and pendulum velocity for all scenarios. Also, the proposed FOPID-FOAC controller produced least Max.OS. Also, the quantified results as a percentage reduction regarding the error and time performance indices given in Tables 22, 23, 24 and 25 affirm this superiority of the proposed controller. Besides, Table 26 lists the computation time for the five controllers in terms of the IP system stabilizing issue. Regardless the proposed FOPID-FOAC controller has a larger computation time, but it’s still acceptable for the IP system with a sampling period of \(10\ ms\). Similar to example one, the statistical analysis of the performance indices for the proposed FOPID-FOAC algorithm regrading scenario 1 for 50 times is presented in Table 27.
The response of the IP system for the proposed FOPID-FOAC under \(30\%\) increase in pendulum mass and 15N external disturbance (Inverted pendulum system, Scenario2)
Variation of performance indices values with uncertainties levels for pendulum angle (Inverted pendulum system, Scenario2)
Variation of performance indices values with uncertainties levels for pendulum velocity (Inverted pendulum system, Scenario2)
5 Conclusions
In this study, the main purpose is to develop a machine learning-based online tuning for FOPID parameters that can effectively handle the effect of the parameter uncertainties and disturbances of uncertain nonlinear systems. The main feature of this approach is that the online tuning of the controller parameters can be performed without any need for user-based pre-tuning and prior system dynamic information. We can conclude that the principal objective of this paper is achieved in terms of the following major steps: First, an AC learning algorithm in the framework of fractional-order neural networks is proposed. The FOAC approach is developed by generalizing the regular IAC learning algorithm using fractional-order calculus with adaptive learning rates. Moreover, a generalized RLU activation function is introduced along with the developed FOAC approach. The convergence of the FO learning algorithm of the AC neural network has been confirmed using Lyapunov’s criteria. Second, the proposed FOAC is utilized as an online tuning for the multiparameter control, namely FOPID control. Specifically, the proposed FOAC algorithm is developed to learn the error-to-action mapping that aims to find the best FOPID parameters by maximizing the reward function. Third, an exhaustive simulation study has been carried out using two problems of nonlinear control systems, the tracking issue of the 2-DOF helicopter system and the stabilization problem of the inverted pendulum system. Fourth, by a comparative study with FOPID, FOPID-GWO, FOPID-IAC, and FOPID-DDPG controller approaches, the proposed controller has been offered a less reduction in the error performance measurements (i.e., IAE, and ISE) and the time response performance indices (i.e., Max. OS, settling time, and rising time). In particular, by employing the proposed FOPID-FOAC for the 2-DOF helicopter system, the improvements reached a reduction of about 30.65% IAE, 32.83% ISE, 6.65% rising time, 10.15% Max.OS and 8.245% settling time compared to the other control methods. For the IP system, the improvements reached a reduction of about 43.83% IAE, 47.58% ISE, 11.16% rising time, 48.08% Max.OS and 10.72% settling time compared to the other control methods. Moreover, the results also show that the proposed FOPID-FOAC controller is more capable of dealing with ambiguity in parameter variation and disturbances than all controllers included in the comparative study. Finally, we can affirm that the use of the proposed FOPID-FOAC is applicable and promising for uncertain nonlinear systems. At the same time, the shortcoming of this technique is its relatively long computation time. Hence, in future work, the investigation of low computation fractional-order actor-critic algorithms should be considered.
Data Availability Statement
Data sharing not applicable to this article as no data sets were generated or analyzed during the current study.
References
Aguilar CZ, Gómez-Aguilar J, Alvarado-Martínez V, Romero-Ugalde H (2020) Fractional order neural networks for system identification. Chaos, Solitons & Fractals 130:109444
Akbarimajd A (2015) Reinforcement learning adaptive pid controller for an under-actuated robot arm. Int J Integrated Eng 7(2)
Al-Saggaf UM, Mehedi IM, Mansouri R, Bettayeb M (2017) Rotary flexible joint control by fractional order controllers. Int J Control Autom Syst 15(6):2561–2569
Arya Y (2020) A novel cffopi-fopid controller for agc performance enhancement of single and multi-area electric power systems. ISA Trans 100:126–135
Badri V, Tavazoei MS (2013) On tuning fractional order [proportional-derivative] controllers for a class of fractional order systems. Automatica 49(7):2297–2301
Bai W, Li T, Tong S (2020) Nn reinforcement learning adaptive control for a class of nonstrict-feedback discrete-time systems. IEEE Trans Cybernet 50(11):4573–4584
Barth JM, Condomines JP, Bronz M, Lustosa LR, Moschetta JM, Join C, Fliess M (2018) Fixed-wing uav with transitioning flight capabilities: model-based or model-free control approach? a preliminary study. In: 2018 International Conference on Unmanned Aircraft Systems (ICUAS), pp. 1157–1164. IEEE
Boubertakh H, Tadjine M, Glorennec PY, Labiod S (2010) Tuning fuzzy pd and pi controllers using reinforcement learning. ISA Trans 49(4):543–551
Busoniu L, Babuska R, De Schutter B, Ernst D (2017) Reinforcement learning and dynamic programming using function approximators. CRC press, US
Carlucho I, De Paula M, Acosta GG (2020) An adaptive deep reinforcement learning approach for mimo pid control of mobile robots. ISA Trans 102:280–294
Chen M, Lam HK, Shi Q, Xiao B (2019) Reinforcement learning-based control of nonlinear systems using lyapunov stability concept and fuzzy reward scheme. IEEE Trans Circuits Syst II Exp Briefs 67(10):2059–2063
Dwivedi P, Pandey S, Junghare A (2017) Performance analysis and experimental validation of 2-dof fractional-order controller for underactuated rotary inverted pendulum. Arab J Sci Eng 42(12):5121–5145
Fei J, Wang Z (2020) Multi-loop recurrent neural network fractional-order terminal sliding mode control of mems gyroscope. IEEE Access 8:167965–167974
Fu X, Li S, Fairbank M, Wunsch DC, Alonso E (2014) Training recurrent neural networks with the levenberg-marquardt algorithm for optimal control of a grid-connected converter. IEEE Trans Neural Netw Learn Syst 26(9):1900–1912
George MA, Kamath DV (2020) Design and tuning of fractional order pid (fopid) controller for speed control of electric vehicle on concrete roads. In: 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), pp. 1–6. IEEE
Gheisarnejad M, Khooban MH (2020) An intelligent non-integer pid controller-based deep reinforcement learning: Implementation and experimental results. IEEE Trans Industr Electron 68(4):3609–3618
Görges D (2017) Relations between model predictive control and reinforcement learning. IFAC-PapersOnLine 50(1):4920–4928
Hassan RO, Mostafa H (2021) Implementation of deep neural networks on fpga-cpu platform using xilinx sdsoc. Analog Integr Circ Sig Process 106(2):399–408
Hou Z, Xiong S (2019) On model-free adaptive control and its stability analysis. IEEE Trans Autom Control 64(11):4555–4569
Huang L, Deng L, Li A, Gao R, Zhang L, Lei W (2021) A novel approach for solar greenhouse air temperature and heating load prediction based on laplace transform. J Build Eng 44:102682
Huang X, Guo Z, Song M, Zeng X (2021) Accelerating the sm3 hash algorithm with cpu-fpga co-designed architecture. IET Comput Dig Tech 15(6):427–436
Huang X, Naghdy F, Du H, Naghdy G, Todd C (2015) Reinforcement learning neural network (rlnn) based adaptive control of fine hand motion rehabilitation robot. In: 2015 IEEE Conference on Control Applications (CCA), pp. 941–946. IEEE
Ibraheem GAR, Azar AT, Ibraheem IK, Humaidi AJ (2020) A novel design of a neural network-based fractional pid controller for mobile robots using hybridized fruit fly and particle swarm optimization. Complexity 2020
Jang B, Kim M, Harerimana G, Kim JW (2019) Q-learning algorithms: a comprehensive classification and applications. IEEE Access 7:133653–133667
Johnson T, Zhou S, Cheah W, Mansell W, Young R, Watson S (2020) Implementation of a perceptual controller for an inverted pendulum robot. J Intell Robot Syst 99(3):683–692
Karakoyun M, Ozkis A, Kodaz H (2020) A new algorithm based on gray wolf optimizer and shuffled frog leaping algorithm to solve the multi-objective optimization problems. Appl Soft Comput 96:106560
Khater AA, El-Nagar AM, El-Bardini M, El-Rabaie N (2019) A novel structure of actor-critic learning based on an interval type-2 tsk fuzzy neural network. IEEE Trans Fuzzy Syst 28(11):3047–3061
Kokologiannaki CG (2010) Properties and inequalities of generalized k-gamma, beta and zeta functions. Int J Contemp Math Sci 5(14):653–660
Kumar P, Hati AS (2021) Deep convolutional neural network based on adaptive gradient optimizer for fault detection in scim. ISA Trans 111:350–359
Kumar R, Sinha N (2021) Voltage stability of solar dish-stirling based autonomous dc microgrid using grey wolf optimised fopid-controller. Int J Sustain Energ 40(5):412–429
Lawrence NP, Forbes MG, Loewen PD, McClement DG, Backström JU, Gopaluni RB (2022) Deep reinforcement learning with shallow controllers: An experimental application to pid tuning. Control Eng Pract 121:105046
Lewis FL, Vrabie D, Vamvoudakis KG (2012) Reinforcement learning and feedback control: Using natural decision methods to design optimal adaptive controllers. IEEE Control Syst Mag 32(6):76–105
Liu JG, Yang XJ, Feng YY, Cui P (2020) New fractional derivative with sigmoid function as the kernel and its models. Chin J Phys 68:533–541
Liu TK, Juang JG (2009) A single neuron pid control for twin rotor mimo system. In: 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, pp. 186–191. IEEE
Ma J, Coogler K, Suh M (2020) Inquiry-based learning: development of an introductory manufacturing processes course based on a mobile inverted pendulum robot. Int J Mech Eng Educ 48(4):371–390
Mahmoud TA, Abdo MI, Elsheikh EA, Elshenawy LM (2021) Direct adaptive control for nonlinear systems using a tsk fuzzy echo state network based on fractional-order learning algorithm. J Franklin Inst 358(17):9034–9060
Matouk AE, Elsadany A, Ahmed E, Agiza H (2015) Dynamical behavior of fractional-order hastings-powell food chain model and its discretization. Commun Nonlinear Sci Numer Simul 27(1–3):153–167
Mbihi MD, Moffo BL, Nneme LN (2021) Design and virtual simulation of an optimal pid/lqrt-pso control system for 2wd mobile robots. algerian journal of signals and systems (ajss) 6(2):98–111
Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw 69:46–61
Mohammadzadeh A, Sabzalian MH, Zhang W (2019) An interval type-3 fuzzy system and a new online fractional-order learning algorithm: theory and practice. IEEE Trans Fuzzy Syst 28(9):1940–1950
Mokhtari SA (2022) Fopid control of quadrotor based on neural networks optimization and path planning through machine learning and pso algorithm. Int J Aeronaut Space Sci pp. 1–16
Monje CA, Chen Y, Vinagre BM, Xue D, Feliu-Batlle V (2010) Fractional-order systems and controls: fundamentals and applications. Springer Science & Business Media, Berlin
Mughees A, Mohsin SA (2020) Design and control of magnetic levitation system by optimizing fractional order pid controller using ant colony optimization algorithm. IEEE Access 8:116704–116723
Munagala VK, Jatoth RK (2021) Design of fractional-order pid/pid controller for speed control of dc motor using harris hawks optimization. In: Intelligent Algorithms for Analysis and Control of Dynamical Systems, pp. 103–113. Springer
Norsahperi N, Danapalasingam K (2020) Particle swarm-based and neuro-based fopid controllers for a twin rotor system with improved tracking performance and energy reduction. ISA Trans 102:230–244
Okazaki R, Tabata T, Sakashita S, Kitamura K, Takagi N, Sakata H, Ishibashi T, Nakamura T, Ajima Y (2020) Supercomputer fugaku cpu a64fx realizing high performance, high-density packaging, and low power consumption. Fujitsu Technical Review pp. 2020–03
Oostwal E, Straat M, Biehl M (2021) Hidden unit specialization in layered neural networks: Relu vs. sigmoidal activation. Physica A 564:125517
Patel R, Deb D, Modi H, Shah S (2017) Adaptive backstepping control scheme with integral action for quanser 2-dof helicopter. In: 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), pp. 571–577. IEEE
Petráš I (2011) Fractional-order nonlinear systems: modeling, analysis and simulation. Springer Science & Business Media, Berlin
Pezol NS, Rahiman MHF, Adnan R, Tajjudin M (2021) Comparison of the crone-1 and fopid controllers for steam temperature control of the essential oil extraction process. In: 2021 IEEE International Conference on Automatic Control & Intelligent Systems (I2CACIS), pp. 253–258. IEEE
Pirasteh-Moghadam M, Saryazdi MG, Loghman E, Kamali A, Bakhtiari-Nejad F (2020) Development of neural fractional order pid controller with emulator. ISA Trans 106:293–302
Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier
Rais MC, Dekhandji FZ, Recioui A, Rechid MS, Djedi L (2022) Comparative study of optimization techniques based pid tuning for automatic voltage regulator system. Engineering Proceedings 14(1):21
Sedighizadeh M, Rezazadeh A (2008) Adaptive pid controller based on reinforcement learning for wind turbine control. In: Proceedings of world academy of science, engineering and technology, vol. 27, pp. 257–262. Citeseer
Shah P, Agashe S (2016) Review of fractional pid controller. Mechatronics 38:29–41
Shalaby R, El-Hossainy M, Abo-Zalam B (2019) Fractional order modeling and control for under-actuated inverted pendulum. Commun Nonlinear Sci Numer Simul 74:97–121
Sharma R, Pfeiffer CF (2017) Comparison of control strategies for a 2 dof helicopter. In: Proceedings of the 58th Conference on Simulation and Modelling (SIMS 58), pp. 271–279
Shi JZ (2020) A fractional order general type-2 fuzzy pid controller design algorithm. IEEE Access 8:52151–52172
Singh AP, Deb D, Agarwal H (2019) On selection of improved fractional model and control of different systems with experimental validation. Commun Nonlinear Sci Numer Simul 79:104902
Song D, Han J, Liu G (2012) Active model-based predictive control and experimental investigation on unmanned helicopters in full flight envelope. IEEE Trans Control Syst Technol 21(4):1502–1509
Song R, Xiao W, Zhang H, Sun C (2014) Adaptive dynamic programming for a class of complex-valued nonlinear systems. IEEE Trans Neural Netw Learn Syst 25(9):1733–1739
Su X, Xia F, Liu J, Wu L (2018) Event-triggered fuzzy control of nonlinear systems with its application to inverted pendulum systems. Automatica 94:236–248
Sun Q, Du C, Duan Y, Ren H, Li H (2019) Design and application of adaptive pid controller based on asynchronous advantage actor–critic learning method. Wireless Networks pp. 1–11
Sutton RS, Barto AG (2018) Reinforcement learning: An introduction. MIT press, USA
Tepljakov A (2017) Fractional-order modeling and control of dynamic systems. Springer, Berlin
Tepljakov A, Alagoz BB, Yeroglu C, Gonzalez E, HosseinNia SH, Petlenkov E (2018) Fopid controllers and their industrial applications: a survey of recent results. IFAC-PapersOnLine 51(4):25–30
Tepljakov A, Alagoz BB, Yeroglu C, Gonzalez EA, Hosseinnia SH, Petlenkov E, Ates A, Cech M (2021) Towards industrialization of fopid controllers: a survey on milestones of fractional-order control and pathways for future developments. IEEE Access 9:21016–21042
Tripathi S, Shrivastava A, Jana KC (2020) Self-tuning fuzzy controller for sun-tracker system using gray wolf optimization (gwo) technique. ISA Trans 101:50–59
Wang J, Wen Y, Gou Y, Ye Z, Chen H (2017) Fractional-order gradient descent learning of bp neural networks with caputo derivative. Neural Netw 89:19–30
Wang J, Yang G, Zhang B, Sun Z, Liu Y, Wang J (2017) Convergence analysis of caputo-type fractional order complex-valued neural networks. IEEE Access 5:14560–14571
Wang S, Diao R, Xu C, Shi D, Wang Z (2020) On multi-event co-calibration of dynamic model parameters using soft actor-critic. IEEE Transactions on Power Systems
Xiao B, Lam HK, Yu Y, Li Y (2019) Sampled-data output-feedback tracking control for interval type-2 polynomial fuzzy systems. IEEE Trans Fuzzy Syst 28(3):424–433
Xie Y, Tang X, Song B, Zhou X, Guo Y (2019) Model-free tuning strategy of fractional-order pi controller for speed regulation of permanent magnet synchronous motor. Trans Inst Meas Control 41(1):23–35
Xiong Y, Guo L, Huang Y, Chen L (2020) Intelligent thermal control strategy based on reinforcement learning for space telescope. J Thermophys Heat Trans 34(1):37–44
Yakoub Z, Amairi M, Chetoui M, Saidi B, Aoun M (2017) Model-free adaptive fractional order control of stable linear time-varying systems. ISA Trans 67:193–207
Yang LH, Huang BH, Hsu CY, Chen SL (2019) Performance analysis of an earth-air heat exchanger integrated into an agricultural irrigation system for a greenhouse environmental temperature-control system. Energy and Build 202:109381
Yao X, Wang Z, Huang Z (2021) A stability criterion for discrete-time fractional-order echo state network and its application. Soft Comput 25(6):4823–4831
Yeroğlu C, Ateş A (2014) A stochastic multi-parameters divergence method for online auto-tuning of fractional order pid controllers. J Franklin Inst 351(5):2411–2429
Zennir Y, Mechhoud EA, Seboui A, Bendib R (2018) Optimal pso-pi\(\lambda\)d\(\mu\) multi-controller for a robotic wrist. Algerian J Sig Syst 3(1):22–34
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shalaby, R., El-Hossainy, M., Abo-Zalam, B. et al. Optimal fractional-order PID controller based on fractional-order actor-critic algorithm. Neural Comput & Applic 35, 2347–2380 (2023). https://doi.org/10.1007/s00521-022-07710-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-022-07710-7