Fractional-order fuzzy sliding mode control of uncertain nonlinear MIMO systems using fractional-order reinforcement learning

Abstract

This paper introduces a novel approach aimed at enhancing the control performance of a specific class of unknown multiple-input and multiple-output nonlinear systems. The proposed method involves the utilization of a fractional-order fuzzy sliding mode controller, which is implemented through online fractional-order reinforcement learning (FOFSMC-FRL). First, the proposed approach leverages two Takagi–Sugeno–Kang (TSK) fuzzy neural network actors. These actors approximate both the equivalent and switch control parts of the sliding mode control. Additionally, a critic TSK fuzzy neural network is employed to approximate the value function of the reinforcement learning process. Second, the FOFSMC-FRL parameters undergo online adaptation using an innovative fractional-order Levenberg–Marquardt learning method. This adaptive mechanism allows the controller to continuously update its parameters based on the system’s behavior, optimizing its control strategy accordingly. Third, the stability and convergence of the proposed approach are rigorously examined using Lyapunov theorem. Notably, the proposed structure offers several key advantages as it does not depend on knowledge of the system dynamics, uncertainty bounds, or disturbance characteristics. Moreover, the chattering phenomenon, often associated with sliding mode control, is effectively eliminated without compromising the system’s robustness. Finally, a comparative simulation study is conducted to demonstrate the feasibility and superiority of the proposed method over other control methods. Through this comparison, the effectiveness and performance advantages of the approach are validated.

Introduction

Nonlinear MIMO control algorithms face various challenges such as unknown dynamics, external disturbances, parametric uncertainties, and variations, which can compromise control performance and even destabilize the closed-loop system [1]. To address such issues, advanced nonlinear control theories, such as backstepping control [2], H-infinity loop-shaping [3], and sliding mode control (SMC) [4], have been proposed in the literature. SMC is one of the most widely used techniques due to its robustness [5]. It is known as a powerful nonlinear control technique that drives system states onto a sliding surface and maintains it there to achieve the desired closed-loop performance. Fundamentally, the SMC structure involves three stages: selecting the sliding surface, introducing the switching law, and the equivalent law. The sliding surface captures the desired performance in the state variable space [6], while the switching law drives the system state trajectories towards and maintains them on the sliding surface. However, designing the equivalent law requires knowledge of the controlled system dynamics, which can be challenging, particularly for MIMO nonlinear systems. Additionally, SMC can induce high-frequency vibrations, known as chattering, which can compromise dynamic stability [7]. With the advent of fractional calculus, researchers started to study fractional-order SMC (FOSMC) methods to address these limitations [8].

Literature review

In the literature, numerous studies have been conducted to construct efficient design methods for FOSMC in the situation of uncertainties or disturbances [9, 10]. The combination of SMC and fuzzy logic controller (FLC) is described as a robust control to address the stabilization and tracking control problems of disturbed MIMO systems [11,12,13]. In [14], FO adaptive fuzzy SMC (FOFSMC) was introduced where optimal parameters of fuzzy membership were obtained using the bat optimization algorithm. An optimal FO fuzzy backstepping SMC approach for fully and under-actuated systems was presented in [15]. A FO adaptive double-loop fuzzy SMC was introduced in [16] for a MIMO system with unknown uncertainty. In [17], a fuzzy fractional-order terminal sliding mode control was presented based on the boundary layer approach to trade-off between chattering elimination and control performances. Most of these methods, however, necessitate an exact dynamic model, which isn’t present for highly nonlinear systems [18]. As a result, FOSMC will perform poorly since it’s difficult to determine the equivalent control law in the absence of model information. Furthermore, the sliding surface parameters are already obtained offline so they are not suitable for systems with variable operating conditions.

Due to the enormous potential flexibility and adaptability of neural networks, the online learning control using neural networks has provided significant enhancement to the FOSMC approaches for nonlinear systems [19]. The most significant contribution of neural networks in FOSMC is their ability to approximate the unknown nonlinear dynamics of the controlled system, which can improve the control performance and robustness. By leveraging neural networks, sliding mode controllers can effectively handle the uncertainties and disturbances that are typically encountered in real-world applications. This capability has made neural-network-based FOSMC an increasingly popular choice in a wide range of applications. In [20], a recurrent neural network-based FOSMC was developed for improving the control performance of dynamic systems. Using a fuzzy wavelet neural network, an adaptive FO non-singular terminal SMC as well as an adaptation scheme for tuning the switching law gains were developed in [21]. To address the issue of unknown model parameters, a FOSMC using a radial basis function (RBF) neural network estimator (FOSMC-NE) was developed [22]. Adaptive FOSMC using RBF for nonlinear systems was introduced also in [23]. Besides, among machine learning methods, the reinforcement learning (RL) method can be used for online learning control by modifying an agent’s actions based on interactions with the environment [24]. Accordingly, the development of SMC for uncertain nonlinear systems was conducted using the online RL approach [25,26,27,28,29,30]. Indeed, RL algorithms are divided into three categories: policy iteration, value iteration, and actor-critic iteration (AC) [31]. Neural networks have shown significant promise in RL tasks for approximating these categories. Common techniques for training neural networks include gradient descent (GD), conjugate gradient (CG), Gauss-Newton (GN), and Levenberg–Marquardt (LM) [32]. LM provides an excellent trade-off between the speed of the GN and the stability of the GD methods. These learning methods are focused mainly with integer-order nature.

One of the current trends that can significantly improve the performance of online learning-based control methods is the use of fractional-order calculus [33]. In [34], the authors present an online tuning of FOPID controller parameters using a newly developed actor-critic method called fractional-order actor-critic, where a gradient method with a fractional-order upgrade design based on Lyapunov’s theorem was established. A competitive evolution algorithm, called population extreme optimization, and a fractional-order GD learning approach were combined to create an adaptive fractional-order back-propagation neural network in [35]. An adaptive law using fractional-order calculus was developed in [36] to adapt the readout set of weights of an adaptive controller-based on a fuzzy echo state neural network. However, few RL results have been reported for successfully controlling the systems, and transferring RL into real-world applications remains a fairly open problem.

Contributions and organization

Online learning controllers offer numerous benefits and advantages for controlling MIMO systems [37,38,39,40]. Firstly, these controllers possess the capability to adapt and learn from the system’s behavior in real-time, allowing them to effectively handle the complex dynamics inherent in MIMO systems. This adaptability ensures improved control performance and robustness. Secondly, online learning control can learn from past experiences and iteratively enhance control actions, resulting in superior performance characterized by reduced tracking errors and faster response times compared to fixed controllers. Lastly, learning controllers can effectively address MIMO nonlinearities by employing advanced learning algorithms and approximation techniques. Hence, the focus of this paper is to introduce an online fractional-order fuzzy sliding mode controller for MIMO nonlinear systems with unknown dynamics. The proposed scheme introduces a significant innovation by employing a fractional-order reinforcement learning technique, which significantly enhances the adaptability and real-time performance of the sliding mode controller. The proposed fractional-order reinforcement learning method incorporates the following key elements: (1) two TSK fractional-order fuzzy actor networks, namely the TSK fractional-order fuzzy sliding mode control (TSK-FOFSMC) actor network and the TSK fractional-order fuzzy equivalent control (TSK-FOFEC) actor network. These networks perform the online approximation of the two control components of the FOSMC: the switching control part and the equivalent control part. (2) Additionally, a TSK fractional-order fuzzy critic network (TSK-FOFCN) is introduced to estimate the value function essential for online reinforcement learning. Moreover, the online adaptation of the proposed scheme parameters is conducted using a developed fractional-order Levenberg–Marquardt learning method (FOLM). In summary, the proposed scheme contributes to the following aspects:

• 1. Different from existing works [22, 25,26,27,28,29,30], the proposed method incorporates the fractional-order derivative into the reinforcement learning process via the development of the FOLM learning algorithm. This enables the controller to adapt and respond to intricate system behaviors that may not be adequately captured by integer-order derivatives. Further, a rigorous proof of bounds for the proposed FOLM method is provided based on Lyapunov’s stability theory.

• 2. In contrast to the existing sliding mode fuzzy control system designs [11, 12, 17], the utilization of TSK fractional-order fuzzy networks within a fractional-order rule consequence in the proposed scheme enhances nonlinear approximation, adaptability to uncertainties in MIMO systems, and offers fractional-order flexibility.

• 3. The efficacy of the developed FOFSMC-FRL controller is validated by applying it to a 2-DOF helicopter system [41]. Furthermore, the performance of the proposed FOFSMC-FRL controller is compared to two other controllers: the FOFSMC based on conventional integer-order RL (FOFSMC-IRL) and the FOSMC-NE as given in [22].

The remainder of this paper is structured into six sections. “Problem formulation” introduces the problem formulation. The proposed FOFSMC-FRL control method is detailed in “Structure of the proposed method”. “Online learning of the proposed method” presents the online FOLM learning method and the stability convergence for the developed control strategy. In “Results and discussion”, the simulation results have been described, which demonstrate the superior performance of the FOFSMC-FRL in comparison to other two control methods. “Conclusions” puts forward the conclusion of the proposed work, followed by the references.

Problem formulation

According to [42], the MIMO nonlinear affine systems are described as follows:

$$\begin{aligned} \dot{x}_{i,j}&=f_{i,j}(\bar{x}_{i,j})+g_{i,j}(\bar{x}_{i,j})x_{i,j+1}+d_{i,j}, 1\le j\le n-1 \nonumber \\ \dot{x}_{i,n}&=f_{i,n}(\bar{x}_{i,n})+g_{i,n}(\bar{x}_{i,n})u_{i}+d_{i,n}, \quad n\ge 2 \nonumber \\ y_i&=x_{i,1}, i=1, 2,\ldots , m, \end{aligned}$$

(1)

where

(2)

where $x_{i,j}\in \mathbb {R}^{m\times n}$ are the states of the MIMO nonlinear system with $\bar{x}_{i,j}=\left[ x_{i,1},\ldots ,x_{i,j},\ldots ,x_{i,n}\right] ^\mathrm{{T}} \in \mathbb {R}^{n}$ is the $i^{th}$ subsystem state vector; $y_i$ and $u_i$ are the outputs and the inputs of the $i^{th}$ subsystem with being $\bar{y}_i$ and $\bar{u}_i\in \mathbb {R}^{m}$ are the outputs and the inputs vectors, respectively; The functions and are totally nominal nonlinear functions of ${f}_{i,j}(.)\in \mathbb {R}^{n}$ and ${g}_{i,j}(.)\in \mathbb {R}^{n\times n}$ of Eq. (1), respectively; $d_{i,j}\in \mathbb {R}^{n}$ is the unknown bounded disturbance.

Rewrite the system model of Eq. (1) as

(3)

where $D_{i,j}=\vartriangle f_{i,j}(\bar{x}_{i,j})+\vartriangle g_{i,j}(\bar{x}_{i,j})x_{i,j+1}+d_{i,j}$ and $D_{i,n}=\vartriangle f_{i,n}(\bar{x}_{i,n})+\vartriangle g_{i,n}(\bar{x}_{i,n})u_{i}+d_{i,n}$ describe the lumped uncertainty encompassing parameter and external disturbances.

In this article, the following assumptions are given for the system in Eq. (1) [23, 29, 43].

Assumption 1

f(x) and g(x) are unknown nonlinear and bounded functions; g(x) doesn’t equal “0” for all values of x, and all states are measured.

Assumption 2

The lumped parameter $D_{i,j}$ satisfies $|D_{i,j}|\le D_d$ with $D_d$ being a positive constant.

Assumption 3

The desired trajectory $x_{i,d}(y_{id})$ and its derivative $\dot{x}_{i,d}(\dot{y}_{id})$ are known and bounded.

In MIMO systems, the control problem is to obtain a control law so that the output signal $x_{i,1}$ tracks a reference signal $x_{i,d}$ and all the closed-loop signals are bounded. Assuming that all parameters for the MIMO system are well known, the ideal FOSMC can be designed as given below.

Define the error tracking and its derivative as

$$\begin{aligned} \begin{aligned} e_{i,1}=x_{i,1}-x_{i,d} \end{aligned} \end{aligned}$$

(4)

$$\begin{aligned} \begin{aligned} \dot{e}_{i,1}=\dot{x}_{i,1}-\dot{x}_{i,d}, \end{aligned} \end{aligned}$$

(5)

A fractional-order sliding surface can be given as

$$\begin{aligned} \begin{aligned} s_{i}=\lambda _{i_1} e_{i,1}+\lambda _{i_2} {D^{\xi _i-1}e_{i,1}}, \ \ \ 0<\xi _i<1, \end{aligned} \end{aligned}$$

(6)

where $\lambda _{i_1}, \lambda _{i_2}$ are designed parameters. $\left( \xi _i-1\right)$ is the fractional-order of fractional-order operation.

The derivative of the sliding surface is

$$\begin{aligned} \begin{aligned} \dot{s}_{i}{=}\lambda _{i_1} \dot{e}_{i,1}{+}\lambda _{i_2} {D^{\xi _i}e_{i,1}}. \end{aligned}\nonumber \\ \end{aligned}$$

(7)

Substituting from Eq. (3) into Eq. (7), and setting $\dot{s}_i=0$, yields the equivalent signal as

(8)

To compensate for the lumped uncertainty and external disturbance, the switching controller is employed as

(9)

where $\rho _{i}$ is a computable positive constant to compensate for uncertainty and disturbance.

According to [44], the control law of fractional-order sliding is formed by summing the above two parts.

$$\begin{aligned} \begin{aligned} u_i(k)&=u_{e_i}(k)+u_{s_i}(k), \end{aligned} \end{aligned}$$

(10)

where $u_{e_i}(k)$ and $u_{s_i}(k)$ are the equivalent and the switching control signals, respectively.

Substituting from Eqs. (8) and (9), the FOSMC signal can be written as

(11)

Select a Lyapunov function as

$$\begin{aligned} \begin{aligned} V_{i}=\frac{1}{2} s_{i}^Ts_{i}. \end{aligned} \end{aligned}$$

(12)

The derivative of $V_{i}$ is

(13)

Substituting from Eq. (11) into Eq. (13), yields

$$\begin{aligned} \begin{aligned} \dot{V}_{i}&=-\rho _{i}\parallel s_{i} \parallel +\parallel s_{i} \parallel \lambda _{i_1} D_{i,j}. \end{aligned} \end{aligned}$$

(14)

For $\rho _{i}>\parallel \lambda _{i_1}\parallel D_{d}$, $\dot{V}_{i}$ will be

$$\begin{aligned} \begin{aligned} \dot{V}_{i}\le -\parallel s_{i} \parallel \left( \rho _{i}-\parallel \lambda _{i_1}\parallel D_{d}\right) . \end{aligned} \end{aligned}$$

(15)

Accordingly, the closed loop system with the controller in Eq. (11) is asymptotically stable. However, a large $\rho _{i}$ will result in a serious chattering problem. Alternatively, sign$\left( s_{i}\right)$ is replaced by the hyporbolic function to smooth the control signal, output and states [45]. Hence, the control action is given by

(16)

However, imperfect tracking and disturbance rejection occur when sign$(s_i)$ is replaced with $\tan h\left( \frac{s_{i}}{\phi _{i}}\right)$ [46]. Moreover, obtaining the bounds of the lumped uncertainty and external disturbance is difficult. Furthermore, if the functions and are unknown, the controller in Eq. (16) will not be realized. As a result, the performance of sliding-mode control will suffer and may not perform well due to the difficulty in calculating the switching and the equivalent control laws, especially for MIMO systems.

Motivated by these mentioned problems, an online fractional-order reinforcement learning algorithm for fractional-order fuzzy sliding mode control is presented in the next section.

Structure of the proposed method

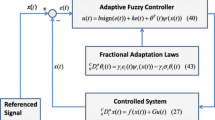
The scheme adopted is illustrated in Fig. 1 to address the challenges associated with nonlinear systems. This includes tackling issues related to unknown system dynamics and external disturbances. The proposed FOFSMC-FRL method mainly relies on employing reinforcement learning to approximate the parts of the fractional-order sliding mode controller within a newly developed framework that utilizes fuzzy logic. Moreover, the conventional reinforcement learning algorithm is reconstructed based on fractional-order calculus, leading to the development of a new algorithm for fractional-order reinforcement learning. Essentially, the FOFSMC-FRL scheme comprises three main components: the TSK-FOFSMC actor, the TSK-FOFEC actor, and the TSK-FOFCN critic. The TSK-FOFSMC actor is responsible for the online approximation of the switching control part, while the TSK-FOFEC actor is utilized for the online approximation of the equivalent control part. Additionally, the TSK-FOFCN is introduced to estimate the value function for online learning within the proposed scheme. Both actors and critic use fractional-order derivatives (FOD) to describe the consequences of the rules.

Fig. 1

The proposed FOFSMC-FRL control structure

Based on the actor-critic reinforcement learning control approach, the proposed design approach assumes the two parts (i.e., switching and equivalent parts) of the $i^{th}$ FOSMC for the MIMO system in Eq. (1) can be approximated as

$$\begin{aligned} \begin{aligned} u_{s_i}(k)&=f_s(\varTheta ^{*}_{s},X_{s_i})+\zeta _a(k)\\ u_{e_i}(k)&=f_e(\varTheta ^{*}_{e},X_{e_i})+\zeta _a(k), \ \ \vert \zeta _a(k)\vert \le \epsilon . \end{aligned} \end{aligned}$$

(17)

By considering Eqs. (8) and (9), the input vectors $X_{s_i}$ and $X_{e_i}$ can be defined as

$$\begin{aligned} \begin{aligned} X_{s_i}&=\left[ e_{i,1}(k),{{D^{\xi _i-1}e_{i,1}}}(k)\right] ^\mathrm{{T}}\\ X_{e_i}&=\left[ e_{i,1}(k),{{D^{\xi _i-1}e_{i,1}}}(k),y_i(k),\dot{x}_{i,d}\right] ^\mathrm{{T}}. \end{aligned} \end{aligned}$$

(18)

In the proposed controller, the two functions $f_s(.)$ and $f_e(.)$ are implemented using TSK-FOFSMC and TSK-FOFEC actors networks, respectively. Thus, $\varTheta ^{*}_{s}$ and $\varTheta ^{*}_{e}$ are the actor’s network parameters that can be optimized based on the following RL optimization problem

$$\begin{aligned} \begin{aligned} \varTheta ^{*}_{s}&=\arg \ \underset{\varTheta _{s}}{\min } \left[ \underset{X_s}{\sup }\ \Vert v_{c}(k)-R_a(k)\Vert \right] \\ \varTheta ^{*}_{e}&=\arg \ \underset{\varTheta _{e}}{\min } \left[ \underset{X_e}{\sup }\ \Vert v_{c}(k)-R_a(k)\Vert \right] . \end{aligned} \end{aligned}$$

(19)

In the design method, $R_a(k)$ is located as “0” indicating that the RL reward signal r(k) is successful. $v_c(k)$ is the value function. Moreover, the value function can be approximated as

$$\begin{aligned} \begin{aligned} v_{c}(k)&=f_c(\varTheta ^{*}_{c},X_c)+\zeta _c(k), \ \ \vert \zeta _c(k)\vert \le \epsilon , \end{aligned} \end{aligned}$$

(20)

where $X_c$ is the input vector of the critic network and it is assumed as

$$\begin{aligned} \begin{aligned} X_c=\left[ u_i(k),e_{i,1}(k),{{D^{\xi _i-1}e_{i,1}}}(k)\right] . \end{aligned} \end{aligned}$$

(21)

Also, $f_c(.)$ is implemented using TSK-FOFCN critic network and its parameters $\varTheta ^{*}_{c}$ can be optimized based on the following optimization problem

$$\begin{aligned} \begin{aligned} \varTheta ^{*}_{c}&=\arg \ \underset{\varTheta _{c}}{\min } \left[ \underset{X_c}{sup}\ \Vert v_{c}(k-1)-r(k)-\gamma v_{c}(k)\Vert \right] . \end{aligned} \end{aligned}$$

(22)

Practically, $\varTheta ^{*}_{s}$,$\varTheta ^{*}_{e}$, and $\varTheta ^{*}_{c}$ are unknown and its estimation values are used and updated by proposing a FOLM learning method in the next section. The structures of TSK-FOFSMC, TSK-FOFEC, and TSK-FOFCN are given in the following subsections.

The TSK-FOFSMC actor structure

First, we consider the control of nonlinear system in Eq. (1). To derive the FOSMC control law in Eq. (16), we use fuzzy system $f_s(\varTheta ^{*}_{s},X_{s_i})$ as mentioned in Eq. (17) to approximate the switching control law $u_{s_i}(k)$. Based on the FOD, the proposed TSK-FOFSMC rule for MIMO systems is generalized as

$$\begin{aligned} \begin{aligned} Rule^p:&\textit{ If } e_{i,1}(k) \textit{ is } A^p\textit{ and } D^{\xi _i-1}e_{i,1}(k) \textit{ is } A^p\\&\textit{Then} \ D^{\beta _{s_i}}u_{s_i}^{p}(k)=\rho _{i}^{p}(k) tanh\\ {}&\left( \frac{e_{i,1}(k)+D^{\xi _i-1}e_{i,1}(k)}{\phi _{i}^{p}(k)}\right) , \ \ \ \ \ p=1,2,\dots {.},p_{max} \ \ \ \end{aligned}\nonumber \\ \end{aligned}$$

(23)

where $p_{\max }$ is the number of fuzzy rules and $\bar{A}=\left[ A^1,\dots {.},A^{p_{\max }}\right]$ are fuzzy sets to realize a mapping from an input linguistic vector $\bar{x}_{s_{i}}=\left[ e_{i,1}(k),{D^{\xi _i-1}e_{i,1}}(k)\right] ^\mathrm{{T}}$ to an output linguistic scalar $u_{s_i}^p(k)$. The parameters $\rho _{i}^{p}$ and $\phi _{i}^{p}$ are the rule’s consequent coefficients. $\beta _{s_i}$ is the rule’s consequent fractional-order parameter.

Based on the Grunwald–Letnikov (GL) definition for FOD [47], the numeric solution for the FO differential equation of the rule consequence can be obtained as

$$\begin{aligned} \begin{aligned} \ u_{s_i}^{p}(k)=&\rho _{i}^{p}(k) tanh\left( \frac{e_{i,1}(k)+D^{\xi _i-1}e_{i,1}(k)}{\phi _{i}^{p}(k)}\right) \\ {}&-\sum _{q=1}^{k}c^{(\beta _{s_i}(k))}_{q} u_{s_i}^{p}(k-q). \end{aligned} \end{aligned}$$

(24)

Hence, the fuzzy rule in Eq. (23) can be rewritten as

$$\begin{aligned} \begin{aligned} Rule^p:&\textit{ IF } e_{i,1}(k) \textit{ is } A^p\textit{ and } D^{\xi _i-1}e_{i,1}(k) \textit{ is } A^p \\ {}&\textit{Then} \ u_{s_i}^{p}(k)=\rho _{i}^{p}(k) tanh\\ {}&\left( \frac{e_{i,1}(k)+D^{\xi _i-1}e_{i,1}(k)}{\phi _{i}^{p}(k)}\right) -\sum _{q=1}^{k}c^{(\beta _{s_i}(k))}_{q} u_{s_i}^{p}(k-q) \ \ \ \end{aligned} \end{aligned}$$

(25)

Corollary 1

In the proposed TSK-FOFSMC actor, the rules’ consequences are typically introduced similarly to the switching function of FOSMC. Thus, the coefficients of both the switching law and the boundary layer become the coefficients of the rules’ consequences. In addition, using the FOD can effectively avoid the chattering phenomenon caused by the switching control, achieving high precision tracking performance, and reducing the steady-state tracking error.

The proposed TSK-FOFSMC actor network can be structured into four layers, as shown in Fig. 2. The description of these layers can be given as follows.

Fig. 2

The schematic of the TSK-FOFSMC actor network

The input layer This layer accepts the input variables of the TSK-FOFSMC actor, which are defined as

$$\begin{aligned} \begin{aligned} X_{s_{i}}=\left[ e_{i,1}(k),{D^{\xi _i-1}e_{i,1}}(k)\right] ^\mathrm{{T}}. \end{aligned} \end{aligned}$$

(26)

The membership function layer Each neuron in this layer represents a Gaussian membership function to execute the fuzzification operation as

$$\begin{aligned} \begin{aligned} \mu ^{p}_{s_i}(X^r_{s_{i}})&=\exp \left( -\frac{1}{2}\left( \frac{X^r_{s_{i}}-c^{p}_{s_i}(k)}{\sigma ^{p}_{s_i}(k)}\right) ^2\right) ,\\&\quad r=1,2\ \ \ p=1,2,\dots {.}p_{\max }, \end{aligned} \end{aligned}$$

(27)

where $\sigma ^{p}_{s_i}(k)$; $c^{p}_{s_i}(k)$ are the standard deviation and the center of the pth neuron, respectively.

The rule layer In this layer, each neuron performs the t-norm operation as

$$\begin{aligned} \begin{aligned} \tau ^{p}_{s_i}(k)=\prod _{r=1}^{r=2}{\mu ^{p}_{s_i}(X^r_{s_{i}})}. \end{aligned} \end{aligned}$$

(28)

The output layer This layer is responsible to give the crisp output $u_{s_{i}}(k)$ as

$$\begin{aligned} \begin{aligned} u_{s_{i}}(k)&=\frac{\sum _{p=1}^{p_{\max }}\tau ^{p}_{s_i}(k) u_{s_{i}}^{p}(k)}{\sum _{p=1}^{p_{\max }}\tau ^{p}_{s_i}(k)}, \end{aligned} \end{aligned}$$

(29)

where $u_{s_{i}}^{p}(k)$ is calculated as

$$\begin{aligned} \begin{aligned} u_{s_i}^{p}(k)=&\rho _{i}^{p}(k) tanh\left( \frac{e_{i,1}(k)+D^{\xi _i-1}e_{i,1}(k)}{\phi _{i}^{p}(k)}\right) \\ {}&-\sum _{q=1}^{k}c^{(\beta _{s_i}(k))}_{q} u_{s_i}^{p}(k-q) \ \ \ \end{aligned} \end{aligned}$$

(30)

The TSK-FOFEC actor structure

To obtain the FOSMC control law stated in Eq. (16), we employ the TSK-FOFEC actor network as a fuzzy system represented by $f_e(\varTheta ^{*}_{e},X_{e_i})$, indicated by Eq. (17), to approximate the corresponding equivalent control law $u_{e_i}(k)$. Hence, by defining the input of this network as $X_{e_i}=\left[ e_{i,1}(k),{D^{\xi _i-1}e_{i,1}}(k),y_i(k),\dot{x}_{i,d}\right] ^\mathrm{{T}}$, the IF-Then rule for the proposed TSK-FOFEC network can be given as

$$\begin{aligned} Rule^p:&\textit{ If } X^1_{e_{i}}(k) \textit{ is } B^p\ldots X^z_{e_{i}}(k)\textit{ is } B^p\ldots \nonumber \\&\textit{ and } X^{z_{\max }}_{e_{i}}(k)\textit{ is } B^p \nonumber \\ {}&\textit{Then} \ \ \ \ {D^{\beta _{e_i}}u_{e_i}^{p}(k)}=\sum _{z=1}^{z_{\max }}Q^{z,p}_{i}(k)X^z_{e_{i}}(k), \nonumber \\&\quad p=1,2,\dots {.},p_{\max }, \end{aligned}$$

(31)

where $p_{\max }$ is the number of fuzzy rules and $\bar{B}=\left[ B^1,\dots {.},B^{p_{\max }}\right]$ are the fuzzy sets. The parameters $Q^{z,p}_{i}(k)$ are the rule’s consequent coefficients, which are described by crisp numbers. $\beta _{e_i}(k)$ is the rule’s consequent fractional-order parameter. Also, using the numeric solution for the FO differential equation, the fuzzy rule given in Eq. (31) can be modified as

$$\begin{aligned} Rule^p:&\textit{ If } X^1_{e_{i}}(k) \textit{ is } B^p\ldots X^z_{e_{i}}(k)\textit{ is } B^p\ldots \nonumber \\&\quad \textit{ and } X^{z_{\max }}_{e_{i}}(k)\textit{ is } B^p\nonumber \\ {}&\textit{Then} \ \ \ \ u_{e_i}^{p}(k)=\sum _{z=1}^{z_{\max }}Q^{z,p}_{i}(k)X^z_{e_{i}}(k)\nonumber \\&\quad -\sum _{q=1}^{k}c^{(\beta _{e_i}(k))}_{q} u_{e_i}^{p}(k-q), \nonumber \\&\quad p=1,2,\dots {.},p_{\max }. \end{aligned}$$

(32)

Hence, the structure of the proposed TSK-FOFEC actor-network can be depicted in Fig. 3. Like the TSK-FOFSMC actor, the TSK-FOFEC consists of four layers, which are as follows. The first layer only accepts the input variables $X_{e_i}$ for the network. The second layer represents the membership functions for the input variables, which are obtained by using the following Gaussian function

Fig. 3

The schematic of the TSK-FOFEC actor network

$$\begin{aligned} \begin{aligned} \mu ^{p}_{e_{i}}(X^z_{e_{i}})&=\exp \left( -\frac{1}{2}\left( \frac{X^z_{e_{i}}-c^{p}_{e_i}(k)}{\sigma ^{p}_{e_i}(k)}\right) ^2\right) ,\\&\quad z=1\dots {.}z_{\max }, \end{aligned} \end{aligned}$$

(33)

where $z_{\max }$ is the number of inputs; $\sigma ^{p}_{e_i}(k)$ and $c^{p}_{e_i}(k)$ are the standard deviation and the center of the pth neuron, respectively. By the third layer, the strength of each fuzzy rule is obtained as

$$\begin{aligned} \begin{aligned} \tau ^{p}_{e_{i}}(k)=\prod _{z=1}^{z=z_{\max }}{\mu ^{p}_{e_{i}}(X^z_{e_{i}})}. \end{aligned} \end{aligned}$$

(34)

Accordingly, the crisp value of the equivalent term of the proposed SMC is given by the output layer as

$$\begin{aligned} \begin{aligned} u_{e_{i}}(k)&=\frac{\sum _{p=1}^{p_{\max }}\tau ^{p}_{e_i}(k) u_{e_{i}}^{p}(k)}{\sum _{p=1}^{p_{\max }}\tau ^{p}_{e_i}(k)}, \end{aligned} \end{aligned}$$

(35)

where $u_{e_{i}}^{p}(k)$ is calculated as

$$\begin{aligned} \begin{aligned} u_{e_i}^{p}(k)&=\sum _{z=1}^{z_{\max }}Q^{z,p}_{i}(k)X^z_{e_{i}}(k)-\sum _{q=1}^{k}c^{(\beta _{e_i}(k))}_{q} u_{e_i}^{p}(k-q),\\&\quad p=1,2,\dots {.},p_{\max }. \end{aligned}\nonumber \\ \end{aligned}$$

(36)

Finally, the ith output for the proposed FOFSMC-FRL controller can be derived by the summation from the outputs of the two actor networks.

$$\begin{aligned} \begin{aligned} u_i(k)&=u_{e_i}(k)+u_{s_i}(k). \end{aligned} \end{aligned}$$

(37)

The TSK-FOFCN critic structure

The TSK-FOFCN critic network is represented using a fuzzy system called $f_c(\varTheta ^{*}_{c},X_c)$. This fuzzy system is used as an approximate for the value function $v_{c}(k)$ for the RL approach of the proposed FOFSMC-FRL controller, as indicated by Eq. (20). The input of this network is as in Eq. (21). Based on the fractional-order derivative, the IF-Then rules for this network are proposed in the following form

$$\begin{aligned} \begin{aligned} Rule^p:&\textit{ If } X^1_{c}(k) \textit{ is } G^p \ldots X^m_{c}(k)\textit{ is } G^p \ldots \textit{ and }\\&X^{m_{\max }}_{c}(k)\textit{ is } G^p\\&\textit{Then} \ \ \ \ {D^{\beta _{c}}v_{c}^{p}(k)}=w_{c}^{p}(k). \end{aligned} \end{aligned}$$

(38)

By using the numeric solution for the fractional-order differential equation of the rule consequence, the above fuzzy rule can be redefined as

$$\begin{aligned} Rule^p:&\textit{ If } X^1_{c}(k) \textit{ is } G^p\ldots X^m_{c}(k)\textit{ is } G^p\ldots \textit{ and }\nonumber \\&X^{m_{\max }}_{c}(k)\textit{ is } G^p\nonumber \\&\textit{Then} \ \ \ \ v_{c}^{p}(k)=w_{c}^{p}(k)-\sum _{q=1}^{k}c^{(\beta _{c}(k))}_{q} v_{c}^{p}(k-q), \nonumber \\&\quad p=1,2,\dots {.},p_{\max }, \end{aligned}$$

(39)

where $p_{\max }$ is the number of fuzzy rules and $\bar{G}=\left[ G^1,\dots {.},G^{p_{\max }}\right]$ are fuzzy sets. $w_{c}^{p}(k)$ are the rule’s consequent parameters and $\beta _{c}(k)$ is the rule’s consequent fractional-order parameter. The structure of the TSK-FOFCN critic network has four layers, as shown in Fig. 4.

Fig. 4

The schematic of the TSK-FOFCN critic network

The output of this network can be given as

$$\begin{aligned} \begin{aligned} v_{c}(k)&=\frac{\sum _{p=1}^{p_{\max }}\mu ^{p}_{c}(\bar{X}_{c}(k)) v_{c}^{p}(k)}{\sum _{p=1}^{p_{\max }}\mu ^{p}_{c}(\bar{X}_{c}(k))}, \end{aligned} \end{aligned}$$

(40)

where $\mu ^{p}_{c}(\bar{X}_{c}(k))$ is the rule firing strength which is calculated by

$$\begin{aligned} \begin{aligned} \mu ^{p}_{c}(\bar{X}_{c}(k))=\exp \left( -\frac{1}{2}\left( \frac{\left\Vert \bar{X}_{c}(k)-\bar{c}^{p}_{c}(k)\right\Vert ^2}{\left( \sigma ^{p}_{c}(k)\right) ^2}\right) \right) , \end{aligned} \end{aligned}$$

(41)

where $\sigma ^{p}_{c}(k)$ and $\bar{c}^{p}_{c}(k)=\left[ c^{1,p}_{c}(k),\dots {.},c^{m_{\max },p}_{c}(k))\right]$ are the standard deviation and the center vector of the pth neuron, respectively.

and

$$\begin{aligned} \begin{aligned} v_{c}^{p}(k)&=w_{c}^{p}(k)-\sum _{q=1}^{k}c^{(\beta _{c}(k))}_{q} v_{c}^{p}(k-q), \\&\quad p=1,2,\dots {.},p_{\max }. \end{aligned} \end{aligned}$$

(42)

Online learning of the proposed method

In this section, a FOLM learning method is developed for the online learning updating of the proposed scheme parameters, including the actors and critic neural network parameters. In comparison to the classical LM, the newly developed FOLM can effectively decrease the system’s uncertainty influence by providing more DOF for the learning parameters. This section also investigates the convergence analysis of the developed learning algorithm.

Updating laws

Actually, the updating laws of the FOFSMC-FRL controller parameters using the developed FOLM learning are conducted based on the minimization of the cost function defined in Eq. (43).

$$\begin{aligned} \begin{aligned} T(\varTheta (k))=\frac{1}{2}\zeta ^T\left( \varTheta (k)\right) \zeta \left( \varTheta (k)\right) , \end{aligned} \end{aligned}$$

(43)

where $\varTheta (k)=\left[ \varTheta _a(k),\varTheta _{c}(k)\right]$ contains the actors and critic network parameters such that

$$\begin{aligned} \varTheta _a(k)= & {} \bigg [c^{p}_{s_i}(k),\sigma ^{p}_{s_i}(k),\rho _{i}^{p}(k),\phi _{i}^{p}(k),\beta _{s_i}(k),\xi _i(k),\nonumber \\{} & {} c^{p}_{e_i}(k),\sigma ^{p}_{e_i}(k),Q^{z,p}_{i}(k),\beta _{e_i}(k)\bigg ] \end{aligned}$$

(44)

$$\begin{aligned} \varTheta _{c}(k)= & {} \left[ w_{c}^{p}(k),c^{m,p}_{c}(k),\sigma ^{p}_{c}(k),\beta _{c}(k)\right] . \end{aligned}$$

(45)

$\zeta (k)=\left[ \zeta _a(k),\zeta _{c}(k)\right]$ contains the learning errors for actors and critic networks. The actors’ parameters, defined in Eq. (44), are updated using the error occurred between the required ultimate objective, $R_a(k)$, and the approximate $v_{c}(k)$ function from the critic as

$$\begin{aligned} \begin{aligned} \zeta _a(k)=v_{c}(k)-R_a(k). \end{aligned} \end{aligned}$$

(46)

The critic’s parameters, defined in Eq. (45), are updated using the prediction error of the critic element as

$$\begin{aligned} \begin{aligned} \zeta _c(k)=v_{c}(k-1)-r(k)-\gamma v_{c}(k). \end{aligned} \end{aligned}$$

(47)

The RL reward signal r(k) is defined as [48]

$$\begin{aligned} \begin{aligned} r(k)=\varPi _{1_{i}}(k)+\varPi _{2_{i}}(k), \end{aligned} \end{aligned}$$

(48)

where

$$\begin{aligned} \begin{aligned} \varPi _{1_{i}}(k)&={\left\{ \begin{array}{ll} 0&{} \vert {e_{i,1}(k)}\vert \le \varepsilon \\ \varepsilon -\vert {e_{i,1}(k)}\vert &{} \mathrm{{otherwise}} \end{array}\right. } \\ \varPi _{2_{i}}(k)&={\left\{ \begin{array}{ll} 0&{} \vert {e_{i,1}(k)}\\ \vert \le \vert {e_{i,1}(k-1)}\vert \\ \vert {e_{i,1}(k-1)}\vert -\vert {e_{i,1}(k)}\vert &{}\mathrm{{otherwise}} \end{array}\right. }, \end{aligned} \end{aligned}$$

(49)

where $\varepsilon$ is a small value.

Based on the cost function defined Eq. (43), the updating rule for the proposed FOFSMC-FRL parameters can be obtained using the classical LM method as

$$\begin{aligned} \begin{aligned} \bigtriangleup \varTheta (k) =&-\left[ J^T(\varTheta (k))J(\varTheta (k))+\eta _g I\right] ^{-1}\\ {}&\times J^T(\varTheta (k)) \zeta (\varTheta (k)) \ \ \ \end{aligned} \end{aligned}$$

(50)

Here, this rule can be modified according to the fractional-order calculus as

$$\begin{aligned} \begin{aligned} D^{\alpha _g}\varTheta (k)=&-\left[ J^T(\varTheta (k))J(\varTheta (k))+\eta _g I\right] ^{-1}\\ {}&\times J^T(\varTheta (k)) \zeta (\varTheta (k)) \ \ \ \end{aligned} \end{aligned}$$

(51)

where $J^\mathrm{{T}}(.)$ is the Jacobian matrix containing the first derivatives of the actors and critic errors with respect to their parameters; $\eta _g=\left[ \eta _a,\eta _c\right]$ are the learning rates parameters; $\alpha _g=\left[ \alpha _a,\alpha _c\right]$ are the fractional-order operators. The suffix “g” defines a general for the two actors and the critic. The Jacobian row elements considering the critic and actor tuning parameters are calculated as

$$\begin{aligned} J(\varTheta _{c}(k))= & {} \frac{\partial \zeta _c(k)}{\partial \varTheta _c(k)} \end{aligned}$$

(52)

$$\begin{aligned} J(\varTheta _{a}(k))= & {} \frac{\partial \zeta _a(k)}{\partial \varTheta _a(k)}. \end{aligned}$$

(53)

By employing the GL definition of fractional-order calculus, the numeric solution for the FO differential equation in Eq. (51) can be given as

$$\begin{aligned} \begin{aligned} \varTheta (k+1)&={D^{\alpha _g}\varTheta (k)}-\sum _{q=1}^{k}c^{(\alpha _g)}_{q}\varTheta (k+1-q). \end{aligned} \end{aligned}$$

(54)

Consequently, the fractional-order updating rule of the proposed FOFSMC-FRL controller parameters can be rewritten as

$$\begin{aligned} \begin{aligned} \varTheta (k+1)=&-\left[ J^\mathrm{{T}}(\varTheta (k))J(\varTheta (k))+\eta _g I\right] ^{-1}\\ {}&{\times } J^\mathrm{{T}}(\varTheta (k)) \zeta (\varTheta (k)){-}\sum _{q=1}^{k}c^{(\alpha _g)}_{q} \varTheta (k{+}1{-}q). \end{aligned}\nonumber \\ \end{aligned}$$

(55)

Hence, the updating laws for critic and actor parameters using the FOLM method are given in Eq. (56) and Eq. (57), respectively.

$$\begin{aligned} \varTheta _{c}(k+1)= & {} -\left[ J^\mathrm{{T}}(\varTheta _{c}(k))J(\varTheta _{c}(k))+\eta _{c} I\right] ^{-1}\nonumber \\{} & {} \times J^\mathrm{{T}}(\varTheta _{c}(k)) \zeta _c(\varTheta _{c}(k))\nonumber \\{} & {} -\sum _{q=1}^{k}c^{(\alpha _{c})}_{q} \varTheta _{c}(k+1-q) \end{aligned}$$

(56)

$$\begin{aligned} \varTheta _a(k+1)= & {} -\left[ J^\mathrm{{T}}(\varTheta _a(k))J(\varTheta _a(k))+\eta _a I\right] ^{-1}\nonumber \\{} & {} \times J^\mathrm{{T}}(\varTheta _a(k)) \zeta _a(\varTheta _a(k))\nonumber \\{} & {} -\sum _{q=1}^{k}c^{(\alpha _a)}_{q} \varTheta _a(k+1-q). \end{aligned}$$

(57)

For critic and actor update laws, the derivatives in the Jacobian matrix $J(\varTheta _{c})$ and $J(\varTheta _a)$ are described in “Appendix A”.

It was remarkable that, the two parameters $\eta _g$ and $\alpha _g$ guide the algorithm. If $\alpha _g$ is set to “1”, the regular integer-order LM method is performed; otherwise, the FOLM is performed. Hence, $\alpha _g$ values are selected empirically in this paper. In contrast, if $\eta _g$ is a high number, Eqs. (56) and (57) approximate the fractional-order GD technique; if it is a small number, Eqs. (56) and (57) approximate the fractional-order GN technique. Obviously, the FOLM algorithm can combine the merits of the fractional-order GD and the fractional-order GN techniques while avoiding their drawbacks. Here, the parameter $\eta _g$ is adaptively selected using Lyapunov theory. The convergence analysis is discussed in the following subsection.

Convergence analysis

Based on the following theorem, the convergence of the proposed method is examined using Lyapunov theory.

Theorem 1

The following constraints should be provided in the learning rates to assure convergence of the rules indicated by Eqs. (56) and (57)

$$\begin{aligned} \begin{aligned} \eta _g\ge \frac{1}{2}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2. \end{aligned} \end{aligned}$$

(58)

Proof

A discrete-type Lyapunov function candidate can be given in the following form

$$\begin{aligned} \begin{aligned} O(k)=0.5 \zeta ^2(k) \end{aligned} \end{aligned}$$

(59)

The change of such Lyapunov function is provided as

$$\begin{aligned} \begin{aligned} \vartriangle O(k)=O(k+1)-O(k). \end{aligned} \end{aligned}$$

(60)

For stable learning, $\vartriangle O(k)$ should be less than “0”. Hence, the $\vartriangle O(k)$ is obtained as

$$\begin{aligned} \begin{aligned} \vartriangle O(k)=0.5\left[ \zeta ^2(k+1)- \zeta ^2(k)\right] . \end{aligned} \end{aligned}$$

(61)

The $\vartriangle O(k)$ error difference can be expressed as

$$\begin{aligned}{} & {} \vartriangle \zeta (k)= \zeta (k+1)- \zeta (k) \end{aligned}$$

(62)

$$\begin{aligned}{} & {} \vartriangle O(k)=0.5\left[ (\zeta (k)+\vartriangle \zeta (k))^2- \zeta ^2(k)\right] \end{aligned}$$

(63)

$$\begin{aligned}{} & {} \vartriangle O(k)=\vartriangle \zeta (k)\left[ \zeta (k)+\frac{\vartriangle \zeta (k)}{2}\right] \end{aligned}$$

(64)

$$\begin{aligned}{} & {} \zeta (k+1)= \zeta (k)+\left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) ^\mathrm{{T}}\varTheta ^{(\alpha _g)}(k). \end{aligned}$$

(65)

From Eq. (51), we can write

$$\begin{aligned} \begin{aligned} D^{\alpha _g}\varTheta (k)=&-\left( \left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) ^T\frac{\partial \zeta (k)}{\partial \varTheta (k)}+\eta _gI\right) ^{-1}\\ {}&\times \left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) ^T \zeta (k) \ \ \ \end{aligned} \end{aligned}$$

(66)

The $\vartriangle O(k)$ can be rewritten as

$$\begin{aligned} \begin{aligned} \vartriangle O(k)=&\left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) D^{\alpha _g}\varTheta (k)\\ {}&\times \left[ \zeta (k)+\frac{1}{2}\left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) D^{\alpha _g}\varTheta (k)\right] \ \ \ \end{aligned} \end{aligned}$$

(67)

By multiplying both sides of Eq. (66) by $\left( \frac{\partial \zeta (k)}{\partial \varTheta }\right)$, hence

$$\begin{aligned} \begin{aligned} \left( \frac{\partial \zeta (k)}{\partial \varTheta }\right) {D^{\alpha _g}\varTheta (k)}=\left( \frac{\partial \zeta (k)}{\partial \varTheta }\right) \varnothing \left( \frac{\partial \zeta (k)}{\partial \varTheta }\right) ^\mathrm{{T}} \zeta (k), \end{aligned} \end{aligned}$$

(68)

where

$$\begin{aligned} \begin{aligned} \varnothing =-\left( \left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) ^\mathrm{{T}}\frac{\partial \zeta (k)}{\partial \varTheta (k)}+\eta _gI\right) ^{-1} \end{aligned} \end{aligned}$$

(69)

$\square$

Lemma 1

(Matrix inversion lemma) [49, 50] Matrix E, F, G and H have appropriate dimension and E is invertible, then we have

$$\begin{aligned} \begin{aligned} \left( E+FGH\right) ^{-1}=&E^{-1}-E^{-1}F\left( G^{-1}+HE^{-1}F\right) ^{-1}\\ {}&\times HE^{-1} \ \ \ \end{aligned} \end{aligned}$$

(70)

where matrix $E \in \mathbb {R}^{N\times N}$, matrix $G \in \mathbb {R}^{M\times M}$, matrix $H \in \mathbb {R}^{M\times N}$, and matrix $F\in \mathbb {R}^{N\times M}$.

Fig. 5

The control structure for the 2-DOF helicopter system

According to Lemma 1, Eq. (69) can be rewritten as

$$\begin{aligned} \begin{aligned} \varnothing =&-\eta _g^{-1}I+\eta _g^{-2}\left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) ^T\\ {}&\times \left( I+\frac{\partial \zeta (k)}{\partial \varTheta (k)}\eta _g^{-1}\left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) ^T\right) ^{-1}\frac{\partial \zeta (k)}{\partial \varTheta (k)} \\=&-\eta _g^{-1}I+\eta _g^{-1}\left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) ^T\\ {}&\times \left( \eta _gI+\frac{\partial \zeta (k)}{\partial \varTheta (k)}\left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) ^T\right) ^{-1}\frac{\partial \zeta (k)}{\partial \varTheta (k)} \ \ \ \end{aligned} \end{aligned}$$

(71)

Property 1

[51] If A is a non-singular square matrix, there is an existence of $n\times n$ matrix $A^{-1}$, which is called the inverse matrix of A such that it satisfies the property

$$\begin{aligned} \begin{aligned} AA^{-1}=A^{-1}A=I, \end{aligned} \end{aligned}$$

where I is the Identity matrix.

It’s worth noting that the matrix E is represented by $\eta _gI$. Then, according to Property 1, the invertible of matrix E can be guaranteed.

Using Eqs. (71) and (68), we obtain

$$\begin{aligned} \begin{aligned} \left( \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right) {D^{\alpha _g}\varTheta (k)}&= -\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2 \zeta (k)\\&\quad +\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^4\\&\quad \times \left( \eta _gI+\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2\right) ^{-1}\zeta (k). \end{aligned} \end{aligned}$$

(72)

The $\vartriangle O(k)$ can be rewritten as

$$\begin{aligned} \begin{aligned} \vartriangle O(k)=&-\frac{1}{2} \zeta (k)^2\Biggr (\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2-\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^4\\ {}&\times \left( \eta _g^{-1}I+\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2\right) ^{-1}\Biggr )\\ {}&\times \biggr (2-\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2+\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^4\\ {}&\times \left( \eta _g^{-1}I+\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2\right) ^{-1}\Biggr ) \ \ \ \end{aligned} \end{aligned}$$

(73)

Since

$$\begin{aligned} \begin{aligned} 0\le \left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2. \end{aligned} \end{aligned}$$

(74)

Thus

$$\begin{aligned} \begin{aligned} \eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^4 \le \left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2+\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^4. \end{aligned} \end{aligned}$$

(75)

By multiplying both sides of Eq. (75) by $\left( \eta _gI+\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2\right) ^{-1}$, we get

$$\begin{aligned} \begin{aligned}&\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^4\left( \eta _gI+\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2\right) ^{-1}\\&\quad \le \eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2. \end{aligned} \end{aligned}$$

(76)

So that

$$\begin{aligned} \begin{aligned} 0\le&\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2 -\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^4\\ {}&\times \left( \eta _gI+\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2\right) ^{-1} \ \ \ \end{aligned} \end{aligned}$$

(77)

Hence, in order that $\vartriangle O(k)\le 0$

$$\begin{aligned} \begin{aligned} 0\le&2-\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2+\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^4\\ {}&\times \left( \eta _g^{-1}I+\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2\right) ^{-1} \ \ \ \end{aligned} \end{aligned}$$

(78)

Thus, the following constraint for the stability is

$$\begin{aligned} \begin{aligned} 0\le 2-\eta _g^{-1}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2, \end{aligned} \end{aligned}$$

(79)

which means

$$\begin{aligned} \begin{aligned} \eta _g\ge \frac{1}{2}\left\Vert \frac{\partial \zeta (k)}{\partial \varTheta (k)}\right\Vert ^2. \end{aligned} \end{aligned}$$

(80)

The proof of Theorem 1 is now complete. The parameter $\eta _g$ is now written as $\eta _g(k)$, which is updated online during algorithm implementation to ensure stability (which verifies that the Hessian matrix is inverted) and rapid convergence of the FOLM method. Hence, the updating laws for critic and actor parameters using the FOLM method are given in Eq. (81) and Eq. (82), respectively.

$$\begin{aligned} \varTheta _{c}(k+1)= & {} -\left[ J^\mathrm{{T}}(\varTheta _{c}(k))J(\varTheta _{c}(k))+\eta _{c}(k) I\right] ^{-1}\nonumber \\{} & {} \times J^\mathrm{{T}}(\varTheta _{c}(k)) \zeta _c(\varTheta _{c}(k))\nonumber \\{} & {} -\sum _{q=1}^{k}c^{(\alpha _{c})}_{q} \varTheta _{c}(k+1-q) \end{aligned}$$

(81)

$$\begin{aligned} \varTheta _a(k+1)= & {} -\left[ J^\mathrm{{T}}(\varTheta _a(k))J(\varTheta _a(k))+\eta _a(k) I\right] ^{-1}\nonumber \\{} & {} \times J^\mathrm{{T}}(\varTheta _a(k)) \zeta _a(\varTheta _a(k))\nonumber \\{} & {} -\sum _{q=1}^{k}c^{(\alpha _a)}_{q} \varTheta _a(k+1-q). \end{aligned}$$

(82)

Fig. 6

System response for the proposed FOFSMC-FRL under staircase trajectory tracking (Scenario 1)

Fig. 7

Convergence of the trajectory tracking error to “0” for the proposed FOFSMC-FRL (Scenario 1)

Fig. 8

System response for the proposed FOFSMC-FRL under external disturbance (Scenario 2)

Fig. 9

Convergence of the trajectory tracking error to “0” for the proposed FOFSMC-FRL (Scenario 2)

Results and discussion

The FOFSMC-FRL scheme is examined in this section as a novel control strategy that combines three different control techniques: FOSMC, fuzzy logic, and online reinforcement learning. To evaluate the efficacy of the proposed FOFSMC-FRL scheme, the following nonlinear state-space model of a 2-DOF helicopter MIMO system is used [52].

$$\begin{aligned} \begin{aligned} \dot{x}=f(x)+g(x)u, \end{aligned} \end{aligned}$$

(83)

where

$$\begin{aligned} \begin{aligned} f(x)&=\; \begin{bmatrix}\dot{\phi }\\ \frac{-m_\mathrm{{heli}}\cos (\phi )[w_{\vartheta }^2l_{cm}^2\sin (\phi )+gl_{cm}]-B_{p}w_{\phi }}{J_{eq,p}+m_\mathrm{{heli}}l_{cm}^2}\\ \dot{\vartheta }\\ \frac{2m_\mathrm{{heli}}w_{\phi }w_{\vartheta }l_{cm}^2\sin (\phi )\cos (\phi )-B_{y}w_{\vartheta }}{J_{eq,y}+m_\mathrm{{heli}}l_{cm}^2\cos ^2(\phi )} \end{bmatrix}\\ g(x)&= \begin{bmatrix}0&{}0\\ \frac{1}{J_{eq,p}+m_\mathrm{{heli}}l_{cm}^2}&{}0\\ 0&{}0\\ 0&{}\frac{1}{J_{eq,y}+m_\mathrm{{heli}}l_{cm}^2\cos ^2(\phi )} \end{bmatrix}\\ u&= \begin{bmatrix}u_{p}&u_{y} \end{bmatrix}^\mathrm{{T}}, \end{aligned} \end{aligned}$$

(84)

where $u_{p}$ and $u_{y}$ are the inputs which are defined as

$$\begin{aligned} \begin{aligned} u_{p}&=k_{pp}V_{mp}+k_{py}V_{my}\\ u_{y}&=k_{yp}V_{mp}+k_{yy}V_{my}, \end{aligned} \end{aligned}$$

(85)

where $\bar{x}=\left[ \phi ,w_{\phi },\vartheta ,w_{\vartheta }\right] \in \mathbb {R}^4$ is the system state vector; $\left[ V_{mp},V_{my}\right] \in \mathbb {R}^2$ are the voltage signals applied to pitch and yaw motors; $\bar{y}=\left[ \phi ,\vartheta \right] \in \mathbb {R}^2$ is the system output vector; $\phi$ is the pitch angle; $\vartheta$ is the yaw angle. The 2-DOF helicopter parameters are [52]: $l_{cm}=0.1855$ m is the distance between the center of mass and the pivot point; $m_\mathrm{{heli}}=1.3872$ kg is the total moving mass; $J_{p}=0.0384$ kg m$^2$ is the moment of inertia about the pitch axis; $J_{y}=0.0431$ kg m$^2$ is the moment of inertia about the yaw axis; $g=9.81$ m s$^2$ is the acceleration due to gravity; $k_{pp}=0.2041$ Nm/V is the torque constant on pitch axis from pitch motor/propeller; $k_{yy}=0.072$ Nm/V is the torque constant on yaw axis from yaw motor/propeller; $k_{py}=0.0068$ Nm/V is the torque constant on pitch axis from yaw motor/propeller; $k_{yp}=0.0219$ Nm/V is the torque constant on yaw axis from pitch motor/propeller; $B_p=0.8$ N/V is the damping friction factor about pitch axis; $B_y=0.318$ N/V is the damping friction factor about yaw axis. The sampling time is 10 ms.

Figure 5 depicts the control structure for the 2-DOF helicopter handled by two FOFSMC-FRL loops. The first control loop forces the system to follow and track the pitch, while the second forces it to track the yaw. The hyper-parameters of the FOFSMC-FRL are as follows: $\alpha _1=0.9978$; $\alpha _2=0.9897$; $\gamma =0.99$.

Three scenarios are run to evaluate the developed FOFSMC-FRL. In scenario 1, the pitch and yaw are given a reference trajectory. The performance of the proposed FOFSMC-FRL is evaluated in scenario 2 under external disturbances. In scenario 3, the uncertainty rejection capability is investigated.

The comparison involves two perspectives regarding the proposed approach. In the first perspective, we compare the proposed FOFSMC-FRL controller to the FOFSMC-IRL controller to evaluate the impact of fractional-order reinforcement learning on enhancing the performance of the fractional-order fuzzy sliding mode control approach. To ensure a fair comparison, the structure of the FOFSMC-IRL controller remains the same as the proposed FOFSMC-FRL controller, with two distinct differences. Firstly, the FOFSMC-IRL controller utilizes the conventional Levenberg–Marquardt learning method, whereas the proposed FOFSMC-FRL controller employs the developed fractional-order Levenberg–Marquardt learning method. Secondly, the FOFSMC-IRL controller describes the consequences of rules for the actors and critic without utilizing FOD (Fractional Order Differentiation), while the proposed FOFSMC-FRL controller incorporates FOD to describe the consequences of rules for the actors and critic. In the second perspective, we compare the proposed FOFSMC-FRL controller to the FOSMC-NE controller [22], which employs an RBF neural network as an estimator to approximate the system model and solve the problem of unknown model parameters. To conduct a thorough assessment of the quantitative results, two performance indices are used: integral of square error (ISE) and integral of absolute value of error (IAE) defined in Eq. (86). All simulations are run on Windows 10 (64 bit) with MATLAB 9.2 using Intel Core i3, CPU (2.4 GHz) having RAM (4 GB).

$$\begin{aligned}{} & {} \mathrm{{IAE}}=\sum _{k=1}^\mathrm{{MaxIter}} \vert e(k)\vert \nonumber \\{} & {} \mathrm{{ISE}}=\sum _{k=1}^\mathrm{{MaxIter}} \left( e(k)\right) ^2. \end{aligned}$$

(86)

Scenario 1: Trajectory tracking

This scenario describes the system response when the reference staircase trajectory is applied for pitch and yaw axes, as indicated by the black line. Figures 6 and 7 show the system response for trajectory tracking in both axes, and the trajectory tracking error convergence, for the FOFSMC-IRL, FOSMC-NE, and proposed FOFSMC-FRL controllers.

As presented in Fig. 6a, b, all control approaches track the reference output. However, the proposed FOFSMC-FRL controller significantly outperforms the other controllers. Figure 6c shows that the proposed method produces much smooth control action. The tracking error, shown in Fig. 7a, b, can be attained in finite time for all controllers. Meanwhile, the tracking error of the proposed method is converged much faster compared to the other controllers. Thus, two definite outcomes can be established: (1) Under FOFSMC-FRL, both angles track the reference output with fewer fluctuations and slighter steady-state errors; (2) the FOFSMC-FRL introduces smoother and less oscillating angles.

Scenario 2: Disturbance rejection

In this part, the disturbance rejection performance of the 2-DOF helicopter is tested under sudden disturbances with 30 V and − 30 V added to the pitch and yaw motors, respectively. The disturbance equals to 125% of the maximal pitch and yaw motor input. The pitch and yaw motors receive 10 ms pulses at $t=5$ s and $t=20$ s, respectively, to imitate the disturbance. Figures 8 and 9 illustrate the response of both angles and the trajectory tracking error convergence, respectively, under external disturbance for the FOFSMC-IRL, FOSMC-NE and the proposed FOFSMC-FRL controllers.

Figure 8a, b shows that the proposed FOFSMC-FRL controller stabilizes both angles much faster than any other controllers. In addition, the proposed FOFSMC-FRL exhibits less and smaller fluctuations in both angles. Furthermore, less control effort is required when applying the proposed method as shown in Fig. 8c. In comparison to the other controllers, Fig. 9a, b shows that the tracking error can converge to “0” in a short time. Thus, the results demonstrated that the proposed FOFSMC-FRL controller outperforms the FOFSMC-IRL and FOSMC-NE controllers over a large disturbance.

Scenario 3: Uncertainty suppression

Here, the controlled system is subject to uncertainty in terms of 20% rise of $m_\mathrm{{heli}}$ and 20% drop of $l_{cm}$ at $t=5$ s. Figures 10 and 11 illustrate the system response of both angles and the trajectory tracking error convergence, respectively, under the applied uncertainty.

Fig. 10

System response for the proposed FOFSMC-FRL under uncertainty (Scenario 3)

Fig. 11

Convergence of the trajectory tracking error to “0” for the proposed FOFSMC-FRL (Scenario 3)

Figures 10 and 11 confirm the findings of the previous two scenarios. The proposed FOFSMC-FRL controller, as depicted in Fig. 10a, b maintains the desired trajectories with fewer oscillations. Furthermore, Fig. 10c shows that the curves of the control input are bounded, smooth, and without chattering. Meanwhile, the tracking error of the proposed FOFSMC-FRL is converged much faster compared to the other controllers, as shown in Fig. 11a, b. As a result, the 2-DOF helicopter system has better uncertainty suppression performance by using the proposed FOFSMC-FRL.

To illustrate the performance of the proposed FOFSMC-FRL, Tables 1 and 2 show the IAE and ISE error performance indices for both angles for all compared controllers. Figures 12 and 13 illustrate the graph that represents the disparity for each performance index value for all controllers.

Table I Comparison of error performance indices for the pitch angle

Table II Comparison of error performance indices for the yaw angle

Fig. 12

Variation in pitch angle performance indices values

Fig. 13

Variation in yaw angle performance indices values

Tables 1 and 2 and Figs. 12 and 13 indicate that the proposed FOFSMC-FRL records the smallest ISE and IAE values for both angles for all test-scenarios.

Computation time for helicopter system is calculated using Table 3. The proposed FOFSMC-FRL controller books longer computation time, suitable for helicopter system within 10 ms sample period.

Statistical analysis

To showcase the significance of the experimental results, a statistical analysis is carried out. First, a quantitative analysis is presented as a reduction percentage (RP) regarding the IAE and ISE performance indices to evaluate how the proposed FOFSMC-FRL algorithm improves the IAE and ISE performance indices compared to other control methods. Second, the statistical analysis of the error performance measurements in terms of the best value, the worst value, the mean value, and the standard deviation is performed.

Tables 4 and 5 present the improved percentage of the quantified results in performance indices by employing the proposed FOFSMC-FRL algorithm compared to the other control methods. Figures 14 and 15 show the graph representation of the quantified results.

From the observed values in Tables 4 and 5 and Figs. 14 and 15, it’s clear that the proposed FOFSMC-FRL significantly improves the adaptation capabilities compared to the other controllers. This ensures that the proposed FOFSMC-FRL is more reliable and performs much better.

The statistical analysis of the error performance measurements is reported in Tables 6, 7, 8, 9, 10 and 11 for all scenarios in terms of the best value, the worst value, the mean value, and the standard deviation. Furthermore, Figs. 16, 17, 18, 19, 20 and 21 represent the 3-dimensional (3-D) histogram graph representation of the statistical analysis results. The analysis is calculated with 50 runs.

Table III Comparison of computation time for the different controllers

Table IV The quantified results for all scenarios regarding the pitch angle

Table V The quantified results for all scenarios regarding the yaw angle

Fig. 14

The graph representation of the quantified results for all scenarios regarding the pitch angle

Fig. 15

The graph representation of the quantified results for all scenarios regarding the yaw angle

As seen in Tables 6, 7, 8, 9, 10 and 11 and Figs. 16, 17, 18, 19, 20 and 21, with the same number of runs, the proposed FOFSMC-FRL controller has better best value and mean value, showing that it can achieve better accuracy. Moreover, the proposed FOFSMC-FRL has a low standard deviation, which means that the data are clustered closely around the mean (more reliable), while the other controllers have a high standard deviation, indicating that the data are widely spread (less reliable). Thus, from observed values, it cames to the end that the proposed FOFSMC-FRL algorithm is superior than the compared algorithms. Hence, it is strongly recommended for the control of the unknown MIMO systems.

Table VI The statistical analysis results for the pitch angle regarding scenario 1

Table VII The statistical analysis results for the yaw angle regarding scenario 1

Table VIII The statistical analysis results for the pitch angle regarding scenario 2

Table IX The statistical analysis results for the yaw angle regarding scenario 2

Table X The statistical analysis results for the pitch angle regarding scenario 3

Fig. 16

The 3-D histogram graph representation of the statistical analysis results for the pitch angle regarding scenario 1

Fig. 17

The 3-D histogram graph representation of the statistical analysis results for the yaw angle regarding scenario 1

Fig. 18

The 3-D histogram graph representation of the statistical analysis results for the pitch angle regarding scenario 2

Fig. 19

The 3-D histogram graph representation of the statistical analysis results for the yaw angle regarding scenario 2

Fig. 20

The 3-D histogram graph representation of the statistical analysis results for the pitch angle regarding scenario 3

Fig. 21

The 3-D histogram graph representation of the statistical analysis results for the yaw angle regarding scenario 3

Table XI The statistical analysis results for the yaw angle regarding scenario 3

Conclusions

This paper presents a novel scheme for the adaptive control of unknown nonlinear systems using the fractional-order fuzzy sliding mode controller with online fractional-order reinforcement learning and adaptive learning rates. The proposed FOFSMC-FRL is a combination of three different control techniques: FOSMC, fuzzy logic, and online reinforcement learning. The FOSMC provides a robust control strategy that can handle uncertainties and disturbances in the nonlinear system, while the fuzzy logic system adapts the control policy to changes in the system dynamics. The online reinforcement learning component learns the optimal control strategy for the system through a reward-based algorithm. The FOFSMC-FRL controller’s parameters are optimized using the developed FOLM learning method, and the Lyapunov theorem has been used to achieve the stability criteria for the learning rates. The simulation study with the 2-DOF helicopter system has demonstrated the efficacy of the proposed FOFSMC-FRL controller as regards tracking accuracy and robustness against external disturbances. In terms of error performance measures (i.e., ISE and IAE), the controller outperforms both the FOFSMC-IRL and FOSMC-NE controllers. In particular, the quantified results showed that using the proposed FOFSMC-FRL reduced IAE and ISE by roughly 42.39% and 49.79%, respectively, in comparison to all other control approaches. Hence, the results demonstrate the potential of combining different control techniques to design more effective and robust controllers for complex unknown nonlinear systems. However, the proposed method has fixed the value of fractional-orders for the actors and criticizing updating laws, which is a disadvantage. To address this issue, future work of this research will include investigating the optimality of the actors and critic updating laws with low computation time, which can result in better performance and more robustness against disturbances.

Appendix A

For the critic update law, the derivatives in the Jacobian matrix $J(\varTheta _{c})$ are derived as follows

$$\begin{aligned} \frac{\partial \zeta _c}{\partial w_{c}^{p}(k)}= & {} \frac{\partial \zeta _c}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial v^p_{c}(k)}\frac{\partial v^p_{c}(k)}{\partial w_{c}^{p}(k)}\nonumber \\= & {} \frac{\mu _{c}^{p}(k)}{\sum _{p=1}^{p_{\max }}\mu _{c}^{p}(k)} \end{aligned}$$

(87)

$$\begin{aligned} \frac{\partial \zeta _c}{\partial c^{m,p}_{c}(k)}= & {} \frac{\partial \zeta _c}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial c^{m,p}_{c}(k)}\nonumber \\= & {} \left( \frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{\max }}\mu _{c}^{p}(k)}\right) \mu _{c}^{p}(k)\left( \frac{X^{m}_{c}-c^{m,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\right) \nonumber \\ \end{aligned}$$

(88)

$$\begin{aligned} \frac{\partial \zeta _c}{\partial \sigma ^{p}_{c}(k)}= & {} \frac{\partial \zeta _c}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial \sigma ^{p}_{c}(k)}\nonumber \\= & {} \left( \frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{\max }}\mu _{c}^{p}(k)}\right) \mu _{c}^{p}(k)\left( \frac{\left\Vert \bar{X}_{c}-\bar{c}^{p}_{c}(k)\right\Vert ^2}{\left( \sigma ^{p}_{c}(k)\right) ^3}\right) \nonumber \\ \end{aligned}$$

(89)

$$\begin{aligned} \frac{\partial \zeta _c}{\partial \beta _{c}(k)}= & {} \frac{\partial \zeta _c}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial v^p_{c}(k)}\frac{\partial v^p_{c}(k)}{\partial \beta _{c}(k)}\nonumber \\= & {} \frac{\mu _{c}^{p}(k)}{\sum _{p=1}^{p_{\max }}\mu _{c}^{p}(k)}\sum _{q=0}^{k}L^{\beta _{c}(k)}_{c_{q}}v_{c}^{p}(k-q) \end{aligned}$$

(90)

where $L^{\beta _{c}(k)}_{c_{q}}$ is the binomial coefficient defined as

$$\begin{aligned} \begin{aligned} L^{\beta _{c}(k)}_{c_{q}}={\left\{ \begin{array}{ll} 0&{} q=0\\ -\frac{c_{q-1}^{(\beta _{c}(k))}}{q}&{} q>0 \end{array}\right. } \end{aligned} \end{aligned}$$

(91)

It’s worth noting that $\frac{\partial \zeta _c}{\partial u_i(k)}$ is given by

$$\begin{aligned} \begin{aligned} \frac{\partial \zeta _c}{\partial u_i(k)}=&\frac{\partial \zeta _c}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\\=&\sum _{p=1}^{p_{max}}\Biggr (-\left( \frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{max}}\mu _{c}^{p}(k)}\right) \mu _{c}^{p}(k)\\ {}&\times \left( \frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\right) \Biggr ) \ \ \ \end{aligned} \end{aligned}$$

(92)

For the actors update laws, the derivatives in the Jacobian matrix $J(\varTheta _a)$ are derived as follows

$$\begin{aligned} \frac{\partial \zeta _a(k)}{\partial c^{p}_{s_i}(k)}= & {} \frac{\partial \zeta _a}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\frac{\partial u_i(k)}{\partial u_{s_i}(k)}\nonumber \\{} & {} \times \frac{\partial u_{s_i}(k)}{\partial \tau _{s_i}^{p}(k)}\frac{\partial \tau _{s_i}^{p}(k)}{\partial \mu _{s_i}^{p}(k)}\frac{\partial \mu _{s_i}^{p}(k)}{\partial c^{p}_{s_i}(k)}\nonumber \\ {}{} & {} =\Biggr (\sum _{p=1}^{p_{max}}\Biggr (-\left( \frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{max}}\mu _{c}^{p}(k)}\right) \nonumber \\ {}{} & {} \times \mu _{c}^{p}(k)\left( \frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\right) \Biggr )\Biggr )\left( \frac{u_{s_i}^{p}(k)-u_{s_i}(k)}{\sum _{p=1}^{p_{max}}\tau _{s_i}^{p}(k)}\right) \nonumber \\ {}{} & {} \times \left( \frac{\tau _{s_i}^{p}(k)}{\mu _{s_i}^{p}(k)}\right) \left( \mu _{s_i}^{p}(k)\left( \frac{X^{r}_{s_{i}}-c^{p}_{s_i}(k)}{\left( \sigma ^{p}_{s_i}(k)\right) ^2}\right) \right) \ \ \ \end{aligned}$$

(93)

$$\begin{aligned} \frac{\partial \zeta _a(k)}{\partial \sigma ^{p}_{s_i}(k)}= & {} \frac{\partial \zeta _a}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\nonumber \\ {}{} & {} \times \frac{\partial u_i(k)}{\partial u_{s_i}(k)}\frac{\partial u_{s_i}(k)}{\partial \tau _{s_i}^{p}(k)}\frac{\partial \tau _{s_i}^{p}(k)}{\partial \mu _{s_i}^{p}(k)}\frac{\partial \mu _{s_i}^{p}(k)}{\partial \sigma ^{p}_{s_i}(k)}\nonumber \\ {}{} & {} =\Biggr (\sum _{p=1}^{p_{max}}\Biggr (-\Biggr (\frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{max}}\mu _{c}^{p}(k)}\Biggr )\nonumber \\ {}{} & {} \times \mu _{c}^{p}(k)\Biggr (\frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\Biggr )\Biggr )\Biggr )\Biggr (\frac{u_{s_i}^{p}(k)-u_{s_i}(k)}{\sum _{p=1}^{p_{max}}\tau _{s_i}^{p}(k)}\Biggr )\nonumber \\ {}{} & {} \times \Biggr (\frac{\tau _{s_i}^{p}(k)}{\mu _{s_i}^{p}(k)}\Biggr )\Biggr (\mu _{s_i}^{p}(k)\Biggr (\frac{\left( X^{r}_{s_{i}}-c^{p}_{s_i}(k)\right) ^2}{\left( \sigma ^{p}_{s_i}(k)\right) ^3}\Biggr )\Biggr ) \ \ \ \end{aligned}$$

(94)

$$\begin{aligned} \frac{\partial \zeta _a(k)}{\partial \rho _{i}^{p}(k)}= & {} \frac{\partial \zeta _a}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\nonumber \\ {}{} & {} \times \frac{\partial u_i(k)}{\partial u_{s_i}(k)}\frac{\partial u_{s_i}(k)}{\partial u_{s_i}^{p}(k)}\frac{\partial u_{s_i}^{p}(k)}{\partial \rho _{i}^{p}(k)}\nonumber \\ {}{} & {} =\Biggr (\sum _{p=1}^{p_{max}}\Biggr (-\Biggr (\frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{max}}\mu _{c}^{p}(k)}\Biggr )\nonumber \\ {}{} & {} \times \mu _{c}^{p}(k)\Biggr (\frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\Biggr )\Biggr )\Biggr )\nonumber \\ {}{} & {} \times \Biggr (\frac{\tau _{s_i}^{p}(k)}{\sum _{p=1}^{p_{max}}\tau _{s_i}^{p}(k)}\Biggr )\Biggr (tanh\Biggr (\frac{\zeta _{i,1}+e^{\left( \xi _i(k)-1\right) }_{i,1}}{\phi _{i}^{p}(k)}\Biggr )\Biggr ) \ \ \ \end{aligned}$$

(95)

$$\begin{aligned} \frac{\partial \zeta _a(k)}{\partial \phi _{i}^{p}(k)}= & {} \frac{\partial \zeta _a}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\nonumber \\ {}{} & {} \times \frac{\partial u_i(k)}{\partial u_{s_i}(k)}\frac{\partial u_{s_i}(k)}{\partial u_{s_i}^{p}(k)}\frac{\partial u_{s_i}^{p}(k)}{\partial \phi _{i}^{p}(k)}\nonumber \\ {}{} & {} =\Biggr (\sum _{p=1}^{p_{max}}\Biggr (-\Biggr (\frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{max}}\mu _{c}^{p}(k)}\Biggr )\nonumber \\ {}{} & {} \times \mu _{c}^{p}(k)\Biggr (\frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\Biggr )\Biggr )\Biggr )\nonumber \\ {}{} & {} \times \Biggr (\frac{\tau _{s_i}^{p}(k)}{\sum _{p=1}^{p_{max}}\tau _{s_i}^{p}(k)}\Biggr )\Biggr (-\frac{\rho _{i}^{p}(k)\left( \zeta _{i,1}+e^{\left( \xi _i(k)-1\right) }_{i,1}\right) }{\left( \phi _{i}^{p}(k)\right) ^2}\nonumber \\ {}{} & {} \times sech^2\Biggr (\frac{\zeta _{i,1}+e^{\left( \xi _i(k)-1\right) }_{i,1}}{\phi _{i}^{p}(k)}\Biggr )\Biggr ) \ \ \ \end{aligned}$$

(96)

$$\begin{aligned} \frac{\partial \zeta _a(k)}{\partial \beta _{s_i}(k)}{} & {} \frac{\partial \zeta _a}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\nonumber \\ {}{} & {} \times \frac{\partial u_i(k)}{\partial u_{s_i}(k)}\frac{\partial u_{s_i}(k)}{\partial u_{s_i}^{p}(k)}\frac{\partial u_{s_i}^{p}(k)}{\partial \beta _{s_i}(k)}\nonumber \\ {}{} & {} =\Biggr (\sum _{p=1}^{p_{max}}\Biggr (-\Biggr (\frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{max}}\mu _{c}^{p}(k)}\Biggr )\nonumber \\ {}{} & {} \times \mu _{c}^{p}(k)\Biggr (\frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\Biggr )\Biggr )\Biggr )\nonumber \\ {}{} & {} \times \Biggr (\frac{\tau _{s_i}^{p}(k)}{\sum _{p=1}^{p_{max}}\tau _{s_i}^{p}(k)}\Biggr )\Biggr (\sum _{q=0}^{k}h^{\beta _{s_i}(k)}_{s_{q}}u_{s_i}^{p}(k-q)\Biggr ) \ \ \ \nonumber \\ \end{aligned}$$

(97)

where $h^{\beta _{s_i}(k)}_{s_{q}}$ is the binomial coefficient defined as

$$\begin{aligned} h^{\beta _{s_i}(k)}_{s_{q}}= & {} {\left\{ \begin{array}{ll} 0&{} q=0\\ -\frac{c_{q-1}^{(\beta _{s_i}(k))}}{q}&{} q>0 \end{array}\right. } \end{aligned}$$

(98)

$$\begin{aligned} \frac{\partial \zeta _a(k)}{\partial \xi _i(k)}= & {} \frac{\partial \zeta _a}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\frac{\partial u_i(k)}{\partial u_{s_i}(k)}\nonumber \\{} & {} \frac{\partial u_{s_i}(k)}{\partial u_{s_i}^{p}(k)}\frac{\partial u_{s_i}^{p}(k)}{\partial \xi _i(k)}\nonumber \\= & {} \left( \sum _{p=1}^{p_{\max }}\left( -\left( \frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{\max }}\mu _{c}^{p}(k)}\right) \right. \right. \nonumber \\{} & {} \left. \left. \mu _{c}^{p}(k)\left( \frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\right) \right) \right) \left( \frac{\tau _{s_i}^{p}(k)}{\sum _{p=1}^{p_{\max }}\tau _{s_i}^{p}(k)}\right) \nonumber \\{} & {} \times \left( \frac{\rho _{i}^{p}(k)\left( \sum _{q=0}^{k}o^{(\xi _i(k)-1)}_{s_{q}}\zeta _{i,1}(k-q)\right) }{\phi _{i}^{p}(k)}\right. \nonumber \\{} & {} \left. sech^2\left( \frac{\zeta _{i,1}+e^{\left( \xi _i(k)-1\right) }_{i,1}}{\phi _{i}^{p}(k)}\right) \right) \end{aligned}$$

(99)

where $o^{(\xi _i(k)-1)}_{s_{q}}$ is the binomial coefficient defined as

$$\begin{aligned} o^{(\xi _i(k)-1)}_{s_{q}}= & {} {\left\{ \begin{array}{ll} 0&{} q=0\\ -\frac{c_{q-1}^{(\xi _i(k)-1))}}{q}&{} q>0 \end{array}\right. } \end{aligned}$$

(100)

$$\begin{aligned} \frac{\partial \zeta _a(k)}{\partial c^{p}_{e_i}(k)}= & {} \frac{\partial \zeta _a}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\frac{\partial u_i(k)}{\partial u_{e_i}(k)}\nonumber \\{} & {} \frac{\partial u_{e_i}(k)}{\partial \tau _{e_i}^{p}(k)}\frac{\partial \tau _{e_i}^{p}(k)}{\partial \mu _{e_i}^{p}(k)}\frac{\partial \mu _{e_i}^{p}(k)}{\partial c^{p}_{e_i}(k)}\nonumber \\= & {} \left( \sum _{p=1}^{p_{\max }}\left( -\left( \frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{\max }}\mu _{c}^{p}(k)}\right) \right. \right. \nonumber \\{} & {} \left. \left. \mu _{c}^{p}(k)\left( \frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\right) \right) \right) \left( \frac{u_{e_i}^{p}(k)-u_{e_i}(k)}{\sum _{p=1}^{p_{\max }}\tau _{e_i}^{p}(k)}\right) \nonumber \\{} & {} \times \left( \frac{\tau _{e_i}^{p}(k)}{\mu _{e_i}^{p}(k)}\right) \left( \mu _{e_i}^{p}(k)\left( \frac{X^{z}_{e_{i}}-c^{p}_{e_i}(k)}{\left( \sigma ^{p}_{e_i}(k)\right) ^2}\right) \right) \nonumber \\ \end{aligned}$$

(101)

$$\begin{aligned} \frac{\partial \zeta _a(k)}{\partial \sigma ^{p}_{e_i}(k)}= & {} \frac{\partial \zeta _a}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\frac{\partial u_i(k)}{\partial u_{e_i}(k)}\frac{\partial u_{e_i}(k)}{\partial \tau _{e_i}^{p}(k)}\nonumber \\ {}{} & {} \frac{\partial \tau _{e_i}^{p}(k)}{\partial \mu _{e_i}^{p}(k)}\frac{\partial \mu _{e_i}^{p}(k)}{\partial \sigma ^{p}_{e_i}(k)}\nonumber \\ {}{} & {} =\Biggr (\sum _{p=1}^{p_{max}}\Biggr (-\Biggr (\frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{max}}\mu _{c}^{p}(k)}\Biggr )\nonumber \\ {}{} & {} \mu _{c}^{p}(k)\Biggr (\frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\Biggr )\Biggr )\Biggr )\Biggr (\frac{u_{e_i}^{p}(k)-u_{e_i}(k)}{\sum _{p=1}^{p_{max}}\tau _{e_i}^{p}(k)}\Biggr )\nonumber \\ {}{} & {} \times \Biggr (\frac{\tau _{e_i}^{p}(k)}{\mu _{e_i}^{p}(k)}\Biggr )\Biggr (\mu _{e_i}^{p}(k)\Biggr (\frac{\left( X^{z}_{e_{i}}-c^{p}_{e_i}(k)\right) ^2}{\left( \sigma ^{p}_{e_i}(k)\right) ^3}\Biggr )\Biggr ) \ \ \ \nonumber \\ \end{aligned}$$

(102)

$$\begin{aligned} \frac{\partial \zeta _a(k)}{\partial Q^{z,p}_{i}(k)}= & {} \frac{\partial \zeta _a}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\frac{\partial u_i(k)}{\partial u_{e_i}(k)}\nonumber \\{} & {} \times \frac{\partial u_{e_i}(k)}{\partial u_{e_i}^{p}(k)}\frac{\partial u_{e_i}^{p}(k)}{\partial Q^{z,p}_{i}(k)}\nonumber \\ {}{} & {} =\Biggr (\sum _{p=1}^{p_{max}}\Biggr (-\Biggr (\frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{max}}\mu _{c}^{p}(k)}\Biggr )\nonumber \\ {}{} & {} \times \mu _{c}^{p}(k)\Biggr (\frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\Biggr )\Biggr )\Biggr )\Biggr (\frac{\tau _{e_i}^{p}(k)}{\sum _{p=1}^{p_{max}}\tau _{e_i}^{p}(k)}\Biggr )X^{z}_{e_{i}} \ \ \ \nonumber \\ \end{aligned}$$

(103)

$$\begin{aligned} \frac{\partial \zeta _a(k)}{\partial \beta _{e_i}(k)}= & {} \frac{\partial \zeta _a}{\partial v_{c}(k)}\frac{\partial v_{c}(k)}{\partial \mu _{c}^{p}(k)}\frac{\partial \mu _{c}^{p}(k)}{\partial u_i(k)}\frac{\partial u_i(k)}{\partial u_{e_i}(k)}\nonumber \\ {}{} & {} \times \frac{\partial u_{e_i}(k)}{\partial u_{e_i}^{p}(k)}\frac{\partial u_{e_i}^{p}(k)}{\partial \beta _{e_i}(k)}\nonumber \\ {}{} & {} =\Biggr (\sum _{p=1}^{p_{max}}\Biggr (-\Biggr (\frac{v_{c}^{p}(k)-v_{c}(k)}{\sum _{p=1}^{p_{max}}\mu _{c}^{p}(k)}\Biggr )\nonumber \\ {}{} & {} \times \mu _{c}^{p}(k)\Biggr (\frac{X^{1}_{c}-c^{1,p}_{c}(k)}{\left( \sigma ^{p}_{c}(k)\right) ^2}\Biggr )\Biggr )\Biggr )\nonumber \\ {}{} & {} \times \Biggr (\frac{\tau _{e_i}^{p}(k)}{\sum _{p=1}^{p_{max}}\tau _{e_i}^{p}(k)}\Biggr )\Biggr (\sum _{q=0}^{k}h^{\beta _{e_i}(k)}_{e_{q}}u_{e_i}^{p}(k-q)\Biggr ) \ \ \ \end{aligned}$$

(104)

where $h^{\beta _{e_i}(k)}_{e_{q}}$ is the binomial coefficient defined as

$$\begin{aligned} \begin{aligned} h^{\beta _{e_i}(k)}_{e_{q}}={\left\{ \begin{array}{ll} 0&{} q=0\\ -\frac{c_{q-1}^{(\beta _{e_i}(k))}}{q}&{} q>0 \end{array}\right. } \end{aligned} \end{aligned}$$

(105)