1 Introduction

Fuzzy systems have been extensively applied in multiple areas, including decision analysis, automatic control, and system modeling [1]. The membership functions are responsible for mapping the input variables of the fuzzy system. These mappings are then inputted into the fuzzy rules. The generated fuzzy rules are responsible for deciding which action to take. Consequently, designing a fuzzy system structure is one of the most critical processes in FS applications and can be considered a complex optimization problem. Generating the fuzzy rules in a Takagi–Sugeno–Kang Fuzzy System (TSK-FS) and selecting the parameters in these rules are considered an optimization problem that enhances system accuracy. However, fuzzy rule generation is problematic and time-consuming. Therefore, the traditional computation and statistical approaches [2] for automatically generating fuzzy rules cannot enhance the FS performance.

Nature-inspired optimization methods provide an efficient way to find the optimal solution in complex real-world problems [3], such as the optimal design of fuzzy systems and classification problems. Nature-inspired optimization algorithms can be inspired by animal behaviors or evolutionary concepts based on individuals' populations.

Extraordinary efforts have been made to optimize the design of TSK-FSs using evolutionary algorithms (EAs) [4], various genetic algorithms (GAs) [5,6,7], and nature-inspired optimization algorithms such as particle swarm optimization (PSO) [8,9,10], ant colony optimization (ACO) [11], the gravitational search algorithm (GSA) [12], and the grey wolf optimizer (GWO) [13,14,15].

GWO is a relatively new nature-inspired optimization algorithm that mimics grey wolves' social hierarchy and their hunting mechanisms in the wild. The main advantage of GWO lies in its reduced number of search parameters, which results in its superiority on different optimization problems, including optimal tuning of PID-fuzzy controllers [16], training multi-layer perceptrons [17], and optimization benchmarks [18].

This advantage has motivated several researchers [19,20,21,22,23,24] to hybridize two or more meta-heuristics to improve the performance of GWO for optimizing FSs. The authors of [19] recently proposed gDE-GWO, which is a hybridization of GWO and differential evolution (DE) mutation [20]. In [21], the GWO was improved by altering the equation for finding the following positions of the wolves; then, the IGWO with Fuzzy PID controller was applied to power system load frequency control (LFC). Tawhid et al. [22] proposed the hybrid algorithm HGWOGA, which combined the GA and GWO algorithms to minimize a simplified model of a molecule's energy function. A modified version of the GWO algorithm was proposed in [23], namely, the MGWO-based cascade PI-PD controller; the authors assigned more importance to the alpha wolves to find the optimal solution during the iterations.

This paper aims to introduce a hybrid Genetic–Grey Wolf Optimization (GGWO) algorithm for TSK-FS optimization through five main stages. The contributions of the proposed GGWO lie in two main directions.

First, the standard GWO is improved [13] by embedding the GA's crossover and mutation operations to overcome the premature convergence of poor exploitation of solutions in the standard GWO. It will help optimize the search process to find the next locations for the wolves and optimal solutions during iteration. Also, this hybridization accelerates the exploration process and reaches the best solution in a reasonable time.

Second, because designing a fuzzy system can be considered an optimization problem, GGWO is used to optimize TSK-FSs by designing their structure, using rule generation, and optimizing the parameters for each fuzzy rule in the TSK-FSs. The proposed algorithm shows promising performance in optimizing FS compared to other optimization algorithms, as demonstrated in Sect. 5.

The main contribution is summarized as follows.

  • A new hybrid nature-inspired algorithm is proposed, namely Genetic–Grey Wolf Optimization (GGWO) algorithm, to optimize TSK-FSs.

  • GGWO is applied to overcome the premature convergence and poor solution exploitation of the standard GWO.

  • Using genetic crossover and mutation operators accelerates the exploration process and efficiently reaches the best solution (rule generation) within a reasonable time.

  • The proposed GGWO is tested on several benchmark functions compared with other nature-inspired optimization algorithms.

  • The result of simulations applied to the fuzzy control of nonlinear plants shows the superiority of GGWO in designing TSK-FSs with high accuracy compared with different optimization algorithms.

This paper's remainder is organized as follows. Section 2 describes related studies in fuzzy system optimization and introduces the GWO. In Sect. 3, the first-order TSK-FS is defined as a model that can be formulated as an optimization problem; its main goal is to find the optimal convenient solution. Section 4 describes the proposed GGWO. Section 5 presents GGWO simulation results compared to other optimization algorithms, and Sect. 6 concludes the paper.

2 Related work

When designing the structure of TSK-FSs, there are several considerations, including accuracy and interpretability [25]. To preserve a fuzzy model's accuracy, the number of fuzzy rules must be determined, and the parameters in each fuzzy rule must be selected appropriately. Also, constraints that optimize the interpretability of TSK-FSs must be considered. Several studies have been proposed to optimize the design process for TSK-FS models. In [26], generating fuzzy rules was presented based on a fuzzy genetic system. In [10], a constrained PSO algorithm (C-PSO) was proposed to set linear constraints to enhance interpretability while preserving a TSK-FS model's accuracy. Juang et al. [9] proposed a hierarchical cluster-based multispecies particle swarm optimization (HCMSPSO) algorithm for TSK-FS optimization; the authors designed both the structure (the number of rules) and the parameters of an FS. In [27], the authors proposed a new approach for generating accurate and interpretable fuzzy rules: using only fuzzy labels to build transparent knowledge-based systems. In [28], a fuzzy genetic programming approach called FGPRL was proposed to determine the fuzzy rules' size and adjust the controller parameters based on reinforcement learning.

Recently, many researchers [29,30,31,32,33,34] have investigated the optimization algorithms in TSK-FS models and fuzzy rules as follows: Deng et. al. [34] investigated a monotonic relation between the inputs and outputs of the TSK-FS model and presented a Tikhonov regularization strategy to avoid the loss. In [29], the authors used sparse regressions to train high-order TSK-FS models. The sparse regressions used offer regularization; it means that it can be used when the variables number increases the observations. Adequate monotonicity conditions for zero-order TSK-FS models with membership functions generated by cubic splines are proposed in [35], the model concerned with the optimization problems.

Wu et al. [36] proposed three influential optimization techniques based on neural networks for training TSK-FS models: the MBGD with regularization, DropRule, and AdaBound (MBGD-RDA). In [37], the authors improved the MBGD-RDA proposed in [36] by using fuzzy c-means clustering and AdaBound, in a new algorithm named FCM-RDpA, to optimize the parameters used in generating the rules. Wang et al. [38] proposed an aggregation method using fuzzy neural networks for TSK-FS models, namely TSKFNN. The authors implemented AdaBoost to gain a combination of trusty rules to generate prediction models using a number of real datasets.

In [39], the authors proposed a graph-based TSK-FS model to predict hemodialysis patients' adequacy.

2.1 Grey Wolf Optimizer (GWO)

The GWO is a nature-inspired optimization algorithm that Seyedali Mirjalili first proposed in 2014 [13]. The GWO algorithm mimics the social hierarchy of grey wolves and their hunting mechanisms in the wild. The wolves' hunting mechanisms are used to represent a path to the solution of the optimization problem.

Grey wolves tend to live in packs. To simulate the wolf social hierarchy, suppose that there are each pack of wolves contains four different types of wolves: alpha (α), beta (β), delta (δ), and omega (ω); thus, the wolves can be categorized into four classes. The population of search agents (wolves) is categorized according to their fitness function. This hierarchy's mathematical model is designed by considering the wolf with the best fitness function as the alpha wolf (The leader). The second-best fitness is the beta wolf, and the third-best solution is the delta wolf. Any other solution will be considered the omega wolves (the lowest-ranked wolves), who will follow the other three types. This hierarchy is updated in every iteration to change the solutions. The hunting mechanisms of the grey wolves are mathematically modeled via the following steps.

2.1.1 Searching for the prey

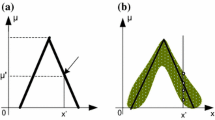
The search process (exploration) is implemented based on α, β, and δ. Their positions are varied randomly to foster a global search for prey. The coefficient vectors \(\vec{A}\) are assigned random values ranging from \(- 1 > \overrightarrow {A }\) > 1, and the coefficient vectors \(\vec{C}\) are assigned random values from [0 to 2], as shown in Fig. 1a, to enable the wolves to find more suitable prey.

Fig. 1
figure 1

a Effect of the coefficient vectors \({\text{A}}^{ \to } \;{\text{and}}\;{\text{C}}^{ \to }\)and b Position vectors of the grey wolves around the prey

Full size image

2.1.2 Encircling prey

Grey wolves encircle their prey during a hunt; the following equations simulate the encircling process:

$$\vec{D} = \left| {\vec{C} . \vec{V}_{p\left( i \right)} - \vec{V}_{\left( i \right)} } \right|$$
(1)
$$\vec{V}_{{\left( {i + 1} \right)}} = \vec{V}_{p\left( i \right)} - \overrightarrow {A } \cdot \overrightarrow {D }$$
(2)

where \({ }\vec{V}_{p}\) is the position vector of the prey, i indexes the current iteration, and \({ }\vec{V}_{ }\) indicates the position vector of a grey wolf. \(\overrightarrow {{A{ }}}\) and \(\vec{C}\) are calculated as follows:

$${\vec{\text{A}}} = 2 {\vec{\text{a}}}.{\vec{\text{r}}}_{ 1} - {\vec{\text{a}}}$$
(3)
$$\vec{C} = 2. \overrightarrow {r }_{2}$$
(4)

During the iterations, the values of \({\vec{\text{a}}}\) vary from 0 to 2 and \({\vec{\text{r}}}_{{{ }1}}\) and \(\overrightarrow {{r{ }}}_{2} { }\) are assigned random values from 0 to 1 to allow the wolves to update their positions around the prey's location using (1) and (2), as shown in Fig. 1b. In Fig. 1b, suppose that the location of a grey wolf is (X, Y) and the location of the prey is (\(X^{\prime}\),\({ }Y^{\prime}\)): the wolves can then update their positions based on prey's location.

2.1.3 Hunting the prey

The alpha wolf is responsible for the hunting process [40] (exploitation), because in most cases, the α wolf leads the pack and can detect the location of prey. However, to mathematically model the optimum location of the prey, the first three best solutions are obtained from the alpha (α), beta (β), and delta (δ) wolves and are calculated as follows:

$$\begin{gathered} \vec{D}_{{\upalpha }} = \left| {\overrightarrow {{C_{1} }} . \vec{V}_{{\upalpha }} - \vec{X}} \right| \hfill \\ \vec{D}_{{\upbeta }} = \left| {\overrightarrow {{C_{2} }} . \vec{V}_{{\upbeta }} - \vec{X}} \right| \hfill \\ \vec{D}_{{\updelta }} = \left| {\overrightarrow {{C_{3} }} . \vec{V}_{{\updelta }} - \vec{X}} \right| \hfill \\ \end{gathered}$$
(5)
$$\begin{gathered} \vec{V}_{1} = \vec{V}_{{\upalpha }} - \overrightarrow {{A_{1} }} \cdot \left( {\overrightarrow {{D_{{\upalpha }} }} } \right) \hfill \\ \vec{V}_{2} = \vec{V}_{{\upbeta }} - \overrightarrow {{A_{2} }} \cdot \left( {\overrightarrow {{D_{{\upbeta }} }} } \right) \hfill \\ \vec{V}_{3} = \vec{V}_{{\updelta }} - \overrightarrow {{A_{3} }} \cdot \left( {\overrightarrow {{D_{{\updelta }} }} } \right) \hfill \\ \end{gathered}$$
(6)

Then, the other agents (wolves) must update their positions based on the positions of the three best search agents (α, β, δ) as shown in the following equation:

$$\vec{V}_{{\left( {i + 1} \right)}} = \frac{{\vec{V}_{1} + \vec{V}_{2} + \vec{V}_{3} }}{3}$$
(7)

Thus, the α, β, and δ wolves determine the prey's position, and the other wolves sequentially update their positions around the prey.

2.1.4 Attacking the prey

When the wolves surround the prey, it stops moving. Then, the grey wolves attack the prey to finish the hunting process. To simulate the attacking process, the value of \({\vec{\text{a}}}\) is decreased; as a result, the value of \(\overrightarrow {{\text{A }}}\) also decreases. The result of the attack process is shown in Fig. 2. \(\overrightarrow {{\text{A }}}\) is considered as having a value from 2a to -2a. The next position of the grey wolf will be between its current location and the location of the prey if the value of \(\overrightarrow {{\text{A }}}\) is between 1 and − 1.

Fig. 2
figure 2

Proposed Genetic Grey Wolf Optimization (GGWO) algorithm

Full size image

3 Problem statement

This section describes the first order TSK-FS [41] to be optimized and shows the mathematical functions for the TSK-FS model; these include the fuzzy rules in the following form:

$${\mathbb{R}}_{j} :If x_{1} \left( m \right) \;{\text{is}}\; A_{j1} , \;{\text{and}} \ldots .{\text{ and}}\;\; x_{p} \left( m \right) \;{\text{is}}\; A_{jp}$$
(8)

THEN \(y is {\mathbb{Z}}_{j} \left( x \right) = a_{j0} + a_{j1} x_{1} + \ldots + a_{jp} x_{p}\). where \({\mathbb{R}}_{j}\) is the \(j^{th}\) rule, \(\in\) \({\mathbb{R}}^{n}_{ }\), \(A_{jp}\) are the fuzzy sets, \(y \in {\mathbb{R}}\), and \(j\) ranges from [1 to c]:

$$A_{jp} \left( {x_{p} } \right) = \exp \left( {\left( {\frac{{X_{p} - V_{jp} }}{{\sigma_{jp} }}} \right)^{2} } \right)$$
(9)

where \(V_{jp}\) and \(\sigma_{jp}\) are the parameters of the fuzzy set, and \(a_{jp} \in A_{jp}\), where p ranges from [1 to IS] and \(IS\) is the dimension of the input space.

Suppose a dataset x = {\(x_{1} , \ldots ..x_{n} \} .\) The strength of fuzzy rule j is calculated as follows:

$${\Phi }_{j} \left( {\vec{x}} \right) = \mathop \prod \limits_{i = 1}^{n} {\mathcal{M}}_{ji } (x_{i} )$$
(10)
$${\Phi }_{j} \left( {\vec{x}} \right) = \exp \left\{ { - \mathop \sum \limits_{i = 1}^{n} \left( {\frac{{X_{p} - V_{jp} }}{{\sigma_{jp} }}} \right)^{2} } \right\}$$
(11)

Gaussian fuzzy sets represent local information efficiently and contain continuous derivatives of the values. In first-order TSK FSs, the consequent function \({\mathbb{Z}}_{j} \left( x \right)\) is set to a linear function of the input variables. The output of the system is given by:

$$\hat{y} = {\raise0.7ex\hbox{${\mathop \sum \nolimits_{j = 1}^{c} \left[ {\mathop \prod \nolimits_{P = 1}^{IS} A_{jp} \left( {x_{p} } \right){\mathbb{Z}}_{j} \left( x \right) } \right] }$} \!\mathord{\left/ {\vphantom {{\mathop \sum \nolimits_{j = 1}^{c} \left[ {\mathop \prod \nolimits_{P = 1}^{IS} A_{jp} \left( {x_{p} } \right){\mathbb{Z}}_{j} \left( x \right) } \right] } {\mathop \sum \nolimits_{k = 1}^{c} \left[ {\mathop \prod \nolimits_{P = 1}^{IS} A_{kp} \left( {x_{p} } \right)} \right]}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\mathop \sum \nolimits_{k = 1}^{c} \left[ {\mathop \prod \nolimits_{P = 1}^{IS} A_{kp} \left( {x_{p} } \right)} \right]}$}}$$
(12)

where c is the number of rules in the FS. The proposed GGWO algorithm's main goal is to optimize the parameters used in each fuzzy rule and specify the number of rules c.

4 The proposed hybrid Genetic–Grey Wolf optimizer (GGWO) algorithm

The proposed GGWO algorithm optimizes the fuzzy system in the five main stages shown in Fig. 2. (1) initial population, (2) fitness function evaluation stage, (3) exploration stage, (4) exploitation stage, and (5) termination stage.

For the GGWO algorithm, a hybrid combination of the GA [42] and the GWO [13] is proposed in this paper. This hybridization aims to overcome the premature convergence and the poor exploitation of solutions of the standard GWO algorithm by using crossover and mutation operations during the exploitation and exploration stages of the GWO algorithm. It will optimize the process of searching for the optimal solutions. The GGWO operating sequence starts by randomly generating the search agents (wolves) that form the pack of grey wolves. Each wolf in the pack is assigned to a position in the vector \({ }\overrightarrow {{V_{i} \left( m \right)}}_{ }\) as follows:

$$\overrightarrow {{V_{i} \left( x \right)}}_{ } = [ v_{i}^{1} \left( x \right) .. v_{i}^{2} \left( x \right).. v_{i}^{{curnt^{i} }} \left( x \right) ]^{T} \quad i = 1,2. \ldots N$$
(13)

where N is the total number of search agents (wolves), \(v_{i}^{{curnt^{i} }} \left( x \right)\) is the position of the \(i^{th}\) wolf in the pack, \(curnt^{i}\) is the index of the current iteration, and \(x\) ranges from 1 to a predefined maximum number of iterations, \(x_{max}\).

Several chromosomes represent these solutions. Partitioning a solution into several chromosomes allows diversity during the wolves' search process for the optimal solution. In the initial population stage, each solution is represented by several genes.

\({\mathbb{G}}{\text{W}}_{{{\varvec{ij}}}}\). An initial process to generate the random solutions \({\mathbb{G}}{\varvec{w}}_{{{\varvec{ij}}}}\) is applied based on the upper and lower boundary, as shown in Eq. (14).

$${\mathbb{G}}{\varvec{W}}_{{{\varvec{ij}}}} = {\mathbb{G}}{\varvec{W}}_{{{\varvec{LOwj}}}} + \fancyscript{r} \times \left( {{\mathbb{G}}{\varvec{W}}_{{{\varvec{Upj}}}} - {\mathbb{G}}_{{{\varvec{WLOwj}}}} } \right)$$
(14)

where is a random value ranging from 0 to 1, i = 1, 2… \({\mathcal{P}}_{{{\mathcal{S}}ize}}\), \({\mathcal{P}}_{{{\mathcal{S}}ize}}\) is the population size (based on the number of wolves), and j = 1, 2, …. \(g_{n}\).

Based on the problem's fitness function, the chromosomes with the highest fitness values will gradually supplant the chromosomes with the lowest fitness values.

This paper calculates the fitness function in terms of the RMSE between the desired and actual outputs. In the proposed GGWO, the number of rules c in the fuzzy system equals the number of genes \({\text{g}}_{{\text{n}}}\) represented, as shown in Fig. 3.

Fig. 3
figure 3

The fuzzy rule representations with their corresponding parameters

Full size image

The reason is that each rule has several parameters to be optimized that cannot be divided into different genes. Consequently, the fitness function for a fuzzy rule directly influences the overall performance of the FS. Suppose that each parameter of the jth rule in (8) is optimized by the jth gene; then, these parameters are denoted as the elements of a gene position vector \(\overrightarrow {{{\mathbb{G}}{\varvec{W}}}}_{{\varvec{j}}}\) for the first-order TSK FSs, as follows:

$$\overrightarrow {{{\mathbb{G}}{\varvec{W}}}}_{{\varvec{j}}} = [ V_{j1} , \sigma_{j1} , \ldots , V_{j1} , \sigma_{j1, } a_{j0} , a_{j1} , \ldots , a_{jn} ]$$
(15)

The overall performance of the FS is directly affected by the genes' fitness in the fuzzy results. In the fitness function evaluation stage, each gene's fitness function is calculated in the fuzzy rules during each iteration to find the optimal solution that represents the highest fitness solution obtained.

The search process terminates when it reaches a predefined maximum number of iterations (\(x_{max}\)). Several genes represent each solution (grey wolf). To determine whether a new fuzzy rule should be generated, the rule strength \(\Phi_{j} \left( {\vec{x}} \right)\) is calculated by (11) for each upcoming data item \(\vec{x}\left( k \right)\):

$$\rho = Max_{i} \{ {\Phi }_{j} \left( {\vec{x}\left( k \right)} \right){ }i = 1, \ldots .c$$
(16)

where c is the number of rules. The rule with the maximum strength (whose \(\Phi_{j} \le \Phi_{ThrS}\)) will be generated, where \({\Phi }_{ThrS} \in \left[ {0,1} \right]\) is a predefined threshold.

In GGWO, the newly generated rule will cause new genes to be developed. When a determination is made that a fuzzy rule should be generated, the centre and width of the Gaussian fuzzy set are denoted by:

$$V_{j1} = x_{i} \left( 0 \right)\quad {\text{and}}\quad \sigma_{j1} = \sigma_{initW} \quad i = 1,2, \ldots n$$
(17)

where \(\sigma_{initW}\) is the initial width of the fuzzy set, and

$$V_{{\left( {c + 1} \right)i}} = x_{i} \left( k \right)\quad i = 1,2, \ldots n$$
(18)
$$\sigma_{{\left( {c + 1} \right)i}} = \Theta \left\{ { - \mathop \sum \limits_{j = 1}^{n} \left( {\frac{{x_{ip} \left( k \right) - v_{ip} }}{{\sigma_{ip} }}} \right)^{2} } \right\}$$
(19)

where \(\Theta\) is the overlap degree between two rules (\(\Theta > 0\) and is a predefined value). Based on (18) and (19), the GGWO algorithm's genes will be initialized for each rule. Selecting the fitness function is the most crucial step in the optimization process: it is the guide for evaluating the population's solutions. The fitness value for each gene is calculated as follows:

$${\mathcal{F}\mathfrak{i}\mathfrak{t}}{ }\left( {{\mathbb{G}}w_{i} } \right) = \mathop \sum \limits_{i = 1}^{{g_{n} }} \frac{1}{{(y_{i} - \hat{y}_{{{\varvec{i}} }} )^{2} }}$$
(20)

The fitness values are assigned different weights. Then, the fitness function is evaluated for each solution, as shown below:

$${\mathcal{F}\mathfrak{i}\mathfrak{t}}{ }\left( {{\mathbb{G}}w_{ij} } \right) = \mathop \sum \limits_{i = 1}^{{{\mathcal{P}}_{{{\mathcal{S}}ize}} }} \mathop \sum \limits_{j = 1}^{{g_{n} }} \frac{1}{{(y_{i} - \hat{y}_{{{\varvec{i}} }} )_{j}^{2} }}$$
(21)

The search agents (wolves) share the fitness value assigned to the search space. The search agents return to the original solutions and choose new solutions, after which their new fitness values \({\mathcal{F}\mathfrak{i}\mathfrak{t}}{ }(N{\mathbb{G}}{\text{w}}_{ij} )\) are evaluated. Then, these new fitness values are compared with the previous values. When the new values are greater than the old ones, the search agents replace the old values with the new solution values. Otherwise, they retain the old solutions.

In the wolf social hierarchy sub-stage, the solutions are classified into different classes based on their fitness functions, as shown in Fig. 4.

Fig. 4
figure 4

Proposed fitness evaluation algorithm (social hierarchy)

Full size image

The solution with the highest fitness function is the alpha wolf (the leader), the solution with the second-best fitness is the beta wolf, and the one with the third-best fitness is the delta wolf. All other solutions are considered omega wolves (the lowest-ranked wolves), following the three different types. Each iteration of the search process consists of two main stages: an exploration stage and an exploitation stage. In the exploration stage, the wolves' main goal is to search and encircle the prey.

In the exploration stage of the proposed GGWO, the GA processes of crossover and mutation are applied to each population to increase the search's diversity and to overcome the premature convergence of the standard GWO algorithm and its poor exploitation of solutions. In the standard GWO algorithm, a random variable \({\vec{\text{a}}}\) is varied from [0 to 2] to determine the prey's location and the alpha wolves.

As shown in Fig. 2, during the prey encirclement substage, the parent solution \(P_{s}\) is assigned to the highest fitness values using (19) and the Neighbour solution \(N_{s}\) is assigned randomly using roulette wheel selection [43]. Then, a crossover is conducted between \(N_{s}\) and \({ }P_{s}\). The \(N_{s}\) and \({ }P_{s}\). solutions are combined to produce one or more children, based on the value of a crossover rate (CR), which is predefined parameter. To determine the nearest solution to the parent, GGWO calculates the value of \(\vec{D}\) based on \({\vec{\text{a}}}\). and \({\vec{\text{r}}}_{{{ }1}}\) using \(N_{s}\), as own in Fig. 5.

Fig. 5
figure 5

Crossover operation on the (GGWO) algorithm

Full size image

The mutation operation is used during the search process for prey (solutions) as defined in the following algorithm:

figure a

where \(New_{ij}\) is the new solution generated, \(PS_{ij}\) is the parent solution, \({{\varvec{\upalpha}}}_{{{\mathbf{ij}}}}\) is a random number in the range [− 1,1], and \(RS_{ij}\) is the random solution selected.

In the exploitation stage, the top three wolves (α, β, and δ) determine the optimum prey location. The top three solutions obtained are calculated as follows:

$$v_{i}^{S} \left( x \right) = \left[ {v_{1}^{{{\text{S}},}} \left( x \right) \ldots v_{2}^{S,} \left( x \right) \ldots v_{i}^{{{\text{S}},}} \left( x \right)} \right],S \in \left\{ {\alpha ,\beta ,\delta } \right\}$$
(22)

The selection process for the three-vector solutions are calculated as follows:

$${\mathcal{F}\mathfrak{i}\mathfrak{t}}_{{\upalpha }} { }\left( {v_{ }^{{\upalpha }} \left( x \right)} \right) = {\text{Max}}_{i = 1..n} {\mathcal{F}\mathfrak{i}\mathfrak{t}}_{{{\alpha i}}} { }\left( {v_{i}^{{\upalpha }} \left( x \right)} \right)| v^{\alpha } \left( x \right) \in V_{i} \left( x \right)$$
(23)
$${\mathcal{F}\mathfrak{i}\mathfrak{t}}_{{\upbeta }} { }\left( {v_{ }^{{\upbeta }} \left( x \right)} \right) = Max_{i = 1..n} {\mathcal{F}\mathfrak{i}\mathfrak{t}}_{{{\beta i}}} { }\left( {v_{i}^{{\upbeta }} \left( x \right)} \right)| v_{ }^{{\upbeta }} \left( x \right) \in V_{i} \left( x \right) \left\{ {v_{ }^{{\upalpha }} \left( x \right)} \right\}$$
(24)
$${\mathcal{F}\mathfrak{i}\mathfrak{t}}_{{\updelta }} { }\left( {v_{ }^{{\updelta }} \left( x \right)} \right) = Max_{i = 1..n} {\mathcal{F}\mathfrak{i}\mathfrak{t}}_{{{\delta i}}} { }\left( {v_{i}^{{\updelta }} \left( x \right)} \right)| v_{ }^{{\updelta }} \left( x \right) \in V_{i} \left( x \right)\backslash \left\{ {v_{ }^{{\upalpha }} \left( x \right),{ }v_{ }^{{\upbeta }} \left( x \right)} \right\}$$
(25)

where the following condition must be applied:

$${\mathcal{F}\mathfrak{i}\mathfrak{t}}_{{\upalpha }} { }\left( {v_{ }^{{\upalpha }} \left( x \right)} \right) > {\mathcal{F}\mathfrak{i}\mathfrak{t}}_{{\upbeta }} { }\left( {v_{ }^{{\upbeta }} \left( x \right)} \right) > {\mathcal{F}\mathfrak{i}\mathfrak{t}}_{{\updelta }} { }\left( {v_{ }^{{\updelta }} \left( x \right)} \right)$$
(26)

A uniform crossover operation is applied between the three vectors to select and update their positions and the prey's position, as shown in Fig. 2. Finally, the best three wolves make the other wolves (omega ω) update their positions according to the best three wolves' positions.

After attacking the prey with several wolves, the GGWO checks the mobility of the prey. When the agents (wolves) confirm that the prey is at location (\(X^{\prime}\),\(Y^{\prime}\)), the leader agent decreases the value of \({\vec{\text{a}}}\), which leads to a decrease in \({\vec{\text{A}}}\), to begin the attacking process.

5 Experimental evaluation

This study evaluated the proposed GGWO algorithm's effectiveness through several simulated experiments and analytical results, as shown in the following subsections. The algorithms were applied on an Intel(R) Core (TM) i7 CPU with 16 GB RAM and 2.81 GHz clock speed using MATLAB R2019a.

The parameters used in the experiments to evaluate the proposed GGWO algorithm can be categorized into common parameters, which are the GA and GWO's parameters defined to achieve a balance between convergence and number of genes\solutions.

The main goal of the GGWO algorithm is to optimize the parameters of the fuzzy rules generated for TSK-FSs. These parameters are problem dependent like \(\Theta\): the overlap degree between two rules, \({\Phi }_{ThrS} ,{ }\sigma_{initW} :\) the thresholds used, \(\Phi_{j} :\) the maximum strength. These parameters are optimized during the implementation, and experiment five shows the influence of changing these parameters on the performance of the algorithms.

To guarantee the fairness of the comparative results, the values of the parameters used in all algorithms are set the same as follows: The maximum number of iterations is 500; the population size is 30. The crossover and mutation rate is 0.7 and 0.01, respectively. The main parameters are set as shown in Table 1.

Table 1 GGWO parameters
Full size table

In addition, an experiment is implemented to test the influence of changing the parameter crossover rate on the accuracy and time of classification in different problems used through the evaluation, as shown in Figs. 6 and 7.

Fig. 6
figure 6

Influence changing parameter crossover rate CR on the GGWO accuracy in different problems

Full size image
Fig. 7
figure 7

Influence changing parameter crossover rate CR on the GGWO Timing in different problems

Full size image

As shown from Figs. 6 and 7, it is concluded that choosing a CR rate of more than 0.6 improves the classification accuracy, but it starts to be stable in accuracy degree when CR's value is from 0.7 to 0.9. However, increasing simulation time is shown when the CR exceeds 0.7. The results displayed in the figures confirm that the value of 0.7 seems to be an acceptable comprise between accuracy and timing, as this value is adapted in the most published work.

5.1 Experiment one: test the efficiency of the proposed GGWO using benchmark functions

The performance of the GGWO algorithm is evaluated using some standard benchmark functions [13]. In this experiment, the GGWO algorithm is tested using nine benchmark functions due to space limitations. \(F_{1}\), \(F_{2}, F_{3}\) , \(F_{4},\) and \(F_{5}\) are unimodal functions while \(F_{8}\), \(F_{9}\), \(F_{10 },\) and \(F_{11}\) are multimodal functions. These functions were selected both for their simplicity and to allow GGWO's results to be compared with other algorithms' results. The nine functions are listed in Table 2. The best solution (\(F_{min}\)) obtained for \(F_{8}\) is 418.9829 \(\times\) 5, while the \(F_{min}\) for the other functions is zero. The dimensions of the nine functions are 30, and the boundary of the search space (range) of each function is listed in Table 2.

Table 2 Benchmark functions
Full size table

The average (Avg) and standard deviation (StD) are calculated for each function using thirty runs, as shown in Table 3. To verify the obtained results, GGWO is compared with Original GWO [13], IGWO [21], PSO [8], GSA [12], and MGWO [23].

Table 3 Results of the benchmark functions by GGWO compared with other algorithms
Full size table

Results' analysis for experiment one: The exploitation and exploration stages of GGWO are tested using unimodal and multimodal functions, respectively. As shown in Table 3, the proposed GGWO algorithm outperforms all the other algorithms on the unimodal functions f1, f2, f3, and f4, reflecting the superiority of GGWO in the exploitation stage. In function f5, the average value obtained by GGWO is better than other algorithms, while the standard deviation obtained by IGWO is better than GGWO. The superiority of GGWO's results occurs from the usage of the GA operators (crossover and mutation) in the exploitation stage in the GGWO algorithm. In addition, GWOA achieves competitive results on the multimodal benchmark functions compared to GWO [13], IGWO [21], PSO [8], GSA [12], and MGWO [23]. Most of the competitive algorithms suffer from becoming trapped in local optima; in contrast, the combination of GA and GWO in the proposed GGWO enhances the search process during the exploration stage and makes the algorithm reach the optimal solution within a reasonable time compared to GWO [13], IGWO [21], PSO [8], MGWO [23], FCM-RDpA [37], MBGD-RDA [36], and TSKFNN [38] algorithms as shown in Fig. 8.

Fig. 8
figure 8

Simulation Time of GGWO Compared to other algorithms

Full size image

From the results obtained in Fig. 8, it is found that the simulation time of the GGWO algorithm is less than that of the GWO algorithm due to the crossover and mutation operation implemented in GWO, which determines the position of a Grey wolf faster.

5.2 Experiment two: test the efficiency of the proposed GGWO in TSK-FS optimization

This experiment uses an optimization example to test the performance of GGWO. The results obtained are compared with those obtained by other optimization algorithms using the same examples. The RMSE is the metric used to evaluate the algorithms on the fuzzy control examples, as shown below.

5.2.1 Example 1: nonlinear plant-tracking control

In this example, the plant to be controlled is described by

$$y_{ } \left( {k + 1} \right) = \frac{{y_{ } \left( k \right)}}{{1 + y^{2}_{ } \left( k \right) }} + u^{3} \left( k \right)$$
(27)

where − 2 \(\le y_{ } \left( k \right) \le 2\), y (0) = 0, u(k) is the control input, and − 1 \(\le y_{ } \left( k \right) \le 1\). The main goal is to control the output u(k) to track the following desired trajectory:

$$y_{d } \left( k \right) = \sin \left( {\frac{\pi k}{{50}}} \right). \cos \left( {\frac{\pi k}{{50}}} \right) 1 \le k \le 250$$
(28)

using a fuzzy controller system. In ANT [11], the ACO was used to select the consequent part of TSK-FSs from a predefined discrete set but could not track the trajectory in (26). The designed fuzzy controller inputs are \(y_{d } \left( {k + 1} \right)\) and \(y_{ } \left( k \right).\) And the output is u(k). For this tracking problem, RMSE is used for performance evaluation, where

$${\text{RMSE}} = \sqrt {\frac{{\mathop \sum \nolimits_{k = 0}^{249} (y_{d } \left( {k + 1} \right) - y\left( {k + 1} \right))^{2} }}{250}}$$
(29)

In this experiment, the optimization process is implemented through fifty runs and the maximum number of iterations is set to 500. The threshold \({\Phi }_{ThrS}\) is set to 0.0004. The average number of fuzzy rules (genes) is 6.

Figure 7 shows the RMSEs of the proposed GGWO algorithm compared to the PSO [8], GWO [13], IGWO [21], ANT [11], HCMSPSO [9], FCM-RDpA [37], MBGD-RDA [36], and TSKFNN [38] algorithms. To verify the performance of GGWO through comparisons with other algorithms, the number of rules and the threshold \({\Phi }_{ThrS}\) are set to the same values in all simulations, and the algorithms were limited to a maximum of 500 iterations. Figure 9 reveals the significant superiority of GGWO over the GWO-based, PSO, and ANT colony algorithms.

Fig. 9
figure 9

Performance of GGWO compared to other GWO-based algorithms in Example 1

Full size image

In addition, the tracking control results of GGWO and other algorithms using a first-order TSK-type fuzzy controller are compared and reported in Table 4.

Table 4 Tracking control (RMSE) by different ALGORITHMS ON Example 1
Full size table

Table 4 shows the averages (Avg) and standard deviations (StD) of the RMSEs over 50 runs. The GGWO achieves the smallest average RMSE. Moreover, Fig. 10 shows the RMSE values of each iteration obtained by different algorithms during the first-order TSK-type fuzzy system's optimization.

Fig. 10
figure 10

Root-Mean-Squared-Error (RMSE) values on each iteration obtained by different algorithms in Example 1

Full size image

The obtained results demonstrate the increased capability of the proposed GGWO algorithm compared to the PSO [8], GWO [13], IGWO [21], ANT [11], and HCMSPSO [9] algorithms. These results occur because of the previous modifications to the standard GWO algorithm. Figures 11 and 12 show the initial distributions of the fuzzy sets for the two input variables and the fuzzy sets' distributions after optimization by GGWO.

Fig. 11
figure 11

Initial distributions of the rules in the input space by the rule generation method

Full size image
Fig. 12
figure 12

The final distributions of the rules in the input space after optimization by GGWO

Full size image

The * represents the fuzzy rules in the input space while the circles and ovals determine the distribution of the rules among the input space. Figure 11 shows the initial distributions of the fuzzy rules in the input space. Then, the final distributions of the rules in the input space are optimized after implementing the GGWO algorithm, as shown in Fig. 12.

Figure 13 shows the best fuzzy control results of the GGWO on Example 1, showing the desired and the actual tacking output using the GGWO algorithm.

Fig. 13
figure 13

Fuzzy control results of the GGWO in Example 1

Full size image

5.2.2 Experiment three: testing the accuracy of the GGWO algorithm when applied to three real datasets

This experiment uses different datasets taken from the UC Irvine Machine Learning Repository, namely, Abalone [44], Airfoil [45], and PowerPlant [46]. Abalone dataset is used to predict the age of Abalone from physical measurements by cutting the shell through the cone, staining it, and counting the number of rings through a microscope. This task consumes time and effort, so other different measurements have been used to easily predict the age. Abalone dataset consists of eight input variables: sex, length, diameter, height, whole weight, shucked weight, viscera weight and shell weight; however, the first input variable is neglected because it is a trichotomous variable. The output variable is the number of rings that predict the age of Abalone. The dataset contains 4177 samples. Table 5 summarizes the properties of the three datasets used in the experiments.

Table 5 Description of the datasets used in the experiments
Full size table

This experiment's main goal is to test the accuracy of the GGWO algorithm when implemented on real datasets. The proposed algorithm is compared to different algorithms, namely FCM-RDpA [37], MBGD-RDA [36], TSKFNN [38], DE [47], Artificial Bee Colony (ABC) [48], which perform unconstrained optimization, as well as with the C-PSO [10], which performs constrained particle swarm optimization. The abalone dataset data are divided as follows: 70% are used as a training set and 30% as a test set.

Examples of the Abalone dataset's fuzzy partitions are illustrated in Fig. 14, where VW, W, M, S, and VS stand for Very Weak, Weak, Medium, Strong, And Very Strong, respectively. The rule base equivalent to the fuzzy partitions of the abalone dataset in Fig. 12 is shown in Table 6.

Fig. 14
figure 14

Examples of fuzzy partitions of the dataset Abalone

Full size image
Table 6 Rule base equivalent to the fuzzy partitions of the abalone dataset in Fig. 12
Full size table

The grid partitioning is implemented to divide the input space into a number of fuzzy partitions, each of which is specified by a membership function for each feature dimension. Figure 14 illustrates the input space fuzzy partitions for the Abalone dataset. In the implemented first-order TSK FSs, the Gaussian membership function represents the local information efficiently and contain continuous derivatives of the values. The consequent function \({\mathbb{Z}}_{j}\left(x\right)\) is set to a linear function of the input variables. The output of the system is given by Eq. (12).

Samples of the membership functions of the fuzzy partitions in the fuzzy rules generated by GGWO are shown in Fig. 15. The fuzzy rules can be described as shown in Table 6.

Fig. 15
figure 15

Sample of membership functions of the fuzzy partitions in fuzzy rules generated by GGWO

Full size image

From Fig. 14, as the number of rules (c) increases, the probability of finding the best solution (\({F}_{min}\)) decreases. To test the accuracy of GGWO, the average RMSE for training and testing data in abalone dataset is calculated and listed in Table 7, along with the number of rules for which it achieves the best accuracy and the time taken by the GGWO algorithm to compute all the attributes of the dataset.

Table 7 Optimal number of rules, computational cost, and RMSE values
Full size table

In addition, the average RMSE for the GGWO algorithms and a different number of iterations on Abalone, Airfoil, and PowerPlant dataset are shown in Figs. 16, 17 and 18, respectively. The results obtained are compared to FCM-RDpA [37], MBGD-RDA [36], TSKFNN [38], GWO [13], IGWO [21], and HCMSPSO [9] algorithms.

Fig. 16
figure 16

Average RMSE for the GGWO algorithms along with different iterations on PowerPlant dataset compared to other algorithms

Full size image
Fig. 17
figure 17

Average RMSE for the GGWO algorithms along with different iterations on Abalone dataset compared to other algorithms

Full size image
Fig. 18
figure 18

Average RMSE for the GGWO algorithms along with different iterations on Airfoil dataset compared to other algorithms

Full size image

The previous figures show that the GGWO algorithm performed the best among the other algorithms in the three datasets. The TSK-FS were trained well from the GGWO algorithm during the iteration. These results ensured that hybridizing the GA with GWO was useful in optimizing the learning rates, which in turn facilitated achieving enhanced learning performances.

To guarantee the fairness of the comparative results, the parameters of all algorithms are equalized as follows: The maximum number of iterations is 500, the population size is 30. The crossover and mutation rate is 0.7 and 0.01, respectively.

In addition, the computational cost in secs for the GGWO algorithm is calculated and compared with the algorithms that had the closest RMSE to our results, namely FCM-RDpA [37], MBGD-RDA [36], and TSKFNN [38] algorithm. Figure 19 shows the computational cost in seconds for the GGWO algorithm implemented into Abalone, Airfoil, and PowerPlant datasets.

Fig. 19
figure 19

Computational cost in seconds for the GGWO algorithm implemented into Abalone, Airfoil and PowerPlant datasets

Full size image

The results show that the proposed algorithms were the faster among other algorithms in the three datasets.

Furthermore, to validate the obtained results, the GGWO results are compared with the results obtained by (DE) [47], (ABC) [48], and C-PSO [10], as shown in Fig. 20.

Fig. 20
figure 20

RMSE for the GGWO algorithms within each fold on abalone compared to other algorithms

Full size image

Figure 20 shows that the proposed GGWO algorithm results are comparable to those obtained by the specifically designed hybrid algorithms.

5.2.3 Experiment four: test the classification accuracy of the proposed GGWO-ANN algorithm

An Optimized Artificial Neural Network, proposed in [49], had been implemented along with GGWO algorithm to optimize the classification performance for the three datasets: Abalone, Airfoil, and PowerPlant. To validate the proposed GGWO-ANN algorithm, the results obtained are compared to MRC-TSK-FSC [35], FCM-RDpA [37], MBGD-RDA [36], SVM [13], and TSKFNN [38] algorithm. Table 8 summarizes the accuracy obtained, in terms of mean values and standard deviation, when implementing the ANN in different datasets.

Table 8 Classification accuracy of GGWO-ANN compared to different algorithms
Full size table

The results show that the classification performance of GGWO-ANN is promising in the datasets with a relatively large number of instances. However, in the dataset with a few instances, as in Airfoil dataset, the accuracy is not the best among the other algorithms. The recent MRC-TSK-FSC [35] algorithm outperforms the GGWO-ANN performance. A deep study for different datasets will be considered in future work.

5.2.4 Experiment Five: test the influence of the control parameters \({\upsigma }_{{{\text{initW}}}}\), \({\Phi }_{{{\text{ThrS}}}}\), and \({\Theta }\) on the performance of GGWO

During the TSK-FS optimization process, GGWO relies on some selected parameters: \(\sigma_{initW}\) is the initial width of the fuzzy set, \({\Phi }_{ThrS}\) is a predefined threshold for rule generation decision, and \({\Theta }\) is the degree of overlap between two rules. These three parameters (\({\upsigma }_{{{\text{initW}}}}\), \({\Phi }_{{{\text{ThrS}}}}\), and \({\Theta }\)) have large effects on the optimization performance because they influence the number of generated rules. In other words, the selection of the \({\Phi }_{ThrS}\), \(\sigma_{initW}\), \({\Theta }\) parameters directly affects the optimization performance of GGWO. In this experiment, the effects of changing the values of these parameters on the overall optimization performance of the proposed GGWO are investigated by calculating the resulting RMSE. The influence of \({\Phi }_{ThrS}\) and \({\Theta }\) is illustrated by examining the nonlinear plant-tracking control problem in Example 1. Figure 21 shows the GGWO performance for different values of \({\Phi }_{ThrS}\), and the results are compared to HCMSPSO [9], C-PSO [10], MGWO [23], and IGWO [21].

Fig. 21
figure 21

Influence of changing parameter \({\Phi }_{ThrS}\) on GGWO Performance

Full size image

Figures 22 and 23 show the RMSE values obtained by GGWO when optimizing the nonlinear plant-tracking control problem using different values of \({\Theta }\) and \({\Phi }_{ThrS}\), respectively. The results are compared to HCMSPSO [9], C-PSO [10], MGWO [23], and IGWO [21].

Fig. 22
figure 22

Influence of changing parameter \(\Theta\) on GGWO Performance

Full size image
Fig. 23
figure 23

Influence of changing parameter \({\sigma }_{initW}\) on GGWO Performance

Full size image

As the figures show, the RMSE values remain stable as the values of \({\Phi }_{ThrS}\), \(\sigma_{initW}\) and \({\Theta }\) increase until they reach a specific value. Subsequently, the RMSE values increase as the values of \({\Phi }_{ThrS} , \sigma_{initW,}\) and \({\Theta }\) increase. Consequently, this value can be considered as a threshold value for the GGWO. In addition, the previous figures show that GGWO achieves performance gains compared to the other algorithms.

To evaluate the performance of GGWO, other optimizing algorithms are also tested on the same dataset, examples and parameters. The experiments showed the RMSE, simulation time, computational cost, and the final distributions of the rules for different algorithms. The smaller RMSE, the less simulation time and the less computational cost indicate that the algorithm has better performance. It can be seen from the experiments that GGWO obtains the smallest RMSE in Abalone, PowerPlant, and Airfoil datasets and has a better performance compared to others in running the functions, with less timing compared to others.

6 Conclusion

This paper proposed a hybrid GGWO algorithm for first-order TSK-FS optimization. GGWO combines the crossover and mutation operations of GA with the exploration and exploitation stages of GWO. This combination has been shown to have several advantages: (1) partitioning the solution into several genes (chromosomes) improved the diversity search of GGWO; (2) the combination maintains a balance between solution exploitation and exploration; (3) the exploration process is accelerated and reaches the best solution in less time; (4) the GGWO algorithm overcomes the tendency of premature convergence and the poor exploitation of solutions in the standard GWO algorithm. Unimodal and multimodal benchmark functions are used to demonstrate the GGWO's efficiency. The results validate that GGWO achieves better values than other nature-inspired optimization algorithms. In addition, GGWO is applied to generating fuzzy rules for TSK-FSs and optimizing the parameters for each fuzzy rule. GGWO tunes all the free parameters in the designed TSK-FSs. The simulation results show that the GGWO can optimally design TSK-FSs and achieve higher accuracy than other optimization algorithms. We intend to apply GGWO algorithm to different multi-objective optimization, multi-constraint optimization, and dynamic uncertainty.