Abstract
Large amount of data are generated from in-situ monitoring of additive manufacturing (AM) processes which is later used in prediction modelling for defect classification to speed up quality inspection of products. A high volume of this process data is defect-free (majority class) and a lower volume of this data has defects (minority class) which result in the class-imbalance issue. Using imbalanced datasets, classifiers often provide sub-optimal classification results, i.e. better performance on the majority class than the minority class. However, it is important for process engineers that models classify defects more accurately than the class with no defects since this is crucial for quality inspection. Hence, we address the class-imbalance issue in manufacturing process data to support in-situ quality control of additive manufactured components. For this, we propose cluster-based adaptive data augmentation (CADA) for oversampling to address the class-imbalance problem. Quantitative experiments are conducted to evaluate the performance of the proposed method and to compare with other selected oversampling methods using AM datasets from an aerospace industry and a publicly available casting manufacturing dataset. The results show that CADA outperformed random oversampling and the SMOTE method and is similar to random data augmentation and cluster-based oversampling. Furthermore, the results of the statistical significance test show that there is a significant difference between the studied methods. As such, the CADA method can be considered as an alternative method for oversampling to improve the performance of models on the minority class.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Additive manufacturing (AM) is “a process of joining materials to make objects from 3D model data, usually layer upon layer, as opposed to subtractive manufacturing methodologies” [15]. It leads (1) to manufacture products that have complex geometries and designs (2) to produce light-weight customized products as well as (3) to reduce the cost and lead time [4, 31]. However, there are still some persisting problems with AM, such as porosity and cracks. To address these problems, in-situ process monitoring has been used for quality inspection [13]. One of the ways of in-situ monitoring is to capture the process with cameras (for instance melt-pool), and then use the captured data to analyse the deviations in the process to find out irregularities (checking defects) in welding. Using this data, several research studies focused on finding more efficient ways for quality inspection with prediction modelling to reduce the manual time-consuming verification process [4, 10, 11, 21, 33].
When using these prediction models, it is important for process engineers that a model correctly classifies images with defects more accurately compared to those ones with no defects since this is crucial for quality inspection. Large amount of data are generated from the monitoring processes and such data can be used to train models. However, one of the problems is that a high volume of these process data does not have any defects (majority class), and a lower volume of data has defects (minority class). Furthermore, it is expensive and time-consuming to collect more defect images since it involves a manual labelling process. Using the imbalanced datasets, standard classifiers often provide sub-optimal classification results i.e. better performance for the majority class than for the minority class. Therefore, we aim to address the class-imbalance issue in manufacturing data to support in-situ quality control of additive manufactured components.
One of the approaches to address the class imbalance problem is by using resampling approaches to obtain the required class balance [20, 22]. Two resampling approaches are undersampling and oversampling. In the undersampling approach, the size of the majority class is reduced to balance with the minority class. The undersampling approach is conventional and simple. However, it suffers from some information loss for the majority class. In the oversampling approach, the size of the minority class is increased to balance with the majority class. This approach does not lose any information in the majority class. However, replicating the original data (i.e., digital images in our case) randomly for oversampling might miss different sub-class distributions in a single class. In this case, a clustering-based oversampling approach has been shown to be suitable since it helps to identify sub-class distributions in a single class by clustering images.
Hence, we choose the oversampling approach with clustering to balance our datasets. We propose an oversampling method, cluster-based adaptive data augmentation (CADA) to improve the performance of classifiers for the minority class. Unlike existing clustering approaches, the proposed method oversamples by learning from misclassified instances. We believe that identifying sub-class distributions in a single class using clustering together with learning from misclassified instances improve the performance of classifiers. The rationale behind this assertion is that there might be some clusters of images that are easier to classify than other clusters. Hence, if we can get some information regarding these images, we can choose which clusters need to be oversampled instead of oversampling every cluster (i.e., the adaptivity aspect in CADA). For the performance comparison of the proposed method, we use random oversampling (ROS), random data augmentation (RDA), cluster-based oversampling (COS) and synthetic minority oversampling technique (SMOTE).
For extracting features from images, in our previous study [10], we conducted a study to explore several hand-crafted feature extraction methods with small sample datasets to use them in the current study. In the latter study, we investigated the performance of random forests (RF) models using the polar transformation (PT), the histogram of oriented Gradients (HOG), the HARALICK descriptors, the local binary patterns (LBP), and naive XY-projections. The results show that PT was better compared to other methods for our use-case image datasets. Hence, we use that study knowledge [10], PT for feature extraction and RF for building the models in our current study. More details of the previous study and results can be found in [10].
2 Aim and scope
This paper aims to address the class-imbalance issue in manufacturing data to support in-situ quality control of additive manufactured components. For this, we propose an adaptive augmentation approach (a data-centric approach), CADA, for oversampling to deal with the class-imbalance issue. We compare the proposed method with selected state-of-the-art oversampling methods. For the experimental investigations, we use melt-pool image datasets which are captured while manufacturing using the Laser Melt Deposition (LMD) method. The setup of the LMD experiment and robot control parameters are out of the scope of this study. Furthermore, the scope is limited to investigate and compare the performance of the oversampling methods, and hence only one classifier is selected to train the models. For the generalization of the proposed method, we use publicly available casting manufacturing image data for quality inspection.
3 Related work
Class-imbalance occurs in classification tasks when some classes have considerably more instances than other classes. These classes are typically called majority and minority classes, respectively. The class-imbalance issue is a very important problem in many domains such as fraud detection, medical diagnosis, and industrial manufacturing [20]. It arises due to limited access to data collection for certain reasons [29]. Wang et al., have stated that class-imbalance is one of the challenges with surface defects datasets since they are generally small because it is costly to collect more samples [32]. That study gave an example that the ratio of no-defects and defects can be highly imbalanced ranging with 9:1 proportions. Hence, it is difficult to use standard classification algorithms since they can be overwhelmed by majority classes and ignore the minority classes [7]. One of the approaches to address the class-imbalance is to use data-centric approaches (also known as pre-processing approaches) [20, 22]. For instance, Cateni et al., have adapted a resampling approach for the class-imbalance to inspect defects on the surface of metal sheets that are captured by cameras [5].
Undersampling approaches such as random undersampling and cluster-based oversampling have been used to obtain the class balance [20, 22, 28, 34]. However, the information loss of the majority class is a problem when using undersampling approaches. Furthermore, there might be another issue with undersampling in some applications where the majority class has very few samples. Hence, undersampling of this class may result in reducing the size of datasets even further which might make it difficult to train an accurate classifier.
Oversampling approaches have been introduced to increase the size of the minority class to obtain balanced class datasets. Initially, random oversampling to duplicate samples for the minority class has been used. However, overfitting is the main issue with using this method [18]. To overcome this issue, SMOTE has been introduced by Chawla [6]. Bach et al., conducted a comparative study with SMOTE and provided insights into this method [2]. Nafi et al., have conducted a study with SMOTE and generalized adversarial networks (GAN) to address class-imbalance issues. The authors of that study state that SMOTE interpolated images are blur compared to GAN’s generated synthetic images [30].
Cluster-based approaches have been used for oversampling to learn complexities when a single class has different sub-class data distributions [23]. Although clustering could be helpful when identifying sub-class distributions in a single class for oversampling, there might be some clusters of images that are easier to classify than the other clusters. Hence, if we can get some information regarding the clusters (for instance, which type of images are needed for a classifier to learn better in the minority class) then we can choose which clusters need to be oversampled instead of oversampling every cluster. Furthermore, if we replicate the images by choosing images randomly from these clusters, overfitting could be an issue similar to random oversampling. Hence, in our proposed method, we apply rotation augmentation on images to avoid overfitting.
There are eight studies reported in [20] which have addressed the class-imbalance issue in infrastructure and industrial manufacturing. Out of these, we found one related study which adapted a resampling approach for class-imbalance to inspect defects on the surface of metal sheets captured by cameras [5]. Furthermore, Houtum et al., proposed the adaptive weighted uncertainty sampling (AWUS) to address the class-imbalance issue in an additive manufacturing application (direct-energy-deposition). The authors have conducted thorough experiments using 28 datasets and concluded that AWUS reduces the number of necessary annotations compared to random sampling [21]. Although machine learning (ML) technologies have been applied in design and other applications such as automation control systems and telecommunications [14], adopting these ML technologies in AM has been introduced recently [17, 24]. Hence, there are challenges with AM data such as data labelling, small sample sizes, and class-imbalance which need to be addressed effectively to build accurate models for quality inspection.
4 In-situ quality control of AM component in aerospace use case
Laser melt deposition (LMD) is one of the popular AM processes. A part is built by melting a surface with a laser beam while simultaneously applying metal wire or powder in the LMD process [12]. For quality assurance, this process in captured with a camera. This captured data contains melt-pools that are created when the material is melted with a laser beam. Robot control parameters (for instance, the distance of nozzle in relation to the substrate and the wire feed rate) are adjusted in order to have a improve the quality of welding. The recorded melt-pool video will later be used to manually analyze the deviations (instability) in the welding process that could lead to defects. Since this instability of welding process data used as an indicator for defects, we refer this as defects classification task.
The criteria to identify non-defective (good) from defective (bad) melt-pool images are as follows:
-
Stubbing: The welding process is considered as bad if the distance of nozzle is too small or the wire feed is too high.
-
Dripping: Dripping is considered as bad welding. It arises if the height is too large or the wire feed is too low, since the wire melts very quickly.
-
Smooth metal transfer: This is considered as good welding means that the process of melt-pool is stable when the distance and wire feed speed are adjusted perfectly.
By looking at images guided by the above criteria, process engineers check the defects (in-site quality control) visually to learn about the robot control parameters in order to have better quality of manufacturing. However, the gained knowledge regarding defects or their potential causes is not often stored and re-used for future production pipelines. Furthermore, the visual inspection process is prone to human-inaccuracy due to the time consuming and tedious work it requires. Therefore, we aim to support in-situ quality control with an attempt to automate the manual inspection using melt-pool data to speed up defect analysis.
5 Methods
In this section, we present our proposed method and other oversampling methods for performance comparisons. Furthermore, we describe the methods that we use for feature extraction, clustering and classification.
5.1 Oversampling techniques
5.1.1 The proposed method (CADA)
CADA oversamples by learning from misclassified instances of the minority class from a classifier that is trained on imbalanced datasets. The assumption is that identifying the misclassified instances of minority classes provides data understanding (for example, which instances are hard to classify), which then serves as input for an adaptive data augmentation instead of a random sampling approach for oversampling.
We have three phases in the CADA oversampling process; Fig. 1 shows the schematic workflow. First, we build a classifier using an original imbalanced dataset. We use the existing RF method to build the classifier. For this, we randomly select 70% of data to train and 30% of data to validate the model with n number of experimental runs (we choose n to be 10 in our experiments which is proportional to the size of the dataset and is computationally feasible). For each experiment, we identify misclassified samples (false positives) that we pass forward to Phase 3.
In Phase 2, we cluster the minority class using the existing Affinity Propagation clustering algorithm. Since we have an image dataset, we first need to extract features from the images for clustering. For this purpose, we did some preliminary investigations using deep features extracted by pre-trained models (i.e., VGG16 and ResNet50) and also with handcrafted feature extraction methods. By manually inspecting clusters, we ended up choosing VGG16 for extracting the deep features from the minority class. The idea with clustering is to find clusters whose sample images have been repeatedly misclassified the most, and which have more instances of misclassified images (identified in Phase 1) compared to the original images. Furthermore, the benefit of clustering is to pin-point those original images which are similar to these identified misclassified images to have them both augmented in Phase 3.
In Phase 3, we use rotation augmentations of images for oversampling. We choose image rotations as they suit our studied datasets and application. Instead of oversampling all clusters, we select the clusters which are identified in Phase 2 to balance the class distribution of minority class with the majority class to form a new training dataset.
5.1.2 SMOTE
In the synthetic minority oversampling technique (SMOTE), the minority class is oversampled by generating synthetic samples based on the original data. SMOTE performs linear interpolation in minority class samples that are close to each other. A brief explanation of SMOTE is as follows. First, it takes each minority class (let’s call the first sample \(i_{original}\)) and then searches for its nearest neighbours (samples) of the minority class. The default number of nearest neighbours parameter k is 5 (given in the original paper) [6]. We also used the default value for this parameter in our study. Second, depending on the size of the oversampling, it selects the samples randomly from the k nearest neighbours (let’s call the first sample from k \(i_{neighbour}\)). Third, it takes the difference between the sample \(i_{original}\) and its neighbour sample \(i_{neighbour}\). Later, this difference is multiplied by a random number which is selected from 0 and 1, and is added to the sample \(i_{original}\) to create a new synthetic sample \(i_{new}\) as shown in the following equation.
5.1.3 Random oversampling
In random oversampling (ROS), the samples are added by replicating randomly selected samples from the minority class with replacement. We choose a random image from the original minority dataset until the required number of images needed to balance the minority class with the majority class are reached. The process of repetition of the same data can induce a bias towards training data and is prone to overfitting. This method has been widely used for comparison studies for oversampling techniques [6, 8, 20, 22, 28].
5.1.4 Random data augmentation
In random data augmentation (RDA), new samples are instantly created by randomly rotating images. The RDA rotates an image clockwise with a given number of degrees [27]. We rotate an image that is chosen randomly and then we add the rotated image for oversampling to balance the dataset. We choose the number of rotations of each image based on the size of the samples which are needed to achieve the desired balance.
5.1.5 Cluster based oversampling
Cluster-based methodologies have been used for both undersampling and oversampling [1, 8]. In cluster-based oversampling (COS), the minority class is initially clustered and then oversampling is performed based on the clustered images. In our study, we use the affinity propagation clustering method proposed in [16]. Once images are clustered, we augment these images by applying rotation. Our approach differs from existing methods in which the same images are selected randomly from the clusters for oversampling. We believe that oversampling the same images might induce overfitting similar to ROS.
5.2 Feature extraction technique: polar transformation
Original images are transformed to polar coordinate system using the Cartesian-to-polar transformation (PT). The pixel number, contrast and calibration are copied to the PT images. The PT uses x-coordinate values of an image in the Cartesian space to calculate the radius r and the y-coordinate values to represent the angel, theta \(\theta \).
The center point in the original image needs to be specified for PT [19]. For this, let us denote the original image dimensions as (M, N) with the coordinates (X, Y). The center point which PT uses to calculate the distance to is \(\left( \left\lceil \frac{M}{2}\right\rceil \mathrm { },\left\lceil \frac{N}{2}\right\rceil \right) \) for gray-scale images [10]. After this, the PT operates on this new center treating it as the origin (0,0), and we choose 360 degrees data (x-values start from 0 to positive radius values). The polar transformed image has a height of 360 due to the circular scan, and the width depends on the original image dimensions. For our experiments, we extract the XY-projections of the polar transformed image, which are then concatenated to form the final feature vector input for training a classification model.
We believe that PT is useful to extract shape features from images containing round shaped objects. In our previous study, we investigated PT’s applicability for feature extraction using a melt-pool image dataset and a public dataset of shapes [10]. The results suggest that PT is suitable for shape object images and performed better compared to other feature extraction techniques (Histogram of Oriented Gradient, the HARALICK descriptors, the Local Binary Patterns and the naive XY-projections of images). Hence, we selected PT for this work to extract features from the studied datasets.
5.3 Clustering: affinity propagation
The affinity propagation (AP) clustering algorithm is based on a concept of message passing between data samples until convergence [16]. For example, a dataset is described with a small number of exemplars (most representatives of other samples). The messages sent between pairs represent the suitability for one sample to be an exemplar of the other. This information is updated in response to the values from other pairs, and it continues to update iteratively until the final exemplars are selected to give the final clusters. The reason for choosing this algorithm is that it selects the number of clusters based on the data. Hence, we do not require to determine the number of clusters beforehand.
5.4 Classifier: random forests
We use RF to construct image classification models, a brief description of its underlying concept is as follows: RF is an ensemble method that is a combination of multiple methods which can handle can handle nominal, categorical and continuous data [3]. Hence, it is used for both regression and classification. The RF method contains several decision trees and each tree represents a model. The tree is built using a deterministic algorithm by selecting random samples and a random set of variables from the training dataset. For this, two hyperparameters of RF are needed to build a forest. These are (1) Ntree: the number of trees to grow in the forest, and (2) Mtry: the number of features which are randomly selected for all splits in a tree.
6 Experimental design
The experiment aims to determine which sampling method improves the performance of the classifier for the minority class for quality inspection of products. In this section, we present our experimental design which includes datasets description, sampling techniques, hyperparameter configurations, evaluation procedure, performance measures and experimental setup.
6.1 Datasets
We used three labelled binary image datasets for the experiments. The first and second datasets (D1 and D2) contain melt-pool images of additive manufacturing process in aerospace engineering. The images of D1 and D2 are selected from two layers of the welding process. The first layer is used for training and the second layer is used as a test dataset. Both layers have melt-pool images with the same characteristics, however, we add synthetic samples to the first layer (train data D1) to train the model, and we evaluate the performance of the model on a real-world scenario using the second layer data (unseen test data D2). The first dataset D1 contains 50 grey images for training and the second dataset D2 has 140 images for training. D2 is an extension of D1, hence, D1 is a subset of D2. The reason for this selection of sample sizes is that we want to explore small datasets since the size of the minority class samples are generally small and it is costly to collect more samples. The test set for both D1 and D2 has 78 images. The output of these D1 and D2 datasets has two classes which are good (no defect) or bad (defective) melt-pool samples are shown in Fig. 2.
The third dataset D3 has grey scale product images (of size 512x512) from casting manufacturing process and it is publicly availableFootnote 1. These images are used for quality inspection by inspecting casting defects. The casting defects are defined as undesired irregularity in a metal casting process such as blow holes, pinholes, shrinkage defects, pouring metal defects etc. Although D3 has 1300 images, we select 140 images for training and 70 images for testing similar to D2 since we want to simulate the experiments in the same manner as we did with our domain dataset D2. We use clustering for both classes and then randomly select samples for D3 (out of 1300). The labels of D3 are whether the casting is without a defect or has a defect as shown in Fig. 3.
6.2 Sampling techniques
We use the proposed method CADA, SMOTE, ROS, and COS for oversampling of the minority class. These methods’ details are presented in Sect. 5. The sample size of the majority class is selected based on the availability of defect images (minority class) and the percentage of synthetic samples for our domain. The idea is to use the smallest possible size of the minority class samples since we do not have enough defect images. This is the reason that we investigate the performance of models using different size datasets (D1 and D2) by changing the ratio of synthetic samples (50%, 60%, 70%, 80%) for oversampling. We choose the number of augmented samples for these ratios based on the size of our studied datasets.
6.3 Hyperparameters and configuration selection
We selected the number of trees (Ntree hyperparameter) for RF to be 130. The reason for choosing this number is that in a previous study, it states that increasing the number of trees can decrease the forest error rate [9, 25]. These two studies [9, 25] have studied Ntree hyperparameter and provided some insights about setting the Ntree parameters, based on these, we choose the value of 130 for Ntree. For the Affinity Propagation clustering algorithm, we choose the default settings of Python Sklearn moduleFootnote 2.
6.4 Evaluation procedure
For each studied dataset, we have a training set to train the model which includes synthetic augmented data for the minority class using each of the studied sampling techniques. For testing the model, we have a separate test set which does not have any synthetic or augmented data. In other words, the test set has all original samples. The reason for this type of evaluation procedure is to evaluate the performance of the model on a real-world scenario using unseen test data since the training sets have synthetic samples. For example, using the cross-validation approach includes evaluation on synthetic samples which is not suitable for our case.
6.5 Performance metrics
We use the Area Under the Curve (AUC), sensitivity and F-score to evaluate the studied models’ performance. In the following, we describe these metrics briefly.
AUC: this gives the measure of the classifier ability to distinguish between classes. The higher the value of AUC is, the better is the performance of the classifier to differentiate between positive and negative classes. We use this measure to identify which model has better performance to distinguish the classes when using different oversampling method.
Sensitivity: this refers to the true positive rate and measures how well a positive class is predicted. The reason for choosing this measure is that predicting the positive class (defect) is more important than predicting the negative class (no defect) in our case. Furthermore, we investigate which sampling method gives better sensitivity since we oversample the positive class.
Where TP is true positive (positive class and positive prediction) and FN is false negative (positive class but negative prediction). In our case, the positive class represents an image with defects and the negative class represent an image with no defects.
F-score: this measures the harmonic mean of precision and recall, and it is used for imbalanced classification. Since the baseline model uses imbalanced data, we choose F-score to establish a fair performance comparison between the baseline model and the other studied models.
Where Precision, shown in Eq. 4, summarizes the fraction of samples that are assigned to the positive class which belongs to the positive class. The recall is the same as the sensitivity.
6.6 Experiment setup
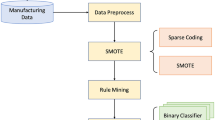
We used the following procedure, which is also shown in Fig. 4, to conduct the experiments. We start by applying sampling methods on imbalanced data for oversampling the minority class. Since we have image datasets, we extract features using polar transformation from each sample (image). Subsequently, we build classification models using RF and evaluate the performance of the models on the test dataset (which is original and does not have any synthetic data) using the selected evaluation metrics. We repeat the aforementioned procedure for all studied oversampling methods to determine the best-performed models.
7 Results and analysis
In this section, we present the experimental results for the use-case melt-pool image datasets (D1 and D2), and the casting manufacturing image dataset (D3). Table 1 shows the sensitivity of models for D1, D2 and D3 when changing the percentage of augmented data. Figure 5, 6 and 7 show the bar plot for the sensitivity results which are also shown numerically in Table 1. These results show that when using CADA, the model yields the best sensitivity compared to the baseline and other methods for D1 and D2. Furthermore, the model with COS has the same sensitivity as the model with CADA when the percentage of augmented data is 80%. For D3, the model with CADA yields the best performance compared to other methods when the percentage of augmented data is 50% and 60%. The models with CADA, COS and RDA methods have the same performance when augmenting 70% and 80% of the data in D3.
Table 2 shows the F-score for D1, D2 and D3. Table 3 shows the area under curve (AUC) for D1, D2 and D3. The F-score and AUC results for D1 show that the model with CADA outperformed the baseline model, ROS, RDA, SMOTE, and it has the same performance as the model with COS when the percentage of augmented data is 80%. For D2, the model with CADA yields the best F-score and AUC compared to other methods. Similar to D1, the F-score of D3 shows that the CADA model outperformed the baseline model, ROS, RDA, SMOTE models and has the same performance as the COS model when the percentage of augmented data is 80%. The AUC of D3 shows that CADA, SMOTE and RDA model have the same AUC when the percentage of augmented data is 50% and 60%. For the rest (70% and 80%), the CADA model yields the best AUC compared to other methods.
7.1 Analysis
Since we oversample the minority class, the sensitivity gives us an idea of how accurate the minority class is classified when using the oversampling methods. Hence, we present the analysis for sensitivity results. Figure 5, 6 and 7 show the bar plots for the sensitivity (recall) of all datasets. The percentage of augmented data or the ratio of synthetic samples is varied to observe how the ratio of augmentation affects the performance of the models. The bar plots for the F-score and AUC results are shown in Appendix A.
Ratio 50–50 and 40–60: The minority class is oversampled with 50 and 60% of synthetic samples for all datasets. The 50 and 40% are the percentages of original images. From the sensitivity plots (Fig. 5, 6 and 7), we can observe that the CADA model has better sensitivity compared to all the methods. The augmented data based on learning from misclassified instances and clustering clearly improve the performance of the models. By analysing the misclassified images of D1 and D2, we observed that the appearance of defect melt-pool images is very close to the images with no defects. We learned that these images are difficult to classify. Hence, we augmented this type of images when training to be able to accurately classify them. Due to the confidentiality of datasets D1 and D2, we did not include any of these images in the paper apart from the examples in Fig. 2. Nevertheless, we have the third dataset D3 where we have also observed similar patterns. The dataset D3 has casting product images and an example of images is shown in Fig. 3. Figure 8 shows an example of these images.
Ratio 30–70 and 20–80: The minority class is oversampled with 70 and 80% of synthetic samples for all datasets. For the ratio of 30–70%, when we have a sample size of 50 (dataset D1), the CADA model performed better than other models as shown in Fig. 5. However, when we have the ratio of 20–80 for D1, the CADA and COS models classified the same number of true positives. For D2, CADA and RDA models classified the same number of true positives. When the percentage of augmented data is high, there will be very few original samples. For instance, for the ratio 20–80% of D1, we have 5 original images and 20 synthetic samples for the minority class. In this case, CADA, COS and also ROS (as shown also in D1, D2, D3 cases) can have the same performance since all these three methods use image rotation to augment synthetic samples.
7.2 Statistical analysis
We performed statistical analysis to see if there is any significant difference between the performance of the studied oversampling methods regardless of the data augmentation ratio. For this analysis, we use the sensitivity, F-score and AUC results of all the methods (baseline, ROS, RDA, SMOTE, COS and CADA). For the statistical significance test of more than two samples, we used Friedman statistical test [26]. The Friedman test is a non-parametric test that ranks the methods for each dataset based on their performance. The statistical hypothesis is:
\(H_o\): All models which are constructed with baseline, ROS, RDA, SMOTE, COS and CADA perform equally well with respect to predictive performance.
\(H_a\): There is a significant difference between models which are constructed with baseline, ROS, RDA, SMOTE, COS and CADA methods.
From the Friedman test, we obtained a p value which is less than a significance level of 0.05, see Table 4. Hence, we reject the null hypothesis and thus, we infer that there is a significant difference between models when constructed with datasets using the studied oversampling methods. Furthermore, we conducted the Nemenyi test for pairwise comparison to see individual differences. Table 4 shows the Nemenyi test results with bold p values where we have pairwise significance difference.
8 Discussions
We have performed the investigations of these methods using three datasets. Two datasets are from our domain and the third one is publicly available. Hence, one must consider that our observations are based on these datasets. Since we have studied two different sample sizes (50 samples in D1 and 140 samples in D2 & D3) and different ratios of augmentation for oversampling, one can get an idea of the studied oversampling methods to choose them to balance datasets.
There is a similarity between ROS and RDA in that, both methods use a random sampling approach. However, the ROS method replicates the same samples that are selected randomly, and the RDA method applies rotations on the images that are selected randomly. As shown in the results, ROS is not an efficient way for oversampling in our case. RDA is a better option compared to ROS if one wants to choose random sampling approaches. Regarding the SMOTE method, it has better performance than ROS in some cases. However, it still does not seem to be suitable for the studied datasets. One may observe that SMOTE has the same AUC as CADA and RDA when having 60% augmentation for dataset D3 in Table 3. However, this model with SMOTE classified more negative samples correctly than the positive class, consequently, it yields low sensitivity (recall) compared to CADA and RDA.
From COS, we learned that balancing samples based on the size of the clusters for oversampling does not really help us getting better performance on the minority class. The reason is that some clusters are easier for a model to classify even though it has a smaller number of images than the other clusters. Hence, in this case, balancing the samples based on cluster size does not contribute either to improve the performance of models. However, this might be not the case when we augment a higher percentage of data (70 and 80%) and have a small number of original samples for oversampling. Hence, the COS method could be suitable in such cases.
With respect to CADA, we observed that it performed the best for 50 and 60% augmentation of the minority class, and it performed similar to COS and RDA for 70 and 80% augmentation. Hence, in summary, the CADA method is suitable in all cases. This can be attributed to learning from misclassified images for oversampling. However, when we have very few original samples, there is a chance that we get all the images as misclassified. Hence, we might not get any information regarding the images which are difficult to classify. In such cases, both COS and RDA can be considered suitable as shown in the results.
Regarding data augmentation in CADA, we selected clusters that have repeated misclassified images. Furthermore, we manually inspected the identified misclassified images for a better understanding of minority samples as it not only helps us to have a better classification of these samples but also gives us an idea on what type of welding process irregularities contribute to the generation of these images. In this study, this kind of analysis is deemed feasible since we have a small number of samples. For larger datasets, the identification of clusters for augmentation can be automated by having a weighted combination of the number of repeatedly misclassified images and the relative ratio of these images in each cluster (i.e., the clusters which have more misclassified images) in order to rank the clusters for per-priority data augmentation. We will look into the applicability of CADA for larger datasets (given their availability) in future work. Furthermore, we believe that CADA will be used to improve the training set even if it is balanced in other applications, and we will look in to this aspect in future work.
Regarding the studied datasets, we observed that there are many image variations in the dataset D3 compared to the rest of the datasets (D1 and D2). This makes it harder to achieve better performance for the models, for example, we obtain the maximum sensitivity of 80%. We believe that the model needs more training data to improve its performance as we did for D1, which is a subset of D2. Nevertheless, our intention is to investigate how the proposed method can be generalized to other datasets when compared to other oversampling methods. Hence, we choose the casting manufacturing process dataset D3. Thus, improving the accuracy of models when using D3 was not our aim in this study.
9 Conclusions
In this study, we proposed the cluster-based adaptive data augmentation (CADA) method for oversampling to address the class-imbalance issue in machine learning for manufacturing data for in-site quality control of products. We investigated the applicability of the proposed method using datasets from additive manufacturing and casting manufacturing by changing the ratio of augmentation. Furthermore, the proposed method is compared with the selected state-of-the-art oversampling methods (ROS, RDA, COS and SMOTE) to determine its applicability. The experimental results show that CADA performed better compared to ROS, SMOTE and equal to RDA and COS. Furthermore, we observed that CADA performed the best for 50 and 60% augmentation of the minority class, and it performed similar to COS and RDA for 70 and 80% augmentation. These results show that the CADA method is suitable in all cases when we are changing the ratio of synthetic samples. Therefore, the CADA method can be considered as an alternative method for oversampling to improve models’ performance on the minority class. Future work could be investigating the applicability of the proposed method on larger image datasets in other applications even if they are balanced to improve training datasets and improve models’ performance. Furthermore, we will include more than one classifier for performance comparison together with data augmentation methods in future work.
Data Availability Statement
The public dataset which we use in our experiments is available https://drive.google.com/drive/folders/1A_3EHO-DMQNaArXQASK9gONFXFENEqL6?usp=sharing.
References
Abouelenien M, Yuan X, Giritharan B, Liu J, Tang S (2013) Cluster-based sampling and ensemble for bleeding detection in capsule endoscopy videos. Am J Sci Eng 2(1):24–32
Bach M, Werner A, Żywiec J, Pluskiewicz W (2017) The study of under-and over-sampling methods’ utility in analysis of highly imbalanced data on osteoporosis. Inf Sci 384:174–190
Breiman L (2001) Random forests. Mach Learn 45(1):5–32
Caggiano A, Zhang J, Alfieri V, Caiazzo F, Gao R, Teti R (2019) Machine learning-based image processing for on-line defect recognition in additive manufacturing. CIRP Ann 68(1):451–454
Cateni S, Colla V, Vannucci M (2014) A method for resampling imbalanced datasets in binary classification tasks for real-world problems. Neurocomputing 135:32–41
Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP (2002) Smote: synthetic minority over-sampling technique. J Artif Intell Res 16:321–357
Chawla NV, Japkowicz N, Kotcz A (2004) Special issue on learning from imbalanced data sets. ACM SIGKDD Explor Newsl 6(1):1–6
Cieslak DA, Chawla NV, Striegel A (2006) Combating imbalance in network intrusion datasets. In: GrC, Citeseer, pp 732–737
Dasari SK, Cheddad A, Andersson P (2019) Random forest surrogate models to support design space exploration in aerospace use-case. In: IFIP international conference on artificial intelligence applications and innovations, Springer, pp 532–544
Dasari SK, Cheddad A, Palmquist J (2020) Melt-pool defects classification for additive manufactured components in aerospace use-case. In: 2020 7th international conference on soft computing & machine intelligence (ISCMI), IEEE, pp 249–254
Dasari SK, Cheddad A, Lundberg L, Palmquist J (2021) Active learning to support in-situ process monitoring in additive manufacturing. In: 2021 20th IEEE international conference on machine learning and applications (ICMLA), IEEE, pp 1168–1173
Emmelmann C, Kranz J, Herzog D, Wycisk E (2013) Laser additive manufacturing of metals. Laser technology in biomimetics. Springer, Berlin, pp 143–162
Everton SK, Hirsch M, Stravroulakis P, Leach RK, Clare AT (2016) Review of in-situ process monitoring and in-situ metrology for metal additive manufacturing. Mater Des 95:431–445
Fan W, Chen Y, Li J, Sun Y, Feng J, Hassanin H, Sareh P (2021) Machine learning applied to the design and inspection of reinforced concrete bridges: resilient methods and emerging applications. Struct, Elsevier 33:3954–3963
Frazier WE (2014) Metal additive manufacturing: a review. J Mater Eng Perform 23(6):1917–1928
Frey BJ, Dueck D (2007) Clustering by passing messages between data points. Science 315(5814):972–976
Fu Y, Downey AR, Yuan L, Zhang T, Pratt A, Balogun Y (2022) Machine learning algorithms for defect detection in metal laser-based additive manufacturing: a review. J Manuf Process 75:693–710
Ganganwar V (2012) An overview of classification algorithms for imbalanced datasets. Int J Emerg Technol Adv Eng 2(4):42–47
Gonzalez RC, Woods RE, Eddins SL (2020) Digital image processing using Matlab, 3rd edition p 810
Haixiang G, Yijing L, Shang J, Mingyun G, Yuanyue H, Bing G (2017) Learning from class-imbalanced data: review of methods and applications. Expert Syst Appl 73:220–239
van Houtum GJ, Vlasea ML (2021) Active learning via adaptive weighted uncertainty sampling applied to additive manufacturing. Addit Manuf 48:102411
Kaur H, Pannu HS, Malhi AK (2019) A systematic review on imbalanced data challenges in machine learning: applications and solutions. ACM Comput Surv (CSUR) 52(4):1–36
Kovács G (2019) An empirical comparison and evaluation of minority oversampling techniques on a large number of imbalanced datasets. Appl Soft Comput 83:105662
Li X, Jia X, Yang Q, Lee J (2020) Quality analysis in metal additive manufacturing with deep learning. J Intell Manuf 31(8):2003–2017
Oshiro TM, Perez PS, Baranauskas JA (2012) How many trees in a random forest? In: International workshop on machine learning and data mining in pattern recognition, Springer, pp 154–168
Sheskin DJ (2020) Handbook of parametric and nonparametric statistical procedures. CRC Press, United States
Shorten C, Khoshgoftaar TM (2019) A survey on image data augmentation for deep learning. J Big Data 6(1):1–48
Sowah RA, Agebure MA, Mills GA, Koumadi KM, Fiawoo SY (2016) New cluster undersampling technique for class imbalance learning. Int J Mach Learn Comput 6(3):205
Sun Y, Wong AK, Kamel MS (2009) Classification of imbalanced data: a review. Int J Pattern Recognit Artif Intell 23(04):687–719
Tajik M, Movasagh S, Shoorehdeli MA, Yousefi I (2015) Gas turbine shaft unbalance fault detection by using vibration data and neural networks. In: 2015 3rd RSI international conference on robotics and mechatronics (ICROM), IEEE, pp 308–313
Wang C, Tan X, Tor SB, Lim C (2020) Machine learning in additive manufacturing: state-of-the-art and perspectives. Addit Manuf 36:101538
Wang J, Ma Y, Zhang L, Gao RX, Wu D (2018) Deep learning for smart manufacturing: methods and applications. J Manuf Syst 48:144–156
Weimer D, Scholz-Reiter B, Shpitalni M (2016) Design of deep convolutional neural network architectures for automated feature extraction in industrial inspection. CIRP Ann 65(1):417–420
Zhang YP, Zhang LN, Wang YC (2010) Cluster-based majority under-sampling approaches for class imbalance learning. In: 2010 2nd IEEE international conference on information and financial engineering, IEEE, pp 400–404
Funding
Open access funding provided by Blekinge Institute of Technology.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dasari, S.K., Cheddad, A., Palmquist, J. et al. Clustering-based adaptive data augmentation for class-imbalance in machine learning (CADA): additive manufacturing use case. Neural Comput & Applic (2022). https://doi.org/10.1007/s00521-022-07347-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00521-022-07347-6