1 Introduction

The progress in technological infrastructures and the awareness about environmental resource consumption are driving a revolution in how energy is supplied [1]. There is a need of not only providing stable energy but also accomplishing efficiency requirements and prediction capabilities to anticipate issues. This is especially important in critical services such as irrigation system [2],

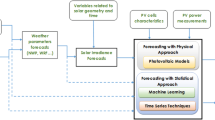
telecommunication stations [3] and defense systems [4], where the system is not fed by the electrical distribution network but a Photo-Voltaic (PV) standalone installation. The energy in these systems is not consumed at the same rate at which is generated so the installation needs an Energy Storage System (ESS) to provide a stable power supply. This stability is subject to unpredictable meteorological phenomena, turning the efficient autonomy into a challenge. The solution involves designing an intelligent system capable of predicting future low power generation scenarios, preserving the infrastructures typically coordinated by low-cost embedded systems. In this sense, data-driven techniques are must. Among others, GPR appears as a promising tool [5, 6] because of the absence of overfitting and the measurement of the uncertainty of the prediction. However, GPR requires a large computational effort, limiting its use in real-time applications. To cope with this, this paper analyzes the performance of different GPR models using a real and large dataset, containing the waveforms of typically measured variables in an ESS of a communication system (see Fig. 1).

Fig. 1
figure 1

PV installation in Sigena, region of Aragón, Spain

Full size image

The problem of feature prediction in ESSs based on Battery Management Systems (BMSs) is a motivating topic. For instance, [7] works in predicting both State of Charge (SoC) and State of Health (SoH) by an Extended Kalman Filter (EKF) and an adaptive observer. A Probabilistic Neural Network is presented in [8] to predict the SoH. Following with the learning tools, [9] proposes a Support Vector Machine (SVM) model for regression. Nevertheless, due to the aforementioned advantages, GPR is a cornerstone in the state-of-the-art discussion. The authors in [10] apply Regular GPR to the prediction of the State-of-Charge (SoC) of a single battery. A similar approach is presented in [11], focused on the voltage prediction in a certain horizon applying a recursive GPR. Another interesting parameter to predict in BMSs is the SoH [12] and the Remaining Useful Live (RUL). In this regard, recent works like [13, 14] explore the use of GPR to determine the aging of Lithium-ion batteries and control their SoH under different life-cycle regimes. Furthermore, the authors of [15,16,17] have proved the convenience of GPR techniques to predict the health of Lithium-ion batteries under uncertain scenarios, modifying the structure of the underlining kernels to better consider empirical and electrochemical knowledge. Despite the great promise of the aforementioned instances, GPR is typically studied with artificial and/or informal datasets.

In contrast, the main contribution of this paper is the extension of GPR in BMS applications to a real, large, complex dataset, where the computational cost and memory use are crucial and a significant level of unpredictability is involved. There are two critical parameters to predict: the evolution of the voltage during the day and the End Of Night (EON) voltage, the latter with especial impact to develop fault-tolerant systems. This study concerns a variety of GPR versions, kernels and hyperparameters and compares the performance with LSTM and NARX techniques.

The outline of the paper is organized as follows. Section II introduces the dataset, detailing its main features. Then, Section III introduces GPR and describes the GPR models developed for this specific application. Section IV provides the results of an exhaustive evaluation of the models and compares with both an LSTM and NARX model. Finally, Section V includes the conclusions.

2 Dataset development

In this Section, we present the real data set used, its main features and the context in which it has been obtained.

The dataset comes from a PV standalone system which provides the energy supply to a communication installation. This installation is part of the hydrographic system of Aragón, Spain, which is managed by the CHE. The base station is located in one of the best Spanish irradiation environments in the Ebro basin (Sigena, Aragón). The standalone installation is powered by 24 lead-acid batteries (VRLA, Exide Classic Solar 2 V 4600Ah C120) with nominal voltage of 2 V in series and for a total nominal voltage of 48 V and a capacity of 4600Ah, shown in Fig. 2. The installation, as it is seen in Fig. 1, has 24 solar panels (Scheuten multi 180P6), with 4680 W of rated power. The equipment of the installation has a typical consumption of 350 W, with occasional peaks up to 550 W.

Fig. 2
figure 2

Group of batteries of the PV standalone system

Full size image

The control system monitors the current, voltage and temperature waveforms of the batteries. PV Standalone system features irregular generation profiles that depend on weather and sun irradiation. They have three main generation-consumption dynamics: day-night cycles, cloudy periods (days or weeks) and the annual dynamic. Therefore, the reliability of the system is subject to.significant uncertainties. In this application in particular, the prediction of a short-term system failure is especially interesting due to the expensive actions needed to restart the system. These critical system failures are mainly related to insufficient charge in the battery and could be detected by predicting an excessive low voltage level in the battery. A GPR based voltage predictor is a suitable option for this task, since it not only provides the prediction, but it also indicates the confidence interval of the prediction [18].

Data have been recorded during 2 years with a sampling rate of one sample every hour. Voltage, current and temperature waveforms are the information available and, as they are the typical variables in this type of installation, this work can be easily extended to similar systems. Below we include a sample instance of the structure and values of the dataset

$$ {\text{Dataset}}\left\{ {\begin{array}{*{20}c} {{\text{Voltage}}} & \to & {\left\{ {\begin{array}{*{20}c} {{\text{Value~}}} & {\mathop \to \limits^{{{\text{e.g.}}}} } & {49.62\;{\text{V}}} \\ {{\text{Date~}}} & {\mathop \to \limits^{{{\text{e.g.}}}} } & {01/01/2008~ - ~00:00} \\ \end{array} } \right.} \\ {{\text{Current}}} & \to & {\left\{ {\begin{array}{*{20}c} {{\text{Value~}}} & {\mathop \to \limits^{{{\text{e.g.}}}} } & { - 7.2~A} \\ {{\text{Date~}}} & {\mathop \to \limits^{{{\text{e.g.}}}} } & {01/01/2008~ - ~00:00} \\ \end{array} } \right.} \\ {{\text{Temperature}}} & \to & {\left\{ {\begin{array}{*{20}c} {{\text{Value~}}} & {\mathop \to \limits^{{{\text{e.g.}}}} } & {6.3\;{^\circ }{\text{C}}} \\ {{\text{Date~}}} & {\mathop \to \limits^{{{\text{e.g.}}}} } & {01/01/2008~ - ~00:00} \\ \end{array} } \right.} \\ \end{array} } \right. $$

Figure 3 shows examples of current waveforms recorded in different weather scenarios, which manifest clear differences. According to the specifications of the client, i.e., the CHE, a failure prediction of 48 h ahead is sufficient to avoid a critical failure, which is tackled by increasing the battery charge voltage level (floating voltage). As the consumption of the installation is nearly constant, the critical moment is the moment just before the sunrise, where the amount of charge is the lowest of the cycle.

Fig. 3
figure 3

Example of the current waveforms recorded in different weather scenarios

Full size image

Our data set is different from others due to the amount of real data available. In this sense, it is noteworthy that there are two different phenomena in the database. The first is the periodical dynamics, which are predictable with an accurate model of a battery. The other is the random events associated with weather from which, due to its inherent quasi-chaotic nature, it is difficult to predict its impact in the batteries. The purely periodical dynamics are related to several phenomena: day/night, yearly and season-based dynamics. Thus, to account for all of them, the training set has been selected according to the greatest period, using a complete year of data. Thanks to the size of the database, tests are performed with data from the next year.

Figure 4. illustrates the voltage waveforms recorded in the installation in 2008, from where it is clear that the floating voltage of the batteries is not constant. This is due to the temperature-regulated charge strategy of the solar regulator. Thus, the information encoded in that strategy provides important knowledge to our problem.

Fig. 4
figure 4

Voltage waveforms from 2008

Full size image

To end up this Section, we introduce the metrics we will use along the paper to evaluate and study the different methods and hyperparameter selections. To evaluate the performance of the models, we choose the Root Mean Square Error (RMSE) and the Maximum Absolute Error (MaxAE) as metrics, defining them as.

$$RMSE\left(l\right)=\sqrt{\frac{1}{{N}_{test}}\sum _{t=1}^{{N}_{test}}{\left({V}_{t+l}-{\widehat{V}}_{t+l}\right)}^{2}},$$
(1)
$$ MaxAE\left( l \right) = \max _{{i = 1, \ldots ,N_{{test}} }} \left| {V_{{t + 1}} - \hat{V}_{{t + 1}} } \right|, $$
(2)

where \({N}_{test}\) refers to the number of test samples and \(l=1,\dots ,M\), where \(M=48\) hours for this work. In addition, we present two additional metrics which refer to RMSE and MaxAE at the end of the night.

$${RMSE}_{EON}\left(l\right)=\sqrt{\frac{1}{{N}_{test}}\sum _{t=1}^{{N}_{test}}{\left({V}_{t+l}^{EON}-{\widehat{V}}_{t+l}^{EON}\right)}^{2},}$$
(3)
$${MaxAE}_{EON}\left(l\right)={\text{max}}_{i=1,...,{N}_{test}}\left|{V}_{t+l}^{EON}-{\widehat{V}}_{t+l}^{EON}\right|.$$
(4)

This value of voltage is crucial in PV standalone systems as it gives the BMS the information of the voltage of the system if no more solar energy can be absorbed.

3 GPR models for large datasets.

In this section we firstly present a brief review of the theory of GPR. After that, three versions of GPR (Regular GPR, Multiple Experts GPR and Sparse GPR) are detailed, connecting with the need of processing large quantities of data.

3.1 A brief introduction to theory

Most of the content of this subsection is adapted from [6] and it should be consulted by readers interested in further details about the mathematical background. Let \(\mathcal{D}=\left(\mathbf{X},\mathbf{y}\right)\) denote a training dataset, comprising \(n\) D-dimensional input and scalar output pairs \(\mathbf{X}={\left\{{\mathbf{x}}_{i}\right\}}_{i=1}^{n}\), where \({\mathbf{x}}_{i} \in R^{D}\) and the corresponding outputs \(\mathbf{y}={\left\{{y}_{i}\right\}}_{i=1}^{n}\), where \(y_{i} \in R\). It is assumed that there is an underlying nonlinear latent function \(f\left(\bullet \right)\), which can be used to parameterize the probabilistic mapping between inputs and outputs

$${y}_{i}=f\left({\mathbf{x}}_{i}\right)+{\varepsilon }_{i},$$
(5)

where \({\varepsilon }_{n}\) denotes zero-mean additive Gaussian noise with variance \({\sigma }_{i}^{2}\), i.e., \({\varepsilon }_{i}\sim \mathcal{N}\left(0,{\sigma }_{i}^{2}\right)\) and \({\left\{{\varepsilon }_{i}\right\}}_{i=1}^{n}\) form an independent and identically distributed (i.i.d) sequence. The GPR main hypothesis relies on assuming a priori that function values behave according to a multivariate Gaussian distribution

$$p\left(\mathbf{f}|{\mathbf{x}}_{1},{\mathbf{x}}_{2},\cdots ,{\mathbf{x}}_{n}\right)=\mathcal{N}\left(0,{\mathbf{K}}_{\mathbf{f},\mathbf{f}}\right)$$
(6)

where, \(\mathbf{f}={\left[f\left({\mathbf{x}}_{1}\right),f\left({\mathbf{x}}_{2}\right),\cdots ,f\left({\mathbf{x}}_{n}\right)\right]}^{T}\) is a vector of latent function values and \(0\) is an \(n\times 1\) vector whose elements are all 0. In addition, \({\mathbf{K}}_{\mathbf{f},\mathbf{f}}\) is a covariance matrix, whose entries are given by the covariance function \({\mathbf{K}}_{i,j}=k\left({\mathbf{x}}_{i},{\mathbf{x}}_{j}\right)\), from now on named kernel function, evaluated at each pair of training inputs.

In GPR, the kernel function plays a major role, since it encodes the prior assumptions about the properties of the underlying latent function that we are trying to model. Indeed, one of the tasks of the designer is to select the kernel which best fits the phenomena modeled. An instance of kernel typically adopted is the Squared Exponential (SE) kernel, defined as

$${k}_{s}\left({\mathbf{x}}_{i},{\mathbf{x}}_{j}\right)={\mathrm{\vartheta }}_{0}^{2}exp\left[-\frac{1}{2}\sum _{d=1}^{D}{\left(\frac{{x}_{id}-{x}_{jd}}{{l}_{d}}\right)}^{2}\right],$$
(7)

where \({x}_{id}\) and \({x}_{jd}\) correspond to the \(d\)-th element of vectors \({\mathbf{x}}_{i}\) and\({\mathbf{x}}_{j}\), respectively, and \(\Theta = \left[ {\vartheta _{0} ,l_{1} , \ldots ,l_{D} } \right]^{T}\) denotes the hyperparameters. Distinctly, \({\mathrm{\vartheta }}_{0}^{2}\) denotes the signal variance and quantifies the variation of the underlying latent function from its mean, and \({l}_{D}\) represents the characteristic length scale for each input dimension. Finally, \({l}_{D}\) fixes the width of the kernel and thereby represents how smooth the functions in the model are.

In addition to the aforementioned kernel function, we incorporate the additive Gaussian white noise term into the selected kernel function

$$k\left({\mathbf{x}}_{i},{\mathbf{x}}_{j}\right)={k}_{s}\left({\mathbf{x}}_{i},{\mathbf{x}}_{j}\right)+{\sigma }_{i}^{2}{\delta }_{ij},$$
(8)

where \({\delta }_{ij}\) denotes the Kronecker delta, which takes value of 1 if \(i=j\) and 0 otherwise. Then, the distribution of \(\mathbf{y}\), conditioned on the latent function values \(\mathbf{f}\) and the input \(\mathbf{X}\), is given by

$$p\left(\mathbf{y}|\mathbf{f},\mathbf{X}\right)=\mathcal{N}\left(\mathbf{f},{\sigma }_{i}^{2}\mathbf{I}\right),$$
(9)

where \(\mathbf{I}\) is an \(n\times n\) identity matrix. Throughout integration over the latent function values \(\mathbf{f}\) and by using (6) and (9) the marginal distribution of \(\mathbf{y}\) can be obtained.

$$p\left(\mathbf{y}|\mathbf{X},\mathrm{\Theta }\right)=\int p\left(\mathbf{y}|\mathbf{f},\mathbf{X}\right)p\left(\mathbf{f}|\mathbf{X}\right)d\mathbf{f}=\mathcal{N}\left(0,{\mathbf{K}}_{\mathbf{f},\mathbf{f}}\right)+{\sigma }_{i}^{2}\mathbf{I}.$$
(10)

Then, the marginal log-likelihood, which refers to the marginalization over the function values \(\mathbf{y}\) can be written as

$$ \begin{gathered} \log p\left( {\user2{y}\left| {\user2{X,}\Theta } \right.} \right) = \frac{1}{2}\user2{y}^{T} \left( {\user2{K}_{{{\mathbf{f,f}}}} + \sigma _{i}^{2} \user2{I}} \right)^{{ - 1}} \hfill \\ \quad - \frac{1}{2}\log \left| {\user2{K}_{{{\mathbf{f,f}}}} + \sigma _{i}^{2} \user2{I}} \right| - \frac{n}{2}\log 2\pi , \hfill \\ \end{gathered} $$
(11)

where \(\left|\bullet \right|\) is the determinant of a matrix. The optimum hyperparameters \(\widehat{\mathrm{\Theta }}\) are found by maximizing the marginal log-likelihood. To do so, we use the partial derivatives of the marginal log-likelihood, from where we obtain that

$$ \begin{gathered} \frac{\partial }{{\partial \theta _{i} }}\log p\left( {{\mathbf{y}}\left| {{\mathbf{X}},\Theta } \right.} \right) = - \frac{1}{2}tr\left( {{\mathbf{K}}_{{{\mathbf{f,f}}}} + \sigma _{i}^{2} {\mathbf{I}}} \right)^{{ - 1}} \frac{{\partial \left( {{\mathbf{K}}_{{{\mathbf{f,f}}}} + \sigma _{i}^{2} {\mathbf{I}}} \right)}}{{\partial \theta _{i} }} \hfill \\ + \frac{1}{2}{\mathbf{y}}^{T} \left( {{\mathbf{K}}_{{{\mathbf{f,f}}}} + \sigma _{i}^{2} {\mathbf{I}}} \right)^{{ - 1}} \frac{{\partial \left( {{\mathbf{K}}_{{{\mathbf{f,f}}}} + \sigma _{i}^{2} {\mathbf{I}}} \right)}}{{\partial \theta _{i} }}\left( {{\mathbf{K}}_{{{\mathbf{f,f}}}} + \sigma _{i}^{2} {\mathbf{I}}} \right)^{{ - 1}} {\mathbf{y}}. \hfill \\ \end{gathered} $$
(12)

It is important to notice that the complexity of computing (11) is dominated by the inversion of \({\mathbf{K}}_{\mathbf{f},\mathbf{f}}+{\sigma }_{i}^{2}\mathbf{I}\), which requires a computational time of \(\mathcal{O}\left({n}^{3}\right)\). Hence, a simple implementation of the GPR is advisable for datasets with up to a thousand training examples.

The characterization in (12) allows the use of any gradient based optimization method to optimize the marginal log-likelihood function (11). It is important to note that, generally, objective functions are nonconvex with respect to the hyperparameters which can lead to convergence to a local optimum. In order to tackle this problem, gradient-based optimization can be performed with different initial points and the optimal hyperparameters that yield the largest marginal log-likelihood can be chosen. Once we obtain the optimal hyperparameters, it is possible to express the joint distribution of the training outputs \(\mathbf{y}\) and the test output \({y}_{\mathrm{*}}\) as

$$p\left(\mathbf{y},{y}_{\mathrm{*}}|\mathbf{X},{x}_{\mathrm{*}},\mathrm{\Theta }\right)=\mathcal{N}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}{\mathbf{K}}_{\mathbf{f},\mathbf{f}}+{\sigma }_{i}^{2}\mathbf{I}& {\mathbf{K}}_{\boldsymbol{*},\mathbf{f}}\\ {\mathbf{K}}_{\mathbf{f},\boldsymbol{*}}& {K}_{\mathrm{*}\mathrm{*}}+{\sigma }_{i}^{2}\end{array}\right]\right),$$
(13)

where the asterisk \(*\) is used as a shorthand for \({f}_{*}\), which is the corresponding latent function value at the test input, \({\mathbf{K}}_{\boldsymbol{*},\mathbf{f}}={\left[k\left({\mathbf{x}}_{1},{\mathbf{x}}_{\mathrm{*}}\right),\cdots ,k\left({\mathbf{x}}_{n},{\mathbf{x}}_{\mathrm{*}}\right)\right]}^{T}\) and \({K}_{\mathrm{*}\mathrm{*}}={k}_{s}\left({\mathbf{x}}_{\mathrm{*}},{\mathbf{x}}_{\mathrm{*}}\right)\). The target of the GPR is to find the predictive distribution of the test output \({y}_{\mathrm{*}}\) which are conditioned on both the dataset \(\mathcal{D}\) and test input \({\mathbf{x}}_{\mathrm{*}}\). Thus, it is possible to marginalize the joint distribution (13) over the training dataset output \(\mathbf{y}\) and to obtain that the predictive distribution of the test output, \({y}_{\mathrm{*}}\), is Gaussian distributed, i.e.,

$$p\left({y}_{\mathrm{*}}|\mathbf{X},\mathbf{y},{\mathbf{x}}_{\mathrm{*}},\mathrm{\Theta }\right)=\mathcal{N}\left({\mu }_{\mathrm{*}},{\mathrm{\Sigma }}_{\mathrm{*}}\right),$$
(14)

where the mean and the covariance of the predictive distribution are given, respectively, in the following

$$ \mu _{ * } = {\mathbf{K}}_{{ * {\mathbf{,f}}}} \left( {{\mathbf{K}}_{{{\mathbf{f,f}}}} + \sigma _{i}^{2} {\mathbf{I}}} \right)^{{ - 1}} {\mathbf{y}}, $$
(15)
$${\mathrm{\Sigma }}_{\mathrm{*}}={\sigma }_{i}^{2}+{K}_{\mathrm{*}\mathrm{*}}-{\mathbf{K}}_{\boldsymbol{*},\mathbf{f}}{\left({\mathbf{K}}_{\mathbf{f},\mathbf{f}}+{\sigma }_{i}^{2}\mathbf{I}\right)}^{-1}{\mathbf{K}}_{\mathbf{f},\boldsymbol{*}}.$$
(16)

This mean, which is effectively the point estimate of the test output, is obtained as a linear combination of the noisy dataset outputs \(\mathbf{y}\). Also, the variance of the predictive distribution, \({\mathrm{\Sigma }}_{\mathrm{*}}\) in (16), serves as a measure of the uncertainty in the estimate of the test output. After performing the inversion of \({\mathbf{K}}_{\mathbf{f},\mathbf{f}}+{\sigma }_{i}^{2}\mathbf{I}\), the computational complexity of the testing stage is \(\mathcal{O}\left(n\right)\) and \(\mathcal{O}\left({n}^{2}\right)\) for the mean \({\mu }_{\mathrm{*}}\) and the variance \({\mathrm{\Sigma }}_{\mathrm{*}}\) respectively, which makes the proposed method highly appropriate for online operation. As a remark, notice that the computation of the inverse of \({\mathbf{K}}_{\mathbf{f},\mathbf{f}}+{\sigma }_{i}^{2}\mathbf{I}\) can be speeded up to improve the computational burden of the online regression. Since \({\mathbf{K}}_{\mathbf{f},\mathbf{f}}\) does not change after training, we can compute \({\mathbf{K}}_{\mathbf{f},\mathbf{f}}^{-1}\) and then use the matrix inversion lemma (Chapter 8 of [6]) to calculate.

\({\left({\mathbf{K}}_{\mathbf{f},\mathbf{f}}+{\sigma }_{i}^{2}\mathbf{I}\right)}^{-1}\) by simply computing online \({{(\sigma }_{i}^{2}\mathbf{I})}^{-1}.\)

Figure 5 shows a first approximation to our prediction problem. All the typical data available in the installation are fed (voltage, temperature and current). However, at first sight, it is not possible to determine the relevance and influence of this data in the prediction, so an extensive discussion and justification of which type of information is really needed is discussed in Section IV.

Fig. 5
figure 5

Schematic block of Regular GPR

Full size image

The output of the GPR model is an estimation of the future sample of voltage data, \({V}_{k+1}\), predicted from L + 1 past samples of voltage \({V}_{k},\cdots ,{V}_{k-L}\), current \({I}_{k},\cdots ,{I}_{k-L}\) and temperature \({T}_{k},\cdots ,{T}_{k-L}\); and future current \({I}_{k+1}\) and temperature \({T}_{k+1}\) samples. Thus, L is the memory length of the number of previous samples processed. Since the power demand of the installation is known, we can feed the GPR models with future current and temperature.

figure a
figure b

waveforms. This data is assembled in a vector \({\mathbf{x}}_{*k}\), of length \(3(L+1)+2\), formatted as:

$$ {\mathbf{x}}_{{{\text{*}}k}} = \left[ {I_{{k + 1}} T_{{k + 1}} V_{k} I_{k} T_{k} V_{{k - 1}} I_{{k - 1}} \cdots T_{{k - L}} \cdots V_{{k - L}} I_{{k - L}} } \right]^{T} $$
(17)

The corresponding mean and variance output from the GPR, given \({\mathbf{x}}_{\mathrm{*}k}\), is denoted as \({\mu }_{\mathrm{*}k}\)(from Eq. (15)) and \({\mathrm{\Sigma }}_{\mathrm{*}k}\)(from Eq. (16)) respectively, using the sub-index k to emphasize that they are the estimations at instant k. The output \({y}_{k}\) of the algorithm is the voltage at the sample \(k+1\)

$${y}_{k}={\mu }_{\mathrm{*}k}={V}_{k+1}.$$
(18)

GPR techniques consist in two processes. In the first part, GPR is trained offline to learn the relationship between the inputs \({\mathbf{x}}_{{k}_{i}}\) and outputs \(\mathbf{y}\). Then, optimal values of the hyperparameters of the chosen kernel are determined through a conjugate gradient method based on a training dataset, \(\mathcal{D}\). In the second part, online voltage prediction of the battery is performed based on voltage, current and temperature measurements of the battery. The mean \({\mu }_{\mathrm{*}k}\) of the predicted distribution represents the estimated voltage \({V}_{k+1}\). Additionally, the standard deviation (\({{\mathrm{\Sigma }}_{\mathrm{*}k}}^{1/2}\)) of the predicted distribution permits us to build a confidence interval to measure the accuracy of the prediction. In this paper, we consider a typical 95% confidence interval [6]

$$ \left[ {V_{{k + 1}} - 1.96\sum {_{{ * k}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } ,V_{{k + 1}} + 1.96\sum {_{{ * k}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } } \right] $$
(19)

The designer can choose the level of confidence interval depending on the particularities of applications. As standard deviation decreases, the confidence interval becomes smaller and it indicates a more accurate prediction. GPR techniques can be used to directly provide the prediction of a variable one sample ahead. In this sense, Algorithms 1 and 2 show the training and estimations stages for the one step predictor. In this model, this means 1 hour in advance. However, as a 48 h prediction is pursued, the GPR versions in this work are implemented in a recursive multi-step form, so recursion will be assumed henceforth.

3.2 Regular GPR

The scope of this method is to obtain the estimated voltage corresponding to \(k+z\) time, until reaching the desired \(M=48\) hours prediction for our purposes. This means that the predicted output of the method corresponds to the expected voltage at time instant\(k+z+1\). Due to the recursive structure, in the first step, what it is estimated is the mean \({\mu }_{*k}^{(1)}\) calculated through (15). This value is then fed back along with voltage, current and temperature at time instants \(k,k - 1, \ldots ,k - L - 1,\) and current and temperature \({I}_{k+1},{T}_{k+1},\) \(I_{{k + 2}} T_{{k + 2}}\) in a one-step prediction algorithm to obtain\({\mu }_{*k}^{(2)}\). This process is repeated until we obtain the \(48\) step-ahead voltage prediction. Regarding the implementation, the training process is the same treated in Algorithm 1. However, in the testing stage vectors are formatted as

$$ {\mathbf{x}}_{{ * k}}^{{\left( z \right)}} = \left[ {I_{{k + m}} T_{{k + m}} {\mathbf{V}}_{k}^{{\left( z \right)}} {\mathbf{I}}_{{kk}}^{{\left( z \right)}} {\mathbf{T}}_{k}^{z} } \right]^{T} $$
(20)

with

$$ {\mathbf{V}}_{k}^{{\left( z \right)}} = \left[ {\mu _{{ * k}}^{{\left( {z - 1} \right)}} \ldots \mu _{{ * k}}^{{\left( 1 \right)}} V_{k} \ldots V_{{k - L + z - 1}} } \right]^{T} $$
(21)
$$ {\mathbf{I}}_{k}^{{\left( z \right)}} = \left[ {I_{{k + m - 1}} \ldots I_{{k + 1}} I_{k} \ldots I_{{k - L + z - 1}} } \right]^{T} $$
(22)
$$ {\mathbf{T}}_{k}^{{\left( z \right)}} = \left[ {T_{{k + m - 1}} \ldots T_{{k + 1}} T_{k} \ldots T_{{k - L + z - 1}} } \right]^{T} $$
(23)

A flowchart of the operational stage of this estimation method is shown in Algorithm 3.

figure c

3.2.1 Train/test dataset selection.

The GPR model is trained with 720 samples of data, i.e., a complete month. To capture all kind of phenomena, the 720 samples come from an equally spaced selection of the original training dataset (the complete year of 2008). In each selection, a complete day is captured in to preserve the temporary properties and waveform features, so the training set can be seen as a cascade of days from different seasons and weather conditions. This set is the input of the training algorithm (Algorithm 1). For testing, the complete month of March 2009 has been used, selected due to the fact that it involves all kinds of uncertain phenomena (both sunny and cloudy periods) since it belongs to a low irradiation season.

3.2.2 Memory length selection.

Prior to applying Algorithms 1 and 3, Memory Length (\(L\)) must be established. The selection of \(L\) is relevant for the final deployment of the algorithm because of its impact in the computational cost. Indeed, we recall that the focus of this paper is to validate GPR techniques in real applications with large quantities of data and evaluate different GPR-based techniques. The final selection of \(L\) should be made considering the available computational resources.

A priori, a larger \(L\) could provide better results because more data are involved in each prediction. The results of an exhaustive preliminary test with a Regular GPR and several \(L\) values are shown in Fig. 6., where RMSE over the predicted voltage is represented to track the performance of the model with respect to \(L\). As there is not a clear optimized value of \(L\) we opted for a technical selection of \(L\) = 15 samples. This value is a compromise between the computational cost and the accuracy of the calculations.

Fig. 6
figure 6

Evolution of the error with the memory length

Full size image

3.2.3 Kernel function selection.

The selection of the kernel used in the GPR model is also required. Conceptually, the kernel is the tool that captures the relationships within the training data. In this application, it is especially difficult to detect these hidden relations because of the 48 h recurrent approach. In non-recurrent previous related works [10, 11] SE kernel exhibits good performances. However, in this work we make an extensive test of different kernels, as proposed in [19]. Table 1 describes the compared kernels. According to the results over the RMSE and MaxAE, the kernel that gives a better performance for our database is the Rational Quadratic (RQ) [20]. Table 2 shows the best results of the tests, where it can be appreciated that more complex kernels do not improve the performance while computational cost is increased. In all cases, Automatic Relevance Determination is used.

Table 1 List of kernels used in the comparison
Full size table
Table 2 Comparative of kernels using Regular GPR
Full size table

3.3 GPR based Multiple Experts

In this Section a modification of the Regular GPR is proposed. The idea is to model different types of canonical current waveforms (related to specific daily dynamics.

during a year), or classes. Several GPR-based “experts” are designed, each one related to a class. A non-supervised clustering algorithm is used for a more accurate classification. Self-Organizing Maps (SOM) [21,22,23] is the selected technique to classify training data in a visual map. To characterize a day, five features are chosen.

  • Voltage at the beginning of the discharge.

  • Voltage at the end of the discharge (at the sunrise of the day).

  • Duration in hours of the charging process.

  • Hours of the discharge.

  • Charge stored.

After training a 10 × 6 SOM by using the SOM Toolbox [24] MATLAB® library, every input pattern (each day) is projected to its closest neuron, in such a way that nearby neurons are tuned to similar patterns (similar days). The resulting SOM can be considered as a two-dimensional picture of the database, where clusters of similar days could be identified. After that, a K-means clustering algorithm [25, 26] has been applied to the outputs of the SOM to establish the different classes obtained. K-means need the number of clusters to make the separation, so for establishing this number of clusters the algorithm has been applied several times changing this parameter.

The results show that using more than five classes does not provide relevant information. Figure 7. is the final result of this process. Each sample is labeled regarding its characteristics in the following classes: low irradiation days, winter days with high SoC, winter days with low SoC, spring days and summer days.

Fig. 7
figure 7

Results of K-means applied to SOM

Full size image

For a better understanding of the differences among the type of days, Fig. 8., shows the mean current waveform of each data related to each type of day. With this tool all the days of the original training database are classified and tagged. For further details, [27] is included as a pointer. Afterward, five GPR experts are designed and trained, using for training days of their corresponding class.

Fig. 8
figure 8

Mean waveforms of the five classes of days from SOM

Full size image

The same parameters obtained with Regular GPR (train size, test set, memory length of 15 h, RQ kernel) are used in the five experts. In the inference stage, after each expert estimates the future sample, one of the experts is chosen and its output is reinjected for the next iteration. As the confidence interval calculated by the GPR provides information about the accuracy of the estimation, the expert with the most accurate confidence interval is selected as the one to provide the final output.

3.4 Sparse GPR

Sparse GPR [5, 28] is a modification of the Regular GPR to be able to process large datasets. For larger datasets, sparsity solves the problem of the computational cost. The computational cost of a regular GPR is reduced by introducing inducing variables and modifying the joint prior distribution, Let \(p\left( {f_{ * } ,{\mathbf{f}}} \right).\) \({\mathbf{u}} = \left[ {u_{0} , \ldots ,u_{m} } \right]^{T}\) denote.

the inducing variables which correspond to a set of input locations \({X}_{\mathbf{u}}\) called inducing points, where \(m\le n\) is the number of inducing points. The inducing points are chosen as a subset of the data points. Given the inducing points, the joint prior distribution, \(p({f}_{\mathrm{*}},\mathbf{f})\) can be rewritten as

$$ p\left( {f_{ * } ,{\mathbf{f}}} \right) = \int {p\left( {f_{ * } ,{\mathbf{f}}\left| {\mathbf{u}} \right.} \right)} p\left( {\mathbf{u}} \right)d{\mathbf{u}}, $$
(24)

where \(p(\mathbf{u})=\mathcal{N}\left(0,{K}_{\mathbf{u},\mathbf{u}}\right)\). For the approximation of \(p({f}_{\mathrm{*}},\mathbf{f})\), it is assumed that \({f}_{\mathrm{*}}\) and \(\mathbf{f}\) are conditionally independent given \(\mathbf{u}\) in the following [5]

$$ p\left( {f_{{\text{*}}} ,{\mathbf{f}}} \right) = \int p\left( {f_{{\text{*}}} ,{\mathbf{f}}{\text{|}}{\mathbf{u}}} \right)p\left( {\mathbf{u}} \right)d{\mathbf{u}}, $$
(25)

Besides, it is assumed that the training conditional \(q\left(\mathbf{f}|\mathbf{u}\right)\) is fully independent and the test conditional keeps exact as

$$ q\left( {{\mathbf{f}}\left| {\mathbf{u}} \right.} \right) = \prod\limits_{{i = 1}}^{n} {p\left( {f_{n} \left| {\mathbf{u}} \right.} \right)} = N\left( {K_{{{\mathbf{f}},u}} ,K_{{{\mathbf{u}},{\mathbf{u}}}}^{{ - 1}} {\mathbf{u}},diag\left[ {K_{{{\mathbf{f}},{\mathbf{f}}}} - Q_{{{\mathbf{f}},{\mathbf{f}}}} } \right]} \right), $$
(26)
$$q\left({f}_{\mathrm{*}}|\mathbf{u}\right)=p\left({f}_{\mathrm{*}}|\mathbf{u}\right),$$
(27)

where \(\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[A]\) denotes the diagonal matrix in which the entries outside the main diagonal are all zero. The distributions in (26) and (27) can be substituted in (25), so that integrating over \(\mathbf{u}\) gives the joint prior

$$ q\left( {{\mathbf{f}},f_{{\text{*}}} } \right) = N\left( {0,{\text{~}}\left[ {\begin{array}{*{20}c} {Q_{{{\mathbf{f}},{\mathbf{f}}}} - {\text{diag}}\left[ {Q_{{{\mathbf{f}},{\mathbf{f}}}} - K_{{{\mathbf{f}},{\mathbf{f}}}} } \right]} & {Q_{{{\mathbf{f}},*}} } \\ {Q_{{*,{\mathbf{f}}}} } & {K_{{*,*}} } \\ \end{array} } \right]} \right), $$
(28)

where \({Q}_{\mathbf{a},\mathbf{b}}={K}_{\mathbf{a},\mathbf{u}}{{K}_{\mathbf{u},\mathbf{u}}}^{-1}{K}_{\mathbf{u},\mathbf{b}}\) is a low-rank matrix (i.e., rank \(m\)). The predictive distribution can be obtained by using the above joint prior distribution,

$$q\left({y}_{\mathrm{*}}|\mathbf{X},\mathbf{y},{\mathbf{x}}_{\mathrm{*}},\mathrm{\Theta }\right)=\mathcal{N}\left({\stackrel{\sim }{\mu }}_{\mathrm{*}},{\stackrel{\sim }{\mathrm{\Sigma }}}_{\mathrm{*}}\right),$$
(29)

where

$$ q\left( {y_{*} |{\mathbf{X}},{\mathbf{y}},{\mathbf{x}}_{*} ,\Theta } \right) = {\mathcal{N}}\left( {\tilde{\mu }_{*} ,\tilde{\Sigma }_{*} } \right), $$
(30)
$${\stackrel{\sim }{\mathrm{\Sigma }}}_{\mathrm{*}}={\sigma }_{i}^{2}+{K}_{\mathrm{*},\mathrm{*}}-{Q}_{\mathrm{*},\mathrm{*}}+{K}_{\mathbf{*},\mathbf{u}}\boldsymbol{\Omega }{K}_{\mathbf{u},\mathbf{*}}.$$
(31)

Here, \(\Omega = \left( {K_{{{\mathbf{u}},{\mathbf{u}}}} + K_{{{\mathbf{u}},{\mathbf{f}}}} \Lambda ^{{ - 1}} K_{{{\mathbf{f}},{\mathbf{u}}}} } \right)^{{ - 1}}\) and\(\mathrm{\Lambda }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[{K}_{\mathbf{f},\mathbf{f}}-{Q}_{\mathbf{f},\mathbf{f}}+{\sigma }_{i}^{2}\mathbf{I}\right]\). Notice that the only matrix requiring inversion is the \(n\times n\) diagonal matrix\(\mathrm{\Lambda }\), which translates into a significant reduction in computational complexity. The computational cost of training becomes\(\mathcal{O}\left({m}^{2}n\right)\), i.e., linear in \(n\) and quadratic in m. Larger values of m should yield to better accuracy at the expense of an increase in the computational requirements. Additionally, the complexity of the testing stages is \(\mathcal{O}\left(m\right)\) and \(\mathcal{O}\left({m}^{2}\right)\) for calculating the mean and the variance, respectively.

Among many different kinds of sparsity algorithms [5, 29], Fully Independent Training Conditional (FITC) seems to get the best performance [30] and, therefore, it is the one used in this work. Regarding the selection of \(m\), several simulations have been made with an increasing number of inducing points. Figure 9 shows that there is almost no need of increasing inducing points beyond \(80\) for our database (RMSE is beyond that point), so \(m=80\) is selected.

Fig. 9
figure 9

Study of the influence of the number of inducing points in the voltage prediction error and the computational time

Full size image

There are several methods to select the position of the inducing points (like the powerful, but time consuming, Farthest Point Clustering (FPC) [31]). However, the most typical approximation is to select equally spaced points because of the low computational cost involved. After that, this subset of data points is also optimized when included in the training stage, along with the other hyperparameters, with the gradient descent algorithm. The other parameters are the same as in the other models. The iterative process of Regular GPR is also carried on with the Sparse GPR.

The number of inducing points is tested up to \(720\) samples because this corresponds to one month of data, the same magnitude used to train Regular and ME models. Algorithm 4 details the flowchart of the Sparse method, similar but not equal to Algorithm 3 for Regular GPR.

As a last remark, one of the advantages of GPR for the application point of view is that it provides the confidence interval in Eq. (19). To verify the performance of the trained model with respect to the actual behavior of the installation we must wait \(M\) hours to compare the measured voltage with the predicted one. This gives a procedure to check the accuracy of the trained model, since with an accurate GPR we should see, at least, a \(95\%\) of the times of the measured voltage lying within the confidence interval.

figure d

4 Results and discussion

In this Section we validate the proposed models in the experimental database. The experiments are implemented in MATLAB©2020a in a 1.8-GHz Intel Core i7-10510U CPU.

In order to test the performance of the three proposed models, it is first necessary to see the relevance of the selection of the input variables. By this, we study which variables (voltage, current and temperature) are relevant to predict future voltage. There are four possibilities:

  • Future current and temperature profiles known.

  • Only future current profile known.

  • Only future temperature profile known.

  • Neither current nor temperature known (not possible in the context of this problem).

In all cases past profiles are known. To test the influence of the input parameters in the prediction we use the Regular GPR, as long as the results are expandable to the other models. The resulting error metrics are listed in Table 3.

Table 3 Error metrics as a function of the inputs considered in the models
Full size table

The results show that temperature has almost no influence on voltage prediction and therefore it can be omitted in future analysis. This is related to the high thermal inertia of the battery pack, since they contain tons of liters of water. Sudden irradiation changes caused by a cloud are not enough to vary relevantly the temperature. In practice, this result helps to reduce the complexity of the system since the matrix dimensions get reduced. As the second method in Table 3 gets similar error metrics to the first method but with less measures, it is chosen to test the models.

Once the future input profile has been chosen, we discuss the performance of the three different algorithms. In contrast with Regular and ME GPR, as Sparse GPR can deal with larger datasets, it is trained with the entire 2008 year. In order to keep a fair comparison between the algorithms, they all are tested with March 2009.

To illustrate the performance of the three methods, in Fig. 10, we show the waveforms obtained with the Regular GPR implementation. The model fits the real waveform accurately even in low irradiation days. These results manifest that there exists a periodic error located at midday which matches with the highest value of the confidence interval and therefore of standard deviation, during a single day. This is because, at this point of the day, any interfering cloud may reduce the irradiation on the panels and, thus, there is a higher uncertainty. The error at the end of the night is low in all cases. This is an intuitive result since clouds do not really have an impact on the irradiation at night (which is nonexistent). As the waveforms from the three GPR models are similar, Table 4 provides quantitative information.

Fig. 10
figure 10

Results of the prediction with Regular GPR and current as the only known future value: a waveforms over the month test, b zoom to the crucial days of the month, c \({RMSE}_{EON}\) obtained in the month test, d \(\mathrm{\Sigma }\) obtained in the crucial days of the month

Full size image
Table 4 Error metrics with only future current profile as input, for a battery with a total nominal voltage of 48 V
Full size table

All methods perform, to a greater or lesser extent, a proper voltage estimation in a month with heterogeneous events. ME GPR improves the RMSE of Regular GPR but.

Sparse GPR gets the better performance of all methods when it comes to this metric. Besides, Regular GPR has the lower MaxAE so it seems to be the most reliable option when the system needs accurate voltage estimation. In the PV standalone application field, where the EON voltage estimation has a strong interest, all methods reduce RMSE and MaxAE values with a noteworthy performance of ME and Sparse. We remark that using GPR for prediction (extrapolation) in PV standalone applications represents a more demanding task than in the typical regression problem (interpolation) because of the uncertainty of the results.

As means of comparison, we apply the same approach to two non GPR related algorithms in this application: Nonlinear Autoregressive Exogenous Model (NARX) networks [32, 33] and Long Short-Term Memory (LSTM) [34, 35], both well-known techniques to process and predict real-time data series. The theoretical and implementation details can be found in [36]. The tests are carried with the same conditions of GPR: the same year for training, the same month for testing, same L and failure prediction of 48 h ahead. The results are in Table 5.

Table 5 Error metrics of GPR techniques vs NARX and LSTM for a battery with a total nominal voltage of 48 V
Full size table

Results are rather similar, which confirms the usefulness of GPR as a prediction tool. Only NARX shows slightly better results predicting EON situations (40 mV better than GPR) but, in contrast, it has higher MaxAE Figs. (1.6 V worse than GPR). Train and test times information are not especially important because they are only related to the design phase of the algorithm. Execution time (Exe. Time), which is the time needed to make one single prediction of a sample, is more important regarding to implementation. However, as a single prediction is carried out each hour, there is enough time for each execution. For example, the most time-consuming technique (ME) spends only 0.61 s. Therefore, the time-scale difference between the execution time and rate of data stream (in the order of \({10}^{3}\)) makes the system robust against failures due to overpassing the computational burden of the installation.

Comparing the execution times in Table 5 it can be seen that the computational improvement of Sparse GPR is of an order of magnitude in both training and test stages. This is reasonable if we consider the theoretical computational complexities of both methods, shown in Table 6.

Table 6 computational cost of Regular and Sparse GPR
Full size table

Besides, it is important to note that GPR algorithms have an advantage over the other techniques, that is, they provide the confidence interval. This measure of the algorithm accuracy enhances the robustness and allows to design more sophisticated fault-tolerant protocols.

5 Conclusion

In this paper, we have analyzed the problem of future voltage estimation in PV standalone installations with three different recursive multistep GPR models: Regular GPR, Multiple Expert GPR and Sparse GPR. In contrast with previous work on the field, a large dataset with voltage, current and temperature from 2 years has been used. We have evaluated the impact of kernel selection, memory length and the influence of the temperature in the behavior of the system. Results have revealed how simple kernels as RQ provide a good trade-off between computational time and error metrics. It has been observed that a short memory length of \(L\) =15 h is good enough to make accurate estimations. We have seen how, due to the high thermal inertia of the battery pack, temperature is not a representative input parameter for the model and can be omitted. Simulation results have shown an RMSE value of 590 mV for Regular GPR, improved to 517 mV and 469 mV for Multiple Experts and Sparse GPR, respectively. Furthermore, with respect to the fault-tolerant application, ME and Sparse models exhibit a robust performance thanks to a low MaxAE and the confidence interval, compared to the results with NARX and LSTM solutions. In future work, we will study the prediction capabilities of these algorithms for SoC and SoH parameters in PV standalone applications and we will extend our proposal to an online version implemented in the real installation. Besides, we will prepare and process the dataset to open it to the general public.