Mining sensor data in a smart environment: a study of control algorithms and microgrid testbed for temporal forecasting and patterns of failure

Abstract

The generation of active power in renewable energy is dependent on several factors. These variables are related to the areas of weather, physical structure, control, and load behavior. Estimating the future value of the active power to be generated is difficult due to their unpredictable character. However, because of the higher precision required of the estimation, this problem becomes more complex if we examine a short-term temporal prediction. This study presents a method for converting stochastic behavior into a stable pattern, which can subsequently be used in a short-term estimator. For this conversion, K-means clustering is employed, followed by Long-Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) algorithms to perform the Short-term estimate. The environment, the operation, and the generated (normal or faulty) signal are all simulated using mathematical models. Weather parameters and load samples have been collected as part of a dataset. Monte-Carlo simulation using MATLAB programming has been realized to conduct an experiment. In addition, the LSTM and the GRU are compared to see how well they perform in this system. The proposed method's end findings outperform the current state-of-the-art.

1 Introduction

A smart grid is an electricity network enabling a two-way flow of electricity and data with digital communications technology. This gives the ability of monitoring, managing, and automatic decision-making. Besides, smart grid uses a wide range of resources based on information technology techniques to enable new and existing guidelines in minimizing energy costs and reducing electricity wastes. According to Ali et al. (2013), the smart grid is one of the most complicated and largest systems considering the design and building processes, although it is one of the easiest to use. It uses all kinds of power plants (including hydro, solar, coal, nuclear, wind turbine, and natural gas, among others), substations, transformers, and high-voltage transmission lines (Hasan et al. 2019), therefore, there is the need for a demand-responsive electrical grid with high efficiency of energy use. The traditional grid uses a one-way limited interaction, in which power flows to the consumers from the power plant. In contrast, the smart grid introduces a two-way interchange in which involve the exchange both information and electricity, in both directions (between consumer and power utilities). The growing network of computers, automation, control, and communications are instrumental in making the grid “greener”, more reliable, more secure and more efficient (Hasan et al. 2019).

These grids could provide a rich dataset that could be used for analyzing and monitoring their activities, but these could also be used to provide an opportunity to use this data in different applications as well, such as using them for sensor data (Jakkula and Cook 2007).

This data could be useful when being set to work with different aspects or dimensions of SmartGrid such as integration with renewable energy sources, management of intermittent power supplies, real-time data responses as well as the energy pricing strategies among others (Jakkula and Cook 2007). As such, it becomes a necessity that we would develop the right tools and methods which could help in conserving the energy by gathering the data from the smart grid using sensors which could then be used to recognize patterns from previous data and forecast or predict in order to conserve energy in the smart grids.

Some of the algorithm that could be used for prediction which are related to deep learning algorithms like Long-short term memory (LSTM), Recurrent Neural Network (RNN), Gated Recurrent Unit (GRU). In this work, the used predictor is the most efficient one of them, in terms of accuracy and delay.

LSTM is an RNN variant that is meant specifically for time series data. The LSTM is used in addressing this problem in addition to empowering RNNs algorithms using internal memory cells (Li et al. 2020).

RNNs are a form of neural networks that adopt the feedback connections in various nodes in remembering the previous time steps values. As such, they can capture the time series data’s temporal behaviour. (Tealab 2018).

GRU is a kind of gated RNN which is largely used in mitigating the gradient vanishing problem of RNNs using gating mechanism in addition to making the structure simpler without interfering with the effect of LSTM neural network (Luo et al. 2021).

GRU addresses the vanishing gradient problem, which are the values used in updating network weights. According to (Agarap 2018), GRU can solve this problem using two gates, the rest gate and the update gate. The gates are instrumental in deciding the information that is allowed to pass to the output in addition to having the ability to be trained for retaining information from farther back, thus allowing it to pass relevant information through a variety of events for making better predictions.

However, since these prediction methods are based on regression techniques, which tries to find a common pattern for the historical samples to use it to predict the future values. Considering our application, the historical samples from the energy generators and also the load of the smart city, may not have a constant pattern. This is due to the stochasticity behavior of the environment. Therefore, in order to convert this dynamicity to a static pattern, in this work, K-Means clustering algorithm is used.

K-means clustering algorithm refers to a simple unsupervised learning algorithm used in solving clustering problems which is useful in clustering analysis. According to (Xu et al. 2020), the algorithm is applied using certain procedures that classify a certain set of data into clusters defined by the letter "K."

Although several works have tackled the problem of the prediction in the SmartGrid context, most of these works focus only on the long-term prediction. The advantage of the long-term prediction is in bringing long-term strategy and planning, However, the methods that are currently used for this task provides in accurate predictions. On the other hands, short and very shorts terms predictions are important for the real-time control of the SmartGrid which requires real-time information from the real load and the natural resources in addition to the physical structure of the solar panels. Moreover, providing an accurate short-term prediction for the generated energy is also a challenging problem. This is due to the fact, that the amount of generated energy depends on several parameters, from the physical components of the unit to the weather conditions. All these parameters are totally stochastic and do not follow any accurate pattern.

Our methodology in this work is to convert the stochastic behavior of the attributes into an accurate pattern using a clustering algorithm (i.e., K-Means). This allows us to be able to identify their fitting curve and use a suitable regression-based algorithm (i.e., LSTM and GRU) for an accurate short-term prediction.

The main objective of this work is to propose a method that allows enhancing the accuracy of the short-term generated power prediction for the SmartGrid environment.

The main contributions to the existing body of knowledge that this study will make include:

• 1. Identify the most useful factors that affects the accuracy of the Smart Grid short term prediction process.

• 2. Implement a model (or a combination of already existing models) for recognizing patterns of failure in the Smart Grid.

• 3. Identification of the best deep learning algorithm to mine data from a synthetic testbed.

• 4. Proposing a solution to provide a comparatively enhanced prediction results using unpattern-able (highly dynamic and stochastic) data.

• 5. Providing a solution that enhances the protection level for smart grid dynamic environment against failures.

• 6. Providing an accurate future value for the short-term prediction in a relatively faster processing time.

2 Literature review

Efficient delivery of energy resources to the smart grid requires a balanced energy demand and supply by developing energy resource management strategies. However, the significant fluctuations in energy demand and supply enhance the challenges in the development of these energy resource management schemes. This problem has been tackled using different approaches.

For instance, this work (Yu et al. 2015) developed several approaches to predict energy supply and demand effectively. The study then develops machine learning-based methods for accurate energy consumption and generation forecasts. Lastly, the study used the prediction results to establish energy consumption upper and lower bounds realizing optimal demand and anomaly detections.

The problem is the smart meters acquire large amounts of data through sophisticated signal processing algorithms. The methodology will be applied in the study for it will the first develops a new classification scheme that categorizes users based on their consumption patterns. The study will then test the proposed and benchmarked models. Additionally, this research uses semi-Markov models to generate more extensive and more realistic test data due to insufficient power consumption data. (Tornai et al. 2016).

The problem is electrical load prediction is a fundamental factor in the planning, operations, and resource management within the grid system. The numerous restructurings of the grid and the integration of new devices to the grid heighten the need for forecasting to better plan for energy supply and demand. The methodology will be applied in the study for it will the first proposes a prediction model capable of predicting load data. Additionally, the study assesses the prediction model’s performance and effectiveness against several metrics. (Chemetova et al. 2017).

The problem is difficulty in harvesting various renewable energy forms led to the use of the smart grids integrated with photovoltaic (PV) power. However, various atmospheric conditions, for instance, rain, affect solar irradiance occurrence. This solution proposes the adoption of wavelet transform and Elman Neural Network (WT- ENN) for short-term solar energy production and irradiance forecasting. The methodology, the first decomposed the original solar irradiance data into consecutive stable wavelet sub-series. Additionally, the study used ENN to optimize the new wavelet coefficients. Lastly, the study reconstructed solar irradiance using the prediction model and the new coefficients. The prediction model’s performance was then assessed using two real-world data solar irradiance datasets. (Huang et al. 2019).

The problem is Smart grid systems allow consumers to use more energy from the grid or vend it back to the grid for other consumers. Smart homes with photovoltaic systems can establish the daily energy yield. This solution recommends the use of multi-layer perceptron based on photovoltaic forecasting on rooftop PV systems. The methodology will be applied, the first suggests the use of multi-layer perceptron-based PV forecasting. The study then trains its historical data, conducts cross-validation, and tests the model using real-world PV data. (Parvez et al. 2020).

The problem is emergence of smart grids offers better integration of power systems between energy producers and consumers. The bidirectional nature of these smart grids calls energy consumption optimization measures to maintain the grid’s reliability and supply–demand balance. The solution evaluates the available short-term energy consumption prediction models to determine next-day energy consumption forecasts at one-hour intervals realizing a 24-point forecast. This methodology conducted a thorough assessment of various high-level machine algorithms adopted to forecast and evaluate the various model instances to determine the most appropriate algorithm for energy consumption forecasting. (Petrican et al. 2018).

The problem is Efficient energy delivery in the smart grid requires adopting energy resource management strategies that balance energy supply and demand. This solution proposes several techniques that accurately model and predict energy production and demand over time. Similarly, the study recommends modeling analyses that statistical output models of energy consumption and machine learning approaches improve prediction accuracy. The methodology, the first the statistical distribution of real-world meter reading data of several houses for over 200 days acquired from Stanford University. (Yu et al. 2014).

The problem is several countries continue to record an increase in their solar power capacity connections to the distribution grids. Adopting the smart grid concept has since contributed to this increase. The solution study suggests a new forecasting model that uses autoregressive models and gradient boosting algorithms. Such promote the alleviation of these constraints and result in point and probabilistic solar power forecasts for medium voltage and low voltage distribution stations. The methodology, the first proposes a model that overcomes the information and communication technology (ICT) limitations to promote solar energy forecasts at secondary substation levels. It then combined the values obtained from various distributed sensors. (Bessa 2014).

The problem is various new technology appliances that consumers currently use in their households overwhelm the existing smart grid infrastructure as they were initially not developed to support these devices. This solution proposes the implementation of various methods energy providers can improve their energy consumption forecasts for households despite their variability in electrical appliance usage. The methodology, the first assesses the existing prediction models ad their significance. It then describes various modeling techniques that assess the existing statistical approaches and machine learning algorithms. (Lauer et al. 2019).

3 Analytical analysis

To realizes our proposed solution, we need first to identify the environment model, which in this case includes a photovoltaic grid. Then the process of generating the energy depending on the physical structure and the weather conditions in addition to the generated signal need to be modelled and then simulated. After this, the generated data are clustered using the K-means clustering algorithm. Finally, LSTM and GRU are used to provide the short-term predictions.

3.1 Environment and PV model

The earth rotates around the sun approximately 8766 h about 365.242 days. Earth is closest to the Sun (147 million km) on January 2, and this point is called perihelion.

Specific point on earth aligned with sun position. It’s determined by two angels; they are altitude angle ($\alpha$) and azimuth angle ${\uptheta }_{s}$

The altitude angle is the angular height of the Sun is measured from the horizontal. The altitude angle can be given by:

$$ sin\alpha = sinL sin\delta + cosL cos\delta cos\omega $$

(1)

where,

$L$: attitude of the location

$\delta$: Angle of declination

$\omega$: Hour angle.

The declination angle is between Earth Sun vector and equatorial plane its calculated degree, arguments to trig function noted in radian mode.

(2)

Noted hour angel ω is the angular displacement of the sun local point is given by:

$$ {\upomega } = 15^{0} { }\left( {{\text{AST}} - 12{\text{h}}} \right){ } $$

(3)

AST the true daily motion of solar time is given by a daily apparent solar motion of true observed sun. AST is constructed on the actual solar day. The two interval falls between two consecutive returns of local meridian and the sun. Solar time is illustrious as,

$$ AST = LMT + E_{0} T \pm 4^{0} /\left( {LSMT - LOD} \right) $$

(4)

$LMT$: Local meridian time

$LOD$: Longitude

$LSMT$: Local standard meridian time

${E}_{0}T$: Equation of time.

$AST$: Apparent solar time

The $LSTM$ is a reference meridian used for a particular time zone, used for Greenwich Mean Time.

$LSTM$ is given by:

$$LSMT={15}^{0}{T}_{GMT}$$

(5)

The ${E}_{0}T$ is the difference between apparent and mean solar times, both taken at a given longitude at the same real instant of time.

${E}_{0}T$ is given by:

$$EoT=9.87\mathrm{sin}\left(2B\right)-7.53 cosB-1.5sinB$$

(6)

where,

$B$ can be given by;

$$B=\frac{2\pi }{365}\left(N-81\right)$$

(7)

where,

$N$: Day number defined as the number of days elapsed in a given year up to a particular date.

Angular displacement of the Sun reference line from the source axis. The azimuth angle can be given by:

$$ sin\theta = \frac{{cos{{\delta sin\omega }}}}{{cos{\upalpha }}} $$

(8)

The solar source model is to estimate the emitted radiation from the Sun. The function of the temperature is described as radiant energy of emitting objects.

We associate radiating energy to the blackbody. A blackbody is defined as a perfect absorber and emitter. A perfect absorber can absorb all of the received energy with any reflections.

Planck’s law describes the wavelengths emitted by a blackbody at a specific temperature as follows:

$${E}_{\lambda }=\frac{3.74\times {10}^{8}}{ {\lambda }^{5}\left[exp\frac{\mathrm{14,40}}{ \lambda T}\right]-1}$$

(9)

${E}_{\lambda }$: Total emissive per unit area of blackbody emission rate (W/m2 µm)

$T$: Absolute temperature of the blackbody (K)

$\lambda$: Wavelength (µm).

Solar radiation value outside the atmosphere varies as the Earth orbits the Sun. Therefore, the distance between the Sun and the Earth must be considered in modeling the extraterrestrial solar radiation. Thus, the (${G}_{ex}$) is given by:

$${G}_{ex}={G}_{0}{\left[\frac{{R}_{av}}{R}\right]}^{2}$$

(10)

where.

${G}_{ex}$: Extraterrestrial solar radiation.

${G}_{0}$: Solar constant

${R}_{av}$: Mean distance between the Sun and the Earth

$R$: Instantaneous distance between the Sun and the Earth depends on the day of the year or day number.

There are different approximations for the factor (${R}_{av}/R)$ in the literature. A recommended approximation can be given by:

$$\left[\frac{{R}_{av}}{R}\right]=1+0.0333 cos\left[\frac{2\pi N}{365}\right]$$

(11)

By substituting Eqs. (11, 10)

The extraterrestrial solar radiation unit of time falling at a right on square meter of a surface can be given by:

$${G}_{ex}={G}_{0}\left(1+0.0333 cos\left[\frac{2\pi N}{365}\right]\right)$$

(12)

Once the surface faces the Sun (normal to a central ray), the solar irradiance falling on, is ${G}_{ex}$, utilizes maximum solar radiation at that distance. If the surface is not normal to the Sun, the solar radiation drops on it will be decrease by cosine of the angle between the surface normal and a central ray from the Sun.

Thus, the extraterrestrial solar radiation on a horizontal surface located in a specific location (${G}_{exH}$) can be calculated by:

$${G}_{exH}={G}_{ex}cos \varphi $$

(13)

where.

$\varphi$: Solar zenith angle.

The solar zenith angle value is equal to the altitude value, and thus Eq. (13) can be rewritten as follows:

$${G}_{exH}={G}_{0}\left[1+0.0333 cos\left[\frac{360N}{365}\right]\right] sinL sin\delta +cosL cos\delta cos\upomega $$

(14)

Finally, the total extraterrestrial solar energy ${E}_{ex}$ (Wh/m2) is calculated as follows:

$${E}_{ex}=\underset{{T}_{sr}}{\overset{{T}_{ss}}{\int }}{G}_{exH}dt$$

(15)

There are several components of a solar radiation on a tilted surface are in addition to the direct (${G}_{B.\beta })$ and diffuse (${G}_{D.\beta }$) solar radiation, reflected solar radiation (${G}_{R})$ is added to form the global solar radiation incident on a tilted surface.

$${G}_{T,\beta }={G}_{B,\beta }+{G}_{D,\beta }+{G}_{R}$$

(16)

The solar energy components on a horizontal surface as follows:

$${G}_{T,\beta }={G}_{B}{R}_{B}+{G}_{D}{R}_{D}+{G}_{T}\rho {R}_{R}$$

(17)

where,

RB, RD, and ${R}_{R}$:are coefficients.

$\rho$: Ground Aledo.

${R}_{B}$: Ratio between global solar energy on a horizontal surface and global solar energy on a tilted surface.

${R}_{D}$: Ratio between diffuse solar energy on a horizontal surface and diffuse solar energy on a tilted surface,

${R}_{R}$: Factor of reflected solar energy on a tilted surface.

The finding of solar energy components on a tilted surface is to estimate the coefficients ${R}_{B}$,${R}_{D}$, and ${R}_{R}$. Used model for calculating ${R}_{B}$ is the Liu and Jordan model [Liu, B.Y. and Jordan, R.C., 1963]

$${R}_{B}=\frac{\mathrm{cos}\left(L-\beta \right)cos\delta sin{\omega }_{ss}+{\omega }_{ss}\mathrm{sin}\left(L-\beta \right)sin\delta }{cosL cos\delta sin{\omega }_{ss}+{\omega }_{ss} sinL sin\delta }$$

(18)

The surfaces in the southern hemisphere, the slope toward the equator ${R}_{B}$ is given as:

$${R}_{B}=\frac{\mathrm{cos}\left(L+\beta \right)cos\delta sin{\omega }_{ss}+{\omega }_{ss}\mathrm{sin}\left(L+\beta \right)sin\delta }{cosL cos\delta sin{\omega }_{ss}+{\omega }_{ss} sinL sin\delta }$$

(19)

The most recommended formula ${R}_{R}$ is:

$${R}_{R}=\frac{1-cos\beta }{2}$$

(20)

${R}_{D}$ Have been classified into isotropic and anisotropic models.

Isotropic radiation has the same intensity regardless of the direction of measurement. Isotropic radiator is a uniform radiation from given point.

Model used of the Liu and Jordan an isotropic diffuse with ${R}_{D}$ been expressed:

$${R}_{R}=\frac{1-cos\beta }{2}$$

(21)

$${R}_{D}=\frac{1}{3\left[2+cos\beta \right]}$$

(22)

$${R}_{D}=\frac{3+\mathrm{cos}(2\beta )}{4}$$

(23)

$${R}_{D}=1-\frac{\beta }{180}$$

(24)

The behavior of isotropy and anisotropy radiation. Isotropy indicates identical properties in all direction moreover measure aligned different axes of materials physical property (absorbance, refractive index, density). On the other hands Anisotropy model is based on anisotropic radiation measurements varies in direction because of radiates nonuniformly in all direction. Anisotropic moles are noted ${R}_{D}$:

$${R}_{D}=\frac{{G}_{B}}{{G}_{T}}{R}_{D}+\left(1-\frac{{G}_{B}}{{G}_{T}}\right)\left(\frac{1+cos\beta }{2}\right)$$

(25)

$${R}_{D}=0.51{R}_{B}+\frac{1+cos TLT}{2}-\frac{1.74}{1.26\pi }\left[sin\beta =\left(\beta \frac{\pi }{180}\right)cos\beta -\pi { sin}^{2}\left(\frac{\beta }{2}\right)\right]$$

(26)

$${R}_{D}=\frac{{G}_{B}}{{G}_{T}}{R}_{B}+\left(1-\frac{{G}_{B}}{{G}_{T}}\right)\left(\frac{1+cos\beta }{2}\right)\left(1+\sqrt{\frac{{G}_{B}}{{G}_{T}}} {sin}^{3}\left(\frac{\beta }{2}\right)\right)$$

(27)

The circuit of a solar cell is a current source connected in parallel with a diode as shown in Figure. The output of the current source is directly related to the light emitted on the cell. Nor current or voltages are produced during darkness of solar cell. During light falls over solar cell it generates diode current Fig. 1.

Fig. 1

source connected in parallel with a diode

a Solar cell is a current

The diode, D, determines the I–V characteristics of the cell. A series resistance, ${R}_{s}$, while the shunt resistance, ${R}_{SH}$

Assumed that ${R}_{s}$ = 0 and ${R}_{SH}$ = infinity. The net current of the cell is the difference between the photocurrent, ${I}_{L}$, and the normal diode current is:

$$I={I}_{L}-{I}_{0}\left({e}^{\frac{q\left(V+I{R}_{s}\right)}{nkT}}-1\right)-\frac{V+I{R}_{s}}{{R}_{p}}$$

(28)

The photocurrent, ${I}_{L}$, depends on reference first and second temperatures, ${T}_{1}$ and ${T}_{2}$, respectively, illustrated by:

$${I}_{L}={I}_{L}\left({T}_{1}\right)+{K}_{0}\left(T-{T}_{1}\right)$$

(29)

where,

$${I}_{L}\left({T}_{1}\right)={I}_{scT1,nom}\left(\frac{G}{{G}_{nom}}\right)$$

(30)

$${K}_{0}=\frac{{I}_{sc{T}_{2}}-{I}_{sc{T}_{1}}}{{T}_{2}-{T}_{1}}$$

(31)

where,

$G$: Present solar radiation

${G}_{nom}$: Solar radiation at the reference test.

The saturation current of the diode, ${I}_{0}$, is given by:

$${I}_{0}={I}_{0{T}_{1}}{\left(\frac{T}{{T}_{1}}\right)}^\frac{3}{n}{e}^{\frac{q{V}_{q{T}_{1}}}{nk\left(\frac{1}{T}-\frac{1}{{T}_{1}}\right)}}$$

(32)

where,

$${I}_{0{T}_{1}}=\frac{{I}_{sc{T}_{1}}}{({e}^{\frac{q{V}_{oc{T}_{1}}}{nk{T}_{1}}}-1)}$$

(33)

The series resistance of a solar cell is given by:

$${R}_{s}=-\frac{dV}{d{I}_{{V}_{oc}}}-\frac{1}{{X}_{V}}$$

(34)

where,

$${X}_{V}={I}_{o{T}_{1}}\frac{q}{nk{T}_{1}}{e}^{\frac{q{V}_{oc{T}_{1}}}{nk{T}_{1}}}$$

(35)

3.2 Operations modelling

A typical V–I characteristic of a solar cell at a certain ambient irradiation, G, and fixed cell temperature.

For a resistive load, the load characteristic is a straight line with slope I/V = 1/R.

If the load is small, the cell operates in the regions M–N of the curve; cell behaves as a constant current source that is almost equal to the short circuit current. When we have high load, the cell function in the P–S zone of the curve and the cell behaves as a constant voltage source that is almost equal to the open circuit voltage.

The short circuit current, ${I}_{sc}$, is the greatest value of current generated by a solar cell. When V = 0 the short circuit condition produced. When the photocurrent is zero, the open circuit voltage corresponds to the voltage drop across the diode. It reflects the voltage of the cell at no light conditions, and it can be expressed as:

$${V}_{oc}=\frac{nkT}{q}ln\left(\frac{{I}_{L}}{{I}_{0}}\right)={V}_{t }ln\left(\frac{{I}_{L}}{{I}_{0}}\right)$$

(36)

where (${V}_{t}=mk{T}_{c}/q$): is known as the thermal voltage.

T: absolute cell temperature.

Cells are connected together in series to increase the voltage. Several of these series strings of cells may be connected together in parallel to increase the current as well. This package is called as a PV module or PV panel.

The relations between a PV module panel, the cell’s voltage (${V}_{c}$) and current (${I}_{c}$) and the module’s voltage (${V}_{m}$) and current (${I}_{m}$) are given by the following equations:

$${I}_{M}={N}_{pM}{I}_{c}$$

(37)

$${V}_{M}={N}_{sM}{V}_{c}$$

(38)

$${\mathrm{R}}_{\mathrm{sM}}{\mathrm{R}}_{\mathrm{sM}}=\frac{{\mathrm{N}}_{\mathrm{sM}}}{{\mathrm{N}}_{\mathrm{pM}}}{\mathrm{R}}_{\mathrm{sc}}$$

(39)

where,

${\mathrm{N}}_{\mathrm{sM}}$: Number of series cells.

${\mathrm{N}}_{\mathrm{pM}}$: Number of parallel cells.

${\mathrm{R}}_{\mathrm{sM}}$: Equivalent series resistance of the PV module.

Most PV manufacturers provide temperature elements for their crystalline PV modules based on the NOCT as the cell temperature (${\mathrm{T}}_{\mathrm{c}}$), which has a standard equation of

$${\mathrm{T}}_{\mathrm{c}}={\mathrm{T}}_{\mathrm{a}}+\frac{\mathrm{G}}{800}\left(\mathrm{NOCT}-20^\circ \mathrm{C}\right)$$

(40)

where,

${T}_{\mathrm{c}}$: Cell temperature.

${T}_{\mathrm{a}}$: Ambient temperature.

$G$: Instant solar radiation.

$NOCT$: nominal operating cell temperature is defined as the temperature reached by the open circuit cells in a photovoltaic module under conditions of 800 W/m2 irradiance on the cell surface, 20 °C air temperature, and 1 m/s wind velocity.

As mentioned in Eq. (28), the characteristic of a PV cell is expressed by its relationship between current and voltage (I–V) and power and voltage (P–V) at specific solar radiation and temperature levels. Assuming the ${\mathrm{R}}_{\mathrm{p}}$ in Eq. (27) is too large, and then the I–V a solar cell expressed as:

$$\mathrm{I}={\mathrm{I}}_{\mathrm{L}}-{\mathrm{I}}_{0}\left[\mathrm{exp}\left(\frac{\mathrm{q}(\mathrm{V}+{\mathrm{IR}}_{\mathrm{s}}}{{\mathrm{nkT}}_{\mathrm{c}}}\right)-1\right]$$

(41)

In addition to that, in order to simplify the characterization of a solar cell, assume that

$$\frac{\mathrm{q}}{\mathrm{nk}}={\mathrm{k}}_{1}$$

(42)

$$\frac{{\mathrm{T}}_{\mathrm{c}}}{{\mathrm{k}}_{1}}=\mathrm{a}$$

(43)

Based on this, Eq. (27) can be rewritten as follows:

$$I={I}_{L}-{I}_{0}\left[exp\left(\frac{q(V+I{R}_{s}}{a}\right)-1\right]$$

(44)

Solving Equation for $V$ results:

$$V=a.ln\left(\frac{{I}_{L}-I}{{I}_{0}}+1\right)-I{R}_{s}$$

(45)

The light‐generated current, ${I}_{ph}$, is linearly proportional to the global solar radiation and is also logarithmically dependent on the operating temperature of cell, ${T}_{c}$. Therefore, ${I}_{ph}$ can be expressed:

$${I}_{L}=\left({k}_{2}+{k}_{3}{T}_{c}\right){G}_{T}$$

(46)

Finally, the diode saturation current depends on the operating temperature of cell ${T}_{c}$: as follows:

$${I}_{0}={k}_{4}{T}_{c}^{3}exp\left(-\frac{{k}_{5}}{{T}_{c}}\right)$$

(47)

Four statistic errors are used, which are.

• (1) ($MAPE$): Mean absolute percentage error.

• (2) ($MBE$): Mean bias error.

• (3) ($MAE$): Mean absolute error.

• (4) ($RMSE$): Root mean square error.

The general accuracy of a neural network can be highlighted by $MAPE$. $MAPE$ can be defined as follows:

$$MAPE=\frac{1}{n}\sum_{t=1}^{n}\left|\frac{M-P}{M}\right|$$

(48)

where,

$M$: Measured data.

$P$: Predicted data.

The information of long‐term performance of the neural network model can also be evaluated by $MBE$. $MBE$ can be calculated as follows:

$$\mathrm{MBE}=\frac{1}{n}\sum_{i=1}^{n}({P}_{i}-{M}_{i})$$

(49)

The mean absolute error $(MAE)$: is a measure of errors between paired observations expressing the same phenomenon. Examples of Y versus X include comparisons of predicted versus observed, subsequent time versus initial time, and one technique of measurement versus an alternative technique of measurement. $MAE$ is calculated as:

$$\mathrm{MAE}=\sum_{i=1}^{n}(\frac{\left|{y}_{i}-{x}_{i}\right|}{n})$$

(50)

where,

${y}_{i}$: Prediction

${x}_{i}$: True value

$n$: Total number of data points

The final statistic error is $RMSE$; it represents the measurement of the variation of the predicted data around the measured data.

The short‐term performance information of the model can be evaluated by $RMSE$:

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}({{P}_{i}-{M}_{i})}^{2}}$$

(51)

3.3 Fault modelling

Photovoltaics (PV) component/module, which involves solar cells connected in series. The equation below illustrates the PV voltage as well as current features.

$$I={I}_{PH}-{I}_{0}\left[\mathrm{exp}\left( \frac{V+{R}_{s}I}{\mathrm{\alpha }{V}_{t}}\right)-1\right]-\frac{V+{R}_{s}I}{{R}_{sh}}$$

(52)

whereby voltage of the PV is denotated by V while the photovoltaics current (output) is denotated by I. Therefore, $V={N}_{cell} {V}_{cell}$;${N}_{cell}$ as well as$I={I}_{cell}$; this refers to the solar cell’s quantity connected in series. The produced PV-photocurrent is represented by$IPH$:${I}_{PH}={I}_{PH},cell {I}_{0 };$. Also, the thermal voltage is represented by ${V}_{t}={N}_{cell}\frac{KT}{q}$ whereas the diode’s reverse saturated I is represented by ${I}_{0}={I}_{0},cell {V}_{t }.$ The parallel as well as series equal or correspondent resistance(s) is denoted by ${R}_{sh}$ as well as ${R}_{s}, respetcively:{R}_{s}={N}_{cell}{R}_{s,cell}$

Whereas ${R}_{sh}={N}_{cell}{R}_{sh,cell}$ (Villalva et al. 2009).

3.3.1 Strategy used to identify faults

This study focuses on detecting photovoltaics system’s faults, which are associated with the degraded photovoltaics array and photovoltaics array’s partial shading, short circuits, as well as open circuits. Silvestre et al. (2014) formulate Eqs. (55, 56) for defining the photovoltaics system’s indicators of current and voltage, as well as describing it using defect feature quantity. The Eqs. (55, 56) are shown below:

$${R}_{V}=\frac{V}{{V}_{oc}}$$

(53)

$${R}_{I}=\frac{I}{{I}_{sc}}$$

(54)

where ${R}_{V}-voltage indcator$, ${whereas R}_{I}-indicator of current/I$ in a photovoltaics module. Similarly, I-is current and V-is voltage of the photovoltaics module in its maximum power point. The photovoltaics array’s short-circuit current is-${I}_{sc}$ whereas the voltage open-circuit is represented as ${V}_{oc}.$ According to (Silvestre et al. 2014), Eqs. 57 and 58 below represents the${V}_{oc}$,${I}_{sc}$

$${I}_{sc}= {N}_{P}(\frac{{I}_{scm\_STC}}{1000}G+{K}_{I}\left(T-{T}_{STC}\right))$$

(55)

$${V}_{oc}= {N}_{s}({V}_{ocm\_STC}+{K}_{V}\left(T-{T}_{STC}\right)+{V}_{t}\mathrm{ln}\left(\frac{\frac{{I}_{sc}}{{N}_{p}}}{{I}_{scm\_STC}}\right))$$

(56)

In which:

${N}_{s}$-refers to the number of the photovoltaic modules of a photovoltaic string

${N}_{P}$-refer to the number of the photovoltaic array’s photovoltaic string

${V}_{t}$-implies the photovoltaics’s thermal voltage.

$T$ − refers to photovoltaics’ temperature

$G$-refers to photovoltaics component that receives irradiations

${K}_{V}$-refers to an open-circuit voltage’s Temperature coefficient

${K}_{I}$-refers to short-circuit current’s Temperature coefficient

At standard testing settings, which are ${T}_{STC}= {25}^{0}C$ [temperature] as well as ${G}_{STC}$ $=1000 W/{m}^{2}$[irradiation], the ${V}_{ocm\_STC}$ -refers to photovoltaics module’s open- circuit voltage whereas ${I}_{scm\_STC}$ refers to the photovoltaic modules short-circuit current.

Silvestre et al. (2014) stated that no fault operations (i.e., no faults in the indicators of current or voltage) in the photovoltaics component as illustrated in Eqs. 55 and 56 is represented in Eqs. 58 and 59 below:

$${R}_{VM}=\frac{{V}_{m}}{{V}_{oc}}$$

(57)

$${R}_{IM}=\frac{{I}_{m}}{{I}_{sc}}$$

(58)

whereby:

${I}_{m, }{V}_{m}$: The photovoltaics module’s output current as well as voltage of the PV system in fault-free operation

${R}_{IM}$: Photovoltaics module’s current indictors of the PV system in fault-free operation

${R}_{VM}$: Photovoltaics module’s voltage indictors of the PV system in fault-free operation

Additionally, Eqs. 61 and 62 below shows the ${V}_{m}$, ${I}_{m}$ of the photovoltaics array at a maximum power point (MPP)during a fault-free state. (Silvestre et al. 2014).

$${I}_{m}= {N}_{P}(\frac{{I}_{mm\_STC}}{1000}G+{K}_{I}\left(T-{T}_{STC}\right))$$

(59)

$${V}_{m}= {N}_{s}({V}_{t}\mathrm{ln}\left(1+\frac{{I}_{sc}-{I}_{m}}{{I}_{sc}}\left({e}^{\frac{{V}_{oc}}{{N}_{s}{V}_{t}}}-1\right)\right)-\frac{{I}_{m}}{{N}_{p}}{R}_{s}$$

(60)

whereby at normal testing conditions:

${R}_{s}$: Photovoltaics component’s series equal resistance.

${I}_{m{m}_{STC}}$: The current at the maximum power point of the photovoltaics module at Standard Test Conditions.

3.3.2 Defining the verges of detecting faults

A. Open-circuit fault

Yahyaoui and Segatto (2017) stated that the faulty string’s I tend to be equivalent with the photovoltaics array’s output current’s decreased percentage, which usually occurs whenever there is a faulty open circuit. Therefore, the I-indicators in this condition is represented in Eq. 63 below:

$${R}_{IO}=\frac{({N}_{p}-1)}{{N}_{p}}\frac{{I}_{m}}{{I}_{sc}}=\alpha {R}_{IM}$$

(61)

where ${R}_{IO}$ -refers to the current indicator when there’s an existence of an open circuit fault in a photovoltaics array where $\alpha$ tend to be:

$$\alpha =1.0-\frac{1.0}{{N}_{p}}$$

(62)

Therefore, the fault detection threshold of open circuit faults is be defined by Eq. 65 (Yahyaoui and Segatto 2017).

$${T}_{IO}=\varepsilon {R}_{IM}$$

(63)

whereby:

$\varepsilon$-refers to a fault detection allowable offset coefficient and $\varepsilon$ $= 2.0\%$ (Silvestre et al. 2014).

${T}_{IO}$-refers to an open circuit fault’s threshold. Silvestre et al. (2014) argued that ${T}_{IO}$ Value should be above the ${R}_{I}-value$ (see Eq. 56), particularly if one or more the photovoltaics strings given has an open circuit fault.

B) Short-Circuits fault

Likewise, if there is an occurrence of short-circuit photovoltaics module in any photovoltaic strings, the short-circuit voltage of the photovoltaics module is equal to the decreased portion of the output voltage of the photovoltaics array. Therefore, the following equation (Eq. 66) is used to calculate voltage indicator Yahyaoui and Segatto (2017).

$${R}_{VS}=\frac{({N}_{s}-1)}{{N}_{s}}. \frac{{V}_{m}}{{V}_{oc}}=\beta {R}_{VM}$$

(64)

where: ${R}_{VS}$-refers to an indicator of voltage in presence of a short-circuit in the photovoltaics occurring within photovoltaics string(s). Equation 67 show $\beta$, illustrated below:

$$\beta =1-\frac{1}{{N}_{s}}$$

(65)

Therefore, the fault detection threshold of short-circuit faults are be defined by (Yahyaoui and Segatto 2017).

$${T}_{VS}=\varepsilon \beta {R}_{VM}$$

(66)

${R}_{V}-value$ (Provided in Eq. 55) should be lower than ${T}_{VS}$ values.

${T}_{VS}$ -refers to short-circuit fault’s threshold whenever one/more photovoltaic module string offered with a short circuit fault.

C) Partial shading fault

Partly shading of photovoltaics array causes drastic decrease in the current output since part of the array receives solar irradiation. Therefore, Eqs. 69 and 70 below are used to calculate the indicators of current and voltage in an event of partly or incomplete shading

$${R}_{VP}=\frac{{V}_{mp}}{{V}_{oc}}$$

(67)

$${R}_{IP}=\frac{{I}_{mp}}{{I}_{sc}}$$

(68)

where:

${I}_{mp}$ refers to a photovoltaics array’s current output at a maximum power point

${V}_{mp}$ refers to a photovoltaics array’s voltage output maximum power point

${R}_{IP}$ refers to fractional shading fault’s the indicators of current

${R}_{VP}$ refers to partly shading fault’s the indicators of voltage

Equation 71 and 72 are used to calculate photovoltaics array’s ${I}_{mp} as well as{ V}_{mp}$ whenever there is a partly shading, where the photovoltaics array receives maximum irradiance in unshaded side.

$$ I_{mp} = N_{p} \left( {\frac{{I_{mm\_STC} }}{1000}G_{P} + K_{I} \left( {T - T_{STC} } \right)} \right) $$

(69)

$${V}_{mp}= {N}_{s}({V}_{t}\mathrm{ln}\left(1+\frac{{I}_{sc}-{I}_{mp}}{{I}_{sc}}\left({e}^{\frac{{V}_{oc}}{{N}_{s}{V}_{t}}}-1\right)\right)-\frac{{I}_{mp}}{{N}_{p}}{R}_{s}$$

(70)

where ${G}_{P}$ -gets photovoltaics optimum irradiance in partial-shading states. Thus, Eq. 73 below is instrumental in detecting and identifying the threshold of faults during a partly-shading.

$${T}_{IP}=\varepsilon {R}_{IP}$$

(71)

where ${T}_{IP}$-refers to the partial-shading fault’s thresholds. ${T}_{IP}$ values should be higher than the ${R}_{I}$ Values (provided in Eq. 56) whenever all or partial shaded for the photovoltaics array.

where ${T}_{IP}$ is the threshold of partial shading faults, and when partial or all shaded for the PV array, the value of ${R}_{I}$ (given as Eq. (56) must be below the value of ${T}_{IP}$ Table 1.

Table 1 Nomenclature

3.4 Problem definition and proposed Model

Having identified the models for the environment, the operation, and the generated signals, now the problem of the accurate generated power prediction can be formulated as below.

$$\mathrm{F}(\mathrm{A}*)=\left(\underset{0\le\upeta \le 1}{\mathrm{max}}P,\upeta , \underset{0\le {Q}_{S}\le 1}{\mathrm{min}}{Q}_{S}\right)$$

The above definition is a min–max-optimization problem, where,

$P$: PV power output (LSTM and GRU Final Comparative Results) Table 3.

$\upeta$: Is conversion efficiency of PV module (Maximum efficiency for GRU and LSTM algorithms) (Durisch et al. 2007) Table 4.

${Q}_{S}$: Respects the thermal energy losses through radiation and convection heat transfer from modules (Castillejo-Cuberos and Escobar 2020; Lave et al. 2015; Van Haaren et al. 2014) Figs. 16, 17.

While the optimization variables can be defined as:

$A = \left\{ {S, \beta , \gamma , h_{r} ,h_{c} , l, G_{T} , V_{WS}, \varphi, } \right.$ θ, , , £, Б, α, $\mu , \xi , \vartheta , \varpi ,$ , }

However, a problem with all these variables can be defined as an NP-Hard problem. And cannot be solved using tradition optimization techniques. Therefore, to solve this problem we will follow the below methodology Table 2.

Table 2 While the definitions of the used notations and their ranges, are illustrated in the below table

After having modelled the environment, the operation and the signals to generate the patterns that is like the real patterns of the physical instruments, this pattern is clustered using k-mean clustering algorithm.

After that, we implement a monte-carlo simulation with the identification of all the bounds of the remained stochastic variables, and the optimization outputs, as mentioned in the above table. Inside the iterations of this simulation, Particle Swarm Optimization (PSO) algorithm, which is a metaheuristic stochastic-based algorithm is applied in order to identify the optimal values of the selected optimization variables.

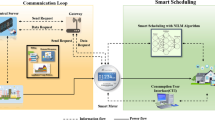
After finding the optimal values of the parameters, these parameters as well as the output values, will be used in addition to the current and previous loads in order to produce the short-term prediction, for example, LSTM or GRU algorithms will be used in this phase. The below figure shows the block diagram of our proposed solution. The below figure summarizes this proposed method Fig. 2.

Fig. 2

Methodology Block Diagram

In the prediction phase,initially LSTM, see Fig. 3a, has been selected with training input is the output of the clustering phase with size of 1400 × 34and then this and 300 hidden layers with three output signals, representing the next or the future temporal values of $n, p$ and the $Qs$ in the LSTM we have used look up in order to use only the most useful or the most related samples in building that pattern. Moreover, GRU, see Fig. 3b, followed the same structure to compare both algorithms using the same benchmark in order to be able to figure out which one provides us with the most accurate future temporal value, and which one provides us with a most with the fastest processing time.

Fig. 3

GRU and LSTM Structures

3.5 Datasets

Regarding the load, we have acquired it from a with short-term slots of a frequency of 5 min which is very useful for our application in short-term prediction. This dataset (Dataset employed by this research can be retrieved from UK Smart Grid Industry 2021–2024) contains 371 samples each sample is 5 min separated from the other sample from the period of the first of January to the second of January in the year in the previous year 2020.This dataset was generated from a real site located in London city in the UK. The exact coordinates are 51.5074° N, 0.1278° W.

4 Implementation and results

The modeling of the sun position for the selected location in London city in the UK, according to the location of the site from which we obtained the datasets which contains the temperature and solar radiation is shown below.

Figure 4 shows, the first plot which is the alpha angle of the sun position from day 0 to day 350. So, for entire year according to the position of the coordinate of London city UK. Where the second plot is the Theta for the period time for the same position for the same location.

Fig. 4

The alpha angle of the sun position

Figure 5, below chooses the hourly extraterrestrial solar radiation profile for 16 days of January, each plots of this 16 plots for a specific date is shown that the plots almost similar to each other but the related plot for corresponding days increase with the increase of that day which means the peak value of each day as increasing according to the day number for example day 1 we have the value around 350 for day 2 its around 360 and so on the big value.the x-axis here is $\left(LMT\right)$ and y -axis the$\left(GextH\right)$.While Fig. 6 shows five minutes step for only one day Fig. 7.

Fig. 5

Five minutes step for only one day

Fig. 6

The hourly extraterrestrial solar radiation

Fig. 7

The solar radiation for one day and Diffuse solar radiation

Figure 7a shows the solar radiation for one day in January for 5 min step. And 7b the diffuse solar radiation for the same period of time also the step time 5 min.

Figure 8 shows sample of the global solar radiation and diffuse solar radiation for sample days, the first day, day number 50, 100, 180, 250, and 360, which choose the variation of the solar radiation in this day. In this result we have used 60 min step so hourly based solar radiation for each day this value helps us to predict the next solar radiation for following minutes.

Fig. 8

Global solar radiation and diffuse solar radiation

Figure 9 shows the 5 min step solar radiation for the same days which also helps us to predict the short-term solar radiation for each 5 min, as we can see the pattern is almost similar, it looks smoother than the previous figure.

Fig. 9

5 min step solar radiation

Figure 10a shows the sun position for 5 min of one day in January the sun position alpha angle and theta angle.

Fig. 10

The sun position alpha angle and theta angle and Sun position and generated power

it shows corresponding voltage, current and power for each sun position Fig. 10. between the sun position and generated power.

It appears from the above figures, that the sun position for the same day in different years is not the same. This is a physical fact that applies on all the natural resources and factors, such as wind, dust, shading, etc. Consequently, and as clearly shown in the figures above, the behavior of the natural factors is totally stochastic and cannot be predicted. Since the generation of the electricity is based and affected by these resources and factors. This leads to the fact, that the prediction of the generated energy based on renewable resources is a challenging problem. Therefore, this work contributes to this field by developing a methodology to allow the process of short-term prediction for the short-term future generated energy that is based on and affected by renewable resources and factors.

4.1 Data Generation and Montecarlo simulation

Figure 11 shows the generated signals that contains1000 normal and 1000 faulty signals, each of which contains 34 features. However, these signals have been also generated using the stochastic features of the Montecarlo simulation. To test the Prediction model Fig. 12.

Fig. 11

Sample traffic from the generated big-data signals

Fig. 12

Pattern Clustering with K-Mean

In This phase we need to know the status of the pattern. Weather this signal is normal or a fault signal. However, in our problem we don't have target. There is no data set with a target. Also, the behavior of the normal traffic and that the behavior faulty traffic in the real life is a little bit of stochastic that does not follow a stable pattern. Therefore, we will not be able to identify the exact features of the input pattern and the target for them. Therefore, our problem can be defined as a clustering problem, In order to solve this clustering problem, We have used k-mean clustering algorithm the previously generated sample traffic have been sent to k-mean clustering algorithm then trained on it after that the clustering algorithm showed as a very clear recognition for the statues of traffic as shown in this figure, the given pattern is found in the first column of the table and then the predicted pattern have been output by k-mean clustering algorithm and as we see here both of them are identical with no any missing values. Therefore, we calculate the loss we have found it very, close to 0 which means that the accuracy is almost 100% (Loss K-means Testing = 2.2204e-16).

4.2 Prediction final results (for LSTM)

the below Fig. 13 shows the plots of the input training and target training, input testing and targeted testing for the prediction process (LSTM). It also shows the output prediction process which is almost exactly as the target testing this also can be improved by showing accuracy, which is almost near to 99.5%.

Fig. 13

The input training and target training input testing and targeted testing for the prediction process (LSTM)

the below Figs. 14 show the prediction finally this classified, or cluster recognized pattern should be sent to the prediction algorithm in order to prediction the Future traffic. For this we have used long short-term memory, which is best reignition technique and we have identified parameters using train and error as shown is this table, however, the training validation and testing process as shown in the figure, after the completion of the training validation and testing process is seen in this figure and as shown, the root mean square error is almost 0.71%.

Fig. 14

Prediction (LSTM model and parameters)

While in the below Fig. 15, GRU is used to do the same prediction task, using the same inputs. This phase is made for a comparison purpose. Where it is clearly noticed that the GRU is slightly faster than the LSTM. But with higher error rate (1%) Table 3.

Fig. 15

Prediction (GRU model and parameters)

Table 3 LSTM and GRU final comparative results

4.3 Identify Qs value

This section illustrates how to identify the ${Q}_{S}$ value. However, in (Castillejo-Cuberos and Escobar 0.2020) it was determined that the overall specific static and dynamic characteristics of solar irradiance for a determined time period, or state, are summarized by the clearness index (${K}_{t}$), the diffuse fraction (K) and the variability of the solar resource. By defining a variable termed the solar resource quality score (${Q}_{S}$), irradiance patterns can be classified in an explicit scheme comparable to clustering techniques but providing a straightforward approach and a simple analytical expression on which to perform the classification, easily translatable across studies, overcoming the issue of data specificity previously discussed.

The only variables needed are the global horizontal irradiance (GHI). The ${Q}_{S}$ is a measure of how close a particular state is from the ideal of full atmospheric clearness (${K}_{t}$ = 1), no attenuation (K = 0) and constant irradiance (variability = 0).

Lave et al. (2015) was used, defined as the probability that a particular ramp rate (RR = $\upmu \left(\frac{GHI}{G \varepsilon \mathrm{sin}(\alpha )}\right)\ge 0.03$) exceeds a given threshold ramp (${RR}_{0}=1000 W/{m}^{2}$ during an evaluation period, and$(\varepsilon =0.02)$.

The Variability Score (CDF based) ${(VS}_{cdf})$ uses the normalized, which is the result of linearly mapping the ${VS}_{cdf}$ from the range 0.002–0.4054 to 0–1 (Castillejo-Cuberos and Escobar 2020), $\left(\Delta t\right)$ temporal resolution timestep

$${VS}_{cdf}=min \left(\sqrt{{\left(\frac{RR}{{RR}_{0}}\right)}^{2}+{(P\left(\left|{RR}_{\Delta t}\right|>{RR}_{0}\right)-1)}^{2}}\right)$$

(72)

where,

$\left(\Delta t\right)=5 mints$.

The quality score (${Q}_{S}$):

$${Q}_{S}=1- \left(\sqrt{\frac{{\left(1-{K}_{t}\right)}^{2}+{K}^{2}+{{(VS}_{cdf})}^{2}}{\sqrt{3}}}\right)$$

(73)

Van Haaren et al. (2014), the Daily Average Ramp Rate (DARR) is calculated as the sum of the absolute value of the changes in irradiance on a minute basis, normalized with an irradiance (G) of 1000 W/m2.

$$\mathrm{DARR}=\sum_{k=1}^{k=371}\frac{\left|{GHI}_{k}-{GHI}_{k-1}\right|}{G}$$

(74)

where,

$$GHI=0<GHI<\left(100+1.5*G*{(sin\alpha )}^{1.2}\right)$$

After implementation the Qs value are determine as shown in the below Figs. 16 and 17:

Fig. 16

Qs values using GRU

Fig. 17

Qs values using LSTM

4.4 Identify efficiency Value:

The maximum power point is given by:

$${P}_{max}={V}_{max}{I}_{max}$$

(75)

The maximum efficiency of a solar cell is expressed as:

$$\eta =\frac{{P}_{max}}{{P}_{in}}=\frac{{I}_{max}{V}_{max}}{A{G}_{a}}$$

(76)

where,

$A$: Area of the PV module,${G}_{a}$: Radiation.

After implementation maximum efficiency for the GRU and LSTM algorithms value are determine as shown in the below Table 4:

Table 4 Maximum efficiency for GRU and LSTM algorithms:

After implementing the optimization algorithm, we have obtained the optimal below values for using LSTM and GRU algorithms. The below tables Illustrate the exact optimal values for the future predicted values of the P, QS, and the efficiency Table 5.

Table 5 Exact optimal values for the future predicted of the P, Qs, and efficiency for using LSTM, GRU algorithms

5 Conclusions and future work

This work addresses the problem of future value estimation based on data with stochastic behaviour. The dependent variables used are the future active generated power, Qs, and the efficiency for the PV grid. While the independent variables are represented with the weather conditions and load behaviour. In this work we proposed a solution based on K-means clustering that converts the stochastic behaviour of the independent variables into a known pattern. Then it becomes easier for either the LSTM or the GRU to use it for the short-term future estimation of the dependant variable. A mathematical model in addition to dataset are used to build a complete environment, with its operation and signals. And mote- Carlo method is used for simulation. As outcomes of a comparative study, we can confirm that although GRU is a fast algorithm, LSTM provides more accurate short-term predictions. Moreover, it’s been concluded that stochasticity is an important factor to be considered in any future estimation process. However, the method proposed in this work shows clear outcomes in solving the stochasticity issue and enhancing the performance of the prediction. Uncertainty in this dynamic environment is an important factor that could be considered in future perspectives.