Abstract
Slope deformation prediction is crucial for early warning of slope failure, which can prevent property damage and save human life. Existing predictive models focus on predicting the displacement of a single monitoring point based on time series data, without considering spatial correlations among monitoring points, which makes it difficult to reveal the displacement changes in the entire monitoring system and ignores the potential threats from nonselected points. To address the above problem, this paper presents a novel deep learning method for predicting the slope deformation, by considering the spatial correlations between all points in the entire displacement monitoring system. The essential idea behind the proposed method is to predict the slope deformation based on the global information (i.e., the correlated displacements of all points in the entire monitoring system), rather than based on the local information (i.e., the displacements of a specified single point in the monitoring system). In the proposed method, (1) a weighted adjacency matrix is built to interpret the spatial correlations between all points, (2) a feature matrix is assembled to store the time-series displacements of all points, and (3) one of the state-of-the-art deep learning models, i.e., T-GCN, is developed to process the above graph-structured data consisting of two matrices. The effectiveness of the proposed method is verified by performing predictions based on a real dataset. The proposed method can be applied to predict time-dependency information in other similar geohazard scenarios, based on time-series data collected from multiple monitoring points.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Geohazard refers to events caused by geological processes that dramatically change environmental conditions and present severe threats to human life, built infrastructures, and even the overall economic system [41]. Slope failures are one of the worst types of geohazards, and occur frequently worldwide [19]. The monitoring of slopes is necessary to adopt adequate prevention measures for the mitigation of human and property damage [7, 40].
Since the 1940s, in-situ monitoring could provide accurate and real-time information on slopes and has been widely employed in slope displacement prediction [61]. Currently, an extensive variety of monitoring systems has been established worldwide [24, 49]. Time-series displacement data collected by monitoring devices generally reflect the deformation and stability characteristics of the slope directly, for instance, to determine whether the slope is accelerating or continuing to slide slowly [8, 20, 34]. These datasets have significant value for developing a high-performance model for obtaining reasonably accurate displacement predictions [18].
Displacement prediction of natural and human-induced slopes, including quarries, open-pit mines, and extensive road excavations, is a common research objective in engineering geology [12]. The slope deformation prediction models mainly include two categories: physically-based models and data-based models [27]. The modeling processes of data-based models are simpler and more accurate than those of physically-based models [28]. Nevertheless, accurate prediction of the deformation behavior of slopes remains a challenge [9, 11]. It is well known that slope failure is the result of the action of nonlinear dynamical systems [39], and its deformation and stability are influenced by multifactorial factors, including geotechnical properties, hydrogeology, geomorphological conditions, climate, weathering, vegetation, and human engineering activities, the interaction, of which renders slope failure randomness, fuzziness, and variability [15, 43]. The influence of these factors can be reflected in the temporal and spatial correlation of slope deformation.
In regards to the temporal correlation of monitoring displacement data, recently, the machine learning model as a data-based model has been widely utilized to predict slope displacements from time-series data. These models can solve the problems of complexity, dynamism, and nonlinear characteristics in nonlinear time series, which thus can be used to predict time-series slope displacement, including artificial neural networks (ANNs) [3, 16, 29, 56], extreme learning machine (ELM) [57], fuzzy logic approach [23], support vector machine (SVM) [32, 42, 52], deep belief network (DBN) [35], and Gaussian process (GP) [38]. These models that consider influencing factors on slope displacement as input and slope displacements as predicted output, have achieved satisfactory performances.
The workflows of these machine learning methods are similar. Several monitoring points are first selected for observation to analyse their deformation, and thus plot the curve of displacement-time, which can reflect different displacement stages for the slope displacement, capture warning indicators of slope failure such as slope displacement falling into the acceleration phase [37, 40]. Subsequently, time-series data from these chosen points will be adopted for modeling, respectively. In other words, each curve shows evolution characteristics from a single monitor point, and each model can predict the displacement of a single monitoring point according to its data.
However, spatial correlations among monitoring points are overlooked by this kind of analysis based on a single point, and thus it is difficult to reveal the displacement changes in the entire monitoring system. Moreover, when some monitoring points are selected for observation, other points where displacement changes are not significant will be ignored, which may leave some potential threats to unnoticed.
To address the above problem, in this paper, we propose a novel deep learning method for predicting the slope deformation, by considering the spatial correlations between all points in the entire displacement monitoring system. The essential idea behind the proposed method is to predict the slope deformation based on the global information (i.e., the correlated displacements of all points in the entire monitoring system), rather than based on the local information (i.e., the displacements of a specified single point in the monitoring system).
First, to obtain the spatial correlation of the monitoring system, we connected all the monitoring points to construct a complete graph (i.e., the fully connected graph) in which each monitoring point serves as a node on the graph, and every pair of distinct nodes is connected by a unique edge. Then, we calculate the weight of the edges (i.e., the similarity between these monitoring points) of each pair of nodes through a spectral clustering method to obtain a weighted adjacency matrix. We term the constructed graph structure a fully connected monitoring network (FCMN).
Next, we used a deep learning method to predict the displacement of the FCMN. Current advances in the deep learning domain make it possible to model the complex spatiotemporal correlation in region-based spatiotemporal prediction [22, 44, 45]. For temporally correlated data, typical models include long-short term memory (LSTM) and gated recurrent units (GRU) . For spatially correlated data, a state-of-the-art model is graph convolutional networks (GCN).
The contributions in this paper can be summarized as follows.
-
(1)
We consider spatial correlation among points in the monitoring system, and connect all monitoring points to construct a fully connected graph FCMN, that is, replace a traditional single-point time series data with the graph-structured data. Thus, our method can predict the displacement in the entire monitoring system.
-
(2)
We further leverage a deep learning architecture called the T-GCN that combines the GCN and GRU [58]. The GCN can capture the spatial correlation based on the topological structure of FCMN. The GRU can complete time-series prediction for slope displacement.
-
(3)
We evaluate the method on a real-world dataset collected from a monitoring system.
The rest of this paper is organized as follows. Section 2 describes the proposed method in detail. Section 3 applies the method in a real case and analyses the results. Section 4 discusses the advantages and shortcomings of the proposed method, and the potential future work. Section 5 concludes the paper.
2 Methods
2.1 Overview
In this paper, we propose a deep learning method using GCN to predict slope deformation based on time-series displacement data; see the workflow of the proposed method in Fig. 1. First, we obtained data from a monitoring device and preprocessed it. Second, we divided the preprocessed data into temporally and spatially correlated data and processed them separately. Third, with the processed spatiotemporal data, we developed a novel deep learning model termed as temporal graph convolutional networks (T-GCN) to predict displacements. The model combines GCN, which can be used for handling spatial correlations, and GRU, which can be used for handling temporal correlations. Finally, we highlighted the motivation for applying the proposed deep learning method in slope deformation prediction.
2.2 Step 1: data acquisition and preprocessing
2.2.1 Data acquisition
Slope displacement data are usually collected from monitoring systems with the use of various types of devices. Common types of devices for deformation monitoring including inclinometer, ground-based synthetic-aperture radar (GBSAR), light detection and ranging (LiDAR), global positioning system (GPS), and fiber sensing cables [5, 13, 17, 53]. The GPS is a radio navigation, timing, and positioning system that has been used extensively for slope surface deformation monitoring. Compared with other devices, GPS devices are more reliable, less expensive, faster, and easier to utilize [47].
2.2.2 Data preprocessing
Once the raw displacement data are collected through the monitoring system, it needs to be preprocessed. Regardless of the method used to build the prediction model, data preprocessing is an essential step in slope displacement prediction, which mainly consists of denoising and normalization [62]. Denoising is used to improve data quality [59, 60]. Normalization makes the data dimensionless [48].
More specifically, the preprocessing of slope displacement data is carried out in three steps. The first step is to check data quality and detect errors in the monitoring data, including analysis of displacement trends and looking for incorrect, inconsistent, missing, or skewed information. The most common method to inspect the data is data profiling, which explores the quality of the data through summary statistics, including checking for missing data values, calculating correlations between variables and the distribution of individual variables [2]. Missing values, outliers, and uncorrelated values are determined from these statistics.
After identifying these incorrect and/or incomplete data, the next step is to clean the data (i.e., denoising), including removing incorrect values and handling missing values. Finally, to improve the data quality, scaling and normalizing the data as well as adjusting the values of the skew distribution are also required. A common normalization method for handling slope monitoring data is to employ max-min normalization [31, 36, 54].
2.3 Step 2: data processing
In this section, we introduce data processing for spatially and temporally correlated displacement data.
2.3.1 Processing of the spatial correlation data
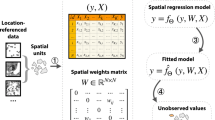
To represent the spatial correlation among points in the entire monitoring system, we use a weighted undirected fully connected graph \(G = (V, E, W)\), and term it as an FCMN. Here, \(V=\left\{ v_{1}, v_{2}, v_{3} \ldots v_{N}\right\} \) is a set of nodes (i.e., monitoring points), and N is the number of monitoring points, in which each node is connected to each of the others (with one edge E between each pair of nodes). The number of edges E is \(n(n\mathrm {-}1)/2\). \(W \in R^{N \times N}\) is a weighted adjacency matrix representing the proximity of the nodes (see Fig. 2).
Considering that the distance between two points in the monitoring system would affect their spatial correlation in the FCMN, we calculate the weighted adjacency matrix using the Gaussian similarity functions based on spatial proximity. The weight \(w_{i j}\) of edge \(e_{i j}\) is calculated based on Eq. (1), which represents the spatial correlation between two nodes (\(v_{i}\), \(v_{j}\)).
where \(\mathrm{{dist}}{}_{i j}\) denotes the distance between monitoring points \(v_{i}\) and \(v_{j}\), and \(\sigma \) is the standard deviation of distances, which controls the width of the neighborhoods [51].
The weighted adjacent matrix can be represented as Eq. (2). A larger weight means that the two nodes have a higher correlation.
An example of building a FCMN in the monitoring system. Assuming that there are seven monitoring points on the slope as shown in the figure, we use the fully connected network to represent it as a graph and then calculate the similarity between any two connected nodes using Gaussian similarity to obtain a weighted adjacency matrix
2.3.2 Processing of the temporal correlation data
To represent the temporal correlation of monitoring points, we constructed a feature matrix \(X \in R^{N \times P}\) containing node time-series information, where P denotes the number of node time-series features (i.e., the length of the historical time series). \(X \in R^{N \times i}\) denotes the displacement on each monitoring point at time i. The input \([X{}_{t-n} , \ldots , X{}_{t-1}, X{}_{t}]\) is a sequence of n historical displacement data. The output \([X{}_{t+1} , \ldots , X{}_{t+T}]\) is the predicted displacement in the next T moments.
After creating the FCMN and feature matrix X, the displacement prediction problem converts to learn the mapping function f that can predict the displacements (see Eq. (3)).
2.4 Step 3: data modeling
In this section, we present more details on the data modeling of the proposed deep learning method for displacement prediction. Three deep learning models are utilized in the data modeling. First, we describe the GCN for spatially correlated data. Second, we describe the GRU for temporally correlated data. Finally, we describe the T-GCN that can deal with spatiotemporal data.
2.4.1 Use of the graph convolutional network (GCN)
In this section, we introduce how to use GCN to capture the spatial correlation from the established FCMN.
Quite recently, GCN has been gaining attentions, which can extend convolutional operations to non-Euclidean domains based on spectral graph theory. GCN is an effective method for capturing spatial correlation in non-Euclidean structures, which can capture local correlations well and maintain shift-invariance [25]. With this advantage, GCN has been gradually applied to spatial modeling in various fields (e.g., traffic road networks).
We describe how GCN extracts spatial correlations from FCMN by employing graph convolution (GC) operations. Structurally, the GCN constructs a filter in the Fourier domain that can act on the nodes of the FCMN and their first-order neighbors to capture the spatial features between the nodes. For any node in FCMN, the GCN can capture the topological relationship between it and its surrounding nodes. Furthermore, the GCN model can encode the topological structure of FCMN and the attributes on the nodes (i.e., displacement of each node). The structure of the GCN is illustrated in Fig. 3. A GCN can stack multiple layers to model higher-order neighborhood interactions in the graph [14]. The propagation rule of the GCN can be expressed as Eq. (4).
where \(H^{(l)} \in R^{N \times P}\) is a node-level output, \(W^{(l)}\) is a weight matrix for the l-th neural network layer, and \(\sigma (\cdot )\) is a nonlinear activation function such as the ReLU. A represents the adjacency matrix, refers to the preprocessing step and denotes taking the average of neighboring node features. \({\hat{A}}=A+I\) is a matrix with a self-connection structure, where I is the identity matrix, and \({\hat{D}}\) is the diagonal node degree matrix of \({\hat{A}}\), i.e., \({\hat{D}}=\sum _{j} {\hat{A}}_{i j}\).
2.4.2 Use of the gated recurrent units (GRU)
In this section, we introduce how to use GRU to capture the temporal correlation from the sequence of feature matrix X.
GRU is a variant of the recurrent neural networks (RNN) and is commonly utilized to analyse time-series data and capture their long-term time correlation. Similar to the RNN structure, GRU has a sequential stepping mechanism, in which the output of the previous unit is used as part of the input of the current unit, thus allowing information to be passed step by step. Using a gating mechanism, GRU made improvements to address the problem of vanishing or exploding gradients in RNN [6]. GRU utilizes the so-called update gate and reset gate to store as much information as possible for as long as possible [10, 26]. Compared to other variants (e.g., LSTM), GRU has a simpler structure and therefore involves fewer parameters, making the training efficient and faster.
The structure of the GRU is illustrated in Fig. 3. Given the current timestep feature matrix \(x_{t}\) as input, \(h_{t-1}\) denotes a hidden state of the previous time step \(t-1\). \(r_{t}\) is the reset gate, which is used to determine the degree of ignoring the status information at the previous moment. \(u_{t}\) is the update gate, which is used to determine how much of the past information at the previous time is passed along to the current status. is a candidate hidden state, that represents the intermediate memory. The governing equations of the GRU can be expressed as Eq. (5).
where the parameters W and b are the weights and deviations in the training process, respectively. The symbol \({\odot }\) indicates pointwise multiplication between tensors. Tanh denotes the hyperbolic tangent function to ensure that the values of the hidden states remain in the interval (\(-1\),1).
2.4.3 Use of temporal graph convolutional network (T-GCN)
To capture the spatial and temporal correlations from the established FCMN at the same time, we employ a T-GCN model. The T-GCN model is a deep learning architecture, including the 2-layer GCN and GRU, which takes the weighted adjacency matrix \(A{}_{\mathrm{w}}\) and feature matrix X as input [58]. Figure 4 illustrates the specific structure of a T-GCN cell and the process of spatiotemporal displacement prediction.
The process of spatiotemporal displacement prediction based on Temporal Graph Convolutional Network (T-GCN). GC represents graph convolution. \(A_{\mathrm{w}}\) represents the weighted adjacent matrix (see Fig. 2)
First, the GCN is used to capture spatial correlation in the FCMN. Here, the graph convolution processes in the 2-layer GCN are represented as f(X, A).
where \(W{}_{0}\) and \(W{}_{1}\) denote the weight matrix in the first two layers; \({\hat{A}}=A+I\) is a matrix with a self-connection structure, where I is the identity matrix and \({\hat{D}}\) is the diagonal node degree matrix of \({\hat{A}}\), i.e., \({\hat{D}}=\sum _{j} {\hat{A}}_{i j}\); \(\sigma (\cdot )\) is a nonlinear activation function such as the ReLU.
Second, the matrix multiplications in the GRU are replaced with the graph convolution (GC). The specific calculation process is expressed as Eq. (7).
where the spatial features of the time step t are denoted as \(f\left( X_{t}, A\right) \) and inputted to the GRU; parameters W and b are the weights and deviations, respectively, in the training process; the symbol \(\mathrm {\odot }\) indicates pointwise multiplication between tensors; Tanh denotes the hyperbolic tangent function to ensure that the values of the hidden states remain in the interval (-1,1).
2.5 Step 4: data application
Slope displacement prediction should be considered as a spatiotemporal prediction task due to its spatial and temporal correlations.
First, the temporal correlation needs to be carefully considered in the prediction of slope displacement for the following reasons. As time passes, a slope continually deforms under the control of local geological conditions, including geomorphology and geological structures, which is mainly reflected in its displacement trend [4]. Typically, displacements exhibit an approximately monotonically increasing function on larger time scales due to the combined effect of the weight of the slope or continuous external forces that persist on the slope for a longer period of time. Displacements increase dramatically before complete destruction [21, 50].
Second, the spatial correlation needs to also be considered in the prediction of slope displacement for the following reasons. Neighboring points tend to have similar displacement trends in an entire monitoring system [55]. This phenomenon implies that the spatial correlation of displacement trends can be influenced by the topological structure of the monitoring system that is deployed on the slope. A reasonable explanation is that the closer the monitoring points are, the more similar their geographic and geological conditions are.
In summary, the objective of this paper is to predict the holistic slope deformation by considering both the spatial and temporal correlations based on the acquired time-series displacement data collected from an entire monitoring system.
3 Results: a real case
In this section, we apply the proposed method to a real-world dataset collected from a monitoring system and evaluate the results.
3.1 Data description
The real case is situated in Dongsheng Coal Field, Ordos, Inner Mongolia, China, where the main coal-bearing strata are part of the middle and lower sections of the Yan’an Group, which are Jurassic deposits. No faults or intrusive magnetite have been found in the mine. According to 2017 Annual Report from the Ordos Municipal Government, the annual coal production of Dongsheng Coalfield amounted to 61.31 million tons. Surface displacements are triggered by mining.
The installation of monitoring devices in the region began in April 2011 to measure the displacements. The monitoring system contains four control points and monitored with GPS receiver. Considering data integrity, we selected 59 monitoring points from the entire monitoring system and collected 9 months of data ranging from May 8th, 2011, to February 12th, 2012, for the displacement prediction. Figure 5 illustrates the layout of the selected monitoring points, which constitute three crossed monitoring lines. Monitoring points R01 \(\mathrm {\sim }\) R24 constitute the R-line, monitoring points A01 \(\mathrm {\sim }\) A18 constitute the A-line, and monitoring points B01 \(\mathrm {\sim }\) R18 constitute the B-line. On each line, the distance between two adjacent points is 20 m. Due to a midway failure at the monitoring device located at point B08, displacement data were collected from a total of 59 monitoring points. The frequency of measurements was once a week. The dataset was also aggregated into a week interval. The dataset contained 29 records for each monitoring device. It should be noted that the last three records were the results of a monthly test.
3.2 Predication of the spatiotemporal displacement
In this section, we use the proposed method to predict displacement based on the real dataset. First, we describe the manipulation of the acquired real dataset. Second, we analyse the spatial correlation of the dataset. Third, we present the metrics for evaluating the prediction model. Finally, we analyse the prediction results.
3.2.1 Data manipulation
We divided the dataset into two parts for manipulation. For spatial correlation data, we connected 59 monitoring points according to the FCMN construction method described above to obtain a 59 \(\times \) 59 weighted adjacency matrix \(A{}_{\mathrm{w}}\), which depicts the spatial relationship between monitoring points in a graphical structure. The values in the matrix represent the similarity among the monitoring points. For time correlation data, we used the Euclidean norm \(\Vert \varvec{x}\Vert _{2}:=\sqrt{x^{2}+y^{2}+z^{2}}\) to integrate the three directions (x, y, z) data collected by GPS into a single displacement value, and constructed a feature matrix X with a size of 59 \(\times \) 29, which represents the displacement of each point over time. Each row is one monitoring point; each column is the displacement value based on the measured frequency.
Furthermore, we performed data preprocessing. First, we set the data interval to once a week and use linear interpolation to handle missing values that appear in the last three months of data. Therefore, the size of the feature matrix changes to 59 \(\times \) 41. Second, we apply the min-max normalization method to scale the displacement values in the range of [0, 1], according to \(x=(x-\min ) /(\max -\min )\). Finally, 70% of data is used for training, and the remaining 30% is used for testing.
3.2.2 Analysis of the spatial correction in the displacement data
We analyzed the dataset was not yet been preprocessed to determine the spatial correlation among the monitoring points. First, we compared the displacement trends of the first point (i.e., R01, A01, B01) in the three monitoring lines. Second, we compared the displacement trends of the first and last points in each monitoring line separately. Then, we compared the displacement trends of neighboring points from the two intersecting regions in the three monitoring lines. Finally, we compared the displacement trends of three sets of nodes (R01 \({\sim }\) R05, R16 \({\sim }\) R17, and R20 \({\sim }\) R24) in the R-line.
The displacement trends of R01, A01, and B01 are illustrated in Fig. 6. Although the three points R01, A01, and B01 are relatively farther away in the monitoring system layout, the displacement trends appeared largely consistent implying a strong spatial correlation among them. The most pronounced variation within several points is R01. One explanation for this is that mining induces perturbation.
The spatial correlation between the two farthest points in the entire monitoring system for each line (i.e., R01 and R24, A01 and A18, B01 and B18) is illustrated in Fig. 7. The A-line and B-line exhibit a strong spatial correlation, which is reflected by the remarkable similarity in displacement trends and displacements between the two farthest points for each line. One explanation for this is that both lines have only 18 points, which implies that the distance between the farthest points is relatively short. The displacements of R24 were substantially larger than those of R01 from August 2011 until October 2011, and then the displacement trends of both points became similar again.
The displacement trends in the two intersecting regions of the three monitoring lines are illustrated in Fig. 8. In the first intersecting region, the displacement trends at the four neighboring points are almost identical, and their displacements are relatively large. In the second intersecting region, point R24 on the R-line and two points on the B-line exhibit different displacement trends. However, the two neighboring points B09 and B10 on the B-line, are almost identical.
The displacement trends of the three sets of monitoring points on the R-line, which is the longest monitoring line, are illustrated in Fig. 9. The displacement trends from the first set of monitoring points (R01, R02, R03, R04, R05) exhibit remarkable similarities that imply a strong spatial correlation among them. Apparently, R05 has a larger displacements. The displacement trends from the second set of monitoring points (R16 and R17) that are randomly selected in the middle of the monitoring line are almost identical. Similarly, the displacement trends from the third set of monitoring points (R20, R21, R22, R23, R24) exhibit remarkable similarities implying a strong spatial correlation among them.
3.2.3 Evaluation metrics of prediction
We evaluate the model performance based on two metrics: (1) Mean absolute error (MAE) and (2) Mean absolute scaled error (MASE).
MAE is the mean absolute error produced by the actual prediction. A smaller MAE value means better performance in the prediction model (see Eq. (8)).
where \(Y_{t}\) and \({\widehat{Y}}_{t}\) denote the actual and predicted displacements.
MASE was substituted for the use of percentage error in evaluating the accuracy of time-series predictions [30]. For time-series data, it is typical to scale the errors using a simple prediction [see Eq. (9)].
where the numerator \(e_{j}\) is the prediction error for a given period, defined as the actual value \(Y_{t}\) minus the actual value from the prior period as the prediction \(Y_{t-1}\): \(e_{j}=Y_{t}-Y_{t-1}\). An important threshold for MASE is 1. MASE \(\mathrm {=}\) 1 implies that the model has the same MAE as a naive prediction (the metric is \(e_{j}\)). MASE \(\mathrm {>}\) 1 implies that the actual prediction does worse than a naive prediction. MASE \(\mathrm {<}\) 1 implies that the actual prediction is better than the naive prediction.
3.2.4 Predicted results
The prediction process includes the determination of model parameters and model training, as well as model performance evaluation. The hyperparameters of the model include the learning rate, batch size, training period, and number of hidden layers. We set the learning rate to 0.01, the batch size to 64, and the training period to 1000. Given the small sample size of our model, there is only one hidden layer with 100 hidden units. We use ReLU as the activation in the GCN and employ the Adam optimizer for minimizing the loss function [33]. All neural network-based approaches are implemented using TensorFlow [1]. The training process of the model was performed on a laptop equipped with the Intel Core i7-8550U CPU and 8 GB of RAM. The input set we used consisted of 5 historical records that were used to predict the displacement over the next 4 weeks.
It should be noted that we used two datasets. One dataset was the uninterpolated dataset Dataset_1; and the other dataset was the interpolated dataset Dataset_2. In Dataset_1, we sampled only the first 26 weeks of data; its feature matrix shape was (59 \(\times \) 26). The feature matrix shape of Dataset_2 was (59 \(\times \) 41). We compared the performance of the model in both datasets. The results are listed in Table 1.
As illustrated in Table 1, the uninterpolated dataset performs better than the interpolated dataset in terms of evaluation metrics. The MASE of the uninterpolated dataset is less than 1, while the interpolated dataset is more than 1.
We focused on the predicted displacement trends based on the displacement data collected from the entire monitoring system, and compared these trends with the observed trends as follows.
The predicted results of Dataset_1 are illustrated in Fig. 10. On 13th November 2011, several monitoring points (R19, R20, R21, R22, R23, R24) had larger measured displacements than the predicted results. On 20th November 2011, the measured displacement of several monitoring points decreased. At the time, their predicted results were similar to the measured displacements. For most points in the entire monitoring system, the prediction results were similar to the measured displacements, which indicates that the results of the prediction of the proposed method were effective. Moreover, the spatial distribution of displacement changes was consistent for the entire monitoring system.
The predicted results of Dataset_2 are illustrated in Fig. 11. Excluding the anomalies in the prediction result at point R11, the spatial distribution of displacement changes is consistent for the entire monitoring system. The prediction results are usually larger than measured displacements.
4 Discussion
The predicted results demonstrate the effectiveness of our proposed method of using deep learning to predict slope deformation based on time-series displacement data. The following section discusses its advantages and some problems and how it can be improved to address the shortcomings.
4.1 Advantage of the proposed deep learning method
The advantage of the proposed method is to consider the spatial correlation of slope displacement predictions. More specifically, in this paper, we consider the spatial correlation of the entire monitoring system and propose a novel method that can predict the displacement of all points with graph-structured data instead of the traditional single point time-series data as input.
To the best of the authors’ knowledge, there is currently no related research work focusing on addressing the prediction of the monitoring system from a holistic perspective. In this paper, we represent the spatial correlation of the entire monitoring system using FCMN and capture its spatial correlation using GCN, which is a state-of-the-art deep learning model. The holistic analysis can predict the deformation based on data collected from the entire monitoring system over time. In addition, the method eliminates the need to select monitoring points, thus increasing efficiency and saving time. It also avoids the selection of a few monitoring points at the expense of others that may pose a potential threat.
4.2 Shortcoming of the proposed deep learning method
The shortcoming of this paper is that the employed displacement datasets are limited. The frequency with which we acquired the datasets was with a weekly; hence, there were only 26 weeks of data. According to the prediction results, for the small sample, a typical interpolation method could deteriorate the performance of the prediction results of the model. Additionally, we did not factor in external influences. When the slope is influenced by irregular factors, e.g., human activities, it may interfere with the predicted results.
4.3 Outlook and future work
In the future, we plan to (1) evaluate the applicability of the proposed deep learning method in other geohazard scenarios for spatiotemporal predictions based on time-series data from an entire monitoring system containing multiple points, (2) handle limited datasets from monitoring systems using different approaches to meet prediction requirements, and (3) consider the effect of influencing factors to extend our method that can learn the correlations between abnormal events and displacement change. Moreover, we will primarily focus on handling small sample datasets.
Limited datasets in geohazard domains might be a prevalent phenomenon. In practice, for some countries or regions, the collection of large geohazard datasets proves to be costly or impracticable. As a consequence, there is often no choice except to utilize a limited dataset with the attempt to achieve as accurate a prediction as possible. For example, a time series analysis may be performed with only records for a specific time period.
Several solutions have emerged in other domains for these limited datasets, including data augmentation, synthetic data, and transfer learning. First, data augmentation refers to increasing the number of data points without changing the data label. For time-series data, variability factors including random noise and active time features can be introduced to increase the length of the time-series [46]. Second, synthetic data are fake data that contain the same patterns and statistical properties as real data. For example, a deep learning model called generative adversarial networks (GAN) can be utilized to generate synthetic data. Finally, transfer learning refers to a framework for using existing relevant data or models in the construction of new models. Transfer learning techniques are useful on the ground that they enable the model to make predictions about new domains or tasks (called target domains) using knowledge learned from another dataset or from an existing model (source domain).
5 Conclusion
In this paper, by considering the spatial correlations between all points in the entire displacement monitoring system, we proposed a novel deep learning method for predicting the slope deformation. The essential idea behind the proposed method is to predict the slope deformation based on the global information (i.e., the correlated displacements of all points in the entire monitoring system), rather than based on the local information (i.e., the displacements of a specified single point in the monitoring system). In the proposed method, (1) a weighted adjacency matrix is built to interpret the spatial correlations between all points; (2) a feature matrix is assembled to store the time-series displacements of all points; (3) one of the state-of-the-art deep learning models, i.e., T-GCN, is developed to process the above graph-structured data consisting of two matrices. To evaluate the effectiveness of the proposed method, we performed predictions based on a real dataset. The results show that: (1) the predicted displacement values for most of the monitoring points are close to the measured displacement values, which verifies the effectiveness of the proposed method; (2) the smaller the measured displacement value, the closer the prediction is to the measured value; and (3) the trend in the spatial distribution of the displacement of the monitoring system remains substantially similar over the different periods of the prediction. Future work is planned to achieve better results for a sufficient sized dataset.
Abbreviations
- ANN:
-
Artificial neural networks
- DBN:
-
Deep belief network
- ELM:
-
Extreme learning machine
- FCMN:
-
Fully connected monitoring network
- GAN:
-
Generative adversarial networks
- GBSAR:
-
Ground-based synthetic-aperture Radar
- GCN:
-
Graph convolutional networks
- GP:
-
Gaussian process
- GPS:
-
Global positioning system
- GRU:
-
Gated recurrent units
- LiDAR:
-
Light detection and ranging
- LSTM:
-
Long short term memory
- RNN:
-
Recurrent neural networks
- SMOTE:
-
Synthesizing minority oversampling Techniques
- SVM:
-
Support vector machine
- T-GCN:
-
Temporal graph convolution networks
References
Abadi M, Agarwal A, Barham P, Brevdo E, Chen Zhifeng aro C, Corrado G, Davis A, Dean J, Devin M, Ghemawat S, Goodfellow I, Harp A, Irving G, Isard M, Jia Y, Kaiser L, Kudlur M, Levenberg J, Zheng X (2016) Tensorflow: large-scale machine learning on heterogeneous distributed systems. arXiv preprint arXiv:1603.04467
Abedjan Z, Golab L, Naumann F (2017) Data profiling—a tutorial. In: Proceedings of the 2017 ACM international conference on management of data (SIGMOD '17). Association for Computing Machinery, New York, NY, USA, pp 1747–1751. https://doi.org/10.1145/3035918.3054772
Afan HA, El-shafie A, Mohtar WHMW, Yaseen ZM (2016) Past, present and prospect of an artificial intelligence (AI) based model for sediment transport prediction. J Hydrol 541:902–913. https://doi.org/10.1016/j.jhydrol.2016.07.048
Anantrasirichai N, Biggs J, Kelevitz K, Sadeghi Z, Wright T, Thompson J, Achim A, Bull D (2020) Deep learning framework for detecting ground deformation in the built environment using satellite INSAR data. arXiv preprint arXiv:2005.03221
Atzeni C, Barla M, Pieraccini M, Antolini F (2014) Early warning monitoring of natural and engineered slopes with ground-based synthetic-aperture radar. Rock Mech Rock Eng 48(1):235–246. https://doi.org/10.1007/s00603-014-0554-4
Bengio Y, Simard P, Frasconi P (1994) Learning long-term dependencies with gradient descent is difficult. IEEE Trans Neural Netw 5(2):157–166. https://doi.org/10.1109/72.279181
Benoit L, Briole P, Martin O, Thom C, Malet JP, Ulrich P (2015) Monitoring landslide displacements with the geocube wireless network of low-cost GPS. Eng Geol 195:111–121. https://doi.org/10.1016/j.enggeo.2015.05.020
Casagli N, Frodella W, Morelli S, Tofani V, Ciampalini A, Intrieri E, Raspini F, Rossi G, Tanteri L, Lu P (2017) Spaceborne, UAV and ground-based remote sensing techniques for landslide mapping, monitoring and early warning. Geoenviron Disasters 4:9–23. https://doi.org/10.1186/s40677-017-0073-1
Chen H, Qin S, Xue L, Yang B, Zhang K (2018) A physical model predicting instability of rock slopes with locked segments along a potential slip surface. Eng Geol 242:34–43. https://doi.org/10.1016/j.enggeo.2018.05.012
Cho K, van Merriënboer B, Bahdanau D, Bengio Y (2014) On the properties of neural machine translation: encoder–decoder approaches. arXiv preprint arXiv:1409.1259. https://doi.org/10.3115/v1/W14-4012
Cho SE (2017) Prediction of shallow landslide by surficial stability analysis considering rainfall infiltration. Eng Geol 231:126–138. https://doi.org/10.1016/j.enggeo.2017.10.018
Crosta G, Agliardi F (2003) Failure forecast for large rock slides by surface displacement measurements. Can Geotech J 40(1):176–191. https://doi.org/10.1139/t02-085
Dikshit A, Satyam DN, Towhata I (2018) Early warning system using tilt sensors in Chibo, Kalimpong, Darjeeling Himalayas, India. Nat Hazards 94(2):727–741. https://doi.org/10.1007/s11069-018-3417-6
Duvenaud D, Maclaurin D, Aguilera-Iparraguirre J, Gómez-Bombarelli R, Hirzel T, Aspuru-Guzik A, Adams R (2015) Convolutional networks on graphs for learning molecular fingerprints. Adv Neural Inf Process Syst (NIPS) 13:2224–2232
Eidsvig U, Papathoma-Köhle M, Du J, Glade T, Vangelsten B (2014) Quantification of model uncertainty in debris flow vulnerability assessment. Eng Geol 181:15–26. https://doi.org/10.1016/j.enggeo.2014.08.006
Fahimi F, Yaseen ZM, El-shafie A (2017) Application of soft computing based hybrid models in hydrological variables modeling: a comprehensive review. Theor Appl Climatol 128(3–4):875–903. https://doi.org/10.1007/s00704-016-1735-8
Fathani T, Karnawati D, Wilopo W (2016) An integrated methodology to develop a standard for landslide early warning systems. Nat Hazards Earth Syst Sci 13(2):2123–2135. https://doi.org/10.5194/nhess-16-2123-2016
Federico A, Popescu M, Elia G, Fidelibus C, Intern G, Murianni A (2012) Prediction of time to slope failure: a general framework. Environ Earth Sci 66(1):245–256. https://doi.org/10.1007/s12665-011-1231-5
Froude MJ, Petley DN (2018) Global fatal landslide occurrence from 2004 to 2016. Nat Hazards Earth Syst Sci 18(8):2161–2181. https://doi.org/10.5194/nhess-18-2161-2018
Fukuzono T (1985) A method to predict the time of slope failure caused by rainfall using the inverse number of velocity of surface displacement. Landslides 22(2):8–13. https://doi.org/10.3313/jls1964.22.2-8
Fukuzono T (1985) A new method for predicting the failure time of a slope. In: Proceedings of 4th international conference and field workshop on landslide, 1985, pp. 145–150
Geng X, Li Y, Wang L, Zhang L, Yang Q, Ye J, Liu Y (2019) Spatiotemporal multi-graph convolution network for ride-hailing demand forecasting. Proc AAAI Conf Artif Intell 33:3656–3663. https://doi.org/10.1609/aaai.v33i01.33013656
Gentili PL, Gotoda H, Dolnik M, Epstein IR (2015) Analysis and prediction of aperiodic hydrodynamic oscillatory time series by feed-forward neural networks, fuzzy logic, and a local nonlinear predictor. Chaos Interdiscip J Nonlinear Sci 25(1):013104. https://doi.org/10.1063/1.4905458
Glade T, Nadim F (2014) Early warning systems for natural hazards and risks. Nat Hazards 70(3):1669–1671. https://doi.org/10.1007/s11069-013-1000-8
Hammond DK, Vandergheynst P, Gribonval R (2011) Wavelets on graphs via spectral graph theory. Appl Comput Harmon Anal 30(2):129–150. https://doi.org/10.1016/j.acha.2010.04.005
Hochreiter S, Schmidhuber J (1997) Long short-term memory. Neural Comput 9(8):1735–1780. https://doi.org/10.1162/neco.1997.9.8.1735
Huang F, Huang J, Jiang S, Zhou C (2017) Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng Geol 218:173–186. https://doi.org/10.1016/j.enggeo.2017.01.016
Huang F, Yin K, He T, Zhou C, Zhang J (2016) Influencing factor analysis and displacement prediction in reservoir landslides—A case study of three gorges reservoir (China). Technical Gazette 23(2):617–626. https://doi.org/10.17559/TV-20150314105216
Huang F, Zhang J, Zhou C, Wang Y, Huang J, Zhu L (2020) A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 17(1):217–229. https://doi.org/10.1007/s10346-019-01274-9
Hyndman RJ, Koehler AB (2006) Another look at measures of forecast accuracy. Int J Forecast 22(4):679–688. https://doi.org/10.1016/j.ijforecast.2006.03.001
Jiang P, Chen J (2016) Displacement prediction of landslide based on generalized regression neural networks with k-fold cross-validation. Neurocomputing 198:40–47. https://doi.org/10.1016/j.neucom.2015.08.118
Kavzoglu T, Sahin EK, Colkesen I (2014) Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 11(3):425–439. https://doi.org/10.1007/s10346-013-0391-7
Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980
Lacasse S, Nadim F (2009) Landslide risk assessment and mitigation strategy. In: Sassa K, Canuti P (eds) Landslides – disaster risk reduction. Springer, Berlin, Heidelberg, pp 31–62. https://doi.org/10.1007/978-3-540-69970-5-3
Li H, Xu Q, He Y, Fan X, Li S (2020) Modeling and predicting reservoir landslide displacement with deep belief network and EWMA control charts: a case study in three gorges reservoir. Landslides 17(3):693–707. https://doi.org/10.1007/s10346-019-01312-6
Lian C, Zeng Z, Yao W, Tang H (2015) Multiple neural networks switched prediction for landslide displacement. Eng Geol 186:91–99. https://doi.org/10.1016/j.enggeo.2014.11.014
Liu Y, Zhang YX (2014) Application of optimized parameters SVM in deformation prediction of creep landslide tunnel. Appl Mech Mater (Trans Tech Publ.) 675:265–268. https://doi.org/10.5194/nhessd-1-5295-2013
Liu Z, Shao J, Xu W, Chen H, Shi C (2014) Comparison on landslide nonlinear displacement analysis and prediction with computational intelligence approaches. Landslides 11(5):889–896. https://doi.org/10.1007/s10346-013-0443-z
Ma J, Tang H, Liu X, Hu X, Sun M, Song Y (2017) Establishment of a deformation forecasting model for a step-like landslide based on decision tree c5. 0 and two-step cluster algorithms: a case study in the three gorges reservoir area, China. Landslides 14(3):1275–1281. https://doi.org/10.1007/s10346-017-0804-0
Ma Z, Mei G, Piccialli F (2020) Machine learning for landslides prevention: a survey. Neural Comput Appl. https://doi.org/10.1007/s00521-020-05529-8
Mei G, Xu N, Qin J, Wang B, Qi P (2020) A survey of internet of things (IOT) for geohazard prevention: applications, technologies, and challenges. IEEE Internet Things J 7(5):4371–4386. https://doi.org/10.1109/JIOT.2019.2952593
Miao F, Wu Y, Xie Y, Li Y (2018) Prediction of landslide displacement with step-like behavior based on multialgorithm optimization and a support vector regression model. Landslides 15(3):475–488. https://doi.org/10.1007/s10346-017-0883-y
Park D, Michalowski RL (2017) Three-dimensional stability analysis of slopes in hard soil/soft rock with tensile strength cut-off. Eng Geol 229:73–84. https://doi.org/10.1680/jgeot.16.P.037
Piccialli F, Giampaolo F, Casolla G, Cola V, Li K (2020) A deep learning approach for path prediction in a location-based IOT system. Pervasive Mobile Comput 66:115–120. https://doi.org/10.1016/j.pmcj.2020.101210
Piccialli F, Somma V, Giampaolo F, Cuomo S, Fortino G (2021) A survey on deep learning in medicine: Why, how and when? Inf Fusion 66:111–137. https://doi.org/10.1016/j.inffus.2020.09.006
Rashid K, Louis J (2019) Times-series data augmentation and deep learning for construction equipment activity recognition. Adv Eng Inform 42:1–12. https://doi.org/10.1016/j.aei.2019.100944
Rawat M, Joshi V, Rawat M, Kumar K (2011) Landslide movement monitoring using GPS technology: a case study of Bakthang landslide, Gangtok, East Sikkim, India. J Dev Agric Econ 3(5):194–200
Segalini A, Valletta A, Carri A (2018) Landslide time-of-failure forecast and alert threshold assessment: a generalized criterion. Eng Geol 245:72–80. https://doi.org/10.1016/j.enggeo.2018.08.003
Segoni S, Battistini A, Rosi A, Catani F, Moretti S, Casagli N, Lagomarsino D, Rossi G (2015) Technical note: An operational landslide early warning system at regional scale based on space-time-variable rainfall thresholds. Nat Hazards Earth Syst Sci 15:853–861. https://doi.org/10.13140/RG.2.1.1683.4087
Voight B (1988) A method for prediction of volcanic eruptions. Nature 332(6160):125–130. https://doi.org/10.1038/332125a0
Von Luxburg U (2007) A tutorial on spectral clustering. Stat Comput 17(4):395–416. https://doi.org/10.1007/s11222-007-9033-z
Wu LC, Kuo C, Loza J, Kurt M, Laksari K, Yanez LZ, Senif D, Anderson SC, Miller LE, Urban JE et al (2017) Detection of American football head impacts using biomechanical features and support vector machine classification. Sci Rep 8(1):1–14. https://doi.org/10.1038/s41598-017-17864-3
Wu Y, Niu R, Lu Z (2019) A fast monitor and real time early warning system for landslides in the Baige landslide damming event, Tibet, China. Nat Hazards Earth Syst Sci Discuss. https://doi.org/10.5194/nhess-2019-48
Xu S, Niu R (2018) Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short-term memory neural network in three Gorges area, China. Comput Geosci 111:87–96. https://doi.org/10.1016/j.cageo.2017.10.013
Yang B, Yin K, Lacasse S, Liu Z (2019) Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 16(4):677–694. https://doi.org/10.1007/s10346-018-01127-x
Yaseen ZM, El-Shafie A, Jaafar O, Afan HA, Sayl KN (2015) Artificial intelligence based models for stream-flow forecasting: 2000–2015. J Hydrol 530:829–844. https://doi.org/10.1016/j.jhydrol.2015.10.038
Yaseen ZM, Sulaiman SO, Deo RC, Chau KW (2019) An enhanced extreme learning machine model for river flow forecasting: state-of-the-art, practical applications in water resource engineering area and future research direction. J Hydrol 569:387–408. https://doi.org/10.1016/j.jhydrol.2018.11.069
Zhao L, Song Y, Zhang C, Liu Y, Wang P, Lin T, Deng M, Li H (2019) T-GCN: a temporal graph convolutional network for traffic prediction. IEEE Trans Intell Transp Syst. https://doi.org/10.1109/TITS.2019.2935152
Zhou C, Yin K, Cao Y, Intrieri E, Ahmed B, Catani F (2018) Displacement prediction of step-like landslide by applying a novel kernel extreme learning machine method. Landslides 15(11):2211–2225. https://doi.org/10.1007/s10346-018-1022-0
Zhu X, Xu Q, Tang M, Nie W, Ma S, Xu Z (2017) Comparison of two optimized machine learning models for predicting displacement of rainfall-induced landslide: a case study in Sichuan province, China. Eng Geol 218:213–222. https://doi.org/10.1016/j.enggeo.2017.01.022
Zhu ZW, Liu DY, Yuan QY, Liu B, Liu JC (2011) A novel distributed optic fiber transduser for landslides monitoring. Opt Lasers Eng 49(7):1019–1024. https://doi.org/10.1016/j.optlaseng.2011.01.010
Zou Z, Yang Y, Fan Z, Tang H, Zou M, Hu X, Xiong C, Ma J (2020) Suitability of data preprocessing methods for landslide displacement forecasting. Stoch Environ Res Risk Assess 34:1105–1119. https://doi.org/10.1007/s00477-020-01824-x
Acknowledgements
This research was jointly supported by the National Natural Science Foundation of China (Grant Nos. 11602235 and 41772326), the Fundamental Research Funds for China Central Universities (2652018091), and Major Program of Science and Technology of Xinjiang Production and Construction Corps (2020AA002). The authors would like to thank the editor and the reviewers for their helpful comments and suggestions.
Funding
Open access funding provided by Università degli Studi di Napoli Federico II within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Please note that a preprint version of this paper has been posted on TechRxiv at: https://doi.org/10.36227/techrxiv.12987995.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ma, Z., Mei, G., Prezioso, E. et al. A deep learning approach using graph convolutional networks for slope deformation prediction based on time-series displacement data. Neural Comput & Applic 33, 14441–14457 (2021). https://doi.org/10.1007/s00521-021-06084-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-021-06084-6