Abstract
Modern medical clinics support medical examinations with computer systems which use Computational Intelligence on the way to detect potential health problems in more efficient way. One of the most important applications is evaluation of CT brain scans, where the most precise results come from deep learning approaches. In this article, we propose a novel correlation learning mechanism (CLM) for deep neural network architectures that combines convolutional neural network (CNN) with classic architecture. The support neural network helps CNN to find the most adequate filers for pooling and convolution layers. As a result, the main neural classifier learns faster and reaches higher efficiency. Results show that our CLM model is able to reach about 96% accuracy, and about 95% precision and recall. We have described our proposed mechanism and discussed numerical results to draw conclusions and show future works.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Medical clinics offer many options to support patients in detection of health problems. Recent advances in computer research brought many new ideas in the field of automated medical support systems. We can notice that clinics are equipped with new devices. New microscopes are used to observe tissues and organs. Multimedia systems help in examinations. Results of screenings and scans are evaluated on monitors which provide high-quality presentation helpful in detailed examinations.
One of the recent fields where computer science is much helpful is radiography or more precisely various forms of RTG and CT screening systems. Among these, brain and lung problems are very important diseases in which faster detection may efficiently benefit from Computational Intelligence models. In [16] was presented how beneficial in robust examination can be a diagnosis based on these methods for treatment of lung and brain metastases, while [10] discussed importance of neuroimaging in brain injury examination and Sheng et al. [36] proposed a system for retina diagnosis. Computer methods applied in medical imaging have two main directions in recent years. One is segmentation of organs from images which helps medicians to concentrate on symptoms, where convolutional neural networks are among the best efficient structures [46]. The second is automated diagnose which gives medicians an additional advice about symptoms to consult. CT scans of head organs are used in various examinations. Therefore we can find many devoted computer methods developed in such fields. In [39] was discussed how to extract midsagittal plane from CT scans of head for facial surgery. Various image completion methods can be used to improve CT registration as presented in Zheng et al. [48]. Another important aspect is to extract tissues which need detailed examination. In this task also computer systems can efficiently help medicians. In [1] was proposed a new and fast brain extraction from CT scans, while derivative of hemorrhage computer segmentation of CT scans was proposed in Ray et al. [30].
Complex neural models are trained to serve as precise advisors in IoT for medical purposes and smart environments. There are many interesting survey papers discussing advances. In [8, 38] was discussed big data analytics approach based on machine learning. Challenges for the development of new models were defined in Lv et al. [23], one of the most important aspect was improved learning model for complex neural architectures. For healthcare and vision systems, as important aspect for the development, was also defined improvement in their construction for image processing [43, 47].
1.1 Related works
Recent years brought new possibilities for Artificial Intelligence. New computer architectures are making it possible to implement complex structures which learn to detect, extract and recognize medical symptoms of dangerous diseases. In [19] was presented a thresholding approach used to train convolutional neural network (CNN) for brain hemorrhages detection from CT scans. Deep learning also serves as predictor in medical examinations of infarct brain volume [32] and online stroke detection [12]. Deep learning is also used in vision assistance [18] and image watermarking [22]. Moreover, it was also shown in Mostapha and Styner [24] that deep learning techniques may have an impact on medical examinations of humans in various age, also in an infant time. Bhandary et al. [2] presented a deep learning framework for CT-based detection.
Among applications of deep learning in medical systems very important are lung scan estimation and brain disorders detection. Interesting studies presenting catalogs of recent approaches were Hu et al. [17] for cancer detection and Chilamkurthy et al. [7] for disorders of head organs. Deep learning techniques are very often used in detection of malfunctions in these two parts of human bodies. Lakshmanaprabu et al. [20] discussed a composition of deep learning model for optimal detection of lung cancer, while in Capizzi et al. [3] we have presented our approach to efficient detection of lung nodules based on fusion of fuzzy rules and probabilistic neural network (PNN). Application of Artificial Intelligence to brain scans is sometimes more difficult since brain CT scan gives much more information. Thus, applied methods are more complex, and the process to extract tissues and to find symptoms of brain disorders is demanding. Deep learning can be used for classification of various brain disorders from CT scans as proven in Gao et al. [13]. Cherukuri et al. [6] discussed how to make segmentation sourced in learning algorithm to detect hydrocephalic malfunctions. In Özyurt et al. [28], deep learning based on convolutional neural network was combined with fuzzy entropy function to stimulate brain tumor detection. In Deepak and Ameer [9], the idea of deep learning for brain tumors detection from CT scans was combined with transfer learning, and that helped to shorten the training time. In Zeng and Tian [44] was proposed an efficient strategy to accelerate structures of convolutional neural networks by reducing unimportant inter-spatial and inter-kernel relations, which helped to speed-up the process of recognition. Different propositions of acceleration were developed for incomplete data or special types of images. In Liu et al. [21] was presented an acceleration technique for images without equivalent labeling from medical examinations, while in Nie et al. [27] a model for infant brain imaging was presented. An improved CNN was used for isotense segmentation. Deep learning models are also developed for IoT interfaces as presented in Xu et al. [42] and Dourado et al. [11], where patients with particular symptoms were analyzed. A broad survey on various implementations of brain tumors detection was presented in Sarmento et al. [33] and Muhammad et al. [25] for intelligent medical health care units.
In this article, we present our novel approach based on combination of convolutional neural network (CNN) with classic neural network (ANN). Proposed novel system is composed in the way that CNN is learning how to use adequate filtering in pooling and convolution layers from classic Neural Network. ANN evaluates results received from CNN and store them in archives, from which the configurations are used in next iterations to improve CNN processing. In this way, we have developed a novel correlation learning mechanism (CLM) which improves the work of CNN by robust selection of the most efficient filtering on the way to precisely detect brain tumors.
2 Proposed model of the developed correlation learning mechanism
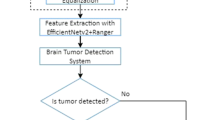
The proposed model of correlation learning mechanism (CLM) is composed of convolutional neural network co-working in training process with classic neural network (ANN). Both neural architectures compose a structure which is learning how to evaluate CT brain scans while exchanging information in the form of palettes of filters for CNN and numerical values describing evaluated image for ANN. The whole idea of CLM is presented in Fig. 1.
2.1 Input to the system
The input CT brain scan image is segmented into 64 squared fragments. This number fits our cpu architecture, where each of fragments can be processed on one core/thread. Also this number in our initial research helped to maintain balance between the speed of learning and the diversity of filter mixing.
2.2 CNN architecture
Each of segments is forwarded to CNN, which is performing filtering operations. For the first iteration of the proposed CLM, we randomly select filters from the pool, while in each next iteration the filters are selected for composed palettes by the developed mechanism. The set of filters used in CLM is presented in Table 1. Size of each applied filter is selected by us empirically in the research experiments to best fit processing and achieve the highest accuracy.
The selected palette is used by CNN in each iteration to configure CT scan processing. It is always selected using the archives according to the best results of loss and accuracy values. Each palette can be understood as a following configuration of CNN part, i.e., the best palette code: [4; 4], c[1; 11; 6; 3], r, [3; 3], c[52; 0; 1; 8] which mean: [4; 4]—pooling max \(4\times 4\), c[1; 11; 6; 3]—convolutional layer with following filter numbers from Table 1, r—ReLU, [3; 3]—pooling max \(3\times 3\), c[52; 0; 1; 8]—convolutional layer with following filter numbers from Table 1. Thus we can define a palette for CNN as a set of layers, their order, type of applied filters, where and when we have pooling, what kind of pooling, where is ReLU, etc. In developed CNN, the palette is changed to a list of possible image transformations and applied to the architecture before processing. Then each input image is evaluated in terms of: Min, Max, sum, median, arithmetic mean and standard deviation, which compose a CNN output numerical description of the CT input image. These values are presented to ANN together with resulting feature maps. Developed CNN part is presented in Fig. 2.
2.3 ANN architecture
At the input of ANN, we have feature maps from convolutional part, which describe the input CT brain scan after transformations and numerical measures of this feature maps represented in statistical values of minimum value, maximum value, arithmetic mean, sum of feature maps impact, median value, and standard deviation value. To improve whole process, CNN does not forward noise or zero values to ANN. Some probability of converting random synapses weights to 0 is also set to avoid over-fitting. There is also slight shuffling between batch data. The network learns from the data. The architecture of hidden ANN part is as follows: \([90]\,[45]\,[10]\,[5]\,[4]\,[2]\), where [] is a layer and the value is the number of neurons. We have selected this architecture empirically in our experiments as the best, since it was the model with the smallest number of layers, which allowed high data compression for the final binary output of ANN. Similarly to previous part of the proposed CLM, the ANN network is a multi-core model for the number of available processor threads. The idea of the data flow in training of ANN classifier is presented in Fig. 3.
2.4 Output of the system
As a result of processing, the CLM returns decision about the input CT scan. Output image is marked by the system to show detected tumors to doctor. Evaluation of the result is done regarding the minimum value of the loss function and the maximum efficiency. Approved palette is stored into the archives, otherwise the new palette composition is performed for CNN and results are recalculated again. The process is performed in fixed number of iterations. In our research experiments, we have set the number of iterations to 120,000. In our initial tests, this number gave the best results for each of input CT scans. In case of recalculation, the best archived palette goes to reshuffling. We have implemented a smart mechanism in which the filter palettes are reshuffled in relation to the results of ANN—the lower ANN efficiency, the more reshuffling we apply to new palettes of CNN.
3 Model development and applied training
3.1 Convolutional neural network
In our system, we have applied CNN model which is using two successive convolution blocks preceded by pooling operations. However, to flatten the final image we used ReLU function between them, as shown in Fig. 2. Because CNN is devoted to image processing, the architecture involves operations on pixels. Pooling operation works to extract features we are searching for. Convolution operation works to improve these results, as visible in sample filtering of CT brain scans in Fig. 7. In our system, we have used two different filter sizes for 17 applied filters presented in Table 1. Convolutional layer is 3-dimensional operator on width, height and depth of the image. The \(\omega\) filter of size \(m\times m\) recalculates color components of the segmented image size \(N\times N\) changing position by step of S pixels. As a result, the size of convolution \(s_{{\textit{output}}}\) relates to the image size
CNN returns feature maps defined for each pixel \(x_{ij}\) on the output of CNN
where \(y^{l-1}\) is pixel value from previous operation on CNN. Pooling basically returns the maximum value of pixels in a grid \(k\times k\), which in our case is \(3\times 3\) for the first block and \(4\times 4\) for the second one. The result of pooling is better extraction of the most important key points. ReLU operation is used to flatten the image in a simple operation of \(\max {0, x}\) for each pixel. As a final output from CNN, we receive the image, which is resized to much smaller with only the highest values of evaluated grids being visible. This kind of simplified image is turned to numerical values forwarded to ANN for detection of brain tumors.
3.2 Neural network
In our research, we have applied ANN composed of 5 hidden layers, input and output, which is shown in Fig. 3. Basically, no matter how many layers we implement in the architecture, the structure of the neural network is similar. The input is receiving vector from CNN where numerical values represent description of segmented CT scan image. Output layer returns decision if brain tumors were detected in the input image or not. Between these, we have hidden layers. Each of them is composed of neurons connected backward and forward with weights scaling the neural signal on each connection. The neuron receives n signals from previous layer neurons \(x_i\) multiplied by the weights \(w_i\) associated with connections which forward their own signal
where \(f_{{\textit{act}}}(e)\) represents activation function. In our CLM model, we used sigmoid unipolar function
whose range is \(\langle 0,1\rangle\) to model decisions about detected (or not detected) brain tumors.
3.3 Back-propagation training algorithm for ANN
The training algorithm is recalculating weights between ANN layers to receive the minimal gradient of the detection error value from cross-entropy function
where y is received value, d is expected value, K—number of neurons on the output, and P—number of samples in training set. In subsequent iterations of the algorithm, weights of connections are recalculated using training dataset. If we define \(w_{mn}\) as a connection weight between neurons \(x_m\) and \(x_n\), the method corrects the weights by propagating back the error value over the network layers. On each of neurons, the received error is a sum of signals from previous ones (from the output side)
where we understand it as a numerical difference between expected and received values, and k represents the number of neurons from previous layer. Using this value, the weights are recalculated in simple equation
where parameter \(\alpha\) controls training speed. At the end of each iteration, the error value is recalculated by Eq. (5). The stop criterion in applied training algorithm is to minimize this value to a certain assumed level. Applied procedure is presented in Algorithm 1.
3.4 Developed multi-threading training model
Proposed CLM was implemented in a parallel form, so that we achieve advance in processing. The more threads we can run on our cpu, the more palettes (configurations of CNN) we can examine in a shorter time. The developed solution is not restricted from the number of threads, so actually the only limit of proposed parallelization is the cpu capacity we can use. Therefore with the development of the latest architectures, our solution will become more and more powerful. Since the calculations are not computationally demanding, it is not necessary to use cpu only. This gives an important advance in case we migrate this solution to gpu, especially to latest architectures developed just for machine learning purposes which have several hundreds of available threads.
The general idea of parallelization is that we generate randomly a set of palettes to be examined. In the first iteration, palettes are generated fully randomly, while in the next iteration we store the best solutions in a database and randomize new palettes for next iterations among them. In this way, on a parallel architecture, we are able to examine a huge variety of configurations to select the best one devoted to our task. The whole idea of parallelization is presented in Fig. 4. From this chart, we can see that before training we create a set of instances, since the ANN training operates also in a parallel manner. The beginning of the algorithm is the division of the input data into fragments. The number of fragments is equal to the number of threads. Ideally, the fragments are of equal size, so the number of input matrices must be divisible by the number of threads. Otherwise, the excess matrix is attached to the initial instances, giving fragments of sizes n and \(n + 1\), where n is the number after total division of the number of input matrices by the number of threads.
The next step is the training loop. At the beginning, n processes are created, where each process has its corresponding piece of data, and common, equal weights of synapses. In the training, each thread changes weights of classifier in a manner adequate to the received data fragment. Then, the processes are merged and synapse weights are averaged by the arithmetic mean. After this step, n processes are again created with new, averaged synapse weights. On their basis, by using forward propagation we create the results of the network for CNN palettes. The one from palettes which gives the highest result is selected and stored in database. For the simplicity, we have assumed that we perform this operations in 100 iterations for each set of instances. However, it is also possible to set a stop criterion in a form of fitness function. This aspect will be further investigated in our next research project. Developed algorithm for multi-threading is presented in Algorithm 2.



Each of the instances is trained by Adam algorithm which performs adaptive moment estimation. This idea has gained many applications due to speed of training and low computational complexity. To train the network, Adam is using 1–2 gradients moments of the error function. In the beginning, we assume that basic formulas of mean and variation are known. Each of coefficients is related to values from previous iteration \(t-1\). The first of formulas is related to the combination of 1st momentum and RMSprop as follows:
where \(\beta\) hyper-parameters are constant in iterations and g represents the value of the error function gradient. Now we calculate correlations of mean and variation \(\hat{m}_t\) and \(\hat{v}_t\) as follows:
which are being used for final weights correction formula in entire network. The equation to recalculate weights \(w_{t}\) is
where \(\eta\) represents applied learning rate and \(\epsilon\) is a constant small value. This method is very efficient since in contrast to other we can recalculate weights in entire network at the same time. The algorithm is presented in Algorithm 3.
Visualization of CNN processing on each of layers from left to right original CT brain scan, pooling, \(\mathrm{pooling}+\mathrm{conv}\), \(\mathrm{pooling}+\mathrm{conv}+\mathrm{pooling}\), \(\mathrm{pooling}+\mathrm{conv}+\mathrm{pooling}+\mathrm{ReLu}\), \(\mathrm{pooling}+\mathrm{conv}+\mathrm{ReLu}+\mathrm{pooling}+\mathrm{conv}\), and \(\mathrm{pooling}+\mathrm{conv}+\mathrm{ReLu}+\mathrm{pooling}+\mathrm{conv}\), respectively
4 Research results
In the research experiments, we have used a dataset Brain MRI Images from Kaggle portal, which was developed for tests on brain tumors detection. In the set, we have 138 scans of healthy patients and 200 scans of patients with tumors. Images are of various quality and size. We have removed from the set images where brain was presented from other perspective and also those with labels and other elements which covered brain tissues, since these were not applicable to our developed computer system. We left in the research set only images which have the very similar outlook as from the typical CT examination in a clinic. As a second dataset, we applied data from [5], where 3064 images present brain tumors: meningioma (708 images), glioma (1426 images), and pituitary (930 images).
4.1 Preprocessing and feature vector composition
All the images used in our research were augmented to improve training process of our proposed CLM model. We have applied some simple augmentation techniques like blur and noise effect. Images were also flipped and shifted to receive the most wide spectrum of training data for our system. Applied augmentation sample results are presented in Fig. 5. Feature vector presented to our CLM model was composed for each of images by using numerical description of image features: min and max values of the pixels. We also used statistical description by median, mean, std. deviation. A model of numerical vector composition is presented in Fig. 6.
4.2 Filtering, feature maps and final detection
For the proposed CNN architecture, we have used filters presented in Table 1. Among all filters developed, CLM system has selected these which give the best result for brain tumor detection. Sample filtering results of these filters on CT scans for healthy patients and patients with brain disorders are presented in Fig. 7. We can see that CLM works well, since filtering results are very well visible in the case of both healthy patients scans (presented in the first two rows) and scans with brain tumors (presented in rows from 3 to 8). Selected filters make tumors more visible in CT images. Therefore other parts of composed CNN architecture can work more efficiently on brain tumors extraction. On the other hand, when no tumors are present, the selected CT scan filters do not extract any tissues of brain, so the final CNN output does not show potential disorders in tissues. That confirms selection of appropriate filters.
As a result of CLM system, the best palette for CNN architecture was composed, see Fig. 2. The developed CLM system has optimized CNN architecture and applied selected filters to construct the best CNN architecture devoted to brain tumors detection as: [4; 4], c[1; 11; 6; 3], r, [3; 3], c[52; 0; 1; 8]. The definition of this palette was presented in Sect. 2. Input CT brain scan processing goes from the optimized CNN architecture in the following steps. As a result of processing the input image, the output of first part feature maps is returned, and sample examples are shown in Fig. 8. This result is forwarded together with statistical measures to ANN, which gives the final decision. Samples of such decision from ANN are presented in Fig. 9. We can see that healthy patients brain tissues were not marked by the system, while images with visible brain tumors (in different sizes from small to big) were correctly detected and the system returned an alert in a form of a red frame on the brain shape. Machine learning metrics for both applied datasets are presented in Table 2. We can see that our developed CLM model metrics reach above 95% accuracy, precision and recall, which prove the value of the developed model. Other metrics show that the proposed model is also very efficient in correct detection of false samples. This is very important in the case of medical system, where applied Computational Intelligence advise on potential treatment, so when the risk of misclassification is reduced, the doctor can better help patients.
In the following charts, we can see a comparison of numerical statistics which describe the proposed CLM efficiency in detection of brain tumors for various number of cpu threads working in our system. Presented charts show how the statistics change (on vertical axis) in relation to the number of cpu threads (on horizontal axis), while the last chart presents the ROC of detection for all threading on our cpu
In the following charts, we can see numerical statistics which describe proposed CLM efficiency in detection of brain tumors for training and test dataset 1. Presented charts show how the statistics change (on vertical axis) during 100 iterations (on horizontal axis) of parallel training process, while the last chart presents the ROC of detection
4.3 Implementation and hardware architecture
Training algorithms Algorithm 1–Algorithm 3 for our CLM model were run with empirically set values of parameters:
-
for Adam: learning rate = 0.00025, \(\beta _1=0.89\), \(\beta _2=0.995\), \(\epsilon =1\mathrm{e}-07\),
-
for BPTA: learning rate = 0.001.
Our hardware architecture was:
-
CPU: AMD Threadripper 2950X 16/32 3.75 Ghz with support for 32 threads on 16 cores with auto threading mode,
-
RAM: 64 GB 3333 Mhz,
-
GPU: 2x RTX 2080.
In research on CLM model, we have developed a fully custom, multithreaded network model implemented entirely in C++ programming language. Applied training algorithms were based on our proposed improvements for the developed multithreading model to improve performance boost. Results of comparison to the standard Tensorflow library algorithms can be seen in Table 3. They show that our implemented model not only scores better in terms of accuracy but also made the score in shorter training time than the Tensorflow equivalent. What’s more, these results were achieved using BPTA compared to Adam in Tensorflow model. Comparing the results on both datasets, we can conclude that our implemented method performs as well or even better than current standard implementations in shorter time needed to train the CLM model. In future works, we plan to expand our research by implementing some other optimization algorithms to improve the performance even more.
4.4 Analysis of numerical results
Let us now discuss numerical results which we obtained in tests of our idea. We would like to discuss the results in three aspects: how the multi-threading influence efficiency of the proposed CLM system, how the best solution statistics prove our result, and in third part we would like to compare our results to other literature solutions.
In Fig. 11, we can see how the process of using multi-threading improves training of CLM. The chart shows how various number of involved cpu threads improve the overall process. We have tested training time for various number of applied cores, and the results show that up to 8 cores training time can be reduced a lot by each new unit, while after that number calculations are not much boosted with new ones. On the other hand, the most efficient option was auto threading which gives the optimal power by using only the necessary number of threads at the time and in result shorten the time of processing to the minimum. In Fig. 10, we can see comparison of statistics for various number of threads. For measures of Sensitivity and Specificity, we don’t see much changes in values. Most thread configurations give very similar results accept for one thread for which most of samples were incorrectly classified as brain tumors. Similar equality in results is visible for accuracy; however, the highest one is visible for auto selected number of threads. Differences in values are visible in charts of Loss and Fallout. Loss function was lowest for auto function, which again shows advantage in comparison with other number of threads set to the CLM system. Fallout value is the best in the case of auto selected number of threads again. In the case of ROC, all thread numbers above 4 show similar efficiency. However, in comparison we can see again an advantage of auto function. As conclusion from this analysis, we have selected auto threading mode as operation setup for CLM system, since it gives the shortest time of training and the best results.
In Fig. 12, we can see how the CLM was improving CNN palettes and therefore ANN ability to detect brain tumors. The results show how the statistics of the proposed solution change during 100 iterations of parallel training. Each of presented statistics improves during following iterations of CLM. The highest improvement is visible in the first 10 iterations, while in the next CLM is adjusting the model to tune it up for final detection. Specificity and sensitivity in all iterations are above 90% which confirms efficiency of the proposed solution. The final value of sensitivity is 88.9%, while specificity is 97.43%. Fallout in all iterations is under 25%, and in the final it goes down to 11.1%. The Loss value is constantly decreasing in each new iteration, while accuracy in avg. value is growing. Both values in the last iterations reach meaningful values of 8.47% and 94.73%, respectively. In Figs. 15 and 16 we can see results for 2nd data set for training and test, both have reached above 95% of accuracy. These results show that proposed CLM works well and it is able to improve \(\mathrm{CNN}+\mathrm{ANN}\) architecture from iteration to iteration. Additionally, we can conclude that with more training data we can provide to the CLM system the better final result composed \(\mathrm{CNN}+\mathrm{ANN}\) architecture will achieve.
Using proposed CLM technique, we obtained results of 100% on validation data (data on which the CLM system was trained) presented in Fig. 13, and 95% on test data (data on which the CLM system has not yet seen) presented in Fig. 14. This result gives conclusion that our solution works well and can be efficiently implemented in image processing systems.
In Table 4, we can see comparisons of our method to other approaches in the field of deep learning for disorders detection from CT scans. From presented results, we can see that our CLM method is surely placed among the best approaches. If we compare numerical statistics, we can see that our method is 1–10% better than most of the methods in the case of accuracy, while there is only one method using deep belief network by [45] which gave just 0.27% higher result. Sensitivity, which reveals how good is the system in identification of brain tumors, is 88.9%. We can find better results; however, the other are devoted to lung nodules which gives our system advantage in the case of brain tumors detection. Specificity, which reveals how good is the system in identification of healthy people, of our solution is 97.43%, which is the best result. That shows CLM has the lowest ration in misleading detection over healthy patients. This is very important conclusion since by using our proposed solution for medical examinations experts will increase confidence that healthy patients will not be bothered unnecessary. These give us assurance that the proposed CLM system works well and has a very high potential for further research and development.
4.5 Conclusions
The proposed CLM model is fast learning from the data. We can see that all statistics show ability of fast and efficient learning. The system gives a novel and easy idea of CNN composition. The palette can be composed from the variety of filters to modify the image and number of grids to extract the most important features. In our research tests, we have used those which gave the best results in brain tumor detection, but the CLM can be also applied to other purposes. Due to parallel implementation, the CLM can evaluate many incoming palettes (configuration of the CNN architecture) in each iteration. The model can be run on various number of threads, so that as a result we receive flexible system composition with possibility to examine broad spectrum of CNN configurations whose performance actually depends only on the type of used cpu. Construction of the system does not limit it only to biomedical research domain but makes it useful model in most image processing and object detection tasks which is another advantage of our idea. Proposed training model was originally tested on brain images; however, it could be easily implemented in other medical fields like lung analysis, sarcoidosis detection and others. What’s more, it could be also used in non-medial tasks, for example luggage CT scans analysis at the airport.
When creating our system, we wanted to obtain high modularity of individual elements; therefore, we can replace CNN with a different method of feature extraction. As for the classification layer, we can replace applied NN with other methods or alternative types of classification, for example SVM.
We propose the flow of information following the standard examination order as shown in Fig. 17. The doctor examines the photograph, the radiologist takes it, and then analyzes the photograph independently with the system located on the server. Then result returns from the server where it is compared with the radiologist’s description. If descriptions match, the system will automatically send the report to the doctor’s room. However, if the descriptions differ, the system will try to draw the radiologist’s attention to the given fragments of the scan. As you can see above, the system is only intended to support radiologist and doctor since professional experience of medicians cannot be replaced.
5 Final remarks
In this article, we present our idea for improved process of deep learning architecture construction for brain tumors detection. The novelty of our proposition is in two main contributions of the developed correlation learning mechanism. Our system is using palettes of CNN architecture to adjust them to the best possible detection result of ANN. This process was implemented in parallel processing model, in which multi-threading mechanism flexibly selects the number of threads. This construction improves whole process of training since efficiency of the CLM is higher in relation to similar approaches and training has much shorter time.
Future works in our project will concentrate on additional improvements for CNN. This part can additionally benefit from multi-threading. From our initial tests, we conclude that parallelization of pooling and convolution can enable better adjustment of palettes. Another idea, good to solve, would be an introduction of special weights to filters on CNN layers since this would make it possible to control the process of filtering so that resulting feature maps can have more details about image key objects, which can improve overall statistics of ANN part.
Author contribution
All authors contributed equally to the research by conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing—original draft, writing—review & editing.
References
Akkus Z, Kostandy P, Philbrick KA, Erickson BJ (2019) Robust brain extraction tool for CT head images. Neurocomputing 392:189–195
Bhandary A, Prabhu GA, Rajinikanth V, Thanaraj KP, Satapathy SC, Robbins DE, Shasky C, Zhang Y-D, Tavares JMRS, Raja NSM (2020) Deep-learning framework to detect lung abnormality–a study with chest X-ray and lung CT scan images. Pattern Recognit Lett 129:271–278
Capizzi G, Sciuto GL, Napoli C, Polap D, Woźniak M (2019) Small lung nodules detection based on fuzzy-logic and probabilistic neural network with bio-inspired reinforcement learning. IEEE Trans Fuzzy Syst 28(6):1178–1189
Causey JL, Zhang J, Ma S, Jiang B, Qualls JA, Politte DG, Prior F, Zhang S, Huang X (2018) Highly accurate model for prediction of lung nodule malignancy with ct scans. Sci Rep 8(1):1–12
Cheng J, Huang W, Ru SC, Wei YY, Yun Z, Wang Z, Feng Q (2015) Enhanced performance of brain tumor classification via tumor region augmentation and partition. PloS ONE 10(10):e0140381
Cherukuri V, Ssenyonga P, Warf BC, Kulkarni AV, Monga V, Schiff SJ (2017) Learning based segmentation of ct brain images: application to postoperative hydrocephalic scans. IEEE Trans Biomed Eng 65(8):1871–1884
Chilamkurthy S, Ghosh R, Tanamala S, Biviji M, Campeau NG, Venugopal VK, Mahajan V, Rao P, Warier P (2018) Deep learning algorithms for detection of critical findings in head ct scans: a retrospective study. Lancet 392(10162):2388–2396
Dartmann G, Song H, Schmeink A (2019) Big data analytics for cyber-physical systems: machine learning for the internet of things. Elsevier, Amsterdam
Deepak S, Ameer PM (2019) Brain tumor classification using deep cnn features via transfer learning. Computers in biology and medicine 111:103345
Douglas DB, Ro T, Toffoli T, Krawchuk B, Muldermans J, Gullo J, Dulberger A, Anderson AE, Douglas PK, Wintermark M (2019) Neuroimaging of traumatic brain injury. Med Sci 7(1):2
Dourado CMJM, Da Silva SPP, Da Nóbrega RM, Filho PPR, Muhammad K, De Albuquerque VHC (2020) An open ioht-based deep learning framework for online medical image recognition. IEEE J Sel Areas Commun
Dourado CMJM Jr, da Silva SPP, da Nóbrega RVM, Barros ACDS, Filho PPR, de Albuquerque VHC (2019) Deep learning IoT system for online stroke detection in skull computed tomography images. Comput Netw 152:25–39
Gao XW, Hui R, Tian Z (2017) Classification of ct brain images based on deep learning networks. Comput Methods Program Biomed 138:49–56
George J, Skaria S, Varun VV et al (2018) Using yolo based deep learning network for real time detection and localization of lung nodules from low dose ct scans. In: Medical imaging 2018: computer-aided diagnosis, vol 10575. International Society for Optics and Photonics, p 105751I
Han G, Liu X, Zheng G, Wang M, Huang S (2018) Automatic recognition of 3D GGO CT imaging signs through the fusion of hybrid resampling and layer-wise fine-tuning CNNs. Med Biol Eng Comput 56(12):2201–2212
Ho K-C, Toh C-H, Li S-H, Liu C-Y, Yang C-T, Lu Y-J, Su T-P, Wang C-W, Yen T-C (2019) Prognostic impact of combining whole-body PET/CT and brain PET/MR in patients with lung adenocarcinoma and brain metastases. Eur J Nucl Med Mol Imaging 46(2):467–477
Hu Z, Tang J, Wang Z, Zhang K, Zhang L, Sun Q (2018) Deep learning for image-based cancer detection and diagnosis–a survey. Pattern Recognit 83:134–149
Jiang B, Yang J, Lv Z, Song H (2018) Wearable vision assistance system based on binocular sensors for visually impaired users. IEEE Internet Things J 6(2):1375–1383
Ker J, Singh SP, Bai Y, Rao J, Lim T, Wang L (2019) Image thresholding improves 3-dimensional convolutional neural network diagnosis of different acute brain hemorrhages on computed tomography scans. Sensors 19(9):2167
Lakshmanaprabu SK, Mohanty SN, Shankar K, Arunkumar N, Ramirez G (2019) Optimal deep learning model for classification of lung cancer on CT images. Future Gener Comput Syst 92:374–382
Liu M, Zhang J, Lian C, Shen D (2019) Weakly supervised deep learning for brain disease prognosis using mri and incomplete clinical scores. IEEE Trans Cybern 50(7):3381–3392
Liu S, Pan Z, Song H (2017) Digital image watermarking method based on dct and fractal encoding. IET Image Process 11(10):815–821
Lv Z, Song H, Basanta-Val P, Steed A, Jo M (2017) Next-generation big data analytics: State of the art, challenges, and future research topics. IEEE Trans Ind Inform 13(4):1891–1899
Mostapha M, Styner M (2019) Role of deep learning in infant brain MRI analysis. Magn Reson Imaging
Muhammad K, Khan S, Del Ser J, de Albuquerque VHC (2020) Deep learning for multigrade brain tumor classification in smart healthcare systems: a prospective survey. IEEE Trans Neural Netw Learn Syst
Nibali A, He Z, Wollersheim D (2017) Pulmonary nodule classification with deep residual networks. Int J Comput Assist Radiol Surg 12(10):1799–1808
Nie D, Wang L, Adeli E, Lao C, Lin W, Shen D (2018) 3-d fully convolutional networks for multimodal isointense infant brain image segmentation. IEEE Trans Cybern 49(3):1123–1136
Özyurt F, Sert E, Avci E, Dogantekin E (2019) Brain tumor detection based on convolutional neural network with neutrosophic expert maximum fuzzy sure entropy. Measurement 147:106830
Raju AR, Pabboju S, Rao RR (2019) Hybrid active contour model and deep belief network based approach for brain tumor segmentation and classification. Sens Rev
Ray S, Kumar V, Ahuja C, Khandelwal N (2018) Intensity population based unsupervised hemorrhage segmentation from brain CT images. Expert Syst Appl 97:325–335
Reza SMS, Mays R, Iftekharuddin KM (2015) Multi-fractal detrended texture feature for brain tumor classification. In: Medical Imaging 2015: computer-aided diagnosis, vol 9414. International Society for Optics and Photonics, p 941410
Robben D, Boers AMM, Marquering HA, Langezaal LLCM, Roos YBWEM, van Oostenbrugge RJ, van Zwam WH, Dippel DWJ, Majoie CBLM, van der Lugt A et al (2020) Prediction of final infarct volume from native CT perfusion and treatment parameters using deep learning. Med Image Anal 59:101589
Sarmento RM, Vasconcelos FFX, Filho PPR, Wu W, De Albuquerque VHC (2019) Automatic neuroimage processing and analysis in stroke–a systematic review. IEEE Rev Biomed Eng 13:130–155
Shaffie A, Soliman A, Fraiwan L, Ghazal M, Taher F, Dunlap N, Wang B, van Berkel V, Keynton R, Elmaghraby A et al (2018) A generalized deep learning-based diagnostic system for early diagnosis of various types of pulmonary nodules. Technol Cancer Res Treat. https://doi.org/10.1177/1533033818798800
Sharif MI, Li JP, Khan MA, Saleem MA (2020) Active deep neural network features selection for segmentation and recognition of brain tumors using MRI images. Pattern Recognit Lett 129:181–189
Sheng B, Li B, Mo S, Li H, Hou X, Wu Q, Qin J, Fang R, Feng DD (2018) Retinal vessel segmentation using minimum spanning superpixel tree detector. IEEE Trans Cybern 49(7):2707–2719
Song QZ, Zhao L, Luo XK, Dou XC (2017) Using deep learning for classification of lung nodules on computed tomography images. J Healthcare Eng 2017
Sun Y, Song H, Jara AJ, Bie R (2016) Internet of things and big data analytics for smart and connected communities. IEEE Access 4:766–773
Tan W, Kang Y, Dong Z, Chen C, Yin X, Su Y, Zhang Y, Zhang L, Xu L (2019) An approach to extraction midsagittal plane of skull from brain CT images for oral and maxillofacial surgery. IEEE Access 7:118203–118217
Xie Y, Xia Y, Zhang J, Song Y, Feng D, Fulham M, Cai W (2018) Knowledge-based collaborative deep learning for benign-malignant lung nodule classification on chest CT. IEEE Trans Med Imaging 38(4):991–1004
Xie Y, Zhang J, Xia Y, Fulham M, Zhang Y (2018) Fusing texture, shape and deep model-learned information at decision level for automated classification of lung nodules on chest CT. Inf Fusion 42:102–110
Xu Y, Holanda G, Fabrício L, de Souza F, Silva H, Gomes A, Silva I, Ferreira M, Jia C, Han T et al (2020) Deep learning-enhanced internet of medical things to analyze brain ct scans of hemorrhagic stroke patients: a new approach. IEEE Sens J
Yang J, Wang C, Jiang B, Song H, Meng Q (2020) Visual perception enabled industry intelligence: state of the art, challenges and prospects. IEEE Trans Ind Inform 17:2204–2219
Zeng L, Tian X (2018) Accelerating convolutional neural networks by removing interspatial and interkernel redundancies. IEEE Trans Cybern 50(2):452–464
Zhang T, Zhao J, Luo J, Qiang Y (2017) Deep belief network for lung nodules diagnosed in CT imaging. Int J Perform Eng 13(8):1358–1370
Zhang X, Wei Y, Yang Y, Huang TS (2020) Sg-one: Similarity guidance network for one-shot semantic segmentation. IEEE Trans Cybern 50(9):3855–3865
Zhang Y, Sun L, Song H, Cao X (2014) Ubiquitous wsn for healthcare: recent advances and future prospects. IEEE Internet Things J 1(4):311–318
Zheng J, Xia K, Zheng Q, Qian P (2019) A smart brain mr image completion method guided by synthetic-ct-based multimodal registration. J Ambient Intell Humaniz Comput 1–10
Acknowledgements
Authors would like to acknowledge contribution to this research from the Rector of the Silesian University of Technology, Gliwice, Poland, under proquality grant No. 09/010/RGJ21/0056.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relations that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Woźniak, M., Siłka, J. & Wieczorek, M. Deep neural network correlation learning mechanism for CT brain tumor detection. Neural Comput & Applic 35, 14611–14626 (2023). https://doi.org/10.1007/s00521-021-05841-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-021-05841-x