Genetic and deep learning clusters based on neural networks for management decision structures

Abstract

Judgments are taken in a structured way; both human and business management decisions involve a hierarchical process that requires a level of compromise between risk, cost, reward, experience and knowledge. This article proposes a management decision structure that emulates the human brain approach based on genetic and deep learning cluster algorithms and the random neural network. Reinforcement learning takes quick and specific local decisions, deep learning clusters enables identity and memory, and deep learning management clusters make final strategic decisions. The presented genetic algorithm transmits the learned information to future generations in the network weights rather than the neurons. Because the subject’s information, a combination of memory, identity and decision data, is never lost but transmitted, the genetic algorithm provides immortality. The management decision structure has been applied and validated in a smart investment Fintech application: an intelligent banker that makes buy and sell asset decisions with an associated market and risk that entirely transmits itself to a future generation. Results are rewarding; the management decision structure with genetics and machine learning based on the random neural network algorithm that emulates the human brain and biology transmits information to future generations and learns autonomously, gradually and continuously while adapting to the environment.

1 Introduction

The brain takes decisions in a structured way, and the striatum is a fundamental area essential in decision making formed of different sections that have distinct roles: the dorsolateral striatum functions in typical actions, the dorsomedial striatum in goal-directed actions and the ventral striatum in motivation [1]; although these three different regions have independent functions, they coordinate between each other during the different stages of decision-making process based on hierarchical reinforcement learning. Similar structured decision-making approach is also applied in business management, company and institution operations and emergency services that require a level of compromise between risk, cost, reward, experience and knowledge.

In addition to our brain hierarchical decision process, biological organisms autonomously learn in a gradual and continuous approach while adapting to the environment using genetic changes to generate new complex structures in organisms [2]. The current structure of the organisms defines the type and level of the future genetic variation that will provide a better adaption to the environment or increased reward to a goal function. Random genetic changes have more probability to be successful in organisms that change in a systematic and modular manner where the new structures acquire the same set of subgoals in different combinations. This approach enables organisms not only to remember their reward evolution but also to generalize goal functions to successfully adapt to future environments [3]. The adaptations learned from the living organisms affect and guide evolution, even though the characteristics acquired are not transmitted to the genome [4]; however, its gene functions are altered and transmitted to the new generation. This method enables learning organisms to evolve much faster.

Successful machine learning and artificial intelligence models have been based on biology emulating the structures provided by nature during the learning, adaptation and evolution when interacting with the external environment. Neural networks and deep learning are based on brain structure which is formed of dense local clusters of the same neurons. Dense clusters perform different functions which are connected between each other with numerous very short paths and few long distance connections [5]. The brain retrieves a large amount of data obtained from the senses; analyzes the material and finally selects the relevant information [6] where the cluster of neurons specialization occurs due to their adaption when learning tasks.

1.1 Research proposal

This article proposes a management decision structure that emulates the brain functions using reinforcement learning and deep learning clusters based on the random neural network. Information in the presented model is learned through the interaction and adaptation to the environment using reinforcement and deep learning. Decisions are taken in a hierarchical way with different learnings specialized in different stages of the decision process:

• Reinforcement learning [7,8,9] takes quick and specific local decisions;

• Deep learning clusters [10,11,12] enable identity and memory;

• Deep learning management clusters [13,14,15,16] make final strategic decisions.

In addition, this article presents a genetic learning algorithm based on the genome and evolution applying extreme learning machine methods [17,18,19,20,21]. Information in the proposed genetic algorithm is transmitted to future generations in the network weights through the combinations of four different nodes rather than the value of nodes themselves. The four nodes represent the genome nucleotides (C, G, A or T) that form the double helix of the DNA where the output layer of nodes replicates the input layer as the genome reproduces replicas of organisms. The genetic learning algorithm fixes the output to four neuron values that represent the four different nucleoids, and it also fixes the network weights to generate four different types of neurons rather than random values as proposed by the ELM theory. Genetic algorithm provides immortality: the entire subject’s information, defined as the combination of memory, identity and decision data, is never lost but transmitted to future generations.

The proposed management decision structure has been applied and validated in a smart investment application: an intelligent banker that makes buy and sell asset decisions with an associated market and risk that entirely transmits itself to a future generation.

The results presented by this article are rewarding and promising: the intelligent banker takes the right decisions, learns the variable asset price, makes profits on specific markets at minimum risk and finally efficiently transmits the information learned to future generations.

1.2 Research structure

This article presents the research background that consists on the genome, artificial neural networks, machine learning, genetic algorithms and extreme machine learning in Sect. 2. The random neural network with reinforcement learning, deep learning clusters, deep learning management clusters and genetic algorithm are defined in Sect. 3. The management decision structure and its application to smart investment in an intelligent banker are presented in Sect. 4, whereas its implementation is described in Sect. 5. The experimental results are shown in Sect. 6 with a cryptocurrency evaluation in Sect. 7. Finally, conclusions and future work are shared in Sect. 8.

2 Research background and literature review

Artificial neural networks, machine learning and genetic algorithms have been applied in economics and finance to make predictions where extreme machine learning have improved the performance of classic neural network models.

2.1 Genome

The genome is the genetic material of an organism; it consists of 23 pairs of chromosomes (1–22, X and Y) for a human cell formed of genes (approximately 21,000 in total) that code for a molecule that has a function or instruction to make proteins as presented by Pellegrini et al. [22]. Furthermore, genes are formed of base pairs (approximately 3 billion in total). The DNA is a double helix formed by the combination of only four nucleotides (cytosine [C], guanine [G], adenine [A] or thymine [T]) where each base pair consists of the combination of two nucleoids G-C and A-T. The genetic code is formed of codons; a sequence consisted of three nucleotides or three-letter words. Proteins that have similar combination of base pairs tend to have a related functionality determination of protein functions from genetic sequences following the research of Suzuki [23].

2.2 Artificial neural networks

Artificial neural networks have been applied to make financial predictions and represent financial models. The bankruptcy prediction capability of several neural network architectures based on different training sets and number of iterations was evaluated by Leshno and Spector [24]; the neural networks are trained with data obtained from different firm’s financial reports where the prediction capability of the neural network is compared against classical discriminant analysis models. Artificial neural networks for a financial distress prediction model are used by Chen and Du [25]; the back propagation learning algorithm is trained with a dataset obtained from the Taiwan Stock Exchange Corporation where the inputs to the neural network are 37 model factor ratios. An artificial neural network with back propagation gradient descent learning algorithm to predict the direction of stock market index movement for the Istanbul Stock Exchange is applied by Kara et al. [26]; the inputs of the feedforward network correspond to ten technical indicators such as moving average or momentum and the output neuron represents the direction of the index movement.

The effectiveness of neural network models in stock market predictions was evaluated by Guresen et al. [27]; the models analyzed are multilayer perceptron, dynamic artificial neural network and hybrid neural networks where the mean square error and mean absolute deviate metrics are used to compare each model. Different artificial neural networks in bankruptcy prediction against traditional Bayesian classification theory are analyzed by Zhang et al. [28]; the method of cross-validation is applied to examine the sample variation between neural networks. Different ways to use prior knowledge such as newspaper headlines and neural networks to improve multivariate prediction ability is investigated by Kohara et al. [29]; the topics are chief Tokio stock exchange price index, exchange rate dollar-yen, interest rate, crude oil price and New York Dow Jones where the inputs to the neural network are the relative topic difference. Regression, artificial neural networks and support vector machines for predicting the S&P 500 Stock Market Price Index are compared by Sheta et al. [30]; they use 27 potential financial and economic variables that impact the stock movement; these variables are used as the input nodes whereas the output node gives the predicted next week value. Artificial neural networks and fuzzy logic for market predictions are included by Khuat et al. [31] where the input layer contains 30 neurons corresponding to 30 close days and the output node is the close price of the next day.

A feedforward multilayer perceptron to predict a company’s stock value is used by Naeini et al. [32]; the network predicts the next day stock value of a company listed in the Tehran Stock Exchange Corporation only based on its stock trade history and without any information of the current market. A hybrid system based on a multiagent architecture to analyze stock market behavior is created by Iuhasz et al. [33] to improve the profitability in a short or medium time period investment; the proposed system compares the results of feed forward and recurrent neural network in terms of accuracy and time performance. The use of neural networks as an alternative to classical statistical techniques for forecasting within the framework of arbitrage pricing theory model for stock ranking is examined by Nicholas et al. [34]; the training and test sets consist of data presented as factors extracted from the balance sheets of the companies in the UK stocks, and the resultant outperformance Y is the output.

A comparative survey of artificial intelligence applications in Finance is presented by Bahrammirzaee [35] that covers artificial neural networks, expert system and hybrid intelligent systems in financial markets, credit evaluation, portfolio management and financial prediction and planning. The use of artificial neural networks in accounting and finance is reviewed by Coakley and Brown [36]; it includes modeling issues and applicability guidelines such as the selection of the learning algorithm, error and transfer functions, architecture and network training. The applications of neural networks in finance are analyzed by Fadlalla and Lin [37]; in particular, the common characteristics of these applications are examined and compared against applications based on statistical and econometrics models. The use of neural networks in finance and economics forecasting is reviewed by Huang et al. [38]; input variables, type of neural network models and performance comparisons are analyzed for the prediction of foreign exchange rates, stock market index and economic growth. Li et al. [39] summarize different applications of artificial intelligence technologies such as neural networks, deep learning and machine leaning in several domains of business administration including finance, retail, manufacturing and management consultancy.

Machine learning has been applied to solve nonlinear models in continuous time in macroeconomics and finance by Duarte [40] where the problem of solving the corresponding nonlinear partial differential equations can be reformulated as a sequence of supervised learning problems. A single variable time-series model that combines two financial volatility metrics to predict and forecast one of them is proposed by Stefani et al. [41]; the method is based on artificial neural networks with a multilayer perceptron in a single-hidden-layer configuration, the k-nearest neighbors as a local nonlinear model used for classification and regression and finally support vector machine in a regression methodology. Deep learning has also been incorporated in long–short-term memory neural networks for financial market predictions by Fischer and Krauss [42] where day returns are calculated for each day at defined stocks. Hasan et al. [43] investigate how to apply hierarchical deep learning models for the problems in finance such as stock market prediction and classification; the deep learning models are based on neural networks, recurrent neural networks with big data finance datasets.

2.3 Genetic algorithms

Genetic algorithms (GA) have been proposed as method to increase learning performance. Overlapping generations (OLG) economies in which agents use genetic algorithms to learn correct decision rules are studied by Arifovic [44]; the results of an OLG model with GA learning against the results of the same model where the agents form expectations via either the sample average of past prices or least squares adaptive algorithms are compared in terms of on equilibrium within inflationary economies. A genetic algorithm to feature discretization in artificial neural networks for the prediction of stock market index was proposed by Kim and Han [45]; the GA is applied to improve the learning algorithm and to reduce the complexity in feature space.

A hybrid model based on genetic algorithm and neural networks to forecast tax collection is applied by Ticona et al. [46]; endogenous and exogenous variables are used as input variables of the neural network for the multistep time series to forecast a hybrid model based on lags of the value of the time series, differences and moving averages. A genetic algorithm-based deep learning method is presented by Hossain and Capi [47]; the GA is used to optimize the deep learning parameters such as the number of hidden units, the number of epochs, learning rates and momentum in learning stage of the hidden layers. A genetic algorithm assisted method for deep learning that improves the performance of a deep autoencoder producing a sparser neural network is presented by David and Greental [48]; the GA population of each chromosome is a set of weights for the autoencoder. The latest deep learning structures and evolutionary algorithms that can be used to train them are reviewed by Tirumala [49]; these include convolutional neural networks, deep belief networks, stacked autoencoders, generative neuroevolution and deep learning using genetic algorithm.

2.4 Extreme learning machine

The learning speed of feedforward neural networks is in general slower than required due to the slow gradient-based learning algorithm that adjusts iteratively the parameters of the networks. A new learning algorithm called extreme learning machine (ELM) for single-hidden-layer feedforward neural networks (SLFNs) which randomly chooses hidden nodes and analytically determines its output weight is proposed by Huang et al. [17]. The output weights linking the hidden layer to the output layer of SLFNs can be analytically determined through simple generalized inverse operation of the hidden layer output matrices; Huang et al. [18] proves that SLFNs work as universal approximators by randomly choose hidden nodes and then only adjusting the output weights linking the hidden layer and the output layer. An ELM architecture for multilayer perceptron is proposed by Tang et al. [19]; the ELM is divided into two main components: self-taught feature extraction followed by supervised feature classification which they are connected by random initialized hidden weights. ELM provides a unified learning platform with extensive methods of feature mappings that can be applied in regression and multiclass classification applications directly, as demonstrated by Huang et al. [20]. An extreme learning machine-based autoencoder is introduced by Kasun et al. [21] which learns feature representations using singular values.

Reservoir computing consists on an input signal that is fed into a fixed or random dynamical system, or reservoir, where the dynamics of the reservoir map the input to a higher dimension, then a retrieval method is trained to read the state of the reservoir and map it to the desired output [50]; the main benefit is that the reservoir is fixed and training is performed only at the retrieval stage therefore the complexity of the computationally demanding neural networks learning algorithms is reduced. An empirical analysis of deep recurrent neural network architectures with stacked layers develops and improves hierarchical dynamics in deep recurrent architectures within the efficient reservoir computing approach [51]; a deep layering of recurrent models provides an effective diversification of temporal representations in the layers of the hierarchy. Deep Echo State Network models consist of a stack of multiple nonlinear reservoir layers that potentially allow the exploitation of the advantages of a hierarchical temporal feature representation at different levels of abstraction while preserving the training efficiency typical of the reservoir computing methodology [52]; however, adding layers to a deep reservoir architecture affects the regime of network’s dynamics toward equally or less stable behaviors. A new architecture, reservoir with random static projections is proposed to improve the performance of Echo State Networks based on the compromise between the amount of nonlinear mapping and short-term memory when applied to time-series data which are highly nonlinear [53]; a similar method is also applied using an ELM whose input is presented through a time delay.

Radial basis function (RBF) networks that have one hidden layer are capable of universal approximation [54]; RBF networks with the same smoothing factor in each kernel node is broad enough for universal approximation. ELMs can be also extended to a RBF network case, which allows the centers and impact widths of RBF kernels to be randomly generated and the output weights to be simply analytically calculated instead of iteratively tuned [55]; the ELM algorithm for RBF networks can complete learning at very fast speed and produce generalization performance very close to support vector machines in many artificial and real benchmarking function approximation and classification applications. The RBF network applies a nonmonotonic transfer function based on the Gaussian density function [56]; while producing robust decision surfaces, the RBF also provides an estimate of how close a test instance is to the original training data, allowing the classifier to identify that a test instance potentially represents a new class while still presenting the most probable classification. Feedforward neural networks using RBF assume that the patterns of the learning environment are separable by hyperspheres [57]; it is demonstrated that their related cost function is local minima free with respect to all the network weights.

3 The random neural network genetic deep learning model

3.1 The random neural network

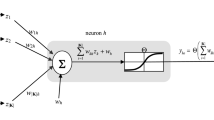
The random neural network (RNN) [7,8,9] represents more closely how signals are transmitted in many biological neural networks where they travel as spikes or impulses, rather than as analogue signal levels. The RNN is a spiking recurrent stochastic model for neural networks. Its main analytical properties are the “product form” and the existence of the unique network steady state solution. The random neural network has also been applied in different genetic models [58,59,60,61,62,63,64,65,66,67].

The RNN is composed of M neurons each of which receives excitatory (positive) and inhibitory (negative) spike signals from external sources which may be sensory sources or neurons (Fig. 1). These spike signals occur following independent Poisson processes of rates λ⁺ (m) for the excitatory spike signal and λ⁻ (m) for the inhibitory spike signal, respectively, to cell $m \in \left\{ {1, \ldots M} \right\}$.

Fig. 1

The random neural network

Neurons interact with each other by interchanging signals in the form of spikes of unit amplitude:

• A positive spike is interpreted as excitation signal because it increases by one unit the potential of the receiving neuron;

• A negative spike is interpreted as inhibition signal decreasing by one unit the potential of the receiving neuron or has no effect if the potential is already zero.

Each neuron accumulates signals and it will fire if its potential is positive. Firing will occur at random, and spikes will be sent out at rate r(i) with independent, identically and exponentially distributed inter-spike intervals:

• Positive spikes will go out to neuron j with probability p⁺(i, j) as excitatory signals;

• Negative spikes with probability p⁻(i, j) as inhibitory signals.

A neuron may send spikes out of the network with probability d(i). We have:

$$d\left( i \right) + \mathop \sum \limits_{j = 1}^{n} \left[ {p^{ + } \left( {i,j} \right) + p^{ - } \left( {i,j} \right)} \right] = 1 \quad {\text{for}}\, 1 \le i \le n$$

(1)

Neuron potential decreases by one unit when the neuron fires either an excitatory spike or an inhibitory spike. External (or exogenous) excitatory or inhibitory signals to neuron i will arrive at rates Λ(i), λ(i), respectively, by stationary Poisson processes. The random neural network weight parameters w⁺(j, i) and w⁻(j, i) are the nonnegative rate of excitatory and inhibitory spike emission, respectively, from neuron i to neuron j:

$$\begin{aligned} & w^{ + } \left( {j,i} \right) \, = \, r\left( i \right)p^{ + } \left( {i,j} \right) \, \ge \, 0 \\ & w^{ - } \left( {j,i} \right) \, = \, r\left( i \right)p^{ - } \left( {i,j} \right) \, \ge \, 0 \\ \end{aligned}$$

(2)

Information is transmitted by the rate or frequency at which spikes travel. Each neuron i, if it is excited, behaves as a frequency modulator emitting spikes at rate w(i, j) = w⁺(i, j) + w⁻(i, j) to neuron j. Spikes will be emitted at exponentially distributed random intervals. Each neuron acts as a nonlinear frequency demodulator transforming the incoming excitatory and inhibitory spikes into potential.

In this model, each neuron is represented at time t ≥ 0 by its internal state k_m(t) which is a nonnegative integer. If k_m(t) ≥ 0, then the arrival of a negative spike to neuron m at time t results in the reduction of the internal state by one unit: k_m(t⁺) = k_m(t) − 1. The arrival of a negative spike to a neuron has no effect if k_m(t) = 0. On the other hand, the arrival of an excitatory spike always increases the neuron’s internal state by 1; k_m(t⁺) = k_m(t) + 1.

The random neural network defines q_i as the probability a neuron i is excited:

$$q_{i} = \frac{{\lambda^{ + } (i)}}{{r\left( i \right) + \lambda^{ - } (i)}} r\left( i \right) = \mathop \sum \limits_{j = 1}^{n} \left[ {w^{ + } \left( {i,j} \right) + w^{ - } \left( {i,j} \right)} \right] \quad {\text{for}}\,1 \le i \le n$$

(3)

where the λ⁺(i), λ⁻(i) for i = 1, …, n satisfy the system of nonlinear simultaneous equations:

$$\begin{aligned} \lambda^{ + } \left( i \right) & = \mathop \sum \limits_{j = 1}^{n} \left[ {q_{j} r(j)p^{ + } (j,i)} \right] + \varLambda (i) \\ \lambda^{ - } \left( i \right) & = \mathop \sum \limits_{j = 1}^{n} \left[ {q_{j} r(j)p^{ - } (j,i)} \right] + \lambda (i). \\ \end{aligned}$$

(4)

3.2 Reinforcement learning algorithm

A random neural network (RNN) [7,8,9] with at least as many nodes as the number of decisions to be taken is generated where neurons are numbered 1, …, j, …, n; therefore, for any decision i, there is some neuron i. Decisions in this RL algorithm with the RNN are taken by selecting the decision j for which the corresponding neuron is the most excited, the one which has the largest value of q_j.

The state q_j is the probability that it is excited, these quantities satisfy the following system of nonlinear equations:

$$q_{j} = \frac{{\lambda^{ + } (j)}}{{r\left( j \right) + \lambda^{ - } (j)}}$$

(5)

The reinforcement learning algorithm used in this model is based on the cognitive packet network presented by Gelenbe [68,69,70,71,72]. Given some Goal G that the agent has to achieve as a function to be optimized and reward R as a consequence of the interaction with the environment, successive measured values of the R are denoted by R_l, l = 1, 2, … and these are used to compute a decision threshold:

$$T_{l} = \alpha T_{l - 1} + \, \left( {1 - \alpha } \right)R_{l}$$

(6)

where α is some constant 0 < α < 1 that can be statically assigned or dynamically updated based on the external observations.

The agent takes the lth decision which corresponds to neuron j and then the lth reward R_l is measured and its associated T_l−1 is calculated where the network weighs are updated as follows for all neurons i ≠ j.

• if T_l−1 ≤ R₁:

  $$\begin{aligned} & w^{ + } \left( {i,j} \right) \, = \, w^{ + } \left( {i,j} \right) \, + \, R_{1} \\ & w^{ - } \left( {i,k} \right) \, = \, w^{ - } \left( {i,k} \right) \, + \frac{{R_{l} }}{n - 2}\quad {\text{if }}k \, \ne \, j \\ \end{aligned}$$

  (7)

• else if R_l < T_l−1:

  $$\begin{aligned} & w^{ + } \left( {i,k} \right) \, = \, w^{ + } \left( {i,k} \right) \, + \frac{{R_{l} }}{n - 2}\quad {\text{if}}\,k \, \ne \, j \\ & w^{ - } \left( {i,j} \right) \, = \, w^{ - } \left( {i,j} \right) \, + \, R_{l} \\ \end{aligned}$$

  (8)

This research uses reinforcement learning to make binary decisions with only two neurons (Fig. 2).

$$q_{0} = \frac{{\lambda^{ + } (0)}}{{r\left( 0 \right) + \lambda^{ - } (0)}}\quad q_{1} = \frac{{\lambda^{ + } (1)}}{{r\left( 1 \right) + \lambda^{ - } (1)}}$$

where

$$\begin{array}{*{20}l} {\lambda^{ + } \left( 0 \right) = q_{1} w_{10}^{ + } + \varLambda_{0} } \hfill & {\lambda^{ + } \left( 1 \right) = q_{0} w_{01}^{ + } + \varLambda_{1} } \hfill \\ {\lambda^{ - } \left( 0 \right) = q_{1} w_{10}^{ - } + \lambda_{0} } \hfill & {\lambda^{ - } \left( 1 \right) = q_{0} w_{01}^{ - } + \lambda_{1} } \hfill \\ {r\left( 0 \right) = w_{01}^{ + } + w_{01}^{ - } } \hfill & { r\left( 1 \right) = w_{10}^{ + } + w_{10}^{ - } .} \hfill \\ \end{array}$$

(9)

On the above equations, w⁺_ij is the rate at which neuron i transmits excitation spikes to neuron j and w⁻_ij is the rate at which neuron i transmits inhibitory spikes to neuron j in both situations when neuron i is excited. Λ_i and λ_i are the rates of external excitatory and inhibitory signals, respectively.

Fig. 2

Reinforcement learning algorithm

3.3 The random neural network with multiple clusters

Deep learning with random neural networks is described by Gelenbe and Yin [10,11,12]. This model is based on the generalized queuing networks with triggered customer movement (G-networks) where customers or tasks are either “positive” or “negative” and customers or tasks can be moved from queues or leave the network. G-networks are introduced by Gelenbe [73, 74]; an extension to this model is developed by Gelenbe et al. [75] where synchronized interactions of two queues could add a customer in a third queue.

The model considers a special network M(n) that contains n identically connected neurons, each which has a firing rate r and external inhibitory and excitatory signals λ⁻ and λ⁺, respectively (Fig. 3). The state of each cell is denoted by q, and it receives an inhibitory input from the state of some cell u which does not belong to M(n); therefore, for any cell $i \, \in \, M\left( n \right)$, there is an inhibitory weight w⁻(u) ≡ w⁻(u,i) > 0 from u to i.

Fig. 3

Clusters of neurons

For any $i,j \, \in \, M\left( n \right)$, we have w⁺(i,j) = w⁻(i,j) = 0, but all whenever one of the neurons fires, it triggers the firing of the other neurons with the following values. As presented in [14,15,16], the potential for each identical neuron is calculated as:

$$q = \frac{{\varLambda + \frac{rq(n - 1)(1 - p)}{n - qp(n - 1)}}}{{r + \lambda + q_{u} w^{ - } \left( u \right) + \frac{rqp(n - 1)}{n - qp(n - 1)}}}$$

(10)

where (10) is a second-degree polynomial in q:

$$0 = q^{2} p(n - 1) \left[ {\lambda + q_{u} w^{ - } \left( u \right)} \right] - q[np(\varLambda + r) + n(\lambda + q_{u} w^{ - } (u)) - p(\varLambda + r) + r] + n\varLambda .$$

(11)

3.4 Deep learning clusters

The deep learning architecture presented in [10,11,12] is composed on C multiple clusters, each of which is made up of a M(n) cluster each with n hidden neurons (Fig. 4). For the cth such cluster, c = 1, …, C, the state of each of its identical cells is denoted by q_c. In addition, there are U input cells which do not belong to these C clusters, and the state of the uth cell u = 1, …, U is denoted by $\bar{q}_{u}$. The cluster network has U input cells and C clusters.

Fig. 4

The random neural network with multiple clusters

The deep learning clusters model defines:

• I = (i_dl1, i_dl2, …, i_dlu), a U-dimensional vector $I \, \in \, \left[ {0,1} \right]^{U}$ that represents the input state $\overline{{q_{u} }}$ for the cell u;

• w⁻(u, c) is the U × C matrix of inhibitory weights from the U input cells to the cells in each of the C clusters;

• Y = (y_dl1, y_dl2, …, y_dlc), a C-dimensional vector $Y \, \in \, \left[ {0,1} \right]^{C}$ that represents the cell state q_c for the cluster c.

Each hidden neuron in the clusters c, with $c \, \in \, \left\{ {1, \ldots ,C} \right\}$ receives an inhibitory input from each of the U input neuron. Thus, for each neuron in the cth cluster, we have inhibitory weights w⁻(u, c) > 0 from the uth input neuron to each neuron in the cth cluster; the uth input neuron will have a total inhibitory “exit” weight, or total inhibitory firing rate $\overline{{r_{u} }}$ to all the clusters which is of value:

$$\overline{{r_{u} }} = n \mathop \sum \limits_{c = 1}^{C} w^{ - } (u, c)$$

(12)

As calculated in (10), the potential for each neuron q_c in cluster C is:

$$q_{c} = \frac{{\varLambda_{c} + \frac{{r_{c} q_{c} (n - 1)(1 - p_{c} )}}{{n - q_{c} p_{c} (n - 1)}}}}{{r_{c} + \lambda_{c} + \mathop \sum \nolimits_{u = 1}^{U} \overline{{q_{u} }} w^{ - } \left( {u,c} \right) + \frac{{r_{c} q_{c} p_{c} (n - 1)}}{{n - q_{c} p_{c} (n - 1)}}}}$$

(13)

The activation function of the cth cluster is defined as:

$$\zeta (x_{c} ) = \frac{{b_{c} }}{{2a_{c} }} - \frac{{\sqrt {b_{c}^{2} - 4a_{c} d_{c} } }}{{2a_{c} }}$$

(14)

where

$$x_{c} = \mathop \sum \limits_{u = 1}^{U} \overline{{q_{u} }} w^{ - } (u, c)$$

(15)

We have:

$$y_{c} = \zeta (x_{c} )$$

The network learns the U × C weight matrix w⁻(u, c) by calculating new values of the network parameters for the input I and output Y using gradient descent learning algorithm which optimizes the network inhibitory weight parameters w⁻(u, c) from a set of input–output pairs (i_u, y_c).

3.5 Deep learning management cluster

The deep learning management cluster was proposed by Serrano et al. [13,14,15,16]. It takes management decisions based on the inputs from different deep learning clusters (Fig. 5). The deep learning management cluster defines:

Fig. 5

The random neural network with a management cluster

• I_mc, a C-dimensional vector $I_{\text{mc}} \in \left[ {0,1} \right]^{C}$ that represents the input state $\overline{{q_{c} }}$ for the cluster c;

• w⁻(c) is the C-dimensional vector of inhibitory weights from the C input clusters to the cells in the management cluster mc;

• Y_mc, a scalar $Y_{\text{mc}} \in \left[ {0,1} \right]$, the cell state q_mc for the management cluster mc.

The activation function of the management cluster mc is defined as:

$$\begin{aligned} \zeta \left( {x_{\text{mc}} } \right) & = \frac{{\left[ {np\left( {\varLambda_{\text{mc}} + r_{\text{mc}} } \right) + n\left( {\lambda_{\text{mc}} + x_{\text{mc}} } \right) - p\left( {\varLambda_{\text{mc}} + r_{\text{mc}} } \right) + r_{\text{mc}} } \right]}}{{2p_{\text{mc}} \left( {n - 1} \right)\left[ {\lambda_{\text{mc}} + x_{\text{mc}} } \right]}} \\ & \quad - \frac{{\sqrt {\left[ {np\left( {\varLambda_{\text{mc}} + r_{\text{mc}} } \right) + n\left( {\lambda_{\text{mc}} + x_{\text{mc}} } \right) - p\left( {\varLambda_{\text{mc}} + r_{\text{mc}} } \right) + r_{\text{mc}} } \right]^{2} - 4p_{\text{mc}} (n - 1)\left[ {\varLambda_{\text{mc}} + x_{\text{mc}} } \right]n\varLambda_{\text{mc}} } }}{{2p_{\text{mc}} \left( {n - 1} \right)\left[ {\lambda_{\text{mc}} + x_{\text{mc}} } \right]}} \\ \end{aligned}$$

(16)

where

$$x_{\text{mc}} = \mathop \sum \limits_{c = 1}^{C} \bar{q}_{c} w^{ - } (c)$$

(17)

we have:

$$y_{\text{mc}} = \zeta (x_{\text{mc}} ).$$

3.6 Genetic learning algorithm model

The proposed genetic learning algorithm on this article is an autoencoder based on the extreme learning machine (ELM) presented by Huang et al. [17,18,19,20,21] for single-layer feedforward networks (SLFN). For N arbitrary distinct samples (x_i, t_i), where x_i = [x_i1, x_i2, … x_in]^T$\in$Rⁿ and t_i = [t_i1, t_i2, … t_im]^T$\in$R^m, an standard SLFN with $N^{{\prime }}$ hidden nodes and activation function g(x) is mathematically modeled as:

$$f_{{N^{{\prime }} }} \left( {x_{j} } \right) = \mathop \sum \limits_{i = 1}^{{N^{{\prime }} }} \beta_{i} g_{i} (x_{j} ) = \mathop \sum \limits_{i = 1}^{{N^{{\prime }} }} \beta_{i} g_{i} \left( {w_{i} \cdot x_{j} + b_{i} } \right) = t_{j} \quad {\text{for}}\, j = 1, \ldots N$$

(18)

where w_i = [w_i1, w_i2, … w_in]^T is the weight vector connecting the ith hidden node and the input nodes, β_i = [β_i1, β_i2, … β_im]^T is the weight vector connecting the ith hidden node and the output nodes, b_i is the threshold of the ith hidden node and g(x) activation function of hidden nodes. The above N equations can be written as:

$$\begin{aligned} & h\left( x \right)\beta = t_{j} \\ & H\beta = T \\ \end{aligned}$$

(19)

where T = [t_i1, t_i2, … t_im]^T are the target outputs and H = [g_i(w₁·x₁ + b₁), g_i(w₂·x₂ + b₂), … g_i(w_n′·x_n′ + b_n′)]^T. The output weights β can be calculated by Eq. 6:

$$\beta = H^{\dag } T$$

(20)

where H^† is the Moore–Penrose generalized inverse of matrix H.

Extreme learning machine [17,18,19,20,21] proves that the input weights and hidden layer biases of SLFNs can be randomly assigned if the activation functions in the hidden layer are infinitely differentiable. In addition, SLFNs can be considered as a linear system where the output weights can be analytically determined through simple generalized inverse operation of the hidden layer output matrices.

The proposed genetic learning algorithm is based on an ELM auto encoder that models the genome as it codes the replica of the organism that contains it. It consists of two instances of the network described in Sect. 3.4. Network 1 is formed of U input neurons and C clusters, and network 2 has C input neurons and U clusters (Fig. 6). The organism is represented as a set of data X which is a U vector $X \, \in \, \left[ {0,1} \right]^{U}$. The genetic learning algorithm fixes C to 4 neurons that represent the four different nucleoids G, C, A and T and it also fixes W₁ to generate four different types of neurons rather than random values as proposed by the ELM theory. The operational complexity of the proposed algorithm is O(n²).

Fig. 6

Genetic learning algorithm

Network 1 encodes the organism, and it is defined as:

• q₁ = (q¹₁, q¹₂, …, q¹_u), a U-dimensional vector $q_{1} \in \left[ {0,1} \right]^{U}$ that represents the input state q_u for neuron u;

• W₁ is the U × C matrix of weights w⁻₁(u,c) from the U input neurons to the neurons in each of the C clusters;

• Q¹ = (Q¹₁, Q¹₂, …, Q¹_c), a C-dimensional vector $Q^{1} \in \left[ {0,1} \right]^{C}$ that represents state q_c for the cluster c where $Q^{1} \, = \,\zeta \left( {W_{1} X} \right)$.

Network 2 decodes the genome, as the pseudoinverse of Network 1, it is defined as:

• q₂ = (q²₁, q²₂, …, q²_c), a C-dimensional vector $q_{2} \in \left[ {0,1} \right]^{C}$ that represents the input state q_c for neuron c with the same value as Q¹ = (Q¹₁, Q¹₂, …, Q¹_c);

• W₂ is the C × U matrix of weights w⁻₂(c,u) from the C input neurons to the neurons in each of the U cells;

• Q² = (q²₁, q²₂, …, q²_u), a U-dimensional vector $Q^{2} \in \, \left[ {0,1} \right]^{U}$ that represents the state q_u for the cell u where Q² = ζ(W₂Q¹) or Q² = ζ(W₂ζ(XW₁)).

The learning algorithm is the adjustment of W₁ to code the organism X into the four different neurons or nucleoids and then calculate W₂ so that resulting decoded organism Q₂ is the same as the encoded organism X:

$$\hbox{min} \left\| {X - \zeta \left( {W_{2} \zeta \left( {XW_{1} } \right)} \right)} \right\| {\text{s}} . {\text{t}} . \,W_{1} \ge 0 (W_{1} {\text{positive definite)}}$$

(21)

Following the extreme learning machine model, W₂ is calculated as:

$$\zeta \left( {XW_{1} } \right)W_{2} = X$$

(22)

we have:

$$W_{2} = {\text{pinv}}\left( {\zeta \left( {XW_{1} } \right)} \right)X$$

(23)

where pinv is the Moore–Penrose pseudoinverse:

$${\text{pinv}}(x) = \left( {x^{T} x} \right)x^{T} .$$

4 Management decision structure: smart investment

The management decision structure combines in a hierarchal way the four presented different learnings: reinforcement learning, deep learning, deep learning management clusters and genetic learning (Fig. 7). This approach enables structured decisions based on shared information where different learnings are specialized in a decision area. Final decisions are taken collaboratively to achieve a bigger reward that includes the entire decision-making chain.

Fig. 7

Management decision structure: smart investment

The smart investment model, named “GoldAI Sachs,” is formed of clusters of intelligent bankers that take local fast binary decisions “buy or sell” on a specific asset based on reinforcement learning (RL) through the interactions and adaptations with the environment where the reward is the profit made. Each asset banker has an associated deep learning (DL) cluster that learns asset identity such as price and reward.

Asset bankers are dynamically clustered to different properties such as investment reward, risk or market type being managed by a market banker deep learning management cluster that selects the best performing asset bankers. The market bankers specialize in learning which asset banker will take the best decision, rather than directly the asset properties.

Finally, a CEO banker deep learning management cluster manages the different market bankers and takes the final structured investment decisions based on the market reward and associated risk prioritizing markets that generate more reward at a lower risk, as any banker would do. The CEO banker genetic algorithm provides immortality: the entire subject’s information, defined as the combination of memory, identity and decision data, is never lost but transmitted to future generations.

4.1 Asset banker reinforcement learning

The asset banker reinforcement learning algorithm used in the proposed model takes only two fast binary local asset investment decisions. Each intelligent banker is formed of two interconnected neurons where the investment decision is taken according to the neuron that has the maximum potential.

“GoldAI Sachs” asset banker reinforcement learning is defined as:

• q₀, neuron 0 for a buy decision

• q₁, neuron 1 for a sell decision

The reward R is based on the economic profit that the asset bankers achieve with the decisions they make, successive measured values of the R are denoted by R_l, l = 1,2…; these are used to compute the predicted reward:

$$PR_{l} = \alpha PR_{l - 1} + \, \left( {1 - \alpha } \right)R_{l}$$

(24)

where α represents the investment reward memory that can be statically assigned or dynamically updated based on the external observations.

If the observed measured reward is greater than the associated predicted reward; reinforcement learning rewards the decision taken by increasing the network weight that point to it; otherwise; it penalizes it:

• if R_l > PR₁:

  $$\begin{aligned} & {\text{Reward}}\,{\text{Buy}}\,{\text{decision:}}\,w^{ + }_{10} = \, w^{ + }_{10} + \left| R \right| \\ & {\text{or}}\,{\text{Reward}}\,{\text{Sell}}\,{\text{decision:}}\,w^{ + }_{01} = \, w^{ + }_{01} + \left| R \right| \\ \end{aligned}$$

  (25)

• Otherwise, if R_l < PR₁:

  $$\begin{aligned} & {\text{Penalise}}\,{\text{Buy}}\,{\text{decision:}}\,w^{ - }_{10} = \, w^{ - }_{10} + \, \left| R \right| \\ & {\text{or}}\,{\text{Penalise}}\,{\text{Sell}}\,{\text{decision:}}\,w^{ - }_{01} = \, w^{ - }_{01} + \, \left| R \right| \\ \end{aligned}$$

  (26)

In addition to the reinforcement leaning, asset bankers make prediction price assets (PPA) based on the previous prediction (PAP) and current price asset (CPA):

$${\text{PPA}}_{l} = \gamma {\text{PAP}}_{l - 1} + \, \left( {1 - \gamma } \right){\text{CPA}}_{l}$$

(27)

where γ represents the asset price prediction memory.

4.2 Asset banker deep learning cluster

Deep learning is used to learn key investment values that generate asset identity. The smart investment model assigns a deep learning cluster per asset banker. Each different deep learning cluster learns the asset reward or profit prediction, the asset price and the asset price prediction.

“GoldAI Sachs” groups asset bankers dynamically into market sectors according to their risk, profit or type. The model defines a set of x asset banker deep learning clusters as:

• I_Banker-x = (i^Banker-x₁, i^Banker-x₂, …, i^Banker-x_u) a U-dimensional vector where i^Banker-x₁, i^Banker-x₂, and i^Banker-x_u are the same banker number x;

• w⁻_Banker-x(u, c) is the $U \times C$ matrix of weights of the deep learning cluster for banker x;

• Y_Banker-x = (y^Banker-x₁, y^Banker-x₂, …, y^Banker-x_c) a C-dimensional vector where y^Banker-x₁ is the reinforcement learning reward prediction, y^Banker-x₂ is the dynamic reward prediction, y^Banker-x₃ is the transaction price, and y^Banker-x_c is the price prediction for banker number x.

4.3 Market banker deep learning management cluster

The market banker deep learning management cluster analyzes the predicted reward from its respective asset banker deep learning clusters, prioritizes their values based on local market knowledge and finally reports to the CEO banker deep learning management cluster the total predicted profit that its market can make.

“GoldAI Sachs” model defines a set of x market banker deep learning management clusters as:

• I_{MarketBanker-x}, a C-dimensional vector $I_{{{{\rm MarketBanker}\text{-}}x}} \in \, \left[ {0,1} \right]^{C}$ with the values of the predicted rewards from asset banker x;

• w⁻_{MarketBanker-x} (c) is the C-dimensional vector of weights that represents the priority of each asset banker x;

• Y_{MarketBanker-x}, a scalar $Y_{{{{\rm MarketBanker}\text{-}}x}} \in \, \left[ {0,1} \right]$ that represents the predicted profit the market banker deep learning management cluster can make.

4.4 CEO banker deep learning management cluster

The CEO banker deep learning management cluster, “AI Morgan” takes the final investment management decision based on the inputs from the market bankers and the associated. The CEO banker selects the markets that can generate better reward at lower risk where the maximum risk is defined as β by the “GoldAI Sachs” board of directors, or other user, where the higher the value the higher risk. β can be statically assigned or dynamically updated based on the external observations.

“GoldAI Sachs” model defines the CEO banker deep learning management cluster:

• I_CEO-Banker, a X-dimensional vector $I_{{{{\rm CEO}}\text{-}{{\rm Banker}}}} \in \, \left[ {0,1} \right]^{X}$ with the values of the set x banker DL management clusters;

• w⁻_CEO-Banker (c) is the C-dimensional vector of weights that represents the risk associated to each market;

• Y_CEO-Banker, a scalar $Y_{{{{\rm CEO}\text{-}{\rm Banker}}}} \in \left[ {0,1} \right]$ that represents the final investment decision.

4.5 CEO banker genetic algorithm

Genetic learning transmits entirely the knowledge acquired from the CEO banker, defined as the combination of memory, identity and decision data, to future banker generations when “AI Morgan” considers itself no longer valid due energy limitations or cybersecurity attacks. Because the CEO banker information is never lost but transmitted to future generations, genetic algorithm provides immortality rather than reinforcement learning applied in fast local decisions or deep learning in identity (Fig. 8).

Fig. 8

“GoldAI Sachs” smart investment model definition

“GoldAI Sachs” model defines genetic learning as an autoencoder where:

• X_Genetic = (x^Genetic₁, x^Genetic₂, …, x^Gentetic_u) a U-dimensional vector where x^Genetic₁, x^Genetic₂, and x^Genetic_u are outputs of the x banker deep learning clusters;

• w⁻_Genetic−1 (u, c) is the U × C matrix of weights of the genetic encoder;

• Y_Nucleoid = (y^Nucleoid₁, y^Nucleoid₂, …, y^Nucleoid_c) a C-dimensional vector where y^Nucleoid₁, …, y^Nucleoid_c is the value of the nucleoid

• w⁻_Genetic−2(c, u) is the C × U matrix of weights of the genetic decoder;

• Y_Generation = (y^Generation₁, y^Generation₂, …, y^Generation_c) a C-dimensional vector where y^Generation₁, …, y^Generation_c is the value of the new banker generation.

5 Smart investment implementation

“GoldAI Sachs” is implemented in Java with eight asset bankers clustered in two different markets; bond market is low reward and therefore low risk, whereas risk market is high reward and high risk.

5.1 Asset banker reinforcement learning and deep learning clusters

Each asset banker has a two-node reinforcement learning algorithm to make local fast decisions “buy or sell” trade on different assets. the banker DL cluster learns the asset properties to create asset identity; it has four inputs cells (u = 4) and four output clusters (c = 4) where the input cell is the normalized value of the x asset banker identification: x (i^Banker-x₁ = 0·x, i^Banker-x₂ = 0·x, i^Banker-x₃ = 0·x, i^Banker-x₄ = 0·x) and the output clusters are the normalized asset properties: (y^Banker-x₁ = reinforcement learning reward prediction, y^Banker-x₂ = dynamic reward prediction, y^Banker-x₃ = transaction price, y^Banker-x₄ = price prediction as shown in Table 1. “GoldAI Sachs” normalizes the DL clusters; the inputs to: x/10 and the outputs to (reward or price/100) + 0.5, respectively, to keep the learning algorithm within the stable region.

Table 1 Asset banker DL cluster implementation

5.2 Market banker deep learning management clusters

“GoldAI Sachs” has two market banker DL management clusters for the bond and commodities market, respectively. The inputs of the market bankers are the predicted asset banker rewards, whereas the output is the predicted reward the market can make. The network weighs are the asset banker priority; i.e., the best asset banker only to be considered with the maximum banker set at 1.0 and others at 0.0 or the four Bankers with the same priority; with all the network weights set at 0.25 as shown in Table 2.

Table 2 Market banker DL management cluster implementation

5.3 CEO banker deep learning management clusters

The input of the CEO banker deep learning management cluster is the market profit provided by the market bankers and its network weight is the risk associated to each market. The smart investment model considers that market risk level is related to the reward the market can generate. The CEO banker, “AI Morgan” starts gradually assessing the reward increasing the risk β from 0.1 up to the maximum risk limit permissible by “GoldAI Sachs” owner or manager. “AI Morgan” then takes the final decision based on a greater predicted reward at the lowest risk β as represented in Table 3.

Table 3 CEO banker DL management cluster implementation

5.4 CEO banker genetic algorithm

Genetic learning algorithm is an autoencoder where the Market’s properties, identity and decisions learned by the banker deep learning clusters are codified into four neurons that represent the 4 nucleoids of the Genome: (cytosine [C], guanine [G], adenine [A] or thymine [T]). These values are transmitted to the next generation in a daily basis.

The input X_Genetic to the genetic algorithm corresponds to a 32-dimensional vector where x^Genetic₁, x^Genetic₂, … x^Genetic₃₂ correspond to the 4 outputs of the 8 asset bankers Y_Banker-xY_{Gene a} is 4-dimensional vector where y^Nucleoid,₁ …, y^Nucleoid₄ is the value of the four different nucleoids. The output of the genetic algorithm Y_Generation corresponds to the input X_Genetic as shown in Table 4.

Table 4 Genetic algorithm implementation

6 Smart investment experimental results

“GoldAI Sachs” is evaluated with eight different assets to assess the adaptability and performance of our proposed smart investment solution for 11 days. The assets are split into the bond market with low risk and slow reward and the derivative market with high risk and fast reward (Fig. 9). Experiments are carried out with reinforcement learning first initialized with a buy decision.

Fig. 9

Smart investment data model

6.1 Asset banker reinforcement learning validation

The profit that each asset banker makes when buying or selling 100 assets for 11 days with the maximum profit, the ratio between both the number of winning decisions against the losing ones and the number of buy decisions against the sell, is shown in Tables 5 and 6. The validation covers three different values of investment reward memory α.

Table 5 Asset banker reinforcement learning validation; α = 0.1

Table 6 Asset banker reinforcement learning validation; α = 0.5 and α = 0.9

The simulation results are almost independent from the value of the investment reward memory α, this is due the reduced complexity in asset price variation. The reinforcement learning algorithm adapts very quickly to variable asset prices where asset 6 shows that the lowest investment memory, α = 0.1, is the optimum value. The profit made in assets that start downward such as asset 2, asset 4, asset 6 and asset 8 is worse than the upward ones because the asset bankers are initialized with a buy decision.

6.2 Asset banker deep learning cluster validation

The asset banker deep learning cluster validation for the eight different assets during the 11 different days is shown in Table 7. The learning algorithm error threshold is set at 1.0E−25. The first value is the final iteration number for learning algorithm number, and the second is the normalized error at 1.0E−26.

Table 7 Asset banker deep learning cluster validation

The learning algorithm of the deep learning clusters is very stable; it achieves a minimum error 1.0E−25 with very reduced iterations.

6.3 Market banker deep learning management cluster validation

The profits generated by the market bankers are shown in Tables 8 and 9 and Figs. 10 and 11. The market bankers take market decisions rather than individual asset decisions form the asset bankers. Market bankers invest 400 assets which is the combination of the four asset bankers purchasing power. The combined profits that the asset bankers can make independently and the profits the bond market manager can obtain are presented; in addition, the maximum values are also shown.

Table 8 Bond market banker profits; α = 0.1

Table 9 Derivative market banker profits; α = 0.1

Fig. 10

Bond market banker accumulative profits; α = 0.1

Fig. 11

Derivative market banker accumulative profits; α = 0.1

The addition of a specialized market banker deep learning management cluster increases the profits almost to the maximum value. Tables 10 and 11 represent the bond and derivative market bankers deep learning management clusters values.

Table 10 Bond market banker deep learning management cluster validation

Table 11 Derivative market banker deep learning management cluster validation

6.4 CEO banker deep learning management cluster validation

The CEO banker, “AI Morgan,” profited at different risks ratios with a total of investment of 800 assets is represented in Table 12. A low risk value β = 0.2 represents 640 assets in the bond market (B) and 160 is the derivative market (D), whereas a high risk value β = 0.8 is 160 assets in the bond market and 640 in the derivative market, respectively.

Table 12 CEO banker profits; α = 0.1

The more risk the CEO banker “AI Morgan” takes, the more profit is able to generate as the investment decisions are directed to the derivative market reaching nearly optimum values. Table 13 and Fig. 12 represent the CEO banker deep learning management clusters values at different risks with the final risk decision.

Table 13 CEO banker deep learning management cluster validation

Fig. 12

CEO banker accumulative profits; α = 0.1

6.5 CEO banker genetic algorithm validation

The genetic algorithm validation for the four different nucleoids (C, G, A, T) during the 10 different days is shown in Tables 14 and 15 with the genetic algorithm error.

Table 14 Genetic algorithm validation

Table 15 Genetic algorithm validation

The genetic algorithm codifies the CEO banker and transmits this information to the next generations with a residual error with only one iteration at a minimum time.

7 Cryptocurrency evaluation

“GoldAI Sachs” is evaluated with seven different assets to assess the adaptability and performance of our proposed smart investment solution for 664 days, from 07/08/2015 to 31/05/2017. The assets are split into the Bitcoin exchange market (BITSTAMP, BTCE, COINBASE, KRAKEN) and the currency market (Bitcoin, Ethereum, Ripple). Reinforcement learning is first initialized with a buy decision.

Cryptocurrency evaluation data has been produced though datasheets obtained from Kraggle; only three different currencies were found (Fig. 13). The values of the different assets within the Bitcoin exchange market are very similar as they trade the same currency, whereas the currency market presents a more disperse set of values.

Fig. 13

Cryptocurrency investment data model

7.1 Asset banker reinforcement learning validation

The profit that each asset banker makes when buying or selling 100 assets for 664 days from year 2015 to 2017 with the maximum profit, the ratio between both the number of winning decisions against the losing ones and the number of buy decisions against the sell, is shown in Tables 16, 17 and 18. The validation covers three different values of investment reward memory α.

Table 16 Asset banker reinforcement learning validation; α = 0.1, year 2015–2017

Table 17 Asset banker reinforcement learning validation; α = 0.5, year 2015–2017

Table 18 Asset banker reinforcement learning validation; α = 0.9, year 2015–2017

The RNN reinforcement learning algorithm adapts very quickly to variable asset prices and makes profits; although not to optimum values. The value of the investment reward memory does not have a mayor impact in the overall profit due to the great adaptation of reinforcement learning algorithm though a high value of investment reward memory generates more profits (Fig. 14).

Fig. 14

Asset banker reinforcement learning validation; α = 0.1; α = 0.5; α = 0.9

7.2 Asset banker deep learning cluster validation

The asset banker deep learning cluster validation for the seven different assets during the 664 different days from year 2015 to 2017 is shown in Table 19. The learning algorithm error threshold is set at 1.0E−25. The first value is the final iteration number for learning algorithm number, and the second is the normalized error at 1.0E−26.

Table 19 Asset banker deep learning cluster validation

7.3 Market banker deep learning management cluster validation

The profit the market bankers can make for the 664 days from year 2015 to 2017 is shown in Tables 20, 21 and 22 where the validation includes three different values of investment reward memory α. The market bankers take market decisions rather than individual asset decisions form the asset bankers. Bitcoin exchange market banker invests 400 assets which is the combination of the four asset bankers purchasing power whereas currency market banker invests 300 assets as there are only three asset bankers.

Table 20 Market banker profits; α = 0.1, year 2015–2017

Table 21 Market banker profits; α = 0.5, year 2015–2017

Table 22 Market banker profits; α = 0.9, year 2015–2017

The Bitcoin exchange market banker does not increase the profits of the market; this is mostly due to the fact that the four Bitcoin exchange asset bankers perform very similarly on almost equal asset conditions therefore with the addition of a market banker, the independent knowledge acquired by each asset banker is lost. However, when the currency asset bankers operate under diverse asset conditions, the addition of a currency market banker increases the market profit due to the right selection of the best performing asset banker. Different values of investment reward memory have an impact on the final profit where a balanced investment reward memory (α = 0.5) between previous and last investment provides optimum results (Figs. 15, 16).

Fig. 15

Exchange market banker profits; α = 0.5

Fig. 16

Currency market banker profits; α = 0.5

Table 23 represents the bond and derivative market bankers deep learning management clusters average values for the 664 days from year 2015 to 2017.

Table 23 Bond and derivative market banker deep learning management cluster validation

7.4 CEO banker deep learning management cluster validation

The CEO banker, “AI Morgan,” profits at different risks ratios β with a total of investment of 700 assets for different investment reward memories α is shown in Tables 24, 25 and 26 for the 664 days from year 2015 to 2017. A risk value β = 0.2 represents 560 assets in the exchange market and 140 in the currency market whereas a risk value β = 0.8 is 140 assets in the exchange market and 560 in the currency market, respectively. This research considers the exchange market as low risk and the currency market as high risk.

Table 24 CEO banker profits; α = 0.1, year 2015–2017

Table 25 CEO banker profits; α = 0.5, year 2015–2017

Table 26 CEO banker profits; α = 0.9, year 2015–2017

The results are consisted with the previous validation the best reward is at α = 0.5. The CEO banker takes the right decisions where the profits increase as the risk increases. Table 27 represents the CEO banker deep learning management clusters values at different risk decisions (Figs. 17, 18).

Table 27 CEO banker deep learning management cluster validation

Fig. 17

CEO banker maximum profits; α = 0.5

Fig. 18

CEO banker profits; α = 0.5

7.5 CEO banker genetic algorithm validation

The genetic algorithm validation for the four different nucleoids (C, G, A, T) average value during the 664 different days from year 2015 to 2017 is shown in Table 28 with the genetic algorithm error. The genetic algorithm codifies the CEO banker with a residual error.

Table 28 Genetic algorithm validation, year 2015–2017

8 Conclusions

This article has presented a management decision structure based on the human brain with its hierarchical decision process. In addition, this article has defined a new learning genetic algorithm based on the genome where the information is transmitted in the network weights rather than through the neurons. The management decision structure has been implemented in a Fintech application: smart investment model that simulates the human brain with reinforcement learning for fast decisions, deep learning to learn properties to create asset identity, deep learning management clusters to make global decisions and genetic to transmit learned information and decisions to future generations.

In the smart investor model, “GoldAI Sachs” asset banker reinforcement learning algorithm takes the right investment decisions; with great adaptability to asset price changes whereas asset banker deep learning learns asset properties and identity. Market bankers success to increase the profit by selecting the best performing asset bankers and the CEO banker, “AI Morgan,” increases the profits considering the associated market risks, prioritizing low risk investment decision at equal profit.

Genetic learning transmits entirely the knowledge acquired from the CEO banker, defined as the combination of memory, identity and decision data, to future banker generations at a minimum error and time. Because the CEO banker information is never lost but transmitted to future generations, genetic algorithm provides immortality. Future work will analyze different methods to improve the performance or increase the profits, of the proposed deep learning cluster structure.

Appendix: Smart investment model—neural schematic