1 Introduction

Efficiency scores of decision-making units (DMUs) is one of the important criteria that managers and policy makers use for future planning to improve the performance of the DMUs. Several parametric and nonparametric methods in measuring efficiency have been proposed, e.g. corrected ordinary least-squares (COLS), stochastic frontier analysis (SFA), data envelopment analysis (DEA) [1]. Perhaps a nonparametric method, DEA, proposed by Charnes et al. [2] is the most popular approach for measuring efficiency. DEA is an evaluation methodology for measuring the relative efficiency of homogenous DMUs when there are multiple inputs and multiple outputs.

Since DEA has been introduced, its application has been verified for solving a wide range of problems. For example, DEA has been applied to evaluate the efficiency of the banks, agriculture, hospitals, universities, airlines, environmental sustainability, supply chain management and many other areas (see Emrouznejad and Yang [3] and Emrouznejad and De Witte [4]).

Here we present the first DEA model has been proposed by Charnes et al. [2].

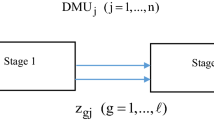
Suppose there are n DMUs, where each \({\text{DMU}}_{j} (j = 1, \ldots ,n)\) consumes m inputs, xij (i = 1, …, m), to produce s outputs, yrj (r = 1, …, s).Considering ur (r = 1, …, s) and vi (i = 1, …, m) as relative importance of each output, and input, respectively, the DEA formulation to calculate the relative efficiency of a given \({\text{DMU}}_{\text{O}}\) is presented as follows [2]:

$$\begin{aligned} & {\text{Max }}\sum\limits_{r = 1}^{s} {u_{r} y_{ro} } \\ & \quad {\text{s.t.}} \\ & \quad \sum\limits_{r = 1}^{s} {u_{r} y_{rj} } - \sum\limits_{i = 1}^{m} {v_{i} x_{ij} } \le 0,\quad j = 1, \ldots ,n \, \\ & \quad \sum\limits_{i = 1}^{m} {v_{i} x_{io} } = 1, \\ & \quad u_{r} > 0,\quad r = 1, \ldots ,s, \\ & \quad v_{i} > 0,\quad i = 1, \ldots ,m \\ \end{aligned}$$
(1)

where xio and yro are the ith input and rth output of under assessing DMU (\({\text{DMU}}_{\text{O}}\)).

Model (1) runs for each DMU, and the efficiency scores are calculated as well as relative importance of inputs and outputs. One of the issues with using DEA is large number of input and output variables when there is not enough number of DMUs. It is a rule of thumb that the relation between the number of DMUs (n) and the number of inputs (m) and outputs (s) is usually be 3(m + s) < n [5]. Accordingly, DEA may not be able to distinguish DMUs if we consider all relevant inputs and outputs, since it requires large number of DMUs. Therefore, researchers usually eliminate some of the variables if number of DMUs is not large enough. However, this means ignoring some information which may leads to incorrect performance evaluation. This is an important shortcoming in DEA, since in the most real-world applications, the number of existing DMUs is not sufficient as compared to number of input and output variables. Researchers have tried to addresses this issue using various approaches, e.g. a multivariate statistical approach for reducing the number of inputs and outputs proposed by [6]. Cook and Zhu [7] proposed a simple ratio analysis for classifying inputs and outputs. Specifically, to overcome the mentioned limitation and to increase the discrimination power of DEA, Rezaee et al. [8] applied the Nash bargaining game model to determine the efficiency of DMUs when the number of DMUs is insufficient, by comparing DMUs while dividing them in two different categories of measures in the competitive environment. In the proposed approach by Rezaee et al. [8] each category of inputs is assumed to act as an independent bargaining player for a better payoff. They have applied the model to measure the efficiency of to 24 thermal power plants.

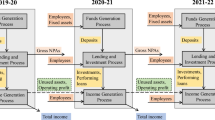
On the other hand, many recent publications focused on network structure of decision-making units. In real-world applications, most DMUs have complex network structure; hence, considering a simple structure which contains only one stage for all DMUs may not be logical. In Fig. 1, three types of classical network DEA structure including typical two-stage, parallel and serial structures are presented (Fig. 1a–c, respectively) [9].

Fig. 1
figure 1

Network structure of DMUs using DEA models.

Full size image

The network DEA models have been applied to evaluate the efficiency of a wide variety of applications, such as universities [10], electricity power production and distribution plants [11], investment trust corporations [12], production systems [13], sustainability of supply chain management systems [14, 15], energy saving and emission reduction [16], banking [17], bus transit systems [18], airlines [19], and insurance industry [20].

It is obvious that analyzing efficiency of complex organizations with network structures is more realistic than non-network structures analysis. Illustrated structures in Fig. 1 clearly show that intermediate inputs and outputs in all stages can be considered by network DEA, whereas the classical DEA model considers the initial inputs and final outputs of a DMU only. Also, the classical DEA model optimizes the efficiency score of a DMU, by calculating the ratio between weighted initial inputs and final weighted outputs. In contrast, in the network DEA models, not only the score of the whole network is calculated but also the efficiency score of each stage is obtained by considering ratios of weighted inputs to weighted outputs in each single stage.

Another important shortcoming of classical DEA is its sensitivity to structure of the network. Applying classic DEA in network structure confronts some conflicts due to the fact that the output of a stage is an input for a subsequent stage; hence, the complexity of this issue must be handled in the model. The issue is that while the classic DEA model tries to maximize the efficiency of first stage by increasing the intermediate outputs in the first stage, the model is expected to decrease these outputs since they are needed for using as inputs in the following stage simultaneously. Some researches applied the classic DEA methodology separately for each stage without considering the link between the two stages to assess the efficiency in network structure DEA. Wang et al. [21] and Seiford and Zhu [22] were the first researchers who studied these conflicts. Other researchers focused on linked network DEA approaches, relational network DEA approach and game theory models (cooperative and non-cooperative approaches) [for more information see Halkos et al. [23]). For example Kao and Hwang [24] proposed an approach which combines efficiency scores of the two stages in a multiplicative (geometric) manner. Chen et al. [25] used a weighted additive model to aggregate two stages and decomposed the efficiency of the overall process. Du et al. [26] proposed a Nash bargaining game model to assess the efficiency of DMUs that have two-stage structure. Specifically, Du et al. [26] considered each stage as a player in Nash bargaining game.

In network DEA models, especially where a DMU has more than two stages (multi-stage structures), beside the problem of conflicts between stages, the number of assessed DMUs should be large enough due to variety number of inputs and output used within sub-networks. In the current paper, we apply two-player and three-player Nash bargaining game model to overcome the shortcomings of classic DEA in the DMUs with network structure when the number of DMUs is not sufficient. Considering the case of bank branches, we first identify the network structure, using the most common input and output variables in the literature and by considering the expert opinions. This structure is presented in Fig. 2 that considered a network with five sub-process; m1 and m2 are the number of inputs in sub-process 1 and sub-process 3, respectively. Where L1 is the number of inputs for sub-process 2 which are outputs from sub-process 1. Also L3 is the number of inputs for sub-process 4 which are outputs from sub-process 3. L2 and L4 are the number of additional inputs in sub-process 2 and sub-process 4, respectively. D1 shows the number of sub-process 5 inputs which are the outputs from sub-process 2 (sub-network 1). D2 represents the number of inputs of sub-process 5 which are output of sub-process 4 (sub-network), where s is the number of outputs from sub-process 5 which are final outputs of network.

Fig. 2
figure 2

Proposed network DEA structure

Full size image

As it can be seen, this network has a hybrid structure of serial network and parallel network. While the trend of sub-processes 1, 2 and 5 (and similarly; sub-process 3, 4 and 5) is a serial network, the trend between sub-processes 1 (and 2) with sub-processes 3 (and 4) is parallel. As shown in Fig. 2, both problems of conflicts between stages and shortage of the number of DMUs may happen in this structure.

In proposed two-player and three-player Nash bargaining game model, we consider two and three distinct sub-networks, respectively. Also, each sub-process is assumed as a player which bargains with other players for a better payoff. Note that this payoff is the efficiency of each individual stage.

The rest of this paper is organized as follows: Sect. 2 provides a review on Nash bargaining game. This is followed by the approach developed for performance assessment of network DEA based on bargaining game model in Sect. 2.2. Also, the theoretical properties of proposed models are discussed in Sect. 2.3. In order to show the capability of the proposed model, a real case study of an Iranian banking system is studied in Sect. 3. Section 4 shows the applicability of the proposed model in measuring efficiency of bank branches by analyzing the results. Finally, conclusion and direction for future research are drawn in Sect. 5.

2 Proposed approach

2.1 Bargaining game

Nash bargaining game model is a cooperative game theory model which first introduced by Nash Jr. [27] for two-person games and extended by Harsanyi [28] for n-person games. Bargaining game model divides the benefits between players based on their competition and bargaining power. The n-person Nash–Harsanyi bargaining game model is:

$$\begin{aligned} & \mathop {\hbox{max} }\limits_{X \in S} \quad \prod\limits_{i = 1}^{N} {(U_{i} (X) - d_{i} )} \\ & \quad {\text{s.t.}}\\ & \quad U_{i} (X) \ge d_{i} \quad \forall i \in \left\{ {1, \ldots ,N} \right\} \\ & \quad X \in S \\ \end{aligned}$$
(2)

where Ui and di are utility and breakdown point of player i, respectively. di is parameters of the model. It should be noted that players would withdraw from the game, if they obtain benefits lower than their breakdown point. In fact, breakdown point is the starting point for bargaining. X is a discrete variable for continuous strategy in game theory context. Ui is the utility of player i in strategy X. S is the feasible set of the model. In model (2), the feasible set must be convex and contain some payoff vectors in a way that benefit of each player is greater than its breakdown point [27].

In this paper, each sub-process and inputs’ category is considered as a player in Nash bargaining game model and the efficiency score for each one is considered as utility of that player. Borrowing the idea of Nash bargaining game model as a one of cooperative models in game theory, the goal of the proposed approach is maximizing the overall efficiency of a sub-network or network by considering the efficiency scores of each sub-network or inputs’ category as a player. We have used the Nash bargaining game model since, firstly, the Nash bargaining model is a cooperative model which chooses a strategy to maximize the utility of all players, simultaneously. Hence, by considering each sub-processes and input categories as the players, the optimal weights to maximize the efficiency of sub-networks can be obtained by considering the weights of inputs/outputs as strategies and efficiency of each sub-process as its utility. Secondly, by dividing the network into sub-networks and sub-networks into sub-process and considering each sub-process as a player, the number of inputs/outputs used for evaluation of each player can be decreased and so DEA can be used even with small number of DMUs.

2.2 Breakdown points in proposed model

The breakdown point is the determining parameter in model (2). Binmore et al. [29] argued that the choice of breakdown point completely depends on players’ viewpoints and is a matter of modeling judgment in Nash bargaining game. To evaluate efficiency of DMUs using proposed game-DEA model in this paper, the breakdown point must be calculated for each category and sub-process which are considered as a player in Nash bargaining game model. To estimate the breakdown points, we use the approach proposed by Du et al. [26]. They added a virtual DMU with the maximum amount of inputs while producing the least amount of output values for each stage. Suppose x max i  = max j{xij}and y min r  = min j{yrj} for each player. Since each DMU uses maximum amount of inputs to produce the least amount of outputs, efficiency scores obtained by classic DEA for (x max i , y min r ) represents the least achievable efficiency for each player. We use this approach to determine breakdown point for each player.

2.3 Network game-DEA model

Consider a network structure process shown in Fig. 2. It is supposed that there are n DMUs where each DMU has five different sub-processes. Because of multi-stage structure of DMUs and the number of inputs and outputs in each sub-process, both problems of conflicts between stages and needed number of DMUs are considered in this study. Note that the sufficient number of DMUs is obtained using Eq. (3), considering the structure shown in Fig. 2:

$$n > 3(m_{1} + m_{2} + L_{1} + L_{2} + L_{3} + L_{4} + D_{1} + D_{2} + s)$$
(3)

where m1, m2, L1, L2, L3, L4, D1, D2 and s are the number of inputs and outputs in each category and sub-network which have been defined in previous section.

In our proposed game-DEA model, we have separated each network (shown in Fig. 2) to three different sub-networks. Also for sub-networks 1 and 2 inputs are divided in two different categories (category m1 and m2 inputs for sub-network 1 and category m3 and m4 inputs for sub-network 2). For sub-network 3, inputs are categorized in “inputs which are outputs from sub-network 1” and “inputs which are from sub-network 2” (see Fig. 3 for more details). It should be noted that dividing a network into sub-networks must be based on the operation within each DMU. The proposed structure is for the case we will be using later in banking efficiency, as it will be shown each sub-network has a defined task. Also, categorizing of inputs must be rational. The procedure of identifying the sub-networks, network’s structure, inputs/outputs and categorizing the inputs is explained in detail in Sect. 3.

Fig. 3
figure 3

Structure of DMUs: sub-networks and categorized inputs

Full size image

In sub-networks 1 and 2, there are two types of inputs, each considered to be a player in sub-process 1 and second sub-process 2. We, therefore, proposed a model to evaluate the efficiency of each sub-network (\(e_{o}^{1} , \, e_{o}^{2}\)) using three-person bargaining game model. The outputs from sub-networks 1 and 2 are considered to be input to sub-network 3, as so we used two players bargaining game model for efficiency assessment (e 3 o ). Finally, efficiency of DMUO, eo, is calculated using geometric mean of \(e_{o}^{1} , \, e_{o}^{2}\) and e 3 o . In the proposed model, the sufficient number of DMUs is:

$$n > \hbox{max} \left\{ \begin{aligned} 3(m_{1} + L_{1} ), \, 3(m_{2} + L_{1} ), \, 3(L_{1} + L_{2} + D_{1} ), \, 3(m_{3} + L_{3} ), \hfill \\ 3(m_{4} + L_{3} ), \, 3(L_{3} + L_{4} + D_{2} ), \, 3(D_{1} + s), \, 3(D_{2} + s) \hfill \\ \end{aligned} \right\}$$
(4)

Therefore, as shown in Eq. (4) in comparison with Eq. (3), the needed number of DMUs in our model is significantly low.

2.3.1 Game-DEA model for sub-network 1

In our proposed game-DEA model, each network is separated (shown in Fig. 2) to three different sub-networks. Also for sub-networks 1 and 2, inputs are arranged in two different categories. For sub-network 1, the first and second types of inputs in sub-process 1 have been considered as two different players. Sub-process 2 is the third player (as shown in Fig. 3). Based on model (2) and in order to assess the efficiency of sub-network 1, the proposed three-person bargaining game DEA model can be expressed as follows: .

$$\begin{aligned} & \hbox{max} \, e_{o}^{1} = \left( {\frac{{\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lo}^{11} } }}{{\sum\nolimits_{i = 1}^{{m_{1} }} {v_{i}^{11} x_{io}^{11} } }} - \theta_{\text{FT}}^{1} } \right)\left( {\frac{{\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lo}^{11} } }}{{\sum\nolimits_{k = 1}^{{m_{2} }} {v_{k}^{12} x_{ko}^{12} } }} - \theta_{\text{ST}}^{1} } \right)\left( {\frac{{\sum\nolimits_{d = 1}^{{D_{1} }} {w_{d}^{1} z_{do}^{1} } }}{{\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lo}^{11} } + \sum\nolimits_{b = 1}^{{L_{2} }} {q_{b}^{12} p_{bo}^{12} } }} - \theta_{\text{Sp}}^{2} } \right) \\ & \quad {\text{s.t.}}\\ & \quad \frac{{\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lo}^{11} } }}{{\sum\nolimits_{i = 1}^{{m_{1} }} {v_{i}^{11} x_{io}^{11} } }} \ge \theta_{\text{FT}}^{1} \\ & \quad \frac{{\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lo}^{11} } }}{{\sum\nolimits_{k = 1}^{{m_{2} }} {v_{k}^{12} x_{ko}^{12} } }} \ge \theta_{\text{ST}}^{1} \\ & \quad \frac{{\sum\nolimits_{d = 1}^{{D_{1} }} {w_{d}^{1} z_{do}^{1} } }}{{\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lo}^{11} } + \sum\nolimits_{b = 1}^{{L_{2} }} {q_{b}^{12} p_{bo}^{12} } }} \ge \theta_{\text{Sp}}^{2} \\ & \quad \frac{{\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lj}^{11} } }}{{\sum\nolimits_{i = 1}^{{m_{1} }} {v_{i}^{11} x_{ij}^{11} } }} \le 1\quad j = 1, \ldots ,n \\ & \quad \frac{{\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lj}^{11} } }}{{\sum\nolimits_{k = 1}^{{m_{2} }} {v_{k}^{12} x_{kj}^{12} } }} \le 1\quad j = 1, \ldots ,n \\ & \quad \frac{{\sum\nolimits_{d = 1}^{{D_{1} }} {w_{d}^{1} z_{dj}^{1} } }}{{\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lj}^{11} } + \sum\nolimits_{b = 1}^{{L_{2} }} {q_{b}^{12} p_{bj}^{12} } }} \le 1\quad j = 1, \ldots ,n \\ & \quad v_{i}^{11} ,v_{k}^{12} ,q_{1}^{11} ,q_{b}^{12} ,w_{d}^{1} > 0,\quad i = 1, \ldots ,m_{1} ,\quad k = 1, \ldots ,m_{2} ,\quad l = 1, \ldots ,L_{1} ,\quad b = 1, \ldots ,L_{2} ,\quad d = 1, \ldots ,D_{1} . \\ \end{aligned}$$
(5)

where \(\theta_{\text{FT}}^{1}\), \(\theta_{\text{ST}}^{1}\) and \(\theta_{\text{SP}}^{2}\) are breakdown points for first category of inputs, second category of inputs and sub-process 2, respectively. First, second and third constraints are bargaining breakdown points constraints, where the efficiency of each category and sub-network must be greater than its breakdown point. Fourth, fifth and sixth constraints are related to efficiency, where the efficiency must be < 1.

Lemma 1

Feasible set of model (5) is convex.

Proof

\((v_{1}^{\prime 11} ,v_{2}^{\prime 11} , \ldots v_{{m_{1} }}^{\prime 11} ,v_{1}^{\prime 12} ,v_{2}^{\prime 12} , \ldots ,v_{{m_{2} }}^{\prime 12} ,q_{1}^{\prime 11} ,q_{2}^{\prime 11} , \ldots ,q_{{L_{1} }}^{\prime 11} ,q_{1}^{\prime 12} ,q_{2}^{\prime 12} , \ldots ,q_{{L_{2} }}^{\prime 12} ,w_{1}^{\prime 1} ,w_{2}^{\prime 1} , \ldots ,w_{{D_{1} }}^{\prime 1} )\) and \((v_{1}^{\prime \prime 11} ,v_{2}^{\prime \prime 11} , \ldots v_{{m_{1} }}^{\prime \prime 11} ,v_{1}^{\prime \prime 12} ,v_{2}^{\prime \prime 12} , \ldots ,v_{{m_{2} }}^{\prime \prime 12} ,q_{1}^{\prime \prime 11} ,q_{2}^{\prime \prime 11} , \ldots ,q_{{L_{1} }}^{\prime \prime 11} ,q_{1}^{\prime \prime 12} ,q_{2}^{\prime \prime 12} , \ldots ,q_{{L_{2} }}^{\prime \prime 12} ,w_{1}^{\prime \prime 1} ,w_{2}^{\prime \prime 1} , \ldots ,w_{{D_{1} }}^{\prime \prime 1} )\) are feasible solutions for model (5). For any λ ∊ [0, 1], we have:

$$\begin{aligned} & \lambda v_{i}^{\prime 11} + (1 - \lambda )v_{1}^{\prime \prime 11} > 0,\quad i = 1, \ldots ,m_{1} \\ & \lambda v_{k}^{\prime 12} + (1 - \lambda )v_{k}^{\prime \prime 12} > 0,\quad k = 1, \ldots ,m_{2} \\ & \lambda q_{l}^{\prime 11} + (1 - \lambda )q_{l}^{\prime \prime 11} > 0,\quad l = 1, \ldots ,L_{1} \\ & \lambda q_{b}^{\prime 12} + (1 - \lambda )q_{b}^{\prime 12} > 0,\quad b = 1, \ldots ,L_{2} \\ & \lambda w_{d}^{\prime 1} + (1 - \lambda )w_{d}^{\prime 1} > 0,\quad d = 1, \ldots ,D_{1} \\ \end{aligned}$$

For example, consider the constraint \(\frac{{\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lo}^{11} } }}{{\sum\nolimits_{i = 1}^{{m_{1} }} {v_{i}^{11} x_{io}^{11} } }} \ge \theta_{\text{FT}}^{1}\), since \(\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lo}^{11} } > 0\) and \(\sum\nolimits_{i = 1}^{{m_{1} }} {v_{i}^{11} x_{io}^{11} } > 0\), then this constraint is equal to \(\theta_{\text{FT}}^{1} \sum\nolimits_{i = 1}^{{m_{1} }} {v_{i}^{11} x_{io}^{11} } \le \sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lo}^{11} }\), for all j = 1,…,n. Therefore, we have:

$$\begin{aligned} & \theta_{\text{FT}}^{1} \sum\nolimits_{i = 1}^{{m_{1} }} {\left[ {\lambda v_{i}^{\prime 11} + (1 - \lambda )v_{1}^{\prime \prime 11} } \right]x_{io}^{11} } = \lambda \theta_{FT}^{1} \sum\nolimits_{i = 1}^{{m_{1} }} {v_{i}^{\prime 11} x_{io}^{11} } + (1 - \lambda )\theta_{FT}^{1} \sum\nolimits_{i = 1}^{{m_{1} }} {v_{1}^{\prime \prime 11} x_{io}^{11} } \\ & \quad \le \lambda \sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{\prime 11} p_{lo}^{11} } + (1 - \lambda )\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{\prime \prime 11} p_{lo}^{11} } = \sum\nolimits_{l = 1}^{{L_{1} }} {\left[ {\lambda q_{l}^{\prime 11} + (1 - \lambda )q_{l}^{\prime \prime 11} } \right]p_{lo}^{11} } \\ \end{aligned}$$

It is assumed that data related to DMUs are positive. The similar proof can be used for other constraints; consequently, the feasible region is convex.□

Now, assume \(t_{1} = \left( {\sum\nolimits_{i = 1}^{{m_{1} }} {v_{i}^{11} x_{io}^{11} } } \right)^{ - 1}\), \(t_{2} = \left( {\sum\nolimits_{k = 1}^{{m_{2} }} {v_{k}^{12} x_{ko}^{12} } } \right)^{ - 1}\), \(t_{3} = \left( {\sum\nolimits_{l = 1}^{{L_{1} }} {q_{l}^{11} p_{lo}^{11} } + \sum\nolimits_{b = 1}^{{L_{2} }} {q_{b}^{12} p_{bo}^{12} } } \right)^{ - 1}\), \(\mu_{l}^{1} = t_{1} q_{l}^{11}\), \(\mu_{l}^{2} = t_{2} q_{l}^{11}\), \(\mu_{d}^{3} = t_{3} w_{d}^{1}\), \(\bar{v}_{i}^{11} = t_{1} v_{i}^{11}\), \(\bar{v}_{k}^{12} = t_{2} v_{k}^{12}\), \(\bar{q}_{l}^{11} = t_{3} q_{l}^{11}\) and \(\bar{q}_{b}^{12} = t_{3} q_{b}^{12}\). Accordingly, we have \(\mu_{l}^{2} = \frac{{t_{2} }}{{t_{1} }}\mu_{l}^{1}\), hence by denoting γ = t2/t1, model (5) converts into the following nonlinear model:

$$\begin{aligned} & \hbox{max} \, e_{o}^{1} = \left( {\sum\limits_{l = 1}^{{L_{1} }} {\mu_{l}^{1} p_{lo}^{11} } - \theta_{\text{FT}}^{1} } \right)\left( {\sum\limits_{l = 1}^{{L_{1} }} {\gamma \mu_{l}^{1} p_{lo}^{11} } - \theta_{\text{ST}}^{1} } \right)\left( {\sum\limits_{d = 1}^{{D_{1} }} {\mu_{d}^{3} z_{do}^{1} } - \theta_{\text{Sp}}^{2} } \right) \\ & \quad {\text{s.t.}}\\ & \quad \sum\limits_{l = 1}^{{L_{1} }} {\mu_{l}^{1} p_{lo}^{11} } \ge \theta_{\text{FT}}^{1} \\ & \quad \gamma \sum\limits_{l = 1}^{{L_{1} }} {\mu_{l}^{1} p_{lo}^{11} } \ge \theta_{\text{ST}}^{1} \\ & \quad \sum\limits_{d = 1}^{{D_{1} }} {\mu_{d}^{3} z_{do}^{1} } \ge \theta_{\text{Sp}}^{2} \\ & \quad \sum\limits_{l = 1}^{{L_{1} }} {\mu_{l}^{1} p_{lj}^{11} } - \sum\limits_{i = 1}^{{m_{1} }} {\bar{v}_{i}^{11} x_{ij}^{11} } \le 0\quad j = 1, \ldots ,n \\ & \quad \gamma \sum\limits_{l = 1}^{{L_{1} }} {\mu_{l}^{1} p_{lj}^{11} } - \sum\limits_{k = 1}^{{m_{2} }} {\bar{v}_{k}^{12} x_{kj}^{12} } \le 0\quad \, j = 1, \ldots ,n \\ & \quad \sum\limits_{d = 1}^{{D_{1} }} {\mu_{d}^{3} z_{dj}^{1} } - \sum\limits_{l = 1}^{{L_{1} }} {\bar{q}_{l}^{11} p_{lj}^{11} } - \sum\limits_{b = 1}^{{L_{2} }} {\bar{q}_{b}^{12} p_{bj}^{12} } \le 0\quad j = 1, \ldots ,n \\ & \quad \sum\limits_{i = 1}^{{m_{1} }} {\bar{v}_{i}^{11} x_{io}^{11} } = 1 \\ & \quad \sum\limits_{k = 1}^{{m_{2} }} {\bar{v}_{k}^{12} x_{ko}^{12} } = 1 \\ & \quad \sum\limits_{l = 1}^{{L_{1} }} {\bar{q}_{l}^{11} p_{lo}^{11} } + \sum\limits_{b = 1}^{{L_{2} }} {\bar{q}_{b}^{12} p_{bo}^{12} } = 1 \\ & \quad \mu_{l}^{1} ,\mu_{d}^{3} ,\bar{v}_{i}^{11} ,\bar{v}_{k}^{12} ,\bar{q}_{1}^{11} ,\bar{q}_{b}^{12} ,\gamma > 0,\quad i = 1, \ldots ,m_{1} ,\quad k = 1, \ldots ,m_{2} ,\quad l = 1, \ldots ,L_{1} ,\quad b = 1, \ldots ,L_{2} ,\quad d = 1, \ldots ,D_{1} . \\ \end{aligned}$$
(6)

Model (6) is nonlinear model in objective function and has (n + 1) constraints.

To standardize efficiency score of sub-network 1 calculated by (6), we use the following equation:

$$e_{o}^{1S} = \frac{{e_{o}^{1} }}{{\mathop {\hbox{max} }\limits_{j} \, e_{j}^{1} }}$$
(7)

Lemma 2

Model (6) is always feasible and the upper bound of its objective function is equal to unit.

Proof

Consider an arbitrary solution as follows:

$$\left\{ {\begin{array}{*{20}c} {\mu_{l}^{1} = \frac{1}{{L_{1} p_{lo}^{11} }},} & {\mu_{d}^{3} = \frac{1}{{D_{1} z_{do}^{1} }},} & {} \\ {\bar{v}_{i}^{11} = \frac{1}{{m_{1} x_{ij}^{11} }},} & {\bar{v}_{k}^{12} = \frac{1}{{m_{2} x_{kj}^{12} }},} & {\forall j} \\ {\bar{q}_{l}^{11} = \frac{1}{{2L_{1} p_{lj}^{11} }},} & {\bar{q}_{b}^{12} = \frac{1}{{2L_{2} p_{bj}^{12} }},} & {\forall j} \\ {\theta_{\text{FT}}^{1} = \theta_{\text{ST}}^{1} = \theta_{Sp}^{2} = 0,} & {} & {} \\ \end{array} } \right.$$

It is clear that above solution is a feasible solution for Model (6).□

2.3.2 Game-DEA model for sub-network 2

Similar to sub-network 1, for sub-network 2, we considered first and second types of inputs in sub-process 3 as two different players and sub-process 4 as third player (as shown in Fig. 3). Similar to the previews subsection, the converted proposed three-person bargaining game-DEA model to assess the efficiency of this sub-network in DMUO can be expressed as:

$$\begin{aligned} & \hbox{max} \;e_{o}^{2} = \left( {\sum\limits_{l = 1}^{{L_{3} }} {\mu_{l}^{1} p_{lo}^{21} } - \theta_{\text{FT}}^{2} } \right)\left( {\sum\limits_{l = 1}^{{L_{3} }} {\gamma \mu_{l}^{1} p_{lo}^{21} } - \theta_{\text{ST}}^{2} } \right)\left( {\sum\limits_{d = 1}^{{D_{2} }} {\mu_{d}^{3} z_{do}^{2} } - \theta_{\text{Sp}}^{4} } \right) \\ & \quad {\text{s.t.}}\\ & \quad \sum\limits_{l = 1}^{{L_{3} }} {\mu_{l}^{1} p_{lo}^{21} } \ge \theta_{\text{FT}}^{2} \\ & \quad \gamma \sum\limits_{l = 1}^{{L_{3} }} {\mu_{l}^{1} p_{lo}^{21} } \ge \theta_{\text{ST}}^{2} \\ & \quad \sum\limits_{d = 1}^{{D_{2} }} {\mu_{d}^{3} z_{do}^{2} } \ge \theta_{\text{Sp}}^{4} \\ & \quad \sum\limits_{l = 1}^{{L_{3} }} {\mu_{l}^{1} p_{lj}^{21} } - \sum\limits_{i = 1}^{{m_{3} }} {\bar{v}_{i}^{21} x_{ij}^{21} } \le 0\quad j = 1, \ldots ,n \\ & \quad \gamma \sum\limits_{l = 1}^{{L_{3} }} {\mu_{l}^{1} p_{lj}^{21} } - \sum\limits_{k = 1}^{{m_{4} }} {\bar{v}_{k}^{22} x_{kj}^{22} } \le 0\quad \, j = 1, \ldots ,n \\ & \quad \sum\limits_{d = 1}^{{D_{2} }} {\mu_{d}^{3} z_{dj}^{2} } - \sum\limits_{l = 1}^{{L_{3} }} {\bar{q}_{l}^{21} p_{lj}^{21} } - \sum\limits_{b = 1}^{{L_{4} }} {\bar{q}_{b}^{22} p_{bj}^{22} } \le 0\quad \, j = 1, \ldots ,n \\ & \quad \sum\limits_{i = 1}^{{m_{3} }} {\bar{v}_{i}^{21} x_{io}^{21} } = 1 \\ & \quad \sum\limits_{k = 1}^{{m_{4} }} {\bar{v}_{k}^{22} x_{ko}^{22} } = 1 \\ & \quad \sum\limits_{l = 1}^{{L_{3} }} {\bar{q}_{l}^{21} p_{lo}^{21} } + \sum\limits_{b = 1}^{{L_{4} }} {\bar{q}_{b}^{22} p_{bo}^{22} } = 1 \\ & \quad \mu_{l}^{1} ,\mu_{d}^{3} ,\bar{v}_{i}^{21} ,\bar{v}_{k}^{22} ,\bar{q}_{l}^{21} ,\bar{q}_{b}^{22} ,\gamma > 0,\quad i = 1, \ldots ,m_{1} ,\quad k = 1, \ldots ,m_{2} ,\quad l = 1, \ldots ,L_{1} ,\quad b = 1, \ldots ,L_{2} ,\quad d = 1, \ldots ,D_{1} . \\ \end{aligned}$$
(8)

It should be noted that all proven lemmas in Sect. 2.3.1 are also valid for model (8).

Similar to Eq. (7), to standardize efficiency score of sub-network 1 calculated by (8) we use the following equation:

$$e_{o}^{2S} = \frac{{e_{o}^{2} }}{{\mathop {\hbox{max} }\limits_{j} \, e_{j}^{2} }}$$
(9)

2.3.3 Game-DEA model for sub-network 3

In sub-network 3, we consider the outputs from sub-network 1 and sub-network 2 as two different players (as shown in Fig. 3). The proposed two-person bargaining game-DEA model to assess the efficiency of sub-network 3 in \({\text{DMU}}_{\text{O}}\) can be expressed as follow:

$$\begin{aligned} & \hbox{max} \, e_{o}^{3} = \left( {\frac{{\sum\nolimits_{r = 1}^{s} {u_{r} y_{ro} } }}{{\sum\nolimits_{d = 1}^{{D_{1} }} {w_{d}^{1} z_{do}^{1} } }} - \theta_{\text{Sp}}^{52} } \right)\left( {\frac{{\sum\nolimits_{r = 1}^{s} {u_{r} y_{ro} } }}{{\sum\nolimits_{h = 1}^{{D_{2} }} {w_{h}^{2} z_{ho}^{2} } }} - \theta_{\text{Sp}}^{54} } \right) \\ & \quad {\text{s.t.}}\\ & \quad \frac{{\sum\nolimits_{r = 1}^{s} {u_{r} y_{ro} } }}{{\sum\nolimits_{d = 1}^{{D_{1} }} {w_{d}^{1} z_{do}^{1} } }} \ge \theta_{\text{Sp}}^{52} \\ & \quad \frac{{\sum\nolimits_{r = 1}^{s} {u_{r} y_{ro} } }}{{\sum\nolimits_{h = 1}^{{D_{2} }} {w_{h}^{2} z_{ho}^{2} } }} \ge \theta_{\text{Sp}}^{54} \\ & \quad \frac{{\sum\nolimits_{r = 1}^{s} {u_{r} y_{rj} } }}{{\sum\nolimits_{d = 1}^{{D_{1} }} {w_{d}^{1} z_{dj}^{1} } }} \le 1\quad j = 1, \ldots ,n \\ & \quad \frac{{\sum\nolimits_{r = 1}^{s} {u_{r} y_{rj} } }}{{\sum\nolimits_{h = 1}^{{D_{2} }} {w_{h}^{2} z_{hj}^{2} } }} \le 1\quad \, j = 1, \ldots ,n \\ & \quad w_{d}^{1} ,w_{h}^{2} ,u_{r} > 0, \\ & \quad d = 1, \ldots ,D_{1} ,\quad h = 1, \ldots ,D_{2} ,\quad r = 1, \ldots ,s. \\ \end{aligned}$$
(10)

It easily can be shown that all proven lemmas in Sect. 2.3.1 are also true for model (10).

Similar to proposed three-person game-DEA models, let \(t_{1} = \left( {\sum\nolimits_{d = 1}^{{D_{1} }} {w_{d}^{1} z_{do}^{1} } } \right)^{ - 1}\), \(t_{2} = \left( {\sum\nolimits_{h = 1}^{{D_{2} }} {w_{h}^{2} z_{ho}^{2} } } \right)^{ - 1}\), \(\mu_{r}^{1} = t_{1} u_{r}\), \(\mu_{r}^{2} = t_{2} u_{r}\), \(\omega_{d}^{1} = t_{1} w_{d}^{1}\) and \(\omega_{h}^{2} = t_{2} w_{h}^{2}\). By these assumptions we have \(\mu_{r}^{2} = \frac{{t_{2} }}{{t_{1} }}\mu_{r}^{1}\); therefore, by denoting γ = t2/t1, model (10) converts into following nonlinear model:

$$\begin{aligned} & \hbox{max} \;e_{o}^{3} = \left( {\sum\limits_{r = 1}^{s} {\mu_{r}^{1} y_{ro} } - \theta_{\text{Sp}}^{52} } \right)\left( {\gamma \sum\limits_{r = 1}^{s} {\mu_{r}^{1} y_{ro} } - \theta_{\text{Sp}}^{54} } \right) \\ & \quad {\text{s.t.}}\quad \sum\limits_{r = 1}^{s} {\mu_{r}^{1} y_{ro} } \ge \theta_{\text{Sp}}^{52} \\ & \quad \gamma \sum\limits_{r = 1}^{s} {\mu_{r}^{1} y_{ro} } \ge \theta_{\text{Sp}}^{54} \\ & \quad \sum\limits_{r = 1}^{s} {\mu_{r}^{1} y_{rj} } - \sum\limits_{d = 1}^{{D_{1} }} {\omega_{d}^{1} z_{dj}^{1} } \le 0\quad \, j = 1, \ldots ,n \\ & \quad \gamma \sum\limits_{r = 1}^{s} {\mu_{r}^{1} y_{rj} } - \sum\limits_{h = 1}^{{D_{2} }} {\omega_{h}^{2} z_{hj}^{2} } \le 0\quad \, j = 1, \ldots ,n \\ & \quad \sum\limits_{d = 1}^{{D_{1} }} {\omega_{d}^{1} z_{do}^{1} } = 1 \\ & \quad \sum\limits_{h = 1}^{{D_{2} }} {\omega_{h}^{2} z_{ho}^{2} } = 1 \\ & \quad \mu_{r}^{1} ,\omega_{d}^{1} ,\omega_{h}^{2} ,\gamma > 0,\quad \, d = 1, \ldots ,D_{1} ,\quad h = 1, \ldots ,D_{2} ,\quad r = 1, \ldots ,s. \\ \end{aligned}$$
(11)

To standardize the efficiency score of sub-network 3 calculated by (11), we use the following equation:

$$e_{o}^{3S} = \frac{{e_{o}^{3} }}{{\mathop {\hbox{max} }\limits_{j} \, e_{j}^{3} }}$$
(12)

2.3.4 Efficiency scores of whole network

Using models 6, 8 and 11, first the efficiency scores of each sub-network have been obtained. Then the efficiency of the entire network is calculated using the average of all sub-networks. Although different approaches can be used for calculating mean value, the weighted sum mean, harmonic mean, geometric mean and weighted geometric mean were used. According to the final results, weighted geometric mean was selected as the best repression for efficiency score of the entire network. The considered procedure for obtaining mean value is as follows:

By assessing the efficiency of sub-networks as explained above, the efficiency of DMUO can be calculated as:

$$E_{o} = \sqrt[{(\alpha_{1} + \alpha_{2} + \alpha_{3} )}]{{(e_{o}^{1S} )^{{\alpha_{1} }} \times (e_{o}^{2S} )^{{\alpha_{2} }} \times (e_{o}^{3S} )^{{\alpha_{3} }} }}$$
(13)

obviously e 1 S o , e 2 S o , e 3 S o  ≤ 1, therefore Eo ≤ 1 for all o ∊ {1,…, n}.

In Eq. (13), α1, α2 and α3 are the importance factors, i.e. weights of sub-network 1, 2 and 3, respectively. In this study, we have got the expert opinion who suggested that sub-network 3 (named profitability stage) is twice more important than the other two sub-networks; hence, we assumed: α3 = 2 is equal to 2 and α1 = α2 = 1. Therefore;

$$E_{o} = \sqrt[4]{{e_{o}^{1S} \times e_{o}^{2S} \times (e_{o}^{3S} )^{2} }} = \sqrt {\sqrt {e_{o}^{1S} \times e_{o}^{2S} } \times e_{o}^{3S} }$$
(14)

To standardize efficiency score of DMUO calculated by (14), we use the following equation:

$$E_{o}^{S} = \frac{{E_{o} }}{{\mathop {\hbox{max} }\limits_{j} \, E_{j} }}$$
(15)

2.4 Algorithm for assessing performance in network DEA

According to above discussions, the algorithm for determining efficiencies of sub-networks and networks is summarized as follows:

figure a

2.5 Assessing networks using the proposed model

We propose a new approach to performance evaluation of DMUs with network structure using DEA. Our proposed model is based on network structure shown in Fig. 3, but indeed, the main idea here is dividing a network into some sub-networks and classifying inputs to several categorizes. Therefore, the proposed approach can be used as a framework for performance assessment in other applications with network structures such as manufacturing, supply chain management, assessment of educational institutions. However, depending on the application, it is important to draw a correct structure of sub-networks and identify suitable inputs and outputs in each stage. In the proposed approach, we could consider any type of networks including: parallel network, series network or even mix of parallel and series approaches as shown in Fig. 4.

Fig. 4
figure 4

Different structure of networks

Full size image

3 A real case study of Iranian banking

In this section, to show ability of proposed approach, models have been applied for performance assessment of 35 selected branches of an Iranian private bank where each branch has a network production system with two different activities, consumer activity and business activity. Each activity contains two sub-processes (see Fig. 5).

Fig. 5
figure 5

Schema of the bank branches structure

Full size image

The under evaluated bank has a professional Research and Development (R&D) group. Some experts of this group have overseen in our research. We were in regular contact with them in each step, and we carefully considered their advices to make sure that selected input/output variables are suitable and the results make sense to the policy makers. The R&D group have some coefficients related to each parameter (inputs and outputs) based on each city and branch. For example, they said business population coefficient is 0.25 (just for example) in Tehran. Therefore, if population of Tehran is 1,000,000 the business population is 250,000. All data which have been gathered from bank and SCI [30] have been verified by experts. SCI is the Statistical Centre of Iran located in Tehran, Iran, which have been established in 1924, to officially collect and validate different statistics.

The first sub-network is named personal or consumer banking (personal or consumer activity). While the second sub-network is named business banking (business activity). The third sub-network is profitability stage of a branch. Sub-process 1 is “The Bureau of Administration and Organization affairs-consumer unit”, which is a managerial unit focusing on consumer banking based on financial and environmental inputs. The inputs and outputs for this sub-process are related to the city which the branch is located as well as size of branches. Sub-process 2 is “Attract consumer investment committee”. In this sub-process, the branch focuses on attracting investment from consumers and manages consumer loans and interests. Sub-process 3 is “The Bureau of Administration and Organization affairs-business unit”. Focusing on business consumers and activities, task of this sub-process is similar to sub-process 1. Finally, sub-process 4 is related to “Attract business investment committee”. In the sub-process 4, the branch focuses on attracting investment from business related consumers, and manages loans and interests related to business activities.

We first identified the most common inputs and outputs used in the literature and proposed them to bank’s R&D group. By gathering experts’ opinion via interviewing and combining this with what has been proposed in the literature, inputs/outputs in each sub-process have been selected. The inputs to the first sub-process are operational cost (millions monetary unit, \(x_{1j}^{11}\)) and fixed assets (millions monetary unit, \(x_{2j}^{11}\)) as financial inputs, income level (millions monetary unit, \(x_{1j}^{12}\)), population (ten thousand, \(x_{2j}^{12}\)) and density (thousand, \(x_{3j}^{12}\)) as environmental inputs. Income level is the amount of monetary or other returns, either earned or unearned, accruing over a given period of time. Per capita income or average income measures the average income earned per person in a given area (city, region, country, etc.) in a specified year. It is calculated by dividing the area’s total income by its total population. Average income level of population of a region is an input for DMUs [31] since it is supposed that high-income level leads to high bank activities. Population density is a measurement of population per unit area or unit volume. It should be noted that when density of a region is high, the number of customers is expected to be more for per capita income-related DMU [31]. There are similar inputs for business sub-network. Business operational cost (millions monetary unit, \(x_{1j}^{21}\)) and business fixed assets (millions monetary unit, \(x_{2j}^{21}\)) as financial inputs, income level (millions monetary unit, \(x_{1j}^{22}\)), population (ten thousand, \(x_{2j}^{22}\)) and density (thousand, \(x_{3j}^{22}\)) as environmental inputs, are considered for sub-process 3. Operational cost is an input parameter since it is an expenses type parameter. It should be noted that the operational costs for consumer banking and business banking are different. The intermediate measures are consumer saving deposit (millions monetary unit, \(p_{1j}^{12}\)), consumer checking deposit (millions monetary unit, \(p_{2j}^{12}\)), personal cost (millions monetary unit, \(p_{1j}^{11}\)) and other operational cost (millions monetary unit, \(p_{2j}^{11}\)) in consumer banking, consumer interest cost (millions monetary unit, \(z_{1j}^{1}\)), consumer loans (millions monetary unit, \(z_{2j}^{1}\)), business saving deposit (millions monetary unit, \(p_{1j}^{22}\)), business checking deposit (millions monetary unit, \(p_{2j}^{22}\)), personal cost (millions monetary unit, \(p_{1j}^{21}\)) and other operational cost (millions monetary unit, \(p_{2j}^{21}\)) in business banking, business interest cost (millions monetary unit, \(z_{1j}^{2}\)) and business loans (millions monetary unit, \(z_{2j}^{2}\)). It is important to have two different deposits (checking & saving) since each type of “Deposit” depends on different activity of bank branches, and it is important for the bank owners to have information about “Deposit level” of each branch and for each type of deposit [32]. Outputs from the network are interest income (millions monetary unit, \(y_{1j}\)), fee income (millions monetary unit, \(y_{2j}\)), fund transfer income (millions monetary unit, \(y_{3j}\)) and returns on assets (in percent, \(y_{4j}\)). Similar to the “Deposit” it is also important to have separate “Income” in the last stage. Data from bank branches are given in Appendix.

It should be noted that the income level, population and density of consumer activities are extracted from Iran’s national statistics center [30] and correspondingly these inputs for business activities are proportional to consumer ones. The sample has been selected based on the feedbacks from bank’s R&D group and due to the industrialization level and geographical properties of the DMU under study.

Table 1 reveals the statistical descriptions of the data set. It is clear that the variance of the selected variables is large because of considering various sizes of sample bank branches. Similarly, large variable ranges and high standard deviations show a high degree of diversity in inputs, intermediate inputs and outputs structures.

Table 1 Statistical description of variables
Full size table

4 Results and analysis

In this section, results of the proposed network approach for bank branches’ efficiency and analysis of the results are presented. The proposed models for sub-networks were coded using GAMS 24.1.2 software. COUENNE solver, as a solver for the non-convex NLP problems, was used for solving the models. The codes of proposed mathematical models were executed on an ASUS laptop with Core i5 due CPU, 2.4 GHz, and Windows Seven using 4 GB of RAM. All proposed models to calculate the efficiency of sub-networks for all of DMUs were feasible. Also mean of running time is 0.802367 s. It should be noted that the efficiency scores of sub-networks and network will be highly dependent on underlying variability of software algorithm. Also, the breakdown points values are very effective factor on obtained efficiency scores. We used the approach proposed by Du et al. [26] to obtain the breakdown points. However, one may use other methods, for example, the breakdown points can be determined by experts or policy makers. But one should be careful about estimation of breakdown points and its variability. Stehlík et al. [33] developed a very efficient method within Basel II initiative to estimate banking thresholds.

First, we have calculated the breakdown points using the proposed method. Results for breakdown points are \(\theta_{\text{FT}}^{1} = 0. 2 0 9\), \(\theta_{\text{ST}}^{1} = 0. 1 3 9\), \(\theta_{\text{Sp}}^{2} = 0. 1 5 0\), \(\theta_{\text{FT}}^{2} = 0. 0 9 7\), \(\theta_{\text{ST}}^{2} = 0. 1 2 3\), \(\theta_{\text{Sp}}^{4} = 0. 1 7 8\), \(\theta_{\text{Sp}}^{52} = 0. 0 7 0\) and \(\theta_{\text{Sp}}^{54} = 0. 1 6 5\). By setting breakdown points and running in the network DEA, efficiency scores of sub-networks and network are obtained for 35 bank branches. Initial results show that 5 DMUs are outliers. The efficiency scores for sub-network 2 in these DMUs were < 0.05. These DMUs were in small cities and did not do significant business activities; therefore, we just evaluated these DMUs as a test to examine the validity of proposed models, since we knew that if the model has been developed correctly it should assign very small efficiency values for these DMUs. Since these five DMUs did not do significant business activities, they have been removed from the analysis. After removing the outliers, the model was run for 30 remaining DMUs. It should also be noted that since these DMUs were inefficient, removing them would not have impact on efficiency of other DMUs. We have also calculated the results from a single DEA model without considering network for comparison purpose (see Table 2). All obtained solutions are the global feasible solutions. Fifth and sixth Columns of Table 2 show the efficiency scores of bank branches by using the proposed approach and classic DEA, respectively. As it is expected, classic DEA scores are equal to 1 for all DMUs. It means that standard DEA is not capable to distinguish efficient DMUs, while the results show proposed model discriminates between DMUs perfectly. Table 2 shows the number of DMUs and conflict between DMUs affecting efficiency scores. This information is useful for identifying the weak sub-networks and DMUs, and can be helpful for improving overall performance of branches. Figure 6 shows efficiency scores of sub-networks and networks for all DMUs. Obviously according to Fig. 6, where efficiency scores of all DMUs from classic DEA are 1, most of the obtained scores from proposed model are < 1, varying in big range that shows the discrimination ability of proposed model between the DMUs. Only DMU 1 has been scored to be full efficient. Analyzing the results for the first five DMUs in the ranking (the DMUs 1, 20, 2, 19 and 30) shows that all of these DMUs have a good performance in the sub-network 3. It indicates the importance of sub-network 3, the profitability stage. For example, even though the DMU 23 has the first rank in the sub-network 2 and third rank in the sub-network 1, it ranked 16th in sub-network 3, as results its overall rank is 12th. Also, the importance of sub-network 3 is observable in the results of five last DMUs (The DMUs 29, 7, 12, 21 and 15). The capability of better discrimination of proposed model can be seen in Fig. 7. Dispersion of consumer banking and business banking performance scores of branches obtained from the sub-network 1 and sub-network 2 models is illustrated in Fig. 7. As seen in this Figure, there are only two DMUs in which their performance scores are more than 0.5 in sub-network 2 and less than 0.5 in sub-network 1. Efficiency score in sub-network 1 is more than sub-network 2 efficiency score for 19 DMUs, which represents poor performance of business banking versus consumer banking for branches. Further, Fig. 8 presents dispersion of sub-networks efficiency versus network efficiency for all DMUs. Only DMU 1 and DMU 2 have been scored more than 0.5 in all sub-networks and network. From Fig. 8, there is not any DMU which its efficiency is more than 0.5 in sub-network 3 and less than 0.5 in the network, which shows the importance of the sub-network 3. Histogram of proposed model scores is presented in Fig. 9. As seen, most branches fall into 0.2–0.299 range and only five branches are scored more than 0.80. From 30 bank branches, only five branches have been scored in all three sub-networks below 0.40. If performance measure below 0.3 is considered as the weakest performance, most DMUs are weak in sub-network 3 (19 DMUs), where only five DMUs have weak efficiency in sub-network 1. Also, the efficiency score in sub-network 2 for 13 DMUs is less than 0.3, which shows that the performance of branches in the business banking is not satisfying. Based on the results, since the importance weight for profitability stage is 2 and the performance of the most branches in this stage is weak, it seems that some affective policies should be considered to improve the performance of DMUs in this stage. For this purpose, first idea is “decreasing the level of inputs” in the sub-network 3. However, when a branch tries to decrease the inputs’ level in the sub-network 3, indeed it decreases the outputs’ values of sub-network 2, which leads to a decrease in the efficiency scores of DMUs in the sub-network 2. Therefore, if the bank managers decide to apply this strategy, they should simultaneously apply some strategies to decrease the inputs in the sub-network 2. Accordingly, in the first strategy managers should try to decrease cost factors including business interest costs, personal costs, and operational costs. The second strategy is “increasing the level of outputs’ in sub-network 3. For this purpose, the bank should adopt some policies to improve the income levels including interest income, fee income, fund transfer income and return on assets. Finally, the third strategy is “increasing the outputs and decreasing the inputs, simultaneously” in the sub-network 3. Based on this strategy, the income levels should be increased and cost level should be decreased.

Table 2 Results of efficiency scores for bank branches
Full size table
Fig. 6
figure 6

Efficiency scores of sun-networks and networks calculated by proposed model

Full size image
Fig. 7
figure 7

Consumer banking efficiency versus business banking efficiency

Full size image
Fig. 8
figure 8

(Note: N Network, SN1 Sub-network 1, SN2 Sub-network 2, SN3 Sub-network 3)

Sub-networks versus network performance.

Full size image
Fig. 9
figure 9

Histogram of efficiency scores

Full size image

In a very low interest environment (with the zero lower bound having been hit in international monetary markets) and an ever-increasing money supply in almost all economies in the world, it is difficult for banks to gain from interest margins [34,35,36]. Efficiency should not only be measured taking into account profitability but the tasks of banks should be considered. As essential part of a countries’ economy, banks work as mediator between those who want to save up money and those who need money for investments. A bank fulfills this task even though it might yield a high ROI from their owner’s point of view, but does not grant so much loans and therefore does not effectively fulfill its job to make money flow in the economy. That is to say, banks that scarify interest margins granting loans to a low interest will most probably yield less rentability, but they do their tasks to efficiently mediate between savers and investors. More interesting would be the construction of a model that defines efficiency by whether or not banks (efficiently) fulfill their role in the economy. In such a model, the lower interest rates, the better for economy and, especially, society since an important part of income inequality, financial crisis and the obligation to grow economically has to do with the money rate if interest [34, 37, 38].

In the proposed network assessment of bank branches, in addition to the profitability, by considering consumer/business deposits and consumer/business loans as inputs/outputs, we have included the money flow also in the performance evaluation of branches. In this research, the under evaluation bank is a private commercial bank which the interest rate for business loans is 18–85%. For managers, the profitability is more important than other tasks such as money flow; hence, sub-network 3 is twice more important than the other two sub-networks.

It should be noted that the proposed approach to obtain breakdown points calculates minimum value of breakdown points. Hence, based on the form of objective functions the efficiency scores have negative relation with breakdown points. Therefore, the obtained efficiency scores, in used breakdown points, are maximum efficiency scores for each DMU in each sub-network and network. According to this, since the maximum efficiency scores of DMUs in the profitability stage are significantly low, bank managements and policy makers should pay more attention on improvement of this stage. It is important to note that for other breakdown points the efficiency scores will be lower and worse than our results.

Hence, it can be concluded that the proposed method not only has managed to deal with complex networks, the corresponding conflicts of stages and insufficient number of DMUs, but also represented a good performance due to improving the discrimination of efficient DMUs as well as precise classification of other DMUs. Although there is only one efficient DMU, it is not unusual. The proposed model is similar to super efficiency model in which the number of efficient DMUs is very low. It should be noted that one of the main goals and advantages of proposed model is increasing the discrimination power. The results show that we have achieved this goal.

5 Summary and conclusion

In this paper, we proposed a novel bargaining game-DEA model for assessing relative efficiency score of network structure processes. We addressed the issue of conflicts between stages, insufficient number of DMUs and additional inputs in the classic DEA models when aping it to network structure. To solve these problems, we divided a network into three different sub-networks. Also, the inputs of sub-networks are classified in two different categories. For each sub-network, a bargaining game structure was constructed. Each category and stage is assumed to be a player in Nash bargaining game. Hence, the proposed model can determine which DMU in which sub-network has better performance. To show abilities of the proposed approach, the model is applied in a real application to measure efficiency of an Iranian private bank branches. It is shown that when the number of network structure DMUs is insufficient for using DEA for performance assessment and there are conflicts between stages, in comparison with classic DEA, our newly developed Nash bargaining game approach yields a better discrimination between efficient and non-efficient DMUs.

In future research, proposed game-DEA approach can be used for performance assessment of network structure of DMUs in several areas of management and engineering. Although the results of DEA depend on under evaluating case study and DMUs, and the obtained results and policies can be different from a set of DMUs to other ones, the proposed approach in this study is a framework which can be used in many other applications of measuring efficiency as long as the application has a network and sub-network structure. Indeed, the main idea of the proposed approach is dividing a network into some sub-networks and classifying inputs to several categories. Sensitivity and stability analysis of efficiencies of the proposed model can be another interesting research stream. Although this real-world case study some assumptions has been assumed based on experts’ opinions in, such as the inputs/outputs, average calculation method, importance weight of each sub-network, the proposed approach can be customized for other networks. From theoretical view, future studies could focus on linearization of the proposed models. From applications view, future research can focus on assessing DMUs by whether or not they efficiently fulfill their role in different aspects, for example, in banking efficiency from different perspectives, such as consumers, governments, bank managers.