Skip to main content
SpringerLink
Log in

Computational and physical aspects of MHD Prandtl-Eyring fluid flow analysis over a stretching sheet

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

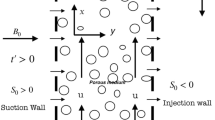
This paper explores the physical and computational aspects of normally applied magnetic field on non-Newtonian Prandtl-Eyring fluid flow over a stretching sheet. The Prandtl-Eyring fluid is a non-Newtonian viscoinelastic fluid model capable of describing zero shear rate viscosity effects. Stretching of a sheet induces the flow (Couette flow). The mathematical formulation of the problem gives a highly non-linear system of partial differential equations. By means of a scaling group of transformations, the partial differential equations are transfigured into ordinary differential equation. The implicit finite difference scheme Keller-Box is implemented to solve the resulting equation. The expression for dimensionless velocity is calculated numerically and inclusive pictures of its physical characteristics are analyzed very concisely and briefly. The influence of different pertinent parameters is displayed via graphs, which are plotted against variation in parameters. Computation of the skin friction coefficient is accomplished, and effects of influential parameters are analyzed via graphs and tables. The accuracy of the present solution is certified by displaying contrast between present and existing literature. It is important to remark that the results have shown excellent agreement up to significant number of digits.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Alfven H (1942) Existence of electromagnetic-hydrodynamic waves. Nature 150:405–406

    Article  Google Scholar 

  2. Rossow VJ (1958) On flow of electrically conducting fluid over a flat plate in the presence of a transverse magnetic field. NACA Tceh Report Server NACA-TN-3971

  3. Abel MS, Mahesha N (2008) Heat transfer in MHD viscoelastic fluid flow over a stretching sheet with variable thermal conductivity, non-uniform heat source and radiation. Appl Math Model 32:1965–1983

    Article  MathSciNet  MATH  Google Scholar 

  4. Shehzad A, Ali R (2012) Approximate analytic solution for magneto-hydrodynamic flow of a non-Newtonian fluid over a vertical stretching sheet. Can J Appl Sci 2:202–215

    Google Scholar 

  5. Ellahi R (2013) The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: analytical solutions. Appl Math Model 37:1451–1457

    Article  MathSciNet  MATH  Google Scholar 

  6. Shahzad A, Ali R (2013) MHD flow of a non-Newtonian power law fluid over a vertical stretching sheet with the convective boundary condition. Walailak J Sci Tech 10:43–56

    Google Scholar 

  7. Khan M, Ali R, Shahzad A (2013) MHD Falkner-Skan flow with mixed convection and convective boundary conditions. Walailak J Sci Tech 10:517–529

    Google Scholar 

  8. Ahmed J, Shahzad A, Khan M, Ali R (2015) A note on convective heat transfer of an MHD Jeffrey fluid over a stretching sheet. AIP Adv DOI:10.1063/1.4935571

  9. Gul T, Islam S, Shah RA, Khan I, Khalid A, Shafie S (2015) Heat transfer analysis of MHD thin film flow of an unsteady second grade fluid past a vertical oscillating belt. PLoS One DOI:10.1371/journal.pone.0103843

  10. Akbar NS, Ebai A, Khan ZH (2015) Numerical analysis of magnetic field effects on Eyring-Powell fluid flow towards a stretching sheet. J Magn Magn Mater 382:355–358

    Article  Google Scholar 

  11. Nadeem S, Mehmood R, Akbar NS (2015) Combined effects of magnetic field and partial slip on obliquely striking rheological fluid over a stretching surface. J Magn Magn Mater 378:457–462

    Article  Google Scholar 

  12. Malik MY, Khan Imad, Hussain Arif, Salahuddin T (2015) Mixed convection flow of MHD Eyring-Powell nanofluid over a stretching sheet: a numerical study. AIP Adv DOI: 10.1063/1.4935639

  13. Nadeem S, Mehmood R, Motsa SS (2015) Numerical investigation on MHD oblique flow of Walter’s B type nano fluid over a convective surface. Int J Therm Sci 92:162–172

    Article  Google Scholar 

  14. Nawaz M, Zeeshan A, Ellahi R, Abbasbandy S, Saman R (2015) Joules and Newtonian heating effects on stagnation point flow over a stretching surface by means of genetic algorithm and Nelder-Mead method. Int J Numer Methods Heat Fluid Flow 25:665–684

    Article  MathSciNet  MATH  Google Scholar 

  15. Malik MY, Salahuddin T, Arif H, Bilal S (2015) MHD flow of tangent hyperbolic fluid over a stretching cylinder: using Keller box method. J Magn Magn Mater 395:271–276

    Article  Google Scholar 

  16. Ellahi R, Rahman SU, Nadeem S, Vafai K (2015) The blood flow of Prandtl fluid through a tapered stenosed arteries in permeable walls with magnetic field. Comm Theo Phy 63:353–358

    Article  MathSciNet  MATH  Google Scholar 

  17. Mehmood R, Nadeem S, Masood S (2016) Effects of transverse magnetic field on a rotating micropolar fluid between parallel plates with heat transfer. J Magn Magn Mater 401:1006–1014

    Article  Google Scholar 

  18. Malik MY, Arif H, Salahuddin T, Awais M (2016) Numerical solution of MHD Sisko fluid over a stretching cylinder and heat transfer analysis. Int J Numeric Methods Heat Fluid flows 26:1787–1801

    Article  MathSciNet  MATH  Google Scholar 

  19. Majeed A, Zeeshan A, Alamri SZ, Ellahi R (2016) Heat transfer analysis in ferromagnetic viscoelastic fluid flow over a stretching sheet with suction. Neural Compu Appl, DOI:10.1007/s00521-016-2830-6

  20. Makinde OD, Animasaun IL (2016) Bioconvection in MHD nanofluid flow with nonlinear thermal radiation and quartic autocatalysis chemical reaction past an upper surface of a paraboloid of revolution. Int J Therm Sci 109:159–171

    Article  Google Scholar 

  21. Makinde OD, Animasaun IL (2016) Thermophoresis and Brownian motion effects on MHD bioconvection of nanofluid with nonlinear thermal radiation and quartic chemical reaction past an upper horizontal surface of a paraboloid of revolution. J Mol Liq 221:733–743

    Article  Google Scholar 

  22. Zeeshan A, Majeed A, Ellahi R (2016) Effect of magnetic dipole on viscous ferro-fluid past a stretching surface with thermal radiation. J Mol Liq 215:549–554

    Article  Google Scholar 

  23. Salahuddin T, Malik MY, Arif H, Bilal S, Awais M (2016) MHD flow of Cattanneo--Christov heat flux model for Williamson fluid over a stretching sheet with variable thickness: using numerical approach. J Magn Magn Mater 401:991–997

    Article  Google Scholar 

  24. Majeed A, Zeeshan A, Ellahi R (2016) Unsteady ferromagnetic liquid flow and heat transfer analysis over a stretching sheet with the effect of dipole and prescribed heat flux. J Mol Liq 223:528–533

    Article  Google Scholar 

  25. Maqbool K, Sohail A, Manzoor N, Ellahi R (2016) Hall effect on Falkner-Skan boundary layer flow of FENE-P fluid over a stretching sheet. Comm Theo Phy 66:547–554

    Article  MathSciNet  Google Scholar 

  26. Ellahi R, Bhatti MM, Pop I (2016) Effects of hall and ion slip on MHD peristaltic flow of Jeffrey fluid in a non-uniform rectangular duct. Int J Numer Methods Heat Fluid Flow 26:1802–1820

    Article  MathSciNet  MATH  Google Scholar 

  27. Ellahi R, Shivanian E, Abbasbandy S, Hayat T (2016) Numerical study of magnetohydrodynamics generalized Couette flow of Eyring-Powell fluid with heat transfer and slip condition. Int J Numer Methods Heat Fluid Flow 26:1433–1445

    Article  MathSciNet  MATH  Google Scholar 

  28. Rehman KU, Malik MY, Salahuddin T, Naseer M (2016) Dual stratified mixed convection flow of Eyring-Powell fluid over an inclined stretching cylinder with heat generation/absorption effect. AIP Adv DOI:10.1063/1.4959587

  29. Khan AA, Muhammad S, Ellahi R, Zaigham Zia QM (2016) Bionic study of variable viscosity on MHD peristaltic flow of Pseudoplastic fluid in an asymmetric channel. J Magn 21:1–8

    Article  Google Scholar 

  30. Ali R, Shahzad A, Khan M, Ayub M (2016) Analytic and numerical solutions for axisymmetric flow with partial slip. Eng Comput 32:149–154

    Article  Google Scholar 

  31. Malik MY, Mair K, Salahuddin T, Imad K (2016) Variable viscosity and MHD flow in Casson fluid with Cattaneo--Christov heat flux model: using Keller box method. Eng Sci Tech Int J 19:1985–1992

    Article  Google Scholar 

  32. Ahmed J, Mahmood T, Iqbal Z, Shahzad A, Ali R (2016) Axisymmetric flow and heat transfer over an unsteady stretching sheet in power law fluid. J Mol Liq 221:386–393

    Article  Google Scholar 

  33. Ahmed J, Begum A, Shahzad A, Ali R (2016) MHD axisymmetric flow of power-law fluid over an unsteady stretching sheet with convective boundary conditions. Results Phy 6:973–981

    Article  Google Scholar 

  34. Awais M, Malik MY, Salahuddin T, Arif H (2017) Magnetohydrodynamic (MHD) flow of Sisko fluid near the axisymmetric stagnation point towards a stretching cylinder. Results in Phys 7:49–56

    Article  Google Scholar 

  35. Arif H, Malik MY, Bilal S, Awais M, Salahuddin T (2017) Computational analysis of magnetohydrodynamic Sisko fluid flow over a stretching cylinder in the presence of viscous dissipation and temperature dependent thermal conductivity. Results in Physics 7:139–146

    Article  Google Scholar 

  36. Bilal S, Rehman KU, Malik MY, Arif H, Mair K (2017) Effects of temperature dependent conductivity and absorptive/generative heat transfer on MHD three dimensional flow of Williamson fluid due to bidirectional non-linear stretching surface. Results in Physics 7:204–212

    Article  Google Scholar 

  37. Darji RM, Timol MG (2011) Similarity solutions of Leminar incompressible boundary layer equations of non-Newtonian Viscoinelastic fluids. Int J Math Ach 2:1395–1404

    Google Scholar 

  38. Akbar NS, Nadeem S, Lee C (2013) Biomechanical analysis of Eyring Prandtl fluid model for blood flow in stenosed arteries. Int J Nonlinear Sci Numer Simul 14:345–353

    Article  MathSciNet  MATH  Google Scholar 

  39. Akbar NS (2013) MHD Eyring--Prandtl fluid flow with convective boundary conditions in small intestines. Int J Biomath DOI: 10.1142/S1793524513500344

  40. Cebeci T, Bradshaw P (1984) Physical and computational aspects of convective heat transfer. Springer, New York, pp 407–413

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Quaid-i-Azam University, Islamabad, 44000, Pakistan

    Arif Hussain, M.Y. Malik, M. Awais & S. Bilal

  2. Department of Mathematics, Mirpur University of Science and Technology, Mirpur, AJK, 10250, Pakistan

    T. Salahuddin

Authors
  1. Arif Hussain
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M.Y. Malik
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Awais
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. T. Salahuddin
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. S. Bilal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Arif Hussain.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hussain, A., Malik, M., Awais, M. et al. Computational and physical aspects of MHD Prandtl-Eyring fluid flow analysis over a stretching sheet. Neural Comput & Applic 31 (Suppl 1), 425–433 (2019). https://doi.org/10.1007/s00521-017-3017-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-017-3017-5

Keywords

Search

Navigation