1 Introduction

Single- and two-phase fluid flow through heterogeneous porous media are important phenomena that occur in many natural and man-made processes (Sahimi 2011; Blunt 2017). Well-known examples include groundwater flow and contamination (Peterson et al. 1999; Selker et al. 2007), soil remediation (Wei et al. 2014), displacement of one fluid by another immiscible fluid (Orr and Taber 1984; Lake 2018), water transmission by building materials, evaporation in soils (Shokri et al. 2024), flow in packed-bed reactors, and ink imbibition in paper (Ghassemzadeh et al. 2001; Ghassemzadeh and Sahimi 2004). Understanding fluid flow, and in particular two-phase flow through porous media, entails solving a complex problem, namely, predicting the continuous paths of the fluid(s) in a disordered pore space. With the enormous increase in the computational power, significant advances have been made in modeling of single- and two-phase fluid flow in porous media. On the experimental side, on the other hand, although visualization of flow paths in real time and investigation of the way by which they are affected by the morphology of the pore space—its pore size distribution, pore connectivity, and surface roughness—have been undertaken, understanding the effect of intrinsic characteristics of the solid matrix, such as its wettability, and that of the flow field, such as the Reynolds number, as well as the rheology of the fluid—Newtonian versus non-Newtonian—remain difficult problems.

A very important problem that has not been studied as extensively, both computationally and by precise experiments and visualization, is the transition of flow from the creeping regime in which Darcy’s law, \({\varvec{\nabla }}P=-(K_e/\mu )\textbf{v}\), is applicable, to flow at larger Reynolds numbers Re in which the relationship between \({\varvec{\nabla }}P\) and v is nonlinear. Here \(K_e\) is the effective Darcy permeability of the pore space, and \(\mu\) is the fluid’s viscosity. Examples of such flows are abundant and include gas flow through a catalytic converter, flow of wastewater that as a fracking fluid is injected into unconventional porous formations, such as shales, flow of high-pressure water injected into geothermal reservoirs, fluid flow in many filtration processes, flow in biological porous materials (Khanafer et al. 2008; Khalili et al. 2010), in nuclear pebble-bed reactors (Dave et al. 2018), and in dense fluidized beds (Lu et al. 2018). In all such problems, the flow regime is no longer linear because, in addition to the viscous forces, the inertial effects are also important. In addition, as recent experiments (Chang et al. 2017) indicated, when the pores have rough surfaces, as almost all pores in natural porous media do, displacement of a wetting fluid by a non-wetting one may give rise to nonlinear flow.

Experimental data (Chauveteau and Thirriot 1967; Tiss and Evans 1989; Johns et al. 2000; Macini et al. 2010) for and visualization (de Camargo et al. 2016) of non-Darcy fluid flow in well-characterized porous media have also been reported. Compared to the Darcy flow in porous media, however, theoretical modeling of the non-Darcy flow, which began over a century ago (Forchheimer 1901), has remained relatively unexplored (Firoozabadi and Katz 1979; Joseph et al. 1982; Hassanizadeh and Gray 1987; Mei and Auriault 1991; Ruth and Ma 1992; Ma and Ruth 1993; Whitaker 1996; Thauvin and Mohanty 1998; Andrade et al. 1999; Cooper et al. 1999; Liu and Masliyah 1999; Chen et al. 2001; Panfilov and Fourar 2006; Hlushkou and Tallarek 2006; Balhoff and Wheeler 2009), even though as early as early 1960s, the effect of turbulence on flow of gases in porous media was studied and reported (Tek et al. 1962). To understand the effect of inertial forces on fluid flow in porous media, one must, in principle, numerically solve the momentum and mass conservation equations in realistic models of heterogeneous porous media—preferably their images as they contain their actual heterogeneity—in order to gain deeper understanding of flow in the transition from the Darcy regime to nonlinear flow at higher Re. Such computations are typically difficult and time consuming. Although several efficient numerical methods, as well as lattice Boltzmann models (Hill et al. 2001; Chai et al. 2010), have been developed that may be used to solve the governing equations at high Reynolds numbers in porous media, many theoretical and computational studies have instead utilized empirical or semi-empirical correlations between the fluid velocity and the macroscopic pressure gradient.

This paper is the first in a series dedicated to a study, by extensive computer simulations, of single- and two-phase flow in a heterogeneous porous medium at Reynolds numbers for which the Darcy’s law and its generalization to two-phase flow breaks down. In the present paper, we focus on the problem in single-phase fluid flow. Many factors contribute to the emergence of a transition from the Darcy to non-Darcy flow, which include the disordered morphology of the pore space that gives rise to highly non-uniform flow fields similar to those in turbulent flow (Sederman et al. 1998), intrinsic flow instabilities (Hill and Koch 2002; Soulaine et al. 2017), and coherent topological patterns (Sederman et al. 1998; Chu et al. 2018) that emerge when the transition to turbulent flow occurs. A good review of the literature is given by Koch and Hill et al. (2001).

The organization of the rest of the paper is as follows. In the next section, we describe models of pore space that we utilize in our study. The details of the numerical simulations are described in Sect. 3, while the results and their implications are presented in Sect. 4. The paper is summarized in the last section.

2 Models of Porous Media

We used two-dimensional (2D) slices of a 3D image of a sandstone in the simulations. The square-shaped image had a length of 365 \(\mu\)m, with its pore space having a porosity of 0.79 and connected from the left to the right side; see Fig. 1. The image was then imported into the COMSOL Multiphysics package whose geometry toolbar provides a number of utility functions for image manipulation. We used the package’s “interpolation curve” function to capture and correctly represent the curved interface between the pores and the solid matrix of the porous medium with a relative tolerance of \(10^{-3}\;\mu\)m. The partition node of the package with various Boolean operations was then utilized to identify the solid and void domains in the images. Once the two domains were identified, they were used in the physics interface of the COMSOL package in order to set up the computational grid for solving the governing equations for fluid flow with specified boundary conditions.

Fig. 1
figure 1

The image of the two-dimensional slice of the sandstone, where the white area shows the pore space

Full size image

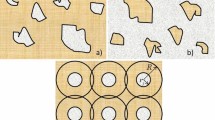
The original morphology of the image was also modified in order to generate several other models of porous media with lower porosities that are typically encountered in nature. According to percolation theory (Sahimi 2023), the lowest possible porosity in 2D disordered porous media with a more or less random morphology that still allows the formation of a sample-spanning cluster of connected pores from the left to the right side of the image is 0.5. Thus, we added at random impermeable solid objects of random sizes to the void domain of the image, in order to generate multiple realizations of the pore space with porosities 0.7, 0.6, and 0.51. Examples of the modified morphology are displayed in Fig. 2.

Note that since we generate the model porous media at lower porosities through stochastic insertion of solid objects in the pore space, one, in principle, can generate an infinite number of such realizations. Each of such realizations will give rise to numerical results that may be different from what we present below. The trends in the variations of the computed properties with the control parameters, such as the porosity, are, however, completely similar among all the realizations. This is because previous simulation of fluid flow through porous media in the same sandstone (Kohanpur et al. 2020; Aljasmi and Sahimi 2021) indicated that the size of the original image is larger then the representative elementary volume (REV) of the sandstone. Thus, the numerical results presented below are representative of the sandstone that we utilize in the simulation [for a discussion of the significance of the REV see, for example, (Wojciech 2019)], and our numerical simulations confirmed this.

It is also crucial to have a smooth interface that separates the void and solid domains in order to ensure that a high-quality and resolved computational grid is generated within the pore space and utilized in the flow simulation. An interface with sharp and pointed corners would result in a low-resolution mesh that can slow down and even prevent, in a reasonable time, convergence of the iterative scheme for solving the discretized governing equations to the true solution.

Fig. 2
figure 2

The structure of the porous medium at three porosities \(\phi\) generated from the original image with porosity of 0.79. White areas show the pores

Full size image

3 Simulation of Fluid Flow

The single-phase flow physics interface of COSMOL, which solves the mass conservation and the Navier–Stokes equations, was utilized to compute the velocity and pressure fields throughout the entire domains, assuming the fluid to be incompressible and Newtonian. The fluid, assumed to be water, was injected into the pore space at the inlet on the left side of the images at a specified pressure, while the pressure on the right side (the outlet) of the models was zero. No-slip boundary condition was imposed on all the inner walls separating the pore space and the solid domain. The boundary conditions at the top and the bottom external edges of the models were either no-flow or symmetric boundary conditions. The former implies that the fluid velocity vector relative to the wall velocity vanishes on the external boundary, whereas the latter prescribes no penetration and vanishing of shear stresses, i.e., the velocity gradient, at the top and bottom boundaries that, roughly speaking, is equivalent to the periodic boundary conditions that are usually used in pore-network models of porous media. Note that since we use the images of a natural sandstone, imposing exact periodic boundary conditions, which eliminate the effect of finite size of a sample porous medium, is not possible.

The Reynolds number that we used in the simulation is defined by

$$\begin{aligned} \textrm{Re}=\frac{\rho D_0 v_m}{\mu (1-\phi )}, \end{aligned}$$
(1)

where \(D_0\) is an appropriate length scale, which can be the mean grain or mean pore-throat size. We used the former, i.e., we took \(D_0\) to be the average diameter of the grains, computed based on the images. They ranged from \(28.2\;\mu\)m for porosity \(\phi =0.79\) to \(22.0\;\mu\)m for \(\phi =0.51\). Here \(\rho\) is the fluid’s density, and \(v_m\) is the mean fluid velocity. Depending on the Reynolds number and the porosity, computational grids with sufficient resolution were superimposed on the pore space of the images, in order to simulate fluid flow. Figure 3 depicts the grid used in the porous medium with the lowest porosity, 0.51. The resulting mesh-based discretized governing equations were solved in a fully-coupled fashion using PARDISO, parallel sparse direct solver. No special tuning of the numerical settings was necessary for achieving convergence of the iterative algorithm that solved the governing equations in the range of the Reynolds number that we studied. The simulations yielded the pressure and velocity fields as the basic outputs, which were then utilizd to compute four important characteristics of interest, namely, the vorticity, the friction drag, the effective permeability, and the relationship between the macroscopic pressure gradient and the mean fluid velocity.

Fig. 3
figure 3

The computational grid in the pore space of the porous medium with porosity of 0.79

Full size image

We carried the flow simulations for a range of the Reynolds number using the “parametric sweep” function in COMSOL, which solves a sequence of stationary or time-dependent flow problems based on a specified range of the parameters of interest, beginning with their smallest values. Thus, a range of the inlet pressures was specified as the main parameter, and all the results for a given model (morphology) were computed through a sequence in a single simulation run for each porosity and several Reynolds numbers.

4 Results and Discussion

We carried out extensive simulation of fluid flow in the models of porous media described above. In what follows, we present the results and discuss their implications.

4.1 Vorticity

The literature on fluid flow in porous media contains various arguments about the root cause of breakdown of Darcy’s law and the transition to nonlinear flow. They include formation of a viscous boundary layer (Whitaker 1996), the interstitial drag force (Hassanizadeh and Gray 1987; Ma and Ruth 1993), singularity of the streamline patterns (Panfilov et al. 2003), separation of flow (Skjetne99), and deformation of streamline patterns and formation of eddies (Fourar et al. 2004; McClure et al. 2010; Panfilov and Fourar 2006). In particular, it has been suggested that one can characterize the departure from the Darcy flow through studying the development of vorticity and formation of eddies as the Reynolds number increases. It has been suggested (Panfilov et al. 2003; Fourar et al. 2004; Panfilov and Fourar 2006; McClure et al. 2010) that, similar to turbulent flow, the departure from Darcy’s law is due to the generation of eddies at microscale. Chaudhary et al. (2011) utilized this idea to study the eddies and gaining understanding of the transition from the Darcy to nonlinear flow. The system that they studied was, however, simple, consisting of axisymmetric pores that had been formed in a staggered pattern of spherical particles.

We computed the overall vorticity \(\omega _z\) through

$$\begin{aligned} \omega _z=\left( \frac{\phi }{S}\right) \int \int \left( \frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\right) dxdy, \end{aligned}$$
(2)

where S is the surface area of the image, and \(v_x\) and \(v_y\) are the components of the fluid velocity vector v. Although we carried out almost all the simulations under steady-state conditions (since we study single-phase flow), to understand how vortical structures are developed in the pore space, we also carried out some simulations under transient conditions. Such simulations are quite time consuming because very small initial time steps, on the order of \(10^{-12}\)s, are required for achieving numerical convergence.

The boundary conditions on the outer edges of the porous medium parallel to the direction of macroscopic pressure gradient do affect the development of the vorticity. In particular, the symmetry (periodic) boundary conditions give rise to dependence of the flow field on the local details of the pore space morphology at the top and bottom edges of the system. Our simulations indicated that the vorticity first develops near the external edges, which then fuels the evolution of fluid mixing in the pore space and increases the strength of the vortical cells. On the other hand, the no-flow boundary conditions at the top and bottom edges suppress the strength of the total vorticity, which is computed over the entire domain, as indicated by Eq. (2).

Figure 4 presents snapshots of the flow field at three distinct times with the Reynolds number, \(\textrm{Re}=14.7\). They indicate that the vortical structures are developed rather quickly around the curved interfaces between the pore and solid phases. Figure 5 presents the local vortical structures at steady state for two Reynolds numbers. It is evident that, with increasing Re, not only the vortical structures spread farther away from the interface between the pores and the solid phase, but that they also become more complex. Figure 6 presents the effect of the porosity on the vortical structures at Re = 10.

Fig. 4
figure 4

Dynamic evolution of vorticity in a portion of the pore space. White areas represent the matrix

Full size image
Fig. 5
figure 5

Evolution of vorticity with the Reynolds number Re. White areas represent the matrix

Full size image
Fig. 6
figure 6

Evolution with porosity of the vorticity at a fixed Reynolds number Re = 10. White areas show the solid matrix

Full size image

We find that, independent of the boundary conditions, the vorticity is very small for small Reynolds numbers at which the Darcy’s law holds, and the effective permeability of the pore space is independent of the macroscopic pressure drop. But, as the deviatons from the Darcy flow begin to emerge, the magnitude of the vorticity also increases rapidly and significantly. This is shown in Fig. 7, where we present the computed vorticity as a function of the porosity and the Reynolds number, using the two aformentioned boundary conditions. The no-flow boundary condition at the top and bottom edges of the porous media suppresses the strength of the total vorticity, which is computed over the entire domain.

On the other hand, the symmetry (periodic) boundary conditions magnify the effect on the vorticity of the local details of the morphology at the external top and bottom edges. Fluid mixing and the development of vortical structures close to the external edges fuel their evolution in the rest of the pore space and increase the strength of vortical cells. Despite such differences, although the magnitudes of the vorticity, computed with the two boundary conditions, are different, the qualitative patterns are quite similar in both cases.

Fig. 7
figure 7

The vorticity, computed by Eq. (2) for the two types of boundary conditions (B.C.), as a function of the porosity and the Reynolds number

Full size image

Several other methods have been proposed in the literature on turbulent flow for characterization of the strength of local swirling and the vorticity. They include the iso-surface of the vorticity magnitude, local clustering of vortex lines (Kim et al. 1987), identification of elongated regions with low pressure (Robinson 1991), regions of complex eigenvalues of the velocity gradient tensor (Chong et al. 1990), the Hessian of the pressure field (Jeong and Hussain 1995), and the second invariant of the velocity gradient tensor (Zhong et al. 1996). Here, in order to further understand the development of the vortical structure in the pore space, we use the method proposed by Chong et al. (1990). In this method, one expresses (Chong et al. 1990; Zhou et al. 1999) the local velocity field v around a point r to linear order as,

$$\begin{aligned} \textbf{v}(\textbf{r}+\delta \textbf{r})=\textbf{v}(\textbf{r})+\textbf{D}\delta \textbf{r}+O(||\delta \textbf{r}||^2), \end{aligned}$$
(3)

where \(\textbf{D}={\varvec{\nabla }}{} \textbf{v}\) is the velocity gradient tensor whose characteristic equation for 3D flow fields is given by

$$\begin{aligned} \lambda ^3+P\lambda ^2+Q\lambda +R=0, \end{aligned}$$
(4)

with P, Q, and R being the three invariants of the tensor D, given by, \(P=-{\varvec{\nabla }}\cdot \textbf{v}\), \(Q=\frac{1}{2}[P^2-\textrm{tr} (\textbf{DD})]\), which is (Ziazi and Liburdy 2022) a quantity that measures the dominance of vorticity over strain, and \(R=-\textrm{det}(\textbf{D})\), where “tr” and “det” denote the trace and the determinant of the tensor. For incompressible fluids, \(P=0\) and, therefore, \(Q=-\frac{1}{2}\textrm{tr}(\textbf{DD})\), in which case, the discriminant \(\Delta\) of the characteristic equation is simply, \(\Delta \equiv R^2/4+Q^3/27\). If \(\Delta >0\), then, D has one real and a pair of conjugated complex eigenvalues. Chong et al. (1990) proposed the use of the region where an eigenvalue pair is complex to characterize the strength of vortices.

Since we simulate 2D systems, Eq. (4) reduces to, \(\lambda ^2+P\lambda +R=0\), with \(P=0\) for an incompressible fluid, and \(R=(\partial v_x/\partial x) (\partial v_y/\partial y)+(\partial v_x/\partial y)(\partial v_y/\partial x)\). For the aforementioned symmertry (periodic) boundary conditions, the two roots of the equation are complex conjugate, \(\lambda =\lambda _r\pm i\lambda _i\), with the imaginary part \(\lambda _i\) representing the local swirling strength (Chong et al. 1990; Ziazi and Liburdy 2022), which may also be interpreted as a measure of the strength of the vorticity. Thus, we computed \(\lambda _i\), with the results shown in Fig. 8, which are consistent with those shown in Fig. 7.

Fig. 8
figure 8

Strength of the vortical structures, computed through 2D version of Eq. (4), as a function of the porosity and the Reynolds number. For no-flow boundary conditions, the same quantity is essentially zero under the same conditions

Full size image

On the other hand, when the no-flow boundary conditions are imposed at the external edges of the porous media, the term R in the characteristic equation for the 2D flow that we study is negative, implying that the two roots are real, and therefore, there are no complex conjugate roots, so that the strength of local swirling and the vorticity is zero.

Another way of understanding the transition from the Darcy regime to the nonlinear one is through studying the growth of the eddies in the pore space with increasing Re and computing their growth rate \(\epsilon\). We define \(\epsilon\) as the ratio of the pore volume occupied by the stationary eddies and the total pore volume of the porous media. Figure 9 presents the results. In a system with uniform morphology (no disorder), such as that studied by Chaudhary et al. (2011), \(\epsilon\) increases monotonically with Re. In the heterogeneous porous medium that we study, however, the behavior of \(\epsilon\) is much more subtle. As Re increases, streamlines form loops and grow, hence \(\epsilon\) increases. Their growth stops when they become large enough to touch the neighboring grain boundaries. Thus, \(\epsilon\) reaches a local maximum. As Re is increased further, however, the heterogeneity of the pore space conspires with the non-uniform fluid velocity field to redistribute some of streamlines, causing \(\epsilon\) to decline, which then grow again toward the next local maximum larger that the previous one. Figure 9 shows four of such cycles or steps. Such a dynamics is not present in a uniform system, because the velocity field is uniform everywhere, so that once \(\epsilon\) reaches a maximum, there is no opportunity for it to reset.

Fig. 9
figure 9

The growth rate \(\epsilon\) of the eddies as a function of the Reynolds number Re. The porosity is 0.51

Full size image

To verify our assertion, we show in Fig. 10, the loops and streamlines developed in the flow with three Reynolds numbers. The figure at the center at Re = 21.6 with larger \(\epsilon\) indicates multiple larger loops than those at Re = 19.4 and Re = 24.7. If the simulations are extended to Re > 24.7, one again obtains increased multiple larger loops. Figure 9 shows the results for Reynolds numbers up to 37, which also indicates the formation of another step at Re = 35.

Fig. 10
figure 10

Loops, streamlines, and the rate of growth \(\epsilon\) of the eddies at three Reynolds number Re. The porosity is 0.51

Full size image

4.2 Drag

We computed the drag D by integrating the shear stress, in order to compute the rate of change of D with respect to the external pressure gradient, or the Reynolds number, i.e., its derivative \(D'\) with respect to either variable, and to understand how it varies with increasing Re. The results are shown in Fig. 11, where \(D'\) has been normalized by its value at Re = 0. As Fig. 11 indicates, for Re < 1, \(D'\) does not change with Re, which is characteristic of the linear flow regime (Darcy’s law). If we examine the formation of eddies in the same interval of Re, we will see that although small eddies are present for Re < 1, \(D'\) does not change with the applied pressure gradient, indicating that the eddies do not grow for very small Re. Note that \(D'\) is larger at the higher porosity of 0.79, since the pore space is more open.

For flows at larger Re, however, \(D'\) begins to decrease, signaling the beginning of the transition from the Darcy regime to nonlinear fluid flow. The decrease in \(D'\) is a consequence of the growth of the eddies. Thus, as emphasized above, the deviation from Darcy’s law is a result of development of vortical structure and the growth of the eddies. We will demonstrate in the next section that the effective permeability also decreases with increasing Re, hence indicating that the mechanism for its reduction is also the growth of the eddies.

Fig. 11
figure 11

The derivative \(D'\) of the frictional drag (normalized by its value at Re = 0) and its dependence on the Reynolds number for two porosities

Full size image

4.3 The Effective Permeability

We define the effective permeability of a porous medium by, \(K_n=(\mu Lv_m)/\Delta P\), where L is the medium’s length, and \(\Delta P\) is the pressure drop across it. Figure 12 presents the results as a function of the Reynolds number and porosity, computed for the two aforementioned boundary conditions. The permebilities have been normalized by their values as \(\textrm{Re}\rightarrow 0\). For very small Reynolds number, the effective permeability remains essentially constant, but for \(\textrm{Re}>\approx \;2\), it begins to decrease, first slowly, and then rather rapidly. Note that the boundary conditions have a very minor effect on the effective permeabilities. A comparison between Figs. 8, 9, 11, and 12 indicates that the vorticity and rate of growth of the eddies begin to rise significantly, and the derivative \(D'\) of the drag begins to decrease, precisely at the same Reynolds number at which the effective permeability begins to decrease strongly, confirming our assertion that studying the vortical structure and the growth of the eddies is a fruitful way of understanding the transition of fluid flow in porous media from the Darcy’s law into a nonlinear regime.

Fig. 12
figure 12

Dependence of the effective permeability on the porosity, the Reynolds number, and the boundary conditions

Full size image

The results so far provide a coherent picture of the mechanism of the reduction in the effective permeability with increasing the Reynolds number. As we showed above, in the Darcy regime, stationary eddies occupy a small and fixed fraction of the pore volume. They grow, however, when Re is above a critical value, \(\textrm{Re}_c=2-3\), with their growth leading to the transition from the Darcy’s law to the nonlinear flow regime. Since the eddies and vortical structure continue to grow above the critical value of Re, they effectively narrow down the flow paths within the pores, hence reducing the effective permeability. This picture is consistent with experimental observations of the Ziazi and Liburdy (2022), who analyzed vorticity locally in their porous medium, which was a packed bed of particles.

We also note that the value Re\(_c\) of the critical Reynolds number depends on the morphology of the pore space, and the manner by which it is defined. Typically, if the length scale \(D_0\) is taken to be the mean pore-throat size, Re\(_c\) will be smaller than its value if \(D_0\) is taken to be the mean grain size.

4.4 Crossover from the Darcy’s Law to Nonlinear Flow

In the literature, the departure from the Darcy’s law due to the effect of inertia has been modeled by the Forchheimer’s equation [see also Brinkman (1949)],

$$\begin{aligned} -{\varvec{\nabla }}P=\left( \frac{\mu }{K_e}\right) \textbf{v}+\beta _F\rho \textbf{v}|\textbf{v}|, \end{aligned}$$
(5)

where \(\beta _F\) is an empirical coefficient for which various correlations have been proposed (Sahimi 2011). One is,

$$\begin{aligned} \beta _F=\frac{1.75(1-\phi )}{D_g\phi ^3}, \end{aligned}$$
(6)

which is for granular media, where \(D_g\) is a typical grain size. Using extensive pore-network simulations, Thauvin and Mohanty (1998) proposed the following correlations:

$$\begin{aligned} \beta _F=1.55\times 10^4\tau ^{3.35}K_e^{-0.98}\phi ^{-0.29}, \end{aligned}$$
(7)

where \(\tau\) is the tortuosity of the pore space (see Ghanbarian-Alavijeh et al. (2013), for a comprehensive review of the literature on the tortuosity). Several other empirical relations that relate \(\beta _F\) to \(K_e\) and porosity \(\phi\) have also been proposed (Sahimi 2011), the accuracy of which is comparable with that of Eq. (6).

On the other hand, by applying the homogenization theory (Sanchez-Palencia 1980; Allaire 1989, 1991a, b, 1992; see also Telega and Wojnar (1998)) to the Navier–Stokes equations in a periodic cell, Mei and Auriault (1991), Wodie and Levy (1991), Cieslicki and Lasowska (1999), and Skjetne and Auriault (1999a) showed that, in the weak inertia regime, the existing data can be accurately represented by

$$\begin{aligned} -{\varvec{\nabla }}P=\frac{\mu }{K_e}{} \textbf{v}+\beta _n\rho \textbf{v}|\textbf{v}|^2, \end{aligned}$$
(8)

where \(\beta _n\) is a generalization of \(\beta _F\) for the nonlinear flow regime. Numerical simulations (Firdaouss et al. 1997; Rojas and Koplik 1998; Andrade et al. 1999; Narváez et al. 2013), as well as experimental studies (Lage et al. 1997; Skjetne and Auriault 1999b), also supported the accuracy of Eq. (8). Whitaker (private communication, May 1993) also derived Eq. (8) in the weak inertia regime.Footnote 1

Adler et al. (2013) proposed two analytical–numerical algorithms in order to study the solution of the Navier–Stokes equations in a three-dimensional channel enclosed by two rough walls, with the roughness amplitude being proportional to \(b\varpi\), where 2b is the mean size of the channel’s flow passage, and \(\varpi\) is a small dimensionless parameter. One algorithm, applicable to small Reynolds number flow, represented the velocity and pressure fields in terms of a double Taylor series in Re and \(\varpi\). The algorithm, with accuracy \(\mathcal{O}(\textrm{Re}^2)\) and \(\mathcal{O}(\varpi ^6)\), together with Padé approximation (see, for example, Brezenski 1996), produced the Forchheimer’s law. The second algorithm, applied to a symmetric channel, took all the terms on Re and \(\varpi\) into account and predicted that the magnitude of the pressure gradient should be an odd function of \(|\textbf{v}|\), implying that at larger Re, the Darcy’s law is corrected by a cubic term in \(|\textbf{v}|\), i.e., Eq. (8). Numerical simulations of Adler et al. (2013) for non-symmetric channels yielded the same cubic correction. Sivanesapillai et al. (2014) also proposed an equation that is consistent with Darcy’s law for small Re, reproduces Forchheimer’s equation for larger Re, and contains leading higher-order terms in the regime of weak inertia.

Here, we present a heuristic derivation of Eq. (8). Consider two-phase disordered materials, including porous materials that consist of the pore and solid phases. If \({\varvec{\nabla }} V\) is an applied voltage gradient across the material and I is the electric flux, then, in the most general form, one has (Sahimi 2003)

$$\begin{aligned} -{\varvec{\nabla }} V=R_\ell \textbf{I}+R_n|\textbf{I}^{m-1}|\textbf{I}, \end{aligned}$$
(9)

where \(R_\ell\) and \(R_n\) are, respectively, the linear and generalized nonlinear resistances (both per unit length), and m is a constant. Clearly, when, \(R_n=0\), one recover’s Ohm’s law, which is the electric analog of the Darcy’s law. It has been shown that (Sahimi 2003) if a disordered material has inversion symmetry, then, one has \(m=3\) in the nonlinear regime, so that

$$\begin{aligned} -{\varvec{\nabla }} V=R_\ell \textbf{I}+R_n|\textbf{I}^2|\textbf{I}. \end{aligned}$$
(10)

This is consistent with Adler et al. (2013) prediction, mentioned above, that the pressure drop (the analog of voltage drop) in the most general case should be an odd function of \(|\textbf{v}|\). If a porous medium’s morphology is random, or if it contains at most short-range correlations, then, it has inversion symmetry. In that case, if we use the analogy between electrical and hydraulic resistances (conductances), i.e., \({\varvec{\nabla }}V\longleftrightarrow {\varvec{\nabla }}P\), \(R_\ell \longleftrightarrow (\mu /K_e)\) and \(\textbf{I}\longleftrightarrow \textbf{v}\), write \(R_n\) as, \(R_n=\rho \beta _n\), and invoke Eq. (10), we obtain Eq. (8), with \(\beta _n\) being a generalization of \(\beta _F\) for the nonlinear flow regime. Note, however, that the units of \(\beta _F\) and \(\beta _n\) are not the same.

Figure 13 compares the results of the numerical simulation of the Navier–Stokes equation with the fits provided by Eqs. (5) and (8) for a porosity of 0.51, and the two types of the boundary conditions—no-flow and periodic—described above. \(\beta _F\) was computed based on Eq. (6), although other correlations for \(\beta _F\) may be used. Figure 14 makes the same comparison as in Fig. 13, but for a porosity of 0.79. For both types of boundary conditions and porosity, Eq. (8) provides very accurate fits of the data, much better than those provided by Eq. (5). Figures 13 and 14 both indicate that the transition from the Darcy’s law to nonlinear flow begins to emerge at a Reynolds number that is about \(2-3\).

Our preliminary simulations indicate that for flow in 3D porous media, the performance of Eq. (8) is significntly better than that of the Forchheimer’s. We should, however, point out that if we treat \(\beta _F\) as an adjustable parameter, rather than estimating it by Eq. (6) or (7) (or other correlations), and fit the numerical data to Eq. (5), the accuracy of the resulting fit would be comparable with what the fit to Eq. (8) provides. But, this means that one must estimate \(\beta _F\) for each porous medium separately. On the other hand, it is possible to theoretically derive an equation that expresses \(\beta _n\) in terms of the effective properties of the same porous media in the linear flow regime, so that, in principle, \(\beta _n\) is not an adjustable parameter. The derivation of the equation for \(\beta _n\) is long and complex, and will be presented in a future paper, where we will also test its accuracy.

Fig. 13
figure 13

Comparison of the correlation between the macroscopic pressure gradient and the Reynolds number (flow velocity), as predicted by the Forchheimer’s equation, the Darcy’s law, and Eq. (8). The porosity is 0.51

Full size image
Fig. 14
figure 14

Same as in Fig. 13, but for porosity, \(\phi =0.79\)

Full size image

5 Summary and Conclusions

Extensive numerical simulations of the Navier–Stokes equations were carried out in order to study the departure from the Darcy’s law for single-phase fluid flow through a disordered porous medium and to understand the effect of inertia. As the models of the porous media, we used 2D slices of an actual 3D image of a sandstone and studied the problem over wide ranges of the porosity and the Reynolds number Re, as well as for two types of boundary conditions. Four main properties of fluid flow, namely, the strength of the vorticity and the eddies, the frictional drag, the effective permeability of the pore space, and the relationship between the macroscopic pressure gradient \({\varvec{\nabla }}P\) and the fluid velocity v, were computed and studied. The numerical simulations indicate that in the range of the Reynolds number Re in which the Darcy’s law is valid, the magnitude \(\omega _z\) of the vorticity is nearly zero. As Re increases, however, so also does \(\omega _z\), and its increase begins at the same Re at which Darcy’s law begins to break down.

Based on the analogy between electrical currents in heterogeneous and nonlinear composites and flow in disordered porous media, we also presented a heuristic derivation of a nonlinear relationship between the macroscopic pressure gradient \({\varvec{\nabla }}P\) and the fluid velocity v that is third order in \(|\textbf{v}|\), unlike the Forchheimer’s equation that is quadratic in \(|\textbf{v}|\). The equation had actually been speculated on in the past based on numerical simulations and experimental data, and had also been derived for simple geometries. The new equation provides accurate representation of the numerical data over the range of Re that we studied, and its predictions are more accurate than those of the Forchheimer’s equation, which has traditionally been used in the studies of the effect of inertia on fluid flow in porous media.

In this paper, we study non-Darcy fluid flow in an image of a sandstone. It remains to be seen whether the nonlinear third-order relation between the pressure gradient and the fluid velocity is applicable to nonlinear fluid flow in other types of porous media. Numerical simulations in this direction are in progress.