1 Introduction

Bearingless Motors (BM) have gained rising attractiveness in the past decade. However, the increased manufacturing effort and the necessary complex position control have limited bearingless motor solutions for industrial use up to now [8]. Especially the motor topologies with special, e.g. conical rotor shapes [7, 15, 21] suffer from that drawback. The most promising topologies for industrial high-speed applications such as pumps or compressors is the bearingless PM synchronous machine. Several prototypes of this topology have reached high speed values up to \({100000\ \mathrm{min}^{-1}}\) [12] and \({60\ \mathrm{kW}}\) [16].

Here, a novel feeding concept of the axial bearing is presented, avoiding the double-cone rotor, but also the extra DC-chopper feeding circuit for the axial bearing coil. This solution reduces the costs, making it a feasible alternative to the use of an extra active magnetic bearing (AMB) circuit or of expensive mechanical high-speed ball-bearings, which require additional maintenance due to lubrification. The concept is based on the reduction of power switches and enables the use of standard 3-phase inverter modules. Thus, the concept can also be applied to higher power classes of several \({100\ \mathrm{kW}}\). Here, a \({1\ \mathrm{kW}/60000\ \mathrm{min}^{-1}}\)-prototype machine was built to evaluate the novel concept.

For power classes \(>1\ \mathrm{kW}\) a slotted 3-phase stator with six actively controlled degrees of freedom is the topology of choice in order to compensate for the rotor forces efficiently. For the use as high-speed drive, small rotor diameters are necessary to keep the mechanical stress in the rotor at a suitable level. For these cylindrical rotors a separate AMB for axial position control, a so-called thrust AMB, is required. This AMB is usually fed by a 4-quadrant chopper which requires four power switches, thus, increasing the system costs.

The novel feeding technique avoids this additional DC supply. The BM is already equipped with two 3-phase stator windings with two star-points, either as one combined torque and suspension winding, like in [17], or as two separated torque and suspension windings, as described in [6]. With the new concept, all six stator winding terminals are used to generate torque, radial and axial force at the same time. This is realized by feeding the axial bearing with a star-point current as superposition of the three zero-sequence phase currents in both 3-phase systems. The principle of feeding an AMB with a zero-sequence current was investigated in a different form already by two research groups.

The Institute for Electric Drives and Power Electronics, Johannes Kepler University Linz, Austria, presented a PM-biased combined radial-axial magnetic bearing, one for each shaft side, where the radial force is generated by a 3-phase winding in [20]. Axial force is generated if a zero-sequence current is injected in the two bearings, weakening or enhancing the PM bias flux in the axial air-gaps on each shaft end. Further, in [4, 5] a so called axial force / torque motor is described, which generates axial force by the interaction of a zero-sequence current in the winding overhangs with a radially magnetized homopolar PM.

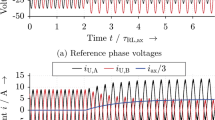
The second research group from Shizuoka University and Tokyo Institute of Technology, Japan, presented a technique in [1] where they feed a PM synchronous machine with a 3-phase current system, applying field-oriented control. In addition they inject a zero-sequence current and put an arbitrary AMB between the star point of the motor winding system and the neutral clamp of the pulse width modulated voltage source inverter (compare Fig. 1a). Hence, the zero-sequence current is used to control the force in the additional AMB by superimposing the zero-sequence current with the phase currents of the machine. In [2, 3] they expand this principle to an outer-rotor 6-pole/6-slot bearingless slice motor with three actively controlled degrees of freedom (\(x\), \(y\), \(\varphi _{\mathrm{z}}\)): A 3-phase 4-pole winding yields the air gap magnetic field for radial force generation. A single-phase 6-pole winding yields the torque generating stator field. This single-phase winding is fed by the star-point current of the suspension winding system, consisting of the zero-sequence currents.

Fig. 1.
figure 1

Different topologies of feeding an axial AMB with a star-point current

Full size image

In contrast to that, the here presented technique is applied to a six degrees of freedom rotor position control. The zero-sequence current is not generated between one star point and the neutral inverter terminal, but between two star points \(\mathrm{Z}_{\mathrm{A}}\) and \(\mathrm{Z}_{\mathrm{B}}\) (see Fig. 1b). This is realized by using the electric scalar potential of the two star points \(\mathrm{Z}_{\mathrm{A}}\) and \(\mathrm{Z}_{\mathrm{B}}\) [9, 18]. This way, the full DC-link voltage can be applied to the axial magnetic bearing. If two bearingless half-motors are used it is also possible to use the difference of four star-point potentials in order to control the axial current \(i_{\mathrm{ax}}\) (Fig. 1c)). This case is not considered here, since the axial voltage requirement for AMB systems is low (compare Fig. 12). Generally, the zero-sequence current feeding can also be used in higher power classes if insulated-gate bipolar transistors (IGBT) instead of the here applied metal oxide semiconductor field-effect transistors (MOSFET) are used as power switches.

2 Prototype bearingless PM synchronous machine

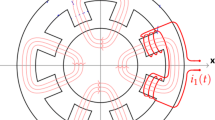
The BM is located on the drive end side (DE), whereas the axial thrust bearing is combined with a radial AMB as “combined” AMB [22] at the non-drive end side (NDE) of the shaft, to allow for a short axial length (Fig. 2). The bearingless permanent magnet (PM) synchronous machine prototype (Table 1) is fed by a two-level \({1.2\ \mathrm{kVA}}\)-inverter at \(150\ \mathrm{V}\)-DC-link voltage with seven current sensors and twelve MOSFET-half-bridges, operated at a switching frequency of \({f_{\mathrm{sw}}=33\ \mathrm{kHz}}\). Eddy current sensors are used for measuring the rotor radial and axial position. The rotor angle \(\gamma _{\mathrm{R}}\) is determined by an analogue Hall-sensor for speed values \({n<10000\ \mathrm{min}^{-1}}\) and by two \(90^{\circ }\)-shifted simple digital Hall-sensors for speed values \({n>10000\ \mathrm{min}^{-1}}\) to reduce the sensor time delay.

Fig. 2.
figure 2

Schematic overview of the considered prototype bearingless PM synchronous machine

Full size image
Table 1. Data of the prototype bearingless PM machine and of the axial AMB
Full size table

The pole pair count \(p_{\mathrm{L}}\) of the suspension winding and \(p\) of the rotor PM fulfill the condition \({p_{\mathrm{L}}=p\pm 1}\) [23] for generating a radial bearing force. With the combination \(p/p_{\mathrm{L}}=1/2\) the PM rotor is composed of a solid magnetic stainless steel shaft, on which a solid \(\mathrm{Sm_{2}Co_{17}}\) PM ring is mounted, magnetized with \({2p=2}\) poles. It is protected against centrifugal forces by a shrink-fit carbon fiber sleeve. The twelve-slot stator is equipped with a distributed integer slot winding with \(q=2\) slots per pole and phase. This so-called “double 3-phase” winding, consisting of the systems A and B (Fig. 1b) serves as a combined drive and suspension winding. It generates two different field waves with \({2p=2}\) for the torque and \({2p_{\mathrm{L}}=4}\) for the radial bearing force. Due to the coil pitching of \(2/3\) the winding factor of the third harmonic field wave component is \({k_{\mathrm{w,3}}=0}\), so that no air gap field results from the zero-sequence current system. The required stator air gap field for the torque and the suspension force generation is excited by the superposition of the phase currents in the two 3-phase systems A and B (Fig. 1b), as explained in [11]. The 4-pole (suspension) field wave with fundamental winding factor \(k_{\mathrm{w,L}}\) occurs if the two 3-phase systems A and B are fed with two “in-phase” current systems (“common-mode feeding”). The 2-pole (drive) field with fundamental winding factor \(k_{\mathrm{w,D}}\) occurs if the two 3-phase systems are fed with two current systems A and B in “phase opposition” (“differential-mode feeding”).

The combined radial-axial AMB at the NDE with PM-biased magnetization is commercially available at KEBA Industrial Automation Germany GmbH. It is composed of a 4-pole radial magnetic bearing and an axial magnetic bearing. The radial magnetic bearing will not be considered hereafter, since it is fed by two standard 4-quadrant choppers in combination with a classical Proportional-Integral-Differential (PID) position controller. It may be omitted if a second BM is used instead [6]. The axial AMB with the resistance \(R_{\mathrm{ax}}\), the inductance \(L_{\mathrm{ax}}\), the force-current coefficient \(k_{\mathrm{F,z}}\) and the stiffness coefficient \(k_{\mathrm{s,z}}\) (Table 1) is also fed by the 3-phase inverters. We use the gravitational rotor force \({m_{\mathrm{R}}\cdot g=8.8\ \mathrm{N}}\) as nominal axial force. For that, we need a stationary Ohmic voltage demand of \({u_{\mathrm{ax}}=0.23\ \mathrm{V}}\), which is a very small value when compared with the speed-dependent induced voltage which can take values up to \({\hat{U}_{\mathrm{p}}=60\ \mathrm{V}}\).

A standard field-oriented, decentralized position control according to [23] is used in the BM for the radial force and the torque, applying controller tuning according the principle of natural stiffness and damping. With this control, the magnetically levitated BM was operated with a turbo-charger fan as load up to its rated speed \(n_{\mathrm{N}}=60000\ \mathrm{min}^{-1}\) [10]. A detailed discussion of the radial and axial position control is given in [10]. The schematic control circuit is shown in Fig. 3 for the axial position control, the speed control and the radial position control at the drive end for the bearingless motor.

Fig. 3.
figure 3

Cascaded control circuit of the axial position control, the speed control and the radial position control at the drive end (i.e. the bearingless PM synchronous motor), where the focus is on the current control

Full size image

3 Applied modulation technique

A carrier-based pulse width modulation (PWM) is used for the feeding of the stator winding of the prototype machine. The modulation of the reference voltage is part of the cascaded current control loop (Fig. 3). Coordinate transformations are required to control the system in the rotor-fixed \(d\)-\(q\)-coordinate frame. In addition to the transformations for simple 3-phase stator windings, here for the double winding systems A and B (Fig. 1b), the transformation (1) is needed due to the combined winding.

$$\begin{aligned} \begin{pmatrix} u_{\mathrm{\alpha ,A}} \\ u_{\mathrm{\beta ,A}} \\ u_{\mathrm{\alpha ,B}} \\ u_{\mathrm{\beta ,B}} \\ \end{pmatrix}&= \begin{bmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ -1 & 0 & 1 & 0 \\ 0 & -1 & 0 & 1 \\ \end{bmatrix} \cdot \begin{pmatrix} u_{\mathrm{\alpha ,D}} \\ u_{\mathrm{\beta ,D}} \\ u_{\mathrm{\alpha ,L}} \\ u_{\mathrm{\beta ,L}} \\ \end{pmatrix} \end{aligned}$$
(1)

The symmetrical drive (subscript: D) and suspension (subscript: L) voltage systems are composed of the voltages in the 3-phase systems A and B. The “common mode feeding” of the systems A and B yields the 3-phase suspension current, whereas a “differential mode feeding” generates the 3-phase drive current system. The natural PWM adapts the mean value of a single-phase voltage over one switching period \(T_{\mathrm{sw}}\). Usually a triangular carrier voltage \(u_{\mathrm{tri}}\) is compared to a reference voltage in order to determine the switching instants (Fig. 4) [13]. For this, the voltage space vector \(\underline{u}_{\mathrm{\alpha ,\beta }}\) for the 3-phase systems A and B must be decomposed into three reference voltage signals \(u_{\mathrm{U,ref}}\), \(u_{\mathrm{V,ref}}\) and \(u_{\mathrm{W,ref}}\) for each of the two 3-phase systems as \(u_{\mathrm{U,A,ref}}\), \(u_{\mathrm{V,A,ref}}\) and \(u_{\mathrm{W,A,ref}}\) and \(u_{\mathrm{U,B,ref}}\), \(u_{\mathrm{V,B,ref}}\) and \(u_{\mathrm{W,B,ref}}\) (Fig. 3, 4). Often the zero-sequence voltage with \(3\cdot f_{\mathrm{s}}\) is added to the sinusoidal reference signal at synchronous frequency \(f_{\mathrm{s}}\) for a higher linear modulation degree \(m_{\mathrm{a}}\) [13]. This is not possible here, because an artificial DC offset \(\pm u_{\mathrm{ax,ref}}/2\) is added to the above noted reference phase voltages, where \(u_{\mathrm{ax,ref}}\approx u_{\mathrm{ax}}\) is the voltage drop over the axial AMB (Fig. 5). This DC offset is of opposite polarity in the two 3-phase systems A and B, so that a DC voltage drop of \(u_{\mathrm{ax}}\) occurs between the two star points \(\mathrm{Z}_{\mathrm{A}}\) and \(\mathrm{Z}_{\mathrm{B}}\). The block diagram of this method is given in Fig. 4. The required voltage transformation (2) shows the integration of the artificial zero-sequence current feeding. It is simple to implement with a carrier-based PWM since it only results in an offset of the reference voltages.

$$\begin{aligned} \begin{pmatrix} u_{\mathrm{U,A}} \\ u_{\mathrm{V,A}} \\ u_{\mathrm{W,A}} \\ u_{\mathrm{U,B}} \\ u_{\mathrm{U,B}} \\ u_{\mathrm{U,B}} \\ \end{pmatrix}&= \begin{bmatrix} 1 & 0 & 0 & 0 & \frac{1}{2} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} & 0 & 0 & \frac{1}{2} \\ -\frac{1}{2} & -\frac{\sqrt{3}}{2} & 0 & 0 & \frac{1}{2} \\ 0 & 0 & 1 & 0 & -\frac{1}{2} \\ 0 & 0 & -\frac{1}{2} & \frac{\sqrt{3}}{2} & -\frac{1}{2} \\ 0 & 0 & -\frac{1}{2} & -\frac{\sqrt{3}}{2} & -\frac{1}{2} \\ \end{bmatrix} \cdot \begin{pmatrix} u_{\mathrm{\alpha ,A}} \\ u_{\mathrm{\beta ,A}} \\ u_{\mathrm{\alpha ,B}} \\ u_{\mathrm{\beta ,B}} \\ u_{\mathrm{ax}} \\ \end{pmatrix} \end{aligned}$$
(2)
Fig. 4.
figure 4

Schematic representation of the classical PWM

Full size image
Fig. 5.
figure 5

Equivalent circuit for the axial current \(i_{\mathrm{ax}}\) (similar to [9])

Full size image

4 Evaluation by measurement and simulation

The proposed method was evaluated at the test bench according to Fig. 6. Time-domain simulations in Simulink, employing the Simscape-Toolbox were used with the settings according to Table 2. The necessary off-time of the high-side MOSFET due to the bootstrap driver circuit is represented by a reduced value of \({U_{\mathrm{DC}}=48\ \mathrm{V}\cdot 0.89}\) according to the measured dead time.

Fig. 6.
figure 6

Test bench for the bearingless PM synchronous prototype machine

Full size image
Table 2. Settings for the numerical simulation in time-domain (power electronic properties at \(100\,\mathrm{C^{\circ }}\) from [14])
Full size table

4.1 Operation at over-modulation

Generally a safe motor operation with the zero-sequence current operation is ensured if the inverter is not driven at its voltage limit, i.e. for modulation degrees \({m_{\mathrm{a}}<1}\). Operation at over-modulation (\({m_{\mathrm{a}}>1}\)) is crucial, since not enough voltage reserve for axial current dynamics may be available. The DC axial current \(i_{\mathrm{ax}}\) in stationary operation exhibits an additional \(3\cdot f_{\mathrm{s}}\)-frequent harmonic component for \({m_{\mathrm{a}}>1}\), since the desired change in star-point potential during the “passive” time sections of the PWM cannot balance the unwanted change in star-point potential during the “active” time sections. This has already been explained in [9].

The rated speed \({n_{\mathrm{N}}=60000 \ \mathrm{min}^{-1}}\) at \({U_{\mathrm{DC}}=150\ \mathrm{V}}\) is also the maximum mechanically allowed speed and is reached with a modulation degree of \(m_{\mathrm{a}}=0.85\) [10].

In order to investigate if a safe operation of the axial bearing even at over-modulation is possible, a reduced DC-link voltage of \({U_{\mathrm{DC}}=48\ \mathrm{V}}\) is applied to enforce over-modulation at reduced speed \(n\). Figure 7 shows the measured third harmonic component of the axial voltage \(\hat{u}_{\mathrm{ax,3}}\) which increases linearly with the modulation degree for \(m_{\mathrm{a}}>1\). The resulting third harmonic of the axial current \(\hat{i}_{\mathrm{ax,3}}\) is given in Fig. 8a, which compares this current oscillation with \(3\cdot f_{\mathrm{s}}\) at \(m_{\mathrm{a}}=1.55\) between measurement and simulation for one electrical period \(1/f_{\mathrm{s}}\). The measured current exhibits an additional current ripple of \({f_{\mathrm{sw}}=33\ \mathrm{kHz}}\). The eddy currents in the axial AMB rotor disk decrease the inductance \(L_{\mathrm{ax}}\) for such high switching frequencies so an increased switching current ripple occurs. The according Fourier voltage harmonic spectrum (Fig. 8b, 8c) shows the amplitude of the \(3\cdot f_{\mathrm{s}}\)-frequent component, which is approximately \({\hat{u}_{\mathrm{ax,3}}\approx 10\ \mathrm{V}}\). Side-bands close to \(2\cdot f_{\mathrm{sw}}\) exhibit rather small values (\({< U_{\mathrm{DC}}/8}\)), when compared to the classical 4-quadrant chopper operation [19]. The increase of the \(3\cdot f_{\mathrm{s}}\)-frequent current component \(\hat{i}_{\mathrm{ax,3}}\) with increasing modulation degree is shown in Fig. 9, proving a good fit between measurement and simulation.

Fig. 7.
figure 7

Measured and simulated fundamental voltage \(\hat{u}_{\mathrm{s,1}}\) and third harmonic component of the axial voltage \(\hat{u}_{\mathrm{ax,3}}\) for varying modulation degree \(m_{\mathrm{a}}\) at \({U_{\mathrm{DC}}=48\ \mathrm{V}}\)

Full size image
Fig. 8.
figure 8

Measured and simulated axial AMB current \(i_{\mathrm{ax}}\), measured (b) and simulated (c) harmonic spectrum of the axial AMB voltage \(u_{\mathrm{ax}}\) at \({m_{\mathrm{a}}=1.55}\) and \({n=25200\ \mathrm{min}^{-1}}\)

Full size image
Fig. 9.
figure 9

Measured and simulated \(3\cdot f_{\mathrm{s}}\)-frequent axial current component \(\hat{i}_{\mathrm{ax,3}}\) for varying speed at \({U_{\mathrm{DC}}=48\ \mathrm{V}}\)

Full size image

This \(3\cdot f_{\mathrm{s}}\)-current component is not crucial for the axial position control since the time constant of the mechanical system is much bigger than the current oscillation period \(1/\left (3\cdot f_{\mathrm{s}}\right )\). This is shown by (3): For the given configuration the ripple in \(z\)-position is \({<1~\upmu \text{m}}\) even for \({\hat{i}_{\mathrm{ax,3}}=1\ \mathrm{A}}\) at \({n=25200\ \mathrm{min}^{-1}}\). Besides that also the eddy currents in the solid rotor part of the axial AMB help to damp such unwanted \(z\left (t\right )\)-oscillations.

$$\begin{aligned} \ddot{z}(t) &= \frac{F_{\mathrm{z}}(t)}{m_{\mathrm{R}}} = \frac{k_{\mathrm{F,z}} \cdot \hat{i}_{\mathrm{ax,3}}}{m_{\mathrm{R}}} \cdot \cos (3 \cdot \omega _{\mathrm{s}} \cdot t) \\ z(t) &= - \frac{k_{\mathrm{F,z}} \cdot \hat{i}_{\mathrm{ax,3}}}{m_{\mathrm{R}}} \cdot \frac{1}{(3 \cdot \omega _{\mathrm{s}})^{2}} \cdot \cos (3 \cdot \omega _{\mathrm{s}} \cdot t) \end{aligned}$$
(3)

4.2 Position control dynamics

The benchmark for the here presented novel axial position control performance is the classical and commercially available 4-quadrant chopper operation. In Fig. 10 a position step responses to a change in reference position of \({\varDelta z=20\ \mathrm{~\upmu \text{m}}}\) at different speed, i.e. at three different modulation degrees \({m_{\mathrm{a}}= 0,\ 0.84, 1.55}\) is shown for the 4-quadrant chopper and the zero-sequence axial current operation in comparison. No significant difference between 4-quadrant chopper operation and zero-sequence current feeding in the settling behavior of the position signal can be recognized. The zero-sequence current based position control dynamics do not depend on the inverter modulation degree \(m_{\mathrm{a}}\). Only a slight oscillation in \(z\) is visible in Fig. 10f for \({m_{\mathrm{a}}=1.55}\).

Fig. 10.
figure 10

Comparison of DC-chopper and zero-sequence current operation of the axial AMB: Measured axial displacement for a step response of \({\varDelta z=20\ \mathrm{~\upmu \text{m}}}\) for different modulation degrees \(m_{\mathrm{a}}\)

Full size image

The Figures 11a, 11b show the axial current response and the torque generating \(q\)-current \(i_{\mathrm{q,D}}\) at the moment of the reference signal step \(z_{\mathrm{ref}}\). In contrast to the 4-quadrant chopper operation, the zero-sequence current feeding (Fig. 11b) shows a coupling between the drive current \(i_{\mathrm{q,D}}\) and the axial current \(i_{\mathrm{ax}}\) as an oscillation of \(i_{\mathrm{q,D}}\) at the moment of the step in \(i_{\mathrm{ax}}\). This is not a magnetic coupling. It only occurs at over-modulation. This is because the high value of \(u_{\mathrm{s,ref}}\) together with the superimposed half axial voltage demand \(u_{\mathrm{ax,ref}}/2\) increase the maximum value of one half-wave of voltage reference signal to values \(>U_{\mathrm{DC}}/2\). The maximum value of the other half-wave is smaller by \(u_{\mathrm{ax,ref}}/2\). This influences the harmonic content of the phase voltages and currents. Low-frequent (\({f<10\cdot f_{\mathrm{s}}}\)) current harmonics occur from voltage harmonics which are in phase opposition in the winding systems A and B, since the axial bearing voltage is given by the difference between the star point potentials in ZA and ZB. This “coupling” does only affect the drive current, but not the suspension current for the radial force because the latter is only influenced by voltage harmonics of A and B in “common mode operation”. Even at stationary operation, these additional ripples of \(i_{\mathrm{q,D}}\) are visible in Fig. 11b when compared to Fig. 11a.

Fig. 11.
figure 11

Comparison of DC-chopper and zero-sequence current operation of the axial AMB: Measured axial AMB current \(i_{\mathrm{ax}}\) and “\(q\)-current-control” drive current \(i_{\mathrm{q,D}}\) for a step response of \({\varDelta z=20\ \mathrm{~\upmu \text{m}}}\) at \(m_{\mathrm{a}}=1.55\)

Full size image

Generally, the required axial current \(i_{\mathrm{ax}}\) takes very low values due to the big force-current coefficient \(k_{\mathrm{F,z}}\) together with the low axial thrust due to the turbo-charger rotor (Table 1). Even in transient situations, there is only a low axial voltage needed (\({u_{\mathrm{ax,ref}}< U_{\mathrm{DC}}/4}\)), which is depicted in Fig. 12. It also shows that the reference voltage ripple in \(u_{\mathrm{ax,ref}}\) as well as in \(u_{\mathrm{q,D,ref}}\) increases at over-modulation in order to compensate for the vanishing voltage reserve.

Fig. 12.
figure 12

Measured reference voltages \(u_{\mathrm{q,D,ref}}\) and \(u_{\mathrm{ax,ref}}\) at zero-sequence current operation for a step response of \({\varDelta z=20\ \mathrm{~\upmu \text{m}}}\) for two different modulation degrees \(m_{\mathrm{a}}\)

Full size image

5 Conclusion

A novel technique for feeding the axial active magnetic bearing in a bearingless PM synchronous machine is presented, so that no 4-quadrant chopper is needed. Instead, the magnetic bearing coil is connected to the two star points of the double 3-phase stator winding in the machine. Simulations and measurements show that this technique is excellently applicable to magnetic bearing applications due to a small voltage demand in the axial active magnetic bearing. The position control dynamics are equal to those of the classical 4-quadrant chopper operation. They do not depend on the inverter modulation degree. At over-modulation an axial current ripple with three-times fundamental frequency occurs which is not harmful since this frequency is much higher than the inverse of the mechanical time constant of the rotor.