1 Introduction

In recent years the Internet-of-Things (IoT) is expanding rapidly. It connects many autonomous nodes, often by using wireless networks. As most of the nodes are battery powered, they need to have a low power consumption in order to extend charging cycles and battery lifetime. The power demand of the devices is mainly defined by the transmitter as it needs energy to transmit data over a range of a few meters. Several approaches have been proposed with the target to reduce power demand in integrated transmitter design as [11] summarizes.

One approach to decrease the power consumption of the transmitter is to correspondingly reduce the complexity as well as the number of components. The simplest architecture just consists of an oscillator that runs at radio frequency. It is switched on and off (OOK, on-off-keying) for information transmission. In this case, the oscillator frequency is not regulated and suffers from high frequency-inaccuracy. The architecture can be used in impulse-radio ultra-wide-band (IR-UWB) transmitters [1, 10] as high frequency accuracy is typically not needed there. Moreover, often IR-UWB transmitters are highly duty-cycled and are transmitting only one pulse during a long time period. Therefore, advanced implementations utilize fast startup oscillators [10].

Narrow-band transmitters need a regulated oscillator in order to fulfill spectral regulations summarized in frequency accuracy and phase noise requirements. Hence, they are often locked to a reference oscillator by using either injection locking or a phase locked loop. Injection locking architectures [4, 9, 12] have the lowest power demand as they are directly locked to the reference oscillator and do not need a regulation loop. In general, as reference oscillators run at a low frequency, this architecture is only suitable for a transmit frequency below 1 GHz. If a higher frequency and flexible frequency adjustment is needed a phase locked loop (PLL) is utilized. Several PLL architectures [5, 8] apply an oscillator directly running at radio frequency. The output signal is either sent directly, or amplified by a power amplifier, depending on the desired output power, to the antenna.

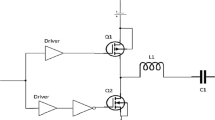
This work proposes a way to further reduce power demand of the transmitter by using frequency multiplication techniques. The general idea is to save power by keeping the frequency of the transmitter components low. Therefore, the oscillator and frequency regulation do not run at radio frequency. The transmit signal is generated directly before the antenna by using either of the two methods—edge-combining or third harmonic extraction. Both methods are shown in this paper and a possibility to integrate them into the power amplifier is proposed as pictured in Fig. 1. A radio frequency signal \(S_{\text{RF}}\) at 2.4 GHz is generated by an eight-stage differential ring oscillator running at 200 MHz. The ring oscillator node signals \(S_{\text{k}\{p|n\}}\) are in a first step used for four times frequency multiplication to an intermediate frequency signal \(S_{\text{IF}}\) at 800 MHz by applying a method called edge-combining. In doing so the time delay output signals of the ring oscillator are connected logically in order to generate pulses. These pulses are added up to generate the radio frequency signal \(S_{\text{RF}}\) as discussed in detail in Sect. 2.1. Similar approaches can be found in [2, 7, 9, 12].

Fig. 1.
figure 1

Edge-combining power amplifier with third-harmonic extraction

Full size image

However, this work goes one step further and additionally extracts the third harmonic frequency from \(S_{\text{IF}}\). For this procedure, the output matching network is utilized to block the fundamental frequency while the third harmonic is matched and thus fed to the output of the transmitter. Therewith, an additional inherent multiplication factor of three is gained, leading to a reduced power consumption especially at a low output power as shown in Sect. 4. The presented methods are suitable for low-power applications where only small output power values needed, for example, body area networks and medical applications.

The paper is structured as follows: Initially, Sect. 2 introduces edge-combining and third harmonic extraction. Then in Sect. 3 an approach is shown how both techniques can be implemented in integrated circuits for switched-mode power amplifiers. Finally, in Sect. 4 an exemplary design is evaluated by simulation and Sect. 5 concludes the work and gives a short outlook.

2 Frequency multiplication techniques

As mentioned in the introduction (cf. Sect. 1) several techniques have been published in order to reduce the power demand of low power integrated transmitters. In this section two methods—edge-combining and third-harmonic extraction—that keep the operating frequency of the transmitter components low and perform frequency multiplication are discussed.

2.1 Edge-combining

Edge-combining uses several time-delayed signals \(S_{\text{k}\{p|n\}}\) at a low frequency \(f_{\text{RO}}\) and connects them logically in order to generate a high frequency signal \(S_{\text{IF}}\). The time-delayed signals \(S_{\text{k}\{p|n\}}\) are generated by a \(K\)-stage delay line having a unity delay of \(\Delta \tau \). To illustrate the method a \(K=4\) pseudo-differential ring oscillator with inverted feedback running at \(f_{\text{RO}} = 1/T_{\text{RO}} = 1/(2k\Delta \tau )\) is utilized as pictured in Fig. 2 on the right side. It generates several \(\Delta \tau \)-shifted single-ended signals \(S_{\text{k}\{p|n\}}\) at its nodes (2 per stage) as plotted on the left side. If the outputs of two consecutive stages (e.g. \(S_{1n}\) and \(S_{2n}\)) are multiplied, a pulse \(P_{1}\) is generated at the points where the signals overlap. In the same manner several \(2\Delta \tau \) time-shifted pulses \(P_{1}\) to \(P_{4}\) are generated as shown in Fig. 2. By adding up the pulses a signal \(S_{\text{IF}}\) having a frequency of \(f_{\text{IF}} = 1/T_{\text{IF}} = 1/(2\Delta \tau )\) is created. In this example the generated frequency \(f_{\text{IF}}\) is 4-times higher (\(m_{\text{EC}}\)) than the oscillator frequency \(f_{\text{RO}}\).

Fig. 2.
figure 2

Edge-combining using a 4-stage differential ring oscillator for 4× frequency multiplication

Full size image

In general, using a \(K\)-stage delay-line results in a frequency multiplication factor \(m_{\text{EC}} = K\) that equals the number of stages. However, the maximum frequency is not dependent on the number of stages but limited by the minimum \(\Delta \tau \) that can be achieved by one delay stage as calculated in (1).

$$ f_{\text{IF}} = m_{\text{EC}} \cdot f_{\text{RO}} = m_{\text{EC}} \cdot \frac{1}{2K\Delta \tau } = \frac{1}{2\Delta \tau } $$
(1)

Edge-combining can be implemented, for example, in hardware by using logical gates as pictured in Fig. 3. The multiplication of the time-delayed signals is performed by an AND-gate and the addition of the pulses is realized as OR-gate. Several other implementation methods are shown in [7]. In this paper the edge combiner is realized by the circuit pictured in Fig. 1 and described in Sect. 3.2.

Fig. 3.
figure 3

Block diagram of the edge-combiner

Full size image

2.2 Harmonic extraction

Every continuously-differentiable periodic continued function \(f(t)\) can be represented by a summation of oscillations at different frequencies and amplitudes also known as Fourier-series

$$ f(t) = a_{0} + \sum _{n=1}^{\infty }\left [ a_{n} \cos (2\pi n f_{1} t) + b_{n} \sin (2\pi n f_{1} t) \right ]. $$
(2)

The output voltages of the ring oscillator, logical gates and also the edge-combiner have a rectangular shaped output signal. A rectangular signal is an odd-signal and thus consists of odd-harmonic frequencies. By additionally having a single-ended signal ranging from e.g. 0–1 V and phase difference of \(\varphi = {0}\circ \) (2) simplifies to

$$ v_{\text{rect}}(t) = a_{0} + \sum _{n=1}^{\infty } a_{n} \cos \left [ 2 \pi (2n-1) f_{0} t \right ] $$
(3)

with the coefficients

$$ a_{0} = \frac{1}{2},\quad a_{n} = \frac{2}{(2n-1)\pi }. $$
(4)

The resulting power spectrum of the rectangular Fourier-series (normalized to the fundamental H1) is plotted in Fig. 4. The signal exhibits power at odd multiples of the fundamental frequency \(f_{1}={800}\) MHz (H1). In order to perform frequency multiplication by the factor \(m_{\text{H3}} = 3\), the third harmonic H3 has to be filtered from the spectrum by a band-pass as illustrated in Fig. 4. The proposed approach uses the output matching network of the switched-mode power amplifier to suppress the fundamental frequency and pass the third harmonic to the antenna (see Sect. 3.3).

Fig. 4.
figure 4

Extraction of the third harmonic from a rectangular signal using a band-pass filter

Full size image

3 Proposed design

Both frequency-multiplication techniques proposed in the previous section (Sect. 2) are integrated into a switched-mode power amplifier. Initially, the basic concept of the amplifier is explained by using a switch that is later on replaced by the edge-combiner and the output matching network is designed in order to extract the third harmonic frequency. Hence, a radio frequency of \(f_{\text{RF}} = {2.4}\) GHz is generated from a ring oscillator frequency of \(f_{\text{RO}} = {200}\) MHz in two steps using the architecture pictured in Fig. 1. At first the edge-combiner performs a frequency multiplication of \(m_{\text{EC}} = 4\) to generate a intermediate frequency signal \(S_{\text{IF}}\) at \(f_{\text{IF}} = {800}\) MHz. In a second step, an additional multiplication by \(m_{\text{H3}}=3\) is performed by extracting the third harmonic. That leads to an overall frequency multiplication factor of \(m = m_{\text{EC}} \cdot m_{\text{H3}} = 12\) and an output signal \(S_{\text{RF}}\) at \(f_{\text{RF}} = {2.4}\) GHz.

3.1 Switched-mode power amplifier

The general block diagram of a switched-mode power amplifier is pictured in Fig. 5. The amplifier consists of a switch—controlled by the rectangular shape input voltage \(V_{\text{in}}\)—and a passive output matching network. In integrated CMOS circuits the switch is realized as a transistor typically showing a drain-source capacitance of \(C_{\text{S}}\), an on-resistance \(R_{\text{ON}}\) and an off-resistance \(R_{\text{OFF}}\). The output matching network provides power matching to the load \(R_{\text{L}}\) and forms the voltage \(V_{\text{D}}\) in order to reduce losses in the switch.

Fig. 5.
figure 5

Concept of switched-mode power amplifier

Full size image

In theory, switched-mode power amplifiers have very low power dissipation \(P_{\text{SW}}=I_{\text{SW}} \cdot V_{\text{D}}\) as either the switch-current \(I_{\text{SW}}\) (ideal: \(R_{\text{OFF}} = \infty \)) or switch-voltage \(V_{\text{D}}\) (ideal: \(R_{\text{ON}} = 0\)) are zero or near to zero. However, in hardware implementations the on-resistance will differ from \(R_{\text{ON}} = {0}~\Omega \) and the off-resistance \(R_{\text{OFF}}\) will be finite. This causes losses in the switch as either a current (off-state) or a voltage (on-state) drop remains. As the switch is realized as a MOS-FET the resistance can be adjusted by the size. A large switch will reduce the on-resistance \(R_{\text{ON}}\) for better efficiency, but will also increase the overall power consumption and output power. For applications with limited power the switch must be designed according to the desired power consumption and output power.

In off-state the voltage \(V_{\text{D}}\) is dependent on the drain-source capacitance \(C_{\text{S}}\) and the output matching network. If the switch is opened while \(C_{\text{S}}\) is charged, the energy stored on the capacitor \(C_{\text{S}}\) will be lost from the system through the switch. That leads to a increased power dissipation and reduced efficiency. To avoid this effect zero voltage switching needs to be applied. That means that the capacitor \(C_{\text{S}}\) is discharged and the switch-voltage \(V_{\text{D}}\) is zero when the switch is opened. For this reason the matching network is designed in order to form the switch-voltage \(V_{\text{D}}\) to be zero at the switching points. Hence, the drain capacitance \(C_{\text{S}}\) is compensated, leading to matching the switch impedance including \(C_{\text{S}}\) to the load at the desired output frequency.

3.2 Edge-combiner

To further include the up-conversion procedure in the radio frequency amplifier, the switch of the switched-mode amplifier is replaced by the edge-combiner. The resulting circuit is shown in Fig. 1. The edge-combiner consists of four branches connected at the node \(V_{\text{D}}\). Each branch is built up as a stacked NMOS-transistor pair. The gates of the transistors are connected to the ring oscillator nodes \(S_{\text{k}\{p|n\}}\) as shown in Fig. 1 and Fig. 2. If the gate voltages, e.g. \(S_{1n}\) and \(S_{2n}\), of both transistors located in one branch are pulled high to the supply voltage \(V_{\text{DD}}\), the branch gets conductive and pulls the node voltage \(V_{\text{D}}\) to the ground potential. Thereby a pulse \(P_{1}\) is created (see Fig. 2). Like the first branch the other branches are used to generated the pulses \(P_{2}\) to \(P_{4}\). As the branches alternately pull the drain voltage \(V_{\text{D}}\) to ground a frequency \(f_{\text{IF}}\) of four times (\(m_{\text{EC}} = 4\)) the oscillator frequency \(f_{\text{RO}}\) is formed at node \(V_{\text{D}}\). The edge-combiner shows the same behavior as having a single switch that is switched with a frequency of \(f_{\text{IF}}\). Therefore it can be modeled as a switch having a parallel connected gate capacitance of \(C_{\text{S}}\) resulting in an output impedance of \(Z_{\text{S}}\).

3.3 Output matching-network

For the presented design, the output matching network is designed to extract the third-harmonic frequency of the edge-combiner output \(S_{\text{IF}}\) (node voltage \(V_{\text{D}}\)) and perform an additional frequency multiplication by the factor \(m_{\text{H3}} = 3\). A further target of the matching network is to suppress the fundamental frequency \(f_{1} = f_{\text{IF}} = {800}\) MHz at its input as good as possible. Simultaneously, the third-harmonic frequency \(f_{3} = f_{\text{RF}}\) is matched to the load \(R_{\text{L}}\) to compensate the drain capacitance \(C_{\text{S}}\). Moreover, the matching network needs to incorporate the functionality of a bias-tee and provide the supply voltage \(V_{\text{DD}}\) as well as a dc-block to avoid a direct current flowing into the load \(R_{\text{L}}\).

The matching network is realized by the circuit shown in Fig. 1. \(L_{1}\) and \(C_{1}\) are designed to be a short at \(f_{\text{RF}} = f_{3}\). However, by connecting \(L_{2}\) in parallel to \(L_{1}\) and \(C_{1}\) a high resistance is created at the fundamental \(f_{\text{IF}} = f_{1}\). \(L_{\text{RFC}}\) is needed to provide the supply voltage and \(C_{\text{DC}}\) is used as direct-current block. Moreover, \(L_{\text{RFC}}\) and \(C_{\text{DC}}\) are used to match the edge-combiner output to the load \(R_{\text{L}}\).

In order to analyze the network and derived the values for its components, the output matching network is simplified to the circuit shown in Fig. 6. The edge-combiner is modeled as a rectangular voltage source having an input impedance of \(Z_{\text{S}} = (43.6 - j45.3)\,\text{$\Omega $}\) (derived by extracted layout simulation) at the desired output frequency \(f_{\text{RF}}\). The output matching network is divided into two impedance values \(Z_{\text{F}}\) and \(Z_{\text{L}}\) connected in series in order to reduce calculation complexity. The impedance \(Z_{\text{F}}\) is designed to realize a filter effect. It provides a high impedance at the fundamental frequency and a short at the third harmonic. In contrast \(Z_{\text{L}}\) is an equivalent representation of the load combined with the matching/biasing components \(L_{\text{RFC}}\) and \(C_{\text{DC}}\). The requirements on \(Z_{\text{D}} = Z_{\text{F}} + Z_{\text{L}}\) of the matching network are summarized in Table 1. \(Z_{\text{F}}\) and \(Z_{\text{L}}\) are dependent on the frequency \(f\) and components \(L_{1}\), \(C_{1}\), \(C_{2}\), \(L_{\text{RFC}}(f)\) and \(C_{\text{DC}}(f)\) are calculated in (5) and (6), respectively.

$$ Z_{\text{F}}(f) = \frac{2 \pi f L_{2} \left [ C_{1} L_{1} (2 \pi f)^{2} -1 \right ]}{\left (C_{1} L_{2} + C_{1} L_{1}\right ) (2 \pi f)^{2} -1} $$
(5)

Considering (5) the high impedance at \(f_{\text{IF}}\) is calculated by setting the denominator to zero (\(Z_{\text{F}}^{-1} = 0\)) and hence generating a pole at \(f_{\text{IF}}\). Moreover, a short at \(f_{\text{RF}}\) is achieved by setting \(Z_{\text{F}} = 0\) and thus bring \(L_{1}\) and \(C_{1}\) into resonance at \(f_{\text{RF}}\). As calculating the values under given criteria provides one degree of freedom, \(L_{2}\) is chosen to be 9.6 nH, and then \(L_{1} = {1.25}\) nH and \(C_{1} = {3.51}\) pF are calculated.

Fig. 6.
figure 6

Equivalent small-signal circuit of the edge-combining amplifier

Full size image
Table 1. Requirements on the output matching network impedance
Full size table

The equivalent load impedance \(Z_{\text{L}}(f)\) is derived in (6). The values are calculated in order to match the third harmonic \(f_{\text{RF}}\) to the load \(R_{\text{L}}\) and thereby compensate the source capacitance \(C_{\text{S}}\).

$$ Z_{\text{L}} (f) = \frac{2 \pi f L_{\text{RFC}} \left ( j 2 \pi f C_{\text{DC}} R_{\text{L}} +1 \right )}{j (2 \pi f)^{2} C_{\text{DC}} L_{\text{RFC}} + C_{\text{DC}} R_{\text{L}} 2 \pi f - j } $$
(6)

Therefore, \(Z_{\text{L}}\) needs to be the conjugate complex value of \(Z_{\text{S}}\) as already shown in Table 1 (note that \(Z_{\text{F}}(f_{\text{RF}})=0\) and has no influence on \(Z_{\text{D}}\) at \(f_{\text{RF}}\)). As mentioned before, the value for \(Z_{\text{S}}(f_{\text{RF}})\) was determined to be \((43.6 - j45.3)\,\Omega \) by simulation with the extracted layout of the edge-combiner circuit. Consequently, the values for \(L_{\text{RFC}}\) and \(C_{\text{DC}}\) are calculated to be 3.1 nH and 1.47 pF, respectively. The resulting frequency-dependent impedance values \(Z_{\text{F}}\), \(Z_{\text{L}}\) and their summation \(Z_{\text{D}}\) are plotted in Fig. 7. It can be observed that the impedance \(Z_{\text{D}}\) has the desired pole at \(f_{\text{IF}} = {800}\) MHz and a value of \(Z_{\text{D}}(f_{\text{RF}}) = (43.6 + j45.3)\,\Omega \). Hence, the derived circuit fulfills the requirements summarized in Table 1. However, in the above consideration all passive components are ideal elements neglecting parasitics. As shown next in Sect. 4, the extracted component models will have parasitic effects that cause power dissipation and mismatch. Therefore, the lossy component values are adjusted due to the simulation results.

Fig. 7.
figure 7

Calculated impedance of the filter \(Z_{\text{F}}\) (- - -), the load \(Z_{\text{L}}\) (⋯) and the resulting output matching network \(Z_{\text{D}}\) (—)

Full size image

4 Simulation results and discussion

The proposed edge-combining amplifier with third-harmonic extraction is implemented in a 180 nm 1P6M CMOS process. To evaluate the expected performance of the proposed concept, post-layout parasitic extraction models of the main circuits are utilized. The edge-combining amplifier is driven by ring oscillator signals running at a frequency of \(f_{\text{RO}} = {200}\) MHz. It generates an intermediate frequency of \(f_{\text{IF}} = {800}\) MHz after the edge-combiner and results in an radio frequency signal of \(f_{\text{RF}} = {2.4}\) GHz after the third-harmonic frequency extraction by the matching network. The ideal component values derived in Sect. 3 are replaced by extracted simulation models incorporating the parasitic resistance values in the capacitors and the quality-factor of the inductors ranging from 5 to 10. In order to correct the matching of the output network, the inductor \(L_{\text{RFC}}\) and the capacitor \(C_{\text{DC}}\) are adjusted to 2.51 nH and 1.7 pF, respectively. The resulting input impedance of the output matching network \(Z_{\text{D}}\) in comparison to the calculated network is shown in Fig. 8. It can be seen that the imaginary pole at the fundamental frequency (\(f_{\text{IF}} = {800}\) MHz) turns to some extent into a resistance (real valued) which causes leakage of the fundamental frequency to the desired output found at the third harmonic.

Fig. 8.
figure 8

Comparison between the calculated (- - -) and simulated impedance \(Z_{\text{D}}\) of the output matching network with ideal (⋯) and extracted (—) components

Full size image

As described in Sect. 3, either the drain voltage \(V_{\text{D}}\) or drain current \(I_{\text{D}}\) need to be zero in order to (at least approximately) have no power dissipation in the transistors of the edge-combiner. Figure 9 pictures the simulated drain current and voltage alternating inversely as desired. However, a small offset remains due to the finite on- and off-resistance of the transistors, especially when they come out of strong inversion. The switching points of the edge-combiner are marked in Fig. 9 using vertical lines. They are located at the drain voltage minimums which offer near-to-zero voltage switching to further reduce losses (see Sect. 3.1). This additionally shows that the drain impedance values are matched properly as described in Sect. 3. The resulting output voltage of the amplifier (at the antenna port) is given in Fig. 10.

Fig. 9.
figure 9

Output voltage \(V_{\text{D}}\) and current \(I_{\text{D}}\) of the edge-combiner

Full size image
Fig. 10.
figure 10

Output voltage of the edge-combining amplifier at the antenna port

Full size image

The output power of the harmonics is derived using a harmonic-balance simulation. The result is plotted together with the output matching S22 in Fig. 11. The power of the fundamental frequency \(f_{\text{IF}} = {800}\) MHz is suppressed to \(P_{1}={-22}\) dBm, which lies 11 dB below the power \(P_{\text{out}} = {-11.8}\) dBm of the desired third harmonic at \(f_{\text{RF}} = {2.4}\) GHz. The spectral behavior shows a high nonlinearity. However, the transmitter is used in low output-power applications for short-range communication, together with duty cycling. Hence, the nonlinearities will barely disturb other devices. Moreover, the linearity can be further improved by using a narrow-band antenna or external filter.

Fig. 11.
figure 11

Simulated harmonic power (•) and S22-parameter (- - -) at the amplifier output

Full size image

The power demand of the amplifier is \(P_{\text{PA}} = {2.39}\) mW, which results in a drain efficiency of \(\eta =P_{\text{out}}/P_{\text{PA}} = {3.2}\) % due to the high losses in the passive elements of the fully integrated circuit. The amplifier efficiency seems very low at the first look, but the overall transmitter power consumption is lower compared to traditional architectures where all components are utilized at radio frequency. This is discussed in the following paragraphs by comparing the power demand of transmitters using different frequency multiplication methods—ring oscillator running directly at 2.4 GHz (RO at RF), applying edge-combining (only EC), applying third harmonic extraction (only H3), and combining edge-combining with third harmonic extraction (EC and H3), respectively. The values taken for the following discussion are gained from a fully implemented and simulated edge-combining transmitter.

The total power \(P_{\text{TX}}\) of the transmitter is composed by constant power demand \(P_{\text{const}}\), a frequency-dependent power demand \(P_{\text{freq}}\) (switched components like ring oscillator and parts of the PLL) and the power demand of the power amplifier \(P_{\text{PA}}\) having an efficiency of \(\eta \)

$$ P_{\text{TX}} = P_{\text{const}} + P_{\text{freq}} + P_{\text{PA}} = P_{\text{const}} + k \cdot P_{\text{RO, $f_{0}$}} + \frac{P_{\text{out}}}{\eta }. $$
(7)

The constant power contribution stays the same for all multiplication methods and is in this case \(P_{\text{const}} = {1}\) mW. The frequency-dependent power increases linearly with frequency. The lowest considered oscillator frequency \(f_{\text{RO,1}} = {200}\) MHz is achieved using edge-combining together with third-harmonic extraction. At this frequency the frequency-dependent power demand is modelled to be \(P_{\text{RO,1}} = {1.3}\) mW. If just edge-combining (\(\kappa =3\)) or third harmonic extraction (\(\kappa =4\)) is used the frequency of the oscillator needs to be increased by the factor \(\kappa \) to get a radio frequency of \(f_{\text{RF}}={2.4}\) GHz. By mainly having switched components also the frequency-dependent power demand scales by \(\kappa \) and is calculated by \(P_{\text{freq}}=\kappa \cdot P_{\text{RO,1}}\).

Switched-mode power amplifiers without third-harmonic extraction have higher efficiencies \(\eta \) between 30–40 % [3, 6] compared to using third-harmonic extraction. The efficiency for running the ring oscillator at radio frequency and just using the edge-combiner for frequency multiplication is here considered as 40 %.

The power demand \(P_{\text{TX}}\) of the transmitters, depending on the output power \(P_{\text{out}}\), is calculated with (7) and pictured in Fig. 12. The values for \(f_{\text{RO,}\kappa }\), \(\kappa \) and \(\eta \) are summarized in Table 2. It can be seen that at an output power below -10 dBm the edge-combiner combined with third harmonic extraction has the lowest power consumption, even with the poor amplifier efficiency of \(\eta = {3.2}\) %. With increasing output power, the efficiency of the PA becomes more important and using only the edge-combiner has the lowest power demand in this case.

Fig. 12.
figure 12

Power dissipation of different frequency-multiplication methods

Full size image
Table 2. Power-consumption model parameters used with (7) for evaluation in Fig. 12
Full size table

5 Conclusion

This paper describes a design of ultra-low-power transmitters that are able to reduce the overall power consumption by using frequency-multiplication techniques. The edge-combining principle in conjunction with third-harmonic extraction is discussed and the utilization of frequency-multiplication techniques is demonstrated by a harmonic edge-combining amplifier that generates an radio-frequency signal of 2.4 GHz from a ring oscillator running at merely 200 MHz. The transmitter’s capability to reduce the overall power consumption—by keeping the operation frequency of the transmitter components low, even when the efficiency of the amplifier suffers—is demonstrated. The concept of the third-harmonic extraction edge-combining amplifier was demonstrated by simulations for a 180 nm 1P6M CMOS process. The proposed transmitter uses on-chip matching and can be fully integrated as it does not require any external components. Especially at low RF output powers, which are typical for short-range medical and body-area network applications, the proposed edge-combining techniques improves the efficiency and overall power consumption of the transmitter.