Observer-based sliding mode control of hydraulic cylinders in the presence of unknown load forces

Abstract

A laboratory hydraulic setup consisting of a coupled actuating and load cylinder is investigated in order to emulate real world working conditions of heavy equipment such as excavators and loaders. An observer-based control scheme is proposed to regulate the position of the actuating cylinder. It relies on on-line identification of unknown parameter as well as reconstruction and compensation of unknown load forces, such that the performance of the closed position feedback loop is superior compared to classical control strategies. The applied method exploit ideas of variable structure systems in the design of both, the observer and the parameter identification scheme.

Zusammenfassung

Im vorliegenden Aufsatz wird ein Hydraulikprüfstand, bestehend aus einem Arbeitszylinder und einem gekoppelten Lastzylinder, betrachtet, um realitätsnahe Arbeitsbedingungen für schwere Geräte wie Bagger und Radlader nachzubilden. Zur Positionsregelung des Arbeitszylinders wird ein beobachterbasiertes Regelgesetz vorgeschlagen. Es beruht auf der Online-Identifikation unbekannter Parameter sowie der Rekonstruktion und Kompensation unbekannter Störgrößen, sodass die Regelgüte des geschlossenen Kreises deutlich besser ist als bei klassischen Regelungskonzepten. Beim Entwurf des Identifikationsalgorithmus als auch beim Beobachterentwurf kommen Ideen strukturvariabler Systeme zum Tragen.

Introduction

Hydraulic actuators are commonly used in industrial applications which demand high forces or torques. They are typically used in positioning systems for heavy equipment, robotics, active suspension systems and aeronautics, see e.g. [12]. Systems actuated by hydraulic circuits offer a number of appealing features such as high power-to-weight-ratio, modular design, high precision and durability. Especially industrial machines, like excavators or material handlers, operating in harsh environmental conditions, are almost exclusively driven by hydraulic actuators. As documented by numerous articles, there is a strong trend of fully or at least partially automating such machines [2, 15]. Automation promises to increase efficiency, productivity as well as safety. This trend requires advanced low-level control strategies allowing precise reference trajectory tracking of positions, velocities and accelerations of hydraulic actuators. However, uncertain load forces, external disturbances, changing operating conditions and the highly nonlinear nature mainly introduced by electrohydraulic components render the control design a rather challenging task and therefore it is as an active research and development field.

The cascaded control strategy proposed in [1] also is exploited in this article. The nonlinear servovalve system is considered in the inner loop where an exact linearization technique is applied. The valve typically is well known, i.e. the parameters are available in data-sheets and, in addition, they remain constant during operation. The integrated servovalve position controller ensures high accuracy operation of a servovalve and therefore exact feedback linearization is an obvious choice for the design of the inner loop controller. The outer loop capturing the mechanical movement is influenced by load forces and possibly time-varying plant parameters like masses and friction coefficients. Hence, a robust control methodology for the design of the outer loop control technique is beneficial. The control approach presented in [14] follows the same idea of cascaded feedback loops. However, the inner loop is driven by a controller designed using a control Lyapunov function and the external disturbances mainly acting on the outer loop dynamics are not compensated, i.e. they are neglected during controller design. In [17] a model reference adaptive control design method using neural networks is discussed. Transient and steady state performance requirements are guaranteed despite the introduced class of uncertainties. Experimental results are demonstrated and show the performance of the proposed method. A combination of an adaptive controller with conventional sliding mode control is presented in [3]. Uncertainties with known structure are estimated and compensated by the adaptive part of the control law, whereas the effect of external disturbances is rejected by a sliding mode controller. The performance of the overall control loop is experimentally demonstrated. An external disturbance estimation and compensation scheme based on a sliding mode observer also is presented in [5]. Therein, it also is written that hydraulic servos are affected by a variety of frictional forces and that there is a need to compensate for the influence of the external disturbances. The incorporated Utkin sliding mode observer, see e.g. [16], provides estimates of the piston velocity and an unknown load force. In contrast to the approach presented in this article the observer is based on the assumption that the load force is slowly time-varying, i.e. its time-derivative is approximately zero. Some information gained by the observer is obtained using lowpass filtered estimates exploiting equivalent control methodology.

The observer based control concept discussed in this paper also relies on sliding mode control (SMC) techniques and consists of two phases. First, a finite-time convergent parameter estimation procedure is carried out at the unloaded plant in order to identify parameters of a friction model. These identified constant parameters are then used for friction force compensation in the applied control loop which is activated in the second phase. Therein, a 3rd-order sliding mode differentiator is implemented estimating unmeasured state variables and the external load force. The latter one is used to compensate the load force in the outer piston position control loop. The inner and outer control loop require full state information, hence, the information of the observer is provided to both loops.

One of the main advantages of sliding mode controlled feedback loops is their insensitivity to so-called matched bounded perturbations and the ability to reconstruct perturbations (unknown inputs) theoretically exact, i.e. within finite time. As reported by Ferreira et al. [4] a control goal may be effectively achieved by one of the following two approaches: The first one aims to design an sliding mode controller. In this case the perturbations are rejected by means of the robust controller. In the second approach, perturbations are exactly estimated by a sliding mode based observer in order to use this information for disturbance compensation in a classically designed control law stabilizing the nominal system, i.e. the system without perturbations. In literature this approach is often called exact output feedback stabilization (EOFS). From a theoretical point of view both approaches give identical results, i.e. regulation of the variable to be controlled. However, it is well known, that in a practical application it is not possible to achieve an ideal sliding mode and the sampling process will unavoidably deteriorate the control performance. The achieved precision of the considered variables is affected by the observer sampling step size, noise bounds, and the controller execution time. Depending on these system characteristics one control strategy may outperforms the other one. Therefore, in this work the second approach, namely the EOFS, is implemented for position reference tracking of a hydraulic differential cylinder subject to unknown load forces. The proposed control law is implemented on a test bench equipped with industrial hydraulic components. It consists of two coupled hydraulic cylinders: one cylinder is regarded as operating cylinder whilst the other one is used to apply certain load profiles. For evaluation purposes a force sensor providing real time measurements of the external load force is installed at the test rig.

The paper is organized as follows: A physically motivated model describing the dynamics of the plant is discussed in Sect. 2. The proposed controller design is outlined in Sect. 3. Experimental results are demonstrated in Sect. 4, followed by a conclusion in Sect. 5.

Plant description and mathematical modeling

The hydraulic actuated piston system is depicted in Fig. 1. A photo of the test bed is provided in Fig. 2. A hydraulic pump supplies the valve with a substantially constant pressure $p_{s}$ which is assumed to be independent on the external load force. The pressure of the tank is denoted by $p_{t}$. The flow $Q_{A}$ and $Q_{B}$ into the cylinder chambers are regulated by a servo valve. The input signal $u$ corresponds to the reference signal of the servo valve position controller. The pressure and the volume in each chamber is denoted by $p_{A}$ and $p_{B}$ respectively $V_{A}$ and $V_{B}$. A typical feature of a differential cylinder is, that it has two differently large effective piston cross sections. The so-called piston ring surface is denoted by $A_{k}$. The ratio between the piston rod cross section and the piston ring surface is denoted by $\alpha$. Due to this characteristic, depending on the direction, the cylinder moves at two different velocities at a constant flow rate $Q$. The control goal is to make the position of the piston rod $x_{p}$ track a certain reference profile in the presence of an unknown load force $F_{{\mathrm{ext}}}$.

Fig. 1.

Schematic representation of the hydraulic actuated piston. The servo valve is supported with a constant supply pressure $p_{s}$. The spool position $x_{\mathrm{spool}}$ is controlled by closed servo-valve position controller. As input serves the reference position denoted by $u$

Fig. 2.

Photo of the hydraulic laboratory test bed

A mathematical model describing the dynamics of the piston movement is derived by applying Newton’s 2nd law of motion, yielding

$$\begin{aligned} m_{t}\ddot {x}_{p}=(p_{A}-\alpha p_{B})A_{k}-F_{r}-F_{\mathrm{ext}}, \end{aligned}$$

(1)

where the parameter $m_{t}$ denotes the total moving mass, i.e. the piston mass plus the mass of the hydraulic medium, $F_{r}$ represents the friction force. The authors Jelali and Kroll [6], Komsta [7] suggest a simplified mathematical model of the form

$$\begin{aligned} \begin{aligned} \dot {\boldsymbol {x}}_{}&=f(\boldsymbol {x})+g(\boldsymbol {x})u+\boldsymbol { \Delta}(\boldsymbol {x},t), \\ y&=h(\boldsymbol {x}), \end{aligned} \end{aligned}$$

(2)

to describe the dynamics of such a hydraulic system where ${\boldsymbol {x}\in\mathbb{R}^{n}}$ is the state vector, $u$ is a scalar control and the scalar variable $y:=x_{p}$ is regarded as the system output. The system state vector is defined as $\boldsymbol {x}= \begin{bmatrix}x_{1}\, & x_{2}\,& x_{3}\,& x_{4} \end{bmatrix} ^{\mathrm{T}}= \begin{bmatrix}x_{p}\, & \dot {x}_{p}\,& p_{A}\,& p_{B} \end{bmatrix} ^{\mathrm{T}}$. The vector fields are given by

$$\begin{aligned} f(\boldsymbol {x})= \begin{bmatrix} x_{2}\\ \frac{A_{k}}{m_{k}}(x_{3}-\alpha x_{4})\\ \kappa_{A}(x_{1}) [-A_{k}x_{2}-K_{li} (x_{3}-x_{4} ) ]\\ \kappa_{B}(x_{1}) [\alpha A_{k}x_{2}-K_{li} (x_{3}-x_{4} ) ]\\ \end{bmatrix} \end{aligned}$$

(3)

and

$$\begin{aligned} g(\boldsymbol {x})= \begin{bmatrix} 0\\ 0\\ \kappa_{A}(x_{1}) c_{v}\sqrt{\xi_{3}(x_{3},u)}\\ -\kappa_{B}(x_{1}) c_{v}\sqrt{\xi_{4}(x_{4},u)} \end{bmatrix} . \end{aligned}$$

(4)

For the sake of a more compact representation the variables

$$\begin{aligned} \kappa_{A}(x_{1}):=\frac{E'}{V_{A}(x_{1})},\qquad \kappa_{B}(x_{1}):=\frac{E'}{V_{B}(x_{1})} \end{aligned}$$

have been introduced. The sign of the input signal $u$ determines the direction of the fluid flow. The two possible cases are taken into account by the piecewise defined function

$$\begin{aligned} \xi_{3}(x_{3},u)= \textstyle\begin{cases} p_{s}-x_{3} & \text{if}\ u\geq0\\ x_{3}-p_{t} & \text{else} \end{cases}\displaystyle \end{aligned}$$

(5)

and

$$\begin{aligned} \xi_{4}(x_{4},u)= \textstyle\begin{cases} x_{4}-p_{t} & \text{if}\ u\geq0\\ p_{s}-x_{4} & \text{else}. \end{cases}\displaystyle \end{aligned}$$

(6)

The volumes in the cylinder chambers $A$ and $B$ are expressed by functions of the cylinder position $x_{1}$, i.e.

$$\begin{aligned} V_{A} &= V_{A,0}+x_{1}A_{k} \end{aligned}$$

(7a)

$$\begin{aligned} V_{B} &= V_{B,0}+x_{1}\alpha A_{k}. \end{aligned}$$

(7b)

The constants $V_{A,0}$ and $V_{B,0}$ denote the so-called dead-volumes and describe the volumes unaffected by the piston movement, e.g. the fluid in the supply lines. The parameter $c_{v}$ represents an orifice coefficient of the valve, $E'$ denotes the bulk modulus of the hydraulic fluid and $K_{li}$ is a leakage coefficient. The friction force and the external load force are considered as perturbations and are summarized in the vector

$$\begin{aligned} \boldsymbol {\Delta}(\boldsymbol {x},t)= - \begin{bmatrix} 0 & & F_{r}(x_{2})+F_{\mathrm{ext}}(t)& & 0 & & 0 \end{bmatrix} ^{\mathrm{T}}. \end{aligned}$$

(8)

The plant parameters are provided in Table 1.

Table 1. Model parameter of the hydraulic pilot plant

Controller design

The controller design basically breaks down into three phases. Firstly, a control loop that input-output linearizes the pressurization dynamics is designed. Then a cascaded control structure, composed of an inner force and an outer position control loop, is derived. In the last step a sliding mode based observer, providing estimates of the unknown system states and load forces is designed. In order to achieve superior estimates of the load force the friction forces are compensated based on a predetermined mathematical model.

Exact linearization of the pressurization subsystem

Consider the pressurization subsystem governed by the last two differential equations in (2) with the output

$$\begin{aligned} y_{F}=F_{L}=A_{k}(x_{3}-\alpha x_{4})=:h_{F}(\boldsymbol {x}), \end{aligned}$$

(9)

i.e. the hydraulic force acting on the piston. Taking its first time derivative yields

$$\begin{aligned} \dot {y}_{F}=\mathcal{L}_{f}h_{F}(\boldsymbol {x})+ \mathcal{L}_{g}h_{F}(\boldsymbol {x})u, \end{aligned}$$

(10)

where $\mathcal{L}_{f}h_{F}(\boldsymbol {x})$ is the Lie derivative of $h_{F}$ with respect to $f$ and $\mathcal{L}_{g}h_{F}(\boldsymbol {x})$ with respect to $g$ (see [13]). The input $u$ appears explicitly in the first time derivative of the output $y_{F}$, i.e. $\mathcal{L}_{g}h_{F}(\boldsymbol {x})\neq0$. Solving relation (10) for the input $u$ gives a linearizing feedback control law of the form

$$\begin{aligned} u = \frac{1}{\mathcal{L}_{g}h_{F}(\boldsymbol {x})} \bigl[v-\mathcal {L}_{f}h_{F}( \boldsymbol {x}) \bigr] \end{aligned}$$

(11)

with the scalar functions

$$\begin{aligned} \mathcal{L}_{f}h_{F}&=A_{k} \bigl(K_{li}(x_{3}-x_{4})-A_{k}x_{2} \bigr) \bigl(\kappa_{A}+\alpha ^{2}\kappa_{B} \bigr), \end{aligned}$$

(12a)

$$\begin{aligned} \mathcal{L}_{g}h_{F}&=A_{k}c_{v} ( \kappa_{A}\sqrt{\xi_{3}}+\alpha A_{k} \kappa_{B}\sqrt{\xi_{4}} ). \end{aligned}$$

(12b)

The variable $v$ is regarded as a new input. The closed loop system exhibits the first order dynamics

$$\begin{aligned} \dot {y}_{F}=v. \end{aligned}$$

(13)

The output $F_{L}$ of the second order pressurization subsystem has relative degree ${\delta=1}$ w.r.t. the input $u$. The first order internal dynamics are rendered unobservable by the control law (11). A discussion showing the asymptotic stability of these dynamics is provided by e.g. Jelali and Kroll [6] and is omitted in this work.

Selecting the new input as

$$\begin{aligned} v = k_{0}(F_{L,d}-F_{L}), \end{aligned}$$

(14)

where $F_{L,d}$ denotes the desired piston force and $k_{0}$ is a positive constant, yields a inner force control loop with closed loop dynamics

$$\begin{aligned} \frac{1}{k_{0}}\dot {F}_{L}+F_{L}=F_{L,d}. \end{aligned}$$

(15)

The authors Ayalew and Kulakowski [1] and Jelali and Kroll [6] suggest to choose the desired piston force as

$$\begin{aligned} F_{L,d}&=m_{k}\ddot {x}_{p,d}-k_{v}({x}_{2}- \dot {x}_{p,d})-k_{p}({x}_{1}-{x}_{p,d}) \\ &\quad +F_{\mathrm{ext}}+F_{r}. \end{aligned}$$

(16)

Thus, a outer feedback loop for position, respectively reference trajectory tacking is obtained. By defining $e:=x_{1}-x_{p,d}$ and making use of dynamic equation of the piston movement

$$\begin{aligned} m_{k}\ddot{x}_{1}=F_{l}-F_{r}-F_{\mathrm{ext}}, \end{aligned}$$

(17)

one gets a differential equation

$$\begin{aligned} m_{k}\ddot {e}_{}+k_{v}\dot {e}_{}+k_{p}e=F_{L}-F_{L,d} \end{aligned}$$

(18)

describing the position error dynamics. Selecting the parameters $k_{v}$ and $k_{p}$ strictly positive will ensure asymptotic stability of the tracking error. The authors Komsta et al. [8] suggest to choose

$$\begin{aligned} k_{p}=\omega_{0}^{2}m_{k},\quad k_{v}=2\omega_{0}m_{k}, \end{aligned}$$

(19)

which ensures second order system behavior, described by the transfer function representation

$$\begin{aligned} G(s)=\frac{\omega_{0}^{2}}{s^{2}+\zeta\omega_{0}s+\omega_{0}^{2}}, \end{aligned}$$

(20)

with damping coefficient $\zeta=1$ and cut-off frequency $\omega_{0}$. Note that this control strategy does not require any knowledge on the piston acceleration. However, implementation of the outer control loop requires knowledge of the external load- and friction force. This information are rarely available in real world applications and therewith need to be estimated.

Finite time convergent parameter estimation of friction force

In order to compensate for the friction effects it is necessary to describe them by a mathematical model. In literature there are a wide number of friction models studied. Most of them are empiric models. A common approach is, to model the friction effects by a static relationship between friction force and velocity, i.e. by a so-called static friction model. In systems operating at low velocity or subject to frequent change of direction, the friction behavior may be described more accurately by a dynamical friction model. However, compared to static models, dynamic friction models usually involve a larger number of parameters which often makes the identification process more complex. The most basic static models are composed of Coulomb friction and linear viscous damping. A suitable static model, describing the friction effects in the considered hydraulic cylinder, may be expressed as

$$\begin{aligned} \hat{F}_{r}=\nu{x}_{2}+F_{c0} \text{sign}({x}_{2}). \end{aligned}$$

(21)

The model involves the two unknown parameters $\nu$ and $F_{c0}$. In order to obtain these parameter an on-line identification procedure is carried out at the unloaded system.

Consider therefore (1) expressed as a system of first order differential equations

$$\begin{aligned} \dot {x}_{1}&=x_{2} \end{aligned}$$

(22a)

$$\begin{aligned} \dot {x}_{2}&=\frac{1}{m_{k}}\bigl(F_{L}-F_{r}(x_{2}) \bigr) \end{aligned}$$

(22b)

Note that (22b) together with (21) can be rewritten in the form

$$\begin{aligned} \dot {x}_{2}=-\frac{1}{m_{k}}\varGamma(t)\theta+\frac{1}{m_{k}}F_{L}, \end{aligned}$$

(23)

where the vector $\varGamma(t)= [{x}_{2} \ \text{sign}(x_{2}) ]$ contains the known piecewise constant functions and $\theta^{\mathrm{T}}= [\nu \ F_{c0} ]$ the constant parameters to be identified. The sliding mode based finite time convergent parameter estimation scheme, proposed by Moreno and Guzman [11] is employed for the on-line identification task. The algorithm is an extension to the recursive Least Squares algorithm in which non-linear injection terms provide for finite time convergence and robust stability properties. A major advantage of this algorithm is that it provides bounded estimation errors even if persistence of excitation is not guaranteed. The estimator reads as

$$\begin{aligned} \dot {\hat{x}}_{2}&=-k_{1}\phi(e_{x_{2}})+\frac{1}{m_{k}} \varGamma(t)\theta +\frac{1}{m_{k}}F_{L} \end{aligned}$$

(24a)

$$\begin{aligned} \dot {\hat{\theta}}_{}&=-k_{2}\phi(e_{x_{2}}) \varGamma(t)^{\text{T}}, \end{aligned}$$

(24b)

with the injection terms

$$\begin{aligned} \phi_{1}&=\mu_{1}|e_{x_{2}}|^{\frac{1}{2}} \mathrm{sign}(e_{x_{2}})+\mu _{2}e_{x_{2}},\quad \mu_{1},\mu_{2}>0 \end{aligned}$$

(25a)

$$\begin{aligned} \phi_{1}&=\frac{\mu_{1}^{2}}{2}\text{sign}(e_{x_{2}})+ \frac{3}{2}\mu_{1}\mu _{2}|e_{x_{2}}|^{\frac{1}{2}} \mathrm{sign}(e_{x_{2}})+\mu_{2}^{2}e_{x_{2}} \end{aligned}$$

(25b)

and the error signal $e_{x_{2}}=\hat{x}_{2}-x_{2}$. Selecting proper positive constant parameters $k_{1}$ and $k_{2}$ will ensure finite time convergence of the closed loop error dynamics

$$\begin{aligned} \dot {e}_{x_{2}}&=-k_{1}\phi(e_{x_{2}})+ \frac{1}{m_{k}}\varGamma(t){e}_{\theta } \end{aligned}$$

(26a)

$$\begin{aligned} \dot {e}_{\theta}&=-k_{2}\phi(e_{x_{2}})\varGamma(t)^{\text{T}}, \end{aligned}$$

(26b)

where the parameter estimation error is defined as ${e}_{\theta}=\hat {\theta}-\theta$.

For the identification task the sinusoidal reference signal $x_{p,d} = 0.06\sin(0.5\pi t)+0.02\sin(3.5\pi t)$ is applied to the unloaded real world closed loop system. The reference signal and the measured position is depicted in the lower plot in Fig. 3. The upper plot shows the evolution of the estimated parameters. The coulomb friction coefficient takes the final value $F_{c0}\approx20$ N, the viscous friction coefficient $\nu \approx 83.3~\mbox{N}\,\mbox{s/m}$. In order to validate the model, the evolution of the friction force $F_{r}$ is calculated off-line from Eq. (22b). Due to the accurate reference tracking it is reasonable to analytically calculate the acceleration of the piston by two times differentiating the reference signal w.r.t. time to avoid numerical differentiation of the measured signals. Note that the pressures $p_{A}$ and $p_{B}$ are available from real time measurements. The obtained values are plotted together with the on-line identified characteristic curve of the friction model in Fig. 4.

Fig. 3.

Convergence of the friction model parameters and reference signal with the measured piston position during the on-line identification procedure

Fig. 4.

Friction model with parameters obtained from the on-line identification compared to off-line calculated data

Sliding mode based state observation and unknown load force estimation

The next design step aims to develop a sliding mode observer that provides both, an estimate of the unmeasured system state, i.e. the piston velocity $x_{2}$, and the external load force $F_{\mathrm{ext}}$. The observer is based on higher order sliding mode (HOSM) differentiators of arbitrary order proposed by Levant [9]. A HOSM differentiator allows real time robust exact time-differentiation of the measured system output up to any desired order $n$ supposing that its $n$th derivative has known Lipschitz constant $L$. An exact differentiator provides output signals $z_{i}$ $(i=0,1,\ldots,n)$ coinciding with the first $n$ time-derivatives of a noise-free input signal $x_{0}$ within finite time. Denoting the estimation error by

$$\begin{aligned} \sigma_{0}&:=z_{0}-x_{0}, \end{aligned}$$

(27)

the recursive form of the $n$th order HOSM differentiator is written as

$$\begin{aligned} \begin{aligned} \dot {z}_{0}&=-\mu_{0}|\sigma|^{\frac{n}{n+1}} \mathrm{sign}(\sigma )+z_{1}, \\ \dot {z}_{1}&=-\mu_{1} |\sigma|^{\frac{n-1}{n+1}}\mathrm{sign}(\sigma )+z_{2}, \\ &\vdots \\ \dot {z}_{n}&=-\mu_{n} \mathrm{sign}({\sigma}). \end{aligned} \end{aligned}$$

(28)

The estimation error dynamics is captured by the differential inclusion

$$\begin{aligned} \begin{aligned} \dot {\sigma}_{i}&=-\mu_{i}| \sigma|^{\frac{n-i+1}{n+1}}\mathrm {sign}(\sigma)+\sigma_{i+1}, \\ \dot {\sigma}_{n}&\in-\mu_{n}\mathrm{sign}({\sigma})+[-L,L], \end{aligned} \end{aligned}$$

(29)

where $\sigma_{i}:=z_{i}-x_{i}$ and

$$\begin{aligned} \dot {x}_{k-1}=x_{k} \quad\text{with } k=1,\ldots,n+1. \end{aligned}$$

(30)

It is well known that the accuracy of this differentiator in the presence of noise is given by

$$\begin{aligned} |\sigma_{i}|=\mathcal{O} \bigl(\varepsilon^{\frac{n+1-i}{n+1}} \bigr) \end{aligned}$$

(31)

which is shown to be asymptotically optimal in the presence of infinitesimal input noises, see [10]. For the implementation at the hydraulic setup it is more likely to consider a discrete time version of the differentiator. Typically, the Euler numerical scheme is applied to obtain a discrete time version of (28). However it is known from literature, that this causes differentiation accuracy deterioration and therefore, in this paper, a proper discretization scheme preserving the accuracy properties of (28) is used. This discrete time differentiator is given by

$$\begin{aligned} \begin{aligned} {z}_{i,k+1}&={z}_{i,k}-\tau \mu_{0}|\sigma|^{\frac{n-i}{n+1}}\mathrm {sign}(\sigma)+\sum \limits _{j=1}^{n-i}\frac{\tau^{j}}{j!} z_{j+i,k} \\ {z}_{n,k+1}&=z_{n,k}-\tau\mathrm{sign}({\sigma}), \end{aligned} \end{aligned}$$

(32)

see [10]. Under constant sampling, with sampling step size $\tau$, the accuracies

$$\begin{aligned} |\sigma_{i}|\leq\bar{\mu}_{i}\rho^{n-i+1},\quad \rho=\mathrm{max}\bigl\{ \tau,\,\varepsilon^{\frac{1}{n+1}}\bigr\} \end{aligned}$$

(33)

are established in finite time. Therein the positive constants $\bar{\mu}_{i}$ depend only on the differentiator parameters $\mu_{i}$.

For the design purpose consider the dynamics of the piston movement captured by Eq. (17) expressed as

$$\begin{aligned} \dot {x}_{1}&=x_{2}, \\ \dot {x}_{2}&=\frac{1}{m_{k}} (F_{L}-F_{r}-F_{\mathrm{ext}} ), \end{aligned}$$

(34)

where $x_{1}$ is measured. In order to reconstruct the piston velocity $x_{2}$ and the bounded external load force $F_{\mathrm{ext}}$ a differentiator of minimum order two is required. Motivated by relation (33), a 3rd order differentiator is implemented. Hence, the order artificially is increased by one which yields improved estimates in the presence of noise and sampling. In particular the observer for system (35) based on the differentiator reads as

$$\begin{aligned} \begin{aligned} \dot {z}_{0}&=-\mu_{0}|z_{0}-x_{1}|^{\frac{3}{4}} \mathrm {sign}(z_{0}-x_{1})+z_{1}, \\ \dot {z}_{1}&=-\mu_{1}|z_{0}-x_{1}|^{\frac{1}{2}} \mathrm {sign}(z_{0}-x_{1})+z_{2}+ \frac{1}{m_{k}} (F_{L}-\hat{F_{r}} ), \\ \dot {z}_{2}&=-\mu_{2}|z_{0}-x_{1}|^{\frac{1}{4}} \mathrm {sign}(z_{0}-x_{1})+z_{3}, \\ \dot {z}_{3}&=-\mu_{3}\mathrm{sign}(z_{0}-x_{1}). \end{aligned} \end{aligned}$$

(35)

Introducing the observer estimation error $e_{0}:=z_{0}-x_{1}$ the estimation error dynamics is given by

$$\begin{aligned} \begin{aligned} \dot {e}_{0}&=-\mu_{0}|e_{0}|^{\frac{3}{4}} \mathrm{sign}(e_{0})+e_{1}, \\ \dot {e}_{1}&=-\mu_{1}|e_{0}|^{\frac{1}{2}} \mathrm{sign}(e_{0})+e_{2}, \\ \dot {e}_{2}&=-\mu_{2}|e_{0}|^{\frac{1}{4}} \mathrm{sign}(e_{0})+e_{3}, \\ \dot {e}_{3}&=-\mu_{3}\mathrm{sign}(e_{0})+ \frac{1}{m_{k}}\ddot {F}_{\mathrm{ext}}. \end{aligned} \end{aligned}$$

(36)

where $e_{1}:=z_{1}-x_{2}$, $e_{2}:=z_{2}+\frac{F_{\mathrm{ext}}}{m_{k}}$ and $e_{3}=z_{3}+\frac{1}{m_{k}}\dot {F}_{\mathrm{ext}}$. It should be noted, that the friction force $F_{r}$ is assumed to be compensated by $\hat{F}_{r}$ exactly and it is supposed that

$$\begin{aligned} \bigl\vert \ddot {F}_{\mathrm{ext}}(t)\bigr\vert \leq L m_{k}, \qquad\forall t\geq0. \end{aligned}$$

(37)

Note that the structure of Eq. (36) is equivalent to (29). Hence, the estimation errors converge to zero within finite time. Consequently the velocity and the external force are recovered by

$$\begin{aligned} \hat{x}_{2}=z_{1}, \qquad\hat{F}_{\mathrm{ext}}=m_{k}z_{2}, \end{aligned}$$

(38)

respectively. According to the discrete time differentiator in Eq. (32) the observer is implemented as

$$\begin{aligned} \begin{aligned} {z}_{0,k+1}&={z}_{0,k}- \tau\mu_{0}|e_{0,k}|^{\frac{3}{4}}\mathrm {sign}(e_{0,k}) \\ &\quad +\tau z_{1,k}+\frac{\tau^{2}}{2}z_{2,k}+ \frac{\tau ^{3}}{3!}z_{3,k}, \\ {z}_{1,k+1}&={z}_{1,k}-\tau\mu_{1}|e_{0,k}|^{\frac{2}{4}} \mathrm {sign}(e_{0,k}) \\ &\quad +\tau z_{2,k}+\frac{\tau^{2}}{2}z_{3,k}+\tau \frac {1}{m_{k}} (F_{L}-\hat{F_{r}} ), \\ {z}_{2,k+1}&={z}_{2,k}-\tau\mu_{2}|e_{0,k}|^{\frac{1}{4}} \mathrm {sign}(e_{0,k})+\tau z_{3,k}, \\ {z}_{3,k+1}&={z}_{3,k}-\tau\mu_{3} \mathrm{sign}(e_{0,k}). \end{aligned} \end{aligned}$$

(39)

Implementation and validation of the developed controller on the test rig

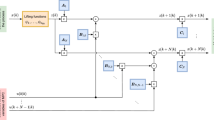
A block diagram of the overall control structure is provided in Fig. 5. The controller is composed of the cascaded control structure consisting of the inner force feedback loop and the outer position control loop. The unknown piston velocity ${x}_{2}$ and the load force $F_{\mathrm{ext}}$ are estimated by the HOSM observer. The discussed control concept is implemented such that the feedback loop is activated after a sufficiently long time period and hence the differentiator does not undesirable excite the control loop during the transient phase of the differentiator. Note that after finite time the outputs can be considered as exact direct measurements. Therefore the separation principle holds, see [9]. The unknown friction force is compensated via a static friction model.

Fig. 5.

Block diagram of the overall control structure

Implementation

The developed controller is implemented on a programmable logic device (PLC) from company Bernecker & Rainer. The PLC is connected via TCP/IP to a PC and supports automatic code generation from Matlab/Simulink environment. The sampling time is set to $\tau=1\mbox{ ms}$. The parameters for the cascaded control structure are selected as ${k_{0}=125}$, ${k_{p}=1.1054\cdot10^{4}}$ and ${k_{v} = 175}$. According to Fig. 5, the parameters are summarized in the vector $\boldsymbol {k}^{\mathrm{T}}=[k_{p}\,k_{v}\,m_{k}]$. The reference vector $\boldsymbol {x}_{d}=[x_{p,d}\,\dot {x}_{p,d}\,\ddot {x}_{p,d}]$. The differentiator parameters are set to ${\mu_{0}=15}$, ${\mu_{1}= 85}$, ${\mu_{2}=212.8}$ and ${\mu_{3}=200}$. The pressures $p_{A}$ and $p_{B}$ are measured by pressure to voltage transducers, where the pressure range 0–100 bar is mapped into a 0–10 V voltage interval. The supply pressure $p_{p}$ is adjusted at 60 bar via a pressure relief valve. The piston position is measured using a linear potentiometer which is attached to the piston rod. The position can be varied from 0–0.47 m. A 300 kg compression/tension load cell is mounted in-between load and working piston rod.

Experimental results

Two experiments are undertaken in order to validate the performance of the proposed controller. In the first experiment a sinusoidal load force is applied and the working cylinder is supposed to change its position according to a desired reference. As reference trajectory a so-called sine-squared function is used. In the second experiment an almost constant load force is applied while the working cylinder tracks a sinusoidal reference trajectory. Both experiments are carried out twice using the proposed control strategy with and without disturbance compensation. In order to compare the proposed compensation with a strategy not including any of the above mentioned sliding mode based concepts the piston velocity $x_{2}$ is obtained by a linear differentiation filter of the form

$$\begin{aligned} G_{d}(s)=\frac{s}{1+sT_{f}}. \end{aligned}$$

(40)

Using $s\approx\frac{1-z^{-1}}{\tau}$, the continuous time transfer function (40) becomes

$$\begin{aligned} G_{d}(s)=\frac{1-z^{-1}}{(\tau+T_{f})-T_{f}z^{-1}}, \end{aligned}$$

(41)

which can be implemented on the PLC. The positive constant $T_{f}$ is selected such that an acceptable trade-off between noise attenuation and the phase shift of the signal to be differentiated is achieved. In this context the choice $T_{f}=0.03$ was selected.

The results of the first experiment, obtained with the sliding mode based control strategy, are shown in Fig. 6a, respectively in Fig. 6b for the comparison strategy not using any disturbance compensation. The blue line in the upper subplots illustrates the reference trajectory for the piston position, the red line the measured position. The initial value is set 0.1 m, the desired final position is 0.18 m. The second subplots show the reference trajectory for the piston velocity and the estimated velocity obtained from differentiator, respectively from the filter given in Eq. (41). The last subplot depict the measured external load force and, in the case of activated disturbance estimator, its estimated value. It can be seen, that without incorporating the estimates of external forces in the control law, the load stiffness is reduced significantly. The load stiffness is defined as the ability of the cylinder to yield as less as possible under external load forces. The robust control strategy is capable to significantly improve this stiffness and therewith achieve superior reference trajectory tracking of the piston position and velocity in the presence of unknown load forces.

Fig. 6.

Comparison of the control strategy with and without disturbance compensation

The results of the second experiment are summarized in Fig. 7a and Fig. 7b. As a reference trajectory the sinusoidal signal $x_{p,d}=0.02\sin(2\pi t)+0.1$ is applied. Similarly to the first experiment, it can be clearly seen that the load stiffness and therewith the tracking performance can be significantly improved with the sliding mode based robust control strategy.

Fig. 7.

Experimental results using a sinusoidal position reference signal

Conclusion

In this work a sliding mode based control concept for position regulation of hydraulic cylinder was proposed. It is mainly composed of three parts: A nonlinear state feedback controller linearizing the pressurization system, a cascaded control structure consisting of a inner force control and an outer position control loop and an observer. The observer employs a higher order sliding mode robust exact differentiator that provides estimates of the unknown piston velocity and the external load force theoretically exact in finite time. The friction effects in the cylinder are compensated by a static friction model. The involved parameters are identified by an on-line identification scheme which also relies on SM techniques. In contrast to an off-line identification algorithm, the on-line parameter identification can be easily carried out during operation or in some kind of start up procedure. In this manner friction effects caused by wearing or changing operating conditions may be taken into account.

The proposed control strategy was implemented on a laboratory test bench which is equipped with industrial components. The external load force was applied by a second force controlled hydraulic cylinder. For the implementation of the observer, a discretization scheme that preserves the asymptotic accuracies of the continuous time differentiator was used. The discretization of the differentiator also reveals that its implementation is straightforward. It has been shown that the disturbance compensation improves the position tracking performance.

The captured load and friction force information may be processed further in extended applications such as payload estimation in heavy equipment or fault detection strategies.