1 Introduction

The numerical simulation of continuous casting is state-of-the-art. It has become an essential tool for developing and improving the casting process concerning quality and productivity. By simulating the process, researchers can optimize the casting conditions to improve the quality of the final product, reduce waste and energy consumption, and increase the productivity of the process. The simulation can also be used to troubleshoot problems that may occur during the process, allowing for faster and more efficient solutions to be implemented. At Montanuniversität Leoben, the developed numerical models, databases, measurement techniques, and laboratory experiments are interconnected within the non-commercial offline platform “m2CAST”. The implementation of heat transfer coefficients (HTC) as thermal boundary conditions in a local resolution is a key factor for precise simulation results. The so-called Nozzle Measuring Stand (NMS) as well as different regression models, are a proper way to solve this challenge [1,2,3].

2 m2Cast—Continuous Casting Development Platform

The non-commercial offline software m2CAST is designed to connect physical experiments and numerical simulations to predict quality-relevant factors. M2Cast is divided into three main parts, namely preprocessing, solver, and postprocessing. A schematic illustration is given in Fig. 1.

Fig. 1
figure 1

Schematic structure including preprocessing, solver, and the linked experiments in postprocessing

Full size image

In the first step, all data necessary for solving the 2d FV solver are collected and provided in the preprocessing. This includes thermodynamic data from the material module m2MAT, which are determined with the help of DSC measurements and calculations using FactSage 8.0. Within the caster configurator, the dimensions and geometry of the casting slab-comprising factors, like local strand thickness, strand width as well as the mesh size, must be defined. The thermal boundary conditions of the mold and the secondary cooling conditions are specified as temperature-dependent local Heat Transfer Coefficients (HTC). The chosen parameters of the nozzles in the secondary cooling zone of the casting machine are characterized experimentally using the NMS, which provides information about water impact density (WID) and the resulting HTC within the spray zone.

As mentioned before, a 2D Finite-Volume (FV) model computes the temperature distribution along the entire length of the strand. The computation assumes geometric symmetry and applies to only half of the slab’s width. Nonetheless, this approach allows the consideration of differing HTC and cooling strategies on the fixed and loose sides of the strand. The computed thermal history then serves as the foundation for experimental simulations, which are represented in the area of post-processing [1].

3 Nozzle Measuring Stand

A significant influencing parameter of the solidification calculation can be found in the selected cooling conditions of the secondary cooling zone. The Chair of Ferrous Metallurgy at Montanuniversität Leoben (MUL) has engineered a device called the Nozzle Measuring Stand (NMS) for generating local heat transfer coefficients (HTC) in spray cooling. The operational parameters encompass the water flow rate, air pressure, the spacing between nozzles, and the distance between the nozzle and the test sample. The experimental arrangement is divided into three zones (depicted in Fig. 2). Zone 1 features a cylindrical steel sample, an inductive heating unit, and a movable sample carrier controlled by linear axes. Zone 2 constitutes the “wet zone”, where spray nozzles are securely positioned to replicate the precise distance from the nozzle tip to the sample according to the dimension of the caster. These nozzles direct their spray upwards to measure HTC and downwards to quantify water distribution (WD). Lastly, Zone 3 accommodates the essential technical components, including the air and water supply, as well as the cooling mechanism for the induction device. [4, 5].

Fig. 2
figure 2

Scheme of so-called “Nozzle Measuring Stand” with different zones drawn within

Full size image

To enhance the understanding of the overlapping spray cone zone (Fig. 3), a configuration involving two nozzles with distinct water-air circuits has been implemented. This setup facilitates the creation of two separate and manageable water circuits for spray cooling.

Fig. 3
figure 3

Schematic drawing explaining overlapping and relevant distances Nx, Nz

Full size image

The equipment installed and the sensors employed, within specified ranges and tolerances, are detailed in Table 1.

TABLE 1 List of equipment and sensor installed at the nozzle measuring stand
Full size table

3.1 Local Spray Water Distribution

For assessing local water distribution (WD) in spray cooling, one or two nozzles are strategically positioned in an inverted manner at a defined distance from a patternator. This distance corresponds to the separation between the nozzle tip and the strand in the industrial setting (Nz). In situations involving two nozzles, the spacing between the nozzles must be adjusted accordingly (Nx). The patternator comprises 7 × 100 cells, each with a 10 mm x 10 mm inlet area. These cells collect the water, while the nozzles operate at specific flow rates, pressures, and distances. Following a predetermined period of time, the patternator is removed, and digital image processing software computes the WD, culminating in the so-called water impact density (WID) for the given nozzle parameters. The fundamental concept of this measurement method is illustrated in Fig. 4. This test setup provides the measurement of a local water impingement density [4, 5].

Fig. 4
figure 4

a Principle measurement of WID with two nozzles, b Exemplary 3D water distribution result of two nozzles

Full size image

3.2 Local Heat Transfer Coefficient

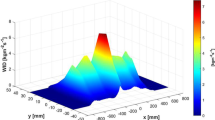
To conduct unsteady measurements of HTC, a test sample is exposed to controlled heating using an inductive heating unit, as illustrated in Fig. 3. The austenitic steel sample material’s temperature is restricted to 1200 °C. Three thermocouples are strategically positioned at varying distances from the surface to capture the internal temperature variations within the specimen. The linear motion unit moves the test sample across the spray cone. To calculate the HTC, an inverse heat conduction model called maximum a posteriori (MAP) is employed. The cylindrical sample body is thermally insulated, enabling the simplification of the heat conduction to a one-dimensional problem. Repeating such a measurement at different positions across the spray width leads to a 3-dimensional distribution of heat transfer coefficients for the specified spray parameters, which is shown exemplarily in Fig. 5. [4,5,6].

Fig. 5
figure 5

a Principle test setup for HTC measurement, b Exemplary 3D HTC distribution result of two nozzles measurement

Full size image

4 Implementation of NMS Measurements

The precision of numerical simulations relies on factors like grid size and boundary conditions. To achieve the highest possible resolution, the offline model m2Cast focuses on fine grid resolution. Ensuring localized HTC resolution and knowing the HTC values for nearly all positions corresponding to predetermined surface temperatures is crucial. Employing regression models emerges as a clear solution. Multiple regression models are explored for this purpose. The input characteristics comprise data triplets involving HTC, water impact density (WID), and surface temperature (Tsurf) from WID and HTC measurements across different positions. A single measurement can generate seven datasets according to the seven measuring grids used in the patternator. The basic allocation of these triplets, along with additional features such as initial temperature, nozzle distances, spray parameters, and more, is depicted in Fig. 6, starting with several measurements at different positions across the spray cone (a) and assembling measured WID and surface temperature Tsurf with calculated HTC values at the same position (b). Table 2 exemplifies the information and data behind the measurements. These supplementary features stem from specific test conditions. The dataset employed for constructing the models encompassed approximately 3000 records, while a set of 600 unknown data records was used to evaluate the regression models. The creation of the regression models was carried out using Matlab.

Fig. 6
figure 6

Principle of creating data triplets. (a HTC results at different positions across spray cone, b Assembling of HTC, Tsurf, and WID at the same position)

Full size image
TABLE 2 Excerpt of additional input features for regression
Full size table

4.1 Exponential Gaussian Process Regression

Exponential Gaussian Process Regression (EGPR) is a variant of Gaussian Process Regression (GPR), a popular probabilistic approach for regression tasks. GPR models the relationship between input variables and output variables as a Gaussian process, which is a collection of random variables that have a joint Gaussian distribution. In GPR, the prediction of the output variable is made based on a mean function and a covariance function, which describes the correlation between input variables. The covariance function is modified to include an exponential term that captures the effect of the distance between input variables on their correlation. The exponential term is added to the standard squared exponential covariance function used in GPR. This modification allows the EGPR model to better capture long-range correlations between input variables, which may be missed by standard GPR. However, as with any machine learning technique, the performance of EGPR depends on the quality and quantity of data, the choice of hyperparameters, and the appropriateness of the model assumptions for the specific application. The result for the developed model between predicted and measured values is shown in Fig. 7. The root mean square error (RMSE) amounts to around 60 [Wm−2K−1] [7].

Fig. 7
figure 7

Correlation of HTCpredicted (HTCpred) and HTCmeasured (HTCmeas) for test data set using EGPR model

Full size image

For a deeper understanding of the applicability of the regression model, a dataset, unknown for the model, with two different casting speeds were investigated. In Fig. 8a, the measured surface temperatures with the corresponding (calculated) HTC course are given. In Fig. 8b, there are the HTC values gained by the EPGR regression model embedded in the results of the testset (transparent grey).

Fig. 8
figure 8

Correlation of HTC for two different casting speeds using an EGPR regression model

Full size image

According to the explanation in Section 4 (seven datapoints gained from one measurement), Fig. 8b shows seven marks for each casting speed. The root mean square error (RMSE) for these datapoints is under 35 [Wm−2K−1].

5 Simulation Results

Studying nozzles experimentally is essential for establishing precise boundary conditions in continuous casting machines. Nonetheless, gauging the complete water dispersion poses challenges, often leading to the practice of assessing a fraction of sprayed water and adjusting the dispersion accordingly. This approach can lead to notable disparities between computed and measured distributions, particularly in regions with overlapping sprays (Fig. 9). Thus, it becomes imperative to experimentally determine the actual spray water distribution.

Fig. 9
figure 9

Difference of WID in the case of scaling; blue line measured, red line calculated

Full size image

In the software m2CAST, comparative computations underscore the significance of empirically determining the heat transfer coefficient (HTC), particularly in regions where sprays overlap. When the water impact is more intense, the surface temperature in Fig. 10b is lower than what the calculated water impact distribution (WID) suggests. These cold spots elevate the potential for crack formation, underscoring the importance of accurate HTC assessment.

Fig. 10
figure 10

m2Cast simulation for corresponding WID. (a calculated and (b) measured given in Fig. 10)

Full size image

Another simulation result is given in Fig. 11. The underlying water distributions are shown in Fig. 11. In Fig. 11a, the ground condition for a conventional continuous casting machine close under the mold is given. This setting leads to a high maximum in the area of overlapping. By optimizing the nozzle to nozzle distance (Nx) from 190 mm up to 260 mm, the maximum of the WID can be minimized to about 15 kgm−2s−1.

Fig. 11
figure 11

Optimization of the WID by raising nozzle to nozzle distance from (a) 190 mm to (b) 260 mm

Full size image

The effects of this optimization were also investigated with our simulation software m2CAST. Figure 12a shows the position of the cutout, which is shown in detail on the right. Case (a) represents the general setting, and the optimization is shown in case (b). Due to the higher water impingement density in the overlap zone, the surface temperature in case (a) is significantly lower (dark area). Such low surface temperatures are avoided by optimizing the nozzle to nozzle spacing (Nx). The possibility of cracks is reduced.

Fig. 12
figure 12

Detail from simulation result for optimized nozzle to nozzle distance

Full size image

6 Conclusion

The non-commercial casting development platform m2CAST is a powerful tool for the prediction of factors relevant for quality. With the help of the so-called Nozzle Measuring Stand the Chair of Steel Metallurgy at the Montanuniversität Leoben has the ability to measure and investigate the cooling conditions in the secondary cooling zone with a high local resolution. The implementation of these measurements as boundary conditions through regression models offers low errors in the prediction of required heat transfer coefficients for precise simulation results [1].