Bidirectional normalized $q$-rung orthopair fuzzy projection and extended TOPSIS approach to multiattribute group decision making

Abstract

$q$-rung orthopair fuzzy sets ($q$-ROFSs), as a generalization of intuitionistic fuzzy sets (IFSs) and Pythagorean fuzzy sets (PFSs), can depict uncertain attitudes more flexibly and bear decision information more extensively. Innumerable fuzzy assessment verdicts that exceed IFSs or PFSs can be captured by $q$-ROFSs. To make the evaluation process more adaptive, in this article, we explore the application of $q$-ROFSs to multiattribute group decision making (MAGDM) by employing the technique for order preference by similarity to ideal solution (TOPSIS) approach. In view of the comprehensive tool of projection method for measuring the proximity of decision vectors, we further propose innovative bidirectional normalized projection measures that consider not only distance but also spatial angle to replace traditional distance measures such as Hamming and Euclidean. A new extension of TOPSIS methodology is then addressed in the context of MAGDM with $q$-ROFSs, which eliminates the transformation and aggregation steps to ensure less information loss. At length, the effectiveness and superiority of the proposed framework are demonstrated by an example of ship equipment reliability evaluation with comparative analysis, and future research directions are also suggested.

1 Introduction

Multiattribute decision making (MADM) is the process of analyzing, calculating, and judging feasible alternatives based on certain attributes and information with the help of specific tools, techniques, and methods, then selecting the best outcome to achieve a particular goal (Ning 2022; Liang and Xu 2017). MADM is an essential branch of modern decision science, which is often adopted to solve real-world problems such as strategy planning, reliability evaluation, supplier selection, and investment decisions. It has received extensive attention from many scholars in the past decade (Yue 2012; Zhang and Xu 2014; Liu et al. 2018a; Zhou 2022). In addition, due to the high complexity of many actual engineering and management situations, it is challenging for a single decision maker (DM) to investigate all crucial aspects of the decision process. As a result, organizations often employ a group of experts to form a decision committee and conduct multiattribute group decision making (MAGDM). A large number of MAGDM literature have achieved considerable success in practice (Ju et al. 2019; Liu et al. 2020; Liu et al. 2022).

The relevant studies have greatly enriched the toolbox of MAGDM and enlarged the related research fields. However, as Garg (2022) points out, uncertainty and ambiguity always play a dominant role in human decision activities. A new MAGDM approach should be developed that allows maximum flexibility and adaptability of the constraint relationship between membership degree ($\mu$) and non-membership degree ($\nu$) to fully and accurately depict the evaluation results with uncertain information delivered by DMs.

Regarding the description method of fuzzy objects (FOs), Zadeh (1965), Bellman and Zadeh (1970) addressed fuzzy sets (FSs) theory with the concept of membership degree and applied it to decision making in the 1960s. After that, Atanassov (1986) extended FSs to intuitionistic fuzzy sets (IFSs) by adding non-membership degree together with membership degree, which can more comprehensively portray the attitudes of DMs, such as support, opposition, and abstention. Nevertheless, restricted by the condition of $0\le \mu +\nu \le 1$, there are many FOs beyond the processing range of IFSs. To expand the applicability, Yager (2014) stretched IFSs to Pythagorean fuzzy sets (PFSs) by stretching the constraint of $0\le \mu +\nu \le 1$ to $0\le {\mu }^{2}+{\nu }^{2}\le 1$. Making the values of $\mu +\nu$ up to $\sqrt{2}$ is possible (discussed in Sect. 2), which allows PFSs to handle and describe more FOs and be widely studied. For instance, Mahmood and Ali (2022) developed a method to multiattribute decision making problems under interaction aggregation operators based on complex PFSs. Büyüközkan and Göçer (2021) modeled an integrated methodology based on the PFSs and simple additive weighting operator to measure the performance of software development project. Garg (2018, 2019a, b) presented more than seven aggregation operators for PFSs and applied them to solve the group decision making problems. Pythagorean fuzzy Aczel-Alsina average aggregation operators are surveyed and explored to solve multiple attribute decision making problems by literature (Senapati 2022).

Although PFS is impressive, it still cannot cover all legal FOs, where “legal” means that $\mu$ and $\nu$ are within $\left[\mathrm{0,1}\right]$, and when one of them takes $1$, the other must take $0$ at the same time. Consider an extreme but legal example where a DM provides preference value about an attribute with $\mu =0.99$ and $\nu =0.99$, then clearly $0.99+0.99\nleqq 1$ and ${0.99}^{2}+{0.99}^{2}\nleqq 1$ hence exceeds IFSs and PFSs. To overcome the above shortcomings, Yager (2017) further stretched PFSs to $q$-rung orthopair fuzzy sets ($q$-ROFSs) by further stretching the constraint of $0\le {\mu }^{2}+{\nu }^{2}\le 1$ to $0\le {\mu }^{q}+{\nu }^{q}\le 1 (q\ge 1)$. Making the values of $\mu +\nu$ infinitely close to $2$ is possible (discussed in Sect. 2), which allows $q$-ROFSs to handle and signify any legal FO via adjusting the parameter $q$. The preference value in the aforementioned extreme example can be captured by $q$-ROFSs as the constraint condition ${0\le 0.99}^{69}+{0.99}^{69}\le 1 (q=69)$ holds. Motivated by the ability of $q$-ROFSs, some researchers utilized this structure for the MAGDM problems. For example, Zhang et al. (2022) established two kinds of MAGDM methods based on q-rung orthopair fuzzy N-soft aggregation operators. Xu et al. (2021) suggested an interval-valued q-rung orthopair uncertain linguistic power Muirhead mean operators and linguistic scale functions based MAGDM method. Liu et al. (2021a) introduced a new class of point-weighted aggregation operators to aggregate linguistic $q$-rung orthopair fuzzy information. Cubic $q$-rung orthopair fuzzy power average operator and dual hesitant $q$-rung orthopair fuzzy 2-tuple linguistic Maclaurin symmetric mean aggregation operator are employed for MAGDM problems by literature Wang et al. (2020) and Naz et al. (2022), respectively.

It is noted that $q$-ROFSs can capture all the legal FOs, thus equipping DMs with one of the most flexible and adaptable structures. Moreover, search result from Clarivate Analytics’ web of science in Fig. 1 shows that $q$-ROFSs-based MAGDM studies are lacking, and this paper is intended to enrich this topic.

Fig. 1

Search result from the Web of Science on September 17, 2023

From the preceding discussion, you may have noticed that most of the relevant existing literature focuses on the development of various aggregation approaches (Chen et al. 2023a; Chen et al. 2019; Chen 2023), which usually necessitate normalization and transformation. Some decision information might be lost during the aggregation operation. Therefore, a new MAGDM approach based on $q$-ROFSs should be developed, thus directly wielding the original decision data to produce evaluation outcomes rather than relying on aggregation operators.

Regarding the decision making framework, it is noted that TOPSIS (technique for order performance by similarity to ideal situation) can effectively exploit the original evaluation information (Biswas et al. 2019; Wang et al. 2021), which excludes aggregation and secondary treatment to minimize information loss. There are no restrictions on data type and sample size (Liu et al. 2018b; Karabašević et al. 2020; Yang and Pang 2018). The TOPSIS model includes a thorough consideration of both the positive ideal solution (PIS) and the negative ideal solution (NIS). Alternatives are ranked by their closeness to PIS and NIS. TOPSIS is suitable for prudent (risk avoidance) situations as it makes decisions that not only achieve as much benefit as possible but also avoid as much risk as possible (Yue 2014). Since the appearance of TOPSIS, it has been extensively scrutinized by researchers. Keikha (2022) described an extended TOPSIS method based on generalized hesitant fuzzy numbers and their general distance, Hamming distance, and Euclidean distance measures in solving MADM problems. Karaaslan and Hunu (2020) focused on a MAGDM algorithm based on the TOPSIS approach under the type-2 single-valued neutrosophic environment and Hausdorff, Hamming, and Euclidean distance measures. Hussian and Yang (2019) constructed normalized versions of Hamming and Euclidean distance and applied them to fuzzy TOPSIS. Another three kinds of TOPSIS with different distance measures are examined by literature Ye and Chen (2021), Ali et al. (2021), and Corrente and Tasiou (2023).

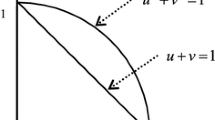
These studies have contributed significantly to the development of TOPSIS technology. However, most performance rankings depend only on the distance factor, which has limitations in determining the proximity of alternatives to PIS and NIS. Consider the example in Fig. 2 below. The distances between vectors ${\boldsymbol{\alpha }}_{1}$ and ${\boldsymbol{\alpha }}_{2}$, as well as between vectors ${{\varvec{\beta}}}_{1}$ and ${{\varvec{\beta}}}_{2}$, are both equal to the length of the red vector ${\varvec{\gamma}}$. Nevertheless, the first case is due to the difference between two vectors of identical length and similar direction, characterized by a smaller angle ${\theta }_{\alpha }$ between ${\boldsymbol{\alpha }}_{1}$ and ${\boldsymbol{\alpha }}_{2}$. The second case arises from the difference between two vectors of identical length but nearly opposite directions, resulting in a larger angle ${\theta }_{\beta }$ between ${{\varvec{\beta}}}_{1}$ and ${{\varvec{\beta}}}_{2}$. Obviously, the similarity between ${\boldsymbol{\alpha }}_{1}$ and ${\boldsymbol{\alpha }}_{2}$ is more remarkable under the condition of the same distance. Therefore, relying solely on distance measures to assess the proximity of two decision vectors is incomplete. Their angular factors should also be considered. A new MAGDM approach based on $q$-ROFSs and improved TOPSIS should be developed that enables a more comprehensive ranking of alternatives and decision matrices to achieve a more complete picture of the relationships between decision objects.

Fig. 2

Example of distance measure limitation

Regarding the similarity measure, it is noted that all the alternatives, PIS and NIS, can be regarded as vectors in the decision space. The inner product and projection are exactly the comprehensive measurements we are looking for, which can measure not only the distance but also the angle between two decision objects (Yue 2022). Wu et al. (2018) offered a linguistic fuzzy projection model for multi-criteria decision-making. Wang et al. (2018) adopted a practical method based on projection measure to define DMs’ weights. Wei et al. (2016) proposed a projection model for multiple attribute decision making with picture fuzzy information. However, this article finds that the conventional projection method is not always reasonable. For specific reasons, please refer to Example 1 in Sect. 3. To solve this problem, Yue (2022, 2020, 2019a, b) recently contributed more than eight normalized projection measures to solve the MADM or MAGDM problem in the field of software reliability assessment. Another normalized projection method was also presented by Liu et al. in the literature Liu et al. (2021b). However, this article still identifies the implicit drawbacks of these methods. For specific reasons, please refer to Example 2 in Sect. 3. Therefore, a new projection measure that is more reasonable and compatible with $q$-rung orthopair fuzzy vectors ($q$-ROFVs) should be developed.

Motivated by these research issues, this study is devoted to developing a new MAGDM method under the $q$-rung orthopair fuzzy environment with the following main contributions.

• 1. A novel bidirectional normalized projection measure is proposed to overcome various problems of existing projection measures.

• 2. The proposed bidirectional normalized projection measure is extended to $q$-rung orthopair fuzzy decision matrices and replaces the traditional distance measure such as Hamming or Euclidean in TOPSIS.

• 3. A new MAGDM method on the basis of $q$-ROFSs and improved TOPSIS is constructed to fill the gap since only a few related techniques have been reported so far to the best of our knowledge.

The remainder of this paper is organized as follows: Sect. 2 reviews some preliminaries related to the proposed model. Section 3 describes the research questions (RQs) and research objectives (ROs) through specific examples. In Sect. 4, a novel bidirectional normalized projection measure is introduced and extended to $q$-ROFSs decision matrices. In Sect. 5, a new MAGDM methodology is offered. Section 6 provides a detailed assessment process to ship equipment reliability, and a comparative analysis is prepared with current techniques. Conclusions and future directions are in Sect. 7.

2 Basic concepts

This section presents the basic definitions, properties, and operational laws of IFS, PFS, $q$-ROFS, and projection measure.

Definition 1

Let $X$ be the universe of discourse. An IFS $I$ on $X$ is displayed as (Atanassov 1986).

$$I=\left\{<x, I\left({\mu }_{I}\left(x\right),{\nu }_{I}\left(x\right)\right)>|x\in X\right\},$$

(1)

where ${\mu }_{I}\left(x\right),{\nu }_{I}\left(x\right):X\to [\mathrm{0,1}]$ denote the degree of membership and non-membership of $x$ to $I$, respectively, and $\forall x\in X$, it holds that $0{\le \mu }_{I}\left(x\right)+{\nu }_{I}\left(x\right)\le 1.$ The degree of hesitation of $x$ to $I$ is ${{\pi }_{I}\left(x\right)=1-\mu }_{I}\left(x\right)-{\nu }_{I}\left(x\right)$. For simplicity, the mathematical symbol $\alpha =\left({\mu }_{I}\left(x\right),{\nu }_{I}\left(x\right)\right)$ is called intuitionistic fuzzy number (IFN) (Zeshui 2007).

Definition 2

Let $X$ be the universe of discourse. A PFS $P$ on $X$ is given as (Yager 2014)

$$P=\left\{<x,P\left({\mu }_{P}\left(x\right),{\nu }_{P}\left(x\right)\right)>|x\in X\right\},$$

(2)

where ${\mu }_{P}\left(x\right),{\nu }_{P}\left(x\right):X\to [\mathrm{0,1}]$ denote the degree of membership and non-membership of $x$ to $P$, respectively, and $\forall x\in X$, it holds that $0\le {\left({\mu }_{P}\left(x\right)\right)}^{2}+{\left({\nu }_{P}\left(x\right)\right)}^{2}\le 1.$ The degree of hesitation of $x$ to $P$ is ${\pi }_{P}\left(x\right)=\sqrt{1-{\left({\mu }_{P}\left(x\right)\right)}^{2}-{\left({\nu }_{P}\left(x\right)\right)}^{2}}$. For simplicity, the mathematical symbol $\beta =\left({\mu }_{P}\left(x\right),{\nu }_{P}\left(x\right)\right)$ is called Pythagorean fuzzy number (PFN) (Zhang and Xu 2014).

According to Definition 2, we have

$${\left({\mu }_{P}\left(x\right)\right)}^{2}+{\left({\nu }_{P}\left(x\right)\right)}^{2}\le 1\Rightarrow {\mu }_{P}\left(x\right)\le \sqrt{1-{\left({\nu }_{P}\left(x\right)\right)}^{2}}\Rightarrow {\mu }_{P}\left(x\right)+{\nu }_{P}\left(x\right)\le {\nu }_{P}\left(x\right)+\sqrt{1-{\left({\nu }_{P}\left(x\right)\right)}^{2}},$$

then let

$$\frac{d}{{d}_{{\nu }_{P}\left(x\right)}}\left({\nu }_{P}\left(x\right)+\sqrt{1-{\left({\nu }_{P}\left(x\right)\right)}^{2}}\right)=1-\frac{{\nu }_{P}\left(x\right)}{\sqrt{1-{\left({\nu }_{P}\left(x\right)\right)}^{2}}}=0,$$

we get ${\nu }_{P}\left(x\right)=1/\sqrt{2}$ and $\mathrm{max}\left({\nu }_{P}\left(x\right)+\sqrt{1-{\left({\nu }_{P}\left(x\right)\right)}^{2}}\right)=1/\sqrt{2}+\sqrt{1-(1/\sqrt{2}{)}^{2}}=\sqrt{2}$. Note that $0\le {\mu }_{P}\left(x\right),{\nu }_{P}\left(x\right)$, one can obtain

$$0\le {\mu }_{P}\left(x\right)+{\nu }_{P}\left(x\right)\le \sqrt{2}.$$

(3)

Definition 3

Let $X$ be the universe of discourse. A $q$-ROFS $Q$ on $X$ is defined as (Yager 2017)

$$Q=\left\{<x,Q\left({\mu }_{Q}\left(x\right),{\nu }_{Q}\left(x\right)\right)>|x\in X\right\},$$

(4)

where ${\mu }_{Q}\left(x\right),{\nu }_{Q}\left(x\right):X\to [\mathrm{0,1}]$ denote the degree of membership and non-membership of $x$ to $Q$, respectively, and $\forall x\in X$, $q\ge 1$, it holds that $0\le {\left({\mu }_{Q}\left(x\right)\right)}^{q}+{\left({\nu }_{Q}\left(x\right)\right)}^{q}\le 1.$ The degree of hesitation of $x$ to $Q$ is ${\pi }_{Q}\left(x\right)=\sqrt[q]{1-{\left({\mu }_{Q}\left(x\right)\right)}^{q}-{\left({\nu }_{Q}\left(x\right)\right)}^{q}}$. For simplicity, the mathematical symbol $\gamma =\left({\mu }_{Q}\left(x\right),{\nu }_{Q}\left(x\right)\right)$ is called $q$-rung orthopair fuzzy number ($q$-ROFN) (Garg and Chen 2020). When the value of $q$ is equal to $1$ or $2$, $q$-ROFN reduces to IFN or PFN.

According to Definition 3, we have

$${\left({\mu }_{Q}\left(x\right)\right)}^{q}+{\left({\nu }_{Q}\left(x\right)\right)}^{q}\le 1\Rightarrow {\mu }_{Q}\left(x\right)\le {\left(1-{\left({\nu }_{Q}\left(x\right)\right)}^{q}\right)}^\frac{1}{q}\Rightarrow {\mu }_{Q}\left(x\right)+{\nu }_{Q}\left(x\right)\le {\nu }_{Q}\left(x\right)+{\left(1-{\left({\nu }_{Q}\left(x\right)\right)}^{q}\right)}^\frac{1}{q}$$

and

$$\underset{q\to \infty }{\mathrm{lim}}\left({\nu }_{Q}\left(x\right)+{\left(1-{\left({\nu }_{Q}\left(x\right)\right)}^{q}\right)}^\frac{1}{q}\right)=\left\{\begin{array}{c}1+{\nu }_{Q}\left(x\right)<2, 0\le {\nu }_{Q}\left(x\right)<1\\ 1, {\nu }_{Q}\left(x\right)=1\end{array}\right..$$

Note that $0\le {\mu }_{Q}\left(x\right),{\nu }_{Q}\left(x\right)$, one can obtain

$$0\le {\mu }_{Q}\left(x\right)+{\nu }_{Q}\left(x\right)<2.$$

(5)

We summarize the evolution of the fuzzy constraints in Table 1 based on Ineqs. (3) and (5).

Table 1 Evolution of the fuzzy constraints

Definition 4

Let $\gamma =\left({\mu }_{Q},{\nu }_{Q}\right)$,${\gamma }_{1}=\left({\mu }_{Q1},{\nu }_{Q1}\right)$, ${\gamma }_{2}=\left({\mu }_{Q2},{\nu }_{Q2}\right)$ be three $q$-ROFNs, then (Garg and Chen 2020; Liu and Wang 2018; Peng et al. 2018),

• 1. ${\gamma }_{1}\subseteq {\gamma }_{2}$ if ${\mu }_{Q1}\le {\mu }_{Q2}$ and ${\nu }_{Q1}\ge {\nu }_{Q2}$;

• 2. ${\gamma }_{1}={\gamma }_{2}$ if ${\gamma }_{1}\subseteq {\gamma }_{2}$ and ${\gamma }_{2}\subseteq {\gamma }_{1}$;

• 3. ${\gamma }_{1}+{\gamma }_{2}=\left({\left({\left({\mu }_{Q1}\right)}^{q}+{\left({\mu }_{Q2}\right)}^{q}-{\left({\mu }_{Q1}\right)}^{q}{\left({\mu }_{Q2}\right)}^{q}\right)}^{1/q},{\nu }_{Q1}{\nu }_{Q2}\right)$, $q\ge 1$;

• 4. $\lambda \gamma =\left({\left(1-{(1-({\mu }_{Q}{)}^{q})}^{\lambda }\right)}^{1/q},{\left({\nu }_{Q}\right)}^{\lambda }\right)$, $q\ge 1$, $\lambda >0$;

Definition 5

Let $\widetilde{\upxi }=\left(\left({\mu }_{Q\widetilde{\xi }}^{1},{\nu }_{Q\widetilde{\xi }}^{1}\right),\left({\mu }_{Q\widetilde{\xi }}^{2},{\nu }_{Q\widetilde{\xi }}^{2}\right),\cdots ,\left({\mu }_{Q\widetilde{\xi }}^{n},{\nu }_{Q\widetilde{\xi }}^{n}\right)\right)$ and $\widetilde{\psi }=\left(\left({\mu }_{Q\widetilde{\psi }}^{1},{\nu }_{Q\widetilde{\psi }}^{1}\right),\left({\mu }_{Q\widetilde{\psi }}^{2},{\nu }_{Q\widetilde{\psi }}^{2}\right),\cdots ,\left({\mu }_{Q\widetilde{\psi }}^{n},{\nu }_{Q\widetilde{\psi }}^{n}\right)\right)$ be two $n$-dimensional $q$-ROFVs, $\left({\mu }_{Q\widetilde{\xi }}^{1},{\nu }_{Q\widetilde{\xi }}^{1}\right),\cdots ,\left({\mu }_{Q\widetilde{\xi }}^{n},{\nu }_{Q\widetilde{\xi }}^{n}\right), \left({\mu }_{Q\widetilde{\psi }}^{1},{\nu }_{Q\widetilde{\psi }}^{1}\right),\cdots ,\left({\mu }_{Q\widetilde{\psi }}^{n},{\nu }_{Q\widetilde{\psi }}^{n}\right)$ are $q$-ROFNs, then (Liu et al. 2020; Liu et al. 2021b).

$$ \Pr j_{{\tilde{\psi }}} \tilde{\xi } = \frac{{\tilde{\xi }\tilde{\psi }}}{{\left| {\tilde{\psi }} \right|}} $$

(6)

is the projection measure of the vector $\tilde{\xi }$ onto the vector $\tilde{\psi }$, where $\left|\widetilde{\psi }\right|=$ is the module of vector $\tilde{\psi }$, where $\tilde{\xi }\tilde{\psi } = \mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{q} } \right)$ is the inner product of vector $\tilde{\xi }$ and vector $\tilde{\psi }$, and $\pi_{{Q\tilde{\xi }}}^{i} = \sqrt[q]{{1 - \left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{q} - \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{q} }}$, $\pi_{{Q\tilde{\psi }}}^{i} = \sqrt[q]{{1 - \left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{q} - \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{q} }}$.

In general, the larger the projection value of $\Pr j_{{\tilde{\psi }}} \tilde{\xi }$ in Eq. (6), the closer the vector $\tilde{\xi }$ is to $\tilde{\psi }$ (Liu et al. 2021b).

3 Research questions and objectives

RQs and ROs are illustrated below in this section.

As mentioned above, in general, the projection value is positively related to the degree of vector closeness. However, some exceptions were found in this research under the $q$-rung orthopair fuzzy environment. One of them is shown in the following example.

Example 1.

Let $\tilde{\xi } = \left( {\left( {0.7,0.3} \right),\left( {0.6,0.1} \right)} \right)$ and $\tilde{\psi } = \left( {\left( {0.8,0.4} \right),\left( {0.7,0.2} \right)} \right)$ be two $q$-ROFVs (suppose $q=3$). According to Definition 5, it is easy to calculate

$$\left| {\tilde{\psi }} \right| = \sqrt {0.8^{6} + 0.4^{6} + \left( {1 - 0.8^{3} - 0.4^{3} } \right)^{2} + 0.7^{6} + 0.2^{6} + \left( {1 - 0.7^{3} - 0.2^{3} } \right)^{2} } = 0.9924$$

, $\tilde{\xi }\tilde{\psi } = 0.7^{3} \times 0.8^{3} + 0.3^{3} \times 0.4^{3} + \left( {1 - 0.7^{3} - 0.3^{3} } \right) \times \left( {1 - 0.8^{3} - 0.4^{3} } \right) + 0.6^{3} \times 0.7^{3} + 0.1^{3} \times 0.2^{3} + \left( {1 - 0.6^{3} - 0.1^{3} } \right) \times \left( {1 - 0.7^{3} - 0.2^{3} } \right) = 1.0267$, and $\tilde{\psi }\tilde{\psi } = 0.8^{3} \times 0.8^{3} + 0.4^{3} \times 0.4^{3} + \left( {1 - 0.8^{3} - 0.4^{3} } \right) \times \left( {1 - 0.8^{3} - 0.4^{3} } \right) + 0.7^{3} \times 0.7^{3} + 0.2^{3} \times 0.2^{3} + \left( {1 - 0.7^{3} - 0.2^{3} } \right) \times \left( {1 - 0.7^{3} - 0.2^{3} } \right) = 0.9849$. It follows that $\Pr j_{{\tilde{\psi }}} \tilde{\xi } = 1.0346$ and $\Pr j_{{\tilde{\psi }}} \tilde{\psi } = 0.9924$. Therefore, $\Pr j_{{\tilde{\psi }}} \tilde{\xi } > \Pr j_{{\tilde{\psi }}} \tilde{\psi }$, which implies that the closeness of $\tilde{\xi }$ to $\tilde{\psi }$ is higher compared to the closeness of $\tilde{\psi }$ to itself. However, we should realize that no other vector can be closer to oneself than itself. It’s an apparent contradiction. In addition,

$$\left| {\tilde{\xi }} \right| = \sqrt {0.7^{6} + 0.3^{6} + \left( {1 - 0.7^{3} - 0.3^{3} } \right)^{2} + 0.6^{6} + 0.1^{6} + \left( {1 - 0.6^{3} - 0.1^{3} } \right)^{2} } = 1.0840$$

, $\tilde{\xi }\tilde{\xi } = 0.7^{3} \times 0.7^{3} + 0.3^{3} \times 0.3^{3} + \left( {1 - 0.7^{3} - 0.3^{3} } \right) \times \left( {1 - 0.7^{3} - 0.3^{3} } \right) + 0.6^{3} \times 0.6^{3} + 0.1^{3} \times 0.1^{3} + \left( {1 - 0.6^{3} - 0.1^{3} } \right) \times \left( {1 - 0.6^{3} - 0.1^{3} } \right) = 1.1750$, thus we have $\Pr j_{{\tilde{\xi }}} \tilde{\xi } = 1.0839$. It follows that $\Pr j_{{\tilde{\xi }}} \tilde{\xi } \ne \Pr j_{{\tilde{\psi }}} \tilde{\psi } \ne 1$. This is an apparent defect.

From Example 1, some RQs are raised as follows.

RQ 1: Projection measure based on Eq. (6) cannot always reflect the closeness of two $q$-ROFVs.

RQ 2: The projection measure based on Eq. (6) is not normalized. That is, the projection value of Eq. (6) does not always satisfy the condition $0 \le \Pr j_{{\tilde{\psi }}} \tilde{\xi } \le 1$. You may notice that both $\Pr j_{{\tilde{\psi }}} \tilde{\xi } = 1.0346$ and $\Pr j_{{\tilde{\xi }}} \tilde{\xi } = 1.0839$ in Example 1 are greater than 1.

RQ 3: The projection value of a $q$-ROFV to itself based on Eq. (6) may be different. As shown in Example 1, $\Pr j_{{\tilde{\xi }}} \tilde{\xi } = 1.0839$ is not equal to $\Pr j_{{\tilde{\psi }}} \tilde{\psi } = 0.9924$, and neither of them is equal to 1. It is unreasonable and counterintuitive.

To improve the projection measure of Eq. (6), recent literature (Yue 2022, 2020) proposed the following normalized projection measures and applied them to picture fuzzy vectors:

$$ {\text{NPyueI}}_{{\tilde{\psi }}} \tilde{\xi } = \frac{{\left| {\tilde{\xi }} \right|^{2} + \left| {\tilde{\psi }} \right|^{2} }}{{\left| {\tilde{\xi }} \right|^{2} + \left| {\tilde{\psi }} \right|^{2} + \left| {\tilde{\xi }\tilde{\psi } - \left| {\tilde{\psi }} \right|^{2} } \right|}}, $$

(7)

$$ {\text{NPyueII}}_{{\tilde{\psi }}} \tilde{\xi } = \frac{{\min \left\{ {\tilde{\xi }\tilde{\psi },\left| {\tilde{\psi }} \right|^{2} } \right\}}}{{\max \left\{ {\tilde{\xi }\tilde{\psi },\left| {\tilde{\psi }} \right|^{2} } \right\}}} $$

(8)

Recent literature (Liu et al. 2021b) proposed the following normalized projection measure and applied it to $q$-ROFVs:

$$ {\text{NPliu}}_{{\tilde{\psi }}} \tilde{\xi } = \frac{{\frac{{\tilde{\xi }\tilde{\psi }}}{{\left| {\tilde{\psi }} \right|}}}}{{\frac{{\tilde{\xi }\tilde{\psi }}}{{\left| {\tilde{\psi }} \right|}} + \left| {\left| {\tilde{\psi }} \right| - \frac{{\tilde{\xi }\tilde{\psi }}}{{\left| {\tilde{\psi }} \right|}}} \right|}}. $$

(9)

However, this research still finds implicit defects in the above methods described by the following example and RQ.

Example 2.

Let $\widetilde{\upxi }$ and $\widetilde{\psi }$ be the same $q$-ROFVs as in Example 1. We have that $\left| {\tilde{\xi }} \right|^{2} = 1.0840^{2}$, $\left| {\tilde{\psi }} \right|^{2} = 0.9924^{2}$, and $\tilde{\xi }\tilde{\psi } = 1.0267$. According to Eq. (7), we can calculate ${\text{NPyueI}}_{{\tilde{\psi }}} \tilde{\xi } = \frac{{1.0840^{2} + 0.9924^{2} }}{{1.0840^{2} + 0.9924^{2} + \left| {1.0267 - 0.9924^{2} } \right|}} = 0.9810$ and ${\text{NPyueI}}_{{\tilde{\xi }}} \tilde{\psi } = \frac{{0.9924^{2} + 1.0840^{2} }}{{0.9924^{2} + 1.0840^{2} + \left| {1.0267 - 1.0840^{2} } \right|}} = 0.9357$. It follows that ${\text{NPyueI}}_{{\tilde{\psi }}} \tilde{\xi } > {\text{NPyueI}}_{{\tilde{\xi }}} \tilde{\psi }$, which indicates that the closeness degree of $\tilde{\xi }$ to $\tilde{\psi }$ is greater than the closeness degree of $\tilde{\psi }$ to $\tilde{\xi }$. Analogously, according to Eq. (8), we can calculate ${\text{NPyueII}}_{{\tilde{\psi }}} \tilde{\xi } = \frac{{\min \left\{ {1.0267,0.9924^{2} } \right\}}}{{\max \left\{ {1.0267,9924^{2} } \right\}}} = 0.9593$ and ${\text{NPyueII}}_{{\tilde{\xi }}} \tilde{\psi } = \frac{{\min \left\{ {1.0267,1.0840^{2} } \right\}}}{{\max \left\{ {1.0267,1.0840^{2} } \right\}}} = 0.8738$. It follows that ${\text{NPyueII}}_{{\tilde{\psi }}} \tilde{\xi } > {\text{NPyueII}}_{{\tilde{\xi }}} \tilde{\psi }$, which also suggests that the closeness of $\tilde{\xi }$ to $\tilde{\psi }$ is higher compared to the closeness of $\tilde{\psi }$. to $\tilde{\xi }$. Similarly, according to Eq. (9), we can calculate ${\text{NPliu}}_{{\tilde{\psi }}} \tilde{\xi } = \frac{{\frac{1.0267}{{0.9924}}}}{{\frac{1.0267}{{0.9924}} + \left| {0.9924 - \frac{1.0267}{{0.9924}}} \right|}} = 0.9608$ and ${\text{NPliu}}_{{\tilde{\xi }}} \tilde{\psi } = \frac{{\frac{1.0267}{{1.0840}}}}{{\frac{1.0267}{{1.0840}} + \left| {1.0840 - \frac{1.0267}{{1.0840}}} \right|}} = 0.8738$. It follows that ${\text{NPliu}}_{{\tilde{\psi }}} \tilde{\xi } > {\text{NPliu}}_{{\tilde{\xi }}} \tilde{\psi }$, which still means that the closeness of $\tilde{\xi }$ to $\tilde{\psi }$ is higher compared to the closeness of $\tilde{\psi }$ to $\tilde{\xi }$. However, we should note that the proximity of $\tilde{\xi }$ and $\tilde{\psi }$ is mutual, which must be the same value. It’s an obvious contradiction.

From Example 2, one more RQ is raised as follows.

RQ 4: Normalized projection measures of Eqs. (7), (8), and (9) are not commutative. That is to say, the closeness degree of $\tilde{\xi }$ to $\tilde{\psi }$ is inconsistent with the closeness degree of $\tilde{\psi }$ to $\tilde{\xi }$.

These RQs promote the following ROs:

RO 1: Construct a reliable projection measure between any $q$-ROFVs $\tilde{\xi }$ and $\tilde{\psi }$ such that the larger the projection value, the closer the vector $\tilde{\xi }$ is to $\tilde{\psi }$.

RO 2: Construct a normalized projection measure between any $q$-ROFVs $\tilde{\xi }$ and $\tilde{\psi }$ such that $0 \le \Pr j_{{\tilde{\psi }}} \tilde{\xi } \le 1$.

RO 3: Construct a reasonable projection measure between any $q$-ROFVs $\tilde{\xi }$ and $\tilde{\psi }$ such that $\Pr j_{{\tilde{\xi }}} \tilde{\xi } = \Pr j_{{\tilde{\psi }}} \tilde{\psi } = 1$.

RO 4: Construct a commutative projection measure between any $q$-ROFVs $\tilde{\xi }$ and $\tilde{\psi }$ such that $\Pr j_{{\tilde{\psi }}} \tilde{\xi } = \Pr j_{{\tilde{\xi }}} \tilde{\psi }$.

4 Presented bidirectional normalized projection measure

To address RQ1 ~ RQ4, this study presents a new bidirectional normalized projection measure as the following definition.

Definition 6

Let $\tilde{\xi } = \left( {\left( {\mu_{{Q\tilde{\xi }}}^{1} ,\nu_{{Q\tilde{\xi }}}^{1} } \right),\left( {\mu_{{Q\tilde{\xi }}}^{2} ,\nu_{{Q\tilde{\xi }}}^{2} } \right), \cdots ,\left( {\mu_{{Q\tilde{\xi }}}^{n} ,\nu_{{Q\tilde{\xi }}}^{n} } \right)} \right)$ and $\tilde{\psi } = \left( {\left( {\mu_{{Q\tilde{\psi }}}^{1} ,\nu_{{Q\tilde{\psi }}}^{1} } \right),\left( {\mu_{{Q\tilde{\psi }}}^{2} ,\nu_{{Q\tilde{\psi }}}^{2} } \right), \cdots ,\left( {\mu_{{Q\tilde{\psi }}}^{n} ,\nu_{{Q\tilde{\psi }}}^{n} } \right)} \right)$ be two $n$-dimensional $q$-ROFVs, $\left( {\mu_{{Q\tilde{\xi }}}^{1} ,\nu_{{Q\tilde{\xi }}}^{1} } \right), \ldots ,\left( {\mu_{{Q\tilde{\xi }}}^{n} ,\nu_{{Q\tilde{\xi }}}^{n} } \right), \left( {\mu_{{Q\tilde{\psi }}}^{1} ,\nu_{{Q\tilde{\psi }}}^{1} } \right), \ldots ,\left( {\mu_{{Q\tilde{\psi }}}^{n} ,\nu_{{Q\tilde{\psi }}}^{n} } \right)$ are $q$-ROFNs, then

$$ {\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\xi } = \left( {\frac{{\tilde{\xi }\tilde{\psi } + \left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}{{2\left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}} \right)^{\sigma } $$

(10)

is the bidirectional normalized projection measure between $q$-ROFVs $\tilde{\xi }$ and $\tilde{\psi }$, where $\left| {\tilde{\xi }} \right| = \sqrt {\mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{2q} } \right)}$ is the module of vector $\tilde{\xi }$, $\left| {\tilde{\psi }} \right| = \sqrt {\mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{2q} } \right)}$ is the module of vector $\tilde{\psi }$, $\tilde{\xi }\tilde{\psi } = \mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{q} } \right)$ is the inner product of vector $\tilde{\xi }$ and vector $\tilde{\psi }$, $\pi_{{Q\tilde{\xi }}}^{i} = \sqrt[q]{{1 - \left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{q} - \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{q} }}$, $\pi_{{Q\tilde{\psi }}}^{i} = \sqrt[q]{{1 - \left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{q} - \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{q} }}$, and $\sigma$ is the distinguishing index of the presented measure. The distribution range of the projection values of a set of alternatives can be changed by adjusting $\sigma$ (refer to Sect. 6.3 for details) to obtain a better evaluation, and $\sigma$ is equal to 4 by default in the discussion of this paper.

Theorem 1

For two $q$-ROFVs $\tilde{\xi } = \left( {\left( {\mu_{{Q\tilde{\xi }}}^{1} ,\nu_{{Q\tilde{\xi }}}^{1} } \right),\left( {\mu_{{Q\tilde{\xi }}}^{2} ,\nu_{{Q\tilde{\xi }}}^{2} } \right), \ldots ,\left( {\mu_{{Q\tilde{\xi }}}^{n} ,\nu_{{Q\tilde{\xi }}}^{n} } \right)} \right)$ and $\tilde{\psi } = \left( {\left( {\mu_{{Q\tilde{\psi }}}^{1} ,\nu_{{Q\tilde{\psi }}}^{1} } \right),\left( {\mu_{{Q\tilde{\psi }}}^{2} ,\nu_{{Q\tilde{\psi }}}^{2} } \right), \ldots ,\left( {\mu_{{Q\tilde{\psi }}}^{n} ,\nu_{{Q\tilde{\psi }}}^{n} } \right)} \right)$, Eq. (10) satisfies:

• 1. ${\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\xi } = {\text{BNPjia}}_{{\tilde{\xi }}} \tilde{\psi }$;

• 2. ${\text{BNPjia}}_{{\tilde{\xi }}} \tilde{\xi } = {\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\psi } = 1$;

• 3. $0 \le {\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\xi } \le 1$.

Proof.

${\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\xi } = \left( {\frac{{\tilde{\xi }\tilde{\psi } + \left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}{{2\left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}} \right)^{\sigma } = \left( {\frac{{\tilde{\psi }\tilde{\xi } + \left| {\tilde{\psi }} \right|\left| {\tilde{\xi }} \right|}}{{2\left| {\tilde{\psi }} \right|\left| {\tilde{\xi }} \right|}}} \right)^{\sigma } = {\text{BNPjia}}_{{\tilde{\xi }}} \tilde{\psi }$. Theorem 1.1 holds, anthe result supports RO 4.

$$\begin{aligned} {\text{BNPjia}}_{{\tilde{\xi }}} \tilde{\xi } & = \left( {\frac{{\tilde{\xi }\tilde{\xi } + \left| {\tilde{\xi }} \right|\left| {\tilde{\xi }} \right|}}{{2\left| {\tilde{\xi }} \right|\left| {\tilde{\xi }} \right|}}} \right)^{\sigma } = \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{q} } \right) + \mathop \sum \nolimits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{2q} } \right)}}{{2\mathop \sum \nolimits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{2q} } \right)}}} \right)^{\sigma } = 1 \\ & = \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{q} \left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{q} } \right) + \mathop \sum \nolimits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{2q} } \right)}}{{2\mathop \sum \nolimits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{2q} } \right)}}} \right)^{\sigma } \\ & = \left( {\frac{{\tilde{\psi }\tilde{\psi } + \left| {\tilde{\psi }} \right|\left| {\tilde{\psi }} \right|}}{{2\left| {\tilde{\psi }} \right|\left| {\tilde{\psi }} \right|}}} \right)^{\sigma } = {\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\psi } \\ \end{aligned}$$

. Theorem 1.2 holds, and the result supports RO 3.

According to Definition 6, $\tilde{\xi }\tilde{\psi },\left| {\tilde{\xi }} \right|,\left| {\tilde{\psi }} \right| \ge 0$. Hence, ${\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\xi } \ge 0$. Furthermore, from the perspective of the inner product, it’s obvious that $\tilde{\xi }\tilde{\psi } \le \left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|$. Then, ${\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\xi } = \left( {\frac{{\tilde{\xi }\tilde{\psi } + \left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}{{2\left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}} \right)^{\sigma } \le \left( {\frac{{\left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right| + \left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}{{2\left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}} \right)^{\sigma } = 1$. Therefore, $0 \le {\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\xi } \le 1$. In addition, the rigorous algebraic proof process is detailed in Appendix A. Theorem 1.3 holds, and the result supports RO 2.

Theorem 2

The projection value of Eq. (10) is monotonic with respect to the membership degree ${\mu }_{Q}$ and non-membership degree ${\nu }_{Q}$ in $q$-ROFN, respectively.

Proof. Firstly, we examine the monotonic relationship between the projection value of Eq. (10) and the membership degree ${\mu }_{Q}$. In this situation, let the non-membership degree ${\nu }_{Q}$ of $q$-ROFN ${\gamma }_{1}=\left({\mu }_{Q1},{\nu }_{Q}\right)$ remain unchanged, and ${\mu }_{Q1}$ sliding in the range $\left[\mathrm{0,1}\right]$ based on the initial value to obtain $q$-ROFN ${\gamma }_{2}=\left({\mu }_{Q2},{\nu }_{Q}\right)$. We have

$$ BNPjia_{{\gamma_{2} }} \gamma_{1} = \left( {\frac{{\gamma_{1} \gamma_{2} + \left| {\gamma_{1} } \right|\left| {\gamma_{2} } \right|}}{{2\left| {\gamma_{1} } \right|\left| {\gamma_{2} } \right|}}} \right)^{\sigma } = \left( f \right)^{\sigma } , $$

where

$$f=\frac{{\left({\mu }_{Q1}\right)}^{q}{\left({\mu }_{Q2}\right)}^{q}+{\left({\nu }_{Q}\right)}^{q}{\left({\nu }_{Q}\right)}^{q}+\left(1-{\left({\mu }_{Q1}\right)}^{q}-{\left({\nu }_{Q}\right)}^{q}\right)\left(1-{\left({\mu }_{Q2}\right)}^{q}-{\left({\nu }_{Q}\right)}^{q}\right)}{2\sqrt{{\left({\mu }_{Q1}\right)}^{2q}+{\left({\nu }_{Q}\right)}^{2q}+{\left(1-{\left({\mu }_{Q1}\right)}^{q}-{\left({\nu }_{Q}\right)}^{q}\right)}^{2}}\sqrt{{\left({\mu }_{Q2}\right)}^{2q}+{\left({\nu }_{Q}\right)}^{2q}+{\left(1-{\left({\mu }_{Q2}\right)}^{q}-{\left({\nu }_{Q}\right)}^{q}\right)}^{2}}}+\frac{\sqrt{{\left({\mu }_{Q1}\right)}^{2q}+{\left({\nu }_{Q}\right)}^{2q}+{\left(1-{\left({\mu }_{Q1}\right)}^{q}-{\left({\nu }_{Q}\right)}^{q}\right)}^{2}}\sqrt{{\left({\mu }_{Q2}\right)}^{2q}+{\left({\nu }_{Q}\right)}^{2q}+{\left(1-{\left({\mu }_{Q2}\right)}^{q}-{\left({\nu }_{Q}\right)}^{q}\right)}^{2}}}{2\sqrt{{\left({\mu }_{Q1}\right)}^{2q}+{\left({\nu }_{Q}\right)}^{2q}+{\left(1-{\left({\mu }_{Q1}\right)}^{q}-{\left({\nu }_{Q}\right)}^{q}\right)}^{2}}\sqrt{{\left({\mu }_{Q2}\right)}^{2q}+{\left({\nu }_{Q}\right)}^{2q}+{\left(1-{\left({\mu }_{Q2}\right)}^{q}-{\left({\nu }_{Q}\right)}^{q}\right)}^{2}}}.$$

Thus,

$$\frac{\partial }{\partial {\mu }_{Q1}}\left(f\right)=\frac{q{\left({\mu }_{Q1}\right)}^{q-1}\left(3{\left({\nu }_{Q}\right)}^{2q}-2{\left({\nu }_{Q}\right)}^{q}+1\right)\left({\left({\mu }_{Q2}\right)}^{q}-{\left({\mu }_{Q1}\right)}^{q}\right)}{2{\left({\left({\mu }_{Q1}\right)}^{2q}+{\left({\left({\mu }_{Q1}\right)}^{q}+{\left({\nu }_{Q}\right)}^{q}-1\right)}^{2}+{\left({\nu }_{Q}\right)}^{2q}\right)}^\frac{3}{2}\sqrt{{\left({\nu }_{Q}\right)}^{2q}+{\left({\left({\nu }_{Q}\right)}^{q}+{\left({\mu }_{Q2}\right)}^{q}-1\right)}^{2}+{\left({\mu }_{Q2}\right)}^{2q}}}.$$

Let $\delta ={\left({\nu }_{Q}\right)}^{q}\in \left[\mathrm{0,1}\right]$, we get

$$3{\left({\nu }_{Q}\right)}^{2q}-2{\left({\nu }_{Q}\right)}^{q}+1=3{\delta }^{2}-2\delta +1,$$

$$\frac{d}{d\delta }\left(3{\delta }^{2}-2\delta +1\right)=6\delta -2,$$

and

$$\frac{{d}^{2}}{d{\delta }^{2}}\left(3{\delta }^{2}-2\delta +1\right)=6>0.$$

Hence, $3{\delta }^{2}-2\delta +1$ is a concave function and takes its minimum value at $\delta ={\left({\nu }_{Q}\right)}^{q}=\frac{1}{3}$, that is, $\underset{0\le {\left({\nu }_{Q}\right)}^{q}\le 1}{\mathrm{min}}\left(3{\left({\nu }_{Q}\right)}^{2q}-2{\left({\nu }_{Q}\right)}^{q}+1\right)=3\times {\left(\frac{1}{3}\right)}^{2}-2\times \left(\frac{1}{3}\right)+1=\frac{2}{3}>0$. In addition, $q{\left({\mu }_{Q1}\right)}^{q-1}\ge 0$, ${\left({\left({\mu }_{Q1}\right)}^{2q}+{\left({\left({\mu }_{Q1}\right)}^{q}+{\left({\nu }_{Q}\right)}^{q}-1\right)}^{2}+{\left({\nu }_{Q}\right)}^{2q}\right)}^\frac{3}{2}\ge 0$, and $\sqrt{{\left({\nu }_{Q}\right)}^{2q}+{\left({\left({\nu }_{Q}\right)}^{q}+{\left({\mu }_{Q2}\right)}^{q}-1\right)}^{2}+{\left({\mu }_{Q2}\right)}^{2q}}\ge 0$. Consequently, the sign of $\frac{\partial }{\partial {\mu }_{Q1}}\left(f\right)$ is determined by $\left({\left({\mu }_{Q2}\right)}^{q}-{\left({\mu }_{Q1}\right)}^{q}\right)$. When ${\mu }_{Q1}<{\mu }_{Q2}$, $\left({\left({\mu }_{Q2}\right)}^{q}-{\left({\mu }_{Q1}\right)}^{q}\right)>0$, $\frac{\partial }{\partial {\mu }_{Q1}}\left(f\right)>0,$ $f$ monotonically increasing, i.e., the bidirectional normalized projection value of ${\gamma }_{1}$, ${\gamma }_{2}$ gradually increases as ${\mu }_{Q1}$ approaches ${\mu }_{Q2}$ from small to large; When ${\mu }_{Q1}>{\mu }_{Q2}$, $\left({\left({\mu }_{Q2}\right)}^{q}-{\left({\mu }_{Q1}\right)}^{q}\right)<0$, $\frac{\partial }{\partial {\mu }_{Q1}}\left(f\right)<0,$ $f$ monotonically decreasing, i.e., the bidirectional normalized projection value of $\gamma_{1}$, $\gamma_{2}$ gradually decreases as $\mu_{Q1}$ moves away from $\mu_{Q2}$ from small to large; When $\mu_{Q1} = \mu_{Q2}$, $\left( {\left( {\mu_{Q2} } \right)^{q} - \left( {\mu_{Q1} } \right)^{q} } \right) = 0$, $\frac{\partial }{{\partial \mu_{Q1} }}\left( f \right) = 0,$ i.e., $\gamma_{1}$, $\gamma_{2}$ coincide, ${\text{BNPjia}}_{{\gamma_{1} }} \gamma_{1} = {\text{BNPjia}}_{{\gamma_{2} }} \gamma_{2} = \left( f \right)^{\sigma }$ obtains the maximum value $1$, which means ${\gamma }_{1}$, ${\gamma }_{2}$ have the highest similarity with themselves.

Analogously, we examine the monotonic relationship between the projection value of Eq. (10) and the non-membership degree ${\nu }_{Q}$. We can obtain the same conclusion. Therefore, Theorem 2 holds, and the result supports RO 1.

For the same $q$-ROFVs $\tilde{\xi } = \left( {\left( {0.7,0.3} \right),\left( {0.6,0.1} \right)} \right)$ and $\tilde{\psi } = \left( {\left( {0.8,0.4} \right),\left( {0.7,0.2} \right)} \right)$ in Example 1, we have already calculated that $\left| {\tilde{\xi }} \right| = 1.0840$, $\left| {\tilde{\psi }} \right| = 0.9924$, and $\tilde{\xi }\tilde{\psi } = 1.0267$. According to Eq. (10), ${\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\xi } = {\text{BNPjia}}_{{\tilde{\xi }}} \tilde{\psi } = \left( {\frac{1.0267 + 1.0840 \times 0.9924}{{2 \times 1.0840 \times 0.9924}}} \right)^{4} = 0.9119$, ${\text{BNPjia}}_{{\tilde{\xi }}} \tilde{\xi } = {\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\psi } = 1$ and ${\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\xi } < {\text{BNPjia}}_{{\tilde{\psi }}} \tilde{\psi }$. These outcomes comply with the principles of RO1 ~ RO4, which is precisely what we expected.

Equation (10) can resolve the various problems encountered in Examples 1 ~ 2 and can be extended to more generic situations where we define the bidirectional normalized projection of one decision matrix onto another as follows.

Definition 7

Let ${\varvec{X}}={\left({x}_{kj}\right)}_{t\times n}$ and ${\varvec{Y}}={\left({y}_{kj}\right)}_{t\times n}$ be two $t\times n$ $q$-rung orthopair fuzzy matrices ($q$-ROFMs), then

$$ BNPjia_{Y} X = \left( {\frac{XY + \left| X \right|\left| Y \right|}{{2\left| X \right|\left| Y \right|}}} \right)^{\sigma } $$

(11)

is the bidirectional normalized projection measure between matrix $X$ and $Y$, where $x_{kj} = \left( {\left( {\mu_{Qx} } \right)_{kj} ,\left( {\nu_{Qx} } \right)_{kj} } \right)$ and $y_{kj} = \left( {\left( {\mu_{Qy} } \right)_{kj} ,\left( {\nu_{Qy} } \right)_{kj} } \right)$ are $q$-ROFNs $\left( {k = 1,2, \cdots ,t;j = 1,2, \cdots ,n} \right)$. $XY = \mathop \sum \limits_{k = 1}^{t} \mathop \sum \limits_{j = 1}^{n} \left( {\left( {\mu_{Qx} } \right)_{kj} } \right)^{q} \left( {\left( {\mu_{Qy} } \right)_{kj} } \right)^{q} + \left( {\left( {\nu_{Qx} } \right)_{kj} } \right)^{q} \left( {\left( {\nu_{Qy} } \right)_{kj} } \right)^{q} + \left( {\left( {\pi_{Qx} } \right)_{kj} } \right)^{q} \left( {\left( {\pi_{Qy} } \right)_{kj} } \right)^{q}$ is the inner product of $X$ and $Y$, $\left| X \right| = \sqrt {\mathop \sum \limits_{k = 1}^{t} \mathop \sum \limits_{j = 1}^{n} \left( {\left( {\mu_{Qx} } \right)_{kj} } \right)^{2q} + \left( {\left( {\nu_{Qx} } \right)_{kj} } \right)^{2q} + \left( {\left( {\pi_{Qx} } \right)_{kj} } \right)^{2q} }$ is the module of $X$, $\left| Y \right| = \sqrt {\mathop \sum \limits_{k = 1}^{t} \mathop \sum \limits_{j = 1}^{n} \left( {\left( {\mu_{Qy} } \right)_{kj} } \right)^{2q} + \left( {\left( {\nu_{Qy} } \right)_{kj} } \right)^{2q} + \left( {\left( {\pi_{Qy} } \right)_{kj} } \right)^{2q} }$ is the module of $Y$, $\left( {\pi_{Qx} } \right)_{kj} = \sqrt[q]{{1 - \left( {\left( {\mu_{Qx} } \right)_{kj} } \right)^{q} - \left( {\left( {\nu_{Qx} } \right)_{kj} } \right)^{q} }}$, $\left( {\pi_{Qy} } \right)_{kj} = \sqrt[q]{{1 - \left( {\left( {\mu_{Qy} } \right)_{kj} } \right)^{q} - \left( {\left( {\nu_{Qy} } \right)_{kj} } \right)^{q} }}$, and $\sigma$ is the distinguishing index mentioned above.

5 Presented MAGDM methodology

Based on the proposed bidirectional normalized projection measure and TOPSIS framework, this section develops a new MAGDM methodology under $q$-rung orthopair fuzzy environment.

Let $A=\left\{{A}_{i}|i\in M\right\}$ be a set of alternatives (assessment objectives), where $M=\left\{\mathrm{1,2},\cdots ,m\right\}$; let $U=\left\{{u}_{j}|j\in N\right\}$ be a set of attributes (criteria), where $N=\left\{\mathrm{1,2},\cdots ,n\right\}$; let ${\varvec{w}}=\left({w}_{1},{w}_{2},\cdots ,{w}_{n}\right)$ be an attributes’ weight vector with $0\le {w}_{j}\le 1(j\in N)$ and $\sum_{j=1}^{n}{w}_{j}=1$; let $D=\left\{{d}_{k}|k\in T\right\}$ be a set of DMs (experts), where $T=\left\{\mathrm{1,2},\cdots ,t\right\}$.

The $i$th alternative in set $A$ is evaluated by t DMs with respect to $n$ attributes, which can be described by the following multiattribute group decision matrix:

$${{\varvec{X}}}_{{\varvec{i}}}=\begin{array}{cc}& \begin{array}{ccc}\begin{array}{cc}{u}_{1} & {u}_{2}\end{array}& \cdots & \begin{array}{ccc}{ u}_{j}& \cdots & { u}_{n}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{c}{d}_{1}\\ {d}_{2}\end{array}\\ \begin{array}{c}\vdots \\ {d}_{k}\\ \vdots \end{array}\\ {d}_{t}\end{array}& \left(\begin{array}{ccc}\begin{array}{c}\begin{array}{cc}{x}_{11}^{i}& {x}_{12}^{i}\end{array}\\ \begin{array}{cc}{x}_{21}^{i}& {x}_{22}^{i}\end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}\cdots & {x}_{1j}^{i}& \cdots \end{array}\\ \begin{array}{ccc}\cdots & {x}_{2j}^{i}& \cdots \end{array}\end{array}& \begin{array}{c}{x}_{1n}^{i}\\ {x}_{2n}^{i}\end{array}\\ \begin{array}{cc}\begin{array}{c}\vdots \\ {x}_{k1}^{i}\\ \vdots \end{array}& \begin{array}{c}\vdots \\ {x}_{k2}^{i}\\ \vdots \end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}\vdots & \vdots & \vdots \end{array}\\ \begin{array}{ccc}\cdots & {x}_{kj}^{i}& \cdots \end{array}\\ \begin{array}{ccc}\vdots & \vdots & \vdots \end{array}\end{array}& \begin{array}{c}\vdots \\ {x}_{kn}^{i}\\ \vdots \end{array}\\ \begin{array}{cc}{x}_{t1}^{i}& {x}_{t2}^{i}\end{array}& \begin{array}{ccc}\cdots & {x}_{tj}^{i}& \cdots \end{array}& {x}_{tn}^{i}\end{array}\right)\end{array},i\in M,$$

(12)

where ${{\varvec{X}}}_{{\varvec{i}}}={\left({x}_{kj}^{i}\right)}_{t\times n}(i\in M)$ is $q$-ROFM, ${x}_{kj}^{i}(j\in N,k\in T)$ is the attribute value delivered by $k$ th DM and characterized by $q$-ROFN $\left({\left({\mu }_{Qx}\right)}_{kj}^{i},{\left({\nu }_{Qx}\right)}_{kj}^{i}\right)$, where the ${\left({\mu }_{Qx}\right)}_{kj}^{i}$, ${\left({\nu }_{Qx}\right)}_{kj}^{i}$ express the membership (agreeing, approving) degree and non-membership (disagreeing, disapproving) degree of alternative ${A}_{i}$ on the relevant attribute ${u}_{j}$, respectively. In addition, ${\left({\pi }_{Qx}\right)}_{kj}^{i}=\sqrt[q]{1-{\left({\left({\mu }_{Qx}\right)}_{kj}^{i}\right)}^{q}-{\left({\left({\nu }_{Qx}\right)}_{kj}^{i}\right)}^{q}}$ expresses the hesitation degree. Then the weighted multiattribute group decision matrix of the $i$ th alternative is determined by:

$${{\varvec{Y}}}_{{\varvec{i}}}=\begin{array}{cc}& \begin{array}{ccc}\begin{array}{cc}{u}_{1} & {u}_{2}\end{array}& \cdots & \begin{array}{ccc}{ u}_{j}& \cdots & { u}_{n}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{c}{d}_{1}\\ {d}_{2}\end{array}\\ \begin{array}{c}\vdots \\ {d}_{k}\\ \vdots \end{array}\\ {d}_{t}\end{array}& \left(\begin{array}{ccc}\begin{array}{c}\begin{array}{cc}{y}_{11}^{i}& {y}_{12}^{i}\end{array}\\ \begin{array}{cc}{y}_{21}^{i}& {y}_{22}^{i}\end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}\cdots & {y}_{1j}^{i}& \cdots \end{array}\\ \begin{array}{ccc}\cdots & {y}_{2j}^{i}& \cdots \end{array}\end{array}& \begin{array}{c}{y}_{1n}^{i}\\ {y}_{2n}^{i}\end{array}\\ \begin{array}{cc}\begin{array}{c}\vdots \\ {y}_{k1}^{i}\\ \vdots \end{array}& \begin{array}{c}\vdots \\ {y}_{k2}^{i}\\ \vdots \end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}\vdots & \vdots & \vdots \end{array}\\ \begin{array}{ccc}\cdots & {y}_{kj}^{i}& \cdots \end{array}\\ \begin{array}{ccc}\vdots & \vdots & \vdots \end{array}\end{array}& \begin{array}{c}\vdots \\ {y}_{kn}^{i}\\ \vdots \end{array}\\ \begin{array}{cc}{y}_{t1}^{i}& {y}_{t2}^{i}\end{array}& \begin{array}{ccc}\cdots & {y}_{tj}^{i}& \cdots \end{array}& {y}_{tn}^{i}\end{array}\right)\end{array},i\in M,$$

(13)

where ${{\varvec{Y}}}_{{\varvec{i}}}={\left({y}_{kj}^{i}\right)}_{t\times n}(i\in M)$ is $q$-ROFM, ${y}_{kj}^{i}=\left({\left({\mu }_{Qy}\right)}_{kj}^{i},{\left({\nu }_{Qy}\right)}_{kj}^{i}\right)=\left({\left(1-{\left(1-{\left({\left({\mu }_{Qx}\right)}_{kj}^{i}\right)}^{q}\right)}^{{w}_{j}}\right)}^{1/q},{\left({\left({\nu }_{Qx}\right)}_{kj}^{i}\right)}^{{w}_{j}}\right)(j\in N,k\in T)$ by Definition 4.

According to the idea of TOPSIS, throughout all the weighted multiattribute group decision matrices ${{\varvec{Y}}}_{{\varvec{i}}}(i\in M)$, PIS is determined by

$${{\varvec{Y}}}_{+}=\begin{array}{cc}& \begin{array}{ccc}\begin{array}{cc}{u}_{1} & {u}_{2}\end{array}& \cdots & \begin{array}{ccc}{ u}_{j}& \cdots & { u}_{n}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{c}{d}_{1}\\ {d}_{2}\end{array}\\ \begin{array}{c}\vdots \\ {d}_{k}\\ \vdots \end{array}\\ {d}_{t}\end{array}& \left(\begin{array}{ccc}\begin{array}{c}\begin{array}{cc}{y}_{11}^{+}& {y}_{12}^{+}\end{array}\\ \begin{array}{cc}{y}_{21}^{+}& {y}_{22}^{+}\end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}\cdots & {y}_{1j}^{+}& \cdots \end{array}\\ \begin{array}{ccc}\cdots & {y}_{2j}^{+}& \cdots \end{array}\end{array}& \begin{array}{c}{y}_{1n}^{+}\\ {y}_{2n}^{+}\end{array}\\ \begin{array}{cc}\begin{array}{c}\vdots \\ {y}_{k1}^{+}\\ \vdots \end{array}& \begin{array}{c}\vdots \\ {y}_{k2}^{+}\\ \vdots \end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}\vdots & \vdots & \vdots \end{array}\\ \begin{array}{ccc}\cdots & {y}_{kj}^{+}& \cdots \end{array}\\ \begin{array}{ccc}\vdots & \vdots & \vdots \end{array}\end{array}& \begin{array}{c}\vdots \\ {y}_{kn}^{+}\\ \vdots \end{array}\\ \begin{array}{cc}{y}_{t1}^{+}& {y}_{t2}^{+}\end{array}& \begin{array}{ccc}\cdots & {y}_{tj}^{+}& \cdots \end{array}& {y}_{tn}^{+}\end{array}\right)\end{array},$$

(14)

and NIS is determined by

$${{\varvec{Y}}}_{-}=\begin{array}{cc}& \begin{array}{ccc}\begin{array}{cc}{u}_{1} & {u}_{2}\end{array}& \cdots & \begin{array}{ccc}{ u}_{j}& \cdots & { u}_{n}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{c}{d}_{1}\\ {d}_{2}\end{array}\\ \begin{array}{c}\vdots \\ {d}_{k}\\ \vdots \end{array}\\ {d}_{t}\end{array}& \left(\begin{array}{ccc}\begin{array}{c}\begin{array}{cc}{y}_{11}^{-}& {y}_{12}^{-}\end{array}\\ \begin{array}{cc}{y}_{21}^{-}& {y}_{22}^{-}\end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}\cdots & {y}_{1j}^{-}& \cdots \end{array}\\ \begin{array}{ccc}\cdots & {y}_{2j}^{-}& \cdots \end{array}\end{array}& \begin{array}{c}{y}_{1n}^{-}\\ {y}_{2n}^{-}\end{array}\\ \begin{array}{cc}\begin{array}{c}\vdots \\ {y}_{k1}^{-}\\ \vdots \end{array}& \begin{array}{c}\vdots \\ {y}_{k2}^{-}\\ \vdots \end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}\vdots & \vdots & \vdots \end{array}\\ \begin{array}{ccc}\cdots & {y}_{kj}^{-}& \cdots \end{array}\\ \begin{array}{ccc}\vdots & \vdots & \vdots \end{array}\end{array}& \begin{array}{c}\vdots \\ {y}_{kn}^{-}\\ \vdots \end{array}\\ \begin{array}{cc}{y}_{t1}^{-}& {y}_{t2}^{-}\end{array}& \begin{array}{ccc}\cdots & {y}_{tj}^{-}& \cdots \end{array}& {y}_{tn}^{-}\end{array}\right)\end{array}.$$

(15)

If ${u}_{j}$ is benefit attribute, then ${y}_{kj}^{+}=\left({\left({\mu }_{Qy}\right)}_{kj}^{+},{\left({\nu }_{Qy}\right)}_{kj}^{+}\right)=\left(\underset{1\le i\le m}{\mathrm{max}}\left({\left({\mu }_{Qy}\right)}_{kj}^{i}\right),\underset{1\le i\le m}{\mathrm{min}}\left({\left({\nu }_{Qy}\right)}_{kj}^{i}\right)\right)$ and ${y}_{kj}^{-}=\left({\left({\mu }_{Qy}\right)}_{kj}^{-},{\left({\nu }_{Qy}\right)}_{kj}^{-}\right)=\left(\underset{1\le i\le m}{\mathrm{min}}\left({\left({\mu }_{Qy}\right)}_{kj}^{i}\right),\underset{1\le i\le m}{\mathrm{max}}\left({\left({\nu }_{Qy}\right)}_{kj}^{i}\right)\right)$. If ${u}_{j}$ is cost attribute, then ${y}_{kj}^{+}=\left({\left({\mu }_{Qy}\right)}_{kj}^{+},{\left({\nu }_{Qy}\right)}_{kj}^{+}\right)=\left(\underset{1\le i\le m}{\mathrm{min}}\left({\left({\mu }_{Qy}\right)}_{kj}^{i}\right),\underset{1\le i\le m}{\mathrm{max}}\left({\left({\nu }_{Qy}\right)}_{kj}^{i}\right)\right)$ and ${y}_{kj}^{-}=\left({\left({\mu }_{Qy}\right)}_{kj}^{-},{\left({\nu }_{Qy}\right)}_{kj}^{-}\right)=\left(\underset{1\le i\le m}{\mathrm{max}}\left({\left({\mu }_{Qy}\right)}_{kj}^{i}\right),\underset{1\le i\le m}{\mathrm{min}}\left({\left({\nu }_{Qy}\right)}_{kj}^{i}\right)\right)$.

After that, the closeness of weighted multiattribute group decision matrix ${Y}_{i}(i\in M)$ with PIS or NIS can be calculated according to Eq. (11) as follows:

$$ BNPjia_{{Y_{ + } }} Y_{i} = \left( {\frac{{Y_{i} Y_{ + } + \left| {Y_{i} } \right|\left| {Y_{ + } } \right|}}{{2\left| {Y_{i} } \right|\left| {Y_{ + } } \right|}}} \right)^{\sigma } , $$

(16)

$$ BNPjia_{{Y_{ - } }} Y_{i} = \left( {\frac{{Y_{i} Y_{ - } + \left| {Y_{i} } \right|\left| {Y_{ - } } \right|}}{{2\left| {Y_{i} } \right|\left| {Y_{ - } } \right|}}} \right)^{\sigma } , $$

(17)

where ${Y}_{i}{Y}_{+}=\sum_{k=1}^{t}\sum_{j=1}^{n}\left({\left({\left({\mu }_{Qy}\right)}_{kj}^{i}\right)}^{q}{\left({\left({\mu }_{Qy}\right)}_{kj}^{+}\right)}^{q}+{\left({\left({\nu }_{Qy}\right)}_{kj}^{i}\right)}^{q}{\left({\left({\nu }_{Qy}\right)}_{kj}^{+}\right)}^{q}+{\left({\left({\pi }_{Qy}\right)}_{kj}^{i}\right)}^{q}{\left({\left({\pi }_{Qy}\right)}_{kj}^{+}\right)}^{q}\right)$,

$$\left|{Y}_{i}\right|=\sqrt{\sum_{k=1}^{t}\sum_{j=1}^{n}\left({\left({\left({\mu }_{Qy}\right)}_{kj}^{i}\right)}^{2q}+{\left({\left({\nu }_{Qy}\right)}_{kj}^{i}\right)}^{2q}+{\left({\left({\pi }_{Qy}\right)}_{kj}^{i}\right)}^{2q}\right)}$$

$$\left|{Y}_{+}\right|=\sqrt{\sum_{k=1}^{t}\sum_{j=1}^{n}\left({\left({\left({\mu }_{Qy}\right)}_{kj}^{+}\right)}^{2q}+{\left({\left({\nu }_{Qy}\right)}_{kj}^{+}\right)}^{2q}+{\left({\left({\pi }_{Qy}\right)}_{kj}^{+}\right)}^{2q}\right)}$$

, ${\left({\pi }_{Qy}\right)}_{kj}^{i}=\sqrt[q]{1-{\left({\left({\mu }_{Qy}\right)}_{kj}^{i}\right)}^{q}-{\left({\left({\nu }_{Qy}\right)}_{kj}^{i}\right)}^{q}}$, and ${\left({\pi }_{Qy}\right)}_{kj}^{+}=\sqrt[q]{1-{\left({\left({\mu }_{Qy}\right)}_{kj}^{+}\right)}^{q}-{\left({\left({\nu }_{Qy}\right)}_{kj}^{+}\right)}^{q}}$. ${Y}_{i}{Y}_{-}$, $\left|{Y}_{-}\right|$, and ${\left({\pi }_{Qy}\right)}_{kj}^{-}$ are the same as ${Y}_{i}{Y}_{+}$, $\left|{Y}_{+}\right|$, and ${\left({\pi }_{Qy}\right)}_{kj}^{+}$, except all the “$+$” in the corner notations are replaced by “$-$”.

Finally, every alternative ${A}_{i}$ in the set $A$ can be ranked according to the following priority factor:

$$ PF_{i} = \frac{{BNPjia_{{Y_{ + } }} Y_{i} }}{{BNPjia_{{Y_{ + } }} Y_{i} + BNPjia_{{Y_{ - } }} Y_{i} }},i \in M. $$

(18)

The larger the value of ${PF}_{i}$, the closer the ${A}_{i}$ is to PIS, the farther the ${A}_{i}$ is from NIS; consequently, the superior the ${A}_{i}$ is to others.

For clarity, the presented MAGDM algorithm based on above-mentioned extended TOPSIS method and bidirectional normalized projection measure with $q$-rung orthopair fuzzy information is depicted in Fig. 3.

Fig. 3

Schematic diagram of the presented MAGDM methodology

6 Experimental analysis

This section provides an actual evaluation of ship equipment reliability conducted on a teaching-practice ship Yukun of Dalian Maritime University in Liaoning, China. A comparative analysis with current techniques is also prepared to validate the feasibility and practicability of the methodology suggested in this paper.

6.1 Illustrative example

In this application, four sets of equipment on the teaching-practice ship are evaluated and denoted by set $A=\left\{{A}_{1},{A}_{2},{A}_{3},{A}_{4}\right\}$. Four experts (DMs) are from the marine engine department, the maritime safety agency, the shipyard, and the ship management company. DMs comprise a set denoted by $D=\left\{{d}_{1},{d}_{2},{d}_{3},{d}_{4}\right\}$. The evaluation verdicts are delivered by experts through a questionnaire survey and characterized by $q$-ROFNs ($q=3$). The evaluation criteria (attributes) are summarized based on the concerns of all experts and written as $U=\left\{{u}_{1},{u}_{2},{u}_{3},{u}_{4}\right\}=\left\{\mathrm{average trouble}-\mathrm{free running time},\mathrm{quickness of repair process},\mathrm{spare parts cost},\mathrm{ easiness of repair process}\right\}$. The “average trouble-free running time” indicates the capability of the ship equipment to work stably, which is a benefit attribute. The “quickness of repair process” indicates the capability of rapid recovery after the ship equipment fault, which is a benefit attribute. The “$\mathrm{spare parts cost}$” indicates the economic cost of spare parts prepared for possible faults, which is a cost attribute. The “easiness of repair process” indicates the capability of easy recovery after the ship equipment fault, which is a benefit attribute.

The evaluation procedures are based on the schematic in Fig. 3. The original multiattribute group decision matrices ${{\varvec{X}}}_{1}$, ${{\varvec{X}}}_{2}$, ${{\varvec{X}}}_{3}$, and ${{\varvec{X}}}_{4}$ for the four sets of ship equipment established from Step 3 are shown in Table 2.

Table 2 Original multiattribute group decision matrices

In Table 2, the element ${x}_{kj}^{i}=\left({\left({\mu }_{Qx}\right)}_{kj}^{i},{\left({\nu }_{Qx}\right)}_{kj}^{i}\right)$ in ${X}_{i}$ is $q$-ROFN. Since ${u}_{1}$, ${u}_{2}$, and ${u}_{4}$ are benefit attributes, consequently, the larger the ${\left({\mu }_{Qx}\right)}_{k1}^{i}$, ${\left({\mu }_{Qx}\right)}_{k2}^{i}$, and ${\left({\mu }_{Qx}\right)}_{k4}^{i}$, the smaller the ${\left({\nu }_{Qx}\right)}_{k1}^{i}$, ${\left({\nu }_{Qx}\right)}_{k2}^{i}$, and ${\left({\nu }_{Qx}\right)}_{k4}^{i}$, the better the attribute performance. Since ${u}_{3}$ is a cost attribute, the smaller the ${\left({\mu }_{Qx}\right)}_{k3}^{i}$, the larger the ${\left({\nu }_{Qx}\right)}_{k3}^{i}$, the better the attribute performance.

In this application case, the $q$ value is assigned as 3, which is not pre-specified before the expert scoring. Instead, it is found during data statistics that if $q=1$, the underlined data in Table 2 are beyond the processing range due to ${\left({\mu }_{Qx}\right)}_{kj}^{i}+{\left({\nu }_{Qx}\right)}_{kj}^{i}>1$. If $q=2$, the double-underlined data in Table 2 are still beyond the processing range due to ${\left({\left({\mu }_{Qx}\right)}_{kj}^{i}\right)}^{2}+{\left({\left({\nu }_{Qx}\right)}_{kj}^{i}\right)}^{2}>1$. Only when the $q$ value is increased to 3, all the data in Table 2 are captured due to ${\left({\left({\mu }_{Qx}\right)}_{kj}^{i}\right)}^{3}+{\left({\left({\nu }_{Qx}\right)}_{kj}^{i}\right)}^{3}\le 1$, which demonstrates the flexibility and adaptability of the proposed methodology in data collection and processing.

In general, the selection method of the $q$ value should start from 1 and gradually increase $\left(\mathrm{1,2},3,\cdots \right)$ until all pending data are included in the processing range of $q$-ROFN.

For the attributes’ weight vector ${\varvec{w}}=\left({w}_{1},{w}_{2},{w}_{3},{w}_{4}\right)=\left(0.3, 0.2, 0.2, 0.3\right)$ given by DMs based on discussion and negotiation, the weighted multiattribute group decision matrices ${{\varvec{Y}}}_{1}$, ${{\varvec{Y}}}_{2}$, ${{\varvec{Y}}}_{3}$, and ${{\varvec{Y}}}_{4}$ are constructed by Step 4 of the schematic diagram, which are shown in Table 3.

Table 3 Weighted multiattribute group decision matrices

By Step 5 of the schematic diagram, the PIS ${{\varvec{Y}}}_{+}$ and NIS ${{\varvec{Y}}}_{-}$ are calculated and shown in Table 4.

Table 4 PIS and NIS

Then, the bidirectional normalized projections $BNPjia_{{Y_{ + } }} Y_{i}$ and ${\text{BNPjia}}_{{Y_{ - } }} Y_{i}$ of each weighted multiattribute group decision ${{\varvec{Y}}}_{{\varvec{i}}}$ onto the ideal solutions ${{\varvec{Y}}}_{+}$ and ${{\varvec{Y}}}_{-}$ are calculated by Step 6. The priority factors ${PF}_{i}$ of each ship equipment ${A}_{i}$ are calculated by Step 7. The reliability ranking given by Step 8 and relevant calculation results are summarized in Table 5.

Table 5 Bidirectional normalized projections, priority factors, and rankings

The reliability preference order is $A_{2} \succ A_{3} \succ A_{1} \succ A_{4}$, indicating that ship equipment $A_{2}$ is the best, followed by $A_{3}$, $A_{1}$, and $A_{4}$, where “$\succ$” stands for “better than”. In addition, it is worth noting that $BNPjia_{{Y_{ + } }} Y_{i}$ and $BNPjia_{{Y_{ - } }} Y_{i}$ are two other different parameters also reflecting the alternatives' priority. On one hand, the larger the $BNPjia_{{Y_{ + } }} Y_{i}$ value, the closer the alternative is to PIS, the superior the equipment reliability. The ranking result according to $BNPjia_{{Y_{ + } }} Y_{i}$ is $0.996 > 0.888 > 0.707 > 0.619$, that is $A_{2} \succ A_{3} \succ A_{1} \succ A_{4}$. On the other hand, the smaller the $BNPjia_{{Y_{ - } }} Y_{i}$ value, the farther the alternative is to NIS, the superior the equipment reliability. The ranking result according to $BNPjia_{{Y_{ - } }} Y_{i}$ is $0.600 < 0.760 < 0.911 < 0.987$, that is $A_{2} \succ A_{3} \succ A_{1} \succ A_{4}$. Therefore, the reliability preference order based on $BNPjia_{{Y_{ + } }} Y_{i}$ and $BNPjia_{{Y_{ - } }} Y_{i}$ are consistent with $PF_{i}$, which demonstrates the robustness of the proposed methodology in this paper.

6.2 Static comparison with current normalized projection measures

This subsection provides static comparisons with current normalized projection measures. The experimental data are based on the same illustrative example described in Sect. 6.1, as shown in Table 2. The multiattribute group decision making procedure is identical to the schematic in Fig. 3, but the bidirectional normalized projection measure Eq. (11), which is the crux of the proposed methodology, is replaced by other models.

As stated above, Eqs. (7), (8), and (9) are three normalized projection measures proposed in recent literature, and then we will compare our method with each of them, respectively.

According to Eq. (7), our projection measure Eq. (11) will be replaced by

$$ NPyueI_{Y} X = \frac{{\left| X \right|^{2} + \left| Y \right|^{2} }}{{\left| X \right|^{2} + \left| Y \right|^{2} + \left| {XY - \left| Y \right|^{2} } \right|}}, $$

(19)

where $\left| X \right|$, $\left| Y \right|$, and $XY$ are the same as Eq. (11). Consequently, Eq. (16) of Step 6.1 in the schematic is replaced by

$$ NPyueI_{{Y_{ + } }} Y_{i} = \frac{{\left| {Y_{i} } \right|^{2} + \left| {Y_{ + } } \right|^{2} }}{{\left| {Y_{i} } \right|^{2} + \left| {Y_{ + } } \right|^{2} + \left| {Y_{i} Y_{ + } - \left| {Y_{ + } } \right|^{2} } \right|}}, $$

(20)

Equation (17) of Step 6.2 in the schematic is replaced by

$$ NPyueI_{{Y_{ - } }} Y_{i} = \frac{{\left| {Y_{i} } \right|^{2} + \left| {Y_{ - } } \right|^{2} }}{{\left| {Y_{i} } \right|^{2} + \left| {Y_{ - } } \right|^{2} + \left| {Y_{i} Y_{ - } - \left| {Y_{ - } } \right|^{2} } \right|}}, $$

(21)

and Eq. (18) of Step 7 in the schematic is replaced by

$$ PFyueI_{i} = \frac{{NPyueI_{{Y_{ + } }} Y_{i} }}{{NPyueI_{{Y_{ + } }} Y_{i} + NPyueI_{{Y_{ - } }} Y_{i} }}. $$

(22)

Finally, the normalized projections $NPyueI_{{Y_{ + } }} Y_{i}$ and $NPyueI_{{Y_{ - } }} Y_{i}$ of each weighted multiattribute group decision $Y_{i}$ onto the ideal solutions $Y_{ + }$ and $Y_{ - }$, the priority factors $PFyueI_{i}$ of each ship equipment $A_{i}$, and the reliability ranking are calculated and summarized in Table 6.

Table 6 Normalized projections, priority factor, and ranking based on $NPyueI$

Table 6 shows that the reliability order is ${A}_{2}\succ {A}_{3}\succ {A}_{1}\succ {A}_{4}$, indicating that ship equipment ${A}_{2}$ is the best, followed by ${A}_{3}$, ${A}_{1}$, and ${A}_{4}$, which is entirely consistent with the conclusion in Table 5.

Analogously, according to Eq. (8), our projection measure Eq. (11) will be replaced by

$$ NPyueII_{Y} X = \frac{{\min \left\{ {XY,\left| Y \right|^{2} } \right\}}}{{\max \left\{ {XY,\left| Y \right|^{2} } \right\}}}, $$

(23)

where $XY$ and $\left| Y \right|$ are the same as Eq. (11). Consequently, Eq. (16) of Step 6.1 in the schematic is replaced by

$$ NPyueII_{{Y_{ + } }} Y_{i} = \frac{{\min \left\{ {Y_{i} Y_{ + } ,\left| {Y_{ + } } \right|^{2} } \right\}}}{{\max \left\{ {Y_{i} Y_{ + } ,\left| {Y_{ + } } \right|^{2} } \right\}}}, $$

(24)

Equation (17) of Step 6.2 in the schematic is replaced by

$$ NPyueII_{{Y_{ - } }} Y_{i} = \frac{{\min \left\{ {Y_{i} Y_{ - } ,\left| {Y_{ - } } \right|^{2} } \right\}}}{{\max \left\{ {Y_{i} Y_{ - } ,\left| {Y_{ - } } \right|^{2} } \right\}}}, $$

(25)

and Eq. (18) of Step 7 in the schematic is replaced by

$$ PFyueII_{i} = \frac{{NPyueII_{{Y_{ + } }} Y_{i} }}{{NPyueII_{{Y_{ + } }} Y_{i} + NPyueII_{{Y_{ - } }} Y_{i} }}. $$

(26)

Finally, the normalized projections $NPyueII_{{Y_{ + } }} Y_{i}$ and $NPyueII_{{Y_{ - } }} Y_{i}$ of each weighted multiattribute group decision $Y_{i}$ onto the ideal solutions $Y_{ + }$ and $Y_{ - }$, the priority factors $PFyueII_{i}$ of each ship equipment $A_{i}$, and the reliability ranking are calculated and summarized in Table 7.

Table 7 Normalized projections, priority factor, and ranking based on $NPyueII$

Table 7 shows that the reliability order is ${A}_{2}\succ {A}_{3}\succ {A}_{1}\succ {A}_{4}$, indicating that ship equipment ${A}_{2}$ is the best, followed by ${A}_{3}$, ${A}_{1}$, and ${A}_{4}$, which is also entirely consistent with the conclusion in Table 5.

Similarly, according to Eq. (9), our projection measure Eq. (11) will be replaced by

$$ NPliu_{Y} X = \frac{{\frac{XY}{{\left| Y \right|}}}}{{\frac{XY}{{\left| Y \right|}} + \left| {\left| Y \right| - \frac{XY}{{\left| Y \right|}}} \right|}}, $$

(27)

where $XY$ and $\left| Y \right|$ are the same as Eq. (11). Consequently, Eq. (16) of Step 6.1 in the schematic is replaced by

$$ NPliu_{{Y_{ + } }} Y_{i} = \frac{{\frac{{Y_{i} Y_{ + } }}{{\left| {Y_{ + } } \right|}}}}{{\frac{{Y_{i} Y_{ + } }}{{\left| {Y_{ + } } \right|}} + \left| {\left| {Y_{ + } } \right| - \frac{{Y_{i} Y_{ + } }}{{\left| {Y_{ + } } \right|}}} \right|}}, $$

(28)

Equation (17) of Step 6.2 in the schematic is replaced by

$$ NPliu_{{Y_{ - } }} Y_{i} = \frac{{\frac{{Y_{i} Y_{ - } }}{{\left| {Y_{ - } } \right|}}}}{{\frac{{Y_{i} Y_{ - } }}{{\left| {Y_{ - } } \right|}} + \left| {\left| {Y_{ - } } \right| - \frac{{Y_{i} Y_{ - } }}{{\left| {Y_{ - } } \right|}}} \right|}}, $$

(29)

and Eq. (18) of Step 7 in the schematic is replaced by

$$ PFliu_{i} = \frac{{NPliu_{{Y_{ + } }} Y_{i} }}{{NPliu_{{Y_{ + } }} Y_{i} + NPliu_{{Y_{ - } }} Y_{i} }}. $$

(30)

Finally, the normalized projections $NPliu_{{Y_{ + } }} Y_{i}$ and $NPliu_{{Y_{ - } }} Y_{i}$ of each weighted multiattribute group decision $Y_{i}$ onto the ideal solutions $Y_{ + }$ and $Y_{ - }$, the priority factors $PFliu_{i}$ of each ship equipment $A_{i}$, and the reliability ranking are calculated and summarized in Table 8.

Table 8 Normalized projections, priority factor, and ranking based on $NPliu$

Table 8 shows that the reliability order is ${A}_{2}\succ {A}_{3}\succ {A}_{1}\succ {A}_{4}$, indicating that ship equipment ${A}_{2}$ is the best, followed by ${A}_{3}$, ${A}_{1}$, and ${A}_{4}$, which is still entirely consistent with the conclusion in Table 5. Furthermore, although Eqs. (27) and (23) are different normalized projection methods, they compute identical results (including all the calculated results in Tables 7 and 8) from the decision information collected in Sect. 6.1. The reason is that the numerator and denominator of Eq. (27) can be transformed into $\frac{XY}{{XY + \left| {\left| Y \right|^{2} - XY} \right|}}$ after multiplying by $\left| Y \right|$($\left| Y \right| \ne 0$) at the same time and $\left| Y \right|^{2}$ is always greater than ${\varvec{XY}}$ for the data being processed. Therefore, Eq. (27) can be further reduced to $\frac{XY}{{\left| Y \right|^{2} }}$, which is just in accordance with the result obtained by Eq. (23) when $\left| Y \right|^{2}$ is greater than $XY$.

Through the above analysis, we can say that the proposed methodology in this paper is compatible with current techniques, and its conclusions are entirely supported by existing projection models.

6.3 Dynamic comparison with current normalized projection measures

To further investigate the stability and robustness of the proposed bidirectional normalized projection measure when the decision information changes, this subsection extends the static comparison of Sect. 6.2 to the dynamic environment. The experimental data are also from the same illustrative example described in Sect. 6.1, as shown in Table 2.

Suppose the decision verdict of ship equipment ${A}_{1}$ given by the first expert ${d}_{1}$ with respect to the first attribute ${u}_{1}$ is a dynamic parameter. That is to say, the element ${x}_{11}^{1}=\left({\left({\mu }_{Qx}\right)}_{11}^{1},{\left({\nu }_{Qx}\right)}_{11}^{1}\right)$ in decision matrix ${{\varvec{X}}}_{1}$ (the bolded and italicized data in Table 2) is a variable, where ${\left({\mu }_{Qx}\right)}_{11}^{1}\in \left[\mathrm{0,1}\right]$ and ${\left({\nu }_{Qx}\right)}_{11}^{1}=\sqrt[3]{1-{\left({\left({\mu }_{Qx}\right)}_{11}^{1}\right)}^{3}}$ to satisfy the constraint of $q$-ROFN ($q=3$). Other decision data in Table 2 remain unchanged.

To present a clear graph, the horizontal coordinate of the ranking curve is mapped to another variable $\varphi$, such that ${\left({\mu }_{Qx}\right)}_{11}^{1}=\frac{\varphi }{100}$, ${\left({\nu }_{Qx}\right)}_{11}^{1}=\sqrt[3]{1-{\left(\frac{\varphi }{100}\right)}^{3}}$, and $\varphi \in \left[\mathrm{0,100}\right]$. When $\varphi$ is increased from $0$ to $100$, four sets of ship equipment are evaluated by our proposed Eqs. (11), (16), (17), and (18) based on the schematic in Fig. 3, the dynamic reliability ranking of ${A}_{1}$~${A}_{4}$ is shown in Fig. 4.

Fig. 4

Dynamic ranking of ship equipment based on our method

Figure 4 shows that the reliability ranking order ${A}_{2}\succ {A}_{3}\succ {A}_{4}$ is steady as $\varphi$ increases from 0 to 100. The distances between their dynamic curves (marked by orange double arrow lines) remain stable and significant. Since the variable $\varphi$ is within ${A}_{1}$, it should be that the priority factor of ${A}_{1}$ increases as the membership degree ${\left({\mu }_{Qx}\right)}_{11}^{1}$ of benefit attribute value ${x}_{11}^{1}$ increases and the priority factors of ${A}_{2}$, ${A}_{3}$, and ${A}_{4}$ relatively decrease simultaneously. The results are valid and reasonable. Moreover, all dynamic ranking curves are monotonic over the entire definition domain, which demonstrates the robustness of the proposed methodology again in a dynamic sense.

Analogously, if four sets of ship equipment are evaluated by Eqs. (19) ~ (22) based on $NPyueI$ according to the schematic in Fig. 3, the dynamic reliability ranking of ${A}_{1}$~${A}_{4}$ is shown in Fig. 5.

Fig. 5

Dynamic ranking of ship equipment based on Eqs. (19) ~ (22)

Figure 5 shows that the dynamic reliability order relations are entirely consistent with the curves in Fig. 4. However, the distances between curves ${A}_{2}$, ${A}_{3}$, and ${A}_{4}$ (marked by orange double arrow lines) are at least 4.4 times smaller than in Fig. 4, which is not conducive to the distinction of alternatives.

Similarly, if four sets of ship equipment are evaluated by Eqs. (23) ~ (26) based on $NPyueII$ and Eqs. (27) ~ (30) based on $NPliu$ according to the schematic in Fig. 3, the dynamic reliability rankings of ${A}_{1}$~${A}_{4}$ are shown in Fig. 6 and Fig. 7, respectively.

Fig. 6

Dynamic ranking of ship equipment based on Eqs. (23) ~ (26)

Fig. 7

Dynamic ranking of ship equipment based on Eqs. (27) ~ (30)

As explained above, if the condition that $\left| Y \right|^{2} > XY$ is satisfied, then $NPyueII$ and $NPliu$ will get the same result. Therefore, you may have noticed that the dynamic curves of the reliability rankings in Figs. 6 and 7 are almost identical. The order relations of ${A}_{1}$~${A}_{4}$ are entirely consistent with the curves in Fig. 4. Although the distances between curves ${A}_{2}$, ${A}_{3}$, and ${A}_{4}$ (marked by orange double arrow lines in Figs. 6 and 7, respectively) are more significant than in Fig. 5, they are still at least 1.8 times smaller than in Fig. 4.

Through the above analysis, we can say that the proposed methodology in this paper is dynamically supported by the existing projection models and is superior to them with respect to the ability of alternative distinction.

Lastly, the $q$ value is an essential parameter in the $q$-ROFN system. The reason for $q=3$ during the above experiments is that all decision data in Table 2 can be captured at this time. However, if there is still evaluation data given by experts beyond the processing range, the $q$ value needs to be further increased. Moreover, it is known from Definition 3 that if an evaluation data can be captured by $q$-ROFN, $q=\zeta$, then this evaluation data must also be captured by $q$-ROFN, $q=\eta$ ($\eta \ge \zeta \ge 1$), since $0\le {\left({\mu }_{Q}\left(x\right)\right)}^{\eta }+{\left({\nu }_{Q}\left(x\right)\right)}^{\eta }\le {\left({\mu }_{Q}\left(x\right)\right)}^{\zeta }+{\left({\nu }_{Q}\left(x\right)\right)}^{\zeta }\le 1$. Therefore, the above dynamic experiments can be further extended to different $q$ value environments.

If the dynamic experimental procedure remains unchanged, except that the $q$ value is replaced with 5 and 7, the dynamic ranking curves of reliability for the above four methods are shown in Figs. 8 and 9, respectively.

Fig. 8

Dynamic ranking of ship equipment based on four projection measures at $q=5$

Fig. 9

Dynamic ranking of ship equipment based on four projection measures at $q=7$

As shown in Figs. 8 and 9, except for our method, all the other three measures show non-monotonic changes in the ranking values during the increase of $q$ (marked by orange circles in Fig. 8), and the larger the value of $q$, the bigger the non-monotonic deviation (marked by orange circles in Fig. 9). As the $q$ value increases, only the $BNPjia$ measure always remains monotonic, demonstrating the stability and superiority of the proposed method in maintaining monotonicity under different $q$ value environments and verifying the validity of Theorem 2.

One more thing worth noting is that the clustering tendency of ranking curves becomes more and more evident as the $q$ value increases. Especially in Fig. 9b, the clustering effect makes ${A}_{1}$ and ${A}_{4}$ almost indistinguishable in the range of $\varphi \in \left[\mathrm{0,70}\right]$. Nevertheless, our method can significantly improve the clustering phenomenon by adjusting the $\sigma$ value. For example, under the condition of $q=7$ as in Fig. 9, although our model already has the best distinguishing ability among all measures, we can still further improve its leading performance by increasing the $\sigma$ value, as shown in Fig. 10.

Fig. 10

Comparison of distinguishing ability for different projection measures

To provide a clear chart, we select three groups of the nearest distance between curves as the horizontal axis of Fig. 10 for comparison, i.e., ${A}_{2}-{A}_{3}$, ${A}_{3}-{A}_{4}$, and ${A}_{1}-{A}_{4}$, respectively. Due to the considerable difference in the numerical range, we use the relative multiple of the ranking distance as the vertical axis of Fig. 10. That is to say, in each group of comparison data, the minimum value within the group is unit 1. The multiples of the other members relative to that minimum value are marked on the vertical coordinate. It can be easily seen from Fig. 10 that the nearest distance between the most challenging ${A}_{1}$ and ${A}_{4}$ increases by 2.9 times when the $BNPjia$ method is compared to itself with the $\sigma$ value increased from 4 to 15. In addition, dynamic rankings corresponding to various $\sigma$ values are provided in Appendix B to serve as a reference for the adjustment process. Consequently, if the calculated results for a practical assessment are unsatisfactory, improvements can be made by adjusting the $\sigma$ value, further demonstrating the superiority of the explored framework.

7 Conclusions

Regarding the description method of FOs and the decision making framework discussed in the Introduction, this study has proposed a new MAGDM method based on $q$-ROFN, $q$-ROFV, and $q$-ROFM, in which the evaluation results delivered by DMs are fully portrayed and processed without aggregation operators. Regarding the similarity measure discussed in the Introduction, this study has developed an improved TOPSIS approach, in which the traditional distance measures are replaced by projection measures. Regarding the projection model discussed in the Introduction, this study has constructed a new bidirectional normalized projection measure under the $q$-rung orthopair fuzzy environment.

The main novelties and advantages of the established MAGDM method are listed as follows:

• 1. Research questions described in RQ1 ~ RQ4 are addressed by our innovative projection measure, which is not only bidirectional, normalized, and monotonic but also overcomes various deficiencies and defects of traditional projection method as well as existing projection methods in recent literature.

• 2. Under legal data conditions, the maximum degree of freedom is granted to the evaluation experts in the scoring process, and the membership and non-membership degrees assigned by them have a more extensive range of values ($\mu +\nu$ can be infinitely close to 2), thus bringing more flexibility and applicability to the evaluation framework.

• 3. The closeness of the evaluation alternatives to the PIS and NIS is measured in terms of both distance and angle to obtain a more comprehensive evaluation performance.

• 4. Through static and dynamic analyses, experimental results suggested that the proposed methodology is not only supported by current projection techniques but also superior to them with respect to the ability to distinguish alternatives and maintain monotonicity.

Besides the contributions, our model has its limitations indubitably. First, the decision information is only characterized by $q$-ROFNs. Other sophisticated information representations are not involved, which is a restriction. Subsequent studies might extend to interval-valued or linguistic environments. Second, the weight vectors for DMs and attributes are based on average and discussion, respectively, which is a constraint. Potential research might integrate weight estimation models. Finally, with regard to decision making techniques, our attention has primarily been directed towards projection and the TOPSIS. Nonetheless, it is essential to acknowledge that other promising and interesting methodologies, such as VIKOR and ELECTRE III (Chen 2021; Chen et al. 2022; Chen et al. 2023b) deserve more attention and further investigation. Future work might expand more decision making techniques in the shipping industry.

Appendices

Appendix A

The algebraic proof for Theorem 1.3 is given below.

Proof. According to Definition 3, $q \ge 1$, $0 \le \mu_{{Q\tilde{\xi }}}^{i}$, $\nu_{{Q\tilde{\xi }}}^{i}$, $\pi_{{Q\tilde{\xi }}}^{i}$, $\mu_{{Q\tilde{\psi }}}^{i}$, $\nu_{{Q\tilde{\psi }}}^{i}$, $\pi_{{Q\tilde{\psi }}}^{i} \le 1$ (where $i = 1,2, \ldots ,n$). Thus

$$ \begin{aligned} \left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right| - \tilde{\xi }\tilde{\psi } & = \sqrt {\mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{2q} } \right) \times \mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{2q} } \right)} \\ & - \sqrt {\left( {\mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{q} } \right)} \right)^{2} } , \\ \end{aligned} $$

And

$$ \mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{2q} } \right) \times \mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{2q} } \right) - \left( {\mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{q} } \right)} \right)^{2} $$

$$ = \left( {\left( {\mu_{{Q\tilde{\xi }}}^{1} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{1} } \right)^{q} - \left( {\nu_{{Q\tilde{\xi }}}^{1} } \right)^{q} \left( {\mu_{{Q\tilde{\psi }}}^{1} } \right)^{q} } \right)^{2} + \left( {\left( {\mu_{{Q\tilde{\xi }}}^{1} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{1} } \right)^{q} - \left( {\pi_{{Q\tilde{\xi }}}^{1} } \right)^{q} \left( {\mu_{{Q\tilde{\psi }}}^{1} } \right)^{q} } \right)^{2} + \cdots + \left( {\left( {\mu_{{Q\tilde{\xi }}}^{1} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{n} } \right)^{q} - \left( {\pi_{{Q\tilde{\xi }}}^{n} } \right)^{q} \left( {\mu_{{Q\tilde{\psi }}}^{1} } \right)^{q} } \right)^{2} + \left( {\left( {\nu_{{Q\tilde{\xi }}}^{1} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{1} } \right)^{q} - \left( {\pi_{{Q\tilde{\xi }}}^{1} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{1} } \right)^{q} } \right)^{2} + \left( {\left( {\nu_{{Q\tilde{\xi }}}^{1} } \right)^{q} \left( {\mu_{{Q\tilde{\psi }}}^{2} } \right)^{q} - \left( {\mu_{{Q\tilde{\xi }}}^{2} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{1} } \right)^{q} } \right)^{2} $$

$$ + \cdots + \left( {\left( {\nu_{{Q\tilde{\xi }}}^{1} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{n} } \right)^{q} - \left( {\pi_{{Q\tilde{\xi }}}^{n} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{1} } \right)^{q} } \right)^{2} + \cdots \cdots + \left( {\left( {\nu_{{Q\tilde{\xi }}}^{2} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{2} } \right)^{q} - \left( {\pi_{{Q\tilde{\xi }}}^{2} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{2} } \right)^{q} } \right)^{2} + \cdots + \left( {\left( {\nu_{{Q\tilde{\xi }}}^{2} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{n} } \right)^{q} - \left( {\pi_{{Q\tilde{\xi }}}^{n} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{2} } \right)^{q} } \right)^{2} + \cdots \cdots + \left( {\left( {\nu_{{Q\tilde{\xi }}}^{n} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{n} } \right)^{q} - \left( {\pi_{{Q\tilde{\xi }}}^{n} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{n} } \right)^{q} } \right)^{2} \ge 0. $$

A visualization of the relationship between the above variables is shown in Fig. A1.

In Fig. 11, the red arrow connects the first factorization of each squared term, the black line represents the minus sign, and the blue arrow connects the second factorization of each squared term. The result can be matched to the sum of polynomial squares.

Hence, $\mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{2q} } \right) \times \mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{2q} + \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{2q} } \right) \ge \left( {\mathop \sum \limits_{i = 1}^{n} \left( {\left( {\mu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\mu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\nu_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\nu_{{Q\tilde{\psi }}}^{i} } \right)^{q} + \left( {\pi_{{Q\tilde{\xi }}}^{i} } \right)^{q} \left( {\pi_{{Q\tilde{\psi }}}^{i} } \right)^{q} } \right)} \right)^{2}$, then $\left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right| - \tilde{\xi }\tilde{\psi } \ge 0$, that is, $\tilde{\xi }\tilde{\psi } \le \left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|$. In addition, according to Definition 6, $\tilde{\xi }\tilde{\psi },\left| {\tilde{\xi }} \right|,\left| {\tilde{\psi }} \right| \ge 0$, $\sigma = 4$. We have $0 \le \left( {\frac{{\tilde{\xi }\tilde{\psi } + \left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}{{2\left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}} \right)^{\sigma } \le \left( {\frac{{\left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right| + \left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}{{2\left| {\tilde{\xi }} \right|\left| {\tilde{\psi }} \right|}}} \right)^{\sigma } = 1$. Therefore, Theorem 1.3 holds.

Fig. 11

Variable relationships

Appendix B

Dynamic curves corresponding to various $\sigma$ values $\left(\mathrm{0.2,0.5,1},\mathrm{4,10,15,20,25,30}\right)$ under the same coordinate scale and $q$ value ($q=7$) are depicted in Fig. 12 as a reference for the adjustment process.

Fig. 12

Dynamic curves corresponding to various $\sigma$ values $\left(\mathrm{0.2,0.5,1},\mathrm{4,10,15,20,25,30}\right)$