Skip to main content
SpringerLink
Log in

q-Rung orthopair fuzzy N-soft aggregation operators and corresponding applications to multiple-attribute group decision making

  • Fuzzy systems and their mathematics
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

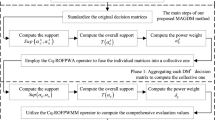
In this paper, by integrating the q-rung orthopair fuzzy set (q-ROFS) with the N-soft set, we first propose a q-rung orthopair fuzzy N-soft set (q-ROFNSS). Based on the q-ROFNSS, we explore the q-rung orthopair fuzzy N-soft weighted average (q-ROFNSWA) operator and q-rung orthopair fuzzy N-soft weighted geometric (q-ROFNSWG) operator, and investigate some properties of the q-ROFNSWG operator and q-ROFNSWG operator including idempotency, monotonicity and boundedness. Finally, two kinds of multiple-attribute group decision-making (MAGDM) methods based on q-rung orthopair fuzzy N-soft aggregation operators are established. In addition, a practical example is provided to illustrate the effectiveness and correctness of the new decision-making approaches. Through comparison with existing methods, the advantages of our method are also elaborated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data availability

The authors confirm that the data supporting the findings of this study are available within the article.

References

  • Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    Article  Google Scholar 

  • Akram M, Adeel A (2018) Fuzzy N-soft sets:a novel model with applications. J Intell Fuzzy Syst 35(4):4757–4771

    Article  Google Scholar 

  • Akram M, Ali G (2019) New decision-making hybrid model:intuitionistic fuzzy N-soft rough sets. Soft Comput 23(20):9853–9868

    Article  Google Scholar 

  • Du WS (2018) Minkowski-type distance measures for generalized orthopair fuzzy sets. Int J Intell Syst 33(4):802–817

    Article  Google Scholar 

  • Fatimah F, Rosadi D, Fajriya Hakim R.B. (2018) N-soft sets and their decision making algorithms. Soft Comput 22(12):3829–3842

    Article  Google Scholar 

  • Garg H (2017) Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int J Intell Syst 32(6):597–630

    Article  Google Scholar 

  • Hussain A (2020) q-Rung orthopair fuzzy soft average aggregation operators and their application in multicriteria decision-making. Int J Intell Syst 35(4):571–599

    Article  Google Scholar 

  • Hussain A (2019) Covering based q-rung orthopair fuzzy rough set model hybrid with TOPSIS for multi-attribute decision making. J Intell Fuzzy Syst 37(1):981–993

    Article  Google Scholar 

  • Hussain A, Ali MI, Mahmood T (2020) Hesitant q-rung orthopair fuzzy aggregation operators with their applications in multi criteria decision making. Iran J Fuzzy Syst 17(3):117–134

    MathSciNet  MATH  Google Scholar 

  • Joshi BP (2018) Interval-valued q-rung orthopair fuzzy sets and their properties. J Intell Fuzzy Syst 35(5):5225–5230

    Article  Google Scholar 

  • Liu PD, Wang P (2017) Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-mttribute decision making. Int J Intell Syst 22(1):259–280

    Google Scholar 

  • Liu PD, Liu J (2018) Some q-rung orthopai fuzzy bonferroni mean operators and their application to multi-attribute group decision making. Int J Intell Syst 33(2):315–347

    Article  Google Scholar 

  • Liu PD, Shyi-Ming C, Peng W (2020) Multiple-attribute group decision-making based on q-rung orthopair fuzzy power maclaurin symmetric mean operators. IEEE Trans Syst Man Cybern Syst 50(10):3741–3756

    Google Scholar 

  • Liu PD, Wang P (2019) Multiple-attribute decision-making based on archimedean bonferroni operators of q-Rung orthopair fuzzy numbers. IEEE Trans Fuzzy Syst 27(5):834–848

    Article  Google Scholar 

  • Liu ZM, Wang S, Liu PD (2018) Multiple attribute group decision making based on q-rung orthopair fuzzy Heronian mean operators. Int J Intell Syst 33(12):2341–2363

    Article  Google Scholar 

  • Maji PK, Biswas R, Roy AR (2001) Fuzzy soft set. J Fuzzy Mathem 9(3):589–602

    MathSciNet  MATH  Google Scholar 

  • Maji PK, Samanta SK (2010) Generalised fuzzy soft sets. Comput Math Appl 59(4):1425–1432

    Article  MathSciNet  Google Scholar 

  • Peng XD, Dai J, Garg H (2018) Exponential operation and aggregation operator for q-rung orthopair fuzzy set and their decision-making method with a new score function. Int J Intell Syst 33(11):2255–2282

    Article  Google Scholar 

  • Wang J, Gao H, Wei GW (2019) Methods for multiple-attribute group decision making with q-rung interval-valued orthopair fuzzy information and their applications to the selection of green suppliers. Symmetry 11(1):131–157

    Article  Google Scholar 

  • Wei GW, Gao H, Wei Y (2018) Some q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision making. Int J Intell Syst 33(7):1426–1458

    Article  Google Scholar 

  • Wang J (2019) Some q-rung orthopair fuzzy Muirhead means with their application to multi attribute group decision making. J Intell Fuzzy Syst 36(2):1599–1614

    Article  Google Scholar 

  • Wang HH (2019) Multi-attribute group decision-making methods based on q-rung orthopair fuzzy linguistic sets. Int J Intell Syst 34(6):1129–1157

    Article  Google Scholar 

  • Riaz M, Aman N, Zareef I (2019) N-soft topology and its applications to multi-criteria group decision making. J Intell Fuzzy Syst 36(6):6521–6536

    Article  Google Scholar 

  • Riaz M, Tehrim ST (2020) Cubic bipolar fuzzy set with application to multi-criteria group decision making using geometric aggregation operators. Soft Comput 24(21):16111–16133

    Article  Google Scholar 

  • Riaz M, Farid HMA, Karaaslan F (2020) Some q-rung orthopair fuzzy hybrid aggregation operators and TOPSIS method for multi-attribute decision-making. J Intell Fuzzy Syst 39(1):1227–1241

    Article  Google Scholar 

  • Riaz M, Hashmi MR (2019) Linear Diophantine fuzzy set and its applications towards multi-attribute decision-making problems. J Intell Fuzzy Syst 37(4):5417–5439

    Article  Google Scholar 

  • Riaz M, Hashmi MR, Pamucar D, Chu YM (2021) Spherical linear Diophantine fuzzy sets with modeling uncertainties in MCDM. Comput Model Eng Sci 126(3):1125-1164

    Google Scholar 

  • Xing YP (2019) Some q-rung orthopair fuzzy point weighted aggregation operators for multi-attribute decision making. Soft Comput 23(4):1627–1649

    MATH  Google Scholar 

  • Xu ZS (2010) Projection models for intuitionistic fuzzy multiple attribute decision-making. Int J Inf Technol Decis Mak 9(2):267–280

    Article  Google Scholar 

  • Xing YP (2020) A new multi-criteria group decision-making approach based on q-rung orthopair fuzzy interaction Hamy mean operators. Neural Comput Appl 32(11):7465–7488

    Article  Google Scholar 

  • Yang XB, Lin TY, Yang JY (2009) Combination of interval-valued fuzzy set and soft set. Comput Math Appl 58(3):521–527

    Article  MathSciNet  Google Scholar 

  • Yang Y, Tan X, Meng CC (2013) The multi-fuzzy soft set and its application in decision making. Appl Math Model 37(7):4915–4923

    Article  MathSciNet  Google Scholar 

  • Yager RR (2017) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222-1230

    Article  Google Scholar 

  • Yager RR, Alajlan N, Bazi Y (2018) Aspects of generalized orthopair fuzzy sets. Int J Intell Syst 33(11):2154–2174

    Article  Google Scholar 

  • Yager RR (2014) Pythagoream membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965

    Article  Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–356

    Article  Google Scholar 

  • Zhang HD, Jiahua DJ, Yan C (2020) Multi-attribute group decision-making methods based on Pythagorean fuzzy N-soft sets. IEEE Access 8:62298–62309

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous referees for their valuable comments and suggestions.

Funding

This study was funded by the National Natural Science Foundation of China (No. 61966032), the Natural Science Foundation of Gansu Province (No. 20JR10RA118), the Fundamental Research Funds for the Central Universities of Northwest MinZu University (No. 31920210025) and the Innovation Team for Operations Research and Cybernetics of Northwest MinZu University.

Author information

Authors and Affiliations

  1. School of Mathematics and Computer Science, Northwest MinZu University, Lanzhou, 730000, Gansu, China

    Haidong Zhang & TaiBen Nan

  2. School of Electrical Engineering, Northwest MinZu University, Lanzhou, 730000, Gansu, China

    Yanping He

Authors
  1. Haidong Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. TaiBen Nan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yanping He
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

HZ contributed to the manuscript preparation and the conception of the study, and made important revisions to the paper; TN wrote the manuscript; and YH performed the experiment and the data analysis.

Corresponding author

Correspondence to Haidong Zhang.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, H., Nan, T. & He, Y. q-Rung orthopair fuzzy N-soft aggregation operators and corresponding applications to multiple-attribute group decision making. Soft Comput 26, 6087–6099 (2022). https://doi.org/10.1007/s00500-022-07126-4

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-022-07126-4

Keywords

Search

Navigation