Abstract
In this paper, we analyze the population diversity of grammatical evolution (GE) on multiple levels of genetic information: chromosome diversity, expression diversity, and output diversity. Thereby, we use a tree-similarity metric from tree-based GP literature to determine similarity of expression trees generated in GE. The similarity of outputs is determined via their correlation. We track the pairwise similarities for all individuals within a generation on all three levels and track the distribution of similarity values over generations. We demonstrate the analysis method using four symbolic regression problem instances and find that the visualization highlights some issues that can occur when using GE such as: large groups of individuals with highly similar outputs, a high fraction of trees with constant outputs, or short and highly similar trees in the early stages of the GE run. Especially in the early phases of GE, we see that a large subset of the population represents equivalent expressions. In early stages, rather short expressions are produced leaving large parts of the chromosome unexpressed. More complex expressions can be derived only after GE has successfully evolved well-working beginnings of chromosomes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Genetic programming (GP) (Koza 1992; Poli et al. 2008) is an optimization technique which evolves a population of tree-encoded solution candidates. Similar to biological evolution, GP depends on two steps of Darwinian evolution: variation due to crossover and mutation, and selection.
Grammatical evolution (GE) is a form of genetic programming where individuals are represented using chromosomes, and decoded into phenotypes by means of a context-free grammar (O’Neill and Ryan 2001). The grammar can be adjusted to the problem instance to be solved and allows integration of prior knowledge. Besides, it is possible to use a classical integer-vector encoding for solution candidates which makes implementation of genetic operators for crossover and mutation trivial.
Recently, some criticisms have been directed to GE. In Whigham (2015), the authors stated that, unlike context-free grammar genetic programming (CFG-GP), the performance of “pure” GE on the examined problems closely resembles that of random search. Besides, the publication of Whigham et al. (2017) introduced a debate that had a significant impact in the community. A peer commentary special section in that paper was published after its publication. The commentary shows that there are different opinions on the affirmations about GE made in the paper. Foster, for instance, defends the importance of the evolutionary process itself in the exploration of the search space, even if the practitioner does not implement fully smart non-disruptive operators and representations (Foster 2017).
However, GE behavior has been extensively analyzed in the research community. In particular, several recent works have analyzed the diversity and redundancy regarding the individuals of the population, extracting interesting conclusions about the relationships between the size of the individuals and the redundancy of the population.
In this paper, we propose a different look at diversity dynamics in GE, specifically for symbolic regression problems. The idea consists of quantifying the population diversity by determining the distributions of pairwise similarities of individuals at three levels of diversity: chromosome diversity, expression diversity, and output diversity. We chose to use these terms instead of the commonly used genotypic diversity and phenotypic diversity because of the intermediate step of genetic expression based on the grammar in GE. This might cause confusion whether the phenotypic diversity refers to diversity of expressions or outputs.
To this aim, we perform an empirical study of the population diversity dynamics of GE on a set of selected symbolic regression benchmark problems. Thereby, we use a tree-similarity measure from GP literature for expression trees produced by GE, and we additionally quantify pairwise similarities on the chromosome level. The main objective is to gain better insights into the population diversity dynamics of GE using visualization of similarities. The GE implementation that is considered in this work is publicly available in a GitHub repository (Adaptive Group BS 2018).
The rest of the paper is structured as follows. Section 2 reviews recent related works on diversity analysis. Section 3 describes the metrics and the analysis that we perform in this work. Section 4 firstly summarizes the benchmark data sets we used and then presents the parameterization of the algorithms. Section 5 shows the experimental results. Finally, Sect. 6 draws the conclusions of the paper.
2 Related work
Population diversity and its progress have long been studied in the GP community. In Burke et al. (2004), the authors provide a good overview of various distance measures in GP, analyzing the correlation between fitness and diversity; and structural versus evaluation-based solutions. Similarity analysis for symbolic regression was for example discussed by Winkler (2010) and Winkler et al. (2018), analyzing similarity dynamics in GP-based symbolic regression.
Regarding GE, a study on the locality of the genotype-phenotype mapping was presented by Rothlauf and Oetzel (2006), where the authors show that in GE neighboring genotypes do not correspond to neighboring phenotypes. They suggested to consider locality issues in GE. However, they also show in Rothlauf and Goldberg (2003) that uniformly redundant representations do not change the behavior of genetic algorithms (GAs) which, as GE, encode the individuals using chromosomes. In particular, they distinguish between redundant representations with similar genotypes, called synonymously redundant (SynR) representations, and redundant representations with dissimilar genotypes, called non-synonymously redundant (non-SynR) representations. They theoretically show that SynR representations do not affect the behavior of evolutionary algorithms. In GE, both types of redundant representations are possible so, according to that previous work, the SynR representations do not affect the evolution. However, the effect of non-SynR representations is not analyzed in GE.
Evolvability, defined as the capacity of an evolutionary algorithm of improving the fitness of an individual (or population) after the application of an operator, is another concept that has been analyzed in the literature in relation with diversity and redundancy. Even in the beginnings of GE, we can find studies that show how genotypic redundancy and, in consequence, degeneracy or fitness neutrality, enhance evolvability. For instance, O’Neill and Ryan (1999), the genetic code degeneracy of GE and its implications for genotypic diversity is analyzed, concluding that genetic diversity is improved as a result of degeneracy for some problems domains. More recently, Medvet et al. (2017) experimentally study GE evolvability mixing problems, mapping functions, genotype sizes, and genetic operators, and they conclude that there are several factors affecting GE evolvability. Among them, authors highlight redundancy.
Other works from Medvet (2017) and Medvet et al. (2018) studied dynamic locality and redundancy in GE. In Medvet (2017), locality and redundancy were studied during the evolution of GE. In Medvet et al. (2018), the authors designed diversity and usage (DU) maps for the analysis of the representation in evolutionary algorithms. Both these works consider those properties at the individual level. Moreover, Bartoli et al. (2019) investigated the effects of two strategies for promoting diversity in Grammar-guided Genetic Programming. The design of those strategies is justified by a previous study of four different approaches: context-free grammar genetic programming (CFGGP) (Whigham 1995), standard grammatical evolution (GE), structured grammatical evolution (SGE) (Lourenço et al. 2016), and weighted hierarchical grammatical evolution (WHGE) (Bartoli et al. 2020). It describes the individuals at three levels in terms of their genotype, phenotype, and fitness, but the focus of the work is not the analysis of diversity but of the promotion strategies. In fact, it should be straight-forward to use the measures for tree similarity and output similarity described below for more fine-grained analysis of the effects of diversity promotion strategies. Compared to the string edit distance used for finding the closest parent by Bartoli et al. (2019) the tree similarity is less sensitive to re-ordering of sub-expressions, e.g., the two expressions \((x_1 + x_2) x_3\) and \(x_3 (x_2 + x_1)\) have a high tree similarity but low string similarity. A simple and efficient algorithm which is equivalent to bottom-up tree-distance and can be used for online diversity control has been described by Burlacu et al. (2019).
In particular, the previously mentioned SGE has introduced even stronger differences among GP, CFG-GP, and GE. In fact, it has been also demonstrated that the high locality of SGE generates low output diversity which produces high redundancy after a number of generations (Bartoli et al. 2019).
Therefore, after the literature review, in our opinion no final conclusion against or in favor of GE can be taken, since its performance is well known, as proven by many successful works applied to different kind of problems (Adamu and Phelps 2009; Hidalgo et al. 2014; Risco-Martín et al. 2014; Mingo and Aler 2018; Cas tejón and Carmona 2018). However, it is also clear that diversity is a key factor in the evolvability of GE, as in other evolutionary algorithms.
Through the genetic expression of chromosomes, GE introduced a separation between the chromosomes and the expressions which allows to have high chromosome diversity even with low expression similarity. This is why we here specifically analyze diversities on all three levels, also including graphical visualization of the process.
3 Population diversity analysis
As we here aim to study the diversity dynamics, we first have to clarify how we define diversity in GE and how we can measure it.
In order to quantify diversity, we calculate all pairwise similarities of GE individuals within the population in each generation.
We calculate similarities on three levels, namely on chromosome level—calculating the similarity of integer vectors, on tree level—comparing trees using the bottom-up tree distance (Valiente 2001), and on phenotype level—calculating the correlation between two individuals’ outputs.
Since our similarity measures are symmetrical, the number of similarity calculations necessary for a population of N individuals is \(\frac{N(N-1)}{2}\). We can quantify the diversity of the population P as the average similarity
where \(Sim(p_1, p_2)\) can be any similarity measure with outputs that range from zero (two completely different objects) to one (identical objects). In our analysis, we not only consider average similarity but track the full distribution of similarities.
3.1 Chromosome similarity
The similarity of two chromosomes \(c_1\) and \(c_2\) is calculated via the Hamming distance. Given two integer vectors, the Hamming distance is calculated as the number of indices at which the vectors have different values. The chromosome similarity is one minus the Hamming distance of the two chromosomes divided by their length to map the similarity to the interval [0, 1]:
Bottom-up mapping between two trees \(t_1\) and \(t_2\) (taken from Valiente (2001)). For each node n the node \(n'\) in the other tree is determined, which has the same structure (subtree structure) as n
Two different individuals of GE (\(f_a=\frac{9+ x_1+x_3}{2.3+x_2}\) and \(f_b = x_3 + \frac{x_1}{x_2} + x_3\)) represented as chromosomes (a, b), corresponding trees (c , d), and the scatter plot of the output values (e). The chromosome similarity of \(f_a\) and \(f_b\) is 0.875, the corresponding tree similarity is 0.4 (\(\frac{3}{(7+8)/2}\)), and their output similarity is 0.65
Two different individuals (\(f_c = \frac{6 \cdot (x_1-1) \cdot x_2}{x_3}\) and \(f_d = \frac{x_3}{(x_1-8)\cdot x_2 \cdot x_3}\)) represented as trees (a, b), and the scatter plot of the output values (c). The tree similarity of \(f_c\) and \(f_d\) is \(\frac{6}{9}\), and their output similarity is 0.064
3.2 Expression similarity
For calculating the similarities of trees defined by GE chromosomes, we use the bottom-up tree distance (Valiente 2001; Winkler et al. 2018; Burlacu et al. 2019). It is based on the largest common forest between trees. It has the advantage of maintaining the same time complexity, namely linear in the size of the two trees regardless of whether the trees are ordered or unordered. An efficient algorithm for the calculation has been described by Burlacu et al. (2019). The tree distance is calculated over the abstract syntax trees after the expression of the chromosomes, and it not dependent on the derivation tree. The algorithm works as follows (Fig. 1):
-
1.
In the first step, it computes the compact directed acyclic graph representation G of the largest common forest
 (consisting of the disjoint union between the two trees). The graph G is built during a bottom-up traversal of F (in the order of non-decreasing node height). Two nodes in F are mapped to the same vertex in G if they are at the same height and their children are mapped to the same sequence of vertices in G. The bottom-up traversal ensures that children are mapped before their parents, leading to \(O(|t_1| + |t_2|)\) time for adding vertices in G corresponding to all nodes in F. This step returns a map \(K : F \rightarrow G\) which is used to compute the bottom-up mapping.
(consisting of the disjoint union between the two trees). The graph G is built during a bottom-up traversal of F (in the order of non-decreasing node height). Two nodes in F are mapped to the same vertex in G if they are at the same height and their children are mapped to the same sequence of vertices in G. The bottom-up traversal ensures that children are mapped before their parents, leading to \(O(|t_1| + |t_2|)\) time for adding vertices in G corresponding to all nodes in F. This step returns a map \(K : F \rightarrow G\) which is used to compute the bottom-up mapping. -
2.
The second step iterates over the nodes of \(t_1\) in level-order and builds a mapping \(M : t_1 \rightarrow t_2\) using K to determine which nodes correspond to the same vertices in G. Thus, for each node n, the node \(n'\) in the other tree is determined, which has the same structure (subtree structure) as n. The level-order iteration guarantees that every largest unmapped subtree of \(t_1\) will be mapped to an isomorphic subtree of \(t_2\); \(|M(t_1,t_2)|\) is the number of branches for which a branch with the same structure was found in the other tree. Finally, the bottom-up distance between trees \(t_1\) and \(t_2\) is calculated as
$$\begin{aligned} \mathrm {BottomUpDistance}(t_1,t_2) = \frac{|M(t_1,t_2)|}{\frac{|t_1| + |t_2|}{2}} \end{aligned}$$(5)Thus, the similarity of \(t_1\) and \(t_2\) is defined as
$$\begin{aligned}&\mathrm {GenotypicSimilarity}(t_1{,} t_2) {=}1 {-} \mathrm {BottomUpDistance}(t_1{,}t_2)\nonumber \\ \end{aligned}$$(6)Due to the division of M by the average tree size of \(t_1\) and \(t_2\), the distance will always be in the interval [0, 1]; thus, also the so calculated genotypic similarity will be in the interval [0, 1].
3.3 Output similarity
Output similarity is calculated with regard to the individuals’ response on the training data. Individuals with the same response are considered similar regardless of their actual structure.
We use the squared Pearson product-moment correlation coefficient to quantify the output similarity of two output vectors \(Y_1\) and \(Y_2\) for the same inputs X:
This function always returns a value in the interval [0, 1]. The similarity for a zero-variance vector and a nonzero variance vector is set to zero; the similarity of two zero-variance functions is set to one.
3.4 Similarity calculation examples
Figure 2 shows two exemplary GE individuals represented as integer vectors. Underneath the figure shows the corresponding trees and functions’ outputs on randomly generated inputs X. The chromosomes are almost identical, but different trees are expressed. However, the function outputs for the two trees are correlated. Accordingly, the chromosome similarity is high (0.875), the tree similarity is 0.4 (3 matching nodes for an average tree size of 7.5), and the function similarity is 0.65.
Figure 3 shows two expression trees. As we see in the figure, the shapes of the trees are similar, but they correspond to different expressions. The nodes which are matched when calculating the bottom-up tree similarity are highlighted. In this example the bottom-up tree similarity is 0.67 (6 matching nodes over 9 total nodes). In Fig. 3c, we see that the functions’ outputs on randomly sampled X are very different and the correlation of outputs is low. Accordingly, the output similarity is almost zero (0.064).
4 Test series
4.1 Problem instances
In the literature, we can find a lot of different symbolic regression problems although some benchmark sets include several functions with similar characteristics (Nicolau 2017). Recently Nicolau et al. (2015) made a study on the difficulty of selecting the appropriate benchmark set. Although different experiments were performed, the main conclusion of this work is that highly non-smooth functions should be avoided. The benchmark function set defined by Vladislavleva explicitly considers extrapolation and interpolation (Vladislavleva et al. 2009). It is also well know that real-world problems are quite different from synthetic benchmarks. Based on the previous considerations and seeking for a small but representative number of benchmarks, we selected four typical symbolic regression problems to perform our study which are also included in the problem instances recommended by White et al. (2013): two instances from the Vladislavleva set, a hard problem in spatial co-evolution (Pagie and Hogeweg 1998) where the shape of the graph is smooth, and the tower problem which contains real-world data for which the true input-output relationship is unknown. Thus, the problem instance set contains three problems with low as well as one problem with medium dimensionality.
-
The Tower data set (Vladislavleva et al. 2009) comes from an industrial problem related to the modeling of chromatography measurements corresponding to the composition of a distillation tower gas. It contains 5000 records and 25 potential input variables; the response variable is the propylene concentration at the top of the distillation tower. The samples were measured by a gas chromatograph and recorded as floating averages every 15 min. The 25 potential inputs are temperatures, flows, and pressures related to the distillation tower.
-
In the spatial co-evolution data set (Pagie and Hogeweg 1998), the target variable is defined as
$$\begin{aligned} F(x,y) = \frac{1}{1 + x^{-4}} + \frac{1}{1 + y^{-4}} \end{aligned}$$(8)In the training data (676 samples), the values for x and y are sampled from − 5 to \(+\) 5 in steps of 0.4; in the test data (1000 samples) x and y are sampled from \([-\,5, \ldots , +\,5]\) randomly.
-
For the Vladislavleva data sets F-5 and F-8, the target variables are defined as functions of the variables x as:
$$\begin{aligned}&F_5(x_1, x_2, x_3) = \frac{30 * ((x_1 - 1) * (x_3 -1))}{x_2 * (x_1 - 10)}\end{aligned}$$(9)$$\begin{aligned}&F_8(x_1, x_2) = \frac{(x_1 - 3)^4 + (x_2 - 3)^3 - (x_2 -3)}{(x_2 - 2)^4 + 10} \end{aligned}$$(10)
In this study, we have ignored the training/test split and used the whole data set for fitness calculation because we are mainly interested in the diversity dynamics and not in producing an optimal model.
The syntactical structure of symbolic expressions is relatively simple. As a consequence, GE grammars for symbolic regression problems are rather flat. We leave a more detailed study for other problem domains with deeper grammars for future work.
4.2 Algorithm parameters
After some preliminary experimentation, we determined the values of the parameters of the GE algorithm shown in Table 1. In particular, the genetic operators are single-point crossover and integer flip mutation (Michalewicz 1996). The mutation operator selects a gene of a chromosome with a probability of 2%, and then, it assigns the gene a uniformly generated random value.
Figure 4 shows the GE grammar. The same grammar has been used for all problem instances. Only the last line, defining the alternatives for input variables is adapted specifically to each problem instance.
Visualization of all pairwise similarities of the GE run shown in Fig. 8 (spatial co-evolution problem). Similarities of all pairs of individuals in the population have been calculated for generations 40, 220, 420, 1100, and 1600. Individuals have been sorted by quality; similarities of the best individuals are shown in the bottom left; similarities of the worst individuals in the top right
5 Experimental results
We have executed 10 GE runs for each problem instance. The experiments were run on a 2.9 GHz Intel Core i7 machine with 16 GB of RAM.
In this section, we first summarize the qualities achieved for the four test instances (Sect. 5.1) and then give a summary of the population diversity progresses on all four problem instances (Sect. 5.2).
5.1 Result qualities
First, to check whether the performance of GE on the benchmark problem instances is acceptable, we analyze the qualities of the final solutions on the training set. We compare the results using the normalized mean of squared errors (NMSE) of the predictions of the best solution.
As we see in Table 2, GE on average obtains NMSE values between 2% (for VF-5) and 20% (for the Tower).
5.2 Population diversity results and discussion
Figures 5, 6, 7, and 8 show the distributions of pairwise similarity values for one selected GE run on each of the benchmark problems. In each generation, we calculate pairwise chromosome, expression, and output similarities of all individuals in the population and build a histogram using 20 bins from 0% similarity to 100% similarity. The red line shows the average similarity.
To facilitate interpretation of the similarity distributions, we also show the average and best quality (in percent) as well as the average size of trees in each generation.
Figure 9 shows the corresponding similarity matrix heatmaps at generations 40, 220, 420, 1100, and 1600 for one of the GE runs on the spatial problem.
The chromosome similarity is almost zero for the first 200 generations and then converges to values between 10 and 25%, which means that this percentage of genes in the chromosomes are exactly equivalent for any pair of individuals. Without selection pressure, the number of equal genes follows a binomial distribution with 256 trials (length of the chromosome) and 1/256 (number of possible alleles) success probability for a trial. The expected value for equal genes for two random chromosomes is therefore only one. The much higher chromosome similarity indicates that certain alleles are fixed.
The chromosome similarity matrices in the top row of Fig. 9 indicate that there is almost no correlation of chromosome similarity with quality. Since the individuals are ordered by quality with the best individuals in the bottom left and the worst in the top right, we would expect larger blocks of highly similar individuals along the diagonal. However, in the chromosome similarity heatmaps this is not apparent. Individuals with similar quality do not have similar chromosomes and vice versa.
For the tree similarities however, the picture is completely different shown in the second rows of Figs. 5, 6, 7 and 8 and the middle row of Fig. 9. For the generated expressions, an interesting phenomenon can be observed: GE produces many equivalent or highly similar expressions from highly dissimilar chromosomes in the first 200 generations. This is caused by the derivation process of expressions from the grammar which stops as soon as a complete sentence is found. Depending on the elements at the beginning of the chromosome, the derivation process might stop early, producing a short expression and ignoring a large part of the chromosome completely. Figures 8 and 9 show that between generations 420 and 1100 GE produced less similar trees from more similar chromosomes than in generations 40–420. This effect is explained by the sudden increase in tree size around generation 300 as larger sections of the genotype became effecting, leading to the observed increase of chromosome similarity and decrease of tree similarity.
Finally, the output similarities shown in the third rows of Figs. 5, 6, 7, and 8 and the bottom row of Fig. 9 have an extremely bi-modal distribution for all problem instances. More than half of individuals in the population produce almost equivalent outputs over all generations. The average output similarity lies in the middle of the two extremes and is mainly determined by the number of similarity values in both classes. This result highlights that the average similarity value alone can be misleading. The GE population contains around 10% highly similar trees producing a constant output (top right square in Fig. 9). The explanation for this is that the grammar has a high probability of producing constants because 3 of 14 rules for expr directly produce a constant. Thus, without selection pressure we expect at least 20% constant expressions. Additionally, constant expressions could be operators with constant arguments. However, with selection pressure the number of constant expressions should reduce quickly as they have the worst possible fitness value. Inspecting the last generation population, we find that only 2% of the expressions are constants. A ratio of 6% are invalid individuals caused either by incomplete derivation, division by zero, or taking the exponential of a large value. For the determination of output similarity, these expressions are handled in the same way as constants. Closer inspection of these invalid individuals shows that only approx. 1% are invalid because of a problem in the derivation process.
For the high-quality individuals, we find that in the early generations (up to 300) they produce effectively the same output from only a few different expressions (bottom left squares in Fig. 9). At around generation 300, the average length of expressions increases, and the algorithm is able to identify a more diverse set of trees, all of which produce very similar outputs. The explanation for this is the redundancy of representation of mathematical expressions, which allow many different representation even for very similar functions.
In Table 3, we show a summary of the all similarity values for the four benchmark problems averaged over the ten independent runs. For each instance, we report the figures calculated for the initial population (generation 1), then similarities during the executions, and at the end of the executions.
It is important to note that the values shown in Table 3 do not show the bi-modal or multi-modal distributions that we observed for output similarities. This highlights the need to look at the distributions of pairwise similarities in depth as we have shown above. From an analysis of the similarity distributions on all heredity levels, we can gain more information about the evolutionary dynamics of these algorithms than when we solely look at average similarities of encoded solutions.
6 Conclusions
Grammatical evolution is a form of genetic programming that represents individuals using chromosomes instead of trees. In this work, we have analyzed and compared the similarity of individuals in GE when applied to symbolic regression problems. We have calculated pairwise similarities of chromosomes, of expressions represented as trees, as well as of the function outputs. We have used a set of four benchmark problem instances to study general dynamics of population diversity. The populations evolved by GE have high chromosome diversity but much lower expression diversity. Especially in the early phases of GE, we observed that a large subset (around 50%) of the population represent exactly the same expressions. This is caused by the rather short expressions that can be derived from the grammar in the beginning—leaving large parts of the chromosome unexpressed.
References
Adamu K, Phelps S (2009) Modelling financial time series using grammatical evolution. In: Proceedings of the workshop on advances in machine learning for computational finance, London, UK
Adaptive Group BS (2018) ABSys JECO (Java Evolutionary Computation) library. https://github.com/ABSysGroup/jeco
Bartoli A, De Lorenzo A, Medvet E, Squillero G (2019) Multi-level diversity promotion strategies for grammar-guided genetic programming. Appl Soft Comput 83:105599
Bartoli A, Castelli M, Medvet E (2020) Weighted hierarchical grammatical evolution. IEEE Trans Cybern 50(2):476–488
Burke EK, Gustafson S, Kendall G (2004) Diversity in genetic programming: an analysis of measures and correlation with fitness. IEEE Trans Evolut Comput 8(1):47–62. https://doi.org/10.1109/TEVC.2003.819263
Burlacu B, Affenzeller M, Kronberger G, Kommenda M (2019) Online diversity control in symbolic regression via a fast hash-based tree similarity measure. In: 2019 IEEE congress on evolutionary computation (CEC), pp 2175–2182. https://doi.org/10.1109/CEC.2019.8790162
Castejón F, Carmona EJ (2018) Automatic design of analog electronic circuits using grammatical evolution. Appl Soft Comput 62:1003–1018
Foster JA (2017) Taking “biology” just seriously enough: commentary on “On the mapping of genotype to phenotype in evolutionary algorithms” by Peter A. Whigham, Grant Dick, and James Maclaurin. Genet Program Evol Mach 18(3):395–398. https://doi.org/10.1007/s10710-017-9296-x
Hidalgo JI, Colmenar JM, Risco-Martín JL, Cuesta-Infante A, Maqueda E, Botella M, Rubio JA (2014) Modeling glycemia in humans by means of grammatical evolution. Appl Soft Comput 20:40–53. https://doi.org/10.1016/j.asoc.2013.11.006
Koza JR (1992) Genetic programming. The MIT Press, Cambridge
Lourenço N, Pereira FB, Costa E (2016) Unveiling the properties of structured grammatical evolution. Genet Program Evolut Mach 17(3):251–289. https://doi.org/10.1007/s10710-015-9262-4
Medvet E (2017) A comparative analysis of dynamic locality and redundancy in grammatical evolution. In: McDermott J, Castelli M, Sekanina L, Haasdijk E, García-Sánchez P (eds) Genetic programming. Springer, Cham, pp 326–342
Medvet E, Daolio F, Tagliapietra D (2017) Evolvability in grammatical evolution. In: Proceedings of the genetic and evolutionary computation conference, pp 977–984
Medvet E, Virgolin M, Castelli M, Bosman PA, Gonçalves I, Tušar T (2018) Unveiling evolutionary algorithm representation with DU maps. Genet Program Evolut Mach 19(3):351–389
Michalewicz Z (1996) Genetic algorithms \(+\) data structures \(=\) evolution programs. Springer, New York
Mingo JM, Aler R (2018) Evolution of shared grammars for describing simulated spatial scenes with grammatical evolution. Genet Program Evolut Mach 19(1):235–270
Nicolau M (2017) Understanding grammatical evolution: initialisation. Genet Progr Evolut Mach 18(4):467–507
Nicolau M, Agapitos A, O’Neill M, Brabazon A (2015) Guidelines for defining benchmark problems in genetic programming. In: 2015 IEEE congress on evolutionary computation (CEC), IEEE, pp 1152–1159
O’Neill M, Ryan C (1999) Genetic code degeneracy: implications for grammatical evolution and beyond. In: Floreano D, Nicoud JD, Mondada F (eds) Advances in artificial life. Springer, Berlin, pp 149–153
O’Neill M, Ryan C (2001) Grammatical evolution. IEEE Trans Evolut Comput 5(4):349–358
Pagie L, Hogeweg P (1998) Evolutionary consequences of coevolving targets. Evolut Comput 5:401–418
Poli R, Langdon WB, McPhee NF (2008) A field guide to genetic programming. http://lulu.com and freely http://www.gp-field-guide.org.uk
Risco-Martín JL, Colmenar JM, Hidalgo JI, Lanchares J, Díaz J (2014) A methodology to automatically optimize dynamic memory managers applying grammatical evolution. J Syst Softw 91:109–123. https://doi.org/10.1016/j.jss.2013.12.044
Rothlauf F, Goldberg DE (2003) Redundant representations in evolutionary computation. Evol Comput 11(4):381–415. https://doi.org/10.1162/106365603322519288
Rothlauf F, Oetzel M (2006) On the locality of grammatical evolution. In: Collet P, Tomassini M, Ebner M, Gustafson S, Ekárt A (eds) Genet Program. Springer, Berlin, pp 320–330
Valiente G (2001) An efficient bottom-up distance between trees. In: Proceedings eighth symposium on string processing and information retrieval, pp 212–219. https://doi.org/10.1109/SPIRE.2001.989761
Vladislavleva EJ, Smits GF, den Hertog D (2009) Order of nonlinearity as a complexity measure for models generated by symbolic regression via pareto genetic programming. IEEE Trans Evol Comput 13(2):333–349. https://doi.org/10.1109/TEVC.2008.926486
Whigham PA et al (1995) Grammatically-based genetic programming. Proc Workshop Genet Program Theory Real World Appl 16:33–41
Whigham PA, Dick G, Maclaurin J, Owen CA (2015) Examining the “Best of Both Worlds” of grammatical evolution. In: Proceedings of the 2015 annual conference on genetic and evolutionary computation, GECCO ’15, ACM, New York, NY, USA, pp 1111–1118. https://doi.org/10.1145/2739480.2754784
Whigham PA, Dick G, Maclaurin J (2017) On the mapping of genotype to phenotype in evolutionary algorithms. Genet Program Evol Mach 18(3):353–361. https://doi.org/10.1007/s10710-017-9288-x
White DR, McDermott J, Castelli M, Manzoni L, Goldman BW, Kronberger G, Jaśkowski W, O’Reilly UM, Luke S (2013) Better gp benchmarks: community survey results and proposals. Genet Program Evol Mach 14(1):3–29. https://doi.org/10.1007/s10710-012-9177-2
Winkler SM (2010) Structural versus evaluation based solutions similarity in genetic programming based system identification. In: González JR, Pelta DA, Cruz C, Terrazas G, Krasnogor N (eds) Nature inspired cooperative strategies for optimization, NICSO 2010, studies in computational intelligence, vol 284, Springer, Granada, Spain, pp 269–282
Winkler SM, Affenzeller M, Burlacu B, Kronberger G, Kommenda M, Fleck P (2018) Similarity-based analysis of population dynamics in genetic programming performing symbolic regression. In: Genetic programming theory and practice XIV, Springer
Acknowledgements
Open access funding provided by University of Applied Sciences Upper Austria. S. M. Winkler and G. Kronberger acknowledge the support of the Austrian Research Promotion Agency (FFG) under Grant #843532 (COMET Project Heuristic Optimization in Production and Logistics) and the support by the Christian Doppler Research Association and the Federal Ministry for Digital and Economic Affairs within the Josef Ressel Centre for Symbolic Regression. This work was partially supported by the Spanish Ministerio de Ciencia, Innovación y Universidades (MCIU/AEI/FEDER, UE) under Grants PGC2018-095322-B-C22 and RTI2018-095180-B-I00, Comunidad de Madrid y Fondos Estructurales de la Unión Europea under Grant P2018/TCS-4566, Madrid Regional Goverment Grant B2017/BMD3773 (GenObIA-CM), Madrid Regional Goverment under Grant Y2018/NMT-4668 (Micro-Stress-MAP-CM) and EU FEDER and Social Funds.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by A. Di Nola.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kronberger, G., Colmenar, J.M., Winkler, S.M. et al. Multilayer analysis of population diversity in grammatical evolution for symbolic regression. Soft Comput 24, 11283–11295 (2020). https://doi.org/10.1007/s00500-020-05062-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-020-05062-9


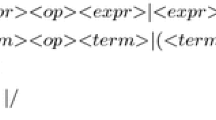





 (consisting of the disjoint union between the two trees). The graph G is built during a bottom-up traversal of F (in the order of non-decreasing node height). Two nodes in F are mapped to the same vertex in G if they are at the same height and their children are mapped to the same sequence of vertices in G. The bottom-up traversal ensures that children are mapped before their parents, leading to
(consisting of the disjoint union between the two trees). The graph G is built during a bottom-up traversal of F (in the order of non-decreasing node height). Two nodes in F are mapped to the same vertex in G if they are at the same height and their children are mapped to the same sequence of vertices in G. The bottom-up traversal ensures that children are mapped before their parents, leading to 




