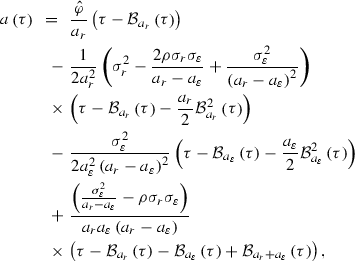Abstract
Catastrophe bonds are financial instruments, which enable to transfer the natural catastrophe risk to financial markets. This paper is a continuation of our earlier research concerning catastrophe bond pricing. We assume the absence of arbitrage and neutral attitude of investors toward catastrophe risk. The interest rate behavior is described by the two-factor Vasicek model. To illustrate and analyze obtained results, we conduct Monte Carlo simulations, using parameters fitted for real data on natural catastrophes. Besides the crisp cat bond pricing formulas, we obtain their fuzzy counterparts, taking into account the uncertainty on the market. Moreover, we propose an automated approach for decision making in fuzzy environment with relevant examples presenting this method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nowadays, natural catastrophes occur more frequently than before. Additionally, they threaten densely populated areas [e.g., tsunami in Japan (2011)]. This results in high values of damages. One can mention Hurricane Andrew (1992) with losses estimated at USD 30 billion [see, e.g., Muermann (2008)]. On the other hand, devastating floods are a significant problem in Europe.
Natural catastrophes losses have a negative impact on financial stability of insurers, e.g., after Hurricane Andrew more than 60 insurance companies became insolvent [see, e.g., Muermann (2008)]. This is caused not only by the huge value of losses, but also the classical insurance mechanisms [see, e.g., Borch (1974)] are not suitable for losses caused by natural disasters. The classical insurance approach applied to the construction of the insurer’s portfolio can lead directly to bankruptcy of this enterprise [see, e.g., Ermoliev et al. (2001); Romaniuk and Ermolieva 2005)].
One of the methods of solving the mentioned above problems is application of other financial and insurance mechanisms. Such instruments are, among others, catastrophe bonds [also called cat bonds, see, e.g., George (1999); Nowak and Romaniuk 2009)]. They transfer risk connected with natural catastrophe losses (i.e., the insurance risk) to financial markets.
The number of papers dedicated to catastrophe bonds pricing is relatively low. A significant problem is the incompleteness of the financial market on which catastrophe instruments are traded. In many papers, simplified models or behavioral finance methods are used. In turn, many stochastic approaches do not take into account the change of probability measure in the martingale method or apply the utility function, which choice can be an additional problem in practice. An interesting stochastic approach proposed by Vaugirard in Vaugirard (2003) overcame the problem of the incompleteness of the financial market. For more detailed references we refer the reader to Nowak and Romaniuk (2013b).
In this paper, we solve the catastrophe bond pricing problem under the assumption of absence of arbitrage on the financial market. We derive and prove the cat bond valuation expressions in crisp case. Then, assuming that some parameters of the model cannot be precisely described, we obtain fuzzy counterparts of the crisp pricing formulas and we apply them to an automatized method of decision making. We illustrate our theoretical results by numerical examples. Our approach in this paper can be treated as an essential extension of Vaugirard’s method. In analogous catastrophe bond valuation formulas considered earlier [see Nowak et al. (2012); Nowak and Romaniuk 2010b, 2013b)], one-factor models of the spot interest rate \(r_{t}\) were used. A new model of \(r_{t}\) proposed in this paper is the two-factor Vasicek model (introduced by Hull and White) with a stochastic process describing deviation of the current view on the long-term level of \(r_{t}\) from its average view. Additionally, in comparison with the mentioned approaches, we introduce more detailed formulas describing prices of cat bonds (see Theorem 2) for arbitrary time moment t, on the basis of Dynkin’s Lemma. For this purpose, we apply zero-coupon bond pricing formulas from Munk (2011). However, the proof of Theorem 2 required considering the case of \(a_{r}=a_{\varepsilon }\) (see Lemma 1, case b), not considered in Munk (2011). Furthermore, contrary to Nowak et al. (2012), Nowak and Romaniuk (2010b), we conduct Monte Carlo simulations, applying real parameters for \(r_{t}\) and distributions of catastrophe losses. We also apply a non-homogeneous Poisson process for quantity of catastrophe events. As mentioned previously, apart from the standard valuation formulas, we obtain their fuzzy counterparts, taking into account the uncertainty on the market. We propose an automated approach for decision making and present examples to illustrate it for a given set of market parameters.
As noted above, applying fuzzy set theory, we consider different sources of uncertainty, not only the stochastic one. In particular, we take into account that volatility parameters and the correlation coefficient, used for description of \(r_{t}\), are determined by fluctuating financial market and often the uncertainty does not have a stochastic character. Therefore, we apply fuzzy counterparts of some market parameters. As result, price obtained by us has the form of a fuzzy number, which can be used for investment decision making. Similar approach was applied in the case of options in Wu (2004) and Nowak and Romaniuk (2010a, 2013c, 2014b), where the Jacod-Grigelionis characteristic triplet [see, e.g., Nowak (2002); Shiryaev 1999)] was additionally used.
The literature devoted to soft computing methods is very rich. Books (Vasant et al. 2012; Vasant 2013a, 2014, 2015) provide a wide overview of soft computing algorithms and their applications. We mention only certain selected examples of the presented approaches, focusing on financial and economic problems. Various optimization methods using soft computing such as fuzzy logic, neural networks, genetic algorithms, and the theory of chaos, in business, finance and economics are discussed in Dostál (2012). An interesting example presented in Dostál (2012) is application of theory of chaos to simulation of market price of a share on the stock market. In Beynon and Clatworthy (2013), the problem of understanding the relationship between company stock returns and earnings components is discussed. The authors apply the classification and ranking belief simplex (CaRBS) and a development of this data analysis technique, called RCaRBS. In turn, the author of Gordini (2014) uses a genetic algorithms approach for small enterprise default prediction modeling. A widely applicable multi-variate decision support model for market trend analysis and prediction, based on a time series transformation method in combination with Bayesian logic and Bayesian network, is presented in Mršić (2014). In Besbes et al. (2015), the authors propose a two-phase mathematical approach, involving the application of a stochastic programming model, to effective product-driven supply chain design. In Vasant (2013b), a new and interesting approach to the industrial production planning problems is discussed. Finally, various generalized soft methods are applied in many other scientific areas, see, e.g., Kowalski et al. (2008), Kulczycki and Charytanowicz (2005, 2010).
Section 2 contains lists of symbols, expressions and operators used in the paper. In Sect. 3, we discuss basic notions and mechanisms connected with catastrophe bonds. In Sect. 4, catastrophe bond pricing formulas are proved for the two-factor Vasicek interest rate model and a necessary theoretical base is presented. Section 5 is devoted to cat bond pricing in fuzzy environment. In Sect. 6, we propose an automated method of decision making with application of the fuzzy valuation expressions. Section 7 is dedicated to algorithms used in Monte Carlo simulations. These algorithms are then applied in Sect. 8 during analysis of some numerical examples of cat bond pricing and automatized decision making.
2 List of symbols, expressions and operators
2.1 List of symbols and expressions in order of appearance
- \(\left( \Omega ,\mathcal {F},P\right) \) :
-
probability space (see Sect. 4),
- P :
-
probability measure (see Sect. 4),
- \({[}0,T^{\prime }{]}\) :
-
time horizon (see Sect. 4),
- T :
-
date of maturity and payoff of catastrophe bonds (see Definition 1, Definition 2),
- \(W_{t}=\left( W_{t}^{1},W_{t}^{2},\ldots ,W_{t}^{n}\right) _{t\in \left[ 0,T^{\prime }\right] }\) :
-
standard, n-dimensional Brownian motion (see Sect. 4),
- \(\left( U_{i}\right) _{i=1}^{\infty }\) :
-
sequence of independent random variables (see Sect. 4),
- \(U_{i}\) :
-
value of losses during ith catastrophic event (see Sect. 4),
- \(\left( \tilde{N}_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\) :
-
compound Poisson process describing aggregated catastrophic losses (see (1)),
- \(\left( N_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\) :
-
Poisson process describing number of catastrophic events (see Sect. 4),
- \(\kappa :{[}0,T^{\prime }{]}\rightarrow \mathbb {R}_{+}\) :
-
intensity function of Poisson process \(\left( N_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\) (see Sect. 4 and Sect. 7.1),
- \(\left( \mathcal {F}_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\) :
-
filtration with respect to which stochastic processes considered in the paper are adapted (see Sect. 4),
- \(\mathcal {F}_{t}^{0}\), \(\mathcal {F}_{t}^{1}\), \(t\in {[}0,T^{\prime }{]}\),:
-
auxiliary \(\sigma \)-fields (see Sect. 4),
- \(\sigma \left( \mathcal {A}\right) \) :
-
\(\sigma \)-field generated by a family \(\mathcal {A}\) of sets or random variables (see Sect. 4),
- \(\mathcal {F}\) :
-
\(\sigma \)-field of events for which probability P is defined (see Sect. 4),
- \(\mathcal {F}_{0}\), \(\mathcal {F}_{T^{\prime }}\) :
-
\(\sigma \)-fields from filtration \(\left( \mathcal {F}_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\) (see Sect. 4),
- \(\left( \Omega ,\mathcal {F},\left( \mathcal {F}_{t}\right) _{t\in \left[ 0,T^{\prime }\right] },P\right) \) :
-
filtered probability space (see Sect. 4),
- \(\left( B_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\) :
-
banking account (see Sect. 4),
- r :
-
risk-free spot interest rate, \(r_t\) denotes the value of the risk-free spot interest rate at moment t (see Sect. 4),
- \(B\left( t,T\right) \) :
-
price at time t of a zero-coupon bond with the maturity date T and the face value equal to 1 (see Sect. 4),
- n :
-
number of levels of catastrophic losses (see Sect. 4),
- \(K_{1}, K_{2},\ldots ,K_{n}\) :
-
levels of catastrophic losses (see Sect. 4),
- \(w_{1},w_{2},\ldots ,w_{n}\) :
-
cat bonds payment decrease coefficients (see Sect. 4),
- \(\tau _{i}:\Omega \rightarrow {[} 0,T^{\prime }{]} ,\;1\le i\le n\),:
-
sequence of stopping times (see Sect. 4),
- \(\displaystyle \inf _{t\in \left[ 0,T^{\prime }\right] }\) :
-
infimum with respect to \(t\in \left[ 0,T^{\prime }\right] \) (see Sect. 4),
- Fv :
-
catastrophe bond face value (see Sect. 4),
- \(\mathrm{IB}_{s}(T,Fv)\) :
-
catastrophe bond with the face value Fv , the date of maturity and payoff T, and a stepwise payoff structure (see Definition 1),
- \(\nu _{\mathrm{IB}_{s}\left( T,Fv\right) }\) :
-
catastrophe bond \(\mathrm{IB}_{s}(T,Fv)\) payoff function (see Sect. 4),
- \(I_A\) :
-
the indicator function of an event A, \(I_A (\omega )\) equals 1 if \(\omega \in A\) and 0 otherwise (see Sect. 4),
- \(\Phi _{i}\), \(i=1,2,\ldots ,n\),:
-
cumulative distribution functions of \(\tau _{i}\) (see Sect. 4),
- \(\Phi \) :
-
sum of cumulative distribution functions of \(\tau _{i}\), \(i=1,2,\ldots ,n\) (see Sect. 4),
- \(K_{0}\) :
-
additional level of catastrophic losses (see Sect. 4),
- \(\mathrm{IB}_{p}(T,Fv)\) :
-
catastrophe bond with the face value Fv , the date of maturity and payoff T, and a piecewise linear payoff structure (see Definition 2),
- \(\nu _{\mathrm{IB}_{p}\left( T,Fv\right) }\) :
-
catastrophe bond \(\mathrm{IB}_{p}(T,Fv)\) payoff function (see Sect. 4),
- Q :
-
probability measure equivalent to P (see Definition 3 and formula (2)),
- \(\bar{\lambda }_{t}=\left( \bar{\lambda }_{1t},\bar{\lambda }_{2t},\ldots ,\bar{\lambda }_{nt}\right) \) :
-
n-dimensional market price of risk process (see Sect. 4),
- \(\lambda _{1}, \lambda _{2},\ldots ,\lambda _{n}\) :
-
constants defining the market price of risk process (see Sect. 4),
- \(\left\| .\right\| \) :
-
the Euclidean norm in \(\mathbb {R}^{n}\) (see Sect. 4),
- \(\int _{0}^{T^\prime }\bar{\lambda }_{t}\mathrm{d}W_{t}\) :
-
Itô integral of \(\bar{\lambda }\) with respect to W (see (2)),
- \(\int _{0}^{T^\prime }\left\| \bar{\lambda }_{t}\right\| ^{2}\mathrm{d}t\) :
-
Lebesgue integral of \(\left\| \bar{\lambda }\right\| ^{2}\) (see (2)),
- \(\frac{\mathrm{d}Q}{\mathrm{d}P}\) :
-
Radon–Nikodym derivative of Q with respect to P (see (2)),
- P-a.s.:
-
P-almost surely (see (2)),
- \(E^{Q}\left( .|\mathcal {F}_{t}^{1}\right) \) :
-
conditional expected value with respect to \(\sigma \)-field \(\mathcal {F}_{t}^{1}\) and probability measure Q (see Sect. 4),
- \(e_{t}\), \(f_{t}\) :
-
conditional expected values of \(\nu _{\mathrm{IB}_{s}\left( T,Fv\right) }\) and \(\nu _{\mathrm{IB}_{p}\left( T,Fv\right) }\) with respect to \(\sigma \)-field \(\mathcal {F}_{t}^{1}\) and probability measure Q (see Sect. 4),
- \(\left( \varepsilon _{t}\right) _{t\in [0,T^{\prime }]}\) :
-
process describing the deviation of the current view on the long-term level of the interest rate \(r=\left( r_{t}\right) _{t\in [0,T^{\prime }]}\) from the average view (see equations (3)),
- \(a_{r}, b_{r}, \sigma _{r}, a_{\varepsilon }, \sigma _{\varepsilon }, \rho \) :
-
parameters of equations (3), describing the risk-free spot interest rate,
- \(x_{1t}, x_{2t}, t\in {[} 0,T^{\prime }{]}\),:
-
state variables describing general form of the spot interest rate process r under Q (see Sect. 4.2),
- \(\xi _{0},\xi _{i},\hat{\varphi }_{i},\vartheta _{i},v_{ij},\hat{\kappa }_{ij},\Gamma _{ij},\) \(i,j\in \left\{ 1,2\right\} \),:
-
constants describing general form of the spot interest rate process r under Q (see Sect. 4.2),
- \(\tilde{W}_{t}^{1}\), \(\tilde{W}_{t}^{2}\) :
-
Q-Brownian motions (see Sect. 4.2),
- \(a,b_{1},b_{2}\) :
-
functions describing the form of the price of a zero-coupon bond (see Theorem 1 and formulas (5)-(7), (10)-(12)),
- \(\lambda \) :
-
constant describing the market price of risk in Lemma 1 and Theorem 2,
- \(\mathcal {B}_{a_{r}}\), \(\mathcal {B}_{a_{\varepsilon }}\), \(\mathcal {B}_{a_{r}+a_{\varepsilon }}\), \(\mathcal {C}\), \(\mathcal {D}\), \(\mathcal {E}\), \(\mathcal {G}\) :
-
auxiliary functions introduced to shorten formulas describing \(B\left( t,T\right) \) in Lemma 1,
- \(\tau \) :
-
arbitrary element of the interval [0, T] (see Lemma 1),
- \(\hat{\varphi }\) :
-
constant given by formula \(\hat{\varphi }=a_{r}b_{r}-\lambda \sigma _{r}\) (see Lemma 1),
- \(\mathrm{IB}_{s}\left( t\right) \), \(\mathrm{IB}_{p}\left( t\right) \) :
-
prices of the catastrophe bonds \(\mathrm{IB}_{s}\left( T,Fv\right) \), \(\mathrm{IB}_{p}\left( T,Fv\right) \) at moment \(t\in [0,T]\) (see Theorem 2),
- \(E^{Q}\left( .|\mathcal {F}_{t}\right) \) :
-
conditional expected value with respect to \(\sigma \)-field \(\mathcal {F}_{t}\) and probability measure Q (see (23)),
- \(E^{Q}\left( .|\mathcal {F}_{0}^{1}\right) \) :
-
conditional expected value with respect to \(\sigma \)-field \(\mathcal {F}_{t}^{0}\) and probability measure Q (see the proof of Theorem 2),
- \(\nu \) :
-
one of the functions \(\nu _{\mathrm{IB}_{s}\left( T,Fv\right) }, \nu _{\mathrm{IB}_{p}\left( T,Fv\right) }\) (see the proof of Theorem 2),
- \(\mathcal {F}_{t}^{0,1}\) :
-
\(\pi \)-system described in the proof of Theorem 2,
- \(\mathcal {A}\) :
-
\(\lambda \)-system described in the proof of Theorem 2,
- \(c_{t}\) :
-
auxiliary function \(c_{t}=\exp \left( -\int _{t}^{T}r_{u}du\right) \), \(t \in [0,T]\), considered in the proof of Theorem 2,
- R :
-
the set of real numbers (see Sect. 5.1),
- \(\tilde{A}\) :
-
an arbitrary fuzzy subset of R (see Sect. 5.1),
- \(\mu _{\tilde{A}}\) :
-
membership function of a fuzzy set \(\tilde{A}\) (see Sect. 5.1),
- \(\tilde{A}_{\alpha }\), \(\alpha \in {[}0,1{]}\),:
-
denotes \(\alpha \)-level set of a fuzzy set \(\tilde{A}\) (see Sect. 5.1),
- \(\tilde{a}_{\alpha }^{L}, \tilde{a}_{\alpha }^{U}\), \(\alpha \in {[}0,1{]}\),:
-
lower and upper bounds of the \(\alpha \)-level set of a fuzzy number \(\tilde{a}\) (see Sect. 5.1),
- \(\tilde{a}=\left( a_{1},a_{2},a_{3}\right) \) :
-
a triangular fuzzy number (see Sect. 5.1),
- \(\mathbb {F}\left( \mathbb {R}\right) \) :
-
the set of all fuzzy numbers (see Sect. 5.1),
- \(f:R\rightarrow R\) :
-
a function considered in Proposition 1,
- \(\tilde{f}:\mathbb {F}\left( \mathbb {R}\right) \rightarrow \mathbb {F}\left( \mathbb {R}\right) \) :
-
fuzzy-valued function induced by f via the extension principle (see Proposition 1),
- \(\tilde{\sigma }_{r}\), \(\tilde{\sigma }_{\varepsilon }\), \(\tilde{\lambda }_{1}\), \(\tilde{\rho }\) :
-
fuzzy counterparts of parameters \(\sigma _{r}\), \(\sigma _{\varepsilon }\), \(\lambda _{1}\), \(\rho \) (see Sect. 5.2),
- \(\tilde{r}_{t}\), \(\tilde{\varepsilon }_{t}\), \(t\in {[}0,T{]}\),:
-
fuzzy random variables corresponding to \(r_{t}\), \(\varepsilon _{t}\), \(t\in \left[ 0,T\right] \) (see Sect. 5.2),
- \(\Sigma \) :
-
the set of symbols \(\Sigma =\{L,U\}\) (see Sect. 5.2),
- \(A_{i}\left( \tau \right) \), \(i=1,2,3,4\),:
-
auxiliary real-valued functions defined on [0, T] (see Sect. 5.2),
- \(\tilde{a}\left( \tau \right) \) :
-
auxiliary fuzzy number-valued function defined on [0, T] (see (24), (25)),
- \(\tilde{\varphi }\), \(\tilde{\sigma }_{1}\), \(\tilde{\sigma }_{2}\), \(\tilde{\sigma }_{3}\), \(\tilde{\rho }_{2}\) :
-
auxiliary fuzzy parameters equal to \(a_{r}b_{r}\ominus \tilde{\lambda }_{1}\otimes \tilde{\sigma }_{r}\), \(\tilde{\sigma }_{r}\otimes \tilde{\sigma }_{r}\), \(\tilde{\sigma }_{r}\otimes \tilde{\sigma }_{\varepsilon }\), \(\tilde{\sigma }_{\varepsilon }\otimes \tilde{\sigma }_{\varepsilon }\), \(\tilde{\rho }\otimes \tilde{\sigma }_{2}\), respectively (see Sect. 5.2),
- \(\tilde{\mathrm{IB}}_{s}\left( t\right) \), \(\tilde{\mathrm{IB}}_{p}\left( t\right) \) :
-
prices of bonds \(\mathrm{IB}_{s}\left( T,Fv\right) \), \(\mathrm{IB}_{p}\left( T,Fv\right) \) at moment \(t\in [0,T]\) for fuzzy parameters (see Theorem 3),
- \(\tilde{\gamma }\left( \tau ,\tilde{r},\tilde{\varepsilon }\right) \) :
-
auxiliary function used in fuzzy pricing formulas of cat bonds (see Theorem 3),
- \(\Xi \) :
-
an arbitrary element of \(\Sigma \) (see Theorem 3),
- \(\tilde{\mathrm{IB}}\left( t\right) \), \(t\in {[}0,T{]}\),:
-
equal to \(\tilde{\mathrm{IB}}_{s}\left( t\right) \) or \(\tilde{\mathrm{IB}}_{p}\left( t\right) \), \(t\in {[}0,T{]}\), (see Sect. 5.3),
- \(\displaystyle \sup _{0\le \alpha \le 1}\) :
-
supremum with respect to \(\alpha \) satisfying the inequality \(0\le \alpha \le 1\) (see Sect. 5.3),
- \(I_{\left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }}\left( c\right) \) :
-
the indicator function of the set \(\left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }\), equal to 1 if \(c\in \left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }\) and 0 otherwise (see Sect. 5.3),
- \(g,h:{[}0,1{]}\rightarrow \mathbb {R}\) :
-
functions of the form \(g(\alpha )=\left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }^{L}\) and \(h(\alpha )=\left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }^{U}\) (see Sect. 5.3),
- \(\sup \) :
-
supremum of a set (see Sect. 5.3),
- \(\beta _{ \tilde{\mathrm{IB}}\left( t\right) }\left( \hat{c}\right) \), \(\delta _{ \tilde{\mathrm{IB}}\left( t\right) }\left( \hat{c}\right) \) :
-
auxiliary functions of a real argument \(\hat{c}\) defined in Sect. 5.3,
- \(\mathbf {B}\), \(\mathbf {A}\), \(\mathbf {H}\), \(\mathbf {R}\), \(\mathbf {S}\) :
-
possible decisions of a financial analyst: Buy, Accumulate, Hold, Reduce, Sell (see Sect. 6),
- V :
-
set of possible decisions of a financial analyst (see Sect. 6),
- \(\hat{C}_{t}\) :
-
current market price of the catastrophe bond (see Sect. 6),
- \(\min \) :
-
two argument minimum function (see Sect. 6),
- \(2^{V}\) :
-
the set of subsets of V (see Sect. 6),
- \(\Lambda :\mathbb {R}^{2}\rightarrow 2^{V}\) :
-
advice choice function defined in Sect. 6,
- \({[}0,1{]}^\mathbb {R}\) :
-
the space of \(\left[ 0,1\right] \)-valued functions defined on \(\mathbb {R}\) (see Sect. 6),
- \({[}0,1{]}^V\) :
-
the space of \(\left[ 0,1\right] \)-valued functions defined on V (see Sect. 6),
- \(\tilde{\Lambda }:{[}0,1{]}^\mathbb {R}\times \mathbb {R}\rightarrow {[}0,1{]}^{V}\) :
-
extended advice choice function (see Sect. 6),
- \(\tilde{l}\) :
-
the membership function of \(\tilde{\Lambda }\left( \tilde{\mathrm{IB}}\left( t\right) ,\hat{C}_{t}\right) \) defined by formulas (39)–(43).
- \(n_S\) :
-
number of simulations (see Sect. 7)
- a, b, c :
-
parameters used in the sinusoidal intensity function (see (44))
- \(\alpha _0\) :
-
starting value of \(\alpha \) (see Algorithm 1)
- \(\alpha _1\) :
-
limiting value of \(\alpha \) (see Algorithm 1)
- \(\Delta \alpha \) :
-
increment of \(\alpha \) (see Algorithm 1)
- \(n_0\) :
-
number of values of \(\alpha \) approximating the fuzzy price (see Sect. 7.2)
- m :
-
number of fuzzy parameters in the interest rate model (see Sect. 7.2)
- \(\epsilon \) :
-
tolerance used in approximation of the membership value (see Sect. 7.3)
- \(\hat{C}_{t}^g\) :
-
initial value of the current price (see Algorithm 4)
- \(\hat{C}_{t}^h\) :
-
limiting value of the current price (see Algorithm 4)
- \(\Delta \hat{C}_{t}\) :
-
increment of the current price (see Algorithm 4)
- \(\mu _{\mathrm{LN}}\) :
-
location parameter of lognormal distribution (see Sect. 8.1.1)
- \(\sigma _{\mathrm{LN}}\) :
-
scale parameter of lognormal distribution (see Sect. 8.1.1)
- \(Q_{\mathrm{LN-NHPP}} (x)\) :
-
xth quantile of the process of losses for NHPP and lognormal distribution (see Sect. 8.1.1)
- \(\Delta \mathrm{IB}_{p} (0)\) :
-
relative percentage change of the cat bond price compared to the reference value (see Sect. 8.1.2)
- \(\Delta \rho \) :
-
relative percentage change of \(\rho \) compared to the reference value (see Sect. 8.1.2)
- \(\Delta a\) :
-
relative percentage change of a compared to the reference value (see Sect. 8.1.3)
- \(\Delta b\) :
-
relative percentage change of b compared to the reference value (see Sect. 8.1.4)
- \(\Delta \sigma _{r}\) :
-
relative percentage change of \(\sigma _{r}\) compared to the reference value (see Sect. 8.1.5)
- \(\Delta \sigma _{\varepsilon }\) :
-
relative percentage change of \(\sigma _{\varepsilon }\) compared to the reference value (see Sect. 8.1.5)
- \(\xi _{\mathrm{GPD}},\beta _{\mathrm{GPD}}\) :
-
parameters of generalized Pareto distribution (GPD) (see Sect. 8.1.6)
- \(Q_{\mathrm{LN-GPD}} (x)\) :
-
xth quantile of the process of losses for NHPP and GPD (see Sect. 8.1.6)
- \(\Delta \xi _{\mathrm{GPD}}\) :
-
relative percentage change of \(\xi _{\mathrm{GPD}}\) compared to the reference value (see Sect. 8.1.7)
- \(\Delta \beta _{\mathrm{GPD}}\) :
-
relative percentage change of \(\beta _{\mathrm{GPD}}\) compared to the reference value (see Sect. 8.1.7)
2.2 List of operators in order of appearance
-
\(\cup \) union of sets (see Sect. 4),
-
\(\wedge \) two-argument minimum function (see Sect. 4),
-
\(\cap \) intersection of sets (see proof of Theorem 2),
-
\(\oplus \), \(\ominus \), \(\otimes \), \(\oslash \) operator of addition, subtraction, multiplication and division of fuzzy numbers (see Sect. 5.1),
-
\(\odot \) one of the operators: \(\oplus \), \(\ominus \), \(\otimes \), \(\oslash \) (see Sect. 5.1),
-
\(\circ \) one of the operators: \(+\), \(-\), \(*\), / of real numbers (see Sect. 5.1),
-
\(\oplus _{int}\), \(\ominus _{int}\), \(\otimes _{int}\) or \(\oslash _{int}\) operator of addition, subtraction, multiplication and division of closed intervals (see Sect. 5.1),
-
\(\odot _{int}\) one of the operators: \(\oplus _{int}\), \(\ominus _{int}\), \(\otimes _{int}\) or \(\oslash _{int}\) (see Sect. 5.1),
-
\(^\prime : \Sigma \rightarrow \Sigma \) the operator defined by: \(L^\prime =U\) and \(U^\prime =L\) (see Sect. 5.2),
-
\(\text { AND }\) logical conjunction (see Sect. 6).
3 Catastrophe bonds
A single catastrophic event, e.g., an earthquake or a hurricane, could result in damages worth of billions of dollars. Therefore, such event could cause problems with reserves for many insurers or even bankruptcy of these enterprises [see Cummins et al. (2002)]. However, daily fluctuations on worldwide financial markets reach also tens of billions of dollars. Then, new instruments were introduced, which could transfer risk from insurance markets to financial markets [see, e.g., Nowak (1999)].
A catastrophe bond (Act-of-God bond, cat bond) is an example of such instruments aimed at ”packaging” risks into a form of tradable assets [see Cox et al. (2000); George 1999); Nowak and Romaniuk 2009)]. The payment function of the cat bond depends on additional random variable called triggering point, which is connected with occurrence or other properties of specified type of natural catastrophe (like the issuer’s actual losses—e.g., losses from flood, insurance industry index, real parameters of catastrophe—e.g., magnitude of earthquake, etc.). If triggering point occurs, then the structure of payments is changed. Other parameters like region and time interval for catastrophic event are described in detail for catastrophe bond. The payments for cat bonds usually depend also on interest rates.
For example, the A-1 bond issued by USAA in 1997 was connected with losses caused by hurricane on the east coast of USA between July 15, 1997 and December 31, 1997. If the value of losses had been more than $ 1 billion, the coupon of the bond would have been lost.
4 Cat bond pricing
This section is devoted to catastrophe bonds pricing in the crisp case, i.e., valuing the catastrophe instruments under the assumption that all the model parameters are crisp. At the beginning, we present selected elements of stochastic analysis, describe the stochastic model of catastrophe losses and introduce Brownian motion, which is used for description of the risk-free spot interest rate. We also define two types of catastrophe bonds and specify assumptions concerning the considered financial market. Subsequently, we discuss the two-factor Vasicek model of the spot interest rate and complete the zero-coupon bond valuation expression for this interest rate model. Finally, we introduce and prove the catastrophe bonds valuation formulas.
We introduce necessary notations and definitions. Let \(\left( \Omega ,\mathcal {F},P\right) \) be a probability space. We assume that time horizon has the form \(\left[ 0,T^{\prime }\right] \), where \(T^{^{\prime }} < \infty \), and we fix a moment \(T \in \left[ 0,T^{\prime }\right] \). Let \(W_{t}=\left( W_{t}^{1},W_{t}^{2},\ldots ,W_{t}^{n}\right) _{t\in \left[ 0,T^{\prime }\right] }\) be standard, n-dimensional Brownian motion.
Let \(\left( U_{i}\right) _{i=1}^{\infty }\) be a sequence of independent random variables with the same distribution and finite second moment. We treat \(U_{i}\) as the value of losses during ith catastrophic event. To describe the aggregated catastrophe losses till moment t, we will use the compound Poisson process given by formula
where \(\left( N_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\) is a Poisson process with a continuous intensity function \(\kappa :\left[ 0,T^{\prime }\right] \rightarrow \mathbb {R}_{+} \).
The filtration \(\left( \mathcal {F}_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\) is defined by equalities
Moreover, we assume that \(\mathcal {F}=\mathcal {F}_{T^{\prime }}\),
and that \(\left( W_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\), \(\left( N_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\) and \(\left( U_{i}\right) _{i=1}^{\infty }\) are independent. Under the above assumptions, the filtered probability space \(\left( \Omega ,\mathcal {F},\left( \mathcal {F}_{t}\right) _{t\in \left[ 0,T^{\prime }\right] },P\right) \) satisfies the usual conditions.
Let \(\left( B_{t}\right) _{t\in \left[ 0,T^{\prime }\right] }\) denote the banking account, satisfying the standard equation
where r is the risk-free spot interest rate. We will denote by the symbol \(B\left( t,T\right) \) the price at the time t of a zero-coupon bond with the maturity date \(T\le T^{\prime }\) and with the face value equal to 1 .
We attempt to introduce definitions of two types of catastrophe bonds with different payoff structures. Let
be levels of catastrophic losses and let
be sequences of constants such that
The constants \({w_i}\) will be called payment decrease coefficients.
In this section, we denote by \(\wedge \) the two-argument minimum function.
Let \(\tau _{i}:\Omega \rightarrow \left[ 0,T^{\prime }\right] ,\;1\le i\le n\) be a sequence of stopping times defined by the formula
Definition 1
By the symbol \(\mathrm{IB}_{s}(T,Fv)\), we denote catastrophe bond with the face value Fv , the date of maturity and payoff T, satisfying the following conditions:
-
(a)
If the catastrophe does not occur in the period \(\left[ 0,T\right] \) (i.e., \(\tau _{1}>T\)), the bondholder is paid the face value Fv.
-
(b)
If \(\tau _{n}\le T \), the bondholder receives \(Fv (1-\sum ^{n} _{i=1}w_{i})\).
-
(c)
If \(\tau _{k-1}\le T < \tau _{k},\;1<k\le n\), the bondholder receives the face value minus the sum of write-down coefficients in percentage \(Fv (1-\sum ^{k-1}_{i=1} w_{i})\).
Clearly, the catastrophe bond \(\mathrm{IB}_{s}(T,Fv)\) payoff function \(\nu _{\mathrm{IB}_{s}\left( T,Fv\right) }\) can be written in the form:
where I is the indicator function.
In the reminder of this section, we will use the following function of the variable T:
where \(\Phi _{i}\) are cumulative distribution functions of \(\tau _{i}\).
To define the second type of cat bond, we introduce an additional constant \(K_{0}\), such that \(0 \le K_{0}<K_{1}\).
Definition 2
By the symbol \(\mathrm{IB}_{p}\left( T,Fv\right) \), we denote catastrophe bond with the face value Fv, the date of maturity and payoff T and the payoff function of the form
The payoff function of the cat bond \(\mathrm{IB}_{p}\left( T,Fv\right) \) is a piecewise linear function of losses \(\tilde{N}_{T}\). If the catastrophe causing significant level of losses does not occur (i.e., \(\tilde{N}_{T}<K_{0} \)), the bondholder receives the payoff equal to its face value Fv. In case when the aggregated losses are not less then \(K_{n}\), the bondholder receives the payoff equal to \(Fv\left( 1-\sum _{i=1}^{n}w_{i}\right) \). If \(K_{j} \le \tilde{N}_{T}\le K_{j+1}\) for \(j=0,1,\ldots ,n\), the bondholder is paid
and when \(\tilde{N}_{T}\) increases in the interval \([K_{j},K_{j+1}]\) the payoff decreases linearly from value \(Fv\left( 1-\sum _{0\le i<j} w_{i+1}\right) \) to value \(Fv\left( 1-\sum _{0\le i\le j}w_{i+1}\right) \).
Definition 3
The family \(\{B\left( t,T\right) \), \(t\le T\le T^{\prime }\}\) is called arbitrage-free family of zero-coupon bond prices with respect to r, if the following conditions hold:
-
(a)
\(B\left( T,T\right) =1\) for each \(T\in \left[ 0,T^{\prime }\right] .\)
-
(b)
There exists a probability measure Q, equivalent to P, such that for each \(T\in \left[ 0,T^{\prime }\right] \), the process of the discounted price of the zero-coupon bond
$$\begin{aligned} B\left( t,T\right) /B_{t}, t\in \left[ 0,T\right] , \end{aligned}$$is a martingale with respect to Q.
Let \(\bar{\lambda }_{t}=\left( \bar{\lambda }_{1t},\bar{\lambda }_{2t} ,\ldots ,\bar{\lambda }_{nt}\right) \) be the n-dimensional market price of risk process. In our model, we assume that \(\bar{\lambda }_{1t}=\lambda _{1} ,\bar{\lambda }_{2t}=\lambda _{2},\ldots ,\bar{\lambda }_{nt}=\lambda _{n} \) are constants. The following Radon–Nikodym derivative defines a probability measure Q equivalent to P:

where \(\left\| .\right\| \) is the Euclidean norm in \(\mathbb {R}^{n}\).
The family of zero-coupon bond prices B(t, T), where \(0\le t\le T\le T^{\prime }\) is arbitrage free with respect to r for Q defined by (2).
In what follows we assume that investors are neutral toward the natural catastrophe risk. Additionally, we introduce the following notations:
From the independence of the payoff function from W [compare Nowak et al. (2012) and Nowak and Romaniuk (2010b)], it follows that
and
4.1 The two-factor Vasicek model
We now introduce the pricing formulas for the catastrophe bonds under the assumption of the two-factor Vasicek model of the spot interest rate. In the mentioned model, the interest rate is described by the system of stochastic differential equations, which in the form proposed by Hull and White [compare Hull and White (1994)] is given by
The process \(\left( \varepsilon _{t}\right) _{t\in [0,T^{\prime }]}\) represents the deviation of the current view on the long-term level of the interest rate \(\left( r_{t}\right) _{t\in [0,T^{\prime }]}\) from the average view. The parameter \(\rho \in \left[ -1,1\right] \) is the correlation coefficient between changes in the interest rate and changes in the process \(\varepsilon \). We assume that all the parameters (except the correlation coefficient \(\rho \)) in the above equations are positive. The proposed model belongs to the class of Gaussian models.
4.2 Cat bonds valuations formulas
In catastrophe bond pricing formulas, we will apply the zero-coupon bond valuation expression from Munk (2011). However, since the author of the mentioned book did not take into account the case of \(a_{r}=a_{\varepsilon }\), we will use the following Theorem 1 (Theorem 8.1 adapted to the two-factor affine interest rate models) from Munk (2011) to complete the zero-coupon bond pricing expression. The complete expression of B(t, T) will be presented in Lemma 1.
Let us assume that the spot interest rate process r under Q has the form
for the dynamics of the vector of state variables given by
where \(\xi _{0},\xi _{i},\hat{\varphi }_{i},\vartheta _{i},v_{ij},\hat{\kappa }_{ij},\Gamma _{ij},\) \(i,j\in \left\{ 1,2\right\} \), are constants and \(\tilde{W}_{t}^{1}\) and \(\tilde{W}_{t}^{2}\) are independent Q-Brownian motions. We additionally assume that
for all possible values of the vector of state variables.
Theorem 1
In an admissible affine model, the price of a zero-coupon bond has the exponential-affine form
where the deterministic functions \(a,b_{1},b_{2}\) satisfy the system of ordinary differential equations
with the initial conditions \(a\left( 0\right) =0,b\left( 0\right) =0\).
Functions a, \(b_1\), \(b_2\) in the above theorem are auxiliary and they are used for description of the price of a zero-coupon bond.
In the following lemma, we assume that
for a constant \(\lambda \) (compare the proof of Theorem 2). To shorten formula describing \(B\left( t,T\right) \), we introduce additional auxiliary functions: \(\mathcal {B}_{a_{r}}\), \(\mathcal {B}_{a_{\varepsilon }}\), \(\mathcal {B}_{a_{r}+a_{\varepsilon }}\), \(\mathcal {C}\), \(\mathcal {D}\), \(\mathcal {E}\), \(\mathcal {G}\).
Lemma 1
Let the risk-free spot interest rate be described by the two-factor Vasicek model. Then, the zero-coupon bond pricing formula has the following affine-exponential form:
where for \(\tau \) \(\in \left[ 0,T\right] \):
-
(a)
in the case of \(a_{r}\ne a_{\varepsilon }\)
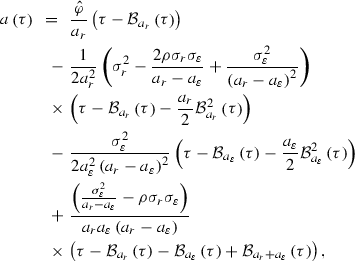 (5)$$\begin{aligned} b_{1}\left( \tau \right) =\mathcal {B}_{a_{r}} \left( \tau \right) , \end{aligned}$$(6)$$\begin{aligned} b_{2}\left( \tau \right) =\frac{1}{ a_{r}-a_{\varepsilon }}\left( \mathcal {B}_{a_{\varepsilon }}\left( \tau \right) -\mathcal {B}_{a_{r}} \left( \tau \right) \right) , \end{aligned}$$(7)$$\begin{aligned} \mathcal {B}_{a_{r}} \left( u\right) \!=\!\frac{1}{a_{r}}\left( 1-e^{-a_{r}u}\right) ,\quad \mathcal {B}_{a_{\varepsilon }}\left( u \right) \!=\!\frac{1}{a_{\varepsilon }}\left( 1-e^{-a_{\varepsilon }u}\right) \nonumber \\ \end{aligned}$$(8)
(5)$$\begin{aligned} b_{1}\left( \tau \right) =\mathcal {B}_{a_{r}} \left( \tau \right) , \end{aligned}$$(6)$$\begin{aligned} b_{2}\left( \tau \right) =\frac{1}{ a_{r}-a_{\varepsilon }}\left( \mathcal {B}_{a_{\varepsilon }}\left( \tau \right) -\mathcal {B}_{a_{r}} \left( \tau \right) \right) , \end{aligned}$$(7)$$\begin{aligned} \mathcal {B}_{a_{r}} \left( u\right) \!=\!\frac{1}{a_{r}}\left( 1-e^{-a_{r}u}\right) ,\quad \mathcal {B}_{a_{\varepsilon }}\left( u \right) \!=\!\frac{1}{a_{\varepsilon }}\left( 1-e^{-a_{\varepsilon }u}\right) \nonumber \\ \end{aligned}$$(8)and
$$\begin{aligned} \mathcal {B}_{a_{r}+a_{\varepsilon }}\left( u \right) =\frac{1}{a_{r}+a_{\varepsilon }}\left( 1-e^{-\left( a_{r}+a_{\varepsilon }\right) u}\right) ; \end{aligned}$$(9) -
(b)
in the case of \(a_{r}= a_{\varepsilon }\)
$$\begin{aligned} a\left( \tau \right)= & {} \frac{\hat{\varphi }}{a_{r}^{2}}\mathcal {C}\left( a_{r} \tau \right) +\frac{1}{8a_{r}^{5}}\left( \sigma _{\varepsilon }^{2}\mathcal {D}\left( a_{r}\tau \right) \right. \nonumber \\&+\left. \rho a_{r}\sigma _{r}\sigma _{\varepsilon }\mathcal {E}\left( a_{r}\tau \right) +a_{r}^{2}\sigma _{r}^{2}\mathcal {G}\left( a_{r}\tau \right) \right) , \end{aligned}$$(10)$$\begin{aligned} b_{1}\left( \tau \right) =\mathcal {B}_{a_{r}} \left( \tau \right) , \end{aligned}$$(11)$$\begin{aligned} b_{2}\left( \tau \right) =\frac{1}{a_{r}^{2}}\left( 1-e^{-a_{r} \tau }-a_{r} \tau e^{-a_{r} \tau }\right) , \end{aligned}$$(12)$$\begin{aligned} \mathcal {B}_{a_{r}} \left( u\right) =\frac{1}{a_{r}}\left( 1-e^{-a_{r}u}\right) , \end{aligned}$$$$\begin{aligned} \mathcal {C}\left( u\right) =e^{-u}+u-1, \end{aligned}$$(13)$$\begin{aligned} \mathcal {D}\left( u\right)= & {} \left( 2u^{2}+6u+5\right) e^{-2u}\nonumber \\&-\,8\left( u+2\right) e^{-u} -4u+11, \end{aligned}$$(14)$$\begin{aligned} \mathcal {E}\left( u\right) =2\left( 2u+3\right) e^{-2u}-8\left( u+3\right) e^{-u} -2\left( 4u-9\right) \nonumber \\ \end{aligned}$$(15)and
$$\begin{aligned} \mathcal {G}\left( u\right) =2\left( e^{-2u}-4e^{-u}-2u+3\right) ; \end{aligned}$$(16)
and \(\hat{\varphi }=a_{r}b_{r}-\lambda \sigma _{r}\) in both cases.
Proof
For the considered two-factor Vasicek model, the system of the ordinary differential equations formulated in Theorem 1 has the form
with the initial conditions \(a\left( 0\right) =0,b\left( 0\right) =0\). The equation (17) has the solution
The solution of (18) in the case of \(a_{r}\ne a_{\varepsilon }\) has the form (7). Moreover, the solution of (19) with \(b_{1}\) and \(b_{2}\) of the form (6) and (7), respectively, is given by (5). The zero-coupon bond pricing formula obtained this way was presented and proved in Munk (2011).
In the case of equal coefficients \(a_{r},a_{\varepsilon }\), the solution of (18) has the form (12). We substitute formulas (11) and (12) into equation (19). Then, we use the equality
to obtain the solution of (19). Applying standard integral operations for right side of (19), we receive the form of \(a\left( \tau \right) \) described by (10) with functions \(\mathcal {C}, \mathcal {D}, \mathcal {E}, \mathcal {G}\) given by (13)-(16) and, finally, the zero-coupon bond pricing formula of the form (4). \(\square \)
Theorem 2
Let \(\mathrm{IB}_{s}\left( t\right) \) and \(\mathrm{IB}_{p}\left( t\right) \) be prices of the catastrophe bonds \(\mathrm{IB}_{s}\left( T,Fv\right) \) and \(\mathrm{IB}_{p}\left( T,Fv\right) \) at moment \(t\in [0,T]\) for the risk-free spot interest rate described by the two-factor Vasicek model. Then
and
where functions \(a,b_{1},b_{2}\) are described by formulas (5)–(7) in the case of \(a_{r}\ne a_{\varepsilon }\) and by (10)–(12) for \(a_{r}=a_{\varepsilon }\).
Proof
We assume that the market price of risk connected with the deviation of the current view on the long-term level of \(r_{t}\) is equal to zero. Then, if \(\lambda _{1}=\lambda \) is a fixed constant, \(\lambda _{2}\) satisfies the following equation:
Therefore, \(\lambda _{2}=-\frac{\rho }{\sqrt{1-\rho ^{2}}}\lambda \). After change of measure according to the formula (2), the Eq. (3) has the form:
where \(\tilde{W}_{t}^{1}\) and \(\tilde{W}_{t}^{2}\) are independent Q-Brownian motions.
Clearly, for each \(t\in [0,T]\)
and, therefore, from Lemma 1, it follows that
where \(a,b_{1},b_{2}\) are described by formulas (5)–(7) in the case of \(a_{r}\ne a_{\varepsilon }\) and by (10)–(12) for \(a_{r}=a_{\varepsilon }\). Moreover, for each \(t\in [0,T]\)
for \(\nu =\nu _{\mathrm{IB}_{s}\left( T,Fv\right) } \text{ or } \nu _{\mathrm{IB}_{p}\left( T,Fv\right) }\). The above formula follows from Dynkin’s Lemma applied to the \(\pi \)-system
and the \(\lambda \)-system \(\mathcal {A}\supset \mathcal {F}_{t}^{0,1}\) of the form
where \(c_{t}=\exp \left( -\int _{t}^{T}r_{u}\mathrm{d}u\right) \). For more details, we refer the reader to the one-factor affine interest rate case considered in Nowak and Romaniuk (2013a). Applying the equality (22) to formula (23), we obtain (20) and (21). \(\square \)
5 Fuzzy approach to catastrophe bonds pricing
In this section, we present and prove the catastrophe bonds pricing formulas, assuming that some model parameters are not precisely known and they are described by fuzzy numbers. We recall basic elements of fuzzy number theory and fuzzy arithmetic. Using Zadeh’s extension principle, we prove fuzzy counterparts of catastrophe bonds valuation expressions introduced in the previous section. Additionally, we derive analytical formulas for \(\alpha \)-level sets of the cat bonds prices. Finally, we discuss a method of computation of values of their membership functions.
5.1 Basic notions and facts
Now we recall some basic notions and facts concerning fuzzy numbers and fuzzy and interval arithmetic.
Let \(\tilde{A}\) be a fuzzy subset of the set of real numbers R. We denote by \(\mu _{\tilde{A}}\) its membership function \(\mu _{\tilde{A}}: R \rightarrow [0,1]\), and by \(\tilde{A}_{\alpha }=\{x:\mu _{\tilde{A}}\left( x\right) \ge \alpha \}\) the \(\alpha \)-level set of \(\tilde{A}\), where \(\tilde{A}_{0}\) is the closure of the set \(\{x:\mu _{\tilde{A}}\left( x\right) >0\}\). \(\tilde{A}\) is called normal if there exists \(x\in R\) such that \(\mu _{\tilde{A}}(x)\).
For a fuzzy number \(\tilde{a}\) [see, e.g., Nowak and Romaniuk (2014b)], the \(\alpha \)-level sets \(\tilde{a}_{\alpha }\), \(\alpha \in [0,1]\), of \(\tilde{a}\) are closed intervals. We denote them by \(\tilde{a}_{\alpha }=\left[ \tilde{a}_{\alpha }^{L},\tilde{a}_{\alpha }^{U}\right] \).
Let \(\odot \) be a binary operator \(\oplus \), \(\ominus \), \(\otimes \) or \(\oslash \) between fuzzy numbers \(\tilde{a}\) and \(\tilde{b}\), corresponding to the related binary operator \(\circ \) between real numbers: \(+\), \(-\), \(\times \) or \(\slash \) via the extension principle. Let \(\odot _{int}\) be a binary operator \(\oplus _{int}\), \(\ominus _{int}\), \(\otimes _{int}\) or \(\oslash _{int}\) between two closed intervals [a, b] and [c, d], defined by
where \(\circ \) is the corresponding to \(\odot _{int} \) operator between real numbers \(+,-,\times \) or \(\slash \) (if the interval [c, d] does not contain zero in the last case).
Let \(\tilde{a},\tilde{b}\) be fuzzy numbers. Then, \(\tilde{a} \odot \tilde{b}\) is also a fuzzy number and the following equalities hold:
if \(\alpha \)-level set \(\tilde{b}_{\alpha }\) does not contain zero for all \(\alpha \in [0,1]\) in the case of \(\oslash \).
A triangular fuzzy number \(\tilde{a}=\left( a_{1},a_{2},a_{3}\right) \) is a fuzzy number with the membership function of the form
We denote by \(\mathbb {F}\left( \mathbb {R}\right) \) the set of all fuzzy numbers. In the further part of this section, we will use the following proposition, proved in Wu (2004).
Proposition 1
Let \(f:R\rightarrow R\) be a function such that for each \(r\in R\) \(\{x:f(x)=r\}\) is a compact set. Then, f induces a fuzzy-valued function \(\tilde{f}:\mathbb {F}\left( \mathbb {R}\right) \rightarrow \mathbb {F}\left( \mathbb {R}\right) \) via the extension principle and for each \(\tilde{\Lambda }\in \mathbb {F}\left( \mathbb {R}\right) \) the \(\alpha \)-level set of \(\tilde{f}(\tilde{\Lambda })\) has the form \({\tilde{f}(\tilde{\Lambda } )}_{\alpha }=\{f(x):x\in \tilde{\Lambda }_{\alpha }\}\).
We will also use fuzzy random variables. For their definition, we refer the reader to Puri and Ralescu (1986).
5.2 Pricing formulas
In practice, some parameters of the financial market (e.g., the market price of risk, the correlation coefficient or the volatility parameters) are not precisely known. Many authors noticed that the uncertainty of the market parameters does not have a stochastic character [see, e.g., Wu (2004)]. Since the parameters are determined by the market which fluctuates from time to time, it is unreasonable to choose their fixed values, obtained from historical data, for later use in pricing formulas. Therefore, to estimate values of the mentioned parameters one can use knowledge of experts, regarding the market price of risk, the correlation coefficient, and the volatility parameters as fuzzy numbers. One can ask experts for forecasts of the parameters values, transfer them into triangular fuzzy numbers, and then use them for estimation of the parameter.
In the remainder of this section, we assume that the above-mentioned parameters are fuzzy numbers of the triangular form. In particular, we introduce fuzzy numbers \(\tilde{\sigma }_{r}\), \(\tilde{\sigma }_{\varepsilon } \), \(\tilde{\lambda }_{1}\), \(\tilde{\rho }\) and fuzzy random variables \(\tilde{r}_{t}\), \(\tilde{\varepsilon }_{t}\), \(t\in \left[ 0,T\right] ,\) in place of their real counterparts \(\sigma _{r}\), \(\sigma _{\varepsilon }\), \(\lambda _{1}\), \(\rho \) and \(r_{t}\), \(\varepsilon _{t}\), \(t\in \left[ 0,T\right] \). We assume that \(\tilde{\sigma }_{r}\) and \(\tilde{\sigma }_{\varepsilon }\) are non-negative fuzzy numbers, i.e., their membership functions are equal to 0 for all negative arguments.
We denote by \(\Sigma \) the set of symbols \(\Sigma =\{L,U\}\) and introduce the operator \(^\prime : \Sigma \rightarrow \Sigma \) by: \(L^\prime =U\) and \(U^\prime =L\).
In the following theorem, we will prove the fuzzy valuation formulas for the two-factor Vasicek interest rate model. Simultaneously, we will correct a simplified version of these formulas from Nowak and Romaniuk (2014a), where only fuzzy volatility parameters were assumed.
To shorten notation, we introduce the following auxiliary real-valued functions defined on [0, T]:
Moreover, we consider an auxiliary fuzzy number-valued function \(\tilde{a}\left( \tau \right) \) defined in the case of \(a_{r}\ne a_{\varepsilon }\) by formula
and in the case of \(a_{r}=a_{\varepsilon }\) by formula
for auxiliary fuzzy parameters
Theorem 3
Assume that \(\tilde{\mathrm{IB}}_{s}\left( t\right) \) and \(\tilde{\mathrm{IB}}_{p}\left( t\right) \) are prices of bonds \(\mathrm{IB}_{s}\left( T,Fv\right) \) and \(\mathrm{IB}_{p}\left( T,Fv\right) \) at moment \(t\in [0,T]\) for the interest rate described by the two-factor Vasicek model and fuzzy parameters \(\tilde{\sigma }_{r}\), \(\tilde{\sigma }_{\varepsilon }\), \(\tilde{\lambda }_{1}\) and \(\tilde{\rho }\). Let for arbitrary \(\tilde{r},\tilde{\varepsilon } \in \mathbb {F}\left( \mathbb {R}\right) \) and \(\tau \in [0,T]\)
where functions \(b_{1}\left( \tau \right) \), \(b_{2}\left( \tau \right) ,\) \(\tilde{a}\left( \tau \right) \) are described by formulas (6), (7), (24) for \(a_{r}\ne a_{\varepsilon }\) and by (11), (12), (25) for \(a_{r}=a_{\varepsilon } \). Then
and
Moreover, for \(\alpha \in [0,1]\) and \(t\in [0,T]\), the following equalities hold:
In the above formulas, for \(\Xi \in \Sigma \),
for \(a_{r}>a_{\varepsilon }\),
for \(a_{r}=a_{\varepsilon }\) and
for \(a_{r}<a_{\varepsilon }\), where
and
Proof
We replace crisp parameters by their fuzzy counterparts and arithmetic operators \(+,-,.\) by \(\oplus \), \(\ominus \), \(\otimes \) in (20) and (21). We obtain formulas (26) and (27). Let \(\alpha \in [0,1]\) and \(\tau \in [0,T]\). Function \(\exp \left( x\right) \) satisfies the assumptions of Proposition 1 and is increasing. Therefore,
i.e., (28) and (29) are satisfied. It is easy to verify the equality (30).
Moreover,
and, therefore, (34) holds. Since \(\tilde{\sigma }_{r}\) and \(\tilde{\sigma }_{\varepsilon }\) are non-negative, (36)–(38) are satisfied. The equalities (31)–(33) follow from the inequalities
and
for \(\tau \in [0,T]\). \(\square \)
5.3 Computational methods
Apart from the forms of \(\alpha \)-level sets of the catastrophe bond price, it is necessary to compute the value of its membership function \(\mu _{\tilde{\mathrm{IB}}\left( t\right) }\left( c\right) \) for arbitrary c. We fix a time moment \(t\in [0,T]\). Let \(\tilde{\mathrm{IB}}\left( t\right) =\tilde{\mathrm{IB}} _{s}\left( t\right) \) or \(\tilde{\mathrm{IB}}_{p}\left( t\right) \).
The equality
describes the membership function of \(\tilde{\mathrm{IB}}\left( t\right) \).
We will use the above formula for computation of the membership function \(\mu _{\tilde{\mathrm{IB}}\left( t\right) }\), applying the method proposed for pricing European options in Wu (2004). From the pricing formulas (see Theorem 3), it follows that the functions \(g,h:[0,1]\rightarrow \mathbb {R}\), where \(g(\alpha )=\left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }^{L}\) and \(h(\alpha )=\left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }^{U}\), are continuous. Moreover, g is increasing, h is decreasing and \(\tilde{\mathrm{IB}}\left( t\right) \) is a normal fuzzy number. The value of \(\mu _{\tilde{\mathrm{IB}}\left( t\right) }\left( c\right) \) can be obtained by solving the optimization problem:

Problem (OP1) can be rewritten to the form:

To solve (OP2), it suffices to consider the following three cases:
-
(i)
If \(g(1)\le c \le h(1)\), then \(\mu _{ \tilde{\mathrm{IB}}\left( t\right) }\left( c\right) =1\).
-
(ii)
If \(c < g(1)\), then one can solve the following relaxed optimization problem:

-
(iii)
If \(c > h(1)\), then one can solve the following relaxed optimization problem:

Problems (OP3) and (OP4) can be solved using bisection search [see Wu (2004)].
In the further part of the paper, we will use the following functions of \(\hat{c}\):
and
One can check that
and
6 Automatized method of decision making
The obtained catastrophe bond pricing formulas can be used for investment decision making. We apply an approach similar to the one used in Piasecki (2014) in another context. We obtain a fuzzy set of possible decisions. A decision maker can choose one of the decisions from its \(\alpha \)-level set for a sufficiently high value of \(\alpha \).
Let \(t\in [0,T]\). For a given \(\alpha \) (e.g., \(\alpha =0.9\)), the \(\alpha \)-level set of \(\tilde{\mathrm{IB}}\left( t\right) \) can be treated by a financial analyst as the interval of the cat bond prices. The financial analyst can choose any value from this interval as the catastrophe bond price with an acceptable membership degree. Such an interval can be a very useful tool for investment decision making.
In particular, apart from a straightforward analysis of \(\alpha \)-level sets of \(\tilde{\mathrm{IB}}\left( t\right) \), the financial analyst can consider the following set of possible decisions:
-
Buy (denoted by \(\mathbf {B}\)), if the price of the catastrophe bond is significantly undervalued;
-
Accumulate (denoted by \(\mathbf {A}\)), if the cat bond is undervalued;
-
Hold (denoted by \(\mathbf {H}\)), if the catastrophe-linked instrument is fairly valued;
-
Reduce (denoted by \(\mathbf {R}\)), if the cat bond is overvalued;
-
Sell (denoted by \(\mathbf {S}\)), if the price of the catastrophe bond is significantly overvalued.
We denote by V the set of the possible decisions
and by \(\hat{C}_{t}\) the current market price of the catastrophe bond. Let \(\mathrm{IB}\left( t\right) =\mathrm{IB}_{s}\left( t\right) \) or \(\mathrm{IB}\left( t\right) =\mathrm{IB}_{p}\left( t\right) \), \(t\in \left[ 0,T\right] .\)
The advice choice function \(\Lambda :\mathbb {R}^{2}\rightarrow 2^{V}\) is defined as follows:
where the symbol \(\text { AND }\) denotes logical conjunction.
Then, by applying the Zadeh extension principle, we obtain the extended advice choice function
The membership function \(\tilde{l}\) of \(\tilde{\Lambda }\left( \tilde{\mathrm{IB}}\left( t\right) ,\hat{C}_{t}\right) \) is defined by formulas:
The financial analyst can choose one of the decisions from the \(\alpha \)-level set \(\tilde{\Lambda }\left( \tilde{\mathrm{IB}}\left( t\right) ,\hat{C}_{t}\right) _{\alpha }\) for a sufficiently high value of \(\alpha \).
7 Algorithms used in simulations
We start from general remarks concerning algorithms which are used in catastrophe bond pricing (see Sect. 7.1 for the crisp case and Sect. 7.2 for the fuzzy case) and in automatized method of decision making (see Sect. 7.3). Then, these algorithms are applied to obtain numerical results in some exemplary cases considered in Sect. 8.
7.1 Cat bond pricing—crisp case
To find the price of the cat bond in the crisp case, we apply Monte Carlo simulations to the results obtained in Theorem 2.
From (20) and (21), it is seen that numerical complexity of the considered model and the related pricing formula depends on two factors: the expected value of the payoff function \(e_t\) or \(f_t\) and the discounting factor related to adopted in this paper two-factor Vasicek model. In the following, Monte Carlo approach is applied to approximate \(e_t\) or \(f_t\). The error of such estimation measured by standard deviation is proportional to \(1 / \sqrt{n_S}\), where \(n_S\) is the number of simulations. But during analysis of the computational complexity, the form (1) of the process \(\tilde{N}_{t}\) should be also taken into account, because the numerical efficiency of simulation of the single trajectory of \(\tilde{N}_{t}\) depends on both types of the Poisson process \(N_t\) and the random distribution of \(U_i\).
We assume that non-homogeneous Poisson process (NHPP) is applied for modeling quantity of losses and that the value of single loss is modeled by lognormal distribution or Pareto distribution. These distributions are commonly used in modeling of risk events in insurance [see, e.g., Chernobai et al. (2006)]. The parameters of the applied distributions were fitted in Chernobai et al. (2006) for real data describing natural catastrophic events in the United States provided by the ISO’s (Insurance Service Office Inc.) Property Claim Services (PCS). The sinusoidal intensity function for NHPP given by the formula
results in a better calibration than simpler homogeneous Poisson process as discussed in Chernobai et al. (2006).
Because of the cyclic form (44) of \(\kappa (t) \), thinning method [see, e.g., Law (2007)] is applied during simulations. Rejection step in this approach results in some loss of the samples generated from the relevant homogeneous Poisson process. For the most straightforward upper bound of (44) given by \(a + b 2 \pi \), the average acceptance rate for the interval [0, T] is equal to
Algorithms for generation of variables from lognormal or Pareto distribution are numerically very fast, like e.g., Marsaglia-Tsang ziggurat algorithm for embedded normal distribution [see Marsaglia and Tsang (2000) for details]. In the case of Pareto distribution, the direct method of inversion of cdf is used. Therefore, to obtain one random variable from the target distribution, only one output from PRNG is sufficient.
Of course other types of NHPP than the formula (44) or other loss distributions could be easily incorporated into the simulation approach. If more complex pdf is necessary, then even Markov Chain Monte Carlo method should be applied.
The whole procedure for finding estimator for \(e_t\) or \(f_t\) constitutes the following algorithm:

In this paper, we assume that the model of interest rates is described by the two-factor Vasicek model. In the following, the parameters for this model fitted in Puhle (2008) are used. Easily seen, two-factor model may be better calibrated to the real-life data than in simpler one-factor approach. Because in Theorem 2, the analytical form of the discount factor is given, then the relevant cat bond price could be directly evaluated without the necessity of subsequent simulations after using Algorithm 1. The price \(\mathrm{IB}_{s}\left( t\right) \) or \(\mathrm{IB}_{p}\left( t\right) \) is straightforward multiplication of the previously estimated expected value of payoffs and the relevant discount factor.
The whole procedure is very fast. We use Intel Core 2 Quad (2.5 GHz) with 4GB RAM, VS Studio 2013 Express compiler, GSL library for random number generation and Mersenne Twister as primary PRNG. Even without sophisticated optimization (like multithreading), finding cat bond price estimator based on sampling 1000000 trajectories takes less than 10 seconds.
7.2 Cat bond pricing—fuzzy case
Now we focus on the cat bond pricing in the fuzzy case. In the following, especially in Sect. 8.2, only triangular fuzzy numbers are considered, but the introduced numerical approach may be also used for other types of LR numbers.
As it is seen from (28) and (29), similarly to the crisp case, the complexity of the considered model and the relevant pricing formulas depends on the (crisp) expected value \(e_t\) or \(f_t\), and the \(\alpha \)-level set related to the discounting factor. The estimator of \(e_t\) and \(f_t\) could be directly found using the Algorithm 1, regardless of the considered value \(\alpha \).
To approximate the fuzzy cat bond price, we fix the value of \(\alpha \) and then find the relevant interval \([g(\alpha ), h(\alpha )] = \left[ \left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }^{L}, \left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }^{U}\right] \) using formulas (28) or (29) depending on the applied payment function. If \(\alpha \) is gradually set to subsequent values, starting from some initial value \(\alpha _0 \in [0,1]\) up to upper bound \(\alpha _1\) (where \(\alpha _1 \in [\alpha _0,1]\)) with given increment \(\Delta \alpha >0\), then the obtained intervals putting on one another form the final output—approximation of the fuzzy cat bond price. It leads us to the following approach:

Apart from the Monte Carlo simulations necessary during the step 1, the computational complexity of the considered fuzzy model directly depends only on method of approximation of the final fuzzy cat bond price. The analytical formulas for endpoints of the \(\alpha \)-level sets of prices are given by Theorem 3. Therefore, for \(n_0\) possible values of \(\alpha \) approximating the fuzzy output, only \(2 n_0 m\) endpoints for \(\alpha \)-level sets of the parameters should be used (where m is number of fuzzy parameters in the model). The above procedure is very fast. Without the first step, using the same platform as in Sect. 7.1, approximation of the fuzzy price for \(n_0=100\) takes 0.054 s.
It should be noted that availability of the fuzzy analytical formulas provided by Theorem 3 is important advantage of the pricing method proposed in this paper. Otherwise, set of even \(n_0 2^m\) possible endpoints for \(\alpha \)-level sets of the parameters should be considered to find fuzzy output.
7.3 Evaluation of the membership values
In this section, we consider the approaches to evaluate membership value \(\alpha \) for the current market price of the cat bond \(\hat{C}_{t}\) which is also useful for automatized decision making introduced in Sect. 6.
As explained in Sect. 5.3, special optimization procedure based on bisection search is used to evaluate membership value \(\alpha \) for the given current market price of the cat bond \(\hat{C}_{t}\), i.e., is used to find \(\mu _{\tilde{\mathrm{IB}}\left( t\right) }\left( \hat{C}_{t}\right) \) solving the problem (OP2) [see also Wu (2004) for detailed description of the relevant algorithm]. In this approach, only the currently used \(\alpha \) varies from step to step of the algorithm, so Monte Carlo estimator of \(e_t\) or \(f_t\) has to be found via Algorithm 1 only once at the beginning of the whole procedure. For the same platform as in Sect. 7.1, evaluation of the membership value for the given \(\hat{C}_{t}\) with tolerance \(\epsilon = 0.00000001\) takes less than 0.01 seconds.
The evaluated membership value could be also used as a source of investment decisions, i.e., to obtain membership functions for the extended advice choice function \(\tilde{\Lambda }\) introduced in Sect. 6.
To calculate the membership functions for various possible decisions from the set V for the fixed current market price \(\hat{C}_{t}\), it is sufficient to evaluate values \(\beta _{ \tilde{\mathrm{IB}}\left( t\right) }\left( \hat{C}_{t}\right) \) and \(\delta _{ \tilde{\mathrm{IB}}\left( t\right) }\left( \hat{C}_{t}\right) \) used in the formulas (39)–(43). Then, we have the following procedure:

Easily seen, even for various \(\hat{C}_{t}\) it is necessary to use Monte Carlo simulations to evaluate \(e_t\) or \(f_t\) only once and then this estimator could be reused. Therefore, the complexity of the main part of Algorithm 3 (apart from the step 1) depends only on the method to solve the problem (OP2), i.e., the bisection search.
To find approximation of the whole membership function for the extended advice choice function \(\tilde{\Lambda }\) for various \(\alpha \) or only for the single fixed value of \(\alpha \), the approach similar to Algorithm 3 could be adopted for the whole range of current prices. As mentioned previously, \(\beta _{ \tilde{\mathrm{IB}}\left( t\right) }\left( \hat{C}_{t}\right) \) and \(\delta _{ \tilde{\mathrm{IB}}\left( t\right) }\left( \hat{C}_{t}\right) \) should be found for \([\hat{C}_{t}^g, \hat{C}_{t}^h]\) starting from some initial value \(\hat{C}_{t}^g < g (0)\) and stopping with \(\hat{C}_{t}^h > h (0)\) with fixed incrementation \(\Delta \hat{C}_{t} >0\). Then, we have the following procedure:

Once again, the most numerically complex part (i.e., Monte Carlo simulations in the step 1) is invoked only once, regardless of the number of points evaluated in the interval \(\left[ \hat{C}_{t}^g, \hat{C}_{t}^h\right] \). For each of this point, the bisection solution in Algorithm 3 is applied only once. Using the same platform as in Sect. 7.1 and for \(n_0=100\), the whole procedure (apart from finding estimators for \(e_t\) or \(f_t\)) takes 0.26 s.
8 Numerical examples and analysis
Based on algorithms introduced in Sect. 7, some numerical examples of cat bond pricing (in both the crisp and the fuzzy environments, see Sects. 8.1 and 8.2, respectively) and automatized decision taking (in the fuzzy case, see Section 8.3) are considered. In each experiment, we conduct \(n_S=1000000\) simulations.
8.1 Cat bond pricing—crisp case
Algorithm 1 from Sect. 7.1 with formulas from Theorem 2 is used to evaluate the cat bond price in the crisp case.
We assume that the face value of the bond in each experiment is set to 1 (one monetary unit assumption) and that the payment function is described by Definition 2. Then, the (crisp) cat bond price \(\mathrm{IB}_{p} (0)\) is given by (21).
8.1.1 Example I.1
As mentioned previously, model of the process of the losses and model of the interest rates are fitted to the real-life data. Then, the parameters of the intensity function (44) are equal to \(a = 30.8750\), \(b=1.6840\) and \(c=0.3396\) [see Chernobai et al. (2006)]. The parameters of the lognormal distribution are set to \(\mu _{\mathrm{LN}} =17.3570\) and \(\sigma _{\mathrm{\mathrm{LN}}} = 1.7643\) [see Chernobai et al. (2006)]. The two-factor Vasicek model is described by the data for term structure of interest rates and \(a_{r}=0.2591\), \(b_{r}=0.0205\), \(\sigma _{r}=0.0073\), \(a_{\varepsilon } = 0.8274\), \(\sigma _{\varepsilon } = 0.0219\), \(\rho = 0.6\), \(r_{0} = 0.025\), \(\varepsilon _{0} = 0\) [see Puhle (2008)].
We set \(n=2\) and \(w_{1} = 0.25, w_{2}=0.5\). The relevant levels of losses (also called triggering points) are connected with surpassing the limits given by quantiles of the cumulated value of losses described by the NHPP process (number of losses) and lognormal distribution (value of each loss). Such xth quantile is denoted by \(Q_{\mathrm{LN}-\mathrm{NHPP}} (x)\). Similar approach was considered in Nowak and Romaniuk (2013b). We assume that \(K_{0} = Q_{\mathrm{LN}-\mathrm{NHPP}} (0.5)\), \(K_{1} = Q_{\mathrm{LN}-\mathrm{NHPP}} (0.75)\) and \(K_{2} = Q_{\mathrm{LN}-\mathrm{NHPP}} (0.95)\). Then, \(\mathrm{IB}_{p} (0)\) is estimated as 0.830485.
In the following, this cat bond price is treated as the reference value for subsequent comparisons. In the next examples, we change values of one or more parameters of the model to verify if these alternations have significant impact on the calculated cat bond prices.
8.1.2 Example I.2
We analyze the relation between the cat bond price and the value \(\rho \) for two-factor Vasicek model, i.e., we find the prices for \(\rho \in [0.1,0.9]\). The other parameters are the same as in Example I.1. Then, only the correlation coefficient for interest rate model is changing. Therefore, we could analyze the situation, e.g., if this parameter is mismatched during the estimation or it will vary in near future compared to the historical data. The outcomes could be also compared with the fuzzification of \(\rho \) considered in Sect. 8.2, which reflects other sources of uncertainty.
The exact cat bond prices \(\mathrm{IB}_{p} (0)\) are given in the third row of Table 1. In the fourth row, the relative percentage change of the actual cat bond price \(\Delta \mathrm{IB}_{p} (0)\) compared to the reference value from Example I.1 is calculated. The relative percentage change \(\Delta \rho \) of the actual \(\rho \) compared to the reference value \(\rho = 0.6\) is given in the second row. As it is seen from Fig. 1, the price as the function of \(\rho \) is increasing and linear, but the variability of the prices is almost negligible (\(\Delta \mathrm{IB}_{p} (0)\) is less than 0.0007 % even for \(\rho = 0.1\)). It should be noted that such numerical analysis is useful and straightforward, because the function of the price depends on \(\rho \) in rather complex way.
Cat bond price \(\mathrm{IB}_{p} (0)\) as the function of parameter a of the intensity function (44) in Example I.3
8.1.3 Example I.3
We analyze the relation between the cat bond price and the value a for the intensity function (44), i.e., we find the prices for the wide interval \(a \in [23,40]\). Then, the overall intensity of the number of losses is lesser or higher than in the case of a fitted to the historical data in Chernobai et al. (2006). Once again, such difference may be caused, e.g., by estimation error or historical data irrelevant for the future. The cat bond price as the function of a is decreasing and almost linear (see Fig. 2 and the third row of Table 2 for some exact values). But in this case the relative percentage changes of price are noticeable (decrease up to almost 9 % for the relative growth of a which is equal to about 26 %). Because of the applied intensity function (44), the overall increase of \(\mathrm{IB}_{p} (0)\) is expected, but the detailed nature of such phenomena has to be numerically determined.
8.1.4 Example I.4
We analyze the relation between the cat bond price and the value b in the intensity function (44), so we find the prices for the wide interval \(b \in [0.5,2.6]\). Then, the intensity of number of losses given by the cyclic part in (44) fluctuates less or more than in the case of historical data from Chernobai et al. (2006), so the number of catastrophes is almost on the same level constantly or more significantly varies from period to period.
Cat bond price \(\mathrm{IB}_{p} (0)\) as the function of parameter b of the intensity function (44) in Example I.4
The cat bond price as the function of b is decreasing and almost linear (see Fig. 3; Table 3) and the relative percentage changes are noticeable, but also lower compared to the previous example (about 6 % decrease of the price if b is increased more than 50 % compared to the reference values from Example I.1). As in the case considered in Sect. 8.1.3, the exact behavior of this function in such setting could be directly analyzed using simulations.
8.1.5 Example I.5
We analyze the relation among the cat bond price and the volatilities \(\sigma _{r}\) and \(\sigma _{\varepsilon }\) in the interest rate model, so we find the prices for \(\sigma _{r} \in [0.001, 0.015]\) and \(\sigma _{\varepsilon } \in [0.005, 0.04]\). The behavior of these parameters is also considered in the fuzzy case in Sect. 8.2. The other parameters are the same as in Example I.1. Therefore, the volatilities vary compared to the historical data from Puhle (2008).
The cuts of the graph (see Fig. 4) for both volatilities (i.e., if one of them is set as constant) seem to be hyperbolic functions. The estimated values of the cat bond prices for \(\sigma _{\varepsilon } =0.0219\) and \(\sigma _{r} = 0.0073\) are given in Tables 4 and 5, respectively. They are also compared there with the reference value from Sect. 8.1.1. For the applied intervals, the relative changes of prices are comparable in scale for both the volatilities.
8.1.6 Example I.6
We apply generalized Pareto distribution (GPD) instead of lognormal distribution for the value of the single loss. The parameters of the GPD are set to \(\xi _{\mathrm{GPD}} =0.8090\), \(\beta _{\mathrm{GPD}} = 5.340 \times 10^{7}\) (see Chernobai et al. (2006)), so they are estimated in the same manner and from the same real-life data as in the previous cases. To enable comparisons, we apply approach similar to Example I.1, so the two-factor Vasicek model is described by the same parameters and we also set \(n=2\) and \(w_{1} = 0.25, w_{2}=0.5\). But the relevant triggering points are given as quantiles of the cumulated value of losses described by the NHPP process and GPD, instead of lognormal distribution. Then, such xth quantile is denoted by \(Q_{\mathrm{GPD}-\mathrm{NHPP}} (x)\). As mentioned previously, we assume that \(K_{0} = Q_{\mathrm{GPD}-\mathrm{NHPP}} (0.5)\), \(K_{1} = Q_{\mathrm{GPD}-\mathrm{NHPP}} (0.75)\) and \(K_{2} = Q_{\mathrm{GPD}-\mathrm{NHPP}} (0.95)\).
In this setting, based on Monte Carlo simulations, the cat bond price is estimated as 0.822337, so the relative percentage change (compared to the reference value from Example I.1) is equal to \(-\)0.9811134458 %. Then in this case, the change of the distribution of the single loss (but with properly estimated parameters) is less significant than, e.g., shift in the parameters discussed in Example I.3.
8.1.7 Example I.7
Similar to the previous cases, the relation among the cat bond price and the parameters \(\xi _{\mathrm{GPD}}, \beta _{\mathrm{GPD}}\) of the distribution of the single loss (given by GPD) is analyzed, so the prices for \(\xi _{\mathrm{GPD}} \in [0.5, 1.1]\) and \(\beta _{\mathrm{GPD}} \in [5.2\times 10^{7}, 5.45\times 10^{7}]\) are found. The other parameters are the same as in Example I.6. Then once again, the parameters of the distribution of the single loss are changed compared to the parameters fitted to the historical data.
As it could be seen (see Fig. 5), the cuts of the graph seem to be hyperbolic (if \(\beta _{\mathrm{GPD}}\) is constant, the exact values are given in the third row of Table 6 for \(\beta _{\mathrm{GPD}} = 5.2\times 10^{7}\)) or almost linear (if \(\xi _{\mathrm{GPD}}\) is constant, see Table 7 for \(\xi _{\mathrm{GPD}} = 0.8\)) in the given intervals of values. The relative percentage changes of prices (compared to the reference value from Example I.6) for both parameters are considerable higher than in all the previous examples (more than 26 % relative reduction of the price if \(\xi _{\mathrm{GPD}}\) is decreased about 38 %). Because of the mentioned hyperbolic shape of function for the fixed \(\beta _{\mathrm{GPD}}\), the possible estimation error or future changes of \(\xi _{\mathrm{GPD}}\) may lead to significant undervaluation of the cat bond price.
8.2 Cat bond pricing—fuzzy case
As noted in Sect. 6, also the fuzzy case of the cat bond prices may be interested for analysts and policyholders because of uncertainty caused by future behavior of the financial market. Therefore, the influence of some fuzzy parameters of the interest rate model on the price is more deeply analyzed using Algorithm 2 introduced in Sect. 7.2.
The overall parameters of the model of losses are the same as in Example I.1—i.e., we assume NHPP of quantity of catastrophic events, and the value of each loss is modeled by lognormal distribution. The applied two-factor Vasicek model arises from parameters considered also in Sect. 8.1.1, and other assumptions about the cat bond are the same as in that setting.
The applied parameters are based on historical data, but because of the uncertainty related to future behavior, the experts’ opinions should be incorporated into estimation of the prices [see, e.g., Nowak and Romaniuk (2014c)].
We focus on three important variables of the interest rate model, namely volatilities \(\sigma _{r}\), \(\sigma _{\varepsilon }\) and the correlation coefficient \(\rho \). They are important part of the model but they could be also wrongly estimated. In the following, only triangular fuzzy numbers are considered, but the similar numerical approach may be also used for other types of LR numbers.
8.2.1 Example II.1
For the parameters \(\sigma _{r}, \sigma _{\varepsilon }, \rho \) we use triangular fuzzy numbers related to the historical values from Puhle (2008). Then, we have
Monte Carlo simulations (see Sect. 7.2) lead to evaluation of the fuzzy cat bond price (see Fig. 6) which is almost triangular and symmetric in its shape.
Fuzzy cat bond price for the triangular fuzzy parameters \(\tilde{\sigma }_{r}, \tilde{\sigma }_{\varepsilon }, \tilde{\rho }\) given by (45) in Example II.1
Fuzzy cat bond price for the triangular fuzzy parameters \(\tilde{\sigma }_{\varepsilon }, \tilde{\rho }\) given by (45) and various \(\tilde{\sigma }_{r}\) ([0.0071, 0.0073, 0.0075] dashed line, [0.0061, 0.0073, 0.0085] solid line, [0.0051, 0.0073, 0.0095] dotted line) in Example II.1
The analyst may be also interested in the behavior of fuzzy numbers. For example, instead of previously used \(\tilde{\sigma }_{r}\), other symmetric triangular fuzzy values of \(\tilde{\sigma }_{r}\) may be used. It is seen from Fig. 7 that for \(\tilde{\sigma }_{r}\) with wider supports, the fuzzy cat bond prices are still LR numbers but with wider supports alike.
8.2.2 Example II.2
Other parameters are also risky factors in the interest rate model, like \(\sigma _{\varepsilon }\). Additionally, experts’ opinions may lead to the triangular fuzzy numbers which are not symmetrical. Therefore, using our numerical approach, example of the fuzzy cat bond price is evaluated for asymmetrical, right-skewed \(\tilde{\sigma }_{\varepsilon } = [0.0119,0.0219,0.0419]\) and \(\tilde{\sigma }_{r} = [0.0071,0.0073,0.0075] \), \( \tilde{\rho } = [0.4,0.6,0.8]\) (see Fig. 8). Then, the fuzzy cat bond price is almost symmetrical but clearly LR, not a triangular, number.
Analysis similar to Example II.1 may be also conducted. The fuzzy cat bond prices evaluated for various asymmetrical values of \(\tilde{\sigma }_{\varepsilon }\) are illustrated in Fig. 9. Once again, for wider support of \(\tilde{\sigma }_{\varepsilon }\), the output fuzzy price has also wider support.
Fuzzy cat bond price for the triangular fuzzy parameters \(\tilde{\sigma }_{r}, \tilde{\rho }\) given by (45) and \(\tilde{\sigma }_{\varepsilon } = [0.0119,0.0219,0.0419]\) in Example II.2
Fuzzy cat bond price for the triangular fuzzy parameters \(\tilde{\sigma }_{r}, \tilde{\rho }\) given by (45) and various \(\tilde{\sigma }_{\varepsilon }\) ([0.0119, 0.0219, 0.0419] dashed line, [0.0019, 0.0219, 0.0619] solid line, [0.0009, 0.0219, 0.0819] dotted line) in Example II.2
8.2.3 Example II.3
For the fixed \(\tilde{\sigma }_{r} = [0.0063,0.0073,0.0083]\) and \(\tilde{\sigma }_{\varepsilon } = [0.0119,0.0219,0.0419]\), the cat bond prices for various types of triangular values \(\tilde{\rho }\) are estimated. In the considered setting, the type of triangular number \(\tilde{\rho }\) (see Fig. 10) has rather moderate effect on the output and both symmetric or asymmetric values of \(\tilde{\rho }\) lead to similar cat bond prices.
8.3 Evaluation of the membership function
Now, we focus on numerical approaches considered in Sect. 7.3. In Sect. 8.3.1, bisection search is used to evaluate membership value \(\alpha \) for the given current market price of the cat bond \(\hat{C}_{t}\). Then, Algorithm 3 is applied in Sect. 8.3.2 to obtain membership functions for the extended advice choice function for the fixed actual cat bond price (i.e., if this current market price with the obtained fuzzy value is compared). Finally, Algorithm 4 is used in Sect. 8.3.3 to find the relevant membership functions for \(\tilde{\Lambda }\) for the whole interval of prices.
8.3.1 Example III.1
As explained in Sect. 7.3, special optimization procedure based on bisection search is used to find membership value \(\alpha \) for the fixed current market price of the cat bond \(\hat{C}_{t}\), i.e., to find \(\mu _{\tilde{\mathrm{IB}}\left( t\right) }\left( \hat{C}_{t}\right) \) solving the problem (OP2). We apply parameters from Sect. 8.2.1 to calculate \(\alpha \) for various \(\hat{C}_{t}\). Some exemplary results for the fixed \(t=0\) are given in Table 8.
8.3.2 Example III.2
Using Algorithm 3, it is possible to evaluate the membership value \(\alpha \) for the extended advice choice function \(\tilde{\Lambda }\) introduced in Sect. 6 for the single fixed current market cat bond price. In Table 9, there are values of \(\alpha \) found for various current market prices \(\hat{C}_{0}\) and possible decisions (to buy/to accumulate/to hold/to reduce/to sell) from the set V. Once again parameters from Sect. 8.2.1 are used to approximate the fuzzy cat bond price.
8.3.3 Example III.3
The whole shape of membership function for each decision from the set V could be also estimated and plotted using Algorithm 4. Applying the parameters from Sect. 8.2.1, the relevant membership functions for the decisions to buy/to accumulate and to hold/to reduce are illustrated in Figs. 11 and 12, respectively.
Additionally, the financial analyst could take relevant decision based on possible recommendations for the fixed value \(\alpha \) of the membership function. The example of such approach is presented in Fig. 13, where \(\alpha = 0.95\) is used. Therefore, knowing the current market price \(\hat{C}_{t}\), the analyst could take his decision based on similar sets.
Decisions (to buy—\(\mathbf {B}\), to accumulate—\(\mathbf {A}\), to hold—\(\mathbf {H}\), to reduce—\(\mathbf {R}\), to sell—\(\mathbf {S}\)) given by the \(\alpha \)-level set of the extended advice choice function for \(\alpha = 0.95\) related to intervals of the current market prices \(\hat{C}_{0}\) in Example III.3
If \(g(\alpha ) = \left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }^{L}\) and \(h (\alpha ) = \left( \tilde{\mathrm{IB}}\left( t\right) \right) _{\alpha }^{U}\) are strictly monotonic functions (as in the previously considered examples), then the simplified approach could be used instead of Algorithm 4. In such case, Algorithm 2 gives the approximation of the fuzzy cat bond price which then leads to the output similar to the one summarized in Fig. 13.
9 Conclusions
The increasing number of natural catastrophes leads to severe problems with stability of insurance industries. Therefore, new financial and insurance instruments are required, such as the catastrophe bonds.
In this paper, we extend our earlier results concerning cat bond pricing. As the model of spot interest rate, we apply the two-factor Vasicek model. We analyze the influence of various parameters on the cat bond price applying Monte Carlo methods.
Moreover, taking into account the uncertainty on the market, we derive fuzzy counterparts of the crisp pricing formulas and present an automated approach for decision making in fuzzy environment with illustrative examples.
References
Besbes K, Allaoui H, Goncalves G, Loukil T (2015) A stochastic approach to product-driven supply chain design. In: Vasant P (ed) Handbook of Research on artificial intelligence techniques and algorithms, IGI Global, pp 82–121
Beynon MJ, Clatworthy M (2013) Analysing the returns-earnings relationship: dempster-shafer theory and evolutionary computation based analyses using the classification and ranking belief simplex. In: Vasant P (ed) Meta-heuristics optimization algorithms in engineering, business, economics, and finance, IGI Global, pp 198–222
Borch K (1974) The mathematical theory of insurance. Lexington Books, Lexington
Cox SH, Fairchild JR, Pedersen H (2000) Economic aspects of securitization of risk. ASTIN Bull 30(1):157–192
Chernobai A, Burnecki K, Rachev S, Trueck S, Weron R (2006) Modeling catastrophe claims with left-truncated severity distributions. Comput Stat 21:537–555
Cummins JD, Doherty N, Lo A (2002) Can insurers pay for the “big one”? Measuring the capacity of insurance market to respond to catastrophic losses. J Bank Finance 26:557–583
Dostál P (2013) The Use of soft computing for optimization in business, economics, and finance. In: Vasant P (ed) Meta-heuristics optimization algorithms in engineering, business, economics, and finance, IGI Global, pp 41–86
Ermoliev YuM, Ermolyeva TYu, McDonald G, Norkin VI (2001) Problems on insurance of catastrophic risks. Cybern Syst Anal 37(2):220–234
George JB (1999) Alternative reinsurance: Using catastrophe bonds and insurance derivatives as a mechanism for increasing capacity in the insurance markets. CPCU J
Gordini N (2014) Genetic algorithms for small enterprises default prediction: empirical evidence from Italy. In: Vasant P (ed) Handbook of research on novel soft computing intelligent algorithms: theory and practical applications, IGI Global, pp 258–293
Hull J, White A (1994) Numerical procedures for implemanting term structure models II: two-factor models. J Deriv, pp 7–16
Kowalski PA, Łukasik S, Charytanowicz M, Kulczycki P (2008) Data-driven fuzzy modeling and control with kernel density based clustering technique. Pol J Environ Stud 17(4C):83–87
Kulczycki P, Charytanowicz M (2005) Bayes sharpening of imprecise information. Int J Appl Math Comput Sci 15(3):393–404
Kulczycki P, Charytanowicz M (2010) A complete gradient clustering algorithm formed with kernel estimators. Int J Appl Math Comput Sci 20(1):123–134
Law AM (2007) Simulation modeling & analysis. McGraw-Hill, New York
Marsaglia G, Tsang WW (2000) The ziggurat method for generating random variables. J Stat Soft 5(8):1–7
Mršić L (2014) Widely applicable multi-variate decision support model for market trend analysis and prediction with case study in retail. In: Vasant P (ed) Handbook of research on novel soft computing intelligent algorithms: theory and practical applications, IGI Global, pp 989–1018
Muermann A (2008) Market price of insurance risk implied by catastrophe derivatives. N Am Actuar J 12(3):221–227
Munk C (2011) Fixed income modelling, Oxford University Press
Nowak P (1999) Analysis of applications of some ex-ante instruments for the transfer of catastrophic risks. IIASA, IR-99-075
Nowak P (2002) On Jacod-Grigelionis characteristics for Hilbert space valued semimartingales. Stoch Anal Appl 20(5):963–998
Nowak P, Romaniuk M (2009) Portfolio of financial and insurance instruments for losses caused by natural catastrophes, In: Wilmowska Z, Borzemski L, Grzech A, Swiatek J (eds) Information systems architecture and technology. IT technologies in knowledge oriented management process, Wroclaw, pp 27–36
Nowak P, Romaniuk M (2010) Computing option price for Levy process with fuzzy parameters. Eur J Oper Res 201(1):206–210
Nowak P, Romaniuk M (2010) Analiza własności portfela złożonego z instrumentów finansowych i ubezpieczeniowych. In: Studia i materiały Polskiego Stowarzyszenia Zarza̧dzania Wiedza̧, vol 31, pp 65–76
Nowak P, Romaniuk M, Ermolieva T (2012) Evaluation of portfolio of financial and insurance instruments: simulation of uncertainty. Lect Notes Econ Math Syst 658:351–366
Nowak P, Romaniuk M (2013) Application of the one-factor affine interest rate models to catastrophe bonds pricing. Research Report, RB/1/2013, SRI PAS, Warszawa
Nowak P, Romaniuk M (2013) Pricing and simulations of catastrophe bonds. Insur Math Econ 52(1):18–28
Nowak P, Romaniuk M (2013) A fuzzy approach to option pricing in a Levy process setting. Int J Appl Math Comput Sci 23(3):613–622
Nowak P, Romaniuk M (2014) Catastrophe bond pricing with fuzzy volatility parameters. In: Köczy LT, Pozna CR, Kacprzyk J (eds) Issues and challenges of intelligent systems and computational intelligence, Springer International Publishing
Nowak P, Romaniuk M (2014) Application of Levy processes and Esscher transformed martingale measures for option pricing in fuzzy framework. J Comput Appl Math 263:129–151
Nowak P, Romaniuk M (2014) Application of the one-factor CIR interest rate model to catastrophe bond pricing under uncertainty. J Autom Mobile Robot Intell Syst 8(3):19–27
Piasecki K (2014) On imprecise investment recommendations. Stud Logic Gramm Rhetor 37(1):179–194
Puhle M (200) Bond portfolio optimization, Springer
Puri ML, Ralescu DA (1986) Fuzzy random variables. J Math Anal Appl 114:409–422
Romaniuk M, Ermolieva T (2005) Application of EDGE software and simulations for integrated catastrophe management. Int J Knowl Syst Sci 2(2):1–9
Shiryaev AN (1999) Essentials of stochastic finance, facts, models, theory, World Scientific
Vasant P, Barsoum N, Webb J (2012) Innovation in power, control, and optimization: emerging energy technologies, IGI Global, Hershey
Vasant PM (2013) Meta-heuristics optimization algorithms in engineering, business, economics, and finance, IGI Global, Hershey
Vasant P (2013) Hybrid mesh adaptive direct search genetic algorithms and line search approaches for fuzzy optimization problems in production planning. In: Zelinka I, Snášel V, Abraham A (eds) Handbook of optimization. Intelligent systems reference library, Springer, Berlin, Heidelberg, pp 779–799
Vasant PM (2014) Handbook of research on novel soft computing intelligent algorithms: theory and practical applications, IGI Global, Hershey
Vasant P (2015) Handbook of research on artificial intelligence techniques and algorithms, IGI Global, Hershey
Vaugirard VE (2003) Pricing catastrophe bonds by an arbitrage approach. Q Rev Econ Finance 43:119–132
Wu H-Ch (2004) Pricing European options based on the fuzzy pattern of Black-Scholes formula. Comput Oper Res 31:1069–1081
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by V. Loia.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nowak, P., Romaniuk, M. Catastrophe bond pricing for the two-factor Vasicek interest rate model with automatized fuzzy decision making. Soft Comput 21, 2575–2597 (2017). https://doi.org/10.1007/s00500-015-1957-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-015-1957-1