Boosted SVM with active learning strategy for imbalanced data

Abstract

In this work, we introduce a novel training method for constructing boosted Support Vector Machines (SVMs) directly from imbalanced data. The proposed solution incorporates the mechanisms of active learning strategy to eliminate redundant instances and more properly estimate misclassification costs for each of the base SVMs in the committee. To evaluate our approach, we make comprehensive experimental studies on the set of $44$ benchmark datasets with various types of imbalance ratio. In addition, we present application of our method to the real-life decision problem related to the short-term loans repayment prediction.

1 Introduction

The imbalanced data phenomenon is known to be one of the fundamental problems in data analysis and prediction. In general, every dataset which exhibits disproportions in the class distribution can be treated as imbalanced. In the context of binary classification problem, we call the majority class to be the one which dominates the training examples and the less prominent one is the minority class. For further consistency we refer to the minority class to as positive and to the major5ity class to as negative. In practice, the imbalanced data issue is observed when disproportion between classes has the impact on the constructed learner that is biased toward majority class. For extremely uneven data distribution, typical learning methods may construct classifiers that have tendency to classify all examples as members of the majority class. The problem of imbalanced data is widely observed in various domains such as medical diagnosis, fraud detection, consumer credit risk assessment and many others (Japkowicz and Stephen 2002).

To solve the manner of the disproportions between classes, various techniques can be applied (He and Garcia 2009). The issue can be solved externally, by applying preprocessing on data before the training procedure. Two techniques are commonly observed in this group: generating artificial examples from minority class (oversampling) and eliminating observations from majority class (undersampling). The most commonly used oversampling technique is SMOTE (Synthetic Minority Over-sampling TEchnique) (Chawla et al. 2002), which generates additional examples situated on the path connecting two neighbors from minority class. Another method in this group is Borderline-SMOTE which is an extension of SMOTE that incorporates in the sampling procedure only the minority data points with a high percentage of the nearest neighbors from majority class (Hui et al. 2005). The policy of undersampling methods is to remove those instances from majority class that are redundant in training procedure and bias the classifier. It is usually performed by random elimination, using $K$-$NN$ algorithm (Mani and Zhang 2003) or evolutionary algorithms (García et al. 2009).

The problem of imbalanced data can be solved directly at the training stage by incorporating proper mechanisms for well-known training methods. In this group, it is possible to distinguish ensemble classifiers such as SMOTEBoost (Chawla et al. 2003), SMOTEBagging (Wang and Yao 2009), RAMOBoost (Chen et al. 2010), which make use of oversampling to diversify the base learners, and models such as UnderBagging (Tao et al. 2006), Roughly Balanced Bagging (Hido et al. 2009), RUSBoost (Seiffert et al. 2010) which apply undersampling before creating each of the component classifiers. In addition to the mentioned learning methods for imbalanced data, other internal techniques are successively applied to construct balanced classifiers, e.g., active learning strategies (Ertekin et al. 2007), granular computing (Tang et al. 2007), or one-sided classification (Manevitz and Yousef 2002).

Beside the internal and external approaches, we can distinguish cost-sensitive techniques that put higher misclassification costs to the minority examples. This group of methods perform inference by assigning weights to each of the examples in the training data as well as adjusting training procedure by introducing different misclassification costs. In this group of techniques, we can identify the algorithms for constructing cost-sensitive models such as decision trees (Drummond and Holte 2000), neural networks (Kukar and Kononenko 1998), SVMs (Morik et al. 1999) and ensemble classifiers (Fan et al. 1999; Wang and Japkowicz 2010; Zięba et al. 2014).

Modern solutions utilize boosted SVM classifiers as high-quality, cost-sensitive predictors (Wang and Japkowicz 2010; Zięba et al. 2014). Despite the high accuracy of prediction of such models confirmed by numerous experiments, the problem of setting proper values of misclassification costs arises during training. To avoid time-consuming calibration of the parameters for each of the classification problems separately, the ratio between negatives and positives is taken as a basis for penalty cost calculation. In such approach, we assume that the value of global imbalance ratio for entire data is similar to the ratio between negatives and positives situated near the borderline. This statement is not always satisfied because of different distribution of examples for different datasets.

To overcome the stated issue, we propose a novel training method for boosting SVM that makes use of active learning strategy to select the most informative examples and more accurately calculate misclassification costs. Each of the base learners of the ensemble is trained on the reduced number of instances, selected to be significant by the previously created component classifier. In this approach, the considered dataset is composed only of the examples situated near the borderline and the penalization terms are calculated basing on local cardinalities of positives and negatives. As a consequence, the consecutive training sets used to construct the base classifiers are more balanced and do not contain redundant and noisy cases.

We identify the borderline examples by introducing the “wide margin” for the base SVM that was created in the previous iteration of constructing the ensemble model. The “wide margin” is the extended “soft margin” obtained in standard training procedure of this component classifier. Therefore, we select all the examples situated in the “wide margin” —the support vectors (beside the “noisy” support vectors located outside) as well as the examples located close to the “soft margin”.

We compare the predictive performance of our solution with other reference methods dedicated to solve the imbalanced data problem. The experiment is carried out for $44$ benchmark datasets. In addition, we apply our training method to the problem of the short-term loans risk analysis and present how to induce reasonable rules from boosting SVM. The short-term loans risk analysis is a typical situation in which data are imbalanced and irregularly distributed.

The paper is organized as follows. In Sect. 2, we describe the novel procedure for constructing boosted SVM. Section 3 contains the results of an experiment showing the quality of the proposed approach. In Sect. 3.2, we present the case study related to the problem of predicting short-term loans risk assessment. The paper is summarized with conclusions in Sect. 4.

2 Methods

2.1 SVM for imbalanced data

The standard SVM¹ is trained by finding the optimal hyperplane $H$ of the following form (Vapnik 1998):

$$\begin{aligned} H : \mathbf {a}^{\top } \phi (\mathbf {x}) + b = 0, \end{aligned}$$

(1)

where $\mathbf {x}$ is the vector of the input values, $\mathbf {a}$ is the vector of the parameters, $b$ is the bias term and $\phi (\cdot )$ is fixed feature-space transformation.

Assume that the training set $\mathbb {S}_{N} =\{\mathbf {x}_{n}, y_{n}\}_{n=1}^{N}$ is given, where $y_n \in \{-1, 1\}$. The problem of training standard SVM can be formulated as the following optimization task:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\min _{\mathbf {a},b}}. &{} Q(\mathbf {a}) = \displaystyle { \frac{1}{2}\mathbf {a}^{T} \mathbf {a} + C \sum _{n=1}^{N} \xi _n} \\ \text {s.t.} &{} y_n(\mathbf {a}^T \phi (\mathbf {x}_{n}) + b) \ge 1 - \xi _n\\ &{} \text {for all } n=1,\ldots , N \end{array} \end{aligned}$$

(2)

where $\xi _{n}$ are slack variables, such that $\xi _{n} \ge 0$ for $n=1,\ldots , N$, and $C$ is the parameter that controls the trade-off between the slack variable penalty and the margin, $C>0$.

The application of the following criterion to imbalanced training data may result in constructing highly biased classifier toward majority class. Therefore, in Zięba et al. (2014), a modified criterion was proposed:

$$\begin{aligned} \begin{array}{rl} \displaystyle {\min _{\mathbf {a},b}}.\ Q(\mathbf {a}) &{}= \displaystyle \frac{1}{2} \mathbf {a}^{\top } \mathbf {a}\\ &{} \displaystyle {+ \frac{C N^2}{2} \Big ( \frac{1}{N_+} \sum _{n \in \mathbb {N}_{+}} w_{n} \xi _{n}} \! +\! \displaystyle {\frac{1}{N_-} \sum _{n \in \mathbb {N}_{-}} w_{n} \xi _{n}} \Big ) \\ \text {s.t.} &{} y_n(\mathbf {a}^T \phi (\mathbf {x}_{n}) + b) \ge 1 - \xi _n \\ &{} \text {for all } n=1,\ldots , N \end{array} \end{aligned}$$

(3)

where $\mathbb {N}_{+} = \{n \in \{1,\dots ,N\} : y_n = 1 \}$ is the set of all positive examples, $\mathbb {N}_{-} = \{n \in \{1,\dots ,N\} : y_n = -1 \}$ is the set of all negative examples, and $N_{+}$, $N_{-}$ are corresponding cardinalities of the sets. Weights $w_n$ are the penalty parameters that fulfill the following conditions:

$$\begin{aligned} \sum _{n=1}^{N} w_{n} = 1 \quad \text { and }\quad w_n > 0 \text { for all } n=1,\ldots , N. \end{aligned}$$

(4)

Notice that weights $w_n$ satisfy the properties of a probability distribution. If we assume equal distribution for $w_n$, i.e., $w_n = \frac{1}{N}$, the accumulated penalization term for the selected positive example is equal $C \frac{N}{2N_+}$ and for chosen negative case is $C \frac{N}{2N_-}$. The cardinality of instances from the positive class is significantly lower than for negative one because of the considered imbalanced data phenomenon. Therefore, the negative receives a higher penalty for improper location relative to the separating hyperplane than the improperly situated positive, and thus the trained classifier is unbiased toward majority class. The classifier trained in this fashion is known as a popular cost-sensitive SVM variation for imbalanced data (further named C-SVM). Parameter $C$ has the same interpretation as for standard SVM. The within-class imbalance issue is handled by applying different values of $w_n$. The process of determining the values of weights will be discussed further in this work.

The stated optimization problem (3) can be formulated in its dual form:

$$\begin{aligned} \begin{array}{rl} \displaystyle {\min _{\varvec{\lambda }}}. &{} Q_{D}(\varvec{\lambda }) = \displaystyle { \sum _{n=1}^{N} \lambda _n - \frac{1}{2} \sum _{i,j=1}^{N}{ \lambda _i \lambda _j y_i y_j k(\mathbf {x}_i , \mathbf {x}_j) } } \\ \text {s.t.} &{} 0 \le \lambda _n \le C \frac{N^2}{2N_+} w_n \\ &{} \displaystyle { \sum _{n=1}^{N}{\lambda _n y_n} = 0 } \\ &{} \text {for all } n=1,\ldots , N, \end{array} \end{aligned}$$

(5)

where $\varvec{\lambda }$ is the vector of Lagrange multipliers. In addition, we have applied the kernel trick, i.e., we have replaced the inner product with the kernel function, $\phi (\mathbf {x}_i)^{\top } \phi (\mathbf {x}_j) = k(\mathbf {x}_i , \mathbf {x}_j)$.

The procedure of classification is made by applying the model:

$$\begin{aligned} h(\mathbf {x}_i) = \mathrm {sign}\Big (\sum _{n \in \mathcal {SV}} y_n \lambda _{n} k(\mathbf {x}_n, \mathbf {x}_i) + b\Big ), \end{aligned}$$

(6)

where $\mathcal {SV}$ denotes the set of indices of the support vectors,² $\mathrm {sign}(a)$ is the signum function that returns $-1$ for $a<0$, and $1$ – otherwise, and the bias parameter is determined as follows:

$$\begin{aligned} b = \frac{1}{N_{\mathcal {SV}}} \sum _{n\in \mathcal {SV}} \Big ( y_{n} - \sum _{m \in \mathcal {SV}} \lambda _{m} y_{m} k(\mathbf {x}_{n}, \mathbf {x}_{m}) \Big ), \end{aligned}$$

(7)

where $N_{\mathcal {SV}}$ is the total number of the support vectors.

2.2 The issue of determining penalty costs

The main drawback of the presented method is a need of incorporating the cardinalities $N_{+}$, $N_{-}$ in the penalty term of the criterion (3) which is minimized to construct the SVM using imbalanced data. The presented method makes the explicit assumption about the ratio between $N_{-}$ and $N_{+}$, so that its growth has very significant impact on the bias degree of the constructed learner. In other words, the higher disproportions between classes are observed, the stronger the tendency of the trained classifier to classify positive examples as negatives. Such an assumption is not always correct in real-life problems. We discuss this issue on a toy example.

Let us consider two artificially generated imbalanced datasets presented in Fig. 1. Both of them have the same cardinality of positive and negative examples, but the distribution over them is noticeable different. In the first case (Fig. 1a), most of the majority examples are situated in the close neighborhood of the separating hyperplane. In the second case (Fig. 1b), the examples from dominating class are clustered far from the classification borderline. Training SVM using the first dataset results in very good predictive accuracy, i.e., the points from two classes seem to be almost perfectly separated. By the introduction of different penalization terms in the training criterion,³ the hyperplane is stabilized in such a form, that two of the minority cases supporting positive class in the region at issue are located on the proper side of the separator and the remaining positive instance was dedicated at the expense of correct classification of a few negatives (see Fig. 1a).

Fig. 1

Optimal hyperplanes for cost-sensitive SVM trained on imbalanced datasets, when: a the most of the majority examples are situated near the hyperplane, b the most of the majority examples are situated far from the hyperplane

On the other hand, if the same type of classifier is trained on the second dataset with the same misclassification costs, the quality of the trained separator is highly debatable. Contrary to the previous case, the considered dataset is balanced in the disputed region, but due to the significantly higher penalty weights for positive examples the classifier is biased toward minority class (see Fig. 1b). As a consequence, the trained classifier “sacrificed” 6 majority points at the expense of 2 correctly classified positives, because the ratio between $N_{+}$ and $N_{-}$ calculated on the entire dataset is equal almost 4. If we associate this result with the ratio of misclassification costs, such debatable behavior of the trained classifier is justified.

From this simple example, we can notice that the ratio between $N_{+}$ and $N_{-}$ does not always inform about how real data are imbalanced in the classification problem. Therefore, it would be essential to propose a technique for selecting informative examples for the training process.

The stated issue can be solved by applying so-called active learning techniques (Settles 2010). These kinds of methods are widely used for given unlabelled data and when the costs of discovering the class labels are too high to receive complete training set. Therefore, there is a need to find the most informative candidates to inquire about objects’ class values. Authors of Ertekin et al. (2007) present the application of the active learning strategy to deal with the imbalanced data issue. In the first step, they generate small pool of the balanced data and train the classifier. Next, they select the most informative example to be incorporated to the training data by applying a novel searching approach. Finally, they correct the location of separating hyperplane by retraining the classifier on the updated data. The entire procedure is repeated until the set of the most informative examples is selected. This approach makes an explicit assumption that the examples located near the borderline tend to be much more balanced than the entire data. Referring to the example presented in Fig. 1a, such a statement is not always satisfied.

2.3 Our Approach

In this work, we propose a boosted SVM with a novel active learning strategy that solves the issue of imbalanced data by proper informative examples selection and misclassification costs estimation. Each of the base SVMs of an ensemble is trained by solving (5) with actual values of weight $w^{(k)}_n$ on the reduced dataset that contains the most informative examples situated near the separating hyperplane. The process of active selection is performed using previously constructed base classifier as an oracle-based selector that makes use of extended margin to locate the most important observations.

The entire procedure is described in Algorithm 1. In the initial step, the starting weights $w_n^{(k)}$ are equal $\frac{1}{N}$. Next, if $k>1$, the dataset $\mathbb {S}_{N_{k}}$ used to construct the $k$-th base learner is determined in the following way:

$$\begin{aligned} \mathbb {S}_{N_{k}} = \{ (\mathbf {x}_n,y_n) \in \mathbb {S}_{N} : y_n y_{k-1}(\mathbf {x}_n) \le 1 + l \}, \end{aligned}$$

(8)

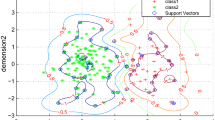
where $y_{k-1}(\mathbf {x}_n)$ represents the output of $(k-1)$-th base SVM and $l$ ($l \ge 0$) is the parameter that stays behind the rescaled distance between extended and separating margins. In the rescaled data space, the width of the margin is equal $2$, and the separating hyperplane is located exactly in the middle, diving it into equidistant space regions. Therefore, the parameter $l$ represents the percentage extension of the margin extracted in the process of training SVM. As a conclusion, the higher value of $l$ is observed, the more examples are selected. Figure 2a presents the exemplary wide margin for an exemplary dataset and Fig. 2b represents the data after the active learning procedure, i.e., the examples selection.

Fig. 2

The application of the wide margin for active selection

The issue of determining the dataset for the first base learner ($k=1$) can be solved by applying one of the typical undersampling techniques. In this work, we recommend to use method called one-sided selection (Kubat and Matwin 1997). The idea of this approach is as follows. First, a negative example is randomly selected from the training set. Next, each of the remaining negatives in the dataset is examined if it is located closer to the selected sample than to any of the positives. If the considered example is located closer to the one of the minority cases, it remains in the training set. Otherwise it is removed from the dataset. This solution is successively applied to identify and eliminate the majority instances located far from the borderline and can be also repeated to eliminate such located examples from the minority class. An exemplary application of the one-sided selection is presented in Fig. 3.

Fig. 3

The application of one-sided selection

Next, after the active learning strategy in the Algorithm 1, the set of base learners $h_{k}$ represented by SVMs is iteratively constructed in the loop. Each of the classifiers is trained on $\mathbb {S}_{N_{k}}$ by solving the optimization problem (5) with actual weight values ($w_n = w^{(k)}_n$ for $n \in \{1,\dots ,N\}$) and with the actual cardinalities of positive examples ($N_{+}=N_{+}^{(k)}, N_{-}=N_{-}^{(k)}$). Therefore, the imbalanced data issue is handled each time the base learner is trained by solving the problem with updated penalization terms calculated basing on cardinalities of positives and negatives situated close to the borderline.

In the following step, the value of error function $e_k$ is calculated using the formula:

$$\begin{aligned} e_k = \frac{E_{Imb}}{\displaystyle {\frac{1}{N_{+}} \sum \nolimits _{n \in \mathcal {N}_{+}}{ w^{(k)}_n}} + \frac{1}{N_{-}}\displaystyle {\sum \nolimits _{n \in \mathcal {N}_{-}}{w^{(k)}_n}}} \end{aligned}$$

(9)

where $E_{Imb}$ is equal:

$$\begin{aligned} E_{Imb}&= \displaystyle {\frac{1}{N_{+}} \sum _{n \in \mathcal {N}_{+}}{w^{(k)}_n I(h_{k}(\mathbf {x}_n)\ne y_n) }} \nonumber \\&+ \displaystyle {\frac{1}{N_{-}}} \displaystyle {\sum _{n \in \mathcal {N}_{-}}{w^{(k)}_n I(h_{k}(\mathbf {x}_n)\ne y_n)}}, \end{aligned}$$

(10)

where $I(\cdot )$ denotes the indicator function. The application of such error function has theoretical justification (see Zięba et al. 2014 for details).

If the error value is lower than $0.5$ it is further used to compute the value of parameter $c_{k}$, which represents the significance of the classifier $h_{k}$ in the committee. The weights are updated using typical AdaBoost procedure to increase the impact of misclassified examples in the training set (Freund et al. 1996). Otherwise, the value of $c_{k}$ is set to $0$ to eliminate the impact of poor learner in the committee, and the weights are reset to the initial values. In addition, the value of parameter $C$ is decreased by multiplying it by $(1-\gamma )$, where $\gamma \in [0,1]$ is an arbitrarily chosen rescaling parameter. As a consequence, the base learners created in the further steps will be more general because of the weaker penalization for incorrectly classified examples.

The output ensemble is composed of the set of base learners with the highest geometric mean (GMean) value. GMean is the typical evaluation criterion for imbalanced data and is described by the equation (Kubat and Matwin 1997):

$$\begin{aligned} GMean = \sqrt{TP_{rate} \cdot TN_{rate}}, \end{aligned}$$

(11)

where $TN_{rate}$ is specificity rate (true negative rate) defined by:

$$\begin{aligned} TN_{rate} = \frac{TN}{TN+FP}, \end{aligned}$$

(12)

and $TP_{rate}$ is sensitivity rate (true positive rate) described by the following equation:

$$\begin{aligned} TP_{rate} = \frac{TP}{TP+FN} \end{aligned}$$

(13)

The meaning of true positive ($TP$), false negative ($FN$), false positive ($FP$) and true negative ($TN$) is explained by confusion matrix (see Table 1), which illustrates prediction tendencies of considered classifier.

Table 1 A confusion matrix

The process of selecting the proper values of parameters is an important issue for training the presented classifier.The $K$ value should be large enough, because we select the subset of base learners with the highest GMean gained on the validation set. As a consequence, the problem of overfitting is handled. For the other parameters, we suggest to use validation set to find their optimal values. Moreover, for the sparsely populated data, we rather recommend to use the linear kernel, than more sophisticated functions, e.g., Radial Basis Functions. By selecting the base learner with lower number of degrees of freedom, we are able to achieve proper model generalization and we avoid overfitting.

3 Experiments

We carry out two experiments:

• Experiment 1: the presented method is evaluated on $44$ benchmark datasets with varying value of imbalance ratio.

• Experiment 2: the presented approach is applied to the real-life decision problem related to the short-term loans repayment prediction.

3.1 Experiment 1: benchmark datasets

3.1.1 Description

In this part of the paper, we examine the quality of the presented approach in comparison to other methods dedicated for imbalanced data on the set of 44 benchmark datasets available in KEEL tool and on website.⁴ Multiclass datasets are modified to obtain two-class imbalanced data by merging some of possible class values (Galar et al. 2012). Detailed description of the datasets is presented in Table 2, where $\mathbf {\#Inst.}$ denotes total number of instances, $\mathbf {\#Attr.}$ is the number of attributes in dataset, $\mathbf {\%P}$ and $\mathbf {\%N}$ represent percentage of positive and negative examples, respectively, and $\mathbf {Imb_{rate}}$ is the imbalance ratio, i.e., the ratio between negative and positive examples.

Table 2 Characteristic of datasets used in experiment (Galar et al. 2012)

As it was noticed in Sect. 2.2, the imbalanced ratio calculated by dividing the cardinalities of the examples from the different classes does not always correspond to the real bias level of the constructed learner trained using typical procedure. To evaluate the real degree of misclassification tendency, we examined the quality of standard SVM trained on each of the datasets. We applied fivefold cross validation and used the GMean as an evaluation criterion. The plot of the results is presented in Fig. 4. It can be observed that the value of imbalanced ratio is weakly correlated with the $GMean$ value achieved by SVM.⁵ For instance, the classifier trained on Ecoli0137vs26 dataset ($ID=42$, $\mathbf {Imb_{rate}}=39.15$) was significantly more balanced ($GMean=0.84$) than the predictor of the same type trained on Haberman data ($ID=11$, $\mathbf {Imb_{rate}}=2.68$, $GMean=0$) despite the fact that the first of them contains only $2.5\,\%$ positives and for the second of the considered benchmarks almost $27.5\,\%$ minority cases were identified. Therefore, the application of the active learning strategy presented in this work for constructing boosted SVM classifier seems to be justified.

Fig. 4

The GMean values for each of the 44 benchmark datasets gained by standard SVM trained with SMO

3.1.2 Methods

The quality of the boosting SVM with active learning strategy (BSIA) was compared with other methods suitable for the imbalanced data:

• SVM (SVM): SVM trained using SMO.

• SVM + SMOTE (SSVM): SVM trained on data oversampled by SMOTE.

• SMOTEBoostSVM (SBSVM): Boosted SVM which uses SMOTE to generate artificial samples before constructing each of base classifiers.

• C-SVM (CSVM): Cost-sensitive SVM described in details in Veropoulos et al. (1999).

• AdaCost (AdaC): Cost-sensitive, ensemble classifier, in which the misclassification cost for minority class is higher than the misclassification cost for majority class (Fan et al. 1999).

• SMOTEBoost (SBO): modified AdaBoost algorithm, in which base classifiers are constructed using SMOTE synthetic sampling (Chawla et al. 2003).

• RUSBoost (RUS): extension of SMOTEBoost approach, which uses additional undersampling in each boosting iteration (Seiffert et al. 2010).

• SMOTEBagging (SB): bagging method, which uses SMOTE to oversample dataset before constructing each of base classifiers (Wang and Yao 2009).

• UnderBagging (UB): bagging method, which randomly undersamples dataset before constructing each of base classifiers (Tao et al. 2006).

• BoostingSVM-IB (BSI): boosted SVM trained with cost-sensitive approach presented in Zięba et al. (2014).

3.1.3 Methodology

As a testing methodology we used fivefold stratified cross validation with a single repetition and each of the methods was tested on the same folds. The values of the training parameters for the reference methods were set basing on the experimental results described in Galar et al. (2012). For BSI and BSIA, we identified the most proper values of the training parameters experimentally by testing their quality on validation set. The quality criterion selected for our studies was GMean because of its very strict penalization for biased models.

3.1.4 Results and discussion

The results of the comprehensive study are presented in Table 3. The analysis of the performance of the considered classifiers leads us to the conclusion that BSIA outperforms other methods by archiving the average GMean value equal $0.8845$. We observed the slight increase of BSIA in comparison to the results obtained by boosted SVM trained without applying additional mechanisms of active selection (BSI). To evaluate the significance of the results, we applied the Holm–Bonferroni method Holm (1979) that is used to counteract the problem of multiple comparisons. First, the set of pairwise Wilcoxon tests is conducted to calculate the $p$ values for the hypothesis about the equality of medians of the both samples. Next, the calculated $p$ values are sorted ascending and the following inequality is examined:

$$\begin{aligned} pval_i \le FWER_i, \end{aligned}$$

(14)

where $pval_i$ represents $i$-th $p$ value in the sequence. The factor $FWER_i$ is familywise error rate and for the given significance level $\alpha$ it can be calculated using the equation:

$$\begin{aligned} FWER_i = \frac{\alpha }{M+1-i}, \end{aligned}$$

(15)

where $M$ is the number of tested hypothesis. If the inequality (15) is satisfied, then the hypothesis about medians equality is rejected. The results for the pairwise tests between BSIA and the reference methods are presented in Table 4. For the set of Wilcoxon test, the $p$ values are lower than the corresponding values $FWER_i$ for a given significance rate $\alpha$ equal $0.05$. Therefore, with the probability equal $95\,\%$, we can say that our approach constructs better predictors than the other methods considered in the experimental studies. To get better insight into the results of GMean, we have presented the boxplot for the best performing methods, including BSIA, see Fig. 5. It can be noticed that BSIA outperforms all methods and performs similarly to UB and BSI. However, it obtains better first quartile in comparison to UB and slightly higher value of minimum of GMean.

Fig. 5

Boxplot for the results of the experiment on the set of the benchmarks according to GMean criterion

Table 3 Results of the experiment on the set of the benchmarks according to GMean criterion

Table 4 Results of Wilcoxon test made between BSIA and reference methods

It is important to highlight that if we select lower significance rate $\alpha$ (e.g. $0.02$) we are not allowed to reject the hypothesis that corresponds to the comparison between BSIA and BSI. Therefore, the deeper analysis of these two methods should be made. The computational complexity of the training procedure for BSI is equal $O(K \cdot N_{svm} \cdot N)$, where $K$ is the total number of base learners, $N_{svm}$ is the maximal number of supporting vectors for each of the constructed SVMs and $N$ is total number of examples in training data. For the BSIA computational complexity is equal $O(K \cdot N_{svm,active} \cdot N_{active})$, where $N_{active}$ represents maximal number of examples selected in the active learning procedure and $N_{svm,active}$ number of detected supporting vectors in the reduced data. Therefore, if the number of active examples is significantly lower than total number of cases ($N_{active}<<N$), the computational costs and memory requirements for training BSIA are visibly lower.

Furthermore, we consider deeper comparison between BSIA and BSI in the context of imbalance ratio. For this purpose, we constructed two subsets of the training datasets considered in the previous experiment. The first one is gained by eliminating 10 datasets with the lowest imbalance ratio and the second one is obtained by excluding 10 datasets with the highest values of imbalance ratio. For the first subset, we gained the mean value of GMean for BSIA equal $0.8924$ and for BSI equal $0.8843$. For the Wilcoxon test, the $p$ value was equal $0.0120$. For the second subset of datasets the mean value of GMean was equal $0.8913$ for BSI and $0.8931$ for BSI2. The $p$ value for that comparison was equal $0.2699$. The presented results show that BSIA outperforms BSI when the imbalance ratio is extremely high. The high quality of BSIA comparing to the results gained by BSI was especially noticeable for datasets Shuttle2vs4 ($ID=35$, $\mathbf {Imb_{rate}}=20.50$) and Ecoli0137vs26 ($ID=42$, $\mathbf {Imb_{rate}}=39.15$) that have high imbalance ratio, but they do not construct as biased learner as for the other sets (see Fig. 4).

3.2 Experiment 2: the short-term loans repayment prediction

3.2.1 Description

In this work, we also consider the problem of 30-day loans risk assessment as a case study for the proposed classifier. The issue of credit risk modeling was initially considered by Durman in 1941, who first proposed the discriminant function that separates “bad” and “good” clients. Recent developments dedicated to solve the problem of constructing decision models that classify credit applicants make use of modern machine learning techniques such as neural networks (West 2000), Gaussian processes (Huang 2011), SVMs (Huang et al. 2007), or ensemble classifiers (Nanni and Lumini 2009). The modern learning methods indicate the necessity to deal with the imbalanced data issue (Huang et al. 2006; Zięba and Świątek 2012), as well as with the need of constructing the comprehensible predictors (Martens et al. 2007).

The short-term loans are typically easier to qualify for, both in terms of income and credit rating, than other types of credits. They are unsecured one-payment loans where no additional collateral is required as a basis for the approval. Moreover, the maximum loan amount varies, depending on the lender, from few hundred to thousands of dollars, relatively to the applicant’s monthly income.

Our goal is to construct the best decision model that can be used to predict whether the applicant will be able to pay the short-term loan. As a suitable model, we recommend to apply boosted SVM trained with the active learning strategy presented in this paper. Therefore, we examined the quality of the solution in comparison to the reference methods on the real-life dataset gathered from a financial institution. In the experiment, we consider the most effective methods (basing on the results presented in Table 3) that deal with the imbalanced data issue: UB, RUS, SSVM and BSI. The intelligibility of the model is extremely important in the loan risk management domain. Therefore, we also took into account two comprehensible models, namely, decision rules inducer JRip and the algorithm for constructing decision trees J48. In addition, we applied the oracle-based procedure of decision rules induction which makes use of the boosted SVM trained with the active learning strategy to relabel the initial data. As the rule inducer we used JRip (we refer this approach in the experiment to as JRip + BSIA). Very similar approach was applied in Craven and Shavlik (1996) for neural netoworks and in Zięba et al. (2014) for SVMs.

The data used in the experiment were composed of 1,146 applicants, each described by $11$ features including gender and age of the client, his monthly income and applied credit amount. We considered two-class problem in which the first class (assumed to be negative) represented the situation in which the consumer made timely repayment of the financial liability and the second class (positive) meant that the client had large problems with settling the debt. We identified a strong imbalance issue with negative/positive ratio equal $7.13$.

3.2.2 Results and discussion

The results of the experiment are presented in Table 5. For the methods that have incorporated mechanisms of dealing with imbalance data issue, the most stable classifier was BSIA that gained the results of $TP_{rate}$, $TN_{rate}$ and $GMean$ near $0.63$. The other reference algorithms were slightly biased either towards minority class (UB, SSVM) or majority class (RUS, BSI) and received lower $GMean$ value than BSIA. The comprehensible models failed completely in loan repayment prediction for the considered dataset and were totally biased toward the majority class. However, the JRip rules inducer trained on the relabelled data by boosted SVM performed comparably to the strongest “black box” imbalance resistant models considered in the experiment. Therefore, we can successfully obtain a comprehensible model using the BSIA as the oracle.

Table 5 Results of the experiment for short-term loans dataset

4 Conclusion and future work

In this work, we proposed the novel method for constructing boosted SVM that makes use of active learning strategy to eliminate redundant instances and more properly estimate the misclassification costs. The outlined method was compared to the ensemble of SVMs as well as to other reference methods that consider the imbalanced data issue. The results obtained within the experiment, i.e., on the representative number of benchmark datasets, supported by the statistical tests show that the presented modification of the training procedure improves the prediction ability of boosted SVM significantly. We also presented the real-life case study related to the problem of the short-term loans repayment prediction for which our solution achieved promising results comparing to other approaches. Moreover, we showed that our approach can be successfully applied as the oracle for rules induction which is an important issue in credit risk assessment.

Furthermore, we plan to adjust our model to the multi-class problem. This issue can be handled by applying a technique that combines two-class models, e.g., one-versus-rest. In addition, it would be beneficial to propose a tuning method for finding optimal width of the “wide margin”. However, we leave investigating these issues as future research.