Some global topological properties of a free boundary problem appearing in a two dimensional controlled ruin problem

Abstract

In this paper a two-dimensional Brownian motion (modeling the endowment of two companies), absorbed at the boundary of the positive quadrant, with controlled drift, is considered. The volatilities of the Brownian motions are different. We control the drifts of these processes and allow that both drifts add up to the maximal value of one. Our target is to choose the strategy in a way, s.t. the probability that both companies survive is maximized. It turns out that the state space of the problem is divided into two sets. In one set the first company gets the full drift, and in the other set the second one. We describe some topological properties of these sets and their separating curve.

1 Introduction

In this paper we investigate the following problem: Given is a two dimensional stochastic process, “living” in the positive quadrant. The individual components of the process are independent Brownian motions, with different volatilities and controllable non negative drift. The total drift should add up to one. The aim of the control is to maximize the probability that the two-dimensional process stays in the positive quadrant, in the following denoted by G, forever. (At least) two economic interpretations are possible: The first one, given by McKean and Shepp in [17], is that a government can influence the drift of the wealth of the companies by a certain tax policy, but the total amount of “support” is bounded by the condition that the sum of the drifts is one. The aim is that both companies should survive. On the other hand, formulating the model a bit different (see Sect. 2), one could also imagine two collaborating companies, again with the aim that both of them survive. Collaborating companies were considered in Actuarial Mathematics recently, also with different objectives, e.g., to maximize expected discounted dividends until ruin, see. e.g. [14] and [16]. For our problem described above, we show that G is separated into two connected sets, where on the one set one has to give the full support to one company, and on the complement full support is provided for the other one. The sets are separated by a $C^1$-curve.

Let us note that, for the case of equal volatilities, it was shown in [17] - by guessing explicitly the value function of the problem - that this separating curve is just the first median, i.e., the optimal strategy is, what they called a push-bottom strategy. This means that full support is given to the weaker company. The authors also mention that the case of different volatilities is open. It is clear that global results on the structure of the solution depend crucially on the boundary conditions of the problem. And indeed, if one replaces the homogeneous boundary data (implied by the “ruin-type problem”) on the finite part of our domain by different ones, our results would not be true any more, see [17] and [12]. Let us finally mention a result, proved in [13], namely that in the case that one of the volatilities appearing in the problem is small one finds, using methods from singular perturbation theory: There exists a function approximating the value function of the problem arbitrary well, and this function is provided explicitly. It turns out that this approximating value function, resp. the corresponding $\epsilon$-optimal strategy, has the properties, which we shall prove in the present paper for the optimal strategy (allowing also general positive volatilities, and not necessarily small ones). Finally, let us mention that one can find some results for the case of correlated Brownian motions, in [15].

Our problem can be seen as a two-phase problem, and the structure of the Hamilton-Jabobi-Bellman (HJB) equation (see Sect. 3) is similar to the one considered in [4]; the difference being that in their case the min-operator applies to two second order elliptic operators, where in our case the max operator applies to elliptic operators with second and first order ingredients, with identical second order ones. In [4] regularity results for their problem were proved. In general it seems that there are not a lot of results in the literature where two different operators appear in the formulation of the FBP, see Sect. 4 of [7]. Moreover, there exists a vast literature concerning regularity and local results for free boundary problems, see e.g. [5] or [19] and the references therein. Results on more global or topological properties seem to be not so numerous. One example would be [9]. Our paper is intended to be a contribution in this direction.

2 The model

We consider the following two-dimensional controlled ruin problem. Let us denote the wealth of two companies by $(X_t)_{t\ge 0}$, resp. $(Y_t)_{t\ge 0}$, and the corresponding two dimensional state process by $(Z_t)_{t\ge 0}$, i.e.

$$\begin{aligned} Z_t = { X_t \atopwithdelims ()Y_t }={x+\int _0^t u_s \, ds+B^{(1)}_t \atopwithdelims ()y+\int _0^t (1-u_s) \, ds+\sigma B^{(2)}_t }. \end{aligned}$$

(1)

Here $(x,y)=:z$ denotes the initial endowment of the companies, $B^{(1)},B^{(2)}$ are independent standard Brownian motions, and $u_t$ is our control processes. We will write G for the positive quadrant, i.e. $G:=\{(x,y)|x>0,y>0\}$, and $\sigma$ denotes a positive constant. Moreover, we define the ruin time $\tau =\inf \{t>0 |Z_t \notin G\}$, i.e. the first time at which one of the two companies is ruined. Finally, we define the set of admissible strategies u as

$$\begin{aligned} {{{\mathcal {U}}}}_{x,y}:= \{ u| u_t = {\hat{u}}(Z_t)\hbox { for a Borel measurable function }{\hat{u}}(z); 0 \le u_t \le 1\}. \end{aligned}$$

(2)

For the unique solution of the SDE’s in (1) above, see [24]. Our aim is to maximize the target functional, given by

$$\begin{aligned} J(x,y,u)={\textbf{P}}_{x,y} \left( \tau =\infty \right) \rightarrow \max , \end{aligned}$$

(3)

where

$$\begin{aligned}{} & {} \tau _1:= \inf \{ t>0 | X_t =0 \}, \nonumber \\{} & {} \tau _2:= \inf \{ t>0 | Y_t =0 \}, \nonumber \\{} & {} \tau := \tau _1 \wedge \tau _2, \end{aligned}$$

(4)

i.e. the probability that both companies survive should be maximized. The value function of the problem is given by

$$\begin{aligned} V(x,y):=\sup _{u\in {{{\mathcal {U}}}}} J(x,y,u). \end{aligned}$$

(5)

Note that, writing the drift vector as ${ 1/2 +{\hat{u}}_t \atopwithdelims ()1/2-{\hat{u}}_t }$, models two collaborating companies with transfer payments ${\hat{u}}$, with the goal that both survive. This is the second interpretation mentioned in the introduction.

3 Preliminary results

Let us start with the definition of an anisotropic Laplacian $\Delta ^{(\sigma )}:=\frac{\partial ^2}{\partial x^2}+\sigma ^2\frac{\partial ^2}{\partial y^2}$. The HJB equation corresponding to our problem then reads

$$\begin{aligned} {{{\mathcal {L}}}} V:= \max \{V_x,V_y\}+\frac{1}{2}\Delta ^{(\sigma )}V=0. \end{aligned}$$

As in [12], Theorem 3.1, Proposition 3.1 and Proposition 3.2, we find the following three results. The proofs are very similar as in [12], but for convenience of the reader we provide them.

Theorem 3.1

There exists a bounded solution $V \in C({\overline{G}}) \cap C^2(G)$ of the system

$$\begin{aligned} {{{\mathcal {L}}}}V=0, \\ V(x,0)= 0,\\ V(0,y)= 0,\\ \lim _{x \rightarrow \infty , y\rightarrow \infty }V(x,y)=1. \end{aligned}$$

Proof

We first consider the problem on a sequence of increasing squares converging to G, i.e. we consider

$$\begin{aligned}{} & {} {{{\mathcal {L}}}}V^{(R)}=0,\hbox {on }Q_{R}:=(0,R)\times (0,R),\nonumber \\{} & {} V^{(R)}(x,y)= w(x,y),\hbox {on }\partial Q_{R}, \end{aligned}$$

(6)

where $w(x,y):=(1-e^{-2x})(1-e^{-2y/\sigma ^2})$ holds. One can check that

$$\begin{aligned} {{{\mathcal {L}}}}w= \max \left( \frac{2e^{-2y/\sigma ^2}}{\sigma ^2}(-1+e^{-2x}), 2e^{-2x}(-1+e^{-2y/\sigma ^2})\right) <0 \end{aligned}$$

holds By Theorem 12.5 of [11], this system has a solution $V^{(R)}\in C^{2,\beta }(Q_{R}) \cap C({\overline{Q_{R}}})$.

We have now

Claim 1. For $0<R_1<R_2$, $V^{(R_1)}\ge V^{(R_2)}$ holds on $Q_{R_1}$.

We first show

$$\begin{aligned} V^{(R_2)}\le V^{(R_1)}=w \end{aligned}$$

(7)

on $\partial Q_{R_1}$. For this it is clearly sufficient that

$$\begin{aligned} V^{(R_2)}\le w \end{aligned}$$

(8)

on ${\overline{Q}}_{R_2}$ holds. We note that the left hand side and the right hand side of (8) coincide on $\partial Q_{R_2}$, and that

$$\begin{aligned} {{{\mathcal {L}}}} w <0,\\ {{{\mathcal {L}}}} V^{(R_2)}=0 \end{aligned}$$

in $Q_{R_2}$ holds. This gives by a classical comparison principle (see e.g. [21], Theorem 2.1.4) assertion (8), hence (7). The same comparison principle proves now Claim 1.

We now denote a strictly increasing sequence of positive numbers tending to infinity as $R_i$, and get, since we have by the maximum principle clearly $V^{(R_i)}\ge 0$ on ${\overline{Q}}_{R_i}$, a monotone decreasing sequence $V^{(R_i)}$, bounded below by zero. We denote its limit by V(x, y), i.e.

$$\begin{aligned} V^{(R_i)}\searrow V \le w \end{aligned}$$

(9)

on ${\overline{G}}$, for $i\rightarrow \infty$. To simplify notation, we shall write in the sequel $V^{(i)}$ for $V^{(R_i)}$, and $Q_{i}$ for $Q_{R_i}$.

The limit V(x, y) clearly fulfills the second and third equation of Theorem 3.1, and we are going to show now that the first one is fulfilled as well.

For fixed $R_1>0$, we have

$$\begin{aligned} V^{(i)}\searrow V \hbox { uniformly on }Q_1\hbox { as }R_i \nearrow \infty \end{aligned}$$

(10)

Define W as the classical solution of the problem

$$\begin{aligned} {{{\mathcal {L}}}}W=0 \text{ in } Q_1,\hspace{1cm}W=V\hbox { on }\partial Q_1. \end{aligned}$$

(11)

Then we must have $W\equiv V$ on $Q_1$, because by the maximum principle,

$$\begin{aligned} |W-V|=\lim _{R_i\rightarrow \infty }\left| W-V^{(i)}\right| = \lim _{R_i\rightarrow \infty }\sup _{\partial Q_{R_1}}\left| W-V^{(i)}\right| =0. \end{aligned}$$

(12)

As V is continuous, and by construction bounded, everything is proved, but the fourth equation of the assertion. We show it now.

Let $v(x,y):=1-e^{-x}-e^{-y/\sigma ^2}$. By plugging in we get

$$\begin{aligned} {{{\mathcal {L}}}}v= \max (e^{-x},\frac{1}{\sigma ^2}e^{-y/\sigma ^2})-\frac{1}{2}\left( e^{-x}+\frac{1}{\sigma ^2}e^{-y/\sigma ^2}\right) \ge 0. \end{aligned}$$

(13)

We consider now

$$\begin{aligned}{} & {} {{{\mathcal {L}}}}{\underline{V}}^{(i)}=0,\hbox {on }Q_{i}=(0,R_i)\times (0,R_i),\nonumber \\{} & {} {\underline{V}}^{(i)}(x,y)= v(x,y),\hbox {on }\partial Q_{i}, \end{aligned}$$

(14)

with a solution ${\underline{V}}^{(i)}\in C^{2,\beta }(Q_{i}) \cap C({\overline{Q_{i}}})$. Exactly as Claim 1, one gets - using the same notation as in the proof of Claim 1 -

Claim 2. For $0<R_1<R_2$, ${\underline{V}}^{(1)}\le {\underline{V}}^{(2)}$ holds on $Q_1$.

Moreover the ${\underline{V}}^{(i)}$ are clearly bounded above by the value 1. We denote the limit of the increasing sequence by $V^*$, i.e. we find

$$\begin{aligned} v \le V^{(i)}\nearrow V^*. \end{aligned}$$

(15)

By construction we have $V^* \le V$, and this together with (15) implies

$$\begin{aligned} v\le V, \end{aligned}$$

(16)

which immediately provides $\lim _{x \rightarrow \infty , y\rightarrow \infty }V(x,y)=1$, since V is bounded above by 1. $\square$

Proposition 3.1

The function V(x, y) constructed in Theorem 3.1 is the value function of our problem (5).

Proof

Using the notation from Sect. 2, we first introduce the stopped process

$$\begin{aligned} R_t^{\tau _1}:=1-e^{-2X^{\tau _1}_t}. \end{aligned}$$

Ito’s Lemma implies

$$\begin{aligned} dR^{\tau _1}_t=2e^{-2X_t^{\tau ^1}}\left( u_t-1\right) \,dt+2e^{-2X_t^{\tau ^1}}dB^{(1)}_t. \end{aligned}$$

Since $u_t \in [0,1]$, $R^{\tau _1}_t$ is a local supermartingale, and because it is bounded from above and below it is a true bounded supermartingale. Hence,

$$\begin{aligned} \lim _{t\rightarrow \infty } R^{\tau _1}_t \end{aligned}$$

exists a.s., and therefore

$$\begin{aligned} \lim _{t\rightarrow \infty } X^{\tau _1}_t \end{aligned}$$

exists a.s.. Clearly, on $\{\tau _1=\infty \}$ $X_t$ can not converge to a finite limit, hence we have

$$\begin{aligned} \lim _{t\rightarrow \infty } X_t=\infty , \hspace{0.8cm}a.s. \end{aligned}$$

on $\{\tau _1=\infty \}$. Analogously, one gets, using

$$\begin{aligned} S_t^{\tau _2}:=1-e^{-\frac{2}{\sigma ^2}Y^{\tau _2}_t}, \end{aligned}$$

$\lim _{t\rightarrow \infty } Y_t=\infty$ a.s., on $\{\tau _2=\infty \}$. Altogether, we end up with

$$\begin{aligned} \lim _{t\rightarrow \infty } X_t=\lim _{t\rightarrow \infty } Y_t=\infty , \end{aligned}$$

on $\{\tau =\infty \}=\{\tau _1=\infty \} \cap \{\tau _2=\infty \}$.

The rest of the proof follows a standard pattern. Let $\rho _N:= \inf \left\{ t>0 |(X_t,Y_t) \notin Q_N \right\}$, where N is large enough, s.t. $(x,y) \in Q_N$. Consider an arbitrary admissible strategy u and apply Ito’s formula to get

$$\begin{aligned} V\left( X_{\tau \wedge \rho _N \wedge t},Y_{\tau \wedge \rho _N \wedge t}\right)= & {} V(x,y) +\int _0^{\tau \wedge \rho _N \wedge t}V_x(X_s,Y_s)u\,ds\\{} & {} +\int _0^{\tau \wedge \rho _N \wedge t}V_y(X_s,Y_s)(1-u)\,ds+\frac{1}{2}\int _0^{\tau \wedge \rho _N \wedge t}\Delta ^{(\sigma )}V(X_s,Y_s)\,ds\\{} & {} + \int _0^{\tau \wedge \rho _N \wedge t}V_x(X_s,Y_s)\,dB^{(1)}_s+\int _0^{\tau \wedge \rho _N \wedge t}\sigma V_y(X_s,Y_s)\,dB^{(2)}_s \end{aligned}$$

Since $V_x$ and $V_y$ are bounded in $Q_N$ the expected value of the stochastic integrals vanishes, and we get

$$\begin{aligned}{} & {} {\textbf{E}}\left[ V\left( X_{\tau \wedge \rho _N \wedge t},Y_{\tau \wedge \rho _N \wedge t}\right) \right] =V(x,y)\nonumber \\{} & {} \qquad +{\textbf{E}}\left[ \int _0^{\tau \wedge \rho _N \wedge t}V_x(X_s,Y_s)u+V_y(X_s,Y_s)(1-u) +\frac{1}{2}\Delta ^{(\sigma )}V(X_s,Y_s)\,ds \right] \nonumber \\{} & {} \quad \le V(x,y), \end{aligned}$$

(17)

where we have used in the last inequality the HJB equation. Letting $N\rightarrow \infty$ (V is bounded !) we find

$$\begin{aligned} {\textbf{E}}\left[ V\left( X_{\tau \wedge t},Y_{\tau \wedge t}\right) \right] \le V(x,y). \end{aligned}$$

Now, since we have $\lim _{x \rightarrow \infty , y\rightarrow \infty }V(x,y)=1$, by Theorem 3.1, the left hand side of the previous inequality tends for $t\rightarrow \infty$

$$\begin{aligned} {\textbf{E}}\left[ {\textbf{1}}_{\{\tau =\infty \}}\right] ={\textbf{P}}(\tau =\infty )=J(x,y,u). \end{aligned}$$

All together we have $J(x,y,u) \le V(x,y)$ for all admissible strategies u.

Using instead of an arbitrary admissible strategy u the strategy

$$\begin{aligned} u^*:= \left\{ \begin{array}{ll} 1,&{} V_x\ge V_y, \\ 0, &{}V_x <V_y, \end{array} \right. \end{aligned}$$

we get in the previous proof an equality instead of an inequality in (17), hence $J(x,y,u^*)=V(x,y)$, concluding our proof. $\square$

Proposition 3.2

The value function V(x, y) fulfills $V \in C^2({\overline{G}} {\setminus } \{(0,0)\})$.

Proof

Let $G_1$ be an arbitrary bounded domain with smooth boundary, s.t. $\overline{G_1}\cap \partial G =:T \ne \emptyset$. Writing the basic PDE as

$$\begin{aligned} \frac{1}{2} \Delta ^{(\sigma )}V =h(x,y):= -\max \left( V_x,V_y\right) , \end{aligned}$$

and viewing the r.h.s. as known inhomogeneity, we get, by applying [11], Corollary 8.36, that $V \in C^{1,\alpha }(G_1 \cup T)$, with arbitrary $\alpha <1$. Hence, we get that h(x, y) is actually an element of $C^\alpha ({\overline{G}}_1)$, (by considering the problem on a slightly larger set $G_2$, with $G_2 \supset {\overline{G}}_1 {\setminus } T$), and we get finally, by [11], Lemma 6.18, $V \in C^{2,\alpha }(G_1 \cup T) \subset C^2(G_1 \cup T)$. Since our set $G_1$ was arbitrary, this suffices. $\square$

The following result (originally) by Hartman and Wintner will be crucial for our paper. So, for convenience of the reader, we state it explicitly.

Theorem 3.2

Let $u \in W^{2,2}_{loc}(\Omega )$ be a non constant solution of

$$\begin{aligned} \sum _{i,j=1}^2 a_{ij}u_{x_i\,x_j}+ \sum _{i=1}^2 b_{i}u_{x_i}=0, \end{aligned}$$

where the $a_{ij}$ are Lipschitz, symmetric in i, j and fulfill a uniform ellipticity condition, $i,j=1,2$. The $b_{i}$ are bounded, $i=1,2$.

For every $x^0 \in \Omega$, there exists an integer $n\ge 1$ and a homogeneous harmonic polynomial $H_n$, of degree n, such that u satisfies, as $x \rightarrow x^0$,

$$\begin{aligned} u(x)=u(x^0)+H_n(K(x^0)\cdot (x-x^0))+O(|x-x^0|^n),\\ Du(x)=DH_n(K(x^0)\cdot (x-x^0))+O(|x-x^0|^{n-1}). \end{aligned}$$

Here, D denotes the gradient, and $K(x^0)$ is the matrix

$$\begin{aligned} K(x^0)=\sqrt{a(x^0)^{-1}}, \end{aligned}$$

with $a(x^0)$ the matrix $a_{ij}$, evaluated at $x^0$.

Moreover, we have

(i) The interior critical points (the zeroes of the gradient of u) are isolated.

(ii) Every interior critical point $x^0$ has a finite multiplicity, that is, for every x in a neighbourhood of $x^0$,

$$\begin{aligned} c_1\,|x-x^0|^m \le |Du(x)| \le c_2\,|x-x^0|^m, \end{aligned}$$

where $c_1,c_2$ are positive constants, $m=n-1$ and n is the integer appearing above.

(iii) If $x^0$ is an interior critical point of multiplicity m, then, in a neighbourhood of $x^0$, the level line $\{x \in \Omega | u(x)=u(x^0)\}$ is made of $m+1$ simple arcs intersecting at $x^0$.

Proof

See [2], Theorem H.-W., Remark 1.1+Remark 1.2. $\square$

4 Main result

Let us start this section with the definition of some functions and sets, which we shall need.

Definition 4.1

$$\begin{aligned}{} & {} D(x,y){:}{=}{V_{x}}(x,y)-{V_{y}}(x,y),\\{} & {} G^{*}{:}{=}{\overline{G}}\setminus \{(0,0)\},\\{} & {} P{:}{=}\{ (x,y) \in G^{*} |\,\, D(x,y)>0\},\,\,\,R:=\{ (x,y) \in G^{*} |\,\, D(x,y)\ge 0\},\\{} & {} N{:}{=}\{ (x,y)\in G^{*} |\,\, D(x,y)<0\},\,\,\,S:=\{ (x,y) \in G^{*} |\,\, D(x,y) \le 0\},\\{} & {} C{:}{=}R \cap {\overline{N}}, \end{aligned}$$

where the closure of N is taken in $G^*$. Note that these sets have the following interpretations: In the set R (N) full drift is given to the X-company (Y-company). R(N) is chosen w.l.o.g.. One could have taken P(S) as well. (The optimal strategy is not always unique in stochastic control problems.) The set C is the set, where the strategy is changed. More precisely, for each point $z \in C$ one finds both types of strategy in each neighbourhood of z. Note that the following topological notions are understood in the trace topology of $G^*$, w.r.t. ${\textbf{R}}^2$, with the sole exception of the second assertion in point c) of the following theorem.

Our main theorem reads now as follows:

Theorem 4.1

One has

a) P and N are simply connected sets.

b) $\{ (x,y)\in G^* |\,\, D(x,y)=0\} \subset {\overline{N}}$, as well as $\{ (x,y)\in G^* |\,\, D(x,y)=0\} \subset {\overline{P}}$, hence $C=\{ (x,y)\in G^* |\,\, D(x,y)=0\}$.

c) C is a $C^1$-curve in $G^*$, and ${\hat{C}}:=C \cup \{(0,0)\}$ is a connected set in the topology of ${\textbf{R}}^2$.

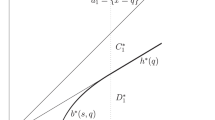
In Fig. 1 one can find a plot of the typical situation, where its topological features are proved in Theorem 4.1.

Fig. 1

plot of a typical situation

We start the proof of the Theorem with several helpful lemmas. Before we do this, we make the following remark, which will be used in the proofs of Lemma 4.1 and Lemma 6.1.

Remark 4.1

Let $R_t:=r+\mu t+\sigma W_t$, where $W_t$ is a standard Brownian motion, and $r,\mu ,\sigma$ are positive constants. Then for $\nu :=\inf \{t>0|R_t <0\}$, one has ${\textbf{P}}(\nu < \infty )=e^{-\frac{2\mu }{\sigma ^2}r}$, see, e.g., [1], Corollary II.2.4.

Lemma 4.1

On the boundary of $G^*$ we have

$$\begin{aligned} \{(0,y)|y>0 \} \subset P,\\ \{(x,0)|x>0 \} \subset N. \end{aligned}$$

Proof

We only show the second relation, the first one works analogously. Using the strategy $u \equiv 1/2$, we get for the target functional

$$\begin{aligned} J(x,\epsilon ,1/2)={\textbf{P}}\left( \tau _1 =\infty \right) {\textbf{P}}\left( \tau _2 =\infty \right) = \left( 1-e^{-x}\right) \left( (1-e^{-\frac{\epsilon }{\sigma ^2}}\right) . \end{aligned}$$

Moreover, we clearly have $J(x,0,u)=0$, for all admissible u, hence $V(x,0)=0$. As V is regular enough by Proposition 3.2, and since we have $V\ge J$, we conclude

$$\begin{aligned} V_y(x,0) \ge J_y(x,0,1/2), \end{aligned}$$

hence

$$\begin{aligned} V_y(x,0) \ge (1-e^{-x})\frac{1}{\sigma ^2} > 0 =V_x(x,0), \end{aligned}$$

finishing our proof. $\square$

The next result concerns the behavior of the function D(x, y) for large values of (x, y). We defer its proof to the Appendix.

Lemma 4.2

Let $P_1$, resp. $N_1$, be the connected component of P, resp. N, including $\{(0,y)|y>0 \}$, resp. $\{(x,0)|x>0 \}$. Then one has

$$\begin{aligned} \lim _{\begin{array}{c} (x,y) \rightarrow \infty \\ {(x,y) \notin P_1 \cup N_1} \end{array} }D(x,y)=0. \end{aligned}$$

By $(x,y) \rightarrow \infty$ we mean $x^2+y^2 \rightarrow \infty$. Let us remark that, since P, resp. N, are locally path wise connected, their connected components and connected path components are the same, see, e.g. [18], Theorem 25.5.

Before we show the simple connectedness of P and N, we need a preparatory result, the proof of which we defer to the Appendix. It is basically a consequence of forming the proper derivative of the HJB equation and known PDE regularity results.

Lemma 4.3

On all simply connected open sets $M\subset G^*$ the function D(x, y) is a distributional solution of

$$\begin{aligned} \frac{1}{2} \Delta ^{(\sigma )} D + {\textbf{1}}_{R} D_x+{\textbf{1}}_{N} D_y =0, \end{aligned}$$

where ${\textbf{1}}$ denotes the indicator function. Moreover, we have, if M is bounded, $D \in W^{2,p}_{loc}(M)$, $1<p<\infty$.

Our next lemma shows, that the sets N and P are (pathwise) connected, i.e. we have

Lemma 4.4

One has $G^*=P_1 \cup N_1 \cup \{ (x,y)\in G^* |\,\, D(x,y)=0\}$, which obviously implies $N_1=N$ and $P_1=P$.

Proof

Let $z \in G^*$. We distinguish several cases.

Case A: $D(z) <0$.

Let ${\hat{N}}$ be the connected component of N, with $z \in {\hat{N}}$.

Case A.1. ${\hat{N}} \cap N_1 =\emptyset$.

In this case we have $D_{/\partial {\hat{N}}}=0$, where $\partial {\hat{N}}$ denotes the boundary of ${\hat{N}}$, and D fulfills $D_y+\frac{1}{2}\Delta ^{(\sigma )}D=0$ on ${\hat{N}}$. Now, the set ${\hat{N}}$ could be unbounded, but we can control the behavior of D on it by Lemma 4.2, i.e.

$$\begin{aligned} \lim _{\begin{array}{c} z \rightarrow \infty \end{array}{z \in {\hat{N}}}}D(x,y)=0. \end{aligned}$$

It allows, to apply the comparison principle in the form of [20], Theorem 10.3, resp. the Remark before Lemma 10.2. This yields $D_{/{\hat{N}}}\equiv 0$, hence $D(z)=0$, a contradiction. So Case A.1 is not possible.

Case A.2. ${\hat{N}} \cap N_1 \ne \emptyset$.

By definition this implies ${\hat{N}}=N_1$, hence $z \in N_1$. Summing up we have in Case A: $z \in N_1$.

Case B: $D(z) >0$.

Analogously one gets here $z \in P_1$, which proves the Lemma. $\square$

Finally, we have

Proposition 4.1

The sets N and P are simply connected.

Proof

We give the proof only for N and argue by contradiction. So assume there exists a closed curve $\gamma \subset N$, and in the interior of $\gamma$ there exists a point $z_0$ with $D(z_0) \ge 0$.

Now, in the interior of the curve $\gamma$ the PDE of Lemma 4.3 holds, and on $\gamma$, D is strictly negative. Moreover, $D(z_0)$ is nonnegative, yielding a maximum in the interior, contradicting the maximum principle, see e.g. [11], Theorem 9.5. $\square$

We turn now to the set C, where the strategy is changed. Here our first result is

Proposition 4.2

We have $\{ (x,y)\in G^* |\,\, D(x,y)=0\} \subset {\overline{N}}$, as well as $\{ (x,y)\in G^* |\,\, D(x,y)=0\} \subset {\overline{P}}$, which implies

$$\begin{aligned} C=\{ (x,y)\in G^* |\,\, D(x,y)=0\}. \end{aligned}$$

Proof

We show only the first and last assertion and argue by contradiction. Assuming the first claim is false, gives the existence of a circle $B:=B(z;\epsilon )$, with $D(z)=0$ and $D_{/B} \ge 0$. On B we have by Lemma 4.3 a $W^{2,p}_{loc}$ solution of

$$\begin{aligned} \frac{1}{2} \Delta ^{(\sigma )} D + D_x =0. \end{aligned}$$

This leaves three possibilities for the vicinity of z:

1.) a $C^1$-curve through z, separating the part with positive D from the part with negative D (the regular case, where the gradient of D at z does not vanish).

This follows from the regularity results in Sect. 3 and the implicit function theorem.

2.) a finite number of curves intersecting at z, which form asymptotically neighbouring sectors, where the sign of D alternates

3.) a constant function D

The cases 2 and 3 follow from the Hartman-Wintner Theorem, see Theorem 3.2.

Obviously, the cases 1 and 2 are not possible, which leaves us with $D_{/B}\equiv 0$.

Now, let M be the connected component of $\{D=0\}$, with $z \in M$, and consider its boundary $\partial M$. Let ${\hat{z}} \in \partial M$, and U a small neighbourhood of ${\hat{z}}$. In U we have again

$$\begin{aligned} \frac{1}{2} \Delta ^{(\sigma )} D + {\textbf{1}}_{R\cap U} D_x+{\textbf{1}}_{N\cap U} D_y =0, \end{aligned}$$

s.t. we can again apply Theorem 3.2 from above. Now, one easily checks that each of the three possibilities above is incompatible with our construction. Indeed, D cannot be constant in the vicinity of ${\hat{z}}$, nor is it possible that a $C^1$-curve through ${\hat{z}}$ separates an area where D is positive from an area, where D is negative. Finally, a finite number of sectors, as described by the Hartman-Wintner result is also impossible. This yields a contradiction and concludes the proof of the first assertion.

The last assertion is easy. Indeed, obviously

$$\begin{aligned} R \cap {\overline{N}} \subset R\cap S =\{ (x,y)\in G^* |\,\, D(x,y)=0\} \end{aligned}$$

holds. Moreover, $\{ (x,y)\in G^* |\,\, D(x,y)=0\} \subset R$ and (by the first assertion) $\{ (x,y)\in G^* |\,\, D(x,y)=0\} \subset {\overline{N}}$, hence $\{ (x,y)\in G^* |\,\, D(x,y)=0\} \subset R \cap {\overline{N}} =C$, finishing the proof. $\square$

Our next result shows, that C is described by a $C^1$-curve.

Proposition 4.3

The set C is given by a $C^1$-curve, i.e. for each point z on C, we can describe the set C locally by a $C^1$-functions, either c(x) or c(y).

Proof

Let z be arbitrary on C, then we can again apply the “Hartman-Wintner” theorem. By the very definition of C, possibility 3.) is excluded. Now assume possibility 2.) is true. Then we would have asymptotically 2k, $k=2,3,4...,n$ sectors in the vicinity of z, where the sign of D alternates. We stick to the case $k=2$, the other cases work analogously. So let the ”sectors” $S_2$ and $S_4$ belong to N. Let $k_1$ be a continuous curve connecting $S_2$ and $\{(x,0)|x>0\}$, and $k_2$ a continuous curve connecting $S_4$ and $\{(x,0)|x>0\}$. Then either a continuous connection (lying entirely in P) from $S_1$ to $\{(0,y)|y>0\}$ or from $S_3$ to $\{(0,y)|y>0\}$ is prohibited by the sets $k_1$, $k_2$ and $\{(x,0)|x>0\}$. This contradicts the path connectedness of P, hence we have a contradiction.

Therefore we remain with possibility 1.), which proves the proposition. $\square$

So far our results concerned the set $G^*$, since we do not know a better regularity result at the origin. In our last proposition we show that, if we affix the origin to the curve C, we get a connected set in the topology of ${\textbf{R}}^2$.

Proposition 4.4

Let ${\hat{C}}:=C\cup \{0\}$, then ${\hat{C}}$ is connected in the topology of ${\textbf{R}}^2$.

Proof

Let $L:=\{(0,y)|y>0\}$, and ${\hat{P}}:=P {\setminus } L$. The set ${\hat{P}}$ is open in ${\textbf{R}}^2$. Moreover, it is path-connected, hence connected. Indeed, let $z_1, z_2 \in {\hat{P}}$. Then there exists a continuous path in P, connecting $z_1$ with $z_2$. We can easily - due to the continuity of D - deform this path to a path connecting the points and lying entirely in ${\hat{P}}$. Summing up we have

$$\begin{aligned} {\hat{P}}\hbox { is an open and connected set in }{\textbf{R}}^2. \end{aligned}$$

(18)

Now, by Proposition 4.2, $S=\{D\le 0 \}$ is connected. Indeed, Proposition 4.2 implies $S={\overline{N}}$, and the closure of the connected set N is connected.

Let $T:=G^c$. Then by, e.g., [3], Ex. 1.3, $S\cup T$ is connected, since S and T have a non empty intersection. As ${\hat{P}}=(S\cup T)^c$, we get by (the only) Theorem of [6],

$$\begin{aligned} \partial {\hat{P}}\hbox { is connected }. \end{aligned}$$

(19)

Our next claim is

$$\begin{aligned} \{0\} \in {\overline{C}}. \end{aligned}$$

(20)

Indeed, if this is not the case, there will exist a circle $B:=B(0;\epsilon )$ in ${\textbf{R}}^2$, s.t. $B\cap C =\emptyset$. W.l.o.g. this would imply $B \cap R =\emptyset$, an obvious contradiction. Hence, (20) is true.

By the definition of C, we have $C \cap {\overline{L}}= \emptyset$, which gives

$$\begin{aligned} {\hat{C}} \cap {\overline{L}}=\{0\}. \end{aligned}$$

(21)

Moreover, we have

$$\begin{aligned} {\overline{C}} \cap L=\emptyset . \end{aligned}$$

(22)

Indeed, assuming that this is false, would give the existence of a $y_0>0$, s.t. $(0,y_0) \in {\overline{C}}$. As $D(0,y_0)>0$, and D is continuous, this is not possible. Hence, we get the validity of (22).

After this preliminary considerations, we finally show the connectedness of ${\hat{C}}$ and argue again by contradiction. So assume we have ${\hat{C}}=C_1 \cup C_2$, with

$$\begin{aligned}{} & {} \overline{C_1}\cap C_2=\emptyset ,\nonumber \\{} & {} \overline{C_2}\cap C_1=\emptyset . \end{aligned}$$

(23)

W.l.o.g. we assume $\{0\} \in C_1$, and $\{0\} \notin \overline{C_2}$, which provides by (21),

$$\begin{aligned} C_2 \cap {\overline{L}} =\emptyset . \end{aligned}$$

(24)

In addition we have $\overline{{\hat{C}}}={\overline{C}}=\overline{C_1}\cup \overline{C_2}$, which yields by (22),

$$\begin{aligned} \overline{C_2} \cap L =\emptyset . \end{aligned}$$

(25)

Finally, we get for the boundary of ${\hat{P}}$, $\partial {\hat{P}}={\hat{C}}\cup L= C_2 \cup \left( C_1 \cup L\right)$, as well as

$$\begin{aligned} \overline{C_2} \cap \left( C_1 \cup L\right) = \left( \overline{C_2} \cap C_1 \right) \cup \left( \overline{C_2}\cap L\right) =\emptyset ,\\ C_2 \cap \overline{\left( C_1 \cup L\right) }= C_2 \cap \left( \overline{C_1} \cup {\overline{L}}\right) = \left( C_2 \cap \overline{C_1}\right) \cup \left( C_2\cap {\overline{L}}\right) = \emptyset , \end{aligned}$$

where we have used (23),(24) and (25). This would give a non connected set $\partial {\hat{P}}$, contradicting (19) and concluding the proof. $\square$

Now we have all the requisites for the

Proof of Theorem 4.1

This is just a consequence of the Propositions 4.1,4.2,4.3 and 4.4. $\square$

5 Concluding remarks

In this section we want to discuss three issues.

Firstly, we want to clarify, what the difference is to the symmetric case considered in [12] and [15], where we have equal volatilities for both companies. In these papers it is crucial, to know explicitly the form of the separating curve, which in these cases is just the first median. Let us remark that in the case of independent Brownian motion, see [12] and [17], and in the case of perfectly correlated Brownian motions [15], one can even calculate the value function in these problems. Now, we do not believe that in our non symmetric case, with different volatilities, it is possible, to find an explicit solution for the separating curve. Hence, we had to go a different path in the present article.

Secondly, compared to other existing models, e.g. such, which involve reflecting diffusions in the positive quadrant, how natural is our model for the wealth of companies? The reflected diffusions are used in Actuarial Mathematics, namely, if one “keeps the companies alive”, by injecting money. In these models the task is to optimize a further business, say reinsurance as in [8], in order to keep the expectation of theses injection minimal. This would be one possibility for optimization in Insurance Mathematics. Another one would be, to give the companies the possibility to invest in the stock market. Then the question is, how to do this, in order to keep the ruin probability as small as possible, see [10]. Now, if one considers more than one company, say two as in our case, two questions appear: How should these companies interact, and what is the optimization criterion? We think that the transfer payments, which we have explained at the end of Sect. 2 and the task of maximizing the probability that both companies survive, are very natural ones.

Thirdly, can we have analogous results, if we consider more general drift structures. Although the present model is widely used in Actuarial Mathematics as “diffusion approximation” for the famous Cramer-Lundberg model in the case of frequent, small claims, it is an interesting and natural question, whether we can get an analogous result, if we replace the present drift structure by a more complicated one, say $(a(X_t)+u_t)\,dt$, with some function a(x) for the first company, and a corresponding expression for the second one. This seems to be a very challenging task and requires probably new methods. On the one hand side, the preliminary result Theorem 3.1, which we formulated in Sect. 3 and proved basically in [12], is not a standard one, mainly because we have an unbounded domain. Hence, we were forced to prove it “by hand” in [12]. Now, the method we have used was to construct appropriate upper and lower solution for the problem on finite domains, and than to go to the limit. It seems that constructing such solutions in the general case is difficult.

On the other hand, and more important, the simple topological structure is probably not true any more. The reason is as follow. It is clear that the topological structure of the solution very much depends on the boundary condition and the behaviour of the solution at infinity (see Lemma 6.2). E.g., if one changes in the symmetric case the boundary condition from zero to some appropriate combination of exponential functions (which corresponds to the problem of maximizing the expected number of surviving companies), it is shown numerically in [17], that the topological structure is different. Indeed, they get four simply connected areas instead of two. Now, in our case the boundary condition remains zero, but the behaviour of the functions at infinity changes, and it seems a really challenging task, to get a sharp control of $V_x$ and $V_y$ at infinity in the general case, which would be an analogue to Lemma 6.2. We leave these problems for further research.

Appendix

The first aim of this Appendix is, to show Lemma 4.2. In order to do this, we need some auxiliary results and start with

Lemma 6.1

One has

$$\begin{aligned} \lim _{y\rightarrow \infty } V(x,y)=1-e^{-2x},&\hbox {unif. for }x\ge 0,\\ \lim _{x\rightarrow \infty } V(x,y)=1-e^{-\frac{2y}{\sigma ^2}},&\hbox {unif. for }y\ge 0. \end{aligned}$$

Proof

We show only the first relation: Let ${\tilde{u}}\equiv 1-\epsilon$, then we find for the corresponding stopping times, ${\textbf{P}}(\tau _1=\infty )=1-e^{-2(1-\epsilon )x}$, and ${\textbf{P}}(\tau _2=\infty )=1-e^{-\frac{2\epsilon }{\sigma ^2}y}$. Moreover, we define the function $g(x,\epsilon )$ by

$$\begin{aligned} g(x,\epsilon ):=(1-e^{-2x})-(1-e^{-2(1-\epsilon )x})=e^{-2(1-\epsilon )x}- e^{-2x}, \end{aligned}$$

and calculate its maximum over ${\textbf{R}}_+$, for fixed $\epsilon$. This gives $0\le g(x,\epsilon ) \le \frac{2\epsilon }{e}$, for $\epsilon$ small enough. Hence,

$$\begin{aligned} \left| J(x,y,{\tilde{u}})-(1-e^{-2x})\right|= & {} \left| {\textbf{P}}(\tau _1=\infty ){\textbf{P}}(\tau _2=\infty )-(1-e^{-2x})\right| \\= & {} \left| \left( 1-e^{-2(1-\epsilon )x}\right) \left( 1-e^{-\frac{2\epsilon }{\sigma ^2}y}\right) -\left( 1-e^{-2x}\right) \right| \\\le & {} \frac{2\epsilon }{e}+e^{-\frac{2\epsilon }{\sigma ^2}y}. \end{aligned}$$

Choosing y large enough, and noting that one clearly has $V(x,y) \le 1-e^{-2x}$, proves the Lemma. $\square$

By the next lemma, we want to control the derivatives of V, for large (x, y), away from the boundary. We find

Lemma 6.2

One has

$$\begin{aligned}{} & {} \lim _{y \rightarrow \infty }\left| \left| V_x-2e^{-2x}\right| \right| _\infty = 0,\,\,\,\hbox {uniformly for }x\ge x_0, \,\,\,\\{} & {} \lim _{x \rightarrow \infty }\left| \left| V_x\right| \right| _\infty = 0,\,\,\,\hbox {uniformly for }y \ge y_0, \\{} & {} \lim _{x \rightarrow \infty }\left| \left| V_y-\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}}\right| \right| _\infty = 0,\,\,\,\,\hbox {uniformly for }y \ge y_0,\,\,\,\\{} & {} \lim _{y \rightarrow \infty }\left| \left| V_y\right| \right| _\infty = 0,\,\,\,\hbox {uniformly for }x \ge x_0, \\{} & {} \lim _{y \rightarrow \infty }\left| \left| V_{xx}+4e^{-2x}\right| \right| _\infty = 0,\,\,\,\hbox {uniformly for }x \ge x_0, \,\,\,\\{} & {} \lim _{x \rightarrow \infty }\left| \left| V_{xx}\right| \right| _\infty = 0,\,\,\,\hbox {uniformly for }y \ge y_0, \\{} & {} \lim _{x \rightarrow \infty }\left| \left| V_{yy}+\frac{4}{\sigma ^4}e^{-\frac{2y}{\sigma ^2}}\right| \right| _\infty = 0,\,\,\,\hbox {uniformly for }y \ge y_0, \,\,\, \\{} & {} \lim _{y \rightarrow \infty }\left| \left| V_{yy}\right| \right| _\infty = 0,\,\,\,\hbox {uniformly for }x \ge x_0, \\{} & {} \lim _{y\rightarrow \infty }\left| \left| V_{xy}\right| \right| _\infty = 0,\,\,\,\hbox {uniformly for }x \ge x_0,\,\,\,\,\,\, \\{} & {} \lim _{x\rightarrow \infty }\left| \left| V_{xy}\right| \right| _\infty = 0,\,\,\,\hbox {uniformly for }y \ge y_0, \end{aligned}$$

where $x_0,y_0 >0$ are arbitrary.

Proof

Let ${\tilde{V}}:=V-(1-e^{-2x}-e^{-\frac{2y}{\sigma ^2}})$. By Lemma 6.1 we have $\lim _{(x,y)\rightarrow \infty }{\tilde{V}}(x,y)=0$. We consider now the function ${\tilde{V}}$ on the circle $B:=B(x_0,y_0;1/2\wedge x_0\wedge y_0)$, for $(x_0,y_0) \in G$, and find obviously

$$\begin{aligned} \left| \left| {\tilde{V}}(x,y)\right| \right| _{L^\infty (B)} \le \epsilon , \end{aligned}$$

(26)

for arbitrary small $\epsilon$, and $||(x_0,y_0)||$ large enough. A simple calculation reveals that ${\tilde{V}}$ fulfills

$$\begin{aligned} F(x,y,{\tilde{V}},D{\tilde{V}},D^2{\tilde{V}}):= \max \left( {\tilde{V}}_x-\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}}, {\tilde{V}}_y-2e^{-2x}\right) +\frac{1}{2}\Delta ^\sigma {\tilde{V}}=0.\nonumber \\ \end{aligned}$$

(27)

We now want to apply Theorem 3.1 of [23] and check the conditions. The conditions (F0)and (F1) are obviously fulfilled. For (F2), we note that $F(x,y,{\tilde{V}},D{\tilde{V}},D^2{\tilde{V}})$ is non increasing w.r.t. ${\tilde{V}}$.

We check the Lipschitz property in ${\tilde{V}},D{\tilde{V}}$:

$$\begin{aligned}{} & {} \left| F(x,y,{\tilde{V}},D{\tilde{V}},D^2{\tilde{V}})-F(x,y,{\widehat{{\tilde{V}}}},\widehat{D{\tilde{V}}},D^2{\tilde{V}}) \right| \nonumber \\{} & {} =\left| \max \left( {\tilde{V}}_x-\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}}, {\tilde{V}}_y-2e^{-2x}\right) - \max \left( \widehat{{\tilde{V}}_x}-\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}}, \widehat{{\tilde{V}}_y}-2e^{-2x}\right) \right| \nonumber \\{} & {} =\left| \max \left( {\tilde{V}}_x, {\tilde{V}}_y+r(x,y)\right) - \max \left( \widehat{{\tilde{V}}_x}, \widehat{{\tilde{V}}_y}+r(x,y)\right) \right| \nonumber \\{} & {} =\left| {\tilde{V}}_x+\max \left( 0, {\tilde{V}}_y-{\tilde{V}}_x+r(x,y)\right) -\widehat{{\tilde{V}}_x} -\max \left( 0,\widehat{{\tilde{V}}_y}-\widehat{{\tilde{V}}_x}+r(x,y)\right) \right| \nonumber \\{} & {} \le \left| {\tilde{V}}_x-\widehat{{\tilde{V}}_x}\right| +\left| \max \left( 0, {\tilde{V}}_y-{\tilde{V}}_x+r(x,y)\right) -\max \left( 0,{\tilde{V}}_y-{\tilde{V}}_x+d+r(x,y)\right) \right| ,\nonumber \\ \end{aligned}$$

(28)

where $r(x,y):=\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}}-2e^{-2x}$, and $d:=\widehat{{\tilde{V}}_y}-{\tilde{V}}_y-\widehat{{\tilde{V}}_x}+{\tilde{V}}_x$ holds. In order to estimate the r.h.s. of (28) we distinguish several cases.

Case 1: ${\tilde{V}}_y-{\tilde{V}}_x+r(x,y)\ge 0,{\tilde{V}}_y-{\tilde{V}}_x+d+r(x,y)\ge 0$. Here one finds

$$\begin{aligned} \hbox {r.h.s. of }(28) \le 2 \left| {\tilde{V}}_x-\widehat{{\tilde{V}}_x}\right| +\left| {\tilde{V}}_y-\widehat{{\tilde{V}}_y}\right| . \end{aligned}$$

Case 2: ${\tilde{V}}_y-{\tilde{V}}_x+r(x,y)\le 0,{\tilde{V}}_y-{\tilde{V}}_x+d+r(x,y)\le 0$.

We get

$$\begin{aligned} \hbox {r.h.s. of }(28) \le \left| {\tilde{V}}_x-\widehat{{\tilde{V}}_x}\right| . \end{aligned}$$

Case 3: ${\tilde{V}}_y-{\tilde{V}}_x+r(x,y)\ge 0,{\tilde{V}}_y-{\tilde{V}}_x+d+r(x,y)\le 0$.

We have

$$\begin{aligned} \hbox {r.h.s. of }(28) \le 2 \left| {\tilde{V}}_x-\widehat{{\tilde{V}}_x}\right| +\left| {\tilde{V}}_y-\widehat{{\tilde{V}}_y}\right| . \end{aligned}$$

Case 4: ${\tilde{V}}_y-{\tilde{V}}_x+r(x,y)\le 0,{\tilde{V}}_y-{\tilde{V}}_x+d+r(x,y)\ge 0$.

One has finally

$$\begin{aligned} \hbox {r.h.s. of }(28where the closure of) \le 2 \left| {\tilde{V}}_x-\widehat{{\tilde{V}}_x}\right| +\left| {\tilde{V}}_y-\widehat{{\tilde{V}}_y}\right| . \end{aligned}$$

Hence, condition (F2) is fulfilled with $K=2$.

For (F3) we observe

$$\begin{aligned} \left| F(x,y,0,0,0) \right| = \left| \max \left( -\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}}, -2e^{-2x}\right) \right| \le K_1(x,y), \end{aligned}$$

with $\lim _{y \rightarrow \infty }K_1(x,y)=0$, uniformly in x, $\lim _{x \rightarrow \infty }K_1(x,y)=0$, uniformly in y, hence

$\lim _{(x,y)\rightarrow \infty }K_1(x,y)=0$. (Note that in the following $K_1$ is a generic function which may vary from place to place.)

Concerning (F4), we have to find an estimate for $\left| \left| \max \left( {\tilde{V}}_x-\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}}, {\tilde{V}}_y-2e^{-2x}\right) \right. \right. \left. \left. +\frac{1}{2}\Delta ^\sigma {\tilde{V}}\right| \right| _{C^\alpha (B)},$ or - since $({\tilde{V}},D{\tilde{V}},D^2{\tilde{V}})$ is fixed - an estimate for $\left| \left| \max \left( -\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}}, A-2e^{-2x}\right) +\frac{1}{2}\Delta ^\sigma {\tilde{V}}\right| \right| _{C^\alpha (B)}$, with $A:={\tilde{V}}_y-{\tilde{V}}_x$.

We assume now a large value of $y_0$ and distinguish several cases. Moreover, we estimate in the following the Lipschitz norm $||\cdot ||_{0,1}$, which is bigger than the Hölder norm, since the radius of our circle is smaller than 1/2.

Case 1: $A \le 0$.

One gets

$$\begin{aligned} \left| \left| \max \left( -\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}},\right. \right. \left. \left. A-2e^{-2x}\right) +\frac{1}{2}\Delta ^\sigma {\tilde{V}}\right| \right| _{0,1} \le K_1(y_0), \end{aligned}$$

with $\lim _{y_0 \rightarrow \infty }K_1(y_0)=0$.

Case 2: $A >0$.

Here we find - using the definition $s(x,y):=\max \left( -\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}},A-2e^{-2x}\right)$ -

$$\begin{aligned} \left| \left| \max \left( -\frac{2}{\sigma ^2}e^{-\frac{2y}{\sigma ^2}}, A-2e^{-2x}\right) +\frac{1}{2}\Delta ^\sigma {\tilde{V}}\right| \right| _{0,1} \le \sup _{(x,y) \in B}\left( \left| s_x(x,y)\right| +\left| s_y(x,y)\right| \right) .\nonumber \\ \end{aligned}$$

(29)

One checks that the r.h.s. of (29) has the upper bound $K_1(y_0)+2A \le K_1(y_0)+2\left( \left| {\tilde{V}}_x\right| +\left| {\tilde{V}}_y\right| \right)$, with $\lim _{y_0 \rightarrow \infty }K_1(y_0)=0$.

As the same considerations hold with large $x_0$ as well, we find that the condition (F4) is fulfilled with $K=2$ and $K_1$ with $\lim _{y \rightarrow \infty }K_1(x,y)=0$, uniformly in x, $\lim _{x \rightarrow \infty }K_1(x,y)=0$, uniformly in y, hence $\lim _{(x,y)\rightarrow \infty }K_1(x,y)=0$. So all the conditions are fulfilled, and we can now apply Theorem 3.1 of [23], to get

$$\begin{aligned} \left| \left| {\tilde{V}}\right| \right| _{2,\alpha ;B}^{(0)} \le N(n,\nu ,K,\alpha ,R_0)\epsilon +K_1(x,y), \end{aligned}$$

where $\epsilon$ stems from inequality (26), and $K_1$ fulfills $\lim _{y \rightarrow \infty }K_1(x,y)=0$, uniformly in x, $\lim _{x \rightarrow \infty }K_1(x,y)=0$, uniformly in y, hence $\lim _{(x,y)\rightarrow \infty }K_1(x,y)=0$. Because of the definition of the norm used in [23], we get the assertion of our lemma, but only away from the boundary. $\square$

Proof of Lemma 4.2:

We start with the definition

$$\begin{aligned} u(x):=\sup \left\{ y_0>0 | D(x,y)<0,\,\, \forall y \in [0,y_0]\right\} , \end{aligned}$$

for $x>0$.

Claim 1: $\lim _{x\rightarrow \infty }u(x)=\infty$.

Let us remark that one obviously has $\left\{ (x,z)| z\in [0,u(x))\right\} \subset N_1$.

Now assume Claim 1 is false. Then we can find a sequence $x_n \rightarrow \infty$, s.t.

$$\begin{aligned} y_n:=u(x_n)\in [0,M], \end{aligned}$$

(30)

for some constant $M>0$, and we have

$$\begin{aligned} D(x_n,y_n)=0. \end{aligned}$$

(31)

By (30), we get the existence of a subsequence $x_{n_k}$, with $\lim _{k\rightarrow \infty }y_{n_k}=\gamma \in [0,M]$.

We now distinguish two cases:

Case A: $\gamma >0$.

For k large enough, we find $y_{n_k} \in [\gamma /2,3\gamma /2]$ and $D(x_{n_k},y_{n_k})=0$. But Lemma 6.2 implies

$$\begin{aligned} \lim _{x\rightarrow \infty } |D+\frac{2}{\sigma ^2}e^{-2y/\sigma ^2}| =0, \end{aligned}$$

uniformly for $y \ge y_0$. Choosing $y_0=\gamma /2$, gives a contradiction.

Case B: $\gamma =0$.

This means, we have $x_{n_k} \rightarrow \infty , y_{n_k}\rightarrow 0$, s.t. $D(x_{n_k},y_{n_k})=0$.

We proceed with

Claim 2: For all $x_0>0,y_0>0$,there exists $\delta (x_0,y_0)>0$, s.t.

$$\begin{aligned} V_y(x,y) \ge \delta >0, \end{aligned}$$

for all $x\ge x_0, y \in [0,y_0]$.

We show now Claim 2: For shorter notation we introduce the points A, B by $A:=(x,y), B:=(x,y+\epsilon )$, for small $\epsilon >0$.

For the starting point A, we use the optimal strategy for the problem (5), i.e. $u_t^{*}$. For B, we take

$$\begin{aligned} {\hat{u}}^B_t:= \left\{ \begin{array}{ll} u_t^{*}(Z_t^B-(0,\epsilon )),&{}\quad t \le \tau ^A,\\ u_t^{*},&{}\quad t > \tau ^A, \end{array} \right. \end{aligned}$$

where $\tau ^A$ denotes the ruin time for the starting point A. This means that, until the ruin time of the process started in A, we use the same strategy for B, so that the two paths move parallel with distance $\epsilon$. After $\tau ^A$ we take the optimal strategy for the path started in B. Hence,

$$\begin{aligned} V(x,y+\epsilon ) \ge J(x,y+\epsilon ,{\hat{u}}^B)= V(x,y)+{\textbf{P}}(H){\textbf{E}}\left[ \int _0^\infty V(z,\epsilon )\, dF^H(z)\right] , \end{aligned}$$

where $H:=\{\tau ^A < \infty , Z^A_{\tau ^A}=(z,0), z>0\}$, i.e. the set where the ruin of the process started in A happens at the $x-$axis. Furthermore, $dF^H$ denotes the conditional distribution of the hitting place at the $x-$axis. Finally, we get

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\frac{V(x,y+\epsilon )-V(x,y)}{\epsilon }= & {} {\textbf{P}}(H)\lim _{\epsilon \rightarrow 0}\frac{1}{\epsilon } {\textbf{E}}\left[ \int _0^\infty V(z,\epsilon )\, dF^H(z)\right] \\\ge & {} {\textbf{P}}(H) {\textbf{E}}\left[ \int _0^\infty \liminf _{\epsilon \rightarrow 0}\frac{V(z,\epsilon )}{\epsilon }\, dF^H(z)\right] \\\ge & {} {\textbf{P}}(H) {\textbf{E}}\left[ \int _0^\infty \frac{1-e^{-z}}{\sigma ^2}\, dF^H(z)\right] \\\ge & {} {\textbf{P}}(H) {\textbf{E}}\left[ \int _{x_0/2}^\infty \, dF^H(z)\right] C(\sigma ,x_0)\\= & {} C(\sigma ,x_0){\textbf{P}}\left( H \cap \left\{ X_{\tau ^A} \ge x_0/2\right\} \right) ) =C(\sigma ,x_0,y_0), \end{aligned}$$

where the C denote some positive constants. Here we have used Fatou’s Lemma in the first inequality, and the last formula in the proof of Lemma 4.1 in the second one. Finally, the last probability in this chain can certainly be estimated below by a positive constant $C(x_0,y_0)$; take, e.g., the probability that the process with drift (1, 1) hits the $x-$axis at values larger than $x_0/2$. This proves Claim 2.

We proceed with

Claim 3: For all $x\ge x_0$, we have uniformly

$$\begin{aligned} V_x(x,\delta ) \rightarrow 0, \end{aligned}$$

for $\delta \rightarrow 0$.

We show Claim 3: Again we introduce the points A, B by $A:=(x,\delta ), B:=(x-\epsilon ,\delta )$, for small $\epsilon >0$. For the starting point A we use the optimal strategy, i.e. $u_t^{*}$. For B we take

$$\begin{aligned} {\hat{u}}^B_t:=u_t^{*}(Z_t^B+(\epsilon ,0)), \end{aligned}$$

i.e., the strategy which is optimal for A. Again, the two paths move parallel with distance $\epsilon$, but since the path started in B is ruined earlier, this definition is already sufficient. Let $\tau ^B$ denote the ruin time for the starting point B. This yields

$$\begin{aligned} V(x-\epsilon ,\delta ) \ge J(x-\epsilon ,\delta ,{\hat{u}}^B)={\textbf{P}}(K):={\textbf{P}}(\{\tau ^B=\infty \}). \end{aligned}$$

Let now $L:=\{\tau ^B<\infty \}\cap \{X^{B,{\hat{u}}^B}=0\}$, i.e. the set where the path started in B hits the $y-$ axis first. Moreover, let $dF^L$ be the conditional distribution for a hitting place z on the $y-$axis. We get

$$\begin{aligned} V(x,\delta )={\textbf{P}}(K)+{\textbf{P}}(L)\int _0^\infty V(\epsilon ,z)\,dF^L(z). \end{aligned}$$

Summarizing, we conclude

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\frac{V(x,\delta )-V(x-\epsilon ,\delta )}{\epsilon }= & {} {\textbf{P}}(L)\int _0^\infty \lim _{\epsilon \rightarrow 0}\frac{V(\epsilon ,z)}{z}\, dF^L(z)\\ {}\le & {} 2 {\textbf{P}}(L)\int _0^\infty \, dF^L(z) =2 {\textbf{P}}(L). \end{aligned}$$

Here the last inequality follows from the fact that the value function is dominated by $(1-e^{-2x})(1-e^{-2y})$, the target functional for the drift (1, 1).

Finally, we note that ${\textbf{P}}(L) \le {\textbf{P}}(\tau _1 < \tau _2)$, with $\tau _1:=\inf \{t |x/2+B^{(1)}_t=0\}$, and $\tau _2:=\inf \{t |\delta +t+B^{(2)}_t=0\}$. Clearly, ${\textbf{P}}(\tau _1 < \tau _2) \rightarrow 0$, for $\delta \rightarrow 0$, uniformly for $x \ge x_0$. This proves Claim 3. Claim 2 and Claim 3 provide a contradiction to $D(x_{n_k},y_{n_k})=0$ in Case B, s.t. Claim 1 is proved.

Defining

$$\begin{aligned} v(y):=\sup \left\{ x_0>0 | D(x,y)>0,\,\, \forall x \in [0,x_0]\right\} , \end{aligned}$$

for $y>0$, analogous considerations give

$$\begin{aligned} \lim _{y\rightarrow \infty }v(y)=\infty . \end{aligned}$$

(32)

Finally, one finds

$$\begin{aligned} \lim _{\begin{array}{c} (x,y) \rightarrow \infty \end{array}{(x,y) \notin P_1 \cup N_1}}D(x,y)= \lim _{x \rightarrow \infty ,y \rightarrow \infty }D(x,y)=0, \end{aligned}$$

where for the first equality we have used Claim 1, resp. (32), and for the second Lemma 6.2. $\square$

Proof of Lemma 4.3

We start with a slight rewriting of the basic PDE, i.e.

$$\begin{aligned} \frac{1}{2}V_{xx}+\frac{\sigma ^2}{2}V_{yy}+V_y+(V_x-V_y)^+=0. \end{aligned}$$

Noting that the distributional derivation of the function $z^+$ is ${\textbf{1}}_{\{z\ge 0\}}$, and that distributional derivatives are interchangeable, see, e.g. [22], 6.12(4), we find, by differentiating first w.r.t. x, then w.r.t. y and subtracting the corresponding equations,

$$\begin{aligned} \frac{1}{2} \Delta ^{(\sigma )} D + {\textbf{1}}_{R} D_x+{\textbf{1}}_{N} D_y =0. \end{aligned}$$

For the regularity statement, we note that the gradient of D on M is bounded by Proposition 3.2. As the same holds for the indicator function, we can use [19], Theorem 1.1. $\square$