Exploring differences in spatial patterns and temporal trends of phenological models at continental scale using gridded temperature time-series

Abstract

Phenological models are widely used to estimate the influence of weather and climate on plant development. The goodness of fit of phenological models often is assessed by considering the root-mean-square error (RMSE) between observed and predicted dates. However, the spatial patterns and temporal trends derived from models with similar RMSE may vary considerably. In this paper, we analyse and compare patterns and trends from a suite of temperature-based phenological models, namely extended spring indices, thermal time and photothermal time models. These models were first calibrated using lilac leaf onset observations for the period 1961–1994. Next, volunteered phenological observations and daily gridded temperature data were used to validate the models. After that, the two most accurate models were used to evaluate the patterns and trends of leaf onset for the conterminous US over the period 2000–2014. Our results show that the RMSEs of extended spring indices and thermal time models are similar and about 2 days lower than those produced by the other models. Yet the dates of leaf out produced by each of the models differ by up to 11 days, and the trends differ by up to a week per decade. The results from the histograms and difference maps show that the statistical significance of these trends strongly depends on the type of model applied. Therefore, further work should focus on the development of metrics that can quantify the difference between patterns and trends derived from spatially explicit phenological models. Such metrics could subsequently be used to validate phenological models in both space and time. Also, such metrics could be used to validate phenological models in both space and time.

Introduction

Climate change is influencing the timing of key biological events. For example, increasingly warm springs are advancing the time of leaf onset of plants (Ellwood et al. 2013; Schwartz et al. 2013) and the migration of animals (Marra et al. 2005; Ault et al. 2011). Monitoring and analysing the timing of plants and animal development events is therefore essential to a better understanding of the Earth system and defining climate change adaptation strategies (Briske et al. 2015; Gerst et al. 2016; Labe et al. 2017). Phenology is the science that studies periodic plant and animal life cycle events (phenophases) and how seasonal and inter-annual variations in environmental conditions affect both (Lieth 1974; Chmielewski 2013). Phenology is also an useful proxy of the impact of climate change on our planet (Doi and Katano 2008; Gordo and Sanz 2010; Zurita-Milla et al. 2017).

Plant phenological models support the study of the impacts of climate change and inter-annual weather variability on vegetated canopies (Badeck et al. 2004; Schwartz et al. 2006; Allstadt et al. 2015). Phenological models can also be used to reconstruct and qualify ground observations (Chuine et al. 2004; Menzel 2005), to estimate species-specific phenology (Chuine et al. 2000), and species performance (Basler 2016). Phenological models are often calibrated using ground and weather observations. Spring plant phenology (SPP) models are particularly interesting (Cayan et al. 2001; Schwartz et al. 2006; Matzarakis et al. 2010; Allstadt et al. 2015). SPP models are widely used to support management decisions and to design suitable adaptation strategies for ecological and agricultural systems (Enquist et al. 2014; Gerst et al. 2016). These uses require phenological models of high quality.

The process of quality control of models starts with their calibration and continues with their validation. Calibration is used to find the values of the model parameters that minimise the error of the model. These values are often derived using specific phenological and environmental datasets. This makes the comparisons between calibrated models challenging. Validation is used to check the error of the calibrated model. The calibration and validation of phenological models over large areas are now possible because we have access to continental-scale gridded weather time series such as daily temperature and large amounts of contemporary volunteered phenological observations (VPOs; (Rosemartin et al. 2015)). Gridded temperature time-series are key inputs to SPP models; they help to generate spatially continuous data from which patterns and temporal trends can be extracted to help evaluate the influence of climate change on plant development (Mehdipoor et al. 2018; Izquierdo-Verdiguier et al. 2018).

SPP models vary in their mathematical formulation as well as in their input variables (Schwartz and Marotz 1988; McCabe et al. 2012; Allstadt et al. 2015). Hufkens et al. (2018) developed a modelling framework that includes a comprehensive list of SPP models and data. They describe historical SPP models such as extended spring indices (SI-x; (Schwartz et al. 2013)), thermal time (TT; (Cannell and Smith 1983)) and photothermal-time (PTT; (Masle et al. 1989; Črepinšek et al. 2006)) and lilac leafing observations. These models have been widely used to study the effect of climate change and global warming on both natural and agricultural ecosystems (Schwartz et al., 1988; Schwartz 1999; Brunsdon and Comber 2012; Richardson et al. 2013; Rosemartin et al. 2015). The framework facilitates both reproducibility and community driven phenology model evaluation and development.

Exploring the effects of using these phenological models improves our understanding of the outputs from SPP models, and consequently improves the quality of the management decisions based on the outputs. Geoscientists have explored the effects of using various models at large scales. However, high resolution and open daily gridded weather data and extensive phenological observations only recently became available (Abatzoglou 2013). As a result, few studies have comprehensively explored the effects of using one or another model on phenological patterns and trends at a high spatial resolution and over large regions. The improvements in large-scale distributed computing and cloud computing facilitate the qualification of SPP models at higher spatial resolution, by using gridded input data (Guo et al. 2010; Mehdipoor et al. 2017).

The quality of phenological models is often assessed using measures of the differences such as the root-mean-square error (RMSE) between the estimated and observed day of the year (DOY) of a phenophase at a number of observations sites. The RMSE is widely used to measure the performance of the models. However, RMSE might be a misleading indicator of average error or variability because RMSE is a function of both the mean of a set of error and their variability that influence the value of RMSE. This prevents a clear assessment of RMSE interpretations (Willmott and Matsuura 2005, Willmott et al. 2009). Moreover, RMSE needs observed DOYs for every grid cell to continuously measure the performance of the models in space, which are not always available. RMSE is often calculated using estimated DOY at a set of locations for which reference observations are available. The RMSE is an average model performance measure, and it can therefore overestimate or underestimate the average model error as a result of the spatial distribution of reference observations (Willmott et al. 2017).

Several studies have shown that phenological patterns and trends derived from various kinds of models may vary considerably (Janssen and Heuberger 1995; García de Cortázar-Atauri et al. 2009; Basler 2016; Chuine et al. 2016). Although researchers and decision makers use metrics such as RMSE to select models, they might not be aware of the effect of selecting models that use error measures such as RMSE. Further, researchers aiming to model plant phenology needs to be cautious in interpreting the results, both in a historical context and especially when looking forward over the next century. Moreover, global change models are able to integrate sophisticated information about land surface model components such as phenological model outputs (Willmott et al. 2009). The output of phenological models must be explored and evaluated to give confidence that global change models will accurately simulate future changes in the land-atmosphere coupling, carbon storage and feedbacks that may affect both weather and ecology.

This study evaluates various SPP models and explores the impact of using one or another model on the phenological patterns and trends that can be extracted by running these models at continental scales. We go beyond model selection and showed various model formulations for the same event. The workflow uses VPOs and gridded time-series temperature over the conterminous US (CONUS). We illustrate the workflow by exploring the effect of using the SI-x, TT and PTT groups of models on the estimation of patterns and trends in DOY of lilac leafing.

Materials and methods

Volunteered observations and temperature data

Two datasets were used to calibrate and validate the selected SPP models. For calibration of the TT and PTT models, we collected historical lilac (Syringa Chinensis ‘Red Rothomagensis’) VPOs and their corresponding temperature data. These VPOs, collected over the period 1961–1994 and containing the geographic location and DOY of first leaf (FL), were originally used to calibrate the SI-x for leafing onset (Schwartz 1997; Ault et al. 2015a, b). In this study, we use the original SI-x lilac leafing model (SI-xLM). The day of lilac FL provides a standard reference of spring plant phenology that can be compared with various locations and years (Caprio 1974; Santer 1985). Furthermore, this phenophase responds directly to changes in temperature and day-length as opposed to changes in other environmental cues (Caprio 1993; Schwartz et al. 2012). The lilac VPOs dataset has a total of 2321 observations collected across 193 sites (known as phenological stations) distributed over the continental US. The corresponding daily maximum and minimum temperatures and a day-length dataset include records from the nearest weather stations to the VPO sites. These weather stations are part of the Global Historical Climatology Network (GHCN).

To validate the selected SPP models and to explore the patterns and trends they produce, we used VPOs from the USA National Phenology Network (USA-NPN) and Daymet gridded temperature time-series, from 2000 to 2014. The USA-NPN dataset contains 899 lilac FL observations that were checked for consistency (Mehdipoor et al. 2015; Rosemartin et al. 2015). The gridded daily maximum and minimum temperatures and day-lengths from Daymet have been available at a 1-km spatial resolution for most of North America since 1980 (Daly et al. 2008; Thornton et al. 2014). Daymet dataset uses spatially-referenced surface measurements of daily maximum and minimum temperature and precipitation from the Global Historical Climatology Network (GHCN) and the land/water mask derived from the NASA SRTM 30 arc second DEM as major inputs (Daly et al. 2008; Thornton et al. 2014). Daymet daily maximum and minimum temperatures and day-length, and SI-x Daymet-based products (Izquierdo-Verdiguier et al. 2018) are available at a 1-km spatial resolution for the continental US from 1980 to 2016. Compared with other datasets such as GridMET (Mitchell et al. 2004) and PRISM (Daly et al. 2008), the higher spatial and temporal resolutions of Daymet helps to better capture temperature regimes across complex topographies, particularly in the western USA (Mehdipoor et al. 2018).

SSP models used

We selected SSP models that were based on temperature and photoperiod because plant phenophases often respond to changes in the daily values of these variables (Caprio 1993; Schwartz et al. 2012). Our selection includes

SI-x_LM

The SI-x models are widely used to study the timing of plant leafing and its changes in the northern hemisphere (Linkosalo et al. 2008; Mehdipoor et al. 2016; Wu et al. 2016; Belmecheri et al. 2017; Hufkens et al. 2018). The outputs of the SI-x model, namely the estimated DOY of FL and first flower of indicator plants such as lilac, are used as an official indicator of climate change in the USA (Schwartz et al. 2006, 2013; Crimmins et al. 2016). SI-xLM was first calibrated about 25 years ago, using the original VPOs and daily minimum and maximum temperatures (Schwartz 1997; Ault et al. 2011; Schwartz et al. 2013; Ault et al. 2015a, b).

The SI-xLM is based on the measure of growing degree hours (GDH: the sum of the hourly temperatures above 31 °F (− 0.5 °C), which is calculated from daily minimum and maximum temperatures. These GDHs are used to define the accumulation of short and long-term variables (Schwartz et al. 2013). Estimators of SI-xLM include days since the 1st of January (MDS0), 5–7 day GDH accumulations (DD57), 0–2 day GDH accumulations (DDE2) and accumulation of the number of high-energy synoptic events, which is defined as a DDE2 greater than 637, (SYNOP). A regression of the form of Eq. 1 was fitted to calibrate SI-xLM coefficients (A1, A2, A3 and A4), using estimators’ values at observed DOYs. For prediction, the calibrated coefficients are used to operationally check the inequalities of Eq. (2) on a daily basis, starting on the 1st of January. For underlying assumptions and a more detailed definition of the SI-x models, please see (Ault et al. 2015a, b).

$$ \frac{1000}{{\mathrm{DOY}}_{\mathrm{Observed}}}={A}_1\frac{\mathrm{MDS}0}{{\mathrm{DOY}}_{\mathrm{Observed}}}+{A}_2\frac{\mathrm{SYNOP}}{{\mathrm{DOY}}_{\mathrm{Observed}}}+{A}_3\frac{\mathrm{DD}57}{{\mathrm{DOY}}_{\mathrm{Observed}}}+{A}_4\frac{\mathrm{DD}\mathrm{E}2}{{\mathrm{DOY}}_{\mathrm{Observed}}} $$

(1)

$$ 3.306\ast \mathrm{MDS}0+13.787\ast \mathrm{SYNOP}+0.201\ast \mathrm{DD}\mathrm{E}2+0.153\ast \mathrm{DD}57\ge 1000 $$

(2)

Thermal time (TT) and thermal time calibrated using a sigmoid temperature response (TTS)

Phenology models are the second group of SPP models considered in this study. These models consider only the role of forcing temperatures (i.e. temperatures at which the plant develops). These models assume that phenophases such as the FL phenophase occur when a critical state of forcing is reached. The state of forcing is modelled as the sum of the daily rate of forcing (R_f), which is purely a function of temperature. We calibrated TT and TTS using Eqs. 3 and 4:

$$ {R}_{f_{TT}}(T)=\left(\begin{array}{cc}0& \mathrm{if}\ T<{T}_b\\ {}T-{T}_b& \mathrm{if}\ T\ge {T}_b\end{array}\right) $$

(3)

$$ {R}_{f_{\mathrm{TTS}}}(T)=\left(\begin{array}{cc}0& \mathrm{if}\ T<{T}_b\\ {}\frac{1}{1+\exp \Big(d\left(T-e\Big)\right)}& \mathrm{if}\ T\ge {T}_b\end{array}\right) $$

(4)

where the T_b is the base temperature (i.e. the minimum temperature required for plant development), T is the daily average temperature, d and e correspond to the slope at the inflection point (width) and the temperature of the mid-response (centre) of the sigmoidal function. For both temperature response functions, the summation of the daily rate of forcing was calculated from the 1st of January (DOY=1) as in inequality 5:

$$ {S}_f\left({t}_s\right)={\sum}_1^{t_s}{R}_f(T)\ge {F}^{\ast } $$

(5)

where t_s represent the DOY at which FL is reached, and F* shows the amount of heat that must be accumulated by the plant to reach that state of forcing S_f(t_s).

Photothermal TT and photothermal TTS

Photothermal TT and photothermal TTS are the third group of models considered in this study. These models depend on the average temperature during day-length (Burghardt et al. 2015). The summation of R_f was converted to photothermal units by adding a photoperiod variable to increase the biological relevance of inequality 5 (Črepinšek et al. 2006). The daily rate of forcing for the PTT models (R_fPPT) is defined as the multiplication of the light period as a proportion of a day to R_f of TT and TTS (Eq. 6). The PTT models, photothermal TT and photothermal TTS, apply the same approach to check if the plant received the amount of heat that is needed to reach a certain state of forcing, as defined in Eqs. 3 and 4, where L_i is the length of day expressed in hours.

$$ {R}_{fPTT}=\frac{L_i}{24}\ {R}_f $$

(6)

Exploring patterns and trends of models

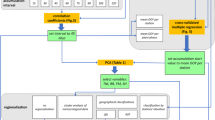
We use the workflow presented in Fig. 1 to analyse and compare the discussed above models. First, we searched for the optimal set of parameters for the TT, TTS, photothermal TT and photothermal TTS models using the VPOs, temperature and day-length datasets used to calibrate SI-x_LM, from 1961 to 1996. In particular, in the first step, we used simulated annealing (SA) to find the models’ parameters (i.e. T_b, e, d and F*). SA is a probabilistic optimization algorithm that performs a search in large multidimensional space (Aarts and Korst 1988). This algorithm is robust against entrapment in local optima (van Laarhoven and Aarts 1987), so we used it to find the optimal set of coefficients that minimizes the objective function. Here, our objective function is the RMSE between the observed and estimated DOY from the calibration dataset. We also used the mean absolute error (MAE) between the observed and estimated DOY from the calibration dataset (Willmott and Matsuura 2005) because this error metric is often used to assess phenological models (Schwartz and Marotz 1988; Zavalloni et al. 2006; Matzarakis et al. 2010). SA uses an initial random set of parameters for the objective function to start its search, then it follows steps within predetermined ranges. In this case, we used a range between [0, 10] for T_b, [− 2, 0] for d, [0, 1000] for F* and [0, 5] for e.

Fig. 1

The main analysis steps for calibrating and comparing models as well as for generating and comparing the spatio-temporal trends

Next, in the second step, SI-x_LM and the calibrated TT, TTS, photothermal TT and photothermal TTS models were validated using contemporary VPOs and Daymet data over the period 2000–2014. This period was selected because consistent VPOs were only available for these years. Daily temperature and day length were extracted for the VPO locations. These data were used to estimate DOY at VPOs locations. The RMSE and MAE of all models were calculated by comparing the observed and estimated DOY. Scatterplots of the observed and estimated DOYs were generated to qualitatively explore the effect on the RMSE and MAE of the model. The scatterplots between the model errors (i.e. subtraction of observed DOY from estimated ones) and geographic coordinates (i.e. latitude and longitude) were generated to analyse the model output further and to help better understand how model errors propagate over space.

In the third step, the average annual rate of change of DOY was calculated for each grid cell across CONUS to reveal variations in spatial and spatio-temporal trends between various geographic locations. Spatially continuous model outputs were only obtained for the two most accurate models to compare the effects of these models on the estimation of their average rate of change. Since we need to calculate daily variables for so many spatial locations (at 1-km resolution for the complete CONUS), we used the Google Earth Engine (GEE) cloud computing platform. The implementation of the SI-x_LM model in the GEE (Gorelick et al. 2017; Izquierdo-Verdiguier et al. 2018) was used to generate annual and average outputs for the models. This helped to explore and compare regional variations between the gridded model outputs. The histograms of the differences were plotted to provide a geographic representation of their distribution.

In the third steps, the annual differences between the two model outputs were spatio-temporally clustered to provide an overview of the effect of the models on spatial and temporal trends in DOY. The annual differences are the pairwise subtraction of grid cell values (i.e. 1-km by 1-km temperature-driven DOY) of the TT product from the SI-x_LM product, from 2000 to 2014. We applied k means clustering in GEE, which is a widely used clustering technique that seeks to minimize the average squared distance between data in the same cluster. For underlying assumptions and details of the GEE k means clustering, please see Arthur and Vassilvitskii 2007. Since the number of clusters cannot be known a priori, we set it to seven as an example. Clusters define regions for which the difference between the estimates of the two models was similar over the selected years. Clusters were mapped and explored to help understand the spatial variation of the regions.

Finally, for both models, the temporal trend in the gridded products was calculated and compared. For each grid cell, the temporal trend was obtained by fitting a linear regression line to the annual products from 2000 to 2014. The slope of the line is the rate of change of the models per year. We calculated the difference between the trends, by subtracting grid cell values of the two models. This highlighted regions where the estimated rates of change were highest. The statistical significance (p value) of these trends was analysed and mapped to show areas showing clear phenological changes. We applied the 2-sided p value test to see if the estimated trend is significantly greater than 0 and if the mean significantly less than 0.

Results and discussion

The SA-calibrated parameters of the TT and PTT models are shown in Table 1. The train RMSE of the models is similar to that which Hunter and Lechowicz (1992) reported. The difference in model parameters indicates that models can be parameterized to provide good predictions; however, their parameters are “biologically meaningless” (Hunter and Lechowicz 1992). The calibrated parameters result in similar minimum values of the RMSE objective function (12 days). These values are similar to the RMSE value calculated using the SI-x_LM (11 days). Such similarities indicate that the results given by selected phenological models can fit the historical data equally well. Similarly, SW has the smallest MAE compared with those of the other models. However, it is worth noting that using the RMSE or the MAE to evaluate the trained models results in a different ranking for the photothermal SW and photothermal UNIFORC models. Further analysis could help to assess if the performance of the selected models is significantly different, for example, via bootstrapping of model statistics (Leung et al. 2003; Noguchi et al. 2011).

Table 1 Calibrated parameters for the TT, TTS, photothermal TT, photothermal TTS models and the corresponding RMSE of the calibration dataset

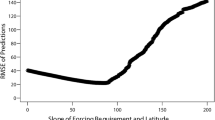
The results of the validation (Fig. 2) shows that the SI-x_LM is more accurate by 2 to 3 days in its estimates than the other models. The MAE also highlighted the similar difference in the error of the models. The visual exploration of scatterplots of both observed and estimated DOY from TTS, photothermal TT and photothermal TTS estimations are more biased to later DOYs than are those of TT and SI-x_LM (Fig. 2). Although there was no significant correlation between the model’s error and geographic gradients (in terms of latitude and longitude), correlation coefficients are higher for TTS than for other leaf models. Figure 2e shows that the TT model produces a higher error in the northern and southern CONUS compared with the centre. This is because for high and low latitudes, the temperature, which is the basis of the TT model, might not be the only driver of lilac FL.

Fig. 2

Scatterplots between observations and predictions by SPP models (first column), latitude and model error (second column) and longitude and models’ error (third column). Estimation errors were calculated by subtracting observed DOY from the estimated ones

The average DOY from SI-x_LM and TT were mapped, generalizing grid cell values into half-months of DOYs (Fig. 3). For both models, DOYs range from January to June across CONUS. Moreover, latitudinal patterns can be observed in the eastern and elevational patterns in the western CONUS. The visual exploration of the generated products shows that DOYs from the SI-x_LM model (Fig. 3a) are different from the results from the TT model (Fig. 3b). In the eastern CONUS, estimated DOYs from TT are earlier in the south, and later in the north than those estimated from SI-x_LM. For example, TT mostly estimates DOY in early May while SI-x_LM estimates it to be in late April. Similarly, in the western CONUS, DOYs driven from TT are earlier in low altitude regions, and later at high altitude regions, compared with DOYs driven from SI-x_LM. TT estimates DOY in early January for most locations in California; however, SI-x_LM estimates this in early February.

Fig. 3

Average DOY of lilac FL generated from a SI-x_LM and b TT, from1980 to 2014

The histogram of difference in DOY for SI-x_LM and TT (Fig. 4) indicates that for most locations in CONUS, the estimated average DOY is 11 days different. At these locations, TT estimates are for earlier dates than those produced by SI-x_LM. Although the RMSE of SI-x_LM and TT were only different by two days, the estimates can show up to a month difference in the West and North West of the CONUS (Fig. 5). For example, in California and Washington states, TT estimates are about 1 month earlier. In the Rocky Mountains, TT estimates are as much as one month later. These differences can be explained by the fact that TT uses only Daymet temperature, for which the interpolation method uses elevation as a key covariant (Daly et al. 2008). Moreover, TT considers only the long-term effects of temperature while SI-x_LM considers both the short-term and long-term effects and the day length. Although these exploratory results tend to show that the performance of models varies in both space and time, further metrics need to be developed to quantify the significant dissimilarity of spatial and temporal variations that are derived from models.

Fig. 4

Histogram of the difference between products generated from SI-x_LM and from TT. The differences are the pairwise subtraction of grid cell values of the TT product extracted from the SI-x_LM product.

Fig. 5

Map of the difference between products generated from SI-x_LM and from TT. The differences are the pairwise subtraction of grid cell values of the TT product resulting from the SI-x_LM product

Spatio-temporal clustering of annual difference in DOY between SI-x_LM and TT resulted in grouping of seven regions that have a similar difference over space and time (Fig. 6). The variability of the cluster type is larger in the eastern CONUS than in the western CONUS, which shows that SI-x_LM and TT perform substantially different in the eastern CONUS. In the eastern CONUS, the elevation gradient and consequently the temperature gradient are lower than in the western CONUS. Thus, compared with the western CONUS, the importance of day length that changes with latitude is higher in the eastern CONUS. As a result, the variability of cluster types is higher in the eastern CONUS, and the clusters have a latitudinal pattern. This is because TT is only based on temperature while SI-x_LM takes the influence of both temperature and day length into account.

Fig. 6

Clustered regions for which the difference between estimates of SI-x_LM and TT remains similar over the years

The regression line fitted to the annual outputs of SI-x_LM and TT, helps to explore spatial variations in the temporal trend (Fig. 7). The slope of the regression lines was mapped by generalizing them in 0.7 increments, which indicates about one week’s change per decade. Both models show advancement in DOY in the most western CONUS, ranging from 1 day to 1 month from 1980 to 2014. Temporal trends (Fig. 7a) driven from SI-x_LM show both advancements and delay in the eastern CONUS while TT driven trends show mostly delay in this part of the CONUS. The geographic pattern of the delay in DOY is consistent with the well-documented ‘warming hole’ in the southeastern USA (Robinson 2002; Kunkel et al. 2006; Meehl et al. 2012; Schwartz et al. 2013).

Fig. 7

Trend maps of DOY of lilac FL from a SI-x_LM and b TT. The trend values show the rate of change of DOY per year

There is a significant trend variation between the outputs from SI-x_LM and TT (Fig. 8). TT shows larger areas with a significant trend in the west coast and south central CONUS compared with SI-x_LM. For example, TT shows significant advancement for most locations in Oregon, while SI-x_LM does not show such advancement in that state. Or, TT estimates significant delay in the southern and western part of Texas. The explanation for this is that TT uses average temperature for which annual variation is higher in the abovementioned regions. In the eastern part of the USA, significant trends between SI-x_LM and TT do not match. Outputs from these models show completely different spatial patterns in estimated delay over the period 2000–2014. However, both models highlight areas in the south eastern CONUS, close to the ‘warming hole’ region, where the secular trend during the past century has been towards later DOY (Meehl et al. 2012; Schwartz et al. 2013).

Fig. 8

Statistical significance (range of p values) for the trends in DOY of lilac FL from a SI-x_LMb TT, shown in Fig. 7

The histogram of difference between the trends in SI-x_LM and TT estimates can be up to a week per decade (Figs. 9 and 10). Difference values are the pairwise subtraction of grid cells values of the trend in SI-x estimated from the trend in TT estimates. The positive differences are more dominant in the western CONUS where the SI-x trend product shows less advancement in DOY compared with the SI-x trends. However, the negative difference values are more concentrated in the eastern CONUS where trends estimated from TT products often show a delay compared with estimated trends from SI-x.

Fig. 9

Histogram of the difference between the trends in SI-x_LM and TT estimates. The differences are the subtraction of the trend in SI-x estimates from the trends in TT estimates

Fig. 10

Map of the difference between the trends in SI-x_LM and TT estimates. The differences are the subtraction of the trend in SI-x estimates from the trends in TT estimates

Conclusions

The analysis of spatial patterns and temporal trends in phenological model outputs is a necessary step in validating them, and to obtain more reliable model predictions that can be used to study climate change and to design management and adaptation strategies for ecological and agricultural systems. This paper not only analyses patterns and trends from observational sites but also analyses spatio-temporal patterns for the complete spatial conterminous US and at a very fine spatial resolution (1 km). Due to the large volume of data, our workflow uses cloud computing and gridded temperate time-series to study phenology at continental scales. Volunteered phenological observations are also used to compare and validate the average and rate of change of DOY across CONUS.

Our results show that errors produced by running SI-xLM and TT models are similar, and that these models are 2 days more accurate than those provided by other spring phenology models considered in this study. However, patterns of DOY which are derived from SI-xLM and TT models are 11 days different in the CONUS. Given that the period under consideration only contains 15 years, this difference is considerable. This demonstrates the importance of spatial-temporal patterns in the model assessment. The spatial variability of the SI-xLM and TT models is higher for the eastern CONUS. However, further correction and tests such as autocorrelation correction and bootstrapping are needed to analyse and compare the effect of the individual models statistically. Further, a longer period of data needs to be analysed to explore field significance further, which evaluate the performance of each model individually. The results also indicate that the estimated rate of change in DOY from SI-xLM and TT can be up to 1 week per decade different across the CONUS. Moreover, our results show that the significance of the rate of change from SI-x and TT is spatially variable in the CONUS.

Therefore, current approaches for validating phenological models based on global statistics such as RMSE cannot be used to gain information about the variability of patterns and trends in different regions. Studies using phenological models and gridded input data to study climate change impact on plant seasonality, and the eventual consequences on other living organisms should check both the spatial and temporal variability at large-scale. Using a model that is found less valid across the study area than another model (i.e. with a “worse” RMSE) may still provide more realistic patterns and trends when compared with the use of large-scale phenological data and/or information. Hence, we recommend applying our workflow to check the reliability of phenological models calibrated for large scale applications because it will help guard against the selection of overfitted models. The workflow presented in this paper can be applied to other phenophases, species and models to explore spatial phenological patterns and trends, and to better understand the impact of climate change on the Earth. It also highlights the need to develop metrics that can quantify the difference between patterns and trends derived from phenological models driven by gridded datasets.