1 Introduction

Predicting water levels of rivers has been an essential task of the hydrological community for the last decades. Forecasting river stages helps to issue flood warnings and supports water resources management. The increasing exposure to river flooding observed in the recent decades (Kundzewicz et al. 2013) highlights the need for accurate water level forecasts. Most models can be classified into two major categories: the physically-based and data-based methods (Beven 2012). The first group of models aims to simulate the nature of physical phenomena. However, they require various types of hydrological and geomorphological data, such as river cross-sections, basin topography and geology (Fatichi et al. 2016). They are also computationally expensive, especially for medium and large river basins. In turn, data-based approaches aim to discover relationships or hidden information in data, primarily by using information available in the data itself (Phan and Nguyen 2020). These models are useful for real-time forecasting because they are often faster and easier to implement than the physically-based methods.

Autoregressive models (AR) are one of the fundamental data-based prediction methods. They were first introduced in hydrology by Box and Jenkins (1970). An AR model expresses a current value as a finite, linear aggregate of previous values and some random noise. AR models, along with their numerous variations such as ARMA and ARIMA, have been widely used in hydrological research (e.g. Abudu et al. 2010; Galavi et al. 2013; Nigam et al. 2014; Sun et al. 2019; Aghelpour and Varshavian 2020; Pan et al. 2020). However, because of the dynamic and complex nature of water flow processes, the use of multivariate techniques, such as the vector autoregressive model (VAR), can be beneficial in accurately modelling time series. The performance of the VAR model in predicting water flows has been demonstrated in numerous studies. Niedzielski (2007, 2010) conducted studies on the upper and middle Odra/Oder river in SW Poland, in which he examined the potentials of multivariate and univariate autoregressive methods applied to regional scale rainfall-runoff modelling. More recently, Niedzielski and Miziński (2017) presented a hydrological ensemble prediction system based on a combination of the AR and VAR models, which was implemented on the Nysa Kłodzka river in SW Poland. Hartini et al. (2015) used the VAR model to analyse the relationship between rainfall and river discharge in Central Java. Zhao et al. (2019) modeled runoff in the Tuwei River basin in the middle reach of the Yellow River, and the VAR approach was used to build a relationship between runoff itself and a few environmental factors.

To make full use of the potential of VAR models, one has to conduct a thorough data analysis and preprocessing. Water level time series often contain no-data gaps, the presence of which can have a deleterious influence on hydrological models and the associated predictions (Harvey et al. 2012). According to Gao et al. (2018), “gap-free time series are a necessary prerequisite for many statistical and deterministic model approaches in hydrology”. The performance of autoregressive models can also be strongly deteriorated by the presence of outliers (Chen and Liu 1993; Nduka 2022), which can cause strong instability of the predictions. However, outlier detection and removal should be carried out with caution (McCuen 2003).

Despite the presence of studies on the use of the VAR model in hydrology, the potential of multiple time series approaches has not been examined in depth (Fathian et al. 2019). For instance, Fathian (2021) fitted several VAR models to daily streamflow data, and various orders of autoregression (5, 9, and 12) have been adopted for rivers located within the same basin, showing how autoregressive order may be vulnerable to local factors. In contrast, Jiang et al. (2023) allowed only very small VAR orders (1 and 2) when investigating the role of land use and climate change in contributing to water resources. This shows that selecting optimal VAR order in hydrological applications remains to be a challenge. Further, scarcity of research on the topic of the instability of autoregressive models in a situation of noisy data has recently been pointed out by Li et al. (2023).

In this study, we present the performance of the VAR model on the middle Odra/Oder river, with the following novelties: (1) we apply a newly-developed and published method for data interpolation (Niedzielski and Halicki 2023), (2) we investigate two different methods for outlier detection and introduce a hydrological criterion for outlier evaluation, (3) we propose an approach to select a fixed VAR order on a basis of a probability distribution of the orders, and (4) we conduct an experiment to study the influence of outliers on the stability of VAR models and, as a consequence, on the accuracy of water level predictions.

Fig. 1
figure 1

Middle Odra/Oder river basin. The location of hydraulic structures is obtained from Polish Topographic Objects Database BDOT10k (2024)

Full size image

2 Study area and data

The Odra/Oder river basin occupies an area of almost 120,000 km2, 90% of which is located in Poland. In this study, we consider the upper Odra/Oder and parts of the middle Odra/Oder basin, with the most downstream outlet in Słubice (Fig. 1). The Odra/Oder river, as well as most of its left tributaries, originates in the Sudetes mountains, with elevations up to 1603 m a.s.l. The flow regime of the mountain rivers is nival-pluvial, with a significant supply of meltwater from the snow thawing, while the right tributaries, located mainly on lowlands, are characterized by a pluvial flow regime, with water supply mainly from rainfall (Wrzesiński 2017). Hydraulic structures are maintained on most of the rivers, including the Odra/Oder river upstream the village of Malczyce. However, dams, which allow human controlled interventions to influence flow, are located predominantly in the upstream part of the basin.

The Odra/Oder river is an important river for the Central Europe. The basin is the third largest in the Baltic Sea catchment area and is home to over 16 million people (Helcom 2018). Further, it is a transboundary river, having its roots in Czech Republic and flowing mainly through Poland and along the Polish-German border. Its modelling is therefore important not only for Polish citizens. The basin has experienced several floods, including a catastrophic flood in 1997 (Dubicki et al. 1999, 2005) followed by another major flood in 2010.

In this study, we use hourly water levels from 27 gauges owned and maintained by the Institute for Meteorology and Water Management — State Research Institute (IMGW-PIB). The time span of gauge measurements ranges from January 2016 to May 2022. Water levels used in this study are values in centimeters above gauge zeros, which are referenced to the Kronsztadt’86 vertical datum. Water level predictions are calculated for six gauges (red triangles on Fig. 1), located on the middle Odra/Oder river between Ścinawa and Słubice gauging stations. This river section is characterized by absence of man-made structures and by water surface slopes ranging from 0.24 to 0.30 m/km (Halicki et al. 2023). Following the approach presented by Niedzielski and Miziński (2017), a corresponding sub-basin (i.e. a list of contributing gauges) was selected for each prediction gauge. Considering the most upstream prediction gauge (6), there are 15 gauges available in its sub-basin. This number increases in the downstream direction, with 17, 18, 19, 26, and 27 gauges available for 5, 4, 3, 2, and 1 prediction gauges, respectively.

The names of the gauges and rivers, as well as basic water levels characteristics, are juxtaposed in Table 1. Standard deviation of water levels on the Odra/Oder river (ranging from 0.50 to 1.02 m) is significantly higher than the standard deviation of water level on the tributaries (ranging from 0.12 to 0.48 m). This is probably related to the absolute water level variation, which ranges from 1.25 m (Jugowice gauge on the Bystrzyca river) to 6.36 m (Racibórz-Miedonia gauge on the Odra/Oder river) and, in general, is much higher on the Odra/Oder gauges.

Table 1 Characteristics of the water level gauging stations in the middle Odra/Oder river basin
Full size table

3 Preprocessing

Three data preprocessing scenarios were proposed in this study, namely: LinAR, EV, and IFO. The first scenario refers to the raw data interpolated with the LinAR method (Section 3.1), while the second and third scenarios refer to the datasets interpolated with LinAR and analysed for outliers with two separate methods (Section 3.2).

3.1 Interpolation

The water level time series used in this paper contain no-data gaps. Furthermore, the outlier detection described in the next section results in the removal of some additional water level measurements. Therefore, we use the LinAR interpolation method (https://github.com/MichalHalicki4/LinAR-interpolation accessed on 24th March 2024) to fill the no-data gaps. The method combines autoregressive models with linear interpolation. The main advantage of LinAR is its ability to reproduce the recent variability of the hydrograph through AR, while still maintaining the gap trend by incorporating the linear interpolation. In terms of accuracy LinAR outperforms the purely linear method for gaps with lengths up to 12 steps (Niedzielski and Halicki 2023). Following this recommendation, short data gaps (0–12 h) were interpolated using LinAR, while medium data gaps (13–72 h) were interpolated using the linear method. Longer gaps were not interpolated.

3.2 Outlier rejection

Water levels measured by IMGW-PIB are provided in near-real time on https://danepubliczne.imgw.pl/ accessed on 24th March 2024. However, these datasets are not preprocessed and checked for outliers by the data provider (personal communication with IMGW-PIB). There are numerous statistical methods for detecting outliers in time series, but most of them require normal, lognormal or Pearson Type III distribution (McCuen 2003). According to Sen and Niedzielski (2010), the empirical distributions of water flow time series in the Odra/Oder river basin are found to be non-Gaussian. We also examined the presence of a Pearson Type III distribution in our dataset, which was found for only a few per cent of the time series. Therefore, the use of statistical outlier detection methods does not seem justified for the analysed gauges.

3.2.1 Extreme values

A solution to the problem of data distribution can be found in the Extreme Values (EV) method (http://www.github.com/markvanderloo/extremevalues accessed on 24th March 2024) developed by van der Loo (2010). One of the parameters required by EV is the underlying distribution, which can be chosen among the following options: normal, lognormal, exponential, Pareto, or Weibull. Next, a data is marked as an outlier when it is unlikely to be drawn from the estimated distribution (Method II, see van der Loo 2010 for method description). We set the the confidence limit (alpha) to 0.001, and the Flim values (quantile limits indicating which data should be used to fit the model distribution) to 0.005–0.995. Finally, only outliers detected in a time series with a R-squared value of the fit higher than 0.95 are considered. Such an approach is applied in a moving window of 240 h. This size has been calibrated on the basis of the percentage of time series that have distribution required by the EV method.

3.2.2 Isolation forest

After applying the EV method we noticed that there exist hydrograph time series, the distributions of which cannot be approximated by one of the EV-required probability laws. The IFO method, for which data do not need to follow a specific distribution, is therefore proposed as a second approach to detect outliers. IFO is an algorithm based on ensemble learning, which is made up of a large number of trees that are called isolation trees (iTree) (Liu et al. 2008). The good performance of this method in detecting outliers in hydrological data has already been presented by Qin and Lou (2019). One of disadvantages of the IFO method is that it needs the contamination parameter to be set manually, which determines the number of outliers detected. In our study, the contamination parameter is of 0.001.

3.2.3 Hydrological evaluation

In order to reduce the number of false outlier detections, we propose a hydrological evaluation criterion. It states that an outlier can only be discarded from the dataset if it has not occurred in any other upstream gauge in the contributing sub-basin within a certain time range. In order to apply the proposed criterion correctly, the following calculations must be carried out. Firstly, the contributing sub-basin for each gauge must be defined. Secondly, the along-river distances between hydrologically connected gauges must be calculated. Finally, the range of water velocities must be estimated. Herein, we use the method for calculating time lag between gauges presented by Halicki and Niedzielski (2022) which, together with distances between the gauges, allows us to obtain flow velocity. Based on these values, we can calculate the time interval for each pair using the following equation:

$$\begin{aligned} \begin{aligned} T_{min} = D / V_{max}, \\ T_{max} = D / V_{min}, \end{aligned} \end{aligned}$$
(1)

where \(T_{min}\) and \(T_{max}\) denote the minimum and maximum time shift values [h], \(V_{min}\) and \(V_{max}\) represent the minimum and maximum water velocities [km/h], and D refers to the distance between two gauges [km]. Consider an artefact \(A_{t_0}\) detected at gauge 6 (Głogów) at a given time \(t_0\). Assuming a flow velocity ranging from 1.5 km/h to 3 km/h and a distance between gauge 6 and the neighbouring gauge 21 (Ścinawa) of 46.5 km, the artefact \(A_{t_0}\) can be discarded (i.e. no longer considered an artefact), if an outlier at gauge 21 has been detected within the time range \([t_0-31h,t_0-15.5h]\). Such outliers are not treated as artefacts, as these values are hydrologically connected. This validation is calculated for each gauge-pair within a sub-basin.

4 VAR model

For each prediction gauge \(g_p\), a multivariate time series of water levels from contributing gauges \(g_c\) (see Section 2) is prepared. Next, each of the time series is differenced and tested for stationarity (Section 4.1). Later, the \(g_c\) time series are tested for cross-correlation with the \(g_p\) water levels (Section 4.2). Only stationary and cross-correlated time series remain in the dataset that is later used to build the VAR model of order p (VAR(p)), which is mathematically described by the equation:

$$\begin{aligned} {\textbf {Y}}_t = {\textbf {a}}_1 {\textbf {Y}}_{t-1} + \cdots + {\textbf {a}}_p {\textbf {Y}}_{t-p} + {\textbf {Z}}_t, \end{aligned}$$
(2)

where \({\textbf {Y}}_t\) is a random vector at the fixed time t, \({\textbf {a}}_j, j = 1, \ldots , p\) denotes the autoregressive coefficient matrices, and \({\textbf {Z}}_t\) is the multivariate white noise vector with mean \({\textbf {m}}\) and covariance matrix \({\textbf {C}}\).

The estimation of the optimal length of the time series is presented in Section 4.3, while the process of determining the VAR order (p) and checking for the autoregressive structure is presented in Section 4.4. Conditions under which the VAR model was fit are juxtaposed in Table 2. Finally, the statistical measures used to assess the quality of water level predictions are described in Section 4.5. All calculations were conducted utilizing Python programming language, with the use of the statsmodels library implementation of the VAR model.

Table 2 Characteristics of VAR model estimation
Full size table

4.1 Stationarity

To build a VAR model, the input dataset must be stationary. This implies that the mean, variance and autocorrelation structure remain constant over time. Initially, we apply the first-order differencing to each input time series \(x_t\) in order to produce residuals \(y_t\), where \(y_t = x_t - x_{t-1}\). Next, we apply two tests to check the stationarity of \(y_t\), namely the augmented Dickey-Fuller test (ADF, Dickey and Fuller 1979) for stationarity and the F-test for the equality of variances. These two tests were selected because the ADF test alone may not always detect non-stationarity, as observed by Niedzielski and Halicki (2023). The significance level assumed for the ADF test was of 0.1, while for the F-test it was 0.01.

4.2 Reduction of the dimension of the VAR model

Decreasing dimension of the VAR model is advisable because it reduces noise in data (signal which does not convey meaningful information produces noise) and to make the computations more efficient (dimension of autoregressive matrix should be as small as possible to facilitate matrix inversion). For instance, Davis et al. (2016) claim that not only large but even moderate model dimensions can lead to noisy estimates and unstable predictions. Also, Wang et al. (2022) accentuate that if a number of univarite time series in mutivariate data as well as lag order are moderately large, the model has too many parameters. In addition, solving multivariate regression models often employs inverting matrices (Kastner and Huber 2020), and thus when the model dimension is large it brings computational burden.

To reduce model dimension, \(m-1\) (where m is an initial model dimension) pairs of time series corresponding to two gauges are analysed using cross-correlation. We build \(m-1\) pairs, each between a given prediction gauge and a contributing gauge (out of \(m-1\) contributing gauges). For lags up to \(\pm 14\), cross-correlations are computed for every pair, and 5% confidence intervals are calculated. Subsequently, if at least one cross-correlation value falls outside the confidence bands, there exists a statistically significant dependency between the two datasets, and therefore model dimension remains unchanged (the contributing gauge remains present in a multivariate time series). In contrast, a given univariate time series corresponding to a contributing gauge can be excluded (decreasing dimension of input multivariate time series by 1) if cross-correlation values for the given pair fall into the corresponding confidence intervals.

4.3 Selecting the optimal moving window size for the VAR model training

To build VAR models for forecasting, there exist two general approaches. The first one involves dividing the dataset into training and test datasets (e.g. Phan and Nguyen 2020), often with 80% for training and 20% for testing. This means that the model is created once on a large amount of data and then applied to a given prediction scenario. The second approach involves constructing a separate model for each prediction (e.g. Alberg and Last 2018; Niedzielski 2007; Niedzielski and Miziński 2017). The model is built on a time series extracted utilizing a moving window, using a specific number of recent observations. Thus, the model can infer the most up-to-date variability of the time series.

In this study, the second approach is used. The optimal number of observations for model estimation was determined based on the results of the stationarity test and cross-correlation analysis. Several time series lengths were tested, including 120, 240, 480, and 720 h. Finally, a length of 720 h was chosen. This provides sufficient information to build the VAR model and allows for the inclusion of a considerable number of stationary and cross-correlated time series in the model.

Fig. 2
figure 2

VAR order selection: (a) VAR order occurrences, (b) accuracy comparison between VAR predictions with order of 4 and 8

Full size image

4.4 Check for autoregressive structure and VAR order selection

The selection of the VAR order p is based on the following criteria: Akaike Information Criterion (AIC, Akaike 1970), Bayesian Information Criterion (BIC, Schwarz 1978), Final Prediction Error (FPE, Akaike 1974), and Hannah-Quinn criterion (HQIC, Hannah and Quin 1979). For each VAR model, we determined four orders based on the criteria described above. We then selected the order chosen by the highest number of criteria. If there were multiple orders with the same number of selections, we selected the order based on the AIC criterion.

Figure 2a shows the distribution of VAR model orders obtained from the six prediction gauges within the study time range. The distribution exhibits a clear bimodal pattern, with modes at \(p=4\) and \(p=8\). To determine the optimal value of p, we analysed the accuracy of two models: VAR(4) and VAR(8). The quality assessment procedure was performed on the LinAR time series, following the procedure description presented in Section 4.5. VAR(8) outperformed VAR(4) on the prediction gauges no. 3, 4, 5, and 6, while VAR(4) showed better accuracy only on the prediction gauges no. 1 and 2, where the performance was clearly affected by a highly deviating prediction (Fig. 2b). Therefore, the VAR order of 8 has been selected and applied in the entire analysis.

To assess the quality of the VAR models, we inspected autocorrelation function of model residuals (Baran and Bacanli 2006), i.e. differences between residuals \(y_t\) and the VAR model fitted to \(y_t\). Based on models built for each week and each prediction gauge (\(\approx \)2000 models) we observe, that the autocorrelation and cross-correlation of the VAR model residuals are low and predominantly do not fall outside confidence bands. We can therefore claim that the structure of the autoregressive models is suitable to describe the residuals \(y_t\). The coefficients of the best fitted model are presented in Table A1 in the Appendix.

4.5 Accuracy assessment statistics

The assessment of the VAR predictions accuracy has been conducted for water level forecasts of length l, for \(l = 1, \dots , 72\). For each l, a time series of water levels predicted for the l-th hour is compared to the corresponding observed values. Each of the time series covers almost the entire time range of the dataset (January 2016 – May 2022), excluding the first 30 days used for estimation of the first VAR model. On average, this gives a total of 55,000 observations for each prediction gauge. Two groups of measures were used to characterize the hydrograph predictions quantitatively, including prediction error statistics as well as prediction performance measures.

The prediction error statistics are calculated to measure how the VAR predictions depart from observed water levels. In this study, we use the mean absolute error (MAE), and the root mean squared error (RMSE), which can be described as:

$$\begin{aligned} MAE = \sum _{i=1}^{n}\frac{|P_t-O_t|}{n}, \end{aligned}$$
(3)
$$\begin{aligned} RMSE = \sqrt{\sum _{i=1}^{n}{\frac{(P_t-O_t)^2}{n}}}, \end{aligned}$$
(4)

where \(P_t\) is the VAR prediction at time t, \(O_t\) is the observed water level at time t, and n is the sample size.

The prediction performance measures include the Nash-Sutcliffe efficiency (NSE, Nash and Sutcliffe 1970), and the index of agreement (d-index, Willmott 1981). Both statistics have been well-described in the context of hydrologic studies by Krause et al. (2005). The NSE and d-index are defined by the following expressions:

$$\begin{aligned} NSE = 1-\frac{\sum _{i=1}^{n}{(P_t-O_t)^2}}{\sum _{i=1}^{n}{(O_t-\bar{O})^2}}, \end{aligned}$$
(5)
$$\begin{aligned} d\text {-}index = 1-\frac{\sum _{i=1}^{n}{(P_t-O_t)^2}}{\sum _{i=1}^{n}{(|P_t - \bar{O}|+|O_t - \bar{O}|)^2}}, \end{aligned}$$
(6)

where \(\bar{O}\) is the mean observed water level. The NSE values range between \(-\infty \) and 1. If the model-based prediction and the observed water levels agree in amplitude, phase and mean, NSE is approximately equal to 1. NSE values of 0 mean that the water level prediction has skills similar to the extrapolation of average computed from the observed data. Negative NSE values indicate that averaging data is even a better approach for predicting water level than employing the model. The d-index represents the ratio of the mean square error to the potential error. The values of the d-index range from 0 (no correlation) to 1 (perfect fit).

Fig. 3
figure 3

Number of outliers detected and rejected hydrologically in water level time series using the (a) Extreme Values and (b) Isolation Forests method

Full size image

5 Results

5.1 Outlier rejection

The numbers of outliers detected are presented in Fig. 3. Considering the EV method, the numbers vary from 322 (gauge 8) to 4 (gauges 10, 14, and 27). The strong variability can be related to the underlying distribution of data which, especially in mountain rivers, did not follow the distributions included in the EV method. On the contrary, the IFO method showed a similar number of outliers in each gauge (from 51 to 58), which is a result of applying the contamination parameter. Both graphs clearly show that the hydrological evaluation allowed to reduce the number of outliers, especially at the Odra/Oder gauging stations with numerous gauges in their contributing sub-basin. For upstream gauges with few or even no gauges in the sub-basins, the impact of evaluating outliers in hydrologically-related gauges was low (see Section 3.2.3 for method description). However, the most important outlier reduction had to be performed on the prediction gauges (1–6). This is because these values are used for validation of VAR predictions and their removal could lead to the omission of real flood signals, which would significantly reduce the reliability of the obtained accuracy.

5.2 Accuracy of VAR predictions

The accuracy (in terms of RMSE and NSE) of the VAR-based water level predictions for selected prognosis lengths is presented in Table 3. The corresponding values of MAE and d-index are presented in Table A2 in the Appendix. The accuracy statistics obtained following the LinAR, EV and IFO scenarios reveal very similar skills for most of the gauges. Considerable discrepancies occur only for gauge 2, where the accuracy of the LinAR scenario is significantly worse than the accuracy of the EV and IFO scenarios.

Table 3 Accuracy of VAR water level predictions in terms of RMSE and NSE for selected prediction lengths
Full size table
Fig. 4
figure 4

Accuracy of VAR predictions for the IFO and LinAR scenarios

Full size image
Fig. 5
figure 5

The impact of an outlier on the VAR predictions

Full size image

The relationship between the prediction accuracy and the prognosis length is also shown in Fig. 4. For the sake of brevity, only LinAR and IFO scenarios are presented, since EV and IFO reveal very similar skills. As can be seen for each gauge and each statistical measure, the accuracy decreases along with the prediction length. When excluding the values clearly influenced by a highly deviating prognosis (shown with arrows on Fig. 4), for the 72-hour predictions the RMSE values range from 19 cm to 43 cm (Fig. 4a), the MAE values range from 13 cm to 31 cm (Fig. 4b), the d-index values range from 0.92 to 0.98 (Fig. 4c), and the NSE values range from 0.69 to 0.92 (Fig. 4d).

The underperformance of the LinAR scenario on gauge 2 is due to a single water level forecast with a large deviation, which has a major impact on all the statistics shown in Fig. 4 and Table 3. It was caused by the presence of an evident outlier on gauge 2, with one value departing from the neighbouring water levels by \(\approx \) 0.5 m (Fig 5c). This unrealistic jump in the hydrograph resulted in an unstable VAR prediction revealing a harmonic-like regular variability, with unrealistic water levels ranging from −200,000 m to 170,000 m. Both outlier detection methods removed the evident artefact and prevented the generation of strongly deviating predictions (Fig. 5a,b).

On gauge 1, a similar case was observed where the accuracy was affected by one highly deviating prediction with future water levels reaching up to 100 m. However, this prediction was not caused by any outlier in the dataset, and therefore all three scenarios produced similar errors. If this prediction is excluded from the analysis, the VAR predictions on gauge 1 would outperform the predictions on all other gauges.

To study the VAR prediction performance during various water levels, we divided the dataset into high (water level > gauge mean \(+\) gauge std.), low (water level < gauge mean − gauge std.), and mean water level (between high and low). For the sake of brevity we consider only the IFO scenario and present such analysis for 12-hour and 24-hour predictions (Table 4). The VAR predictions for upstream gauges were more accurate during high water (gauge 5, 6), while for downstream gauges, lower errors were observed at low water (gauge 1, 2, 3). However, the differences were small and did not exceed 4 cm. Notably, the worst performance during mean water levels was observed in 8 out of 12 cases (Table 4).

5.3 Prediction of rising limb

To assess the performance of the VAR model during peak flow, we selected a period for each prediction gauge that had the largest daily mean difference between consecutive measurements (Fig. 6). Since the prediction error increases for longer forecasts, here we show only the 12-hour and 24-hour predictions. In general, a much better performance can be observed on the downstream gauges, especially for gauge 1 and 2 (Fig. 6a,b). The upstream gauges, in turn, revealed the poorest accuracy and agreement with the observed water levels (Fig. 6e,f). For all gauges, the VAR model underestimated the forthcoming water levels at the beginning of the rising limb, while near the crest, most water levels were overestimated, particularly on gauges 2, 3, and 6 (Fig. 6b,c,f). In all cases the RMSE of the 12-hour predictions was significantly lower than that of the 24-hour predictions. This was particularly evident for gauges 1-4, where the RMSE did not exceed 10 cm and was 2-3 times smaller than the RMSE of the 24-hour predictions. In certain cases the VAR model showed significant instability in consecutive predictions, both during the rising limb (Fig. 6b) and during the falling limb (Fig. 6e,f).

Table 4 Accuracy of VAR water level predictions for high, mean and low water levels
Full size table
Fig. 6
figure 6

12-hour and 24-hour predictions of rising limb (IFO scenario)

Full size image

5.4 Outlier experiment

The VAR model has proven to be prone to evident outliers, which can lead to the generation of highly deviating predictions (gauge 2, Fig. 5). To analyse this problem on the remaining prediction gauges, we conducted an experiment, in which we inserted an artificial outlier into the gauge dataset. After randomly selecting a date for all prediction gauges, we increased one water level by the value of one standard deviation (Table 1). We then applied the EV and IFO outlier detection method and calculated water level predictions for the EV, IFO and LinAR datasets.

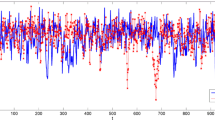
Water levels predicted without outlier detection (LinAR) did not fit into the observed data. For four of the five gauges studied, the prediction revealed a harmonic-like nature with increasing amplitudes, leading to deviations of 5, 10, 20, and even 10,000 m (Fig. 7a,e,g,i). Also the prediction at gauge 3, although not of harmonic nature, deviated strongly from the observed data with an error of \(\approx \) 3 m (Fig. 7c).

In most cases, both the IFO and EV methods successfully detected the artificial outliers, resulting in good forecasts in the aftermath of outlier removal, especially for the first hours into the future (Fig. 7b,d,f,h). An interesting situation occurred on gauge 6, where the outlier was only detected by the IFO method (Fig. 7j). The EV method failed to detect the artefact, because the time series did not follow any of the distributions available in EV. Therefore, the water level prediction in this scenario was the same as in the LinAR scenario and differed from the observed water levels by more than 10,000 m.

Fig. 7
figure 7

Performance of VAR model (following the LinAR, EV, and IFO scenarios) on data with an evident outlier

Full size image

6 Discussion

The results presented in Fig. 2 show superiority of the VAR(8) model over the VAR(4) model for the gauges studied. The river regime is nival-pluvial with a strong snowmelt supply to the baseflow, which can be well modelled by the Moving Average process in the VARMA (Vector Autoregressive Moving Average) models. According to Athanasopoulos and Vahid (2008), any invertible VARMA process can be approximated by a finite long order VAR, therefore our approach (VAR(8)) can be justified. However, the long-order VAR model may contain more noise due to the large number of coefficients. Future studies could consider analysing the performance of the VARMA model for rivers with the nival-pluvial regime.

The accuracy of water level predictions using autoregressive models has been studied on multiple rivers. In a study by Galavi et al. (2013) on the Klang River in Malaysia, the ARIMA model was employed to obtain a 1-day forecast with a NSE of 0.906. In our study, the 24-hour predictions also yielded high NSE values (0.99, 0.98, 0.98, 0.97, 0.94, and 0.87 for gauges 1–6, Table 3). Phan and Nguyen (2020) used the ARIMA model to predict water levels on the Red River in Vietnam. The accuracy of the predictions was verified for different prediction lengths, ranging from 6 hours to 5 days. The RMSE of the 24-hour predictions ranged from 20 to 31 cm, which is of the same order as the accuracies obtained in our study (8 to 28 cm, Table 3). Niedzielski (2007) utilised the VAR model to predict water levels on the Odra/Oder river. The study found that the accuracy of forecasts improves as the distance from the river headwaters increases. This may be due to the increasing amount of explanatory information available in the sub-basin. In our study we observed a similar relationship when excluding gauge 1 from the analysis, the accuracy of which is affected by one strongly deviating forecast.

The effectiveness of autoregressive models in predicting the rising limb of a hydrograph is not unequivocal. According to Niedzielski and Miziński (2017), the VAR model is particularly effective in forecasting a rising limb on the Nysa Kłodzka river. However, Phan and Nguyen (2020) argue that the ARIMA model “failed to forecast the peak and could not capture the data trend”. Other studies on the Odra/Oder river have reported similar findings. Gouweleeuw et al. (2005) utilised an ensemble prediction system to forecast a flood event in 1997 and found, that the peak was underestimated, even after the start of the flood. Niedzielski (2010) found that the VAR model enables to compute accurate predictions at the very beginning phase of peak flows. However, the prediction of maximum discharge is found to be less accurate, or even inaccurate at all. In our study, the VAR model performed well for 24-hour predictions of the rising limb, particularly for the downstream gauges. However, most predictions underestimated the maximum peak. Only a few predictions calculated shortly before the peak flow overestimated the highest water level.

The maximum length of forecasts, for which autoregressive models reveal satisfactory accuracies, is most often recognised as one day (e.g. Galavi et al. 2013; Nigam et al. 2014). The good performance of single models (including autoregressive models) for short predictions are also noticed by Sun et al. (2019). The authors observed, that such models outperform hybrid models within the first 24 hours. Pan et al. (2020) claim that predictions longer than 5 days are not efficient. In our study, a similar relationship between accuracy and forecast length was observed. However, the decrease is more rapid for predictions of upstream gauges than for downstream gauges (Fig. 4). As a result, the optimum length threshold for gauge 6 would be significantly lower than that for gauge 1.

The presence of outliers can strongly affect the accuracy of autoregressive models (e.g Nigam et al. 2014; Nduka 2022). According to Chen and Liu (1993), outliers occurring at the forecast origin have the greatest impact on predictions. The same conclusion can be drawn from Fig. 5 – only the predictions which start just after the outlier occurrence deviate greatly from the observations. The latter predictions are in good agreement with the true water levels and do not seem to be biased by the outlier. The negative impact of outliers on autoregressive models can also be reduced by smoothing. Niedzielski (2010) increased the accuracy of VAR-based predictions of the rising limb by applying a finite impulse response filter, which removes insignificant irregularities and emphasizes the flood wave signal. Pan et al. (2020) also employed smoothing techniques in the preprocessing of hydrograph data to produce water level forecasts. However, it should be noted that smoothing techniques cannot entirely solve the problem of outliers, particularly when they deviate significantly from the neighbouring water levels. Our approach to detecting artefacts and filtering them hydrologically not only increases prediction accuracy but also provides a careful procedure for removing such values. This prevents the omission of real data when building and validating VAR models in hydrology.

7 Conclusion

Autoregressive models have been widely used in hydrology over a few past decades. However, the instability of predictions in situations of data contamination remains a challenge. In this study we produced 72-hour VAR-based predictions of water levels on 6 gauges located on the middle Odra/Oder river. We used the newly-published LinAR method for no-data gap interpolation and, in addition, utilised two separate methods for outlier detection: EV and IFO. We propose a hydrological outlier evaluation criterion that reduces the number of detected outliers by removing (i.e. marking as non-outliers) those that are hydrologically connected. Finally, we evaluated the accuracy of VAR-based predictions of different lengths, assessed the quality of forecasting the rising limb, and examined the VAR model performance on data with artificial outliers. This study provides new data about the possibilities of predicting water levels in the Odra/Oder, which is a transboundary, flood-prone river. Further, we have clearly shown the influence of artificial outliers on the VAR model and studied two separate methods to handle artifacts. The following conclusions can be drawn:

  • Water level predictions for the downstream gauges reveal better skills than predictions for upstream gauges.

  • Applying outlier rejection improved the accuracy of predictions, especially for gauges with evident outliers.

  • The VAR model showed satisfactory skills in predicting the rising limb. However, better accuracies were observed for downstream gauges.

  • Artificial outliers caused instability of VAR-based predictions.

  • IFO method correctly detected all artificial outliers, significantly improving the quality of water level forecasts.

  • Future studies could consider using the VARMA model as the Moving Average component may effectively model the snowmelt-supplied baseflow.