Abstract
Recent research has highlighted the statistical significance and usefulness of trigonometric distribution models for simulating a variety of phenomena. A new set of distributions generated by exponentiated cosine and tangent functions has been introduced. Consequently, two families of distributions called the exponentiated cosine and tan Stacy distributions are derived. Some vital statistical and reliability characteristics are studied. The finite sample characteristics of parameter estimations are compared to the exponentiated cosine and tan distribution generated by four estimation methods: maximum likelihood, ordinary least squares, weighted least squares, and Cramer–von Mises. The methodologies are evaluated using simulation studies. Finally, the practical applications of the proposed trigonometric versions of the Stacy model are examined and applied on two lifetime reliability engineering datasets and another lifetime medical dataset concerning bladder cancer data. These real applications serve to highlight the effectiveness and adaptability of this innovative families within the respective fields compared with other lifetime well-known distribution models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Probability models play a crucial role in statistical analysis by representing the uncertainty and variability of random processes. In recent years, numerous flexible models have been developed and extensively studied, providing a more nuanced understanding of real-world phenomena. As research across various domains, such as reliability, hydrology, survival analysis, biomedical science, medicine, computer science, finance, and others, advances, more complex and adaptable distributions are proposed to better capture the diverse types of data encountered in practical applications. While the majority of these distributions are algebraic in nature, there are some that involve trigonometric functions.
Recently, the families of distributions obtained through "trigonometric transformations" of a given distribution have gained significant attention due to their effectiveness and applicability in diverse situations. These studies influenced the development of various trigonometric distribution families, such as exponentiated sine-G family see Mustapha et al. (2021), hyperbolic sine-Weibull see Kharazmi et al. (2018), sine power Lomax see Nagarjuna et al. (2021), sine-exponential distributions see Kumar et al. (2015), sine Topp-Leone-G family see Al-Babtain et al. (2020), tan- class of distributions see Souza et al. (2021), sine-square distribution see Al-Faris and Khan (2008), hyperbolic cosine-F (HC-F) distribution see Kharazmi and Saadatinik (2016), and sine-generated (SG) family see Kumar et al. (2015), Further, Chesneau et al. (2018) provided the cosine-sine-generated family, Mahmood et al. (2019) introduced the new-sine-generated distribution and highlighted some of the advantages of sine-generated distributions in statistical studies, Jamal and Chesneau (2019), proposed the Polyno-expo-trigonometric distribution, Bakouch et al. (2018) elaborated the new exponential with trigonometric function, and Abate et al. (1995) introduced the weighted-cosine exponential distribution.
Stacy distribution (Crooks 2007) is a flexible probability distribution that has several advantages over other commonly used distributions in statistics. One of the key advantages of the Stacy distribution is its ability to model heavy-tailed and skewed data, which can be particularly useful in fields such as finance and engineering where such data are common. Another advantage is its ability to handle small sample sizes, making it a valuable tool in situations where data are limited. Stacy distribution has been used in a variety of applications, including rainfall modeling, risk analysis, and earthquake engineering. For example, in a study on earthquake ground motion prediction (Iervolinoa et al. 2013; Wu et al. 2023; Chen et al. 2012), the Stacy distribution and it’s special cases specially gamma distribution was found to provide a better fit to the data than other commonly used distributions. Overall, the Stacy distribution is a powerful tool for statistical analysis and modeling, particularly in situations where other distributions may not be appropriate.
The paper is structured as follows: Sect. 2 provides a comprehensive description of the exponentiated cos Generated (ECG) and exponentiated tan generated (ETG) families, including their fundamental principles. The derivation of the Stress-Strength Reliability is presented in Sect. 3. Section 4 defines the EC and ET for the Stacy distribution model and their statistical properties are derived. In Sect. 5, simulation studies have been investigated via maximum likelihood estimation, ordinary least squares, weighted least squares, and Cramer–von Mises. Section 6 is concerned with three real-life applications of the ETS distribution. Finally, Section 7 summarizes the findings and presents conclusions.
2 The exponentiated cos and tan-generated distributions
2.1 Model formulation
One of the most popular methods for extending classical distributions for increased flexibility is the exponentiation method (Gupta et al. 1998). In this paper, the exponentiation method is applied to the tan-G (TG) and cos-G families. Firstly, Souza et al. (2019a) defined the sin-G class using the cumulative distribution function CDF provided by
And Souza et al. (2019b) introduced the cos-G class defined by the CDF generated by
Furthermore, the TG family, introduced by Souza et al. (2021), has CDF as follows:
where \(G\left( {x;\varepsilon } \right)\) is any acceptable CDF of a continuous distribution, and \(\varepsilon\) represents a vector of parameters.
Consequently, in the exponentiated form, the proposed distributions are the exponentiated cos G (ECG) and exponentiated tan G (ETG) distributions which have the forms:
Note that, at \(\mu = 1\), the ECG and ETG family is reduced to the CG and TG family.
The PDF of the ECG and ETG family respectively are as follows
And
where \(g\left( {x;\varepsilon } \right)\) is the PDF of \(G\left( {x;\varepsilon } \right)\).
The survival and the associated hazard rate functions of ECG and ETG families are as follows respectively,
and
moreover, the reversed hazard rate function of ECG and ETG families are respectively as follows,
2.2 Useful expansions
This section presents the PDF of the ETG family in a series expansion form. To achieve this, some preliminary results are necessary. Firstly, the power series is expanded to an integer power, as given by Gradshteyn et al. (2007). It is mentioned in the followed Lemma.
One of the interesting power series is given in Gradshteyn et al. (2007) of the type
Lemma 1.
By taking \(n\) as an integer, the result is obtained.
\(\left( {\sum_{k = 0}^{\infty } a_{k} x^{k} } \right)^{n} = \sum_{k = 0}^{\infty } c_{k} x^{k}\),
where \(c_{0} = a_{0}^{n} ,{ }c_{m} = \left( {\frac{1}{{\left( {ma_{0} } \right)}}} \right)\sum_{k = 1}^{m} \left( {kn - m + k} \right)a_{k} c_{m - k}\) \(for\) \(m \ge 1\).
For technical reasons, the following Lemma is provided. The subsequent lemma offers a series expansion of the exponentiated representation of a tangent term.
Lemma 2.
Let \(\mu > 0\) be real and noninteger, and x such that \(0 < G\left( {x;\varepsilon } \right) < 1\), then:
where \(b_{0} = a_{0}^{\mu - 1} ,b_{m} = \frac{1}{{ m a_{0} }}\mathop \sum \limits_{i = 1}^{\infty } \left( {i\left( {\mu - 1} \right) - m + i} \right)a_{i} b_{m - i} , m \ge 1\)
Proof.
The tangent series expansion can be expressed as follows.
where \(B_{n}\) represent the Bernoulli numbers.
Let \(k = i + 1\)
Let \(a_{i} = \frac{{2^{{2\left( {i + 1} \right)}} \left( {2^{{2\left( {i + 1} \right)}} - 1} \right)}}{{\left( {2\left( {i + 1} \right)} \right)!}} \left| {B_{2i + 2} } \right|\left( {\frac{\pi }{4}} \right)^{2i + 1}\).
Then
To obtain the power series raised to an integer power, refer to Lemma 1.
The required outcome has been achieved, and according (Gradshteyn et al. 2007) the series expansion of \({\text{sec}}^{2} \left( x \right)\) is as follows
Therefore
Let \(k = i + 1\), then
Now, Lemma 2 can be utilized to derive the PDF for ETG specified in Eq. 4 as:
Quantile The skewness and kurtosis of the ECG and ETG families' distribution can be evaluated using their respective quantile functions (QF) as well as to estimate parameters and generate random data that follows the specified distribution. The \(QF\) was also used to compute certain properties of the distribution and measure its goodness of fit. Following various advancements, the ECG and ETG families' \(QF\) are provided respectively
where \(G^{ - 1} \left( {x;\varepsilon } \right)\) is the QF associated with \(G\left( {x;\varepsilon } \right)\). Specifically, the median is
2.3 Moments and entropy of the ETG family
In this section, the moments and Rényi entropy of the ETG family are determined. If \(X\) is a random variable with a distribution belonging to the ETG family, the rth moment of \(X\) can be found by using the traditional method described below:
According to Eq. (6), a series of expansions can be observed
You can find specific moments by specifying \(r = 1, 2, 3, \ldots\).
Entropy is a way to quantify the amount of disorder or randomness in a system. The Rényi entropy of \(X\) is expressed by a mathematical formula
To calculate \(I_{R\left( \rho \right)}\), it is sufficient to calculate \(\mathop \smallint \limits_{ - \infty }^{\infty } f^{\rho } \left( x \right)dx\) and input the result into the logarithmic-integral expression. It can be observed that
The next Lemma is helpful for an expansion of the exponentiated sec term.
Lemma 3.
Let \(\rho > 0\) non-integer and real. Then,
\({\text{where}} \;z_{k}^{**} = z_{k}^{*} \left( {\begin{array}{*{20}c} {2\rho } \\ j \\ \end{array} } \right)\), and \(z_{k}^{*} = \frac{{E_{{2\left( {k + 1} \right)}} }}{{2\left( {k + 1} \right)!}}\left( {\frac{\pi }{4}} \right)^{{2\left( {k + 1} \right)}}\)
Proof.
After some algebraic manipulation of the cosine series expansion with \(n \ge 0\) and the substitution of \(n = k + 1\), \(k \ge 0\), then \(n \ge 1\), as in earlier Lemmas, then obtain.
where \(E_{2n}\) are the Euler numbers given by
where \(z_{k} = \frac{{E_{{2\left( {k + 1} \right)}} }}{{2\left( {k + 1} \right)!}}\left( {\frac{\pi }{4}} \right)^{{2\left( {k + 1} \right)}}\).
For \(j \ge 1\), using Eq. (5),
where \(z_{k}^{*} = z_{0}^{j} and z_{m}^{*} = \left( {\frac{1}{{\left( {mz_{0} } \right)}}} \right)\sum_{k = 1}^{m} \left( {kj - m + k} \right)z_{k} z_{m - k}^{*}\).
Therefore,
which \(z_{k}^{**} = z_{k}^{*} \left( {\begin{array}{*{20}c} {2\rho } \\ j \\ \end{array} } \right)\). Then the expansion mentioned is proven.
But, by slightly modifying Lemma 2 in this case, then
The integral can be computed by \(f^{\rho } \left( x \right)\) to obtain the Rényi entropy by inserting Lemma 3 and Eq. (10) in Eq. (8). Then,
In a similar series expansion way, the Shannon entropy can be stated.
3 Stress-strength reliability of the ETG family
The stress-strength parameter, sometimes referred to as the system performance parameter, is essential for the mechanical performance of a system. The effective design makes sure that the strength is greater than the predicted stress. The performance of the system is determined by the stress-strength parameter given by \(R = P(Y < X)\) if a component is subjected to stress represented by a random variable X and strength symbolized by a random variable Y. Only when the applied stress is greater than the system's capacity will the system break down. R may be used to compare two populations, on the other hand. Stress strength reliability characteristics have applications in engineering, biology, and finance. Among other places, see Kotz and Pensky (2003). Several authors have examined the parameter R in literature from a variety of vantage points.
The expression R is analyzed within the context of the ETG family. Assume that \(X\) and \(Y\) are considered to be independent, that \(X\) has the PDF \(f\left( {x;\mu_{1} ,\varepsilon } \right) ,\) and that \(Y\) has the CDF \(F\left( {y;\mu_{2} ,\varepsilon } \right)\). The following definition follows for the stress-strength reliability parameter:
Consequently,
The comprehensible structure of R makes it suitable for statistical applications and other purposes. An example of R's behavior can be elucidated in one of the following sections, one of the following sections discusses the association of R with a particular distribution from the ETG family.
4 The exponentiated tan stacy (ETS) and exponentiated cosine stacy (ECS) distributions
-
a.
The CDF and PDF for ETS Distribution
According to Eq. (2), the CDF of ETS is derived as follows
where \({\Gamma }\left( z \right) = \mathop \smallint \limits_{0}^{\infty } t^{z - 1} e^{ - t} dt\) is Euler’s Gamma function and \({\upgamma }\left( {a,x} \right) = \mathop \smallint \limits_{0}^{x} t^{a - 1} e^{ - t} dt\) is incomplete Gamma function, and the PDF of ETS distribution is
Theorem 1.
The behavior of the PDF of ETS is summarized as follows:
-
1.
Increasing if \(\alpha ,\theta ,\beta ,\mu > 1\).
-
2.
Decreasing \(\alpha > 1;\theta ,\beta ,\mu < 1\).
-
3.
Unimodal \(\alpha ,\theta ,\beta > 1,\mu < 1\) or \(\alpha ,\theta \left\langle {1;\beta ,\mu } \right\rangle 1\).
-
4.
Bathtub Unimodal \(\alpha \left\langle {1;\theta ,\beta ,\mu } \right\rangle 1\).
Proof.
By obtaining the derivative of the PDF.
When \(\alpha ,\theta ,\beta ,\mu > 1;\) \(f^{\prime}\left( x \right) > 0\) for all \(x\) which implies that \(f\left( x \right)\) is monotonically increasing for all \(x\). But for \(\alpha > 1;\theta ,\beta ,\mu < 1\); \(f^{\prime}\left( x \right) < 0\) which indicates \(f\left( x \right)\) is monotonically decreasing for all \(x\).
By deriving \(L^{\prime} \;{\text{and}}\; L^{\prime \prime }\), where \(L = {\text{ln}}f\left( x \right)\), one obtains:
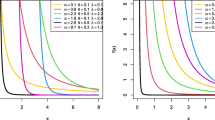
It’s concluded that; for \(\alpha ,\theta ,\beta > 1,\mu < 1\) or \(\alpha ,\theta \left\langle {1;\beta ,\mu } \right\rangle 1\) \(L^{\prime}\) is changed from increasing to decreasing and the sign of the second derivative is negative and visually it has one peak and proved the unimodality of the PDF. On the other side, at \(\alpha \left\langle {1;\theta ,\beta ,\mu } \right\rangle 1\) the PDF changes its sign from negative to positive and then back to negative as \(x\) increases, thus confirming the proof that it is decreasing-increasing–decreasing (Fig. 1).
-
b.
The CDF and PDF for ECS Distribution
The CDF of ECS is provided as follows; from Equation (1),
And the PDF of the ECS distribution is
In the graph, it’s clear that the PDF behavior of ECS distribution is decreasing, increasing, and unimodal (Fig. 2).
4.1 The hazard and survival functions
-
a.
The Hazard and Survival Functions for ETS
The survival function is the probability that a unit will last beyond a certain point in time. To track the duration of a unit throughout its lifetime, the hazard rate is used.
The survival and the hazard functions for the ETS distribution are derived from (12) and (13) as follows:
As a following Theorem, the hazard functions of the ETS distribution have various shapes, which is a very interesting property that characterize its goodness of fit for several lifetime data.
Theorem 2.
The hazard rate function's behavior of ETS is;
-
1.
\(h\left( x \right)\) is increasing when \(\alpha ,\theta ,\beta ,\mu > 1\).
-
2.
\(h\left( x \right)\) is decreasing when \(\alpha ,\theta ,\beta ,\mu < 1\).
-
3.
\(h\left( x \right)\) is bathtub when \(\alpha ,\theta ,\beta > 1;\mu < 1\).
-
4.
\(h\left( x \right)\) is inverted bathtub when \(\alpha ,\mu > 1;\theta ,\beta < 1\).
-
5.
\(h\left( x \right)\) is bimodal when \(\theta ,\beta \left\langle {1;\alpha ,\mu } \right\rangle 1\).
-
6.
\(h\left( x \right){\text{is }}unimodal - bathtub\) when \(\alpha ,\theta \left\langle {1;\beta ,\mu } \right\rangle 1\).
Proof.
In order to investigate the behavior of \(h\left( x \right),\) one can examine the behavior of \(L^{\prime\prime}\) as defined in Eq. (14), with reference to Lemma (5.9) on page 77 of Barlow and Proschan (1975) work, and Lemma (b) presented in Glasser (1980).
Let
Under the stated conditions, \(\alpha ,\theta ,\beta ,\mu > 1\), the function \(\eta^{\prime}\left( x \right) > 0\) therefore, \(\eta \left( x \right)\) has increasing shape and at \(\alpha ,\theta ,\beta ,\mu < 1\) the function \(\eta^{\prime}\left( x \right) < 0\) then \(\eta \left( x \right)\) has decreasing shape. Also the function \(\eta^{\prime}\left( x \right)\) changes its sign from negative to positive as \(x\) increases and \(\alpha ,\theta ,\beta > 1;\mu < 1\); then, \(\eta \left( x \right)\) has a bathtub shape. When, \(\alpha ,\mu > 1;\theta ,\beta < 1\), you can observe that \(\eta^{\prime}\left( x \right)\) changes its sign from positive to negative to positive as \(x\) increases and therefore, \(\eta \left( x \right)\) has inverted bathtub. \(\eta \left( x \right)\) is bimodal as the function \(\eta^{\prime}\left( x \right)\) changes its sign from positive to negative then to positive again then to negative, as \(x\) increases when \(\theta ,\beta \left\langle {1;\alpha ,\mu } \right\rangle 1\).
When \(\alpha ,\theta \left\langle {1;\beta ,\mu } \right\rangle 1\) \(\eta^{\prime}\left( x \right)\) changes its sign from negative to positive then to negative again then to positive, as \(x\) increases, then \(\eta \left( x \right)\) is unimodal-bathtub shape.
Under the specified conditions, where \(\alpha ,\theta ,\beta ,\mu\) are greater than \(1\), the function \(\eta^{\prime}\left( x \right)\) is positive, indicating that \(\eta \left( x \right)\) has an increasing shape. Conversely, when \(\alpha ,\theta ,\beta ,\mu\) are less than \(1\), \(\eta^{\prime}\left( x \right)\) is negative, and \(\eta \left( x \right)\) has a decreasing shape. If \(\alpha ,\theta ,\beta\) are greater than \(1\) and \(\mu\) is less than \(1\), \(\eta^{\prime}\left( x \right)\) changes its sign from negative to positive as \(x\) increases, giving \(\eta \left( x \right)\) a bathtub shape. Similarly, when \(\alpha\) and \(\mu\) are greater than \(1\), and \(\theta\) and \(\beta\) are less than \(1\), \(\eta^{\prime}\left( x \right)\) changes its sign from positive to negative and then to positive again as x increases, resulting in an inverted bathtub shape for \(\eta \left( x \right)\) .
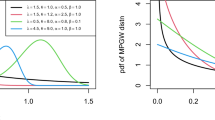
The function \(\eta \left( x \right)\) is bimodal when \(\theta\) and \(\beta\) are less than \(1\) and \(\alpha\) and \(\mu\) are greater than \(1\) because the function \(\eta^{\prime}\left( x \right)\) changes its sign from positive to negative, then to positive again, and finally to negative again as \(x\) increases. Finally, when \(\alpha\) and \(\theta\) are less than 1, and \(\beta\) and \(\mu\) are greater than \(1\), \(\eta^{\prime}\left( x \right)\) changes its sign from negative to positive, then to negative again, and finally to positive as x increases, resulting in a decreasing-unimodal-bathtub shape for \(\eta \left( x \right)\) (Fig. 3).
-
b.
The Hazard Rate and Survival Functions for ECS Distribution
From (15) and (16), the survival and the hazard functions of ECS distribution are obtained by
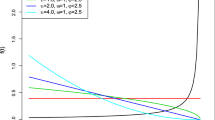
From the study of the hazard function behavior of ECS distribution; It has decreasing, increasing, increasing-bathtub, bathtub, inverted bathtub, and Inverted-bathtub then increasing (Fig. 4).
4.2 Reversed hazard rate function
The reversed hazard rate is a random variable that represents the time passed since a component's failure, given that its lifetime is equal to or less than \(t\). It can also be referred to as inactivity time or time since failure.
The reversed hazard rate function for ETS and ECS distributions are respectively as follows
4.3 Quantile and moments for ETS distribution
The QF for the ETS distribution can be calculated from Eq. (12) as follows;
then
\(\frac{4}{\pi }\tan^{ - 1} \left( {p^{{\frac{1}{\mu }}} } \right) = \left( {1 - \frac{{{\upgamma }\left( {\alpha ,\left( {\frac{x}{\theta }} \right)^{\beta } } \right)}}{{{\Gamma }\left( \alpha \right)}}} \right)\) and \({\Gamma }\left( \alpha \right)\left( {1 - \frac{4}{\pi }\tan^{ - 1} \left( {p^{{\frac{1}{\mu }}} } \right)} \right) = {\upgamma }\left( {\alpha ,\left( {\frac{x}{\theta }} \right)^{\beta } } \right)\).
Then
The QF for ETS distribution can be obtained.
The median for ETS distribution is
Among other quantile-based measures, Bowley's skewness and Moor's kurtosis can be used to analyze the skewness and kurtosis characteristics of ETS distribution. They are characterized respectively by
ETS distribution's moments can be obtained from (7) and computed numerically.
4.4 Asymptotic order statistics
The order statistics from ETS distribution and some of its asymptotic features are the major topics of our current discussion. Let the sample of independent random variables that follows ETS distribution, \(X_{1} ,X_{2} ,X_{3} , \ldots ,X_{n}\), \(n \ge 1\). Let's have a look at \(X_{1:n} ,X_{2:n} , \ldots X_{n:n}\) which are the ordered forms of \(X_{1} ,X_{2} ,X_{3} , \ldots ,X_{n}\).
The PDF of \(X_{j:n}\) is provided for every \(j = 1, 2, \ldots , n\).
Thus, by combining \(F\left( x \right)\) and \(f\left( x \right)\) from Eqs. (12) and (13) into Eq. (24), then
5 Parameter estimation
This section is dedicated to exploring parameter estimates in the absence of any known assumptions. The techniques covered in this section for estimating the parameter include Maximum Likelihood (ML), Least Squares (LS), Weighted Least Squares (WLS), and Cramer–von Mises (CVM) estimation methods.
5.1 (ML) estimation
This section focuses on utilizing maximum likelihood estimation (MLE) for the parameter estimation.
Let \(x_{1} ,x_{2} ,x_{3} \ldots ,x_{n}\) be a random sample of size \(n\) from the ETS distribution with PDF given in (13).
The ETS distribution's log-likelihood function (\({\mathcal{L}}\left( {\alpha ,\theta ,\beta ,\mu } \right))\) is given by.
As a result, the maximum likelihood estimators (MLEs) namely \(\hat{\alpha }\),\(\hat{\theta },\hat{\beta }\) and \(\hat{\mu }\), are the simultaneous solution of the Equations
where \({\text{Meijer}}{\prime} {\text{s }}{\mathcal{G}}\)-function is defined in this case as \({\mathcal{G}}_{2,3}^{3,0} \left( {1,1;0,0,\alpha ;z} \right) = \frac{1}{2\pi i}\mathop \smallint \limits_{ - i\infty }^{ + i\infty } \frac{{{\Gamma }^{2} \left( s \right){\Gamma }\left( {\alpha + s} \right)}}{{{\Gamma }^{2} \left( {1 + s} \right)}}z^{ - s} ds,\) and \({\Psi }\) is the digamma function, formally defined in Gradshteyn et al. (2007) as the logarithmic derivative of the Gamma function \({\Psi }\left( {\text{z}} \right) = \frac{d}{dz}\ln {\Gamma }\left( {\text{z}} \right)\).
and
\(\frac{\partial }{\partial \mu }{\mathcal{L}}\left( {\alpha ,\theta ,\beta ,\mu } \right) = \frac{n}{\mu } + \mathop \sum \limits_{i = 1}^{n} {\text{ln}}\left( {{\text{cot}}\left( {\frac{{\pi \left( {{\Gamma }\left( \alpha \right) + {\upgamma }\left( {\alpha ,\left( {\frac{{x_{i} }}{\theta }} \right)^{\beta } } \right)} \right)}}{{4{\Gamma }\left( \alpha \right)}}} \right)} \right)\).
For a more specific study of the parameter estimates behavior, the following methods will be used for one of interesting special cases of ETS family which is the exponentiated tan exponential (ETE) distribution model.
The PDF of the ETE distribution
5.2 Least squares (LS), weighted least squares (WLS), and Cramer–von Mises (CVM) estimation
Due to Swain et al. (1988), the least square technique is mainly based on decreasing the difference between the vector of uniformed order statistics and the related vector of predicted values.
Let \({\text{y}}_{1} ,{\text{y}}_{2} , \ldots {\text{y}}_{{\text{n}}}\) denote a random sample with parameters from the exponentiated tan exponential (ETE) distribution and let \({\text{y}}_{\left( 1 \right)} ,{\text{y}}_{\left( 2 \right)} , \ldots {\text{y}}_{{\left( {\text{n}} \right)}}\) be the ascending order values of \({\text{y}}_{1} ,{\text{y}}_{2} , \ldots {\text{y}}_{{\text{n}}}\) then,
where, \(F\left( {y_{i} } \right)\) is the CDF for the underling distribution.
-
Least Square Estimator (LSE)
Utilizing these expectations and variances, we can implement two variations of the least squares methods.
By minimizing, the LS estimation may be derived.
where \(G\left( {y_{i} ,\beta } \right)\) is the CDF for ETE distribution.
The Least Squares Estimates (LSE) of \(\theta\), and \(\mu\), denoted as \(\theta\) LSE, and \(\mu\) LSE respectively, can be obtained by implementing a minimization process.
To determine the Least Squares Estimates (LSE), the derivative of Eq. (25) with respect to \(\theta\), and \(\mu\) is obtained then set the result equal to zero.
Subsequently, the Least Squares Estimates (LSE) of the unknown parameters, designated as \(\theta\) LSE, and \(\mu\) LSE respectively, can be acquired by numerically solving Eqs. (26) and (27).
The LS estimate of \(\beta\) is calculated by.
\(\hat{\beta } = {\text{argmax}}_{{\beta \varepsilon \left( {0,\infty } \right)}} LS\left( \beta \right)\).
-
Weighted Least Square Estimator (WLSE)
The WLS estimators can be derived by executing a minimization procedure
where \(\eta_{i} = \frac{{(n + 1)^{2} \left( {n + 2} \right)}}{{\left( {i\left( {n - i + 1} \right)} \right){ }}}\)
The weighted Least Squares Estimates (WLSE) of \(\theta\), and \(\mu\), denoted as \(\theta\) LSE, and \(\mu\) LSE respectively, can be obtained by implementing a minimization process.
To determine the (WLSE), the following Equations are solved numerically
Subsequently,
The WLSE is given by
-
Cramer–Von Mises Estimator (CVME)
The CVM technique is the same as the previous two methods. The following is a description of the CVM function.
The CVM estimators can be derived by executing a minimization procedure
the Cramer–von Mises Estimates (CVME) of \(\theta\), and \(\mu\), denoted as \(\theta\) LSE, and \(\mu\) LSE respectively, can be obtained by implementing a minimization process.
To determine the (CVME), we will first take the derivative of Eq. (31) with respect to \(\theta\), and \(\mu\) then set the result equal to zero then solve numerically;
The CVM estimate is described as follows.
The CVM estimate uses the same method as the WL or LS estimates.
6 Simulation schemes
-
a. ETS model simulation
This section provides a concise analysis of a simulation conducted to evaluate the performance of the Maximum Likelihood Estimator (MLE). To perform the experimental study, a total of 1000 data samples are generated from ETS, with sample sizes of 20, 40, 60,80 and 100 at the nodes \(\upalpha _{0} = 0.5;\uptheta _{0} = 1;\upbeta _{0} = 0.5 ; \upmu _{0} = 1\) and \(\upalpha _{0} = 1;\uptheta _{0} = 0.5;\upbeta _{0} = 1;\upmu _{0} = 0.5\). The bias and mean squared error (MSE) are computed to examine the estimation accuracies. Tables 1 and 2 display the bias and MSE of parameter estimations for various samples size \(n\).
Remark
It is evident from this study that the bias and MSE values are decreasing as long as the sample size increases, which indicates the consistency and the efficiency of the MLE parameter estimation for ETS distribution.
-
b. Exponentiated tan exponential (ETE) Model simulation
An analytical comparison of various estimation techniques for exponentiated tan exponential (ETE) is represented in done and the results are shown in Tables 3 and 4. These techniques encompass the Least Square Estimator, the Weighted Least Square Estimator, and the Cramer–von Mises Estimator. Furthermore, this comparison was conducted under two selected node values; \(\theta_{0} = 0.05;\upmu _{0} = 2\) and \(\theta_{0} = 0.2;\upmu _{0} = 1\).
From Tables 3 and 4, the following remarks can be observed:
At a general look, it can be observed that the three methods are almost equally good in the decreasing behavior of the bias and MSE values as n increases. To be precise, LSE and Cramer–von Mises are better than WLSE for lower bias and MSE values.
7 Real lifetime applications
To examine the performance of fitting the lifetime data for the ETS model, several lifetime data sets from engineering and medical real fields will be used. These datasets vary in terms of size, characteristics, and background, yet all maintain contemporary relevance within their respective fields. For each dataset, the analysis proceeds in the following manner:
-
1.
Data Presentation Each dataset is briefly introduced and described, with relevant background information and references provided for context.
-
2.
Model Comparison The fit of the ETS model is compared with that of other candidate models. This involves calculating the same goodness-of-fit measures for each model and comparing the results. The models are then ranked according to their performance, with the best-fitting model given the highest rank.
-
3.
Results Presentation The results of the analysis, including the parameter estimates and goodness-of-fit measures, are presented in a tabular format for clarity and ease of comparison.
-
4.
Visual Representation A visual comparison is made between the empirical distribution of the data (represented as a histogram) and the fitted probability density functions (PDFs) of the models. This serves to provide a more intuitive understanding of the fit of the models to the data.
The goodness-of-fit tests which used in the comparative study are as follows:
Let us consider the data from the defined distribution model as represented by \(x_{1} ,x_{2} , \ldots x_{n}\) and their corresponding ordered values denoted as \(x_{\left( 1 \right)} ,x_{1} , \ldots ,x_{\left( n \right)}\). Initially, our focus will be on the statistical measures Cramér–von Mises \(\left( {W^{*} } \right),\) Anderson Darling \(\left( {A^{*} } \right)\),and Kolmogorov–Smirnov (K–S) signified as \(\left( {D_{n} } \right)\) These statistical measures are defined as follows:
and
respectively. Consideration is also given to the p value of the K–S test, which is associated with \(D_{n}\). The model exhibiting the minimum value for \(W^{*}\) or \(A^{*}\),and the maximum value for the p value, is selected as the most optimal model in terms of data adequacy.
7.1 Engineering and reliability lifetime data
7.1.1 Data set “1”
The following application describes data for a study of the timing of successive failures of the air conditioning system in a fleet of Boeing 720 jets. The dataset comprises 27 observations, as detailed in reference Proschan (1963). The data was analyzed by Lorenzo et al. (2018) and the observations are recorded as “1, 4, 11, 16, 18, 18, 18, 24, 31, 39, 46, 51, 54, 63, 68, 77, 80, 82, 97, 106, 111, 141, 142, 163, 191, 206, 216.” This study provides valuable insights into the reliability of the air conditioning system in this particular fleet of jets and can be used to inform maintenance and upkeep decisions.
TS (tan Stacy) (Souza et al. 2021), ETS (Exponentiated tan Stacy), CS (cos Stacy) (Souza et al. 2019b), ECS (Exponentiated cos Stacy), SS (sine Stacy) (Souza et al. 2019a), ESS (exponentiated sine Stacy) (Mustapha et al. 2021), SPL (sine Power Lomax) (Nagarjuna et al. 2021), ESW (exponentiated sine Weibull) (Mustapha et al. 2021), and HSW (Hyperbolic sine Weibull) (Kharazmi et al. 2018) are the comparative distribution models which used in this study.
The results of the goodness of fit criteria and tests are as follows:
The analytical results of Table 5 indicate that the ETS model is the most effective, with a highest p value of \(0.99626\) and lowest values for goodness of fit tests. We can also notice that the behavior of ETS is much better that the proposed cosine form.
In Fig. 5, the ETS model's fit is very clear; the corresponding estimated PDF has accurately represented the decreasing circularity of the histogram, compared to the other estimated PDFs.
7.1.2 Data set “2”
This application involves a collection of data on the servicing times for a specific model of windshield. The data was sourced from reference Prabhakar Murthy et al. (2004) and is presented in units of 1000 h. The observations, recorded as “0.046, 1.436, 2.592, 0.140, 1.492, 2.600, 0.150, 1.580, 2.670, 0.248, 1.719, 2.717,0.280, 1.794, 2.819, 0.313, 1.915, 2.820, 0.389, 1.920, 2.878, 0.487, 1.963, 2.950, 0.622, 1.978, 3.003, 0.900, 2.053, 3.102, 0.952, 2.065, 3.304, 0.996, 2.117, 3.483, 1.003, 2.137, 3.500, 1.010, 2.141, 3.622, 1.085, 2.163, 3.665, 1.092, 2.183, 3.695, 1.152, 2.240, 4.015, 1.183, 2.341, 4.628, 1.244, 2.435, 4.806, 1.249, 2.464, 4.881, 1.262, 2.543, 5.140,” provide valuable information on the servicing times for this particular model of windshield. This data can be used to inform maintenance and upkeep decisions, as well as to evaluate the performance of the windshield and identify areas for improvement (Table 6).
It is clear that the ETS model has a better fit for the data with respect to the goodness of fit results. This can be demonstrated as in Fig. 6
7.2 Lifetime medical data (bladder cancer data)
7.2.1 Data set “3”
This study examines an actual dataset of remission times for 128 bladder cancer patients. The data was provided by Saggu and Lee (1994) and is expressed in months. The values in the dataset are shown as "0.08, 2.09, 3.48, 4.87, 6.94, 8.66, 13.11, 23.63, 0.20, 2.23, 3.52, 4.98, 6.97, 9.02, 13.29, 0.40, 2.26, 3.57, 5.06, 7.09, 9.22, 13.80, 25.74, 0.50, 2.46, 3.64, 5.09, 7.26, 9.47, 14.24, 25.82, 0.51, 2.54, 3.70, 5.17, 7.28, 9.74, 14.76, 26.31, 0.81, 2.62, 3.82, 5.32, 7.32, 10.06, 14.77, 32.15, 2.64, 3.88, 5.32, 7.39, 10.34, 14.83, 34.26, 0.90, 2.69, 4.18, 5.34, 7.59, 10.66, 15.96, 36.66, 1.05, 2.69, 4.23, 5.41, 7.62, 10.75, 16.62, 43.01, 1.19, 2.75, 4.26, 5.41, 7.63, 17.12, 46.12, 1.26, 2.83, 4.33, 5.49, 7.66, 11.25, 17.14, 79.05, 1.35, 2.87, 5.62, 7.87, 11.64, 17.36, 1.40, 3.02, 4.34, 5.71, 7.93, 11.79, 18.10, 1.46, 4.40, 5.85, 8.26, 11.98, 19.13, 1.76, 3.25, 4.50, 6.25, 8.37, 12.02, 2.02, 3.31, 4.51, 6.54, 8.53, 12.03, 20.28, 2.02, 3.36, 6.76, 12.07, 21.73, 2.07, 3.36, 6.93, 8.65, 12.63, 22.69." This data provides valuable information on the remission times for bladder cancer patients and can be used to inform medical treatment decisions, as well as to evaluate the effectiveness of different treatment methods.
Table 7 shows that, when compared to the other models, the ETS model has the lowest values for \(W^{*} ,A^{*} ,D_{n} ,and highest KS\) p value (Fig. 7).
8 Conclusion
The paper introduced two generated families of distribution derived through trigonometric functions and used for defining two interesting lifetime models for Stacy distribution named as: exponentiated tan and cos Stacy Distributions (ETS&ECS). These distribution models are themselves families for all special cases of the Stacy distribution, which is one of its advantages for future work. The proposed distribution models are studied due to their behavior for PDF and the hazard functions. The hazard function for both has different interesting shapes: increasing, bathtub, inverted bathtub and others. This indicates their flexibility and applicability for modelling a wide range of lifetime data. Moreover, the statistical and reliability characteristics are obtained not withstanding complexity and giving good results especially for the stress-strength parameter. MLE method gives good properties of consistency and efficiency for ETS distribution’ estimates via the simulation section. One of its special cases is the exponentiated tan exponential (ETE) distribution, which is studied for simulation schemes to examine the parameter estimation properties via different methods. From the introduced study, LS and Cramer–von Mises methods are the best compared with the WLS method. Moreover, the implementation of applications has effectively illustrated these advantages for the proposed ETS model compared with its counterparts within the realms of special reliability engineering data and medical application for bladder cancer data.
References
Abate J, Choudhury GL, Lucantoni DM, Whitt W (1995) Asymptotic analysis of tail probabilities based on the computation of moments. Ann Appl Probab 5(4):983–1007. https://doi.org/10.1214/aoap/1177004603
Al-Babtain AA, Elbatal I, Chesneau C, Elgarhy M (2020) Sine Topp-Leone-G family of distributions: theory and applications. Open Phys 18(1):574–593
Al-Faris RQ, Khan S (2008) Sine square distribution: a new statistical model based on the sine function. J Appl Probab Stat 3(1):163–173
Bakouch HS, Chesneau C, Leao J (2018) A new lifetime model with a periodic hazard rate and an application. J Stat Comput Simul 88(11):2048–2065. https://doi.org/10.1080/00949655.2018.1448983
Barlow F, Proschan R (1975) Statistical theory of reliability and life-testing. Holt, Rinehart, and Winston, New York
Chen C-H, Wang J-P, Wu Y-M, Chan C-H, Chang C-H (2012) A study of earthquake inter-occurrence times distribution models in Taiwan. Nat Hazards 69:1335–1350
Chesneau C, Bakouch HS, Hussain T (2018) Computation A new class of probability distributions via cosine and sine functions with applications. Commun Stat Comput 48(8):2287–2300. https://doi.org/10.1080/03610918.2018.1440303
Crooks GE (2007) The amoroso distribution. Tech. Note 003v1, pp 1–27. https://www.ime.usp.br/~abe/lista/pdfN8FysfgurC.pdf
Glasser R (1980) Bathtub and related failure rate characterizations. J Am Stat Assoc 75:667–672
Gradshteyn I, Ryzhik I, Jeffrey A, Zwillinger D (2007) Table of integrals, series and products, 7th edn. Academic Press, New York
Gupta RC, Gupta PL, Gupta RD (1998) Modeling failure time data by Lehman alternatives. Commun Stat Theory Methods 27(4):887–904. https://doi.org/10.1080/03610929808832134
Iervolinoa I, Giorgiob M, Chioccarelli E (2013) Gamma degradation models for earthquake-resistant structures. Struct Saf 45:48–58
Jamal F, Chesneau C (2019) A new family of polyno-expo-trigonometric distributions with applications. Infin Dimens Anal Quantum Probab Relat Top 22(4):1950027
Kharazmi O, Saadatinik A (2016) Hyperbolic cosine-f family of distributions with an application to exponential distribution. Gazi Univ J Sci 29(4):811–829
Kharazmi O, Saadatinik A, Tamandi M (2018) Hyperbolic sine-weibull distribution and its applications. Int J Math Comput 28:23–334
Kotz M, Pensky S (2003) The stress-strength model and its generalizations: theory and applications. World Science, Singapore
Kumar D, Singh U, Singh SK (2015) A new distribution using sine function-its application to bladder cancer patients data. J Stat Appl Probab 4:417–427
Lorenzo E, Malla G, Mukerjee H (2018) A new test for decreasing mean residual lifetimes. Commun Stat Theory Methods 47(12):2805–2812. https://doi.org/10.1080/03610926.2014.985841
Mahmood Z, Chesneau C, Mahmood Z, Chesneau C, Family ANS (2019) A new sine-G family of distributions: properties and applications. Bull Comput Appl Math 7(1):53–81
Mustapha M, Alshanbari HM, Alanzi ARA, Liu L, Sami W, Chesneau C, Jamal F (2021) A new generator of probability models: the exponentiated sine-g family for lifetime studies. Entropy. https://doi.org/10.3390/e23111394
Nagarjuna VBV, Vardhan RV, Chesneau C (2021) On the accuracy of the sine power Lomax model for data fitting. Modelling 2(1):78–104
Prabhakar Murthy DN, Xie M, Jiang R (2004) Weibull models. Wiley, New York. https://doi.org/10.1002/047147326x
Proschan F (1963) Theoretical explanation of observed decreasing failure rate. Technometrics 5:375–383
Saggu PS, Lee ET (1994) Statistical methods for survival data analysis. Statistician. https://doi.org/10.2307/2348154
Souza L, de O. Júnior WR, De Brito CCR, Chesneau C, Ferreira TAE, Soares LGM (2019a) On the Sin-G class of distributions: theory, model and application. J Math Model 7(3):357–379. https://doi.org/10.22124/jmm.2019.13502.1278
Souza L, Junior WRO, de Brito CCR, Chesneau C, Ferreira TAE, Soares L (2019b) General properties for the Cos-G class of distributions with applications. Eurasian Bull Math 2(2):63–79
Souza L, Chesneau C, Fernandes RL (2021) Tan-G class of trigonometric distributions and its applications. CUBO 23(01):1–20. https://doi.org/10.4067/S0719-06462021000100001
Swain JJ, Venkatraman S, Wilson JR (1988) Least-squares estimation of distribution functions in Johnson’s translation system. J Stat Comput Simul 29(4):271–297. https://doi.org/10.1080/00949658808811068
Wu M-H, Wang J-P, Sung C-Y (2023) Earthquake magnitude probability and gamma distribution. Int J Geosci 14:585–602
Acknowledgements
The authors warmly thank the Editor in Chief and the referees for their valuable and useful comments. Furthermore, we are grateful for Open access funding provided by the Science, Technology and Innovation Funding Authority (STDF) in cooperation with the Egyptian Knowledge Bank (EKB).
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB). The authors have not disclosed any funding.
Author information
Authors and Affiliations
Contributions
Author Contributions Statement The authors of this study have made substantial contributions to the conception, design, acquisition, analysis, and interpretation of data for the manuscript entitled "Simulating Phenomena with Exponentiated Trigonometric Distributions: A Comparative Study of Estimation Methods and Real-World Applications." The specific contributions of each author are as follows: Author 1 (A1): A1 was responsible for the initial conception and design of the study, as well as the development of the overall research framework. A1 also contributed to the selection and implementation of estimation methods, the statistical analysis of the data, and provided critical revisions of the manuscript for important intellectual content. Author 2 (A2): A2 played a key role in the acquisition and analysis of data, as well as the application of the estimation methods to real-world examples. A2 was also involved in the identification and selection of real-world applications for the study, the analysis of the case studies, and the interpretation of results. A2 drafted significant portions of the manuscript and provided crucial feedback on the overall structure and presentation of the paper. Both authors have given their final approval of the version of the manuscript to be published and have agreed to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Corresponding author
Ethics declarations
Conflict of interest
We have no conflict of interest to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hassanein, W.A., Elhaddad, T.A. Simulating phenomena with exponentiated trigonometric distributions: a comparative study of estimation methods and real-world applications. Stoch Environ Res Risk Assess 38, 777–792 (2024). https://doi.org/10.1007/s00477-023-02601-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-023-02601-2