Introduction

In recent years, many classical distributions have been generalized by adding more shape parameters since numerous application in the field of engineering, financial, biomedical and environmental sciences indicated that classical distributions are not suitable to explain the data sets. Hence, there is continual need for the extension of these distributions to make effective progress in the application of these areas. The Weibull distribution with two parameters is a flexible distribution to model different types for lifetime data that exhibit monotone-shaped failure rates. The Weibull distribution can be specified through its cumulative distribution function (cdf) given by

$$\begin{aligned} G(Z)=1-e^{-\upsilon Z^{\omega }}, \quad Z,\upsilon ,\omega >0. \end{aligned}$$
(1)

where \(\upsilon ,\omega \) refer to the scale and shape parameters, respectively. According to Eq. (1), the probability density function (pdf) of the Weibull distribution is given as follows:

$$\begin{aligned} g(Z)=\upsilon \omega Z^{\omega -1}e^{-\upsilon Z^{\omega }}. \end{aligned}$$
(2)

From (1) and (2), the failure rate function (FRF) is obtained as

$$\begin{aligned} h(Z)=\upsilon \omega Z^{\omega -1}. \end{aligned}$$
(3)

Indeed, when \(\omega >1\), the FRF is increasing, whereas \(\omega <1\), it is decreasing, and when \(\omega =1\), it is constant. The Weibull distribution, on the other hand, is incapable to model data that exhibit bathtub-shaped or unimodal-shaped FRFs. The later can be considered as a common situation in industrial and medical applications, for example, electric machine life cycles, human mortality, life cycle of cancer patients, etc. Furthermore, the Weibull distribution may not be a suitable distribution for many of the engineering applications requiring load-bearing capability in the area of material science like strength of brittle materials which include most ceramics, glass, optical fiber and some polymers, and in other numerous applications. However, the strength values are limited where the Weibull distribution requires an unlimited value. Therefore, it is necessary to find generalizations of the Weibull distribution. Several trials have been conducted to define new generalizations of the Weibull distribution by adding several additional shape parameter(s), for instance, see [7, 13, 15, 19]. Broadly speaking, for bringing more flexibility to baseline distribution can be added an extra parameter, so it can be more benefit in exploring tail properties and exhibiting bathtub-shaped failure rate function. Some models for bathtub and unimodal-shaped FRFs are summarized in Table 1.

Table 1 Some models for bathtub-shaped or unimodal-shaped FRFs
Full size table

Note that the generalization is also complex and causes estimation problems, especially when the number of parameters is four or more. In this study, the main purpose is to obtain the more flexible distribution with a few parameters. Recently, a family of distributions has been proposed by Bourguignon [3] called as the Weibull-G “W-G” family by using the Weibull distribution as in (1) and replacing the argument t with \(\frac{G(t;{\varvec{\eta )}}}{\bar{G}(t;{\varvec{\eta }})}\), where \(\bar{G}(t;{\varvec{\eta )}})=1-G(t;{\varvec{\eta )}})\). Its cdf is defined as

$$\begin{aligned} F(t;\upsilon ,\omega ,{\varvec{\eta }})=1-e^{-\upsilon \left[ \frac{G(t;{\varvec{\eta }})}{\bar{G}(t;{\varvec{\eta }})}\right] ^{\omega }}, \quad t\in \mathcal {D}\subseteq \mathcal {R}; \quad \upsilon ,\omega >0, \end{aligned}$$
(4)

where \(G(t;{\varvec{\eta }})\) refers to a parent cdf, which relies on a parameter vector \({\varvec{\eta }}\). The corresponding pdf to (4) is

$$\begin{aligned} f(t;\upsilon ,\omega ,{\varvec{\eta }})=\upsilon \omega g(t;{\varvec{\eta }})\left[ \frac{G(t;{\varvec{\eta }})^{\omega -1}}{\bar{G} (t;{\varvec{\eta }})^{\omega +1}}\right] e^{-\upsilon \left[ \frac{G(t;{\varvec{\eta }})}{\bar{G}(t;{\varvec{\eta }})} \right] ^{\omega }}. \end{aligned}$$
(5)

Assuming that the parent distribution is uniform in the interval \((0,\varphi )\), \(\varphi >0\), then, the cdf is given by

$$\begin{aligned} G(t;\varphi )=\frac{t}{\varphi }, \quad 0<t<\varphi <\infty . \end{aligned}$$
(6)

Then, the corresponding pdf becomes

$$\begin{aligned} g(t;\varphi )=\frac{1}{\varphi }, \quad 0<t<\varphi <\infty . \end{aligned}$$
(7)

Inserting (6) in (4) yields a three-parameter Weibull uniform (WU) distribution with the cdf given by

$$\begin{aligned} F(t)=1-\exp \left[ -\,\upsilon \left( \frac{t}{\varphi -t}\right) ^{\omega }\right] , \quad 0<t<\varphi <\infty ,\quad \upsilon ,\omega >0. \end{aligned}$$
(8)

This distribution is also known as the Kies distribution [8]. The pdf of the WU distribution is given by

$$\begin{aligned} f(t)=\frac{\upsilon \omega \varphi }{(\varphi -t)^2} \left( \frac{t}{\varphi -t}\right) ^{\omega -1}\exp \left[ -\,\upsilon \left( \frac{t}{\varphi -t}\right) ^{\omega }\right] . \end{aligned}$$
(9)

More recently, Cordeiro et al. [6] proposed a generalized Weibull-G “GW-G” family of distributions by substituting the argument t with \(-\,\log _e\{1-G(t;{\varvec{\eta }})\}\) in Eq. (1) and defined the cdf of their family of distributions by

$$\begin{aligned} F(t;\upsilon ,\omega ,{\varvec{\eta }})=1-e^{-\upsilon \left[ -\,\log _e \{1-G(t;{\varvec{\eta }})\}\right] ^{\omega }}, \quad t\in \mathcal {D}\subseteq \mathcal {R};\quad \upsilon ,\omega >0. \end{aligned}$$
(10)

Then, the pdf of the GW-G family is given by

$$\begin{aligned} f(t;\upsilon ,\omega ,{\varvec{\eta }})&=\frac{\upsilon \omega g(t;{\varvec{\eta }})}{1-G(t;{\varvec{\eta }})}\left\{ -\,\log _e\{1-G(t;{\varvec{\eta }})\} \right\} ^{\omega -1}\nonumber \\&\quad \times \,e^{-\upsilon \left[ -\,\log _e \{1-G(t;{\varvec{\eta }})\}\right] ^{\omega }}. \end{aligned}$$
(11)

In this study, a generalization of the WU distribution, referred as a generalized Weibull uniform (GWU) distribution, is obtained. The aim of this generalization is to provide a flexible extension of WU distribution which helps practitioners to model data for different fields. The outline of this work is organized as follows: In Sect. 2, statistical properties of the GWU distribution are obtained including the shapes of the pdf and FRF, quantile function (qf), moments and the moment-generating function. In Sect. 3, the pdf of the order statistics is expressed. In Sect. 4, the parameters of the GWU distribution are estimated by using the method of maximum likelihood estimation (MLE). In Sect. 5, different sample sizes are used to simulate for testing the performance of the MLE, while in Sect. 6, an application real data set is conducted to the GWU distribution where its results are compared with peers of distributions existing in the literature. Finally, Sect. 7 gives concluding remarks.

Main properties of generalized Weibull uniform distribution

Inserting (6) in (10) yields the three-parameter generalized Weibull uniform (GWU) distribution with the cdf given by

$$\begin{aligned} F(t;\upsilon ,\omega ,\varphi )=1-e^{-v\left\{ -\log _e \left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega }}, \quad 0<t<\varphi <\infty , \quad \upsilon ,\omega >0. \end{aligned}$$
(12)

By means of derivation the cdf of T in (12) with respect to T, the pdf of T is found and given in (13)

$$\begin{aligned} f(t;\upsilon ,\omega ,\varphi )=\frac{\upsilon \omega }{\varphi \left( 1-\frac{t}{\varphi }\right) }\left\{ -\log _e\left( 1 -\frac{t}{\varphi }\right) \right\} ^{\omega -1}e^{-v\left\{ -\,\log _e\left( 1 -\frac{t}{\varphi }\right) \right\} ^{\omega }}. \end{aligned}$$
(13)

A random variable T for the pdf in Eq. (13) is defined by \(T\sim \text {GWU}(\upsilon ,\omega ,\varphi )\). R(t), defined by \(1-F(t)\), refers to the probability of an item not failing prior to some time t. For the GWU distribution, R(t) takes the following form:

$$\begin{aligned} R(t;\upsilon ,\omega ,\varphi )=e^{-v\left\{ -\log _e \left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega }},\quad 0<t<\varphi <\infty , \quad \upsilon ,\omega >0. \end{aligned}$$
(14)

Shapes of density function

Here, the shapes of the pdf and FRF of the GWU distribution are discussed. The derivative \(\log _e f(t)\) with respect to t is given by

$$\begin{aligned}&\log _e\quad f(t;\upsilon ,\omega ,\varphi )\nonumber \\& =\log _e \left( \frac{\upsilon \omega }{\varphi }\right) -\log _e \left( 1-\frac{t}{\varphi }\right) +(\omega -1)\log _e\left\{ -\log _e \left( 1-\frac{t}{\varphi }\right) \right\} \nonumber \\& -\,\upsilon \left\{ -\log _e \left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega }\nonumber \\&\frac{\hbox {d}}{\hbox {d}t}\log _e f(t;\upsilon ,\omega ,\varphi )=\frac{\left[ \log _e\left( 1 -\frac{t}{\varphi }\right) +(\omega -1)+\upsilon \omega \left\{ -\,\log _e \left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega }\right] }{\varphi \left( \log _e\left( 1-\frac{t}{\varphi }\right) \right) \log _e\left( \log _e \left( 1-\frac{t}{\varphi }\right) \right) } \end{aligned}$$
(15)

So, the roots of Eq. (15) represent the critical points of the pdf as follows:

$$\begin{aligned} \upsilon \omega \left\{ -\,\log _e\left( 1-\frac{t}{\varphi } \right) \right\} ^{\omega }+\log _e\left( 1-\frac{t}{\varphi }\right) +(\omega -1)=0. \end{aligned}$$
(16)

Herein, there may be more than one root of Eq. (16). If \(t=t_0\) that is a point of inflexion, a local maximum or a local minimum relying on whether \(\frac{\hbox {d}^2}{\hbox {d}t^2}\log _e f(t;\upsilon ,\omega ,\varphi )=0\), \(\frac{\hbox {d}^2}{\hbox {d}t^2}\log _e f(t;\upsilon ,\omega ,\varphi )<0\), \(\frac{\hbox {d}^2}{\hbox {d}t^2}\log _e f(t;\upsilon ,\omega ,\varphi )>0\), where \(\frac{\hbox {d}^2}{\hbox {d}t^2}\log _e f(t;\upsilon ,\omega ,\varphi )\) is given by

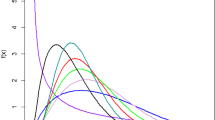
$$\begin{aligned} \frac{\begin{aligned}&\left\{ \log _e\left( 1-\frac{t}{\varphi }\right) \right\} \left\{ \log _e\left( 1-\frac{t}{\varphi }\right) -(\omega -1)\right\} -\upsilon \omega \left\{ -\log _e\left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega } \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \times \left\{ \log _e\left( 1-\frac{t}{\varphi }\right) +(\omega -1)\right\} -(\omega -1) \end{aligned}}{\varphi ^2\left( 1-\frac{t}{\varphi }\right) ^2\left\{ \log _e \left( \frac{\varphi -t}{\varphi }\right) \right\} ^2} \end{aligned}$$

It is difficult to determine the behavior of the density function from Eq. (16); despite this, in Fig. 1, some of the possible shapes are illustrated of the pdf when \(\varphi =2.5\) and for different values of \(\upsilon \) and \(\omega \). For fixed \(\omega <1\), the density is always U-shaped, and as \(\upsilon \) tends to \(0\,(\infty )\), the density function f(t) tends to J (reversed-J) shape, for fixed \(\omega >1\), the right (left)-skewed increases as \(\upsilon \) decreases (increases), and when \(\omega =1\), the density function is monotonically decreasing if \(\upsilon >1\), constant if \(\upsilon =1\) and monotonically increasing if \(\upsilon <1\). Some calculation indicates the limiting behaviors of the pdf, and the limit of the \(f(t;\upsilon ,\omega ,\varphi )\) as \(T\rightarrow \varphi ^{-}\) is 0. Further, the limit of f(t) as \(T\rightarrow 0^{+}\) is given by

$$\begin{aligned} \lim _{t\rightarrow 0^{+}}f(t;\upsilon ,\omega ,\varphi )= {\left\{ \begin{array}{ll} \infty &{}\quad \text {if }\; 0<\omega <1 \\ 0 &{}\quad \text {if }\; \omega >1 \\ \frac{\upsilon }{\varphi } &{}\quad \text {if }\; \omega =1 \end{array}\right. } \end{aligned}$$
Fig. 1
figure 1

Plots of f(t) for selected parameter values of GWU distribution

Full size image

Shape of failure rate function

Based on Eq. (14), the cumulative hazard function H(t) is simply given by

$$\begin{aligned} H(t;\upsilon ,\omega ,\varphi )=\upsilon \left\{ -\log _e \left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega }. \end{aligned}$$

The FRF has other important system’s quantity characterizing life phenomena and characteristic of interest of a random variable defined by

$$\begin{aligned} h(t;\upsilon ,\omega ,\varphi )=\frac{f(t;\upsilon ,\omega ,\varphi )}{R(t;\upsilon ,\omega ,\varphi )}, \end{aligned}$$

h(t) of the GWU distribution takes the following form:

$$\begin{aligned} h(t;\upsilon ,\omega ,\varphi )=\frac{\hbox {d}}{\hbox {d}t}H(t;\upsilon ,\omega , \varphi )=\frac{\upsilon \omega }{\varphi \left( 1-\frac{t}{\varphi } \right) }\left\{ -\,\log _e\left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega -1}. \end{aligned}$$
(17)

Obviously, because through the term \(\left\{ -\,\log _e\left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega -1}\), the shape of FRF relies only on the parameter \(\omega \), also there is no direct effect on the shapes by the remaining two parameters. In order to discuss the shapes of h(t), with respect to t, the derivative of \(\log _e h(t)\) is given by

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\log _e h(t;\upsilon ,\omega ,\varphi ) =\frac{1}{\varphi \left( 1-\frac{t}{\varphi }\right) } \left[ 1-\frac{\omega -1}{\log _e \left( 1-\frac{t}{\varphi }\right) }\right] . \end{aligned}$$
(18)

So, the roots of Eq. (18) represent the critical points of the FRF as follows:

$$\begin{aligned} \log _e\left( 1-\frac{t}{\varphi }\right) -(\omega -1)=0 \end{aligned}$$
(19)

One can obtain the turning point of the FRF \(t_0\) by solving Eq. (19) as follows:

$$\begin{aligned} t_0=\varphi \left[ 1-e^{\omega -1}\right] \end{aligned}$$
(20)

It can be shown from Eq. (17) that when \(\omega \ge 1\), h(t) tends to increase in t, and when \(0<\omega <1\), h(t) tends to decrease for \(t<t_0\) and increase for \(t>t_0\). This implies a bathtub shape for the FRF. However, at a minimum value \(t=t_0\) for the h(t), the value of \(t_0\) decreases as \(\omega \) increases, and \(h(t_0)\) can be obtained after simplification using Eqs. (17) and (20) as

$$\begin{aligned} h(t_0;\upsilon ,\omega ,\varphi )=\frac{\upsilon \omega (1-\omega )^{\omega -1}}{\varphi e^{\omega -1}}. \end{aligned}$$

Although bathtub-shaped FRF are common in reliability and survival analysis, these properties are related to several lifetime distributions, as the GWU distribution.

The limiting behaviors of the FRF can be easily shown from Eq. (17), while the limit of the as h(t) as \(T\rightarrow \theta ^-\) is \(\infty \). Further, the limit of h(t) as \(T\rightarrow 0^+\) is given by

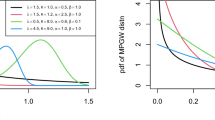
$$\begin{aligned} \lim _{t\rightarrow 0^{+}}h(t;\upsilon ,\omega ,\varphi )= {\left\{ \begin{array}{ll} \infty &{}\quad \text {if }\; 0<\omega <1 \\ 0 &{}\quad \text {if } \;\omega >1 \\ \frac{\upsilon }{\varphi } &{}\quad \text {if } \;\omega =1 \end{array}\right. } \end{aligned}$$

Figure 2 displays several of the possible shapes of \(h(t;\upsilon ,\omega ,\varphi )\) for selected values of \((\upsilon ,\omega ,\varphi )\).

Fig. 2
figure 2

Plots of \(h(t;\upsilon ,\omega ,\varphi )\) for selected parameter values of GWU distribution

Full size image

Figure 2 reveals that the proposed distribution can produce flexible FRF shapes such as increasing, decreasing, bathtub, J, snf reversed-J. This fact implies that the GWU distribution can be very useful to fit different data sets with various shapes.

Transformation

The random variable \(T=\varphi \left[ 1-e^{-Z}\right], \) when a random variable Z is Weibull-distributed with scale parameter \(\upsilon >0\) and shape parameter \(\omega >0\), follows the \(\text {GWU}(v,w,\varphi )\) distribution that helps us to simulate the random variable T in easy way by first simulating the random variable Z and then calculate \(T=\varphi \left[ 1-e^{-Z}\right] \) which has the GWU distribution.

Moment

Assume Z is a random variable possessing the moment-generating function (mgf) \(M_Z(s)=E(e^{sZ})\). One can express \(M_Z(s)\) in a Maclaurin series expansion as

$$\begin{aligned} M_Z(s)=\sum _{v=0}^{\infty }\frac{s^{v}\mu _{v}^{\prime }}{v !} \end{aligned}$$
(21)

so that \(\mu _{v}^{\prime }\) is the coefficient of \(\frac{s^{v}}{v !}\) in expansion (21).

Now, suppose Z is a random variable having the Weibull distribution in Eq. (1) with parameter \(\upsilon \) and \(\omega \), the mgf of Z is given by

$$\begin{aligned} M_Z(s)=\sum _{v=0}^{\infty }\frac{s^{v}\Gamma \left( 1+\frac{v}{\omega }\right) }{v !\upsilon ^{\frac{v}{\omega }}} \end{aligned}$$
(22)

Since the relationship between the random variable Z has the Weibull distribution in Eq. (1) and the random variable T that follows GWU distribution given by \(T=\varphi \left[ 1-e^{-Z}\right] \), the first non-central moment of T is given by

$$\begin{aligned} \mu _{1}^{\prime }=\varphi \left[ 1-E(e^{-Z})\right] =\varphi E\left[ 1-M_Z(-\,1)\right] \end{aligned}$$

Setting \(s=-\,1\) in (22), we have \(M_Z(-\,1)\), and hence, the first non-central moment of T becomes

$$\begin{aligned} \mu _{1}^{\prime }=\varphi \left[ 1-\sum _{v=0}^{\infty } \frac{(-\,1)^v\Gamma \left( 1+\frac{v}{\omega }\right) }{v!\upsilon ^{\frac{n}{\omega }}}\right] =\varphi \left[ \sum _{v=1}^{\infty }\frac{(-\,1)^{v+1}\Gamma \left( 1+\frac{v}{\omega }\right) }{v!\upsilon ^{\frac{n}{\omega }}}\right] \end{aligned}$$
(23)

So, the rth non-central moment of the GWU distribution can be obtained directly from Eq. (22) for \(s=-\,r\) as

$$\begin{aligned} \mu _{r}^{\prime }&=\varphi ^r\left[ 1-E(e^{-rZ})\right] =\varphi ^r\left[ 1-M_Z(-r)\right] \nonumber \\&=\varphi ^r\sum _{v=1}^{\infty }\frac{(-\,1)^{v+1}r^v\Gamma \left( 1+\frac{v}{\omega }\right) }{v!\upsilon ^{\frac{n}{\omega }}}. \end{aligned}$$
(24)

Further, the central moments \(\mu _r\) of T are obtained from Eq. (24) as follows:

$$\begin{aligned} \mu _r=\sum _{i=0}^{r}\left( {\begin{array}{c}r\\ i\end{array}}\right) (-\,1)^r\mu _{i}^{\prime }\mu ^{r-i}, \end{aligned}$$
(25)

For \(r=2,3,4\), Eq. (25) gives \(\mu _2\), \(\mu _3\) and \(\mu _4\), which are of the most interest because of the relations between variance, kurtosis and skewness of the random variables Z. Note that \(\mu _{0}^{\prime }=1\) and \(\mu _{1}^{\prime }=\mu \). Table 2 displays the numerical values for mean, variance, skewness and kurtosis for several values of parameters for the GWU distribution.

Table 2 Mean, variance, skewness and kurtosis for some values of \(\upsilon \) and \(\omega \) with \(\varphi =1\) (*:undefined)
Full size table

Moment-generating function

The result in (25) can be used in (21) to rewrite the mgf as

$$\begin{aligned} M_T(s)=\sum _{v=0}^{\infty }\frac{\varphi ^v s^v}{v!}\sum _{w=1}^{\infty }\frac{(-\,1)^{w+1}v^w\Gamma \left( 1+\frac{w}{\omega }\right) }{w!\upsilon ^{\frac{w}{\omega }}} \end{aligned}$$
(26)

For this section, Eq. (26) represents the main result. The characteristic function \(\Phi (s)=E\left[ e^{isT}\right] \) of T can be obtained from this equation with is in place of s, where \(i=\sqrt{-\,1}\).

Quantile function and simulation

The quantile function of the GWU distribution is obtained by inverting (12) as

$$\begin{aligned} Q(\lambda )=\varphi \left[ 1-\exp \left[ -\left\{ \frac{-\log _e(1-\lambda )}{\upsilon }\right\} ^{\omega }\right] \right] \end{aligned}$$
(27)

Setting \(\lambda =\frac{1}{2}\) in (27) gives the median of the GWU distribution as follows:

$$\begin{aligned} t_{\frac{1}{2}}=\varphi \left[ 1-\exp \left[ -\left\{ \frac{-\log _e(2)}{\upsilon }\right\} ^{\omega }\right] \right] \end{aligned}$$
(28)

Further, setting \(\lambda =\frac{1}{4}\) and \(\lambda =\frac{3}{4}\) gives the lower quartile and upper quartile, respectively. Simulating the GWU random variable is straightforward. If U is a random number following a uniform distribution \(\mathcal {U}(0,1)\), then the random variable

$$\begin{aligned} T=Q(U)=\varphi \left[ 1-\exp \left[ -\left\{ \frac{-\log _e(1-u)}{\upsilon }\right\} ^{\omega }\right] \right] \end{aligned}$$
(29)

will follow a GWU distribution with parameters \(\upsilon \), \(\omega \) and \(\varphi \).

Order statistics

The pdf \(f_{j;n}(t)\) of the jth orders \(T_{(j)}\) is given by

$$\begin{aligned} f_{j;n}(t)=n\left( {\begin{array}{c}n-1\\ j-1\end{array}}\right) f(t)F(t)^{j-1}\{1-F(t)\}^{n-j}, \quad j=1,2,\ldots , n. \end{aligned}$$
(30)

Using

$$\begin{aligned} F(t)^{j-1}&=\left[ 1-e^{-\upsilon \left\{ -\log _e \left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega }}\right] ^{j-1}\nonumber \\&=\sum _{\ell =0}^{j-1}\left( {\begin{array}{c}j-1\\ \ell \end{array}}\right) (-\,1)^{\ell }e^{-\ell \upsilon \left\{ -\log _e\left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega }} \end{aligned}$$
(31)

and

$$\begin{aligned} \{1-F(t)\}^{n-j}=e^{-(n-j)\upsilon \left\{ -\log _e \left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega }} \end{aligned}$$
(32)

and substituting (31) and (32) into (30), we get

$$\begin{aligned} f_{j;n}(t)&=n\left( {\begin{array}{c}n-1\\ j-1\end{array}}\right) \sum _{\ell =0}^{j-1}(-1)^{\ell } \frac{\upsilon \omega }{\varphi \left( 1-\frac{t}{\varphi }\right) } \upsilon \left\{ -\log _e\left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega -1} \nonumber \\&\quad \times \,\,\,e^{-\upsilon (n-j+\ell +1)\upsilon \left\{ -\log _e \left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega }} \end{aligned}$$
(33)
$$\begin{aligned} f_{j;n}(t)&=n\left( {\begin{array}{c}n-1\\ j-1\end{array}}\right) \sum _{\ell =0}^{j-1}\left( {\begin{array}{c}j-1\\ \ell \end{array}}\right) \frac{(-\,1)^{\ell }}{(n-j+\ell +1)}f(t;\upsilon _{n,\ell },\omega ,\varphi ) \end{aligned}$$
(34)

where \(f(t;\upsilon _{n,\ell },\omega ,\varphi )\) is the GWU PDF with parameters \(\upsilon _{n,\ell }=(n-j+\ell +1)\upsilon \), \(\omega \) and \(\varphi \).

Therefore, the rth non-central moment of the jth OS of GWU distribution is given by

$$\begin{aligned} \mu _{r_{j;n}}^{\prime }&=n\left( {\begin{array}{c}n-1\\ j-1\end{array}}\right) \sum _{\ell =0}^{j-1} \left( {\begin{array}{c}j-1\\ \ell \end{array}}\right) \frac{(-1)^{\ell }}{(n-j+\ell +1)}\varphi ^r\nonumber \\&\quad \times \sum _{v=1}^{\infty }\frac{(-1)^{v+1}r^v\Gamma \left( 1+\frac{v}{\omega }\right) }{v!\left\{ (n-j+\ell +1) \upsilon \right\} ^{\frac{v}{\omega }}} \end{aligned}$$
(35)

So, the pdf of the largest order statistics \(T_{(n)}\) is given by

$$\begin{aligned} f_{n;n}(t)&=n\sum _{\ell =0}^{n-1}\left( {\begin{array}{c}n-1\\ \ell \end{array}}\right) (-1)^{\ell } \frac{\upsilon \omega }{\varphi \left( 1-\frac{t}{\varphi }\right) } \left\{ -\log _e\left( 1-\frac{t}{\varphi }\right) \right\} ^{w-1}\nonumber \\&\quad \times \,\, e^{-\upsilon (\ell +1)\left\{ -\log _e\left( 1-\frac{t}{\varphi }\right) \right\} ^{\omega }} \end{aligned}$$
(36)
$$\begin{aligned} f_{n;n}(t)&=n\sum _{\ell =0}^{n-1}\left( {\begin{array}{c}n-1\\ \ell \end{array}}\right) \frac{(-\,1)^{\ell }}{(\ell +1)}f(t;\upsilon _{\ell },\omega ,\varphi ) \end{aligned}$$
(37)

where \(f(t;\upsilon _{\ell },\omega ,\varphi )\) is the pdf of the GWU distribution with parameters \(\upsilon _{\ell }=(\ell +1)\upsilon \), \(\omega \) and \(\varphi \), and the pdf of the smallest order statistics \(T_{(1)}\) is given by:

$$\begin{aligned} f_{1;n}(t)=f(t;\upsilon _n,\omega ,\varphi ) \end{aligned}$$
(38)

where \(f(t;\upsilon _n,\omega ,\varphi )\) is the pdf of the GWU distribution with parameters \(\upsilon _n=n\upsilon \), \(\omega \) and \(\varphi \).

Maximum likelihood estimation

Consider a random sample \(t_1,t_2,\ldots ,t_n\) from \(\text {GWU}(\upsilon ,\omega ,\varphi )\) distribution, and assume \(\Theta =(\upsilon ,\omega ,\varphi )^{T}\) is a vector of the distribution parameter with known \(\varphi \) (since \(t<\varphi \)), then the log-likelihood function denoted by \(\ell (\Theta )\) can be written as

$$\begin{aligned} \ell (\Theta )&=n\left( \log _e(\upsilon )+\log _e(\omega )-\log _e(t_{(n)}) \right) -\sum _{i=1}^{n}\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) -(\omega -1)\nonumber \\&\quad \times \,\,\sum _{i=1}^{n}\log _e\left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}} \right) \right\} -\upsilon \sum _{i=1}^{n}\left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) \right\} ^{\omega } \end{aligned}$$
(39)

Since \(\varphi \) is supposed known, the score vector can be defined by \(U(\Theta )=\left( \frac{\partial }{\partial \upsilon }\ell (\Theta ),\frac{\partial }{\partial \omega }\ell (\Theta )\right) ^{T}\) where the components corresponding to the \(\text {GWU}(\upsilon ,\omega ,\varphi )\) distribution by differentiating Eq. (39) determined the parameters of new model. The elements of the score model are given by

$$\begin{aligned} U_{\upsilon }(\Theta )&=\frac{n}{\upsilon }-\sum _{i=1}^{n} \left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) \right\} ^{\omega } \end{aligned}$$
(40)
$$\begin{aligned} U_{\omega }(\Theta )&=\frac{n}{\omega }+\sum _{i=1}^{n}\log _e \left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) \right\} -\upsilon \sum _{i=1}^{n}\left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}} \right) \right\} ^{\omega }\nonumber \\&\quad \times \,\, \log _e\left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) \right\} \end{aligned}$$
(41)

Setting (40) and (41) to zero and simplifying, we obtain

$$\begin{aligned} \widehat{\upsilon }&=\frac{n}{\sum _{i=1}^{n}\left\{ -\log _e \left( 1-\frac{t_i}{t_{(n)}}\right) \right\} ^{\widehat{\omega }}} \end{aligned}$$
(42)
$$\begin{aligned} \frac{n}{\widehat{\omega }}&=\frac{n}{\sum _{i=1}^{n} \left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) \right\} ^{\widehat{\omega }}} \sum _{i=1}^{n}\left[ \left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) \right\} ^{\widehat{\omega }}\right. \nonumber \\&\quad \,\,\times \,\left. \log _e\left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) \right\} \right] -\sum _{i=1}^{n}\log _e\left\{ -\log _e\left( 1 -\frac{t_i}{t_{(n)}}\right) \right\} \end{aligned}$$
(43)

The solution of Eq. (43) represents the MLE \(\widehat{\omega }\) of \(\omega \). The MLE \(\widehat{\upsilon }\) of \(\upsilon \) can be found by substituting the estimate \(\widehat{\omega }\) in Eq. (42).

The elements of the observed information matrix \(I_n(\Theta )=\{I_{rs}\}\) for \(r;s=\upsilon ,\omega \) are found by

$$\begin{aligned} U_{\upsilon \upsilon }(\Theta )&=-\,\frac{n}{\upsilon ^2} \end{aligned}$$
(44)
$$\begin{aligned} U_{\upsilon \omega }(\Theta )&=-\,\sum _{i=1}^{n}\left\{ -\log _e \left( 1-\frac{t_i}{t_{(n)}}\right) \right\} ^{\omega }\log _e \left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) \right\} \end{aligned}$$
(45)
$$\begin{aligned} U_{\omega \omega }(\Theta )&=-\,\frac{n}{\omega ^2}-\upsilon \sum _{i=1}^{n} \left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) \right\} ^{\omega } \left[ \log _e\left\{ -\log _e\left( 1-\frac{t_i}{t_{(n)}}\right) \right\} \right] ^2 \end{aligned}$$
(46)

For large n, the bivariate normal distribution with zero mean vector 0, and variance-covariance matrix \({\varvec{I_2(\Theta )^{-1}}}\) can be used to approximate the distribution of \({\varvec{\sqrt{n}(\widehat{\Theta }-\Theta )}}\), where \({\varvec{I(\Theta )=\lim _{n\rightarrow \infty }n^{-1}I_n(\Theta )}}\) is the expected. The estimated asymptotic bivariate normal distribution \({\varvec{N_2(0,I(\Theta )^{-1})}}\) of \({\varvec{\widehat{\Theta }}}\) can be used to construct approximate confidence intervals for the distribution parameters. A large sample \({\varvec{100(1-\gamma )\%}}\) confidence intervals for \(\upsilon \) and \(\omega \) are \(\widehat{\upsilon }\pm z_{\frac{\gamma }{2}}\sqrt{\text {var}(\widehat{\upsilon })}\) and \(\widehat{\omega }\pm z_{\frac{\gamma }{2}}\sqrt{\text {var}(\widehat{\omega })}\), respectively, where the \(\text {var}(\cdot )\)’s are the diagonal elements of \({\varvec{I_n(\Theta )^{-1}}}\), and \({\varvec{z_{\frac{\gamma }{2}}}}\) is the upper \({\varvec{\frac{\gamma }{2}}}\)th percentile of the standard normal distribution.

Simulation study

A simulation study is conducted to examine the performance of the MLE method to estimate the GWU distribution parameters. Monte Carlo technique is employed to simulate the GWU random number generation depending on the inversion method, i.e., varieties of the GWU distribution are generated using (29). The simulation study is conducted for nine-parameter incorporation, \(\upsilon =0.5,1.0,1.5\) and \(\omega =0.5,1.0,1.5\) and consider sample sizes with \(n=30,50\) and 100. The process is repeated 5000 times for each parameter incorporation and each sample size.

The average bias \(AB=\frac{1}{5000}\sum _{i=1}^{5000}(\text {estimate}-\text {actual})\) and mean square error \(\hbox {MSE}=\frac{1}{5000}\sum _{i=1}^{5000}(\text {estimate}-\text {actual})^2\) of the MLEs are used to measure the performance.

It can be observed in Table 3 that for all the different sets when we increase n, the bias for \(\upsilon \) and \(\omega \) decreases. The MSEs tend to toward zero when we increase the sample size n. The simulation results validate the performance of the maximum likelihood estimators.

Table 3 MLE, bias and MSE for various parameter values when \(\varphi =1\)
Full size table

Application

Voltage data were employed to illustrate the flexibility of the GWU distribution, in addition to compare the behavior of the new model with other generalization of Weibull distribution. The model selection is achieved by using the maximized log-likelihood, Akaike information criterion AIC and Bayesian information criterion (BIC) given by:

$$\begin{aligned} \text {AIC}= & {} -\,2\mathcal {L}(\widehat{{\varvec{\Theta }}})+2q,\\ \text {BIC}= & {} -\,2\mathcal {L}(\widehat{{\varvec{\Theta }}})+q \ln (n), \end{aligned}$$

where \(\mathcal {L}(\widehat{{\varvec{\Theta }}})\) refers to the log-likelihood function that evaluates at the MLE, while q is the number of parameters and n is the sample size.

Voltage data

The data have been obtained from Meeker and Escobar [10]. They represent the lifetimes of 30 electronic components taken from power-line voltage spikes during electric storms. The data have been previously used by Nadarajah et al. [12] and Tahir et al. [16] (Table 4).

Table 4 Lifetimes of 30 electronic components from Meeker and Escobar [10]
Full size table

The total time on test (TTT) transform plot illustrates that data set has a bathtub-shaped FRF. So, the GWU distribution may be suitable for modeling this data set. Table 5 provides the MLEs of the unknown parameters with corresponding standard errors for different distributions. The values of these statistics in data sets are smaller for the GWU distribution compared to those values of other fitted distributions. The approximate \(95\%\) two-sided asymptotic confidence interval of the parameters \(\upsilon \), \(\omega \) and \(\varphi \), respectively, is: (0.391,0.815) , (0.417, 0.831) and (2030.72, 369.34).

It is concluded that the proposed model provides a goodness of fit for the given data set, which leads to ability to choose the GWU distribution as the best model (Fig. 3).

Table 5 MLEs of the parameters (the standard errors are given in parentheses) to the voltage data and the values of the − log likelihood, AIC and BIC statistics
Full size table
Fig. 3
figure 3

Voltage data set. a TTT- transform plot represents to the voltage data set. b The empirical and estimated cdf of the distribution. c Probability plots. d The expected and observed number of observations

Full size image

Conclusion

The GWU distribution was introduced with the new three parameters. The new model can have bathtub and increasing shapes for the FRF. The new model displays the lifetime data on a bathtub shape as a versatility of FRF. Many structural properties of the GWU distribution have been studied and derived, encompassing the moment, moment-generating function and order statistics. The MLE was used to estimate the asymptotic interval and point estimates of the parameters. One set of real-life data was employed to demonstrate the flexibility of GWU distribution. The encourage results of new model were compared with the results of the others distributions in the literature. Discover revealed that the GWU distribution gives us a better fit than the other lifetime models. It is expected that the new model can be employed in other several sciences.