Spatio-temporal analysis of the extent of an extreme heat event

Abstract

Evidence of global warming induced from the increasing concentration of greenhouse gases in the atmosphere suggests more frequent warm days and heat waves. The concept of an extreme heat event (EHE), defined locally based on exceedance of a suitable local threshold, enables us to capture the notion of a period of persistent extremely high temperatures. Modeling for extreme heat events is customarily implemented using time series of temperatures collected at a set of locations. Since spatial dependence is anticipated in the occurrence of EHE’s, a joint model for the time series, incorporating spatial dependence is needed. Recent work by Schliep et al. (J R Stat Soc Ser A Stat Soc 184(3):1070–1092, 2021) develops a space-time model based on a point-referenced collection of temperature time series that enables the prediction of both the incidence and characteristics of EHE’s occurring at any location in a study region. The contribution here is to introduce a formal definition of the notion of the spatial extent of an extreme heat event and then to employ output from the Schliep et al. (J R Stat Soc Ser A Stat Soc 184(3):1070–1092, 2021) modeling work to illustrate the notion. For a specified region and a given day, the definition takes the form of a block average of indicator functions over the region. Our risk assessment examines extents for the Comunidad Autónoma de Aragón in northeastern Spain. We calculate daily, seasonal and decadal averages of the extents for two subregions in this comunidad. We generalize our definition to capture extents of persistence of extreme heat and make comparisons across decades to reveal evidence of increasing extent over time.

1 Introduction

There is strong evidence of global warming due to the increasing concentration of greenhouse gases in the atmosphere (Lai and Dzombak 2019). This global warming suggests more frequent warm days, more frequent and persistent heat waves (Lemonsu et al. 2014; Alexander 2016) as well as events that break previous records by much larger margins (Fischer et al. 2021; Cebrián et al. 2021). The analysis of heat waves is particularly important due to the potential for serious anthropogenic, environmental, and economic impacts (Amengual et al. 2014; Campbell et al. 2018). Extreme heat raises significant health concerns in humans as it can result in death, change the range or niche for plants and animals, and lead to heat-driven peaks in electricity demands or lost crop income.

A challenge in analyzing heat waves stems from on-going debate over its exact definition. According to the World Meteorological Office (WMO), a period persisting at least three consecutive days of marked unusual hot weather (maximum, minimum and daily average temperature) over a region with thermal conditions above given thresholds based on local climatological conditions can be considered a heat wave. This definition suggests that analyses of heat waves require temperature series at a daily scale, but offers no operational guidance with regard to the various choices of implementation. Khaliq et al. (2005) and Reich et al. (2014) used only maximum temperature, while Keellings and Waylen (2014) and, more recently, Abaurrea et al. (2018) considered both maximum and minimum temperatures.

While there is lack of agreement on heat wave definition in the literature (Perkins and Alexander 2013; Smith et al. 2013), the concept of an extreme heat event (EHE) is explicitly defined, capturing the notion of a period (number of consecutive days) of persistent extremely high temperatures. Specifically, EHE’s are defined locally and are based on exceedance of a suitable local threshold. That is, useful thresholds should be based on local conditions; in the sequel, we adopt the 95th percentile of local daily maximum temperatures, derived using a ten year period. In the context of persistence of exceedance, it is evident that we need to model daily max temperatures since an EHE is defined at a given location as a run of consecutive daily temperature observations exceeding the given threshold for that location. Additionally, daily modeling enables assessment of important behaviors describing the nature of an EHE such as the duration, average exceedance, and maximum exceedance above the threshold. As a result, we define extent in terms of incidence of exceedance on a given day, developed from a daily max temperature model that is able to adequately represent both the central part and the upper tail of the temperature distribution. It is not a model only for the tails or observations above a threshold, i.e., left-truncated data (peaks over thresholds models) or for the extremes (generalized extreme value distribution models). Such modeling addresses different objectives.

Modeling for extreme heat events is customarily implemented using time series of temperatures over a window of time collected at particular locations. However, spatial aspects of this phenomenon are also of interest and should be introduced into the modeling process, particularly with interest in predicting EHE behavior at locations without available time series of temperatures. Since spatial dependence is anticipated in the occurrence of EHE’s, a joint model for time series at different locations that incorporates spatial dependence is needed.

Recent work by Schliep et al. (2021) develops a space-time model based on a point-referenced collection of temperature time series that enables the prediction of both the incidence and the characteristics of the EHE’s occurring at any location in the region. Specifically, it offers direct spatial modeling for daily maximum temperatures which can then be used to characterize the EHE’s. The challenge is that, while the bulk of the distribution, i.e., where most of the data is observed, is not extreme, the main interest for the model lies in the upper tail when attempting to characterize EHE’s (Keellings and Waylen 2015; Shaby et al. 2016). To address this, a specification incorporating thresholding is introduced, i.e., a model which switches between two observed states, one that defines extreme heat days (those above the temperature threshold) and the other that defines non-extreme heat days (those below the temperature threshold). Again, these thresholds are obtained locally and assumed fixed. Importantly, this two-state structure allows temporal dependence of the observations but also permits the parameters controlling the effects of covariates and the spatial dependence to differ between the two states. We briefly review details of this modeling in Sect. 2.4.

With regard to risk assessment, the contribution of this work is to formalize the notion of the spatial “extent” of an extreme heat event and then to illustrate it using output from the Schliep et al. (2021) modeling work. Interest in characterizing the extent of heat waves is clear. For example, Lhotka and Kyselý (2015) proposed an extremity index that captures joint effects of spatial extent, temperature and duration of heat waves. Keellings and Moradkhani (2020) also developed a spatial metric combining heat wave frequency, magnitude, duration and areal extent to analyze the evolution of heat waves across the United States. Rebetez et al. (2009) compared the heatwave extent in Europe in 2003 and 2006. Khan et al. (2019) found an increase of 1.36% of the affected area having both maximum and minimum temperature above the 95th percentile per decade in Pakistan. Lyon et al. (2019) projected the increase in the spatial extent of contiguous US summerheat waves using the CMIP5 archive under RCP4.5 and RCP8.5 scenarios. They found a substantial increase in spatial extent climate model employing projections for 2031–2055. However, all this work analyzes the extent using descriptive approaches and using observed or gridded data with no formal inference from probabilistic modeling.

Some more formal definitions related to the concept of area under extreme conditions have been introduced in the statistical literature. For example, French and Sain (2013) present a method for constructing confidence regions for Gaussian processes that contain the true exceedance regions with some predefined probability. Extending this methodology, Hazra and Huser (2021) obtain confidence regions that contain joint threshold exceedances of surface sea temperatures in the Red Sea, using a semiparametric Bayesian spatial mixed-effects linear model. Bolin and Lindgren (2015) consider excursion sets, which are sets of points in an area where a spatial function is above a given threshold. Sommerfeld et al. (2018) develop confidence regions for these spatial excursion sets with an application to climate and Romero-Béjar et al. (2018) develop quantile-based spatiotemporal risk assessment of exceedances using this concept. Zhong et al. (2020) analyze spatial extent of heatwaves using a model based on max-infinitely divisible processes for annual temperature maxima. However, to our knowledge, the notion of the extent of an EHE has not been explicitly defined as a stochastic object. So, we take this up both conceptually and practically. Given a threshold surface over a specified region, for a given day, the extent of an EHE over the region is the proportion of the area of the region whose daily max temperature for the day is above the associated threshold surface. In the sequel we adopt a static threshold surface in order to assess change in extent over time. With different intentions, time-varying thresholds could be employed.

The basic idea is an extension of the so-called spatial cumulative distribution function (cdf) following the work of Lahiri et al. (1999) and Short et al. (2005). It is also discussed in Section 15.3 of Banerjee et al. (2014). The extent arises as a stochastic integral, i.e., an integral over a realization of a stochastic process. It is a random object as well as a conceptual object in the sense that it can not be observed and it can not be calculated in closed form. However, its moment properties can be calculated and approximate realizations can be obtained through Monte Carlo integration.

Attractively, we can study extents employing realizations from any spatio-temporal model fitted for daily max temperatures. Here, we adopt the model from Schliep et al. (2021) and do not do any additional modeling work. We can provide extents directly from the output of that model fitting. In different words, assessment of extent of an EHE is a post model fitting activity.

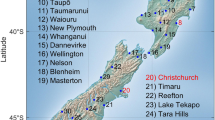
The region over which we study extents is the Comunidad Autónoma de Aragón region in northeastern Spain, located in the Ebro basin (85,362 km$^2$). The Ebro river flows from the NW to the SE through a valley bordered by the Pyrenees and the Cantabrian Range in the north and the Iberian System in the southwest. The maximum elevation is approximately 3400 m in the Pyrenees, 2600 m in the Cantabrian Range and Iberian System, and between 200-400 m in the central valley. In general, the area is characterized by a Mediterranean-continental dry climate with irregular rainfall, and a large temperature range. However, several climate subareas can be distinguished due to the heterogeneous orography and other influences, such as the Mediterranean sea to the east, and the continental conditions of the Iberian central plateau in the southwest. Zaragoza, the largest city in the region, is located in the central part of the valley, and experiences more extreme temperatures and drier conditions.

Our data are observational series from AEMET (the Spanish Meteorological Office). Only long term series with limited missing observations were considered, resulting in daily maximum temperatures for 18 sites across and around the Comunidad Autónoma de Aragón region for the years 1953-2015. The names and locations of the 18 sites are shown spatially in Fig. 1. Data from the years 1953-1962 were used to obtain the location-specific thresholds for extreme heat events; the data for the years 1963-2015 were used in the modeling. Specifically, thresholds were computed as the 95th percentile of daily maximum temperature for the months June, July, and August during the 10 years 1953-1962. Again, our objective is to see change in extent over time which requires a fixed $q(\mathbf{s} )$ threshold surface. While we could use fixed thresholds associated with any time window, using thresholds prior to the start of our modeling, using data not employed in our fitting, seemed to provide a sensible baseline.

The format of the paper is as follows. In Sect. 2, we present the details of the spatial extent and briefly review the Schliep et al. (2021) model. Section 3 shows the rich scope of extents we can calculate and compare. Section 4 provides a brief summary and future work.

2 Formalizing extent of extreme heat

2.1 The definition of extent

The definition of the spatial cdf (Lahiri et al. 1999) is attached to a realization of a stochastic process taking values in $\mathbb {R}$, $\mathcal{Z} = \{Z(\mathbf{s} ): \mathbf{s} \in \mathcal {D}\}$, over a region $\mathcal {D}$ and, for a given w, is

$$\begin{aligned} F_{\mathcal{Z}}(w) = \frac{1}{|\mathcal {D}|}\int _{\mathcal {D}} \mathbf{1} (Z(\mathbf{s} ) \le w) d\mathbf{s} \end{aligned}$$

where $|\mathcal {D}|$ is the area of $\mathcal {D}$. That is, it is the proportion of the realization over $\mathcal {D}$ that lies below w. It behaves like a cdf in the sense that it is nondecreasing and goes to 0 as $w \rightarrow -\infty$ and 1 as $w \rightarrow \infty$. However, since it is a function of the process realization, it is a random variable and arises as a stochastic integral. It differs from the marginal cdf associated with the variable $Z(\mathbf{s} )$ at location $\mathbf{s}$, $P(Z(\mathbf{s} ) \le w)$ which is a constant (as a feature of the distribution of $Z(\mathbf{s} ))$. Like stochastic integrals in general, it can not be calculated explicitly (but it can be approximated using Monte Carlo integration). However, some distributional properties, e.g., mean and variance, can be calculated.

To define the object of interest here, a spatial extent, let $Y_{t}(\mathbf{s} )$ denote the daily max temp for day t at location $\mathbf{s}$. Suppose we consider a subregion $B \subseteq \mathcal {D}$ of the study domain. Then, for a given w, the extent of the EHE in subregion B on day t is:

$$\begin{aligned} Ext_{t}(w;B) = \frac{1}{|B|} \int _{B} \mathbf{1} (Y_{t}(\mathbf{s} ) - q(\mathbf{s} ) \ge w) d\mathbf{s} . \end{aligned}$$

(1)

Here, $q(\mathbf{s} )$ is the threshold surface over B. That is, it is the proportion of B which is experiencing extreme heat at least w degrees above or below (according to the sign of w) associated local thresholds on day t. In fact, it is referred to as a block average (Banerjee et al. 2014) in this case of indicator functions. Evidently, we can choose B as we wish. In Section 3 we consider two subregions of interest for comparison but, with interest in extent at a larger spatial scale, we might also consider the case where $B = \mathcal {D}$. Regardless, since extent captures proportion of incidence within a region, a larger region does not imply a larger extent. However, an alternative definition of extent would specify a region where extent is anticipated to be high (or low) and then calculate the extent in order to provide quantification. EHE is applicable to the extent when $w=0$ and is probably of greatest interest but below, Sect. 3.4, we also look at the extent of more ($w>0$) or less ($w<0$) extreme heat events.

The posterior predictive distribution for $Ext_{t}(w;B)$ is needed for inference. We use a Monte Carlo integration to obtain an approximate realization of it by computing:

$$\begin{aligned} \widetilde{Ext}_{t}(w;B) = \frac{1}{m} \sum _{j=1}^{m} \mathbf{1} (Y_{t}(\mathbf{s} _{j}) - q(\mathbf{s} _{j}) \ge w). \end{aligned}$$

(2)

Here, for a selected set of m locations in B with an associated set of thresholds, $\{q(\mathbf{s} _{j}), j=1,2, \ldots , m\}$, $\{Y_{t}(\mathbf{s} _{j}), j=1,2, \ldots , m\}$ is a posterior predictive realization of daily max temperatures for day t at the locations, $\mathbf{s} _{j}$. If we have a collection of these realizations, then we can obtain posterior samples of $\widetilde{Ext}_{t}(w;B)$ for any choices of w. In this way, with arbitrarily many posterior predictive realizations, we can learn arbitrarily well about the posterior predictive distribution for $Ext_{t}(w;B)$.

To compute (2), given t, we need a realization $\{Y_{t}(\mathbf{s} _j), j=1,2, \ldots , m\}$. To consider arbitrary days within arbitrary years within arbitrary decades, we need a posterior predictive realization of a 50 year daily max time series (1966-2015) for each $\mathbf{s} _j$. Employing the output of the model fitting of Schliep et al. (2021), we can obtain such posterior predictive realizations using composition sampling (Banerjee et al. 2014, Chapter 6). Below, we obtain a collection of 500 such realizations, enabling a posterior predictive distribution for $Ext_{t}(w;B)$ through $\widetilde{Ext}_{t}(w;B)$. These samples yield an empirical summary of the posterior predictive distribution for $Ext_{t}(w;B)$, hence, posterior inference regarding any features of $Ext_{t}(w;B)$ that are of interest.

Note that to compute (2) we first need to create the $q(\mathbf{s} _{j})$. In the sequel, upon a regular gridding of B to fairly fine resolution, we obtained the centroids of the grid cells as our $\mathbf{s} _{j}$’s. Then, gathering elevations for these centroids from a digital terrain map (DTM), we kriged the $q(\mathbf{s} _{j})$. That is, using the thresholds for the observed sites with their associated elevations, we employed a standard kriging model for the thresholds at the $\mathbf{s} _j$ using their associated DTM elevations. Furthermore, we identified an additional 37 stations which had temperature data available between 1953-1962, yielding a total of 55 stations from which we developed the $q(\mathbf{s} )$ surface. In Figure OR.1 in the Online Resource we show the resulting $q(\mathbf{s} )$ surface along with the 55 stations. Fancier kriging could be imagined but here and illustratively, we confine ourselves to the above. Furthermore, we treat all of the kriged $q(\mathbf{s} _{j})$ as fixed in implementing the Monte Carlo integrations.

As a last remark, it is possible to create an empirical extent, employing the form in (2) but using only the available observed sites that are within B. With only 18 stations, only a few will be in B, yielding a single estimate that can assume only a few discrete values and with no uncertainty. In implementing the Monte Carlo integrations for (2) below, we employ $m \approx 6000$ – 8000, yielding much smoother extents and with replication enabling us to see the distribution.

2.2 Some technical details: a digression

Here, we offer some theoretical insight into the distribution of a spatial extent by calculating the first and second moments under an illustrative Gaussian spatial first order autoregression model, a simplified version of the model that we work with in Sect. 2.4. In particular, consider the model

$$\begin{aligned} Y_{t}(\mathbf{s} ) = \mu _{t}(\mathbf{s} ) + \eta (\mathbf{s} ) + \rho (Y_{t-1}(\mathbf{s} ) - (\mu _{t-1}(\mathbf{s} ) + \eta (\mathbf{s} ))) + \epsilon _{t}(\mathbf{s} ) \end{aligned}$$

where $\mu _{t}(\mathbf{s} )$ is a spatio-temporal drift term. Specific choices are adopted in Sect. 2.4. Here, $\eta (\mathbf{s} )$ is a mean 0 Gaussian process with covariance $cov(\eta (\mathbf{s} ),\eta (\mathbf{s} '))=\sigma ^2 h(\mathbf{s} - \mathbf{s} ')$ providing local spatial adjustment to the drift terms as well as spatial dependence across locations. The $\epsilon _{t}(\mathbf{s} )$ are pure errors, independent and identically distributed as $N(0, \tau ^2)$.

Let $Z_{t}(\mathbf{s} ) = Y_{t}(\mathbf{s} ) - \mu _{t}(\mathbf{s} )$ so $Z_{t}(\mathbf{s} ) = \rho Z_{t-1}(\mathbf{s} ) + (1-\rho )\eta (\mathbf{s} ) + \epsilon _{t}(\mathbf{s} )$. Marginalizing over $\eta (\mathbf{s} )$, we obtain

$$\begin{aligned} Z_{t}(\mathbf{s} ) \mid Z_{t-1}(\mathbf{s} ) \sim N(\rho Z_{t-1}(\mathbf{s} ), (1-\rho )^2 \sigma ^2 + \tau ^2). \end{aligned}$$

In fact, the joint distribution of $(Z_{t}(\mathbf{s} ), Z_{t}(\mathbf{s} '))$ given $(Z_{t-1}(\mathbf{s} ), Z_{t-1}(\mathbf{s} '))$ is bivariate normal with mean $\left( \begin{array}{c} \rho Z_{t-1}(\mathbf{s} ) \\ \rho Z_{t-1}(\mathbf{s} ') \\ \end{array} \right)$ and covariance matrix

$$\begin{aligned} \left( \begin{array}{cc} (1-\rho )^{2}\sigma ^{2} +\tau ^{2} &{} (1- \rho )^{2}\sigma ^{2}h(\mathbf{s} - \mathbf{s} ') \\ (1- \rho )^{2}\sigma ^{2}h(\mathbf{s} - \mathbf{s} ') &{} (1-\rho )^{2}\sigma ^{2} +\tau ^{2}\\ \end{array} \right) . \end{aligned}$$

Implementing the customary marginalization over $Z_{t-1}(\mathbf{s} )$, at equilibrium (t large), we have $Z_{t}(\mathbf{s} ) \sim N(0, \phi ^{2}(\rho , \sigma ^{2}, \tau ^{2}))$ where $\phi ^{2}(\rho , \sigma ^{2}, \tau ^{2}) = \frac{(1-\rho )^2 \sigma ^2 + \tau ^2}{1- \rho ^2}$. So, $Y_{t}(\mathbf{s} ) \sim N(\mu _{t}(\mathbf{s} ), \phi ^{2}(\rho , \sigma ^{2}, \tau ^{2}))$. Similarly, we can obtain $cov(Z_{t}(\mathbf{s} ), Z_{t}(\mathbf{s} ')) = \frac{(1-\rho )^2 \sigma ^2 h(\mathbf{s} - \mathbf{s} ')}{1- \rho ^2}$ and hence, the distribution, $[Y_{t}(\mathbf{s} ), Y_{t}(\mathbf{s} ')]$.

Returning to (1), $E\left( Ext_{t}(w;B)\right) =$

$$\begin{aligned}&E\left( \frac{1}{|B|} \int _{B} \mathbf{1} (Y_{t}(\mathbf{s} ) - q(\mathbf{s} ) \ge w) d\mathbf{s} \right) \\&\quad = \frac{1}{|B|} \int _{B} E\left( \mathbf{1} (Y_{t}(\mathbf{s} ) - q(\mathbf{s} ) \ge w)\right) d\mathbf{s} . \end{aligned}$$

However,

$$\begin{aligned}E\left( \mathbf{1} (Y_{t}(\mathbf{s} ) - q(\mathbf{s} ) \ge w)\right) = & P(Y_{t}(\mathbf{s} ) \ge q(\mathbf{s} ) + w) \equiv p_{t}(\mathbf{s} ,w) \\&\quad = \varPhi \left( \frac{\mu _{t}(\mathbf{s} ) - (q(\mathbf{s} ) +w)}{\phi (\rho , \sigma ^{2}, \tau ^{2})}\right) . \end{aligned}$$

So,

$$\begin{aligned} E\left( Ext_{t}(w;B)\right) = \frac{1}{|B|} \int _{B}\varPhi \left( \frac{\mu _{t}(\mathbf{s} ) - (q(\mathbf{s} ) +w)}{\phi (\rho , \sigma ^{2}, \tau ^{2})}\right) d\mathbf{s} . \end{aligned}$$

(3)

Monte Carlo approximation to (3) is straightforward.

Next, we obtain $var(Ext_{t}(w;B))$. Let $g(Y_{t}(\mathbf{s} )) = \mathbf{1} (Y_{t}(\mathbf{s} ) - q(\mathbf{s} ) \ge w)$. Then, by familiar calculation for block averages (see Banerjee et al. 2014, Chapter 7),

$$\begin{aligned} var(Ext_{t}(w;B)) = & \frac{1}{|B|}\int _{B} var(g(Y_{t}(\mathbf{s} ))) d\mathbf{s} \\&\quad + \frac{1}{|B|^{2}} \int _{B}\int _{B} cov(g(Y_{t}(\mathbf{s} )), g(Y_{t}(\mathbf{s} ')))d\mathbf{s} ' d\mathbf{s} . \end{aligned}$$

However, $var\left( g(Y_{t}(\mathbf{s} ))\right) = p_{t}(\mathbf{s} ,w)(1- p_{t}(\mathbf{s} ,w))$. Similarly, $cov(g(Y_{t}(\mathbf{s} )),g(Y_{t}(\mathbf{s} '))) = p_{t}(\mathbf{s} , \mathbf{s} ',w) - p_{t}(\mathbf{s} ,w)p_{t}(\mathbf{s} ',w)$ where $p_{t}(\mathbf{s} , \mathbf{s} ', w) = P(Y_{t}(\mathbf{s} ) \ge q(\mathbf{s} ) + w, Y_{t}(\mathbf{s} ') \ge q(\mathbf{s} ') + w)$, a double integral over the bivariate normal distribution for $Y_{t}(\mathbf{s} )$ and $Y_{t}(\mathbf{s} ')$ given above. So,

$$\begin{aligned} \begin{aligned}&var(Ext_{t}(w;B)) = \frac{1}{|B|} \int _{B}p_{t}(\mathbf{s} ,w)(1- p_{t}(\mathbf{s} ,w))d\mathbf{s} \\&+\frac{1}{|B|^{2}}\int _{B}\int _{B}p_{t}(\mathbf{s} , \mathbf{s} ',w) - p_{t}(\mathbf{s} ,w)p_{t}(\mathbf{s} ',w)d\mathbf{s} 'd\mathbf{s} . \end{aligned} \end{aligned}$$

(4)

Monte Carlo integration for (4) can also be implemented.

2.3 Elaborating extents

In climate applications, such as attempting to assess the effect of global warming on extreme temperatures, the main interest is not usually to characterize the distribution of the extent in a given day $Ext_t(w;B)$ but rather to characterize the behavior of the extent across years or changes in its seasonal pattern. To this end, it is convenient to analyze the distribution of different averages of the daily extent over a given period of time, such as seasons or years. In defining average extents, we will use two time indexes, one for the day within year l and one for the year t,

$$\begin{aligned} Ext_{t,l}(w;B) = \frac{1}{|B|} \int _{B} \mathbf{1} (Y_{t,l}(\mathbf{s} ) - q(\mathbf{s} ) \ge w) d\mathbf{s} . \end{aligned}$$

Then, we can average the daily extent over a period of days within the year, L, and over a period of years, T, as

$$\begin{aligned} \begin{aligned} Av_{ t\in T, l\in L} Ext_{t,l}(w;B) = \frac{1}{n_Tn_L} \sum _{t \in T} \sum _{l \in L} Ext_{t,l}(w;B) \end{aligned} \end{aligned}$$

where $n_T$ and $n_L$ are the number of observations in the periods T and L respectively.

In the analysis of EHE, we consider: (i) decadal averages for a given day l and decade D, $Av_{t \in D} Ext_{t,l}(w;B) = \frac{1}{10} \sum _{t \in D} Ext_{t,l}(w;B)$, (ii) the average extent over the summer months JJA for a given year t, $Av_{l \in JJA} Ext_{t,l}(w;B) = \frac{1}{92} \sum _{l \in JJA} Ext_{t,l}(w;B)$, and (iii) the average extent over the summer months and a decade, $Av_{ t\in D, l\in JJA} Ext_{t,l}(w;B) = \frac{1}{920} \sum _{t \in D} \sum _{l \in JJA} Ext_{t,l}(w;B).$ In calculating these quantities, we replace all integrals by their Monte Carlo approximations, obtaining the values $Av_{ t\in T, l\in L} \widetilde{Ext}_{t,l}(w;B)$. Further, using 500 posterior predictive samples of realizations of $\widetilde{Ext}_{t,l}(w;B)$, we obtain 500 samples of $Av_{ t\in T, l\in L} \widetilde{Ext}_{t,l}(w;B)$ to supply an empirical summary of the posterior distribution of $Av_{ t\in T, l\in L} Ext_{t,l}(w;B)$. In the cases where the average is carried out only over one time index, a bigger size sample is obtained if the distribution is the same in a given period of time. For example, if the distribution of $Av_{l \in JJA} Ext_{t,l}(w;B)$ is taken to be the same for all the years in a decade, $t \in D$, we can obtain a sample of 5000 realizations of $Av_{l \in JJA} \widetilde{Ext}_{t,l}(w;B)$, 500 for each of the 10 years $t \in D$, to consider empirically the posterior distribution of $Av_{l \in JJA} Ext_{t,l}(w;B)$ in D. When it is assumed that the distribution of the ten years in D is the same, we modify notation to $Av_{l \in JJA}^D Ext_{t,l}(w;B)$, and $Av_{l \in JJA}^D \widetilde{Ext}_{t,l}(w;B)$.

Persistence: In the context of global warming, a relevant feature in the analysis of extreme temperatures is persistence. We consider persistence as arising when the probability of being in an extreme heat state at day $l+1$ is higher if we were in an extreme heat state at day l than if we were not. To analyze this feature spatially through the extent, we consider the proportion of B at w degrees above threshold, for both of two consecutive days, l and $l+1$, denoted by ${}^{2}{}Ext_{t,l}(w;B)$ and defined as

$$\begin{aligned} {}^{2}{}Ext_{t,l}(w;B) =&\frac{1}{|B|} \int _{B} \varvec{1}(Y_{t,l}(\mathbf{s} ) -q(\mathbf{s} ) \ge w ) \ \\&\varvec{1}(Y_{t,l+1}(\mathbf{s} ) -q(\mathbf{s} ) \ge w ) d\mathbf{s} . \end{aligned}$$

More generally, ${}^{r}{}Ext_{t,l}(w;B)$ denotes an r-day EHE, that is an EHE persisting for r consecutive days starting at day l, with analogous definition. It is immediate that

$$\begin{aligned} {}^{r}{}Ext_{t,l}(w;B) \le {}^{r-1}{}Ext_{t,l}(w;B) \le \ldots \le Ext_{t,l}(w;B). \end{aligned}$$

This accords with the fact that the extents of two-day EHE’s will be smaller than the extents of one-day EHE’s. Again, we will use a Monte Carlo integration to obtain a realization, e.g., for the $r=2$ case:

$$\begin{aligned} {}^{2}\widetilde{Ext}_{t,l}(w;B) = \frac{1}{m} \sum _{j=1}^{m} \varvec{1}(Y_{t,l}(\mathbf{s} ) -q(\mathbf{s} ) \ge w ) \ \varvec{1}(Y_{t,l+1}(\mathbf{s} ) -q(\mathbf{s} ) \ge w ). \end{aligned}$$

In the analysis for our dataset/study area we confine ourselves to $r=1$ and $r=2$ since the probability of observing runs with $r\ge 3$ is too small to show useful extents.

As with the daily extents, we are usually more interested in the average of ${}^{r}{}Ext_{t,l}(w;B)$ over a time window of l’s, t’s, or both. These averages are defined as above but with ${}^{2}{}Ext_{t,l}(w;B)$. Monte Carlo integrations for these averages are analogous to those for averages of $Ext_{t,l}(w;B)$; we only have to substitute ${}^{r}{}Ext_{t,l}(w;B)$ with $^{r}\widetilde{Ext}_{t,l}(w;B)$.

Useful displays: Displays we will develop for extent and persistence include the following. First, we will consider different subregions of Aragón in order to make comparison between regions. To do this we will examine evolution of extent or persistence across the JJA season. We do this averaged over a decade in order to enable decadal comparison. Further, with posterior predictive samples of extents for each day l within each year t, we will supply the entire posterior predictive distribution of some of these extents and persistences. We will also develop “time to” displays, showing the time to the first day in year t with extent or persistence greater than or equal to a specified v. Lastly, we will examine how extents and persistences vary over choices of w since there can be interest in different specification of local thresholds for extreme heat.

2.4 Reviewing the daily max temperature model

Returning to the notation at the start of this section, let $Y_t(\mathbf {s})$ denote the daily maximum temperature at day t and location $\mathbf {s}$. Schliep et al. (2021) propose a two-state model where the state for a given day defines whether or not the location is experiencing an extreme heat event. Given a threshold, $q(\mathbf{s} )$ at location $\mathbf{s}$, let $U_t(\mathbf {s}) \in \{0,1\}$ denote the state at time t for location $\mathbf {s}$ where a value of 0 denotes the below threshold state and a 1 denotes the above threshold state. So, $U_{t}(\mathbf{s} )$ is a spatial binary time series process reflecting times of transition or state-switching. It is observed for each t at a monitored site but is latent elsewhere. With regard to extents, we note that $Ext_t(0;B) = \frac{1}{|B|} \int _{B} U_{t}(\mathbf{s} )d\mathbf{s}$.

$U_t(\mathbf {s})$ is a Markov process where the state $U_t(\mathbf {s})$ depends only on the previous state $U_{t-1}(\mathbf {s})$. Then, the distribution of $Y_t(\mathbf {s})$ is specified explicitly given $U_t(\mathbf {s})$ and, given the threshold, $U_{t}(\mathbf{s} )$ is a binary function of $Y_{t}(\mathbf{s} )$. Furthermore, the transition probabilities between states are allowed to be a function of previous temperature. This specification ensures transition probabilities to be “local”, i.e., to vary with location and to depend upon the previous day’s maximum temperature at that location. The opposite would be expected if the maximum temperature of the previous day resulted in a non-extreme heat state.

The joint distribution for temperature and state is specified in a first order Markov fashion explicitly as follows. Given $Y_{t-2}(\mathbf{s} )$, and thus, $U_{t-2}(\mathbf{s} )$, for two consecutive time points, $t-1$ and t, the joint distribution $[U_{t-1}(\mathbf {s}),Y_{t-1}(\mathbf {s}), U_{t}(\mathbf {s}), Y_{t}(\mathbf {s})]$ is written as

$$\begin{aligned}&{[}Y_{t}(\mathbf {s})|U_{t}(\mathbf{s} ), Y_{t-1}(\mathbf {s})][U_{t}(\mathbf {s})|Y_{t-1}(\mathbf {s})][Y_{t-1}(\mathbf {s})|U_{t-1}(\mathbf {s}), Y_{t-2}(\mathbf{s} )] \\&\qquad [U_{t-1}(\mathbf {s})|Y_{t-2}(\mathbf{s} )]. \end{aligned}$$

This formulation requires three model specifications: (i) $[Y_{t}(\mathbf{s} )|U_{t}(\mathbf{s} ) = 0, Y_{t-1}(\mathbf{s} )]$, (ii) $[Y_{t}(\mathbf{s} )|U_{t}(\mathbf{s} ) = 1, Y_{t-1}(\mathbf{s} )]$, and (iii) $[U_{t}(\mathbf{s} )|Y_{t-1}(\mathbf{s} )]$. With $q(\mathbf{s} )$ denoting the threshold (quantile) for location $\mathbf{s}$, truncated distributions are needed for (i) and (ii), i.e., $[Y_{t}(\mathbf{s} ) = y]\mathbf{1} ( y < q(\mathbf{s} ))$ and $[Y_{t}(\mathbf{s} ) = y]\mathbf{1} (y \ge q(\mathbf{s} ))$, respectively. For (i), a truncated normal distribution is adopted, with autoregressive centering,

$$\begin{aligned} TN\left( \mu _{t}^{0}(\mathbf{s} )-\rho ^{0}(Y_{t-1}(\mathbf{s} )- \mu _{t-1}^{0}(\mathbf{s} )), \sigma ^{2,0}(\mathbf{s} )\right) \text {I}(-\infty , q(\mathbf{s} )). \end{aligned}$$

Details for $\mu _{t}^{0}(\mathbf{s} )$ are given below.

For (ii), a truncated t-distribution is adopted, with autoregressive centering,

$$\begin{aligned} Tt\left( \mu _{t}^{1}(\mathbf{s} )-\rho ^{1}(Y_{t-1}(\mathbf{s} )- \mu _{t-1}^{1}(\mathbf{s} )), \sigma ^{2,1}(\mathbf{s} )\right) \text {I}(q(\mathbf{s} ), \infty ). \end{aligned}$$

Details for $\mu _{t}^{1}(\mathbf{s} )$ are given below. As an aside, unlike the multivariate normal, the multivariate t-distribution captures upper tail extreme dependence (Chan and Li 2008) which may be desirable in looking at extreme heat events. Further, with multivariate t-distributions in both time and space, tail dependence is inherited in space as well.

Exploratory analysis of the observed data suggested a smaller variance for the above threshold daily maximum temperature distribution than for the below threshold daily maximum temperature distribution. Further, spatially-varying variances are introduced, expecting that variation in say, Jaca (in the Pyrenees in the north of the region) would be different from variation in say, Zaragoza (flat and central in the region).

For (iii) a probit link is employed to define

$$\begin{aligned} \varPhi ^{-1}(p_{t}(\mathbf{s} )) \equiv \varPhi ^{-1}(P(U_{t}(\mathbf{s} )=1|Y_{t-1}(\mathbf{s} ))) \equiv \eta _{t}(\mathbf{s} ) \end{aligned}$$

with $\eta _{t}(\mathbf{s} )$ given below. Putting (i), (ii), and (iii) together, a mixture distribution for $Y_{t}(\mathbf{s} )$ results: (i) a truncated normal distribution for the bulk of the distribution, (ii) a truncated t-distribution for the upper tail of the distribution, and (iii) mixture weights according to $P(U_{t}(\mathbf{s} ) =0)$ or $P(U_{t}(\mathbf{s} ) =1)$, respectively.

As for the specifics of $\mu _t(\mathbf{s} )$ and $\eta _t(\mathbf{s} )$, compacting notation, for $\mu _{t}^{U_t(\mathbf{s} )}(\mathbf{s} )$, Schliep et al. (2021) consider

$$\begin{aligned} \begin{aligned} \mu _{t}^{U_t(\mathbf{s} )}(\mathbf{s} )&= \beta _0^{U_t(\mathbf{s} )} + \beta _0^{U_t(\mathbf{s} )}(\mathbf{s} ) + \gamma _{[\frac{t}{365}]+1}^{U_t(\mathbf{s} )} + \beta _{1}^{U_t(\mathbf{s} )}\text {elev}(\mathbf{s} ) \\&\quad + \beta _{2}^{U_t(\mathbf{s} )}\text {lat}(\mathbf{s} ) + \lambda _{1}\text {sin}(2\pi t/365) + \lambda _{2} \text {cos}(2\pi t/365). \end{aligned} \end{aligned}$$

Here, $\beta _0^{U_t(\mathbf{s} )}$ denotes a global (across the domain for our dataset) intercept and $\beta _0^{U_t(\mathbf{s} )}(\mathbf{s} )$ denotes a local spatial intercept, i.e., providing local adjustment to the global intercept. Each $\beta _0^{U_t(\mathbf{s} )}(\mathbf{s} )$ is modeled as a mean 0 Gaussian process with exponential covariance function. For $\gamma _{[\frac{t}{365}]+1}^{(1)}$, where $[\ ]$ denotes the greatest integer function, thus counting years with this subscript and, as a result, the $\gamma$’s provide annual intercepts to allow for yearly shifts, i.e., for hotter or colder years. The sin and cos terms are introduced to capture annual seasonality with their coefficients reflecting associated amplitudes. This seasonality is critical to ensure that an annual daily maximum temperature trajectory over the course of a year at a location will provide sensible realizations. elev$(\mathbf{s} )$ is the elevation at $\mathbf{s}$ and lat$(\mathbf{s} )$ is the latitude. Finally, $\rho ^{U_t(\mathbf{s} )}$ provides a centered AR(1) specification, bringing in the previous day’s temperature, $Y_{t-1}(\mathbf{s} )$.

For $\eta _{t}(\mathbf{s} )$, Schliep et al. (2021) propose

$$\begin{aligned} \begin{aligned} \eta _{t}(\mathbf{s} ) =&\phi _{0} + \phi _{0}(\mathbf{s} ) + \phi _{1}(Y_{t-1}(\mathbf{s} ) - q(\mathbf{s} )) \\&+ \phi _{2}((Y_{t-1}(\mathbf{s} ) - q(\mathbf{s} ))\mathbf{1} (Y_{t-1}(\mathbf{s} ) - q(\mathbf{s} ) \ge 0)) \\&+ \phi _{3} \text {sin}(2\pi t/365) + \phi _{4} \text {cos}(2\pi t/365). \end{aligned} \end{aligned}$$

Here, centering by the threshold yields more sensible transition probabilities. The threshold, $q(\mathbf{s} )$, can be moved over to the intercept term in order to provide a spatially varying offset. However, the inclusion of $\phi _{0}(\mathbf{s} )$, modeled as a Gaussian process, allows for a richer spatially-varying intercept.

Fig. 1

Location of the stations in the Iberian Peninsula (upper left), names and elevation of the locations (upper right), level curves of elevation (bottom left) and thresholds defining local extreme temperatures (bottom right). Pyrenees (B1) is the area over the upper horizontal line and Ebro valley (B2) the area between the two horizontal lines

We note that, as other common mixture models with a “cut point” to capture skewness, the unconditional density obtained from this model is discontinuous at the threshold. No continuity constraints are needed to smooth the density since this discontinuity does not affect the calculation of the extents over the threshold. This model was satisfactorily validated using out-of-sample prediction of characteristics of extreme values in three locations, see Section 5.2 in Schliep et al. (2021) and a summary in Section OR.2 in the Online Resource.

3 Illustrative summaries

3.1 The data and subregions

We analyze the evolution of the extent over time in two different areas around Aragón, a region located in northeastern Spain. The areas are quite different in topography and temperature, see Fig. 1, where the elevation and the thresholds that define a local EHE are shown.

• B1: Pyrenees, with latitude between 42.5N and 43N and longitude between $-1.9$W and 0.7E. It is a mountainous area with a high variability in elevation. The elevation of the stations varies from 442 to 1645 m asl, but some points in the area are over 3000 m. This leads to a high variability in the thresholds $q(\mathbf{s} )$, that vary from 25.5 to 36 $^\circ$C. This region shows a high biodiversity, including the last glaciers in Spain.

• B2: Central Ebro valley with latitude between 41.5N and 42.5N and longitude between $-1.9$W and 0.7E. This region is more homogeneous both in elevation, ranging from 245 to 546 m, and in temperature. The thresholds $q(\mathbf{s} )$ vary from 33.8 to 37 $^\circ$C. This region is the most populated in Aragón, and the most important farming zones are located here.

With regard to computing extents over these regions, B1 was partitioned into $1km \times 1km$ grid cells yielding, with regard to (2), $m=7881$. B2, a much larger region, was partitioned into $2km \times 2km$ grid cells yielding, with regard to (2), $m=5841$.

The following five observed decades D1: 1966-1975, D2: 1976-1985, D3: 1986-1995, D4: 1996-2005 and D5: 2006-2015, are considered in most of the following analysis to quantify the evolution over time of the different features related to the extent.

Altogether, the posterior predictive time series result in very large data files from which extents and persistences are computed. For instance, for B1, we have 50 years by 92 days by 7881 grid centroids by 500 replicates yielding $1.81263 \times 10^{10}$ points.

In the sequel we present some comparative analysis for the regions B1 and B2. We present in the text the analysis for both regions and displays for the Pyrenees (B1) region, with analogous displays for the Ebro Valley (B2) region in the Online Resource.

3.2 Analysis of the time evolution of the extent

To offer some quantification of global warming, we analyze the evolution of the extent of EHE’s across years. In that regard, we also analyze persistence through the extent of two-day EHE’s. We consider the averages of the extent in the summer period JJA, $Av_{l \in JJA} Ext_{t,l}(0;B)$ and $Av_{l \in JJA}{}^{2}{}Ext_{t,l}(0;B)$. We also compare the evolution in the regions B1 and B2.

Fig. 2

Posterior mean of $Av_{l \in JJA} Ext_{t,l}(0;B)$ (left) and posterior mean of $Av_{l \in JJA}{}^{2}{}Ext_{t,l}(0;B)$ (right) for B1 (red) and B2 (black) and linear trend fitted to the means

Figure 2 shows the plot of the posterior mean of $Av_{l \in JJA} Ext_{t,l}(0;B)$ for B1 and B2 vs. year t. Both regions show an increasing trend; the magnitude of the slope is similar in both regions, although the mean extent in B2 is approximately 1% higher than in B1. The analogous plot for $Av_{l \in JJA}{}^{2}{}Ext_{t,l}(0;B)$ is also shown in Figure 2. Similar conclusions about the extent of two-day EHE’s are obtained, although the magnitude is reduced almost to half, the increase over time is slower, and the difference between the mean extent in the two regions is reduced to 0.5%. These conclusions are in agreement with the analysis of the raw empirical EHE extents using the observed series of temperature, see Figure OR.4 in the Online Resource. However, that figure reveals the limitations of the empirical extent. The plots in Figure OR.4 show the high variability of the empirical extent, and the impossibility of inference to compare the two decades.

To study the entire distribution, we analyze $Av^D_{l \in JJA} Ext_{t,l}(0;B)$ using the 5000 realizations $Av^{D}_{l \in JJA} \widetilde{Ext}_{t,l}(0;B)$. The boxplots of the distribution for each decade in B1 are shown in Fig. 3, and Table 1 gives some summary measures in the two regions. Apart from a small dip in D4, an almost linear increase is observed. Similar conclusions are obtained in B2. With regard to the evolution of the extent of two-day EHE’s, the boxplots of $Av^D_{l \in JJA}{}^{2}{} Ext_{t,l}(0;B)$ in Fig. 3, and Table OR.1 in the Online Resource, confirm that it is quite similar to the evolution of the extent of EHE’s, but smaller and slower in magnitude.

Fig. 3

Top: Boxplots of the posterior density of $Av^D_{l \in JJA} Ext_{t,l}(0;B1)$ (left) and of the posterior density of $Av^D_{l \in JJA}{}^{2}{}Ext_{t,l}(0;B1)$ (right) in the five decades. Bottom: Posterior density of $Av^D_{l \in JJA} Ext_{t,l}(0;B1)$ in D1 (black) and D5 (red). Vertical lines are the posterior means

Table 1 Posterior mean, standard deviation, lower and upper 0.05 quantiles of $Av^D_{l \in JJA} Ext_{t,l}(0;B)$ for the five decades in regions B1 and B2

Table 2 Posterior mean and 90% credible intervals of the increase between D5 and D1 of different averages of the extents, in regions B1 and B2

To better illuminate the global increase of the extent in the summer season, the posterior density for the first and the last decades is shown in Fig. 3 and Figure OR.5, where a shift of the central location and a slightly higher variability is observed. Table 2 summarizes the posterior mean and 90% credible intervals (CI’s) of the difference

$$\begin{aligned} {}^{r}{}\varDelta ^{D5}_{D1}(B)=Av^{D5}_{l \in JJA} {}^{r}{}Ext_{t,l}(0;B)-Av^{D1}_{l \in JJA} {}^{r}{}Ext_{t,l}(0;B) \end{aligned}$$

for $r=1,2$ (superscript $r=1$ is omitted for simplicity) and B1 and B2. In both regions, the interval for the one-day EHE’s contains zero, showing that it is possible that the JJA average extent of one year in the last decade is lower than in the first decade. However, it is unlikely according to the posterior probability $P(\varDelta ^{D5}_{D1}(B)>0 \mid y)$, which is 0.803 in B1 and 0.805 in B2. Similar conclusions are obtained for the two-day EHE’s since $P({}^{2}{}\varDelta ^{D5}_{D1}(B)>0 \mid y)$ are 0.815 in B1 and 0.808 in B2.

Evidence of a significant increase over time in the decadal average is much stronger. Summary measures of the difference of the decadal average,

$$\begin{aligned} {}^{r}{}\varDelta _{D5,D1}(B)&=Av_{t\in D5, l \in JJA} {}^{r}{}Ext_{t,l}(0;B) \\&\quad -Av_{t\in D1, l \in JJA} {}^{r}{}Ext_{t,l}(0;B) \end{aligned}$$

for $r=1,2$ are also shown in Table 2. The CI’s for the one-day EHE’s are narrower than the corresponding CI’s of the yearly averages and do not include zero. The posterior probabilities $P({}^{r}{}\varDelta _{D5,D1}(B)>0 \mid y)$ are essentially 1 in both regions for $r=1,2$, indicating that the decadal average in D5 is significantly higher than in D1 in all the cases.

Another question of interest is the comparison of the increment of the extent between D1 and D5 in the two regions under study. Fig. 2 shows that the trends in B1 and B2 are quite parallel, and that the increase of the JJA average extent between D1 and D5 is quite similar in both regions. The posterior mean of the difference between B1 and B2 of the increase in the yearly average, $\varDelta ^{D5}_{D1}(B1)-\varDelta ^{D5}_{D1}(B2)$, is $-0.002$ and the 90% CI is $(-0.013, 0.009)$ while the CI of the decadal average, $\varDelta _{D5,D1}(B1)-\varDelta _{D5,D1}(B2)$ is $(-0.006, 0.002)$. That means that although there is a shift in the mean value of the average extent in both regions, there is no evidence of a significant difference in the increase of average extent, and both regions show a similar evolution over time.

3.3 Evolution of the seasonal pattern and the beginning of the summer

To analyze the evolution of the seasonal pattern in JJA of the extent $Ext_{t,l}(0;B)$, $l=1,\ldots , 92$, and ${}^{2}{}Ext_{t,l}(0;B)$, Fig. 4 shows the plot vs. day within year of the posterior mean of $Av_{t\in D} Ext_{t,l}(0;B)$ in D1 and D5 in region B1. The seasonal pattern attains the maximum mean extent at the end of July in all cases, and a similar increase of the mean across decades, is observed in both regions. The analogous plot of $Av_{t\in D}{}^{2}{}Ext_{t,l}(0;B)$, see Fig. 4, shows a smoother seasonal pattern of the extent of the two-day EHE’s, and a smaller increase between decades than in the extent of the one-day EHE’s. The same conclusions are obtained in region B2, and the corresponding plots are shown in Figure OR.6 in the Online Resource.

Fig. 4

Posterior means of $Av_{t \in D} Ext_{t,l}(0;B1)$ (left) and $Av_{t \in D}{}^{2}{}Ext_{t,l}(0;B1)$ (right) in D1 (black) and D5 (red), Pyrenees

Table 3 Posterior mean, standard deviation and lower and upper 0.05 quantiles of $Av_{l\in Jn} Ext^{D}_{t,l}(0;B)$, $Av_{l \in Jl} Ext^{D}_{t,l}(0;B)$ and $Av_{l\in Ag} Ext^{D}_{t,l}(0;B)$ in D1 and D5, in regions B1 and B2

The increase between decades is quantified in Table 3 that summarizes the posterior distribution of the monthly averages $Av^D_{l\in Jn} Ext_{t,l}(0;B)$, $Av^D_{l \in Jl} Ext_{t,l}(0;B)$ and $Av^D_{l\in Ag} Ext_{t,l}(0;B)$, in D1 and D5. There is an increase in the posterior mean in the three months with a similar seasonal pattern in both regions: the highest absolute increase, more than 3%, is observed in July and the lowest, around 1.4%, in June. This increase is higher in the upper tail: almost 2% in June and 4% in July. The posterior probability $P(Av^{D5}_{l \in Jn} Ext_{t,l}(0;B)>Av^{D1}_{l \in Jn} Ext_{t,l}(0;B) \mid y)$ is 0.813 in B1 and 0.818 in B2, and in July and August they are 0.805 and 0.804, in both regions.

3.3.1 Time to beginning of EHE’s

An important feature related to the seasonality is the beginning of extreme temperatures in summer, and the analysis of its change across years. To that end, we define the variable $L_{t}(v;B)$, the number of days to the first day l within the period JJA in year t with an extent higher or equal to v, that is the first day l such that $Ext_{t,l}(0;B)\ge v$. If no extent over v is observed in a year, we set $L_{t}(v;B)=92$. Since extents over high thresholds are being analyzed, large extents are very rarely observed so we only consider here $v=0.1$. ${}^{2}{}L_ {t}(v;B)$, the first day with an extent of the two-day EHE’s higher or equal than v, is defined analogously.

Fig. 5

Posterior mean of the first day $L_{t}(0.1;B)$ (left) and posterior mean of the first day ${}^{2}{}L_{t}(0.1;B)$ (right) vs. year, for B1 (red) and B2 (black)

Figure 5 shows the posterior mean of $L_{t}(0.1;B)$ vs. year for B1 and B2, and the the analogous plot for ${}^{2}{}L_{t}(0.1;B)$. A decreasing trend is observed in both variables and in both regions. However, the decrease of the mean of ${}^{2}{}L_{t}(0.1;B)$ across years is much greater, almost 30 days, versus less than 10, but with much higher variability. This variability is likely due to the low incidence of the considered event.

Figure 6 shows the posterior density of the first day, estimated in a decade, $L^{D}_{t}(0.1;B)$, in D1 and D5 in B1; the analogous plot in B2 is shown in Figure OR.7 in the Online Resource. Table 4 summarizes the posterior mean, standard deviation and 90% CI for $L^{D}_{t}(0.1;B)$, for the five decades in the observed period. The mean of the first day between the first and the last decade has decreased almost 7 days in B1 and 8 days in B2. The posterior probability $P(L^{D1}_{t}(0.1;B)> L^{D5}_{t}(0.1;B) \mid y)$, that is the probability that the first day of the summer where more than 10% of the region is under extreme temperatures occurs earlier in the last decade, is 0.775 in B1 and 0.781 in B2.

A summary of ${}^{2}{}L^{D}_{t}(0.1;B)$ analogous to that in Table 4 is presented in Table OR.2 in the Online Resource. Since the probability of a two-day EHE is quite low, it is likely that in a year all the extents of two-day EHE’s are lower or equal than 0.1 and, consequently, the event $P({}^{2}{}L^{D}_{t}(0.1;B)=92\mid y)$ has a positive probability mass. However, this posterior probability decreases over the observed period. In B1, the percentage of years with $L_{t}(0.1;B)=92$ is 0.77 in D1 and 0.31 in D5, and 0.88 and 0.36 in B2. Further evidence that $L^{D}_{t}(0.1;B)$ is decreasing is that, conditionally to the fact that an extent higher than 0.1 occurs in a year, the posterior mean of ${}^{2}{}L^{D}_{t}(0.1;B)$ has decreased more than 5 days between D1 and D5 in both regions.

Fig. 6

Posterior density of $L^D_{t}(0.1;B1)$ for D1 (black) and D5 (red)

Table 4 Posterior mean, standard deviation and lower and upper 0.05 quantiles of $L^D_{t}(0.1;B)$ in D1 and D2, in regions B1 and B2

3.4 Behavior of extent across choices of w

Fig. 7

Posterior mean of $Av_{l \in JJA} Ext_{t,l}(w;B1)$ for $w=-1.5,-1.0,-0.5,0.0,0.5,1.0,1.5$ $^\circ$C and linear trends fitted to the means

The previous sections consider results for $Ext_{t,l}(w;B)$ only at $w=0$, that is the extent corresponding to the threshold used to define an EHE. Here, we consider the effect on extent by adjustment of the local thresholds to lower extreme temperatures and to higher extreme temperatures. To that end, we consider $Ext_{t,l}(w;B)$ for a grid of values over and under the threshold, $w= -1.5, -1.0, -0.5, 0.0, 0.5, 1.0,$ 1.5 $^\circ$C.

To study the evolution across years and across threshold, Fig. 7 shows the posterior mean of $Av_{l \in JJA} Ext_{t,l}(w;B1)$ vs. year for the grid of w values, and the corresponding linear trends fitted to the means. An increasing trend is observed for all the w values but the trend is stronger for smaller w’s. More precisely, the ratio between the slope for $w=-1.5$ and $w=1.5$ is $0.00106/0.00018=5.8$. The finding is that the incidence of extents associated with more extreme thresholds is increasing at a slower rate than that for less extreme thresholds.

This increase over time is not only observed in the mean, but in the entire distribution. As an example, we consider the decadal average of July, where Fig. 8 shows the posterior density of $Av_{t \in D, l \in Jl} Ext_{t,l}(w;B1)$ across w for D1 and D5; the analogous plot for B2 is shown in Figure OR.8 in the Online Resource. It is observed that the shape of the distribution is very similar across w and across decades but, in both cases, there are clear shifts that are not homogeneous across w.

The different evolution across w is observed if we compare the mean difference between decades. For example, in B1, the posterior mean difference

$$\begin{aligned} E\left( Av^{D5}_{l \in Jl} Ext_{t,l}(w;B1)-Av^{D1}_{l \in Jl} Ext_{t,l}(w;B1) \mid y \right) \end{aligned}$$

is 5% for $w=-1.5$, while for $w=1.5$ is 1%. The change is also observed if we compare the mean differences between the range of w values across decades. Again in B1, the posterior mean difference

$$\begin{aligned} E\left( Av^{D}_{l \in Jl} Ext_{t,l}(-1.5;B1)-Av^{D}_{l \in Jl} Ext_{t,l}(1.5;B1) \mid y \right) \end{aligned}$$

is 18% in D5, while in D1 is 14%. These values together with the counterparts for B2 are summarized in Table OR.3 in the Online Resource. The change in the entire distribution is quantified by the posterior probability of the extent for a given w in the last decade being higher than in the first,

$$\begin{aligned} P\left( Av^{D5}_{l \in Jl} Ext_{t,l}(w;B1)>Av^{D1}_{l \in Jl} Ext_{t,l }(w;B1) \mid y \right) . \end{aligned}$$

Table 5 summarizes these posterior probabilities and shows that there is a nonmonotonic decrease across w.

Table 5 Posterior probabilities for a grid of w values, $P\left( Av^{D5}_{l \in Jl} Ext_{t,l}(w;B)>Av^{D1}_{l \in Jl} Ext_{t,l }(w;B) \mid y \right)$, for regions B1 and B2

Fig. 8

Posterior density of $Av_{t \in D, l \in Jl} Ext_{t,l}(w;B1)$ for $w=-1.5, -1.0, -0.5, 0.0, 0.5, 1.0,$ 1.5 and D1 (solid line) and D5 (dashed line)

Figure 9 shows the posterior mean of the average $Av_{t \in D} Ext_{t,l}(w;B1)$ vs. day within year for D1 and D5 in order to compare the seasonal behavior of the extent across w; the analogous plot for B2 is shown in Figure OR.9 in the Online Resource. It can be seen that the seasonal pattern is smoother for larger w. In all the cases, the seasonal pattern is more pronounced in the last decade but the changes across w are not homogeneous, with stronger differences in smaller w values. More precisely, the seasonal pattern for $w=1.5$ in D5 is more pronounced than its counterpart in D1, approaching that of $w=1$ in D1, with probability $P\left( Av^{JJA}_{t \in D5} Ext_{t,l}(1.5;B1) > Av^{JJA}_{t \in D1} Ext_{t,l}(1.5;B1)\mid y \right)$, that is essentially 1, and $P\left( Av^{JJA}_{t \in D5} Ext_{t,l}(1.5;B1) > Av^{JJA}_{t \in D1} Ext_{t,l}(1;B1)\mid y \right) =0.18$. For smaller w values, the differences are higher, with the posterior probabilities comparing the previous averages in $w=-1.5$ and $w=-1.5$, and in $w=-0.5$ and $w=-1.5$ equal to 1; in addition, the seasonal pattern of $w=-1.5$ in D1 is only slightly more pronounced than the pattern in $w=-0.5$ in D5.

Fig. 9

Posterior mean of $Av_{t \in D} Ext_{t,l}(w;B1)$ for $w=-1.5, -1.0, -0.5, 0.0, 0.5, 1.0, 1.5$ for D1 (left) and D5 (right)

4 Summary and future work

Notions of the spatial extent of heat waves and extreme heat events have been considered informally and descriptively in the climate community. Here we have introduced a formal probabilistic definition for extents of extreme heat events. For a specified region, for a given day, the definition of spatial extent takes the form of a block average over the region. It is an average of indicator variables which identify exceedance of a local threshold by the daily max temperature surface for the day at each location within the region. We demonstrate that extents can be calculated through Monte Carlo integration and can be obtained for realizations from arbitrary space-time autoregressive models for daily max temperatures. Using a dataset of daily max temperatures over 50 years, adopting a particular choice of model, working within a Bayesian framework, we obtained posterior predictive samples of daily temperature time series on a fairly fine grid scale to implement the Monte Carlo integrations.

With these samples, we calculated daily, seasonal and decadal averages of the extents for two regions around the Comunidad Autónoma de Aragón in Spain. We generalized these extents to capture extents of persistence of extreme heat. We made comparisons across decades to reveal evidence of increasing extent over time. We also studied other features related to the extent of EHE’s, for example, the first day in the period JJA with an extent higher than a given percentage, and the behaviour of extent across choices of the threshold. Following our approach, other extents yielding other comparisons may be developed according to the interest of the user.

With regard to the regions under study, Pyrenees and Ebro Valley, we found that a clear increase of the extent of EHE’s across time is observed. For example, the posterior probability of the yearly average extent across JJA in the decade 2006–2015 being higher than in 1966-1975 is higher than 0.8. It is also found that the first day of the summer where the extent of EHE’s is higher than 10% has decreased around seven days. The extent of EHE’s defined with all the considered thresholds is increasing, but the incidence of extents associated with more extreme thresholds is increasing at a slower rate than that for less extreme thresholds.

Future work will explore the temporal evolution of geographic extent for different regions to enable comparison. It will also examine the challenges of working with regions at larger spatial scales. Alternatively, with suitable computing capability, we can consider investigating extents at higher spatial resolution than done here. Further, while here we work with actual weather data, another goal is to consider projection of future spatial extent using future climate scenarios.