1 Introduction

Various engineering applications require incorporating values of rainfall intensity and wind speed related to extreme weather events and short time intervals (commonly less than 1 day). In the field of hydrology, these rainfall values are essential for urban drainage designs, runoff prediction and flood management (Adarsh and Reddy 2018; Han and Morrison 2021; Linsley et al. 1975; Toulemonde et al. 2020). Short-duration wind speed is also relevant for assessing wind loads, soil erosion assessments, and many other purposes (Choi 2002; Zhang et al. 2018). These values are also combined with statistical estimates of extreme values (return periods or traditional percentile approaches) to characterise significant adverse events (Brabson and Palutikof 2000; Cui et al. 2021; Linsley et al. 1975; Lombardo et al. 2009; Westra et al. 2014).

More specifically, exhaustive records of both climatic variables (i.e. rain and wind) are indispensable for the study of wind-driven rain (Pérez et al. 2018a, b). This phenomenon is caused by the deviation of raindrops due to wind action that, when impacting building facades, can result in various problems in buildings (Blocken and Carmeliet 2004; Kočí et al. 2017; Orr and Viles 2018). The values of wind and rain associated with short recording intervals and extreme events allow the representative test parameters of the exposure to be established and adequate input data for numerical simulations of the phenomenon to be defined (Blocken and Carmeliet 2008; Kubilay et al. 2013; Pérez et al. 2013).

However, the recording of wind and rainfall data associated with short time intervals has only begun to be generalised with the progressive introduction of automatic weather stations in the twenty-first century. Consequently, these data are not available in many locations, and in other cases, they are not sufficiently representative given their low age (Al Mamun et al. 2018; Fadhel et al. 2017). Where they are recorded, it is usual that only summary data related to broader intervals (hourly, daily, etc.) and obtained from the gathered raw data are available. Therefore, practitioners and researchers have resorted for decades to estimates of these short-interval values obtained from less exhaustive records.

Both rain and wind are stochastic variables, which prevents accurate prediction of values related to different recording intervals for any particular event. However, it is possible to develop statistical approximations that provide reasonable accuracy. In the case of rainfall, although specific empirical correlations have been identified in multiple locations, the generic intensity-duration equation proposed by Linsley et al. (1975) still represents a simplified standard for general purposes and for sites without exhaustive records (Cardoso et al. 2014; Choi 1998; García and Schneider 2001; Sahal and Lacasse 2008). In the case of wind speed, various conversion equations have been defined depending on the climatic context (mainly for obtaining wind gusts), although the generalised equation proposed by Choi is still the most used in the study of wind-driven rain (Choi 1998; Durst 1960; Harper et al. 2010; Sahal and Lacasse 2008; Shu et al. 2015; Van den Bossche et al. 2013).

However, these estimations have limitations that affect their functionality or the accuracy of their results. Thus, many of them are only usable to estimate values for specific short-duration intervals or from records of a specific duration (Choi 2001; Choi and Hidayat 2002; Durst 1960; Harper et al. 2010; Shu et al. 2015). In addition, due to their age, they may be unrepresentative of current climate trends (Allan and Soden 2008; IPCC 2012; Orr et al. 2018). In turn, generic equations can produce inaccuracies because the particularities of the local climatic conditions are not considered. Nevertheless, these generic equations are commonly used at locations without exhaustive records (especially for wind-driven rain applications and general purposes), thus causing undetermined errors in the subsequent calculations that use these estimated values (Blocken and Carmeliet 2010; Cornick and Lacasse 2009; Kpran and Ge 2014; Sahal and Lacasse 2008; Overton 2013).

This research addresses these issues by proposing an alternative estimation procedure capable of determining reliable rainfall intensity and wind speed values (i) calculated from any climatic records usually available; (ii) for any recording interval less than 1 day; and (iii) easily adjusted to the particular conditions of the extreme weather events at each site. For this, 10-min and hourly records gathered between 2008 and 2019 at 109 weather stations in Spain and the Netherlands are analysed. The reliability of this alternative approach when characterising both variables for subdaily intervals and extreme conditions is validated, also comparing its accuracy with that of the most widespread generic equations. Although this alternative approach can provide a clear improvement for applications in the scope of wind-driven rain, it can also be useful in other engineering fields previously mentioned.

2 Background

2.1 Intensity-duration relationships for rainfall

The relationship between the intensity and the duration of extreme rainfall events has been empirically analysed for decades, for example, by obtaining intensity–duration–frequency (IDF) curves (Cardoso et al. 2014; Fadhel et al. 2017; García and Schneider 2001). Although approaches based on probabilistic studies and the scaling property of rainfall have been proposed more recently, empirical equations are widespread tools in hydraulic engineering, which provide reliable predictions of extreme rainfall intensity for specified durations and recurrence periods in locations with the exhaustive records required (Froehlich 2010; Pui et al. 2012; Yu et al. 2004).

Omitting the influence of the recurrence period, most of these empirical intensity-duration relationships are variations of a generic equation, such as that presented in Eq. (1), where Rh (t) represents the average rainfall intensity (mm/h), t is the duration of the considered interval (traditionally specified in minutes), and α, β, χ, δ, and ϕ are empirical coefficients related to the characteristic meteorological events of the site (Cardoso et al. 2014; Froehlich 2010; García and Schneider 2001). Determining these coefficients requires a laborious analysis of climatic records gathered at each location analysed.

$$R_{h \, \left( t \right)} = \frac{\alpha }{{\left( {\beta \cdot t^{\chi } + \delta } \right)^{\phi } }}$$
(1)

Generalising this approach, Linsley et al. (1975) proposed a generic intensity-duration relationship (Eq. (2)) from correlations identified in various rainstorms in Ohio, USA. This equation allows a generic estimation of the subhourly rainfall intensity Rh (t) (mm/h) for a short time interval t (min) from hourly records Rh (60) (mm/h).

$$R_{h \, \left( t \right)} = R_{{h \, \left( {60} \right)}} \cdot \left( \frac{60}{t} \right)^{0.42}$$
(2)

An exponent equal to 0.42 is set by default, although strictly this value should only be used for regular rainfall: for extreme rainfall events, larger exponents should be considered (Choi 2001; Van den Bossche et al. 2013). Therefore, using the generic exponent 0.42 for varied climatic conditions produces a significant uncertainty in the results. However, its use is common in wind-driven rain applications (Choi 1998; Cornick and Lacasse 2009; Overton 2013; Sahal and Lacasse 2008; Van den Bossche et al. 2013).

In turn, other empirical formulae, such as the one established by the Indian Meteorological Department (Eq. (3)), allow estimating hourly rainfall values when only daily rainfall records are available. In this case, Rh (t) represents the rainfall value (mm) for a t-hour duration and Rh (24) represents the daily rainfall record (mm). The use of a constant exponent equal to 1/3 causes uncertainties similar to those already mentioned for Eq. (2). In addition, this generic equation is proposed only for estimates of hourly rainfall values or longer recording intervals (Al Mamun et al. 2018).

$$R_{h \, \left( t \right)} = R_{{h \, \left( {24} \right)}} \cdot \left( \frac{t}{24} \right)^{\frac{1}{3}}$$
(3)

Despite their evident functionality, neither of both generic equations allow rainfall values for any subdaily interval to be estimated. In any case, hourly and daily records are always required for the calculation. In turn, adjusting both generic exponents to achieve greater accuracy would require a similar effort to that of obtaining empirical correlations by location.

2.2 Conversion of wind speed between different recording intervals

For decades it has been developed a whole body of work that provides complex physical models for the combined structure of wind components as well as expressions for their probabilities, correlations, and derivations of their extremes (Cui et al. 2021; Lombardo et al. 2009). However, the study of wind speed values at short time intervals has traditionally focused on obtaining peak wind gusts (i.e. wind speed associated with a duration of 1 to 3 s), given its importance for numerous engineering applications. Eluding complex approaches and for general purposes, the wind gust is commonly defined by the simple use of a dimensionless gust factor Gt,T as expressed in Eq. (4). This factor relates the mean wind speed U (T) (m/s) over a reference period T and the highest average wind speed U (t) (m/s) befallen during a short-duration interval t within this longer period T. Typically, this gust factor can be expressed in terms of: a non-dimensional peak factor Cg representing the number of standard deviations that the maximum gust speed’s magnitude is statistically expected to lie above U(T), consistent with the selected gust duration t; and the quotient between the root-mean-square σ (m/s) of the fluctuating component of wind about the mean and U(T) –so called the turbulence intensity I in this context– (Choi and Hidayat 2002; Harper et al. 2010; Shu et al. 2015).

$$G_{t,T} = \frac{{U_{\left( t \right)} }}{{U_{\left( T \right)} }} = 1 + C_{g} \cdot \frac{\sigma }{{U_{\left( T \right)} }}$$
(4)

Numerous studies have shown that this gust factor depends on aspects such as the mean wind speed, the considered time intervals t and T, the height of the anemometer, the terrain roughness, and the nature of each specific event and its general typology (e.g. regular winds, tropical and extratropical cyclones, monsoons) (Choi 2000; Choi and Hidayat 2002; Durst 1960; Harper et al. 2010; Ishizaki 1983; Lombardo et al. 2014; Shu et al. 2015).

The World Meteorological Organization (WMO) adopts this factor for wind conversions under tropical cyclone conditions, providing tabulated Gt,T values for some terrain types, reference periods T (i.e. 60, 120, 180, 600, and 3600 s) and gust durations t (3, 60, 120, 180, and 600 s) (Harper et al. 2010).

Another of the first and most influential models developed to characterise this gust factor was the so-called ‘Durst curve’, empirically determined from observations made during 44 days between 1928 and 1929 at the Cardington airfield, UK (Durst 1960). This graphical curve provides G t, 3600 values, thus representing the relationship between the wind speed averaged over time t (seconds, time represented in log scale) and the available hourly wind speed (T = 3600 s). Despite its age, the curve is widely used for wind blowing over open terrain and is even included in building standards such as ASCE/SEI 7–16 (2017).

More recently, various mathematical expressions have been proposed to characterise the gust factor as a function of the time interval t and the wind turbulence intensity. Equation (5) represents a generic form of these approaches, where the turbulence intensity value I (-) can be obtained as the standard deviation of the fluctuating wind component about the mean wind speed for the reference period T, divided by that same mean wind speed (Harper et al. 2010).

$$G_{t,T} = 1 + C_{g} \cdot I^{k} \cdot \ln \left( \frac{T}{t} \right)$$
(5)

The non-dimensional coefficients Cg and k adopt different empirical values for specific atmospheric conditions and for a reference period T = 3600 s. For example, Cg = 0.5 and k = 1 were proposed for typhoons (Ishizaki 1983). Cg values ranging from 0.52 to 0.88 were identified by considering tropical thunderstorms in Singapore and fixing a k value equal to 1 (Choi 2000). Five years of wind measurements gathered in Hong Kong also provided Cg = 0.59 and k = 1.14 for monsoons and Cg = 0.55 and k = 1.09 for tropical cyclones (Shu et al. 2015). In any case, implementing these mathematical expressions requires a laborious analysis of the wind turbulence intensity, thus requiring exhaustive available data and a significant calculation effort by location.

By considering in a simplified manner a proportional relationship between the increase in wind speed and the reduction in the logarithmic duration of the recording interval, Choi proposed a generic equation for wind-driven rain applications (Eq. (6)). Thus, the mean wind speed U (t) (m/s) related to a short recording interval t (min) can be estimated from available records of hourly mean wind speed U (60) (m/s) and 3-s gust speed U (0.05) (m/s) (Choi 1998; Choi and Hidayat 2002). The capability for estimating results associated with any t (min) interval and the accuracy due to considering wind data linked to two recording intervals (i.e. gust and hourly records) has enabled the use of the equation as a multipurpose standard in the study of wind-driven rain (Blocken and Carmeliet 2010; Cornick and Lacasse 2009; Kpran and He 2014; Kubilay et al. 2013; Overton 2013; Sahal and Lacasse 2008).

$$U_{\left( t \right)} = U_{{\left( {60} \right)}} + \frac{{\ln \left( \frac{t}{60} \right)}}{{\ln \left( {\frac{0.05}{{60}}} \right)}} \cdot \left[ {U_{{\left( {0.05} \right)}} - U_{{\left( {60} \right)}} } \right]$$
(6)

Finally, another generic estimation was proposed by Lombardo et al. (2014) as a result of the study of various thunderstorms recorded in Texas between 2003 and 2010. In this case, the gust factor for a t interval of 1 s (i.e. G1,T) is defined as a simple polynomial function that depends on the considered reference interval T (s). Analysing 83 extreme thunderstorm events in the same region, Eq. (7) was also considered in good agreement with the experimental G3,T values, considering T (s) values no greater than 3600 s.

$$G_{1 - 3,T} = 0.011 \cdot \ln \left( T \right)^{3} - 0.072 \cdot \ln \left( T \right)^{2} + 0.23 \cdot \ln \left( T \right) + 0.85$$
(7)

3 Material and methods: Analysis of climatic datasets

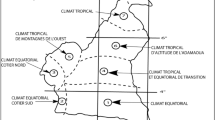
This section assesses the validity and accuracy of the above generic equations, analysing climatic records available at 109 Spanish and Dutch weather stations (see Fig. 1). The Spanish stations are distributed between the regions of Galicia (38 stations), Basque Country (19 stations), and La Rioja (21 stations), all located in the northern part of the country. In turn, the 31 Dutch stations are uniformly distributed throughout the country.

Fig. 1
figure 1

Geographic distribution of the weather stations considered in this research. Analysed stations are shown by crosses

Full size image

The Netherlands and the Spanish regions considered mostly share a temperate ocean climate, given their proximity to the Atlantic Ocean (Peel et al. 2007). However, other types of climates are also present: warm-summer Mediterranean climate in large areas of Galicia and warm-summer humid continental climate in mountainous areas of southeastern Galicia and southern La Rioja.

All these regions are subject to low-pressure areas (i.e. extratropical cyclones) caused by wind circulations in the Ferrel Cell under the influence of the North Atlantic Anticyclone and Icelandic Low, which are more frequent and intense in winter (Serreze et al. 1997). The topography also influences the rainfall and wind speed of these regions. Towards the inland Spanish regions, the rough terrain reduces the influence of oceanic winds. In the case of La Rioja, the mountain ranges locally channel the wind according to the orientation of the Ebro River valley, thus considerably increasing the wind speed (Masson and Bougeault 1996).

The data analysed are not prior to 2008 and are 10 years old (except at the Dutch stations of Valkenburg, Voorschoten and Wilhelmidadorp with 7, 6, and 6 years, respectively). These records have been compiled by the official meteorological networks of each region, following the guidelines set by the WMO (Basque Government 2021; Government of Galicia 2021; Government of La Rioja 2021; KNMI 2021; WMO 2018). Any station with more than 10% missing data was discarded, reaching an average of 2.7% for rainfall intensity records and 0.6% for wind speed records (see the supplementary material for this paper).

The available data belong to different recording intervals: 10-min records in Galicia and Basque Country (57 stations) and hourly records in the Netherlands and La Rioja (52 stations). In addition, the maximum wind gust speed (for the 3-s time interval), associated with every 10-min or hourly interval available, was collected at all stations.

In turn, these records have allowed the production of data series related to other recording intervals, following the aggregation and average criteria established by the WMO (2018). For stations with available 10-min records, 20-, 30-, 40-, 60-, 360-, 480-, 720-, and 1440-min data series were produced. In the Netherlands and La Rioja, 360-, 480-, 720-, and 1440-min data series were produced from the available hourly records.

All these data series allow the annual maximum values of rainfall intensity and wind speed linked to each recording interval to be identified. The rainfall intensity Rh was obtained by dividing the accumulated rainfall (mm) by the duration t (min) of each recording interval, thus presenting typical rainfall intensity units for wind-driven rain applications (i.e. mm/min). In the case of wind speed U, the maximum annual records for each recording interval is expressed in m/s.

These maximum annual records are representative of the extreme weather events characteristic of each location and can also be averaged by the number of years analysed to obtain a single baseline value for each recording interval. As an example, these calculations are presented in Table 1 for one of the stations analysed (Santiago EOAS station, Galicia, Spain), chosen arbitrarily.

Table 1 Example of a regression analysis of the maximum rainfall intensity and wind speed regarding the considered duration, obtained from data series of various recording intervals
Full size table

Finally, using a simple regression analysis based on the least-squares method (LSRA), it can be identified the best-fit relationship between the baseline data of each variable (i.e. the average of maximum annual values of rainfall intensity and wind speed) and the recording interval considered (Kemmer and Keller 2010). A common measure of goodness-of-fit (i.e. the coefficient of determination R2) has been used to determine the best-fit relationships at each location (Devore 2010). The closer this coefficient is to 1, the better the estimation of results related to different intervals (it can also be graphically observed, as in example of Table 1).

In the case of rainfall intensity, it has been found that the 109 analysed stations always present a best correlation of potential type, according to a general form such as presented in Eq. (8). Rh (t) represents the mean rainfall intensity for a t-min duration (mm/min), whereas the coefficients a and b adopt characteristic values at each location.

$$R_{h \, (t)} = a \cdot t^{ - b}$$
(8)

The coefficients of determination R2 obtained for these correlations of potential type have an average value equal to 0.997, ranging from 1.000 (Gilze-Rijen, the Netherlands) to 0.987 (Arrasate, Basque Country). The highest R2 values are identified in the Netherlands and La Rioja, characterised by a lower number of baseline data available for the regression analysis (subhourly records are lacking in both regions). All these coefficients and R2 values are presented in the supplementary material.

For wind speed, the most accurate adjustments are mostly achieved by logarithmic correlations. At some stations, it is also possible to identify an adequate correlation of potential type, although the difference in the R2 values is not significant. Thus, a logarithmic function as presented in Eq. (9) can be adopted as a general form for the wind speed conversion: U (t) (m/s) represents the mean wind speed for a t-min interval of extreme events, whereas the coefficients c and d adopt characteristic values at each location.

$$U_{(t)} = - c \cdot \ln \left( t \right) + d$$
(9)

In this case, the coefficients of determination of this proposed logarithmic correlation range between 1.000 (Pazuengos, La Rioja) and 0.904 (Quimadelos, Galicia), with an average value of 0.980. The worst adjustments are identified in Galicia and Basque Country, characterised by a greater number of points available for the regression analysis (complete series from 10-min data). Again, all these coefficients and R2 values are provided in the supplementary material for this paper.

3.1 Alternative estimation proposal and implementation examples

The high coefficients of determination obtained in all locations using both Eqs. (8) and (9), allow a general and functional approach to be proposed to accurately estimate extreme values of rainfall intensity and wind speed related to any subdaily recording interval. Although multiple series of recording intervals have been produced to adequately identify the type of the best-fit relationships, in practice, only climatic data belonging to two different recording intervals are strictly required to apply the LSRA (i.e. two baseline data), thus obtaining coefficients a, b, c, and d of both equations by location.

With these data (e.g. daily and hourly records or daily and 12-h records, as seen in the implementation cases A and B of Tables 2 and 3), the annual maximum values associated with both recording intervals can be obtained, as well as the average value of these annual maximums. Both resulting baseline data (i.e. only two values by location and variable) are thus representative of the extreme climatic conditions characteristic of the location.

Table 2 Implementation examples of the proposed approach, obtaining the extreme values of rainfall intensity for different recording intervals at the Santiago EOAS station (Santiago de Compostela, Galicia, Spain)
Full size table
Table 3 Implementation examples of the proposed approach, obtaining the extreme values of wind speed for different recording intervals at the Santiago EOAS station (Santiago de Compostela, Galicia, Spain)
Full size table

Through a least-squares regression analysis (which can be automatically performed with the most widely used spreadsheets), it is possible to identify the coefficients a, b, c, and d that best fit both baseline data. In this functional manner, the general Eqs. (8) and (9) can be locally adjusted to accurately estimate the extreme values related to any interval smaller than 1 day, considering the particular conditions of each site and using any record available. Finally, both equations define a reference that can be applied, by means of a simple cross-multiplication and from any starting record, to extrapolate the maximum values associated with another recording interval (see implementation examples in Tables 2, 3).

The percentage error made by these estimates and shown in the tables is determined according to Eq. (10), thus obtaining the absolute errors for each recording interval, which can then be averaged with those of other stations.

$$error = 100 \cdot \left| {\frac{estimation - baseline \, data}{{baseline \, data}}} \right|$$
(10)

Unlike the other generic equations presented in Sect. 2, this alternative approach does not require a high calculation effort for adjusting to the particular conditions of each location (only a few maximum annual records or their average value). In addition, it can be applied from any recording intervals available at the location and for estimating values related to any subdaily interval. In turn, its accuracy can be increased if there are more than two available recording intervals (i.e. more than two baseline values to conduct the regression analysis). As seen in the implementation examples of Table 2 (cases A and B), the rainfall intensity estimation presents similar errors regarding the baseline data, regardless of the recording intervals available at the station. However, for the wind speed estimation (cases A and B in Table 3), it is advisable to have at least hourly records at the location to minimise the error, especially for short time durations.

4 Results and discussion: comparison of maximum rainfall and wind speed estimates obtained by different generic equations

The analysis developed in the 109 locations allows the accuracy of the proposed generic equations to be compared with respect to that of the other generic procedures mentioned in Sect. 2. For this comparison, the average of the maximum annual records associated with each recording interval and location is adopted as a reference. In the Netherlands and La Rioja, where there is a lack of subhourly records, the 10-, 20-, 30- and 40-min baseline values are non-calculable. For the wind speed series, the average maximum annual values linked to a 3-s time interval are added at all stations.

These baseline data are compared at each weather station and for each recording interval, with the estimates provided by the methods described in Sect. 2 and by the alternative approach proposed in Sect. 3.1.

4.1 Comparison with the usual rainfall intensity-duration relationships

First, the accuracy of the rainfall intensity estimates obtained by the following generic procedures is analysed for each station and recording interval:

  • Applying Eq. (2), based on the hourly reference datum available at the station.

  • Applying Eq. (3), based on the daily reference datum available at the station.

  • Applying the proposed Eq. (8), based on the hourly and daily reference data available at the station. Although it would be possible to use another pair of available recording intervals, for uniformity and consistency of the comparison, the same baseline data required by the other procedures have been considered.

The results estimated by each generic procedure have been compared with the observations available at each station and for each recording intervals (average of maximum annual values). An example of this comparative analysis is shown in Table 4 for the same weather station presented in previous tables. As seen, the estimates obtained by Eq. (2) for recording intervals greater than 1 h have been analysed, although this estimation range exceeds the scope intended for the equation. Similarly, the results obtained by Eq. (3) for subhourly recording intervals are also shown. These values are shown in italic font.

Table 4 Example of errors caused by different estimations of rainfall intensity for extreme events and different recording intervals at the Santiago EOAS station (Santiago de Compostela, Galicia, Spain)
Full size table

The same analysis was repeated at each of the 109 stations considered, thus obtaining a global view of the accuracy of the three generic procedures for estimating the subdaily values of extreme rainfall intensity. Table 5 represents the average errors calculated by Eq. (10), further differentiating each region analysed. The lack of available subhourly records at the Netherlands and La Rioja stations prevents this error from being determined in both areas for recording intervals less than 1 h. Finally, the total root-mean-square errors (mm/min) are also shown as an additional comparison metric between different estimation procedures.

Table 5 Comparative summary of the average absolute errors and root-mean-square errors (RMSE) caused by the different estimation procedures for the maximum rainfall intensity at the 109 weather stations considered
Full size table

As observed, Eqs. (2) and (3) are unreliable outside their ranges of use (values shown in italic font in the table), and thus neither are adequate to estimate values in the entire subdaily range. For its part, the proposed Eq. (8) provides more accurate estimates in any subdaily interval, reducing by approximately half the best errors provided by the other procedures in its application ranges. This improved accuracy can be explained by the use of two site-specific data to adjust each particular Eq. (8), thus eliminating the uncertainty associated with the use of generic exponents. In general, the accuracy decreases the lower the recording interval considered, as in Eqs. (2) and (3). Thus, for the stations analysed and according to the considered baseline data (i.e. hourly and daily records), the errors range between 3.5% and 14.0% on average. There are no significant differences between the results of the different regions, although the Basque Country (Spain) has slightly higher errors (ranging from 4.8% to 18.4% on average).

In addition, the proposed approach can be applied from any pair of recording intervals available (not only from the hourly and daily data used here for methodological coherence). This adaptability allows estimations in a wide variety of locations with limited climatic records. In turn, the use of only a few annual maximum records and a regression analysis easily performed by usual spreadsheet programmes involves a reduced calculation effort.

4.2 Comparison with the usual wind speed conversions

Next, similar to the previous point, the accuracy of the wind speed conversions is analysed by the following methods:

  • Applying the tabulated gust factors established by the WMO for tropical cyclone conditions (Harper et al. 2010), based on the hourly reference datum available at the station.

  • Applying the gust factors graphically represented in the Durst curve (ASCE 2017), based on the hourly reference datum available at the station.

  • Applying Eq. (6), based on the 3-s and hourly reference data available at the station.

  • Applying Eq. (7), based on the hourly reference datum available at the station. The estimates obtained for recording intervals greater than 1 h have also been considered, although this estimation range exceeds the scope intended for this equation.

  • Applying the proposed Eq. (9), based on the hourly and daily reference data available at the station.

Table 6 presents a comparative analysis of these errors, showing for clarity the same example station already used in the previous tables. As shown, the Gt,T values tabulated in the WMO guidelines only allow gust and 10-min values (no gust factors are tabulated for the other intervals considered) to be estimated (Harper et al. 2010). In the case of Eq. (7), the results for different recording intervals can be obtained by multiplying several gust factors. For example, U1200 s (20 min) can be obtained as the result of U3600 s (60 min) · G3,T=3660 · 1/G3,T=1200.

Table 6 Example of errors caused by different estimations of wind speed for extreme events and different recording intervals at the Santiago EOAS station (Santiago de Compostela, Galicia, Spain)
Full size table

By repeating this analysis at all stations, it is possible to obtain a global view of the accuracy of these estimation procedures in each region and for any subdaily recording interval. Again, the lack of subhourly records in the Netherlands and La Rioja prevents determining the error for subhourly recording intervals in their stations. The average errors obtained are presented in Table 7 as well as the total root-mean-square errors (as an additional comparison metric between different estimations).

Table 7 Comparative summary of the average absolute errors and root-mean-square errors (RMSE) caused by the different estimation procedures for the maximum wind speed at the 109 weather stations considered
Full size table

The gust factors tabulated by the WMO and those represented by the Durst curve only allow estimates in the subhourly range. In addition, in the case of the former, only the values for 3 s and 10 min can be calculated. Even so, these WMO estimations (proposed for tropical cyclone conditions) are more accurate than those obtained by the Durst curve, defined from regular winds in a climate similar to the regions analysed here. Consequently, there is a need to reconsider the normative use of this curve, especially considering that the values of interest are usually those linked to extreme or adverse events (not regular or average conditions).

In general, the five estimations analysed present reasonable errors, less than 10% for most recording intervals (for the 3-s interval, the error is greater, given the turbulent nature of the variable). In the subhourly range, Eq. (7) presents the highest accuracy, with average errors ranging from 1.3% for 40-min intervals to 12.6% for 3-s intervals. These results confirm the validity of this equation to estimate wind gusts linked to 3-s intervals (not only for 1-s gusts) and, in general, its usefulness in regions other than Texas. Outside its application range, Eq. (7) also maintains adequate accuracy, at least up to the recording interval of 8 h.

In turn, the proposed Eq. (9) also presents a high accuracy, which is also maintained for the entire subdaily range (errors ranging from 1.8% for 40-min intervals to 10.6% for 3-s intervals, considering the hourly and daily baseline data used). Thus, although Eq. (9) is more adaptable than Eq. (7) to estimate values for any subdaily recording interval, it also requires an additional baseline datum (daily data in this analysis) and to determine the coefficients c and d at each site.

Regardless of these functional nuances, it is undeniable that both Eqs. (7) and (9) are more precise than Eq. (6), which is commonly used in wind-driven rain applications. In addition, they do not require exhaustive gust speed data, allowing them to be applied even in locations with limited climatic data. These advantages make both equations a more accurate and adaptable alternative than Eq. (6) for wind-driven rain calculations.

It should be noted that, theoretically, the gust factor Gt,T estimates the highest average wind speed befallen during a short-duration interval t within a longer period T. However, the baseline data used in this analysis do not strictly meet this hypothesis. Each baseline datum is the average of the maximum annual records associated with a specific recording interval (i.e. none of them is associated with a particular climatic event). Nevertheless, the statistical analysis developed is sufficiently representative, also allowing for accurate results based on these gust factors.

Notwithstanding the above, this analysis has only been performed in locations subject to extratropical cyclones and in some specific regions. Although the alternative approach proposed in Sect. 3.1 could be theoretically extrapolated to other regions and extreme climatic conditions (e.g. tropical cyclones, monsoon, etc.), the most appropriate type of general correlation for each variable and the goodness-of-fit reached should be determined first. In addition, it could be necessary to perform an adequate selection of representative wind data by storm types as well as a previous processing of archived reports in more complex atmospheric conditions, such as mixed climates (Cui et al. 2021; Lombardo et al. 2009). In turn, it could be possible to identify generic a, b, c, and d coefficients applicable to sites with similar climates, for which it would be necessary to analyse a greater number of regions and locations before identifying representative patterns. These analyses represent a broad field of research for the future development of this alternative approach.

Similarly, the study has focused on rainfall intensity and wind speed values linked to extreme events, thus ruling out averaged or regular values of less interest for normative purposes in engineering and for fields such as wind-driven rain applications.

5 Conclusions

In this study, an alternative approach was proposed to estimate extreme values of rainfall intensity and wind speed related to any subdaily recording interval. The generic Eqs. (8) and (9) allow the specific conditions of each location to be considered with reduced computational effort (by determining their a, b, c, and d coefficients) and can be applied functionally even in sites with limited climatic data, given the reduced number of required baseline data (i.e. only annual maximum data associated with two subdaily recording intervals whatsoever).

In the case of rainfall intensity, the analysis of recent data collected from a large number of weather stations subjected to extratropical cyclone conditions demonstrates that this alternative approach is more accurate and adaptable than the generic equations traditionally used in fields such as the study of wind-driven rain. In the case of wind speed, the proposed Eq. (9) allows more reliable estimates to be obtained compared with traditional gust factor equations for the entire subdaily range. Only the equation defined by Lombardo et al. provides better accuracies in the subhourly range, also implying a lower calculation effort than the proposed approach.

These results suggest the need to update the procedures currently established in fields such as the study of wind-driven rain to estimate extreme values of rainfall intensity and wind speed related to subdaily intervals and based on limited climatic records. The extension and possible adaptation of this study to other climatic conditions and more complex climates constitutes a future challenge to offer a functional and reliable estimate also in other regions.