Abstract
Representativeness and quality of collected meteorological data impact accuracy and precision of climate, hydrological, and biogeochemical analyses and predictions. We developed a comprehensive Quality Assurance (QA) and Quality Control (QC) statistical framework, consisting of three major phases: Phase I—Preliminary data exploration, i.e., processing of raw datasets, with the challenging problems of time formatting and combining datasets of different lengths and different time intervals; Phase II—QA of the datasets, including detecting and flagging of duplicates, outliers, and extreme data; and Phase III—the development of time series of a desired frequency, imputation of missing values, visualization and a final statistical summary. The paper includes two use cases based on the time series data collected at the Billy Barr meteorological station (East River Watershed, Colorado), and the Barro Colorado Island (BCI, Panama) meteorological station. The developed statistical framework is suitable for both real-time and post-data-collection QA/QC analysis of meteorological datasets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Motivation Quality Assurance (QA) and Quality Control (QC) procedures are commonly used to verify and control environmental monitoring activities to ensure the resulting data provide a representative evaluation of environmental conditions, which are then used for ecohydrological modeling and model validation (van der Heijde and Elnawawy, 1992; QA Guide, 2013). Meteorological data are commonly used as forcing factors in climate, hydrological, and other terrestrial models. Thus, effective QA/QC methods are critical for ensuring the high-level of trust in collected data, because representativeness and quality of field collected time series data may dramatically impact the accuracy and precision of climate, hydrological, and biogeochemical predictions. Examples of meteorological data collected in real time by automated, streaming sensors are temperature, barometric pressure, solar radiation, rainfall, relative humidity, wind speed and wind direction, evapotranspiration, runoff, and soil moisture content. Collected time series data are commonly processed and structured in a unique way, distinct for each type of observations and instrumentation. Although most modern data loggers faithfully record time series data, collected data are usually irregular, and subject to several types of errors: errors of commission, such as incorrect or inaccurate data entered, mistyped data, and malfunctioning of instrumentation, as well as errors of omission, because data or metadata are not properly recorded, for example, due to inadequate documentation, human errors, or anomalies in the field data collection. Collected time series datasets could also be incomplete or imperfect due to different time frequency of measurements, different units of measurements in the same time series, periodic malfunctioning of sensors or changes due to calibration, abnormal values, and data gaps. QA/QC statistical methods are used to ensure consistency in preparation of monitoring data, based on field observations, as inputs for data analysis, modeling, prediction, and decision making. Generally, an application of QA methods is proactive, including the collection of metadata and data maintenance, followed by applying QC methods to improve the quality of data and to provide annotations of the data after the execution of a QC process. The rigorous QA/QC statistical analysis of field collected datasets is a necessary attribute required for the development of consistent and reliable datasets with a specific and aligned time frequency, which are used for modeling and predictions.
General definitions The QA is defined as "part of quality management focused on providing confidence that quality requirements will be fulfilled,” and the QC is defined as “part of quality management focused on fulfilling quality requirements” (ISO, 2015). In particular, the goal of QA is to improve the development and testing processes of the monitoring equipment and sensors to prevent defects or unreliable information arising during the product development lifecycle and its usage. The QA of datasets requires the application of technical and analytical procedures for ensuring the quality in conducting research, and providing confidence that quality requirements will be fulfilled, such as selection of appropriate types of sensors, calibration protocols, software, etc. The QC is performed using a system of routine statistical/numerical activities implemented by the data management team to assess and control the quality of data. Despite the worldwide application of various QA/QC approaches and methods, there are multiple challenging QA/QC problems due to specific features of types of instrumentation and types of collected data, such as duplicates of time stamps and collected data, data gaps, spikes, outliers, abnormal data, etc.
The goal of the current paper is to present an application of a rigorous QA/QC statistical approach for addressing challenging problems of the QA/QC of meteorological and hydrological time series datasets. This approach can be used for both real-time and post-data collection datasets. Two use cases are used to demonstrate the application of the developed approach for solving challenging QA/QC problems of meteorological time series data.
The structure of the paper is as follows. Section 2 provides a literature review of selected QA/QC approaches and methods. Section 3 includes a flowchart of the QA/QC framework, a description of preliminary data exploration, including the datasets and time formatting. Section 4 provides examples of the QA analysis of meteorological data, including the challenging problems of the detection and flagging of extremes and outliers, and Sect. 5 includes examples of the QC analysis of time series, such as imputation of missing data, creation of time series of a desired time frequency, and time series visualization and statistics. Section 6 includes conclusions and directions of future research.
2 Literature review of QA/QC workflows
Over the past 50–60 years, the data collection and usage of meteorological and hydrological observational data have been changed due to automation of monitoring equipment and sensors, so that scientists have been collecting tremendous amounts of data in real time. Currently, the datasets from different sources are retrieved from a few seconds intervals up to a few hours’ periods. There are multiple publications describing the QA/QC procedures implemented in different countries. For example, the Guide on the Global Data-processing System (Guide WMO-No. 305, 2001) is the authoritative reference on all matters related to quality control issues. Recommended minimum standards of quality control at the level of the observing station and at that of the NMC (National Meteorological Centre) are given in the Manual on the Global Data-processing and Forecasting System, WMO No. 485 (WMO, 2019).
The report D1.41 (2014), entitled “User guide containing quality assessment of Arctic weather station and buoy data” includes a selected compilation of Arctic Meteorological Station data from Canada, Finland, Greenland, Iceland, Norway, Russia, and Sweden, as well as buoy data from the International Arctic Buoy Program (IABP) (http://iabp.apl.washington.edu/index.html). All available data from weather stations and data buoys over the Arctic are quality controlled by their original facilities and made available to other project participants. Station data from each source are reprocessed to the standard data format suitable to be used in the ACCESS databank.
Rissanen et al. (2000) provided a survey of different methods used in quality control in the Nordic countries on behalf of the National meteorological services in Denmark, Finland, Iceland, Norway, and Sweden. They emphasized that collecting new data using modern observation methodology and use of data raise new needs for quality assurance and control of collected data. For example, Rissanen et al. (2000) emphasized that data quality flagging is of most importance when using the data, and should be implemented on all levels of the QA/QC.
According to the recommendations of the ASOS Guide (1998) of the National Weather Service of NOAA, there are three cascading levels of quality control, focusing on different temporal and spatial scales. Level 1 is performed on-site, in real-time before observations are transmitted. Level 2 is performed at a Weather Forecast Office (WFO) for a designated area, usually within two hours after the scheduled observation transmission time. Level 3 is performed centrally on all ASOS METAR stations, usually about two hours after the scheduled transmission time.
Publications by Shafer et al. (2000) and Fiebrich and Crawford (2001) described the automated QC that is performed on Mesonet and ARS (Agricultural Research Service of the United States Department of Agriculture) stations (https://www.mesonet.org/index.php/quality_assurance/quality_assurance). Four components compose the Mesonet’s QA system: (1) laboratory calibration and testing, (2) onsite intercomparison, (3) automated QA, and (4) manual QA. Automated QA software is used to evaluate the data received from remote stations, followed by the daily review by a meteorologist, trained in state-of-the-art QA procedures, to examine the suspicious observations detected by other components of the QA system. The Mesonet infrastructure was successfully applied at the OKCNET to perform spatial, step, and persistence tests (McPherson et al. 2007) every minute, and only good and suspect data are delivered in real-time to users. As a result, millions of QA computations are completed on nearly 640,000 unique observations collected daily by OKCNET. To date 97.85% of all OKCNET observations have passed the QA routines as ‘good’ while the remaining 2.15% have been categorized as ‘suspect’, ‘warning’ or ‘failure’. (Basara et al. 2011). The success of OKCNET is contingent upon the quality of the observations collected, continued funding and an increasing number and diversity of end users (http://okc.mesonet.org).
Fiebrich and Crawford (2001) showed that automated QA software, which is supposed to generate QA quality flags of each observation, may fail, resulting in flagging some good observations as erroneous. They showed examples of special problems for automated QA software such as: cold air pooling and “inversion poking,” mesohighs and mesolows, heat bursts, snowfall and snow cover, as well as microclimatic effects produced by variations in vegetation. Range and temporal test thresholds of OKCNET data are used for the automated quality assurance checks (Basara et al. 2011). Meek and Hatfield (1994) presented a series of algorithms similar to the Mesonet’s range, step, and persistence tests, as well as a system of QA flags. Wade (1987) and Fiebrich and Crawford (2001) discussed an approach to a comparison of data from different meteorological stations, based on an evaluation of the standard deviation of observations. Individual quality flags were used to rate the stationarity of the data and to test for development of the turbulent flow field with integral turbulence characteristics (normalized standard deviations). The combination of these two ratings yielded the overall quality of the measurement. Basara et al. (2011) presented a QA/QC approach of time series meteorological data based on the commonly observed range of data and maximum steps allowed between consecutive 5 min observations. The QA/QC methods and guidelines for workflow are being developed by the AQUACOSM (Network of Leading European AQUAtic MesoCOSM Facilities Connecting Mountains to Oceans from the Arctic to the Mediterranean.)
Another example of a sophisticated set of QA/QC tests and flags is AmeriFlux's QA/QC processing pipeline (https://ameriflux.lbl.gov/data/qaqc-tests/). Figure 1 illustrates a flowchart of the QA/QC procedure of the AmeriFlux collected data, indicating that immediately after a flux-met data file is uploaded, it follows one of the paths to an Overall Status/Action.
Flow chart illustrating the QA/QC procedure of the AmeriFlux collected data, showing that after a flux-met data file is uploaded, it follows one of the three paths to an Overall Status and Action. (
Thus, a critical review of existing QA/QC approaches shows that there is no common approach to the QA/QC analysis of meteorological and hydrological data, because different organizations apply different methods depending on the types of data and goals of the further application of QA/QC-ed data.
3 QA/QC approach and a numerical code
3.1 Flowchart and datasets
Our QA/QC process consists of three major phases: Phase I—Preliminary data exploration, i.e., processing of raw datasets, with the most challenging problems of time formatting and combining datasets of different length and different time intervals; Phase II—QA of the datasets, including detecting and flagging of duplicates, outliers, and bad (extreme) data; and Phase III—Imputation of missing values and the development of time series of a desired frequency, visualization and a statistical summary. Numerical analysis is performed using the R programming language, which is widely used for statistical computing and graphics supported by the R Foundation for Statistical Computing (R Core Team, 2021).
A flowchart of the developed QA/QC framework is shown in Fig. 2. The flowchart shows in red the most challenging problems of the QA/QC analysis addressed in this paper. The challenging problems of the Phase I “Data Exploration” include (a) combining individual datasets collected at different sensors with different time duration and time frequency into a single list of files, which is a vectorized function (it can also be achieved by direct concatenation without requiring loops or vectors), and (b) checking the format of dates and converting them to a suitable format for further data analysis. The challenging problems of the Phase II “QA of data” include (a) detecting and flagging outliers and bad/extreme data, and (b) visualization of these data. The challenging problems of the Phase III “QC of data” include imputation of missing data, and (b) creation of the time series of a desired time frequency, including imputation of additional missing data generated during the development of the time series of the desired frequency. The R codes for the whole QA/QC process involving the three phases were developed and tested based on the post-data-collection analysis of meteorological datasets.
In this paper, we demonstrate a QA/QC framework using univariate time series statistical data analysis. The developed QA/QC statistical methods are also appropriate for real-time and post-data-collection QA/QC analysis (all three phases) of meteorological or hydrological datasets. Note that the real time assessment of data quality is recommended to conduct during Phase I (Preliminary data exploration) and Phase II (QA of data), and the post-data-collection analysis includes QC of data.
3.2 Preliminary data exploration
3.2.1 Datasets
Two meteorological datasets representing different end-member ecosystems were analyzed as use cases in this study to demonstrate the utility and effectiveness of our workflow. The Billy Barr dataset represents the mountainous, snow-dominated East River watershed, Colorado, USA (Hubbard et al. 2018). The Billy Barr dataset consists of time series data of the following variables: Solar Radiation, Wind Speed, Wind Direction, Relative Humidity, Temperature, and Precipitation (downloaded from the website https://eastriver.pafbeta.subsurfaceinsights.com/).
The Barro Colorado Island (BCI) dataset from a tropical forest in Panama consists of time series data of Solar Radiation, Wind Speed, Relative Humidity, Temperature, and Precipitation (downloaded from the Smithsonian Tropical Research Institute’s BCI’s website https://biogeodb.stri.si.edu/physical_monitoring/research/barrocolorado).
The challenging problems of these datasets are that meteorological parameters were recorded with different time frequency and for different periods of time. Moreover, the timestamps are different for different variables, which create a problem of combining the QA/QC-ed datasets into a single file for further data analysis and modeling. The time series plots of original time series datasets are shown in Supplementary Information SI-1 in Figures SI-1.1a,b. Figure SI-1.1c shows graphs of time series of meteorological variables for a three-year period from 2018 to 2020 for the BCI station, which were analyzed in this paper. Tables SI-1.1 and SI-1.2 provide summaries of the total number of the data points of meteorological variables along with other statistical parameters of the original datasets. Figures SI-1.2a,b show time series graphs of the time intervals of measurements of the original Billy Barr and BCI datasets. The values of time difference of zero indicate the presence of duplicates, the negative values indicate that the time stamps are not ordered, and a scatter of points is indicative of the irregular time series data. Because the Billy Barr datasets include several time series data in a single file, but the BCI datasets include time series in separate files with different types of information, the preliminary data exploration and preparation of datasets in Phase I were provided differently.
3.2.2 Time formatting and time consistency check
It's common to gather some basic information about the datasets, such as its dimensions, data types and distribution, number of missing data, etc. These can be done using the R functions str(), summary() and is.na()of the base R library, as well as a function desctable() of the library desctable, which were used in this study.
The time format of the Billy Barr meteorological station is given in the format yyyy/mm/dd H:M:S, which is easily converted to the as.POSIXct(%Y-%m-%d %H:%M:%S), representing calendar dates and times (POSIX stands for Portable Operating System for Unix). However, the original time formats of the BCI datasets are given as a string of characters, using a different order of days, months, and years, such as yyyy/mm/dd, or mm/dd/yyyy, or dd/mm/yyyy, which could have been caused by collecting data using new instrumentation, dataloggers, or datalogger programs. Therefore, the first step of the preliminary data exploration is to convert the timestamps to the as.POSIXct time format.
Other problems encountered during the time formatting are the presence of missing timestamps, marked as NAs, duplicates of timestamps, and a non-consecutive order of timestamps. For example, Figure S1-1.2b demonstrates negative values of calculated time intervals of raw data, which indicates breaking the temporal order, i.e., a non-consecutive order of timestamps. These datasets require be sorted/ordered. The time difference (i.e., time interval) is determined using the function diff.POSIXt().
The time consistency check includes the evaluation of the persistence of the time stamps, duplication of timestamps, and the variability of the times intervals. The time stamps are usually given in the format of the local time, while the final dataset is designed to give time stamps in both a local time format and the Coordinated Universal Time (UTC) format, an international standard 24-h timekeeping system. Therefore, the final results of the QA/QC analysis include the timestamp vectors given in both local time (Mountain Times Zone for the Billy Barr station, and Eastern Time Zone for the BCI station), and the UTC format.
4 QA analysis of datasets
4.1 Terminology
Identifying and distinguishing outliers and extreme data in datasets, as well as the difference between them, are among probably one of the most difficult parts of data cleanup. The QA procedure includes detecting and flagging of (a) duplicates of dates and variables, (b) missing data, given as NAs or shown using non-physical values (such as − 999, − 9999, or similar), and (c) outliers and bad data.
The terms "outlier," “bad data,” and "anomaly" do not have common technical definitions in the data mining and statistics literature. For example, Hawkins (1980) defined an outlier as “an observation which deviates so much from the other observations as to arouse suspicions that it was generated by a different mechanism.” Outliers are also referred to as abnormalities, discordants, deviants, or anomalies in the data mining and statistics literature (Aggarwal, 2017). Bad data are usually caused by measurements or input errors, data corruption, but the apparent outliers can be true observations (Kuhn and Johnson, 2013).
Extreme data, which could be bad data (or anomalies), may emerge in time series datasets depending upon the type and a length of the time series. Bad data can appear as (a) a single bad data point, or individual spike, when only one of the measurements in the entire time series will have a large error, or (b) multiple bad data points (or multiple spikes) in time series, when numerous measurements will be in error. For strongly correlated measurements, their errors may significantly affect the estimated value of each other, causing the good measurements to look in error. Multiple bad data can generally be grouped into: non-interacting, with weak relationship between the residuals, which are not significantly affected by each other; and interacting with either a strong correlation between the good and the bad data, or non-conforming, so that it is difficult to recognize the corrupted data and distinguish them from the clean measurements. Other types of spurious data are a level shift, i.e., sudden jumps or unusual events, and a slow drift.
Dealing with these types of data requires the application of different approaches. For example, in the case of a slow drift, i.e., a linear trend of the time series, a linear regression model can be used, and the linear trend can then be subtracted. Then, the apparently bad segment of the time series can be replaced with its residuals. Removing the trend can also be done using a nonparameteric method, such as removing the trend using the first difference function diff().
4.2 Detection and flagging of duplicates
The duplicated()function can be used to determine which elements of a vector or data frame are duplicates of other elements, and returns a logical vector indicating which elements (rows) are duplicates. The other option is to use the function anyDuplicated () that is an efficient shortcut for duplicated(). The distinct() function of the dplyr package in R can be used to eliminate duplicated rows. All duplicated rows are flagged with 1.
4.3 Detection and flagging of extremes and outliers
Conventional approaches developed for random (noisy) datasets with no apparent long-term drift are not applicable for meteorological and hydrological datasets. Criteria for the evaluation of outliers and anomalies are supposed to be different for different scientific and practical applications, because apparent outliers or bad data points may contain valuable information about the process or the data gathering process. The first step in the evaluation of outliers and bad data is to assess whether the data are within a reasonable range (natural overall, seasonal, and instrumental). For example, solar radiation has to be only positive values with the zeros at the night time; rainfall is also only positive values, with zeros at the time of no precipitation, relative humidity is expected to not exceed 100%, and wind direction varies from 0 to 360°.
There are multiple approaches to the detection of outliers, which are noticeably different in value from the others of the time series. (Barnett, 1978). Here are a few examples of the outlier detection techniques: distance-based outlier detection (Hautamaki et al. 2004), generalized dispersion-based outlier detection (Ben-Gal, 2005), depth based outlier detection (Johnson et al. 1998), density-based outlier detection (Ester et al. 1996), a hierarchical cluster analysis, and a Hampel filter that uses a sliding window to go over the data vector, and it calculates the median and the standard deviation expressed as the median absolute deviation (Hampel, 1974; Suomela, 2014). The Hampel approach is based on calculations of the distance from the median in terms of the median absolute deviation (MAD) for symmetrically distributed variables, such as temperature or wind speed, and assigning different distances in case of the unsymmetric distribution, for example, solar radiation, precipitation, or relative humidity.
For long-term meteorological and hydrological data, which exhibit seasonal fluctuations and a long-term trend, we used the runquantile function of the R package “caTools”, which is the moving (i.e., rolling) window calculating quantiles over a vector of the variable. Taking into account the seasonal fluctuations of meteorological parameters, the 6-month moving window was used. The probabilities of 0.999 and 0.001 were selected for the upper and lower extreme values, and 0.975 and 0.025 for the upper and lower outlier values. The selection of the rolling window length and associated thresholds is usually the user’s dependent process, i.e., it is determined by the outlier detections’ goals (e.g., Klein Tank and Können, 2003; Yu et al. 2014). Figures 3a,b show time series graphs depicting outliers and bad data for the rolling window of six months, and statistics of the outliers and extremes are summarized in Tables 1 and 2. To demonstrate the effect of using different lengths of the rolling window, we present the statistical results of calculations of the outliers and extreme values of precipitation at Billy Barr for the rolling windows of 15 and 30 days in Tables SI-1.3 and SI-1.4.
a Time series of the Billy Barr meteorological variables showing the potential outliers and extreme values (calculated using a rolling window of 6 months). Note that the precipitation plot is shown using the semi-logarithmic plot (log-y axis) to more clearly display potential outliers and extreme values. b Time series of the BCI meteorological variables showing the potential outliers and extreme values (calculated using a rolling window of 6 months)
The flagging vectors are combined with the original data sets in the final QA files (given as a series of the CSV or Excel workbook files) to link data-quality flagging with the original data. This approach is used to indicate data quality of the original data, assuming that the original measurements still contain some value. The ‘flags” are generally indicative of underlying problems. The flags may also be used to distinguish between unchecked and checked data, or extremes, which are suspected of being bad or faulty.
5 QC analysis of datasets
5.1 Dealing with duplicate values and extremes
The rows with duplicated Dates/Times can be either extracted or the corresponding values can be aggregated in a single row for a given Date/Time stamp. In the current R code, we extracted rows with duplicated Date/Time stamps, using a function duplicated. We also extracted the rows, in which extremes were identified. The extraction of these rows creates the gaps in time series data. We have conducted imputation of these gaps.
5.2 Imputation of missing values
5.2.1 General approach to imputation of missing values
Missing data, or missing values, occur when no data values are stored for the variable in an observation. Missingness mechanisms and patterns are different for different sites and types of meteorological parameters. Bad data are also usually marked as missing data. Missing time series datasets can be caused by multiple reasons, and missing values and missing time intervals could occur either at random or not at random, i.e., at specific time periods over the course of the year. Imputation of missing data is a challenging problem, because the gap filling techniques are not generic and they are special for different types of meteorological and hydrological variables. Generally speaking, there are three main approaches to handle missing data: (1) Imputation—where values are filled in the place of missing data, (2) omission—where samples with invalid data are discarded from further analysis, and (3) analysis—by directly applying methods unaffected by the missing values. Imputing missing data can be conducted using a univariate or multivariate statistical analysis. There are multiple methods of imputating missing values. In the current paper, examples of using imputation of missing data into a univariate time series by means of the imputeTS package are shown. The imputeTS package provides a univariate time series imputation, and includes several different imputation algorithms. The package can also be used to visualize distribution of missing values, visualize distribution of NA gapsizes, and visualize imputed values. Examples of the visualization of gap imputation are shown in Sect. 5.4. The statistics of the gap sizes in the BCI dataset is given in Table 3.
The application of multivariate imputation of missing values for groundwater levels can be found in the paper by Dwivedi et al. 2021, and for precipitation–in the paper by Mital et al. 2020.
5.2.2 Imputation using the library imputeTs
Imputation was conducted using the na_seadec () function (Seasonally Decomposed Missing Value Imputation) of the ImputeTS package in R, with a the time series frequency of 365, and using the algorithm "interpolation." The function statsNA is used to print statistics of missing values.
5.3 Time series of the desired time frequency
Creation of datasets of the desired time frequency can be provided using the package highfrequency in R. The function aggregateTS() returns an aggregated time series, can handle irregularly spaced timeseries, given as ts, zoo or an xts objects, and returns a regularly spaced time series of the desired frequency. This function is applied over each time interval and provides the mean value for assigned period (for example, "seconds," "minutes," "hours," "days," "weeks." There is also an option to determine whether empty intervals should be dropped. The function returns NA in case of an empty interval. Application of the aggregateTS function for the BCI time series generates a certain number of NAs. Note that the final results of the QA/QC analysis are given not for particular time stamps, but for the time periods for which the data were averaged during preparation of the datasets of the desired frequency. For both sites, the time intervals of the QA/QC-ed datasets are 1 hour. The visualization of the results is demonstrated below in Sect. 5.4.
5.4 Visualization and statistics
A function ggplot_na_distribution() can be used to provide a graphical presentation of the gap filled intervals. The results of using this function to visualize missing intervals are shown in Figure SI-1.3 for the Billy Barr station, and in Figure SI-1.4–for the BCI station. Examples of the visualization of occurrences of NA gap sizes of temperature at both stations are shown in Fig. 4.
The visualization of imputation of mission data, plotted using the function ggplot_na_imputations(), is shown in Figs. 5 and 6.
The visualization of the missing values per interval can be plotted using the function ggplot_na_intervals().
The Billy Barr’s and BCI’s QA/QC Data Profiling Reports were developed using the package DataExplorer, and are given in SI-2. These reports contain the following types of statistical parameters and the results of the statistical analysis:
-
Basic statistics
-
Raw counts
-
Percentages
-
Data structure
-
Missing data profile
-
Univariate distribution
-
Histogram
-
QQ plot
-
Correlation analysis
-
Principal component analysis
The visualization of the data also includes the Box-plot presentation of the correlation between the meteorological variables, which is shown in Figure SI-1.6.
5.5 Comparison of the original and QA/QC-ed datasets
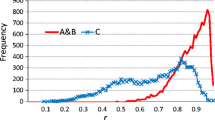
A graphical comparison of the cumulative probability distribution functions for the original and QA/QC-ed datasets is shown in Fig. 7. A quantitative comparison of the original and QA/QC-ed datasets is performed using the Lepage test (Lepage, 1971; Hollander et al. 2014), which is a distribution-free, nonparametric, test for assessing jointly the location (central tendency) and scale (variability) of datasets of different lengths. Calculations are provided using the R package NSM3. Figure 8 and Table SI-1.5 show a set of calculated C statistics and p-values for different variables, indicating that the null hypothesis that the two samples were drawn from the same distribution can be rejected for precipitation, wind direction, wind speed, and solar radiation, as the p-values are less than 0.05. These results illustrate how the meteorological datasets changed after gap filling, removing the extreme values, and creating the desired frequency (1 hour) time series datasets.
6 Conclusions
Numerical modeling commonly requires consistent datasets with a specific and aligned time frequency for different variables. However, the collected time series datasets are often irregular and characterized by different time frequency of measurements, different units of measurements in the same time series, time stamps duplicates, periodic malfunctioning or failure of sensors or changes due to calibration, and missing data. Irregular datasets are also common when the data are multi-modal, with inputs coming from different sources, which are not synchronized with each other, resulting in the non-uniform input data. The other cause of irregularity is due to removing outliers or abnormal values. Moreover, different meteorological parameters from the same meteorological station, representing the same time period, are sometimes collected at different time intervals.
The article presents a framework to perform the entire QA/QC process in the R programming environment. The developed QA/QC workflow includes three consecutive phases: Phase I—Preliminary data exploration, i.e., processing of raw datasets, with the challenging problems of time formatting and combining datasets of different lengths and different time intervals; Phase II—QA analysis of the datasets, including detecting and flagging of duplicates, outliers, and extreme data; and Phase III—imputation of missing values and the development of time series of a desired frequency, visualization and a statistical summary. The developed QA/QC statistical framework and methods are suitable for both real-time (QA analysis during Phases I and II) and post-data-collection QC analysis (Phase III) of meteorological and hydrological datasets. The developed approach allows scientists to obtain QA/QC-ed time series datasets of meteorological drivers with desired time steps. Various criteria and metrics are applied to ensure consistency in the preparation of datasets: time frequency of measurements, descriptive statistics (i.e., max, min, standard deviation, outliers and extremes). The application of the developed framework and methods is demonstrated using two use cases from opposite ends of the meteorological spectrum—the Billy Barr meteorological station (East River Watershed, Colorado) and the Barro Colorado Island (Panama) meteorological station.
References
Aggarwal CC (2017) An introduction to outlier analysis. In: Outlier Analysis. Springer, Cham. https://doi.org/10.1007/978-3-319-47578-3_1
AQUACOSM (2020), Network of leading european AQUAtic MesoCOSM facilities connecting mountains to oceans from the Arctic to the Mediterranean,. https://www.aquacosm.eu/download/Partners-Documentation/aquacosm/sops/AQUACOSM_SOP_7_QAQC_20200527.pdf
Automated Surface Observing System (ASOS) User’s Guide (1998). Source: https://www.weather.gov/media/asos/aum-toc.pdf
Basara JB, Illston BG, Fiebrich CA, Browder PD, Morgan CR, McCombs A, Bostic JP, McPherson RA, Schroeder AJ, Ke C (2011) The Oklahoma City Micronet. Meteorol Appl 18:252–261
Ben-Gal I (2005) Outlier detection. In: Maimon O, Rokach L (eds) Data mining and knowledge discovery handbook. Springer, Boston, MA. https://doi.org/10.1007/0-387-25465-X_7
D1.41 (2014) – User guide containing quality assessment of Arctic weather station and buoy data, Project no. 265863 ACCESS Arctic Climate Change, Economy and Society.
Dwivedi D, Mital U, Faybishenko B, Dafflon B, Varadharajan C, Agarwal D, Williams K, Hubbard S (2021) Imputation of missing high-resolution groundwater data using machine learning and information theory. Accepted for publication at "Journal of Machine Learning for Modeling and Computing." The article ID is JMLMC-38774, 2021
Ester M, Kriegel HP, Sander J, Xu X (1996) A density-based algorithm for discovering clusters in large spatial databases with noise, Publication:KDD'96: Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, pp. 226–231, https://dl.acm.org/citation.cfm?id=3001507
Fiebrich CA, Crawford KC (2001) the impact of unique meteorological phenomena detected by the oklahoma mesonet and ars micronet on automated quality control. Bull Am Meteor Soc 82(10):2001
Guide WMO-No.305 (2001), Guide On The Global Data-Processing System (2001) d1.41
QA Guide (2013) Quality assurance program guide, DOE G 414.1–2B, DOE, 2011–2013
Hampel FR (1974) The influence curve and its role in robust estimation. J Am Stat Assoc 69:382–393
Hautamaki V, Karkkainen I, Franti P (2004) Outlier detection using k-nearest neighbour graph. In Proc. IEEE Int. Conf. on Pattern Recognition (ICPR), Cambridge, UK
Hawkins D (1980) Identification of outliers. Springer, Dordrecht
Hollander M, Wolfe DA, Chicken E (2014) Nonparametric Statistical Methods. Wiley
Hubbard SS, Williams KH, Agarwal D, Banfield J, Beller H, Bouskill N, Brodie E, Carroll R, Dafflon B, Dwivedi D, Falco N, Faybishenko B, Maxwell R, Nico P, Steefel C, Steltzer H, Tokunaga T, Tran PA, Wainwright H, Varadharajan C (2018) The East River, Colorado, Watershed: A mountainous community testbed for improving predictive understanding of multiscale hydrological–biogeochemical dynamics. Vadose Zone J 17:180061. https://doi.org/10.2136/vzj2018.03.0061
ISO (2015), ISO 9000:2015, Quality management systems — Fundamentals and vocabulary (https://www.iso.org/standard/45481.html).
Klein Tank AMG, Können GP (2003) Trends in indices of daily temperature and precipitation extremes in europe, 1946–99. J Clim 16(22):3665–3680
Kuhn M, Johnson K (2013), Applied predictive modeling, Springer, ISBN-13: 978–1461468486
Lepage Y (1971) A combination of Wilcoxon’s and Ansari-Bradley’s statistics. Biometrika 58(1):213–217
Leys C, Ley C, Klein O, Bernard P, Licata L (2013) Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median, Journal of Experimental Social Psychology volume, 49, 4 urlhttp://www.sciencedirect.com/science/article/pii/S0022103113000668
Manual WMO (2019), Manual on the Global Observing System VOLUME I (Annex V to the WMO Technical Regulations) GLOBAL ASPECTS 2003 edition (https://www.wmo.int/pages/prog/www/OSY/Manual/WMO544.pdf)
Meek DW, Hatfield JL (1994) Data quality checking for single station meteorological databases. Agric for Meteor 69:85–109
Mital U, Dwivedi D, Brown JB, Faybishenko B, Painter SL, Steefel CI (2020) Sequential Imputation of Missing Spatio-Temporal Precipitation Data Using Random Forests. Frontiers in Water 2: 20, https://www.frontiersin.org/article/https://doi.org/10.3389/frwa.2020.00020
Rissanen R (2000) (ed) Jacobsson C, Madsen H, Moe M, Pálsdóttir F, Vejen F (2000), Nordic Methods for Quality Control of Climate Data. Nordklim, Nordic co-operation within Climate activities, DNMI Klima Report 10/00.
Shafer MA, Fiebrich CA, Arndt DS, Fredrickson SE, Hughes TW (2000) Quality assurance procedures in the Oklahoma Mesonet. J Atmos Oceanic Technol 17:474–494
Suomela J (2014) Median filtering is equivalent to sorting. https://arxiv.org/pdf/1406.1717.pdf
van der Heijde PKM, Elnawawy OA (1992) Quality assurance and quality control in the development and application of ground-water models, EPA/600/R-93/011.
Vickers D, Mahrt L (1997) Quality control and flux sampling problems for tower and aircraft data. J Atmos Oceanic Tech 14:512–526
Wade CG (1987) A quality control program for surface mesometeorological data. J Atmos Oceanic Technol 4:435–453
Yu Y, Zhu Y, Li S, Wan D (2014) Time series outlier detection based on sliding window prediction. Math Prob Eng. https://doi.org/10.1155/2014/879736
R Software Packages
Package: DescTools, Title: Tools for Descriptive Statistics, Version: 0.99.40. Date: 2021–02–06. Authors: A.Signorell et al
Package: NSM3, Functions and datasets to accompany Hollander, Wolfe, and Chicken—nonparametric statistical methods, Third Edition. Version: 1.16. Authors: G.Schneider, E.Chicken, R. Becvarik
Package: anytime, Title: Anything to 'POSIXct' or 'Date' Converter, Version: 0.3.9, Date: 2020–08–26. Author: D. Eddelbuettel
Package: DataExplorer, Title: Automate Data Exploration and Treatment, Version: 0.8.2. Author: B.Cui
Package: desctable, Title: Produce Descriptive and Comparative Tables Easily, Version: 0.1.9, Authors: M.Wack et al.
Package: dplyr, Title: A Grammar of Data Manipulation, Version: 1.0.4. Authors: H.Wickham
Package: explore, Title: Simplifies Exploratory Data Analysis, Version: 0.7.0, Author: Roland Krasser
Package: highfrequency, Title: Tools for Highfrequency Data Analysis, Authors: Version: 0.8.0.1, K. Boudt et al. 2021–01–11.
Package: imputeTS, Version: 3.0, Date: 2019–07–01, Title: Time Series Missing Value Imputation, Authors: S.Moritz et al.
Package: Lubridate, Title: Make Dealing with Dates a Little Easier, Version: 1.7.9.2. Authors: Vitalie Spinu et al. 2020–11–11.
Package: xts, Version: 0.11–2, Date: 2018–11–05, Title: eXtensible Time Series. Authors: J.A. Ryan et al.
Package: zoo, Version: 1.8–6, Date: 2019–05–27, Title: S3 Infrastructure for Regular and Irregular Time Series (Z's Ordered Observations. Authors: A. Zeileis et al.
R Core Team (2021). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/
Acknowledgements
The peer-review comments and recommendations, which were incorporated into a revised version of the paper, are very much appreciated. The work was funded by the Sustainable Systems Scientific Focus Area (SFA) program and the NGEE Tropics project at Lawrence Berkeley National Laboratory, which are supported by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research, Subsurface Biogeochemical Research Program, through contract No. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declared that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
477_2021_2106_MOESM1_ESM.docx
SI-1. Graphical Presentation and Tables of the Statistical Analysis
SI-2. Billy Barr and BCI Profiling Reports (https://drive.google.com/drive/folders/1cLo5GmVawrZ4shGODegPPtoIcqV7vPV3)
Faybishenko B; Versteeg R; Pastorello G; Dwivedi D; Varadharajan C; Agarwal D (2021): Quality Assurance and Quality Control (QA/QC) of Meteorological Time Series Data for Billy Barr, East River, Colorado USA. Watershed Function SFA. https://doi.org/10.15485/1823516
Supplementary file1 (DOCX 58414 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Faybishenko, B., Versteeg, R., Pastorello, G. et al. Challenging problems of quality assurance and quality control (QA/QC) of meteorological time series data. Stoch Environ Res Risk Assess 36, 1049–1062 (2022). https://doi.org/10.1007/s00477-021-02106-w
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-021-02106-w