Prediction of spatial functional random processes: comparing functional and spatio-temporal kriging approaches

Abstract

We present and compare functional and spatio-temporal (Sp.T.) kriging approaches to predict spatial functional random processes (which can also be viewed as Sp.T. random processes). Comparisons with respect to computational time and prediction performance via functional cross-validation is evaluated, mainly through a simulation study but also on a real data set. We restrict comparisons to Sp.T. kriging versus ordinary kriging for functional data (OKFD), since the more flexible functional kriging approaches pointwise functional kriging (PWFK) and the functional kriging total model coincide with OKFD in several situations. Here we formulate conditions under which we show that OKFD and PWFK coincide. From the simulation study, it is concluded that the prediction performance of the two kriging approaches in general is rather equal for stationary Sp.T. processes. However, functional kriging tends to perform better for small sample sizes, while Sp.T. kriging works better for large sizes. For non-stationary Sp.T. processes, with a common deterministic time trend and/or time varying variances and dependence structure, OKFD performs better than Sp.T. kriging irrespective of the sample size. For all simulated cases, the computational time for OKFD was considerably lower compared to those for the Sp.T. kriging methods.

1 Introduction

In many fields, such as environmental, forestry, climatology, meteorology and medical sciences, it may be of interest to predict a curve at a new spatial location given that such curves have been observed at n other locations, using the information inherent in the spatial dependence between curves. Kriging predictors have a long history of being used to predict objects at new locations based on information observed at a set of other locations, especially for objects that are real- or vector-valued, see e.g. Chilès and Delfiner (2012), Cressie (2015), Cressie and Wikle (2015), and references therein. A kriging predictor is a weighted sum of the objects observed at the n spatial locations, defined to be the best linear unbiased predictor (BLUP) minimizing the mean squared prediction error. Functional kriging predictors, used when the objects are random functions with infinite dimension, were initially discussed by Goulard and Voltz (1993), and further proposed by Giraldo et al. (2010, 2011) and Nerini et al. (2010). In these papers, the expected value of the random functions is assumed to be independent of the spatial location, the so called ordinary functional kriging. More recently, Caballero et al. (2013), Menafoglio et al. (2013), Ignaccolo et al. (2014), and Reyes et al. (2015) have investigated functional kriging methods where the expected value of the random functions may also depend on location.

Here, two kriging approaches to predict spatial functional random processes are compared. A functional random process is a process with stochastic functional objects (curves) $\chi _s=\chi _s(t), t\in T$ over the “time” domain $T\subset {\mathbf {R}}$ at each spatial location $s \in D\subset {\mathbf {R}}^d$. Given that the process has been observed at n different locations, a curve at a new location $s_0$ can be predicted by a functional kriging approach, i.e. as a linear combination of the n observed curves. A spatial functional process can also be viewed as a spatio-temporal (Sp.T.) random process $\{Z(s,t)=\chi _s(t), (s,t)\in D\times T\}$, and hence, a Sp.T. kriging approach could also be used, see e.g. Cressie and Wikle (2015) and Montero et al. (2015). The curve $\chi _{s_0}(t), t \in T$ would then be predicted at a dense grid of values over T, based on linear combinations of a time-grid of values over the observed curves. The question of which approach, functional or Sp.T. kriging, should be used to analyze a particular data set is an important one (with no optimal answer), as pointed out by Delicado et al. (2010). In this paper we compare the two approaches with respect to prediction performance and computational time, mainly by a simulation study but also using a real data set. Prediction performance is evaluated by functional cross-validation. Estimation of the kriging models is made without relying on distributional assumptions.

In Sect. 2 notation and definitions are given. Section 3 presents the functional and Sp.T. kriging approaches, including how to estimate the dependence structure. We also discuss how the functional kriging methods relate to each other, and under which circumstances they may coincide. In particular, we state conditions under which the two functional kriging methods ordinary kriging for functional data and pointwise functional kriging coincide, with proofs given in Appendix 1. A simulation study, comparing the two kriging approaches, is presented in Sect. 4, see also Appendix 2. In Sect. 5 both kriging approaches are applied to the Canadian temperature data, previously analyzed e.g. by Giraldo (2009), Giraldo et al. (2010) and Menafoglio et al. (2013). A discussion and concluding remarks are found in Sect. 6.

2 Preliminaries

A spatial functional random process$\{\chi _s: s\in D \subset {\mathbf {R}}^d\}$ , is a process where, for each given $s \in D$, the observed random element is a functional random variable, $\chi _s$, taking values in an infinite dimensional space, or function space (Giraldo et al. 2010; Delicado et al. 2010). We consider the case where $\chi _s$ for every fixed s is a real-valued function, $\chi _s(t), \; t \in T \subset {\mathbf {R}}$, from the compact set T to ${\mathbf {R}}$ and with $s\in D\subset {\mathbf {R}}^2$. It is usually assumed that the realizations of the curves (functions) $\chi _s(t), t \in T, s\in D$ belong to a separable Hilbert space ${\mathbf {H}}$ of square integrable functions defined on T. Our main focus is on second-order isotropic and stationary spatial functional random processes, that satisfy,

$$\begin{aligned}&\hbox {(i) }\quad E[\chi _s(t)]=m(t) \;{\text{and}}\; Var[\chi _s(t)]=\sigma ^2(t)\; \forall s\in D \;{\text{and}}\; \forall t\in T, \\&\hbox {(ii) }\quad Cov[\chi _{s}(r),\chi _{v}(t)] =C(\Vert s-v\Vert , r, t)\; \forall s, v\in D \;{\text{and}}\; \forall r, t \in T, \end{aligned}$$

(1)

where $\Vert \cdot \Vert$ denotes the (Euclidean) distance measure. A spatial functional random process can also be viewed as a Sp.T. process $Z(s,t)=\chi _s(t)$, where Z(s, t) takes values in ${\mathbf {R}}$, and is mapped from $(s,t) \in D \times T$, cf. Cressie and Wikle (2015). A Sp.T. process is said to be second-order stationary and spatially isotropic if

$$\begin{aligned}&\hbox {(i) } \quad E[Z(s,t)]=m \;{\text{and}}\; Var[Z(s,t)] =\sigma _Z^2\; \forall s\in D \;{\text{and}}\; \forall t\in T, \\&\hbox {(ii) }\quad Cov[Z(s,r),Z(v,t)]=C_Z(\Vert s-v\Vert , \mid r-t\mid )\; \forall s, v\in D \;{\text{and}}\; \forall r, t \in T. \end{aligned}$$

(2)

Note that the class of stationary Sp.T processes is a subset of the class of stationary functional random processes. Section 4.3 gives examples of stationary functional random processes where (1) holds but not (2).

3 Kriging prediction

In this section two kriging approaches to predict spatial functional random processes are described. Section 3.1 presents different functional kriging methods, and under which circumstances they coincide. Section 3.2 describes the Sp.T. kriging approach. In the presentation below, estimation of the kriging models do not rely on distributional assumptions.

3.1 Functional kriging

Unless otherwise stated, we will assume that the spatial functional random process is second-order stationary and isotropic. Within the functional kriging framework, it is of interest to predict the complete random function $\chi _{s_0}(t), t \in T$, at a new location $s_0$, given that a sample of random functions has been observed at n different locations, $s_1, \ldots , s_n$. A functional kriging predictor, ${\hat{\chi }}_{s_0}(t), \; t \in T$, is the best linear unbiased predictor (BLUP) minimizing the mean integrated squared error (MISE)

$$\begin{aligned} \text {MISE}(s_0)=E \left[\int _{T} ({\hat{\chi }}_{s_0}(t)- \chi _{s_0}(t))^2\,dt \right]. \end{aligned}$$

(3)

3.1.1 Ordinary kriging for functional data

Goulard and Voltz (1993) proposed one of the first functional kriging predictors,

$$\begin{aligned} {\hat{\chi }}_{s_0}(t)=\sum _{i=1}^n\lambda _i \chi _{s_i}(t), \; \; t\in T, \end{aligned}$$

(4)

which was further discussed by Giraldo et al. (2007, 2011) and there named ordinary kriging for functional data (OKFD). The optimal kriging weights, $\varvec{\lambda }=(\lambda _1,\ldots,\lambda _n)^{\intercal } \in {\mathbf {R}}^n$, that minimize (3) subject to the unbiasedness condition of the predictor, $\sum _{i=1}^n \lambda _i=1$, satisfy

$$\left( \begin{array}{cc} \Gamma _n & {{\mathbb{1}}_n} \\{\mathbb{1}}_n^{\intercal} &0\\ \end{array}\right)\left(\begin{array}{l} \varvec{\lambda } \\ -\tau \\ \end{array}\right)= \left(\begin{array}{l} {\mathbf {g}}_n \\ 1 \\\end{array}\right),$$

(5)

where $\tau$ is the Lagrange multiplier. Here $\Gamma _n=\{\gamma (h_{ij})\}_{i,j=1}^n$, ${\mathbf {g}}_n=\{\gamma (h_{0j})\}_{j=1}^n$, and $\mathbb {1}_n=(1, \ldots , 1)^{\intercal } \in {\mathbf {R}}^n$, where

$$\begin{aligned} \gamma (h_{ij})=\frac{1}{2}E\left [ \int _{T} (\chi _{s_i}(t)-\chi _{s_j}(t))^2\,dt\right ], \quad \forall\; s_i, s_j\in D, \end{aligned}$$

(6)

with $h_{ij}=\Vert s_i-s_j\Vert$, is called the (isotropic) trace-semivariogram. The trace-semivariogram often satisfies the properties of a classical semivariogram, being a conditional negative definite function (Menafoglio et al. 2013). The trace-semivariogram is in practice unknown and therefore needs to be estimated from the data. This is often done by first estimating the empirical trace-semivariogram for a set of h-values as

$$\begin{aligned} {\hat{\gamma }}(h)=\frac{1}{2\vert N(h)\vert } \sum _{i,j\in N(h)}\int _{T}(\chi _{s_i}(t)-\chi _{s_j}(t))^2\,dt, \end{aligned}$$

(7)

where $N(h)=\{ (s_i,s_j): \Vert s_i-s_j\Vert \in (h-\epsilon ,h+\epsilon )\},$ for some $\epsilon >0$. A parametric variogram model $\gamma (h\mid \theta )$, is then fitted to a set of estimated values $\{{\hat{\gamma }}(h_l),h_l \}$, $l=1,\ldots,L$, by a least squares method, cf. Cressie (2015). Here, the ordinary least squares (OLS) method is used to estimate $\theta$.

The random functions, $\chi _{s_i}(t)$, are typically observed only at a finite number of time points $t_{i1}, \ldots , t_{im_i},$$i=1, \ldots , n$. Goulard and Voltz (1993) suggested to fit a parametric model $\chi _{s_i}(\cdot \mid \alpha _i)$ to the observed values and replace $\chi _{s_i}(t)$ by $\chi _{s_i}(t\mid {\hat{\alpha }}_i)$ in (4) and (7). A non-parametric approach was suggested by Giraldo et al. (2011), where the observed random functions are represented by linear combinations of p known basis functions, $\mathbf{B}(t)=(B_1(t), \ldots , B_p(t))^{\intercal }$, as

$$\begin{aligned} {\tilde{\chi }}_{s_i}(t)=\sum _{k=1}^p a_{ik}B_k(t)=\mathbf{a}_i^{\intercal } \mathbf{B}(t). \end{aligned}$$

(8)

The basis functions could e.g. be B-splines, Fourier or Wavelets. The $\mathbf {a}_i$’s are typically determined by the least squares method, minimizing $\sum _{j=1}^{m_i}(\chi _{s_i}(t_{ij})-\mathbf{a}_i^{\intercal } \mathbf{B}(t_{ij}))^2$. In the final ordinary kriging predictor (4), the estimated trace-semivariogram values are plugged into the kriging weights ($\lambda _i$’s), with ${\tilde{\chi }}_{s_i}(t)$’s replacing the $\chi _{s_i}(t)$’s.

3.1.2 Pointwise functional kriging

Giraldo et al. (2008, 2010) suggested the pointwise functional kriging predictor (PWFK),

$$\begin{aligned} {\hat{\chi }}_{s_0}(t)=\sum _{i=1}^n \lambda _i (t)\chi _{s_i}(t), \quad t \in T, \end{aligned}$$

which allows the $\lambda _i$’s to depend on t. In order to solve the infinite dimensional problem of finding the $\lambda _i(t)$-functions that minimizes (3) subject to the unbiasedness constraint of the predictor, $\sum _{i=1}^n \lambda _i(t)=1$, for all $t \in T$, Giraldo et al. (2008, 2010) represented the $\lambda _i(t)$-functions by a linear combination of K known basis functions,

$$\begin{aligned} \lambda _{i}(t)=\sum _{k=1}^Kb_{ik}B_{\lambda k}(t)= {\mathbf {b}}_i^{\intercal } {\mathbf {B}}_{\lambda }(t), \quad i=1,\ldots,n, \end{aligned}$$

(9)

and the $\chi _{s_i}(t)$’s as in (8). The optimization problem was thus reduced to a multivariate geostatistics problem. The system of $K(n+1)$ equations to be solved in order to find the optimal ${\mathbf {b}}_i$’s is given by Giraldo et al. (2010) when ${\mathbf {B}}_{\lambda }(t)= {\mathbf {B}}(t)$, and for general ${\mathbf {B}}_{\lambda }(t)$ by (29) in Appendix 1, substituting $V[\chi _{s_i}(t)]$ and $Cov[\chi _{s_i}(t),\chi _{s_j}(t)]$ by ${\mathbf {B}}^{\intercal }(t)Var[ {\mathbf {a}}_i] {\mathbf {B}}(t)$ and ${\mathbf {B}}^{\intercal }(t)Cov[ {\mathbf {a}}_i, {\mathbf {a}}_j] {\mathbf {B}}(t)$, respectively. The optimal ${\mathbf {b}}_i$’s are functions of the covariances between the various ${\mathbf {a}}_i$’s, which in practice need to be estimated. Giraldo et al. (2010) suggest estimating these covariances via a linear model of coregionalization (Goulard and Voltz 1992). Note that the ${\mathbf {B}}_{\lambda }(t)$’s need to satisfy the unbiasedness condition

$$\begin{aligned} \sum _{i=1}^n \lambda _i(t)= {\mathbf {c}}^{\intercal } {\mathbf {B}}_{\lambda }(t)=1,\quad {\text{for}}\;{\text{all}}\; t \in T, \end{aligned}$$

(10)

where ${\mathbf {c}}=\sum _{i=1}^n {\mathbf {b}}_i$. B-splines and Fourier basis functions are two admissible choices, that satisfy (10) when ${\mathbf {c}}= {\mathbf {1}}$ and ${\mathbf {c}}=(1, 0, \ldots , 0)^{\intercal }$, respectively. In fact any set of basis functions where one (the first say) basis function is a constant, $B_{\lambda 1}(t)=k$, satisfies (10) for ${\mathbf {c}}=(1/k, 0, \ldots , 0)^{\intercal }$.

3.1.3 Situations when OKFD and PWFK coincide

Here we present situations where PWFK and OKFD coincide. Consider spatial functional random processes that satisfy

$$\begin{aligned}&\hbox {(i)}\quad E[\chi _s(t)]=m(t)\; \forall s\in D \;{\text{and}}\; \forall t\in T, \\&\hbox {(ii)}\quad Cov[\chi _{s}(t),\chi _{v}(t)]=w^2(t)C(s,v)\; \forall s, v\in D \;{\text{and}}\; \forall t \in T, \end{aligned}$$

(11)

where w(t) is a real-valued deterministic function. These type of processes include second-order (isotropic) stationary spatial functional random processes, but also e.g. when $\chi _s(t)$ can be expressed as $\chi _s(t)=m(t)+ w(t)Z(s,t)$, where Z(s, t) is a time stationary Sp.T. process with mean zero and $Cov[Z(s,r),Z(v,t)]=C(s,v,|r-t|)$. Note that for Sp.T. stationary processes $m(t)=m$ and $w^2(t)=1$. Let ${\varvec{\Sigma }}=\{C(s_i,s_j)\}_{i,j=1}^n \in {\mathbf {R}}^{n\times n}$, ${\varvec{\Sigma }}^{-1}=\{\alpha _{ij}\}_{i,j=1}^n$, and $\alpha _{\bullet \bullet }=\sum _{i=1}^n \sum _{j=1}^n \alpha _{ij}$. The following proposition states conditions under which the two functional kriging methods OKFD and PWFK coincide.

Proposition 3.1

Suppose that$\{\chi _s(t), t \in T, s\in D\}$ is a spatial functional random process satisfying (11). Further, assume that$\lambda _{i}(t)= {\mathbf {b}}_i^{\intercal } {\mathbf {B}}_{\lambda }(t),$that the${\mathbf {B}}_{\lambda }(t)$’s satisfy (10) for some constant vector${\mathbf {c}},$that the inverse of the matrix${\mathbf {W}}$exists, where

$$\begin{aligned} {\mathbf {W}}=\int _{T}w^2(t) {\mathbf {B}}_{\lambda }(t) {\mathbf {B}}_{\lambda }^{\intercal }(t)\,dt, \end{aligned}$$

and that${\varvec{\Sigma }}^{-1}$exists with$\alpha _{\bullet \bullet }$being non-zero. Then the optimal kriging weights of PWFK that minimize (3) are unique and satisfy$\lambda _i(t)=\lambda _i,$with${\mathbf {b}}_{i}=\lambda _i {\mathbf {c}},$for all$i=1, \ldots , n,$ and thus coincide with those of OKFD.

The existence of ${\mathbf {W}}^{-1}$ and ${\varvec{\Sigma }}^{-1}$, with $\alpha _{\bullet \bullet }\ne 0$, ensure the existence of a unique solution, see further details in the proof of the proposition given in Appendix 1. In line with Giraldo (2009) we concluded that the computational time for PWFK (using R-code kindly provided by Giraldo et al. (2010)) was substantially larger than for OKFD [using the R-package geofd, see Giraldo et al. (2012)]. We also noted that the estimated PWFK kriging weights always became constant when ${\mathbf {B}}_{\lambda }(t)= {\mathbf {B}}(t)$ were cubic B-splines or Fourier basis functions (after correction of a bug in the R-code).

3.1.4 Functional kriging total model

Giraldo (2009, 2014), and independently Nerini et al. (2010), proposed the functional kriging total model (FKTM),

$$\begin{aligned} {\hat{\chi }}_{s_0}(t)=\sum _{i=1}^n \int _{T}\lambda _i (t, v)\chi _{s_i}(v)dv,\quad t \in T. \end{aligned}$$

(12)

Assuming that the random functions $\chi _{s_i}(t)$ satisfy (8) and that the kriging weights satisfy

$$\begin{aligned} \lambda _{i}(t,v)&= \sum _{k=1}^p\sum _{l=1}^pc_{ik}^lB_{k}(t)B_{l}(v)\\&= {\mathbf {B}}(t)^{\intercal } {\mathbf {C}}_i {\mathbf {B}}(v), i=1,\ldots,n, \end{aligned}$$

Giraldo (2014) proposed a way to determine the $\lambda _i (t, v)$’s (i.e. the ${\mathbf {C}}_i$’s) such that the predictor (12) is unbiased and minimizes (3). Also here, the ${\mathbf {C}}_i$’s are functions of the covariances between the ${\mathbf {a}}_i$’s, which in practice need to be estimated, see Giraldo (2014) for more details.

The FKTM method is computationally heavy compared to OKFD, just like the PWFK method (Giraldo 2009). Moreover, Menafoglio and Petris (2016) showed that if the realizations of $\chi _s(t)$ belong to the Hilbert space of square integrable functions on T (in fact also for general separable Hilbert spaces), and the functional second-order stationary random process is Gaussian, then the kriging weights of FKTM and OKFD agree a.s. for any orthonormal base ${\mathbf {B}}(t)$.

3.2 Spatio-temporal kriging

Since a spatial functional process also can be viewed as a Sp.T. process, $Z(s,t)=\chi _{s}(t)$, taking values in $(s,t) \in D \times T$, it could also be predicted by Sp.T. kriging methods. Given the observed values ${\mathbf {Z}}=(Z(s_1,t_{11}), \ldots , Z(s_1,t_{1m_1}), \ldots , Z(s_n, t_{n1}), \ldots , Z(s_n, t_{nm_n}))^{\intercal } \in {\mathbf {R}}^N$, $N=\sum _{i=1}^n m_i$, the Sp.T. kriging predictor at location $s_0$ and time point $t \in T$,

$$\begin{aligned} {\hat{Z}}(s_0,t)= \sum _{i=1}^n\sum _{j=1}^{m_i}\lambda _{ij} ^tZ(s_i,t_{ij}), \end{aligned}$$

(13)

is defined to be the BLUP minimizing the mean squared prediction error (MSPE)

$$\begin{aligned} \text {MSPE}(s_0,t)=E[({\hat{Z}}(s_0,t)- Z(s_0,t))^2]. \end{aligned}$$

(14)

For Sp.T. processes with constant mean value, the unbiasedness condition implies that $\sum _{i=1}^n\sum _{j=1}^{m_i} \lambda _{ij}^t =1$. The optimal Sp.T. kriging weights $\varvec{\lambda }=(\lambda _{11}^t, \ldots , \lambda _{1m_1}, \ldots , \lambda _{n1}^t, \ldots , \lambda _{nm_n}^t)^{\intercal }$ for processes with unknown constant mean, satisfy the system of $(N+1)$ equations

$$\begin{aligned} \left(\begin{array}{cc} C_N & {\mathbb {1}_N} \\ \mathbb {1}_N^{\intercal } & 0\\ \end{array}\right) \left(\begin{array}{c} \varvec{\lambda } \\ \tau \\ \end{array}\right)= \left(\begin{array}{c} {\mathbf {k}}_N \\ 1 \\ \end{array}\right), \end{aligned}$$

(15)

where $\tau$ is the Lagrange multiplier used to take into account the unbiasedness restriction, $C_N=Var[ {\mathbf {Z}}] \in {\mathbf {R}}^{N \times N}$ is the variance-covariance matrix of ${\mathbf {Z}}$, and ${\mathbf {k}}_N=Cov[ {\mathbf {Z}},Z(s_0,t)] \in {\mathbf {R}}^{N}$. The predictor (13) is referred to as the Sp.T. ordinary kriging predictor, see e.g. Cressie and Wikle (2015). The dependence structure in practice needs to be estimated from the data and is then plugged into the kriging weights ($\lambda _{ij}^t$’s). For second-order stationary and spatially isotropic Sp.T. processes satisfying (2), we have that

$$\begin{aligned} Cov[Z(s,r),Z(v,t)]& = C_Z(\Vert s-v\Vert ,|r-t|) \\& = \sigma _Z^2-\gamma _Z (\Vert s-v\Vert ,|r-t|), \end{aligned}$$

(16)

where $\sigma _Z^2=Var[Z(\cdot ,\cdot )]$ and

$$\begin{aligned}\gamma _Z (\Vert s-v\Vert ,|r-t|) =E[(Z(s,r)-Z(v,t))^2]/2, \quad s, v \in D \text { and } r, t \in T, \end{aligned}$$

is the (spatially isotropic) Sp.T. semivariogram. The dependence structure is typically estimated via the semivariogram as follows. First, an empirical (spatially isotropic) Sp.T. semivariogram is computed from lag classes as

$$\begin{aligned} {\hat{\gamma }}_Z(h,u)=\frac{1}{2\vert N(h,u)\vert }\sum _{(i, j,k,l)\in N(h,u)}(Z(s_i,t_{ik})-Z(s_j,t_{jl}))^2, \end{aligned}$$

where $N(h,u)=\{ (s_i,t_{ik}), (s_j,t_{jl}): \Vert s_i-s_j\Vert \in (h-\epsilon ,h+\epsilon ),$ and $\vert t_{ik}-t_{jl}\vert \in (u-\delta ,u+\delta )\},$ for some $\epsilon , \delta >0$, and $\vert N(h,u)\vert$ is the number of distinct elements in N(h, u). A parametric semivariogram model, ${\gamma }(h,u\vert \theta )$, is then fitted to a set of $\{{\hat{\gamma }}_Z(h_l,u_l), (h_l,u_l)\}, l=1, \ldots , L$ by a least squares method.

In this paper we consider three commonly used types of stationary Sp.T. semivariogram (covariogram) models: the separable model

$$\begin{aligned} C_Z(h,u)=C_s(h)C_t(u), \end{aligned}$$

(17)

modeling the Sp.T. covariance function by the product of a spatial and a temporal covariance function, the product-sum model,

$$\begin{aligned} C_Z(h,u)=kC_s(h)C_t(u)+C_s(h)+C_t(u), \end{aligned}$$

with $k>0$, and the metric Sp.T. covariance model

$$\begin{aligned} C_Z(h,u)=C_{joint}(\sqrt{h^2+(\kappa u)^2}). \end{aligned}$$

More generally, in Sp.T. kriging modeling, the process is often described as

$$\begin{aligned} Z(s,t)= \mu (s,t) + \epsilon (s,t), \end{aligned}$$

where $\mu (s,t)$ is a deterministic trend, and $\epsilon (s,t)$ is a mean zero Sp.T. random field, usually assumed stationary. The trend is typically modeled by

$$\begin{aligned} \mu (s,t)=\varvec{\beta }^{\intercal }\mathbf{x }(s,t), \end{aligned}$$

(18)

where $\mathbf{x }(s,t) \in {\mathbf {R}}^M$ is a set of M known covariates, often chosen to be polynomials of s and t, and $\varvec{\beta } \in {\mathbf {R}}^M$ is an unknown parameter to be determined. When the Sp.T. process has a deterministic (unknown) non-constant trend of the form (18), then the BLUP (13) that minimizes (14) is called the Sp.T. universal kriging predictor, and the kriging weights are functions of both the dependence structure and the covariates evaluated at the observed and predicted locations, see e.g. Cressie and Wikle (2015) Section 4.1.2, page 148. An iterative weighted least squares method may be used to estimate $\varvec{\beta }$ and the Sp.T. variogram parameter $\theta$. Firstly, $\varvec{\beta }$ can be estimated by the OLS method, minimizing

$$\begin{aligned} \sum _{i=1}^n \sum _{j=1}^{m_i} (Z(s_i,t_{ij})-\varvec{\beta }^{\intercal } {\mathbf {x}}(s_i,t_{ij}))^2. \end{aligned}$$

Based on the resulting regression residuals, the Sp.T. semivariogram is then estimated by fitting a parametric Sp.T. semivariogram model to the corresponding empirical Sp.T. semivariogram by a least squares method. The parameter $\varvec{\beta }$ is then re-estimated using a weighted least squares method, taking into account the estimated dependence structure of the residuals (Cressie 2015). The dependence structure (variogram) is again estimated based on the updated residuals, and the whole procedure iterated until convergence. Note that if the deterministic trend only depends on time, such that $\mu (s,t)=m(t)$, the functional kriging methods do not need to specify and estimate the trend, whereas the Sp.T. kriging methods need to.

4 A simulation study

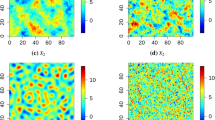
We now present a simulation study that aims to bring light over the relative merits of Sp.T. and functional kriging, with particular focus on Gaussian second-order stationary functional processes in ${\mathbf {R}}^2$. Since the functional kriging methods OKFD, PWFK, and FKTM often coincide for such processes (see Sects. 3.1.3 and 3.1.4) we restrict our comparisons to Sp.T. kriging versus OKFD. Inspired by the setups in Giraldo et al. (2012), Sun and Genton (2012) and Romano et al. (2015), we simulate data from Gaussian processes with three main types of covariance structures. The first two scenarios have stationary isotropic separable and non-separable covariance functions, respectively. The third scenario corresponds to second-order stationary functional (but non-stationary Sp.T.) processes with constant mean. For all three scenarios, several different cases are simulated, with varying strengths of spatial and temporal dependences, see Table 1. The different parameters in Table 1 control the Sp.T. correlation structure. Figure 1 illustrates examples of simulated data for six of the cases, all with constant means.

Table 1 The 24 different types (cases) of simulated Gaussian processes and their parameters: isotropic second-order stationary Sp.T. processes with separable (cases 1–9) and non-separable (cases 10–18) covariance functions, and second-order stationary functional (but non-stationary Sp.T.) processes (cases 19–24) with constant means

For each of the 24 cases, three different sample sizes were considered: small referring to $n=6\times 6$ spatial locations and $m=12$ time points, medium referring to $n=6\times 6$ spatial locations and $m=50$ time points, and large referring to $n=15\times 15$ spatial locations and $m=50$ time points. The number of time points were equally distributed on [0, 1] and the spatial locations were located on a regular grid in $[0,1]\times [0,1]$. Moreover, for cases 1–18, the presence of a deterministic time trend, $m(t)=9+3\sin (2\pi t)$, was also investigated.

For each case, sample size (and trend type), 100 replicates were simulated, using the R-packages RandomFields (Schlather et al. 2015) for cases 1–18 and fda (Ramsay et al. 2009) for cases 19–24. Estimation of the OKFD models was performed using the R-package geofd (Giraldo et al. 2012). The Sp.T. kriging models were estimated using the R-packages gstat (Pebesma 2004) and spacetime (Pebesma et al. 2012).

Functional cross-validation (FCV), suggested by Giraldo et al. (2010, 2011), was used to evaluate the prediction performance. In FCV, the data from each observed spatial location is removed, one at a time, and then predicted at all observed time points by the prediction method using the observed functional data at the remaining locations. The mean squared prediction error (MSPE) is computed as

$$\begin{aligned} \text {MSPE}=\frac{1}{n}\sum _{i=1}^n \sum _{j=1}^{m_i}(Z(s_i,t_{ij})-{\hat{Z}}^{-i}(s_i,t_{ij}))^2/m_i, \end{aligned}$$

(19)

where ${\hat{Z}}^{-i}(s_i,t_{ij})$ denotes the predicted value at location $(s_i,t_{ij})$ based on the functional data with the observations $Z(s_i,t_{ij})$, $j=1, \ldots , m_i$ excluded.

The three main scenarios are now presented in more detail, together with the simulated results.

Fig. 1

Examples of simulated data considering medium sample sizes without a deterministic time trend for: a case 3 ($\alpha =0.1$, $\beta =10$), b case 7 ($\alpha =2$, $\beta =0.1$), c case 10 ($\alpha =0.1$, $\beta =0.1$), d case 18 ($\alpha =2$, $\beta =10$), e case 21 ($\alpha =2$, $p=7$) and f case 22 ($\alpha =0.1$, $p=15$). The larger the value of $\alpha$ and $\beta$ the weaker the spatial and temporal correlation, respectively

4.1 Separable covariance function

Here we evaluate the prediction performance of OKFD and Sp.T kriging models, for the first nine cases in Table 1, which are Gaussian Sp.T processes with separable covariance functions. The spatial covariance function $C_s(h)$ in (17) was chosen to be the exponential covariance function with nugget effect,

$$\begin{aligned} C_s(h)= (1-\nu )\exp {(-\alpha h)}+\nu I\{h=0\}. \end{aligned}$$

The nugget effect $\nu$ was set to 0.04. For parameter $\alpha$, we considered the values 0.1, 0.5 and 2, corresponding to the effective ranges 30, 6 and 1.5 (very strong, medium and weak spatial correlation), respectively. The temporal covariance function $C_t(u)$ in (17) was chosen to be the stable covariance function

$$\begin{aligned} C_t(u)=\exp {(-(\beta u)^ \gamma )}. \end{aligned}$$

(20)

Here, $\gamma$ was fixed to 0.5, while the values for $\beta$ were 0.1, 1, and 10, corresponding to the effective ranges 90, 9 and 0.9 (very strong, medium and weak temporal correlation), respectively.

Given the generated data $Z(s_i,t_j), i=1, \ldots , n, j=1, \ldots , m$, the OKFD model was estimated using Fourier or cubic B-splines with different numbers of basis functions, see Table 10 in Appendix 2 for a detailed specification. For each number and type of basis function the spherical, exponential and stable semivariogram models were fitted to the empirical trace-semivariogram. For each case (1–9) a total of 36, 42 and 42 OKFD models (two types of basis functions $\times$ # different numbers of basis functions $\times$ #trace-semivariograms) were estimated and fitted to the data for small, medium and large sample sizes, respectively. These models were then evaluated by FCV (functional cross-validation) in terms of the MSPE (19), and the minimum MSPE over the models registered. The overall MSPE for each case and sample size was computed as the average minimum MSPEs over the 100 replicates.

Sp.T. ordinary kriging models were estimated for the data sets simulated without a deterministic time trend. First, the separable, product-sum and metric Sp.T. semivariogram models were fitted to the empirical Sp.T. semivariograms. For these three models, all pairwise combinations of the exponential, spherical and stable variograms were considered for the spatial (isotropic), temporal and joint variogram models. It resulted in 9 separable, 9 product-sum and 3 metric Sp.T. semivariogram models. All the Sp.T. ordinary kriging models were evaluated by FCV, the minimum MSPE registered over the different models within each of the three subgroup Sp.T. semivariogram models was obtained, and the overall MSPE was also computed for each case (1–9) and sample size. The Sp.T. models with a product-sum and a metric covariance function were not evaluated for large size samples, due to the large computational time.

The overall MSPEs for the OKFD and the Sp.T. ordinary kriging models for cases 1–9 considering medium sample sizes are presented in Table 2. Corresponding results for small and large sample sizes are reported in Appendix 2, Tables 6 and 7. The last column in Table 2 reports p values from paired two-sided t tests comparing the overall MSPEs between the OKFD and the Sp.T. separable models. The Sp.T. separable kriging models in general had lower overall MSPEs compared to the Sp.T. product-sum and metric models. This was expected, since the simulated data were generated from Sp.T. models with separable covariance functions. Interestingly, the overall MSPE was often (significantly) lower for OKFD compared to the Sp.T. separable models, for small and medium sample sizes (Tables 2, 6). For large sample sizes, the estimated Sp.T. (separable) models often performed better than OKFD (Table 7).

Studying the overall MSPEs in more detail reveals that the weaker the spatial correlation and the stronger the temporal correlation, the better the OKFD performs in relation to the Sp.T. separable model, regardless of the sample size. Case 3 for example, with strong spatial and weak temporal correlation, has significantly lower overall MSPE for the Sp.T. separable model compared to the OKFD model for medium and large sample sizes (Tables 2, 7). On the other hand, for case 7, with weak spatial and strong temporal correlation, the result is reversed.

Table 2 Prediction performance in terms of mean squared prediction errors (MSPEs) for the cases 1–9 (and 1*–9*) without (and with) a deterministic time trend considering medium sample sizes

The numbers in parentheses in Tables 2, 6, and 7, report the average computational time (for estimation and FCV) in seconds over all estimated models and replications when run on a 3.5 GHz Intel Core i7 processor with 32 GB ram memory. It reveals that prediction by and estimation of an OKFD model is substantially faster than the Sp.T. kriging models, regardless of the sample size. The Sp.T. separable models had lower computational time compared to the Sp.T. product-sum and metric models, due to simplifying (Kronecker product) structures of the variance covariance matrix.

Figure 2 presents how the type and number of basis functions used in the OKFD model affects prediction performance (minimum MSPE over the three trace-semivariogram models, averaged over the 100 realizations) for cases 3 and 7 considering medium sample sizes. The number of basis functions turns out to be an important factor for prediction performance, in general with smaller prediction error the more basis functions used. On the other hand, the type of basis functions, Fourier or cubic B-splines, is of less importance. These findings are consistent with all cases (1–9) and for all considered sample sizes.

Fig. 2

Prediction performance (minimum MSPE over the three trace-semivariogram models, averaged over the 100 realizations) for cases 3 and 7 considering medium sample sizes without a deterministic time trend when the estimated OKFD model is based on different numbers (p) of basis functions, being both Fourier and cubic B-spline. The solid black lines represent the corresponding overall MSPE of the Sp.T. separable model

In Fig. 3 box-plots of the differences in (minimum) MSPE between the two kriging approaches (MSPE(Sp.T)-MSPE(OKFD)) for the 100 replicates considering medium sample sizes are presented. From this, it becomes clear that OKFD produces more robust predictions. The Sp.T. separable kriging models produced much higher MSPEs than OKFD for many realizations, especially for small and medium sample sizes.

Fig. 3

Box-plots for cases 1–9 (considering medium sample sizes without a deterministic time trend) of the differences in (minimum) MSPE between the two kriging approaches (MSPE(Sp.T)-MSPE(OKFD)) for the 100 replicates

For the cases 1–9 with a common deterministic (sinusoidal) time trend, the same OKFD models as specified above were used again since these are designed to handle situations where a common deterministic time trend is present. However, predictions by Sp.T. kriging were now performed by universal Sp.T. kriging instead of Sp.T. ordinary kriging, using the same Sp.T. semivariogram models as for the ordinary Sp.T. kriging models. The deterministic time trend in the universal Sp.T. kriging model was specified to be the same as the one simulated from.

Table 2 summarizes the prediction performance of the two kriging approaches for cases 1–9 with deterministic time trend considering medium sample sizes, presented as cases 1*–9*. Corresponding results for small and large sample sizes are reported in Appendix 2, Tables 6 and 7. From these tables, we see that the presence and estimation of a deterministic time trend did not have a large effect on the prediction performance, and more or less gave the same conclusions with respect to the relative performance of the two kriging approaches, regardless of the sample size.

Table 3 Prediction performance in terms of mean squared prediction errors (MSPEs) for the cases 10–18 (and 10*–18*) without (and with) a deterministic time trend considering medium sample sizes

4.2 Non-separable covariance function

Cases 10–18 in Table 1 correspond to Gaussian Sp.T. processes with non-separable covariance functions of the form

$$\begin{aligned} Cov_{\text{ NSEP }}(h,u)& = (1-\nu )(2- C_t(u) )^{-\delta /2}\\&\exp {\left( -\frac{\alpha h}{\sqrt{2-C_t(u)}}\right) } + \nu I\{h=0\}, \end{aligned}$$

with parameters set to $\delta =2$, $\nu =0.04$, and $\alpha =0.1, 0.5$, and 2. The covariance function $C_t(u)$ was chosen to be the stable covariance function (20) with $\gamma =0.5$ and $\beta =0.1, 1$, and 10. The OKFD and the Sp.T. kriging models estimated in Sect. 4.1 were also fitted to the simulated data sets of cases 10–18. Prediction performance of the two kriging approaches was evaluated in the same way as described in Sect. 4.1 and is summarized in Table 3 for the non-separable cases 10–18 (and 10*–18*) for medium sample sizes without (and with) a deterministic time trend, respectively. Corresponding results for small and large sample sizes are reported in Appendix 2, Tables 8 and 9.

In general, we draw similar conclusions as in Sect. 4.1 for the separable cases 1–9 (and 1*–9*): the Sp.T. separable kriging models perform better than the Sp.T. product-sum and metric models; the weaker the spatial correlation and the stronger the temporal correlation, the better the OKFD performs in relation to the Sp.T. (separable) models; OKFD works better than the Sp.T. models for small to medium sample sizes whereas the Sp.T. separable kriging models perform better for large sample sizes; more basis functions in OKFD generally improve prediction performance; computational times are much lower for OKFD; the presence of a deterministic time trend does not change the conclusions.

A more detailed comparison of the overall MSPEs in Table 3, and Tables 8 and 9 reveals that prediction performance of OKFD in general improves in comparison to the Sp.T. separable kriging models for the simulated data sets with non-separable covariance functions (cases 10–18) compared to those simulated from separable covariance functions (cases 1–9). This result was to be expected, since none of the fitted (Sp.T.) kriging models coincide with the models that generated the data for cases 10–18.

4.3 Non-stationary cases

Generation of simulated data sets of second-order isotropic stationary functional, but non-stationary Sp.T. Gaussian processes with constant mean (cases 19–24 in Table 1) were based on the model

$$\begin{aligned} \chi _{s_i}(t)={\mathbf {a}}_i^{\intercal } {\mathbf {B}}(t) +\epsilon _{s_i}(t), \quad i=1,\ldots,n. \end{aligned}$$

(21)

The basis functions ${\mathbf {B}} (t) \in {\mathbf {R}} ^p$ with $p=7$, and 15 cubic B-splines, are defined on equally space knots on the interval [0, 1]. Moreover, ${\mathbf {a}}_i=(a_1(s_i), \ldots , a_p(s_i))^{\intercal }$, where $a_k(s), k=1, \ldots , p$, were chosen to be p independent identically distributed second-order stationary isotropic zero mean Gaussian processes in ${\mathbf {R}}^2$ with exponential covariance function $C(h)=\exp (-\alpha h)$ with $\alpha =0.1, 0.5$ and 2. Hence, the vectors $(a_k(s_1), \ldots , a_k(s_n))^{\intercal }$, $k=1, \ldots , p$, are p independent realizations of a multivariate Gaussian random variable $N_{n}(\mathbf 0 ,{\varvec{\Sigma }})$, where the $n\times n$ covariance matrix equals ${\varvec{\Sigma }}= \{\exp (-\alpha \Vert s_i-s_j\Vert )\}$. The $\epsilon _{s_i}(t)$’s are white noise measurement errors, independent and identically normally distributed with mean 0 and variance 0.04, i.e. $\epsilon _{s_i}(t)\sim N(0,0.04)$.

For each of the $2 \times 3=6$ cases (19–24) and for each such generated data set we fitted the same OKFD models as those fitted in Sect. 4.1. However, for medium and large sample sizes we extended the choices of number of basis functions (see Appendix 2 in Table 11 for a specification), yielding a total of 36, 90 and 90 different estimated OKFD models for small, medium and large sample sizes, respectively. For each case (19–24), sample size, and realization, predictions were made and evaluated by FCV for all models, and the minimum MSPE over the models registered. The overall MSPE for each case and sample size was finally computed as the average minimum MSPE over the 100 replicates. Furthermore, the same Sp.T. ordinary kriging models fitted to the data in Sect. 4.1, were also estimated for these data sets. Additionally, Sp.T. universal kriging models were fitted, with a deterministic time trend specified by a linear combination of the same basis functions that were used to generate the data set. Hence, a total of 18 separable, 18 product-sum and 6 metric Sp.T. kriging models were fitted to the data; predictions evaluated by FCV, the minimum MSPE registered over the models within the three groups of dependence structures, and the overall MSPE computed for each case (19–24) and sample size. As in Sects. 4.1 and 4.2, the Sp.T. models with a product-sum and a metric covariance function were not evaluated for large sample sizes due to large computational times.

Table 4 summarizes the prediction performance of the two kriging approaches for cases 19–24 and all three sample sizes. Note that these simulated data sets have time varying variances and covariances, which the Sp.T. kriging approach is not designed to capture, whereas the OKFD model can handle such situations. We would therefore expect OKFD to perform better than the Sp.T. kriging approach, which is indeed the case. In fact, OKFD has significantly lower overall MSPE for all cases and sample sizes in Table 4 except for cases 22–23 considering small sample sizes. For these two cases the Sp.T. separable kriging model works better. This is coupled to the low number of observations (12) per location for small sample sizes. When the functional representations of the data at each location is formed for the OKFD models, we can thus at most fit a linear combination of 12 basis functions, whereas, the data are generated by 15 B-splines. The functional representations may thus fail to capture the full temporal time dynamics. The Sp.T. universal kriging models on the other hand, do fit a common deterministic time trend using all 15 B-splines. From Table 4, it is also noted that Sp.T. kriging models with fitted metric variograms sometimes had better prediction performance than the Sp.T. separable kriging models, but still worse than the best OKFD models. Moreover, we again note that the computational time for OKFD is much lower than for the Sp.T. models.

Table 4 Prediction performance in terms of mean squared prediction errors (MSPEs) for the cases 19–24 over the different sample sizes

Figure 4 illustrates how the type and number of basis functions used in the fitted OKFD models affect the prediction performance for cases 21 and 22 considering medium sample sizes. Case 21 corresponds to simulated data generated by 7 B-splines with weak spatial dependence, whereas case 22 corresponds to simulated data generated by 15 B-splines with strong spatial dependence. In contrast to the simulated stationary Sp.T. models (cases 1–18) where prediction performance typically increases with the number of basis functions used in the fitted OKFD models, here we observe this phenomena only when Fourier basis functions are used in the fitted OKFD models. For B-splines, the best prediction performance is (naturally) achieved using the same number of B-splines in the OKFD fitted models as used to generate the simulated data set (7 for case 21 and 15 for case 22). In fact, using too many B-splines may give substantially poorer predictions, especially when the spatial dependence is weak, as for case 21, cf. Fig. 4. It can also be noted that the best OKFD model using B-splines has significantly smaller MSPE than the best OKFD model using Fourier basis functions. If the simulated data sets would have been generated by a set of Fourier basis functions instead, we would most likely see the opposite behavior, i.e. that the same Fourier basis functions in the fitted OKFD model as in the data generation model probably would give the best prediction performance, and do better than the OKFD models using B-splines.

For the Sp.T. separable kriging models, it turned out that it was advantageous to use universal kriging, especially for the cases with weak spatial dependence, whereas the prediction performance was about the same for cases with strong spatial dependence (Fig. 4). For the Sp.T. metric model, we observed the opposite behavior, i.e., for cases with weak spatial dependence it was more advantageous to use ordinary kriging instead of universal kriging.

Fig. 4

Prediction performance (minimum MSPE over the three trace-semivariogram models, averaged over the 100 realizations) for cases 21 and 22 considering medium sample sizes when the estimated OKFD model is based on different numbers (p) of basis functions, being both Fourier and cubic B-spline. The solid and dashed black lines represent the corresponding overall MSPE of the Sp.T. separable model with and without an estimated deterministic time trend, respectively. The solid and dashed green lines represent the corresponding overall MSPE of the Sp.T. metric model with and without an estimated deterministic time trend, respectively

We have used FCV to evaluate the prediction performance, where predicted values are compared with the observed values of the process, which include measurement errors. In order to investigate whether comparisons with the true values would change the conclusions, we also computed the MSPEs with respect to the true realizations for cases 19–24 using small sample sizes, see Table 12 in Appendix 2. The MSPEs for the different cases in Table 12 are approximately 0.04 less than the corresponding MSPEs based on the observed processes, presented in Table 4. The difference (0.04) corresponds to the variance of the white noise measurement errors. Furthermore, according to the p values in Tables 4 and 12, the results are consistent. Hence it illustrates that conclusions based on comparing predicted values with the observed values are consistent with those comparing with true values.

5 An application: temperature measurements in Canada

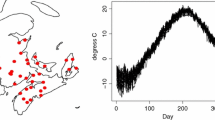
In this section we compare the prediction performance of the OKFD and the Sp.T. kriging models for a meteorological data set, available in the R-package geofd (Giraldo et al. 2012). The data consists of temperature measurements recorded at $n=36$ weather stations at Canada’s Atlantic coast in the Maritime Provinces (Fig. 5, top panel). At each station, the daily mean temperature averaged over the period 1960–1994 (February 29th combined with February 28th) has been recorded. The resulting functional data are displayed in Fig. 5 (bottom panel), connected by light grey lines. All the data except the measurements from Moncton are used to estimate the different models. This place is left as new location used to compare the predictions using the best OKFD and Sp.T. kriging models.

Fig. 5

Locations of the 36 weather stations in the Canadian Maritime provinces (top panel) where the average (over 30 years) daily temperature curves (bottom panel) were registered. The bottom panel also presents the estimated common time trend specified as linear combinations of the first 3 and 7 Fourier basis functions, respectively

Using the R-package geofd, the OKFD model was first estimated using 51, 101, 151, 201, 251, 301 and 351 Fourier basis functions. For each number of Fourier basis functions three semivariogram models (exponential, spherical and stable) were fitted to the empirical trace-semivariogram by the OLS method. Thus, in total we estimated $7 \times 3=21$ OKFD models. Predictions were then made and evaluated by FCV in terms of their MSPEs (19).

The best prediction performance was achieved using the stable trace-semivariogram (Fig. 6, left panel) for all considered numbers of Fourier basis. Figure 6 (right panel) clearly reveals that the prediction error (minimum MSPE over the three trace-semivariogram models) decreases with the number of basis functions used in the fitted OKFD models. Thus, the best performance was attained with 351 Fourier basis functions and its MSPE was 0.5738. The average computational time for an estimated OKFD model based on 51 and 351 Fourier basis functions was less than one and three seconds, respectively.

Fig. 6

Left panel: Empirical trace-semivariogram and the best fitted stable model for the Canadian temperature curves, represented by 351 Fourier basis functions. Right panel: Minimum MSPE over the three trace-semivariogram models for OKFD, based on different numbers of Fourier basis functions. The solid black line represents the MSPE of the best Sp.T. model

The data was further predicted using Sp.T. kriging. Since the data show a clear time trend, universal Sp.T. kriging was first applied. The deterministic time trend was modeled by a linear combination of the 3 (and 7) first Fourier basis functions, and estimated by the OLS method. The dependence structure of the resulting residuals was then estimated by fitting Sp.T. second-order stationary and isotropic semivariogram models to the empirical Sp.T. semivariogram of the residuals. The Sp.T. semivariogram models (separable, product-sum and metric) described in Sect. 3.2 were estimated, letting their corresponding spatial, temporal and joint semivariogram models be altered between the exponential, spherical and stable semivariogram models. This resulted in 9 separable, 9 product-sum and 3 metric Sp.T. semivariogram models. As a comparison we also predicted the original data by Sp.T. ordinary kriging, using the same Sp.T. semivariogram models as for the universal Sp.T. kriging models. Thus, in total we investigated $(9+9+3) \times 3= 63$ Sp.T. kriging models. All models were fitted to the data and predictions evaluated by FCV.

Table 5 presents the best (smallest MSPE) Sp.T. models, within each of the three groups of dependence structure (separable, product-sum and metric), with and without an estimated trend. The numbers in brackets report the corresponding average computational time in seconds over the estimated models. Many of the Sp.T. models have about the same prediction performance, with the exceptions of the Sp.T. metric models with estimated trend, which worked less well. The best Sp.T. models have approximately the same magnitude of MSPE as the best OKFD model (MSPE being 0.5738), but in terms of computational time, an OKFD model (taking 1–3 s to compute) was 100–10,000 times faster to compute compared to a Sp.T. kriging model.

Table 5 Prediction performance of different Sp.T. kriging models for the Canadian weather data

Figure 7 presents the observed daily temperatures at locations Bertrand (the location with the largest prediction error) and Moncton (new location), together with the corresponding predicted values using the best OKFD and Sp.T. kriging models. It emphasizes that there are very small differences between the best OKFD and Sp.T. models in terms of prediction performance.

Fig. 7

Predicted temperatures at locations Bertrand (top) and Moncton (bottom) obtained by the best OKFD model (solid grey line) and the best Sp.T. model (dashed black line) together with the observed (dotted) values

This data set has previously been analyzed by e.g. Giraldo (2009) with the objective to demonstrate and compare the functional kriging methods OKFD, PWFK and FKTM. Giraldo (2009) concluded that the three methods have similar FCV prediction performance when the first 65 Fourier basis functions are used in (8) to represent the $\chi _{s_i}(t)$’s. In Menafoglio et al. (2013) this data set was used to investigate the effect of using universal kriging for functional data (UKFD) instead of OKFD, also by representing the functional data with the first 65 Fourier basis functions. Geodesic distance instead of the Euclidean distance was used to take into account the approximately spherical shape of the Earth. They concluded that UKFD performed better in terms of FCV compared to OKFD. The FCV performance was there computed with respect to the fitted data, thus differing from ours, where raw data has been used.

6 Concluding remarks

In this paper we have presented and compared functional and Sp.T. kriging approaches to predict spatial functional random processes. Comparisons with respect to prediction performance and computational time have been performed, mainly through a simulation study but also using a real data set. We restricted the comparison to Sp.T. kriging versus the functional kriging method OKFD, since the more flexible functional kriging approaches PWFK and FKTM coincide with OKFD in several situations (Sects. 3.1.3 and 3.1.4). Here we also contribute with new knowledge by proving that the kriging weights of OKFD and PWFK coincide under certain conditions, e.g. for all stationary spatial functional random processes, but also for more general processes, cf. Sect. 3.1.3.

The purpose of this study has been to bring light on the relative merits of functional and Sp.T. kriging methods for prediction of spatial functional random processes. While functional kriging predicts complete curves on a given (time) domain, given observations on the same domain, the Sp.T. kriging methods make (a raster of) pointwise predictions of the curves and are not restricted to a given (time) domain. For non-stationary Sp.T. (but stationary functional) processes, e.g. under the presence of a common deterministic time trend and/or time varying variances and dependence structure, functional kriging does not demand any extra modeling, whereas identification and modeling of trend and/or time varying dependence is necessary for Sp.T. kriging. From a modeler perspective, the Sp.T. kriging methods demand more work with a larger risk of choosing a suboptimal model. It should also be pointed out that the functional approach has the possibility to consider other embeddings for the data, i.e. other geometries than L2. In fact, in some cases, the functional approach may completely outperform Sp.T. kriging just because it can account for other data features, such as differential properties in the data or data constraints.

Based on the simulation study and the analysis of the data set, we observed that the prediction performance of OKFD normally was improved when the number of basis functions used to represent the functional data increased. Furthermore, for all considered cases, OKFD was computationally considerably faster than the Sp.T. kriging models. The large matrices that need to be inverted in order to perform Sp.T. kriging prediction at each location, is the major reason for this fact. One way to reduce the computational time for the Sp.T. kriging models could be to use only the local neighborhood (e.g. the k closest neighboring locations) when prediction is made. This can often be done without much loss in prediction performance. Computational time might also be saved if estimation methods based on distributional assumptions are used, both for the functional and Sp.T. kriging methods.

Experience from this study concludes that with respect to prediction performance, OKFD typically performed similarly or better than the Sp.T. kriging models for small and medium sample sizes. This is likely due to the more complex task of finding good estimates of the Sp.T. variogram compared to the trace-variograms used in OKFD, since trace-variograms have one dimension less. The large number of choices of Sp.T. variogram models and parameters to estimate makes the Sp.T. estimation process more vulnerable, especially for small data sets. For larger sample sizes, the Sp.T. kriging starts to perform better for the stationary Sp.T. processes, whereas OKFD continues to work best for the non-stationary Sp.T. (but stationary functional) processes. We also noted a clear tendency for OKFD to perform better relative to Sp.T. kriging, the stronger the temporal- and the weaker the spatial dependence considered.

An interesting extension of this work would be to develop and compare both parametric (relying on distributional assumptions) and non-parametric functional and Sp.T. kriging methods that deals with non-stationary functional processes. In this study we have focused on non-parametric functional and Sp.T. kriging approaches for prediction of stationary spatial functional random processes. The results highlight that OKFD is a good candidate in most situations for prediction of stationary spatial functional random processes, not only for its prediction performance but also for its speed and ease to use.

Appendices

Appendix 1: Proofs

Below we present the proof of Proposition 3.1. However, as the proposition relies on Lemma 1.1 below, we start by stating and proving the lemma before presenting the proof of the proposition.

Lemma 1.1

Consider the following square matrix

(22)

where$\otimes$denotes kronecker product,

$$\begin{aligned} {\varvec{\Sigma }}=\left( \begin{array}{cccc} \sigma _{11}& \sigma _{12} & \cdots & \sigma _{1n}\\ \sigma _{21}& \sigma _{22} & \cdots & \sigma _{2n}\\ \vdots & \vdots & \ddots & \vdots \\ \sigma _{n1} & \sigma _{n2} & \cdots & \sigma _{nn} \end{array} \right) _{n\times n}, \end{aligned}$$

${\mathbf {W}}$is a square$k\times k$matrix,${\mathbf {I}}$is a$k\times k$identity matrix,${\mathbf {0}}$is a$k\times k$zero matrix, and the$\sigma _{ij}$’s are real values. If the inverses of${\varvec{\Sigma }}$and${\mathbf {W}}$exist, and the sum of the$n^2$elements of${\varvec{\Sigma }}^{-1}$is non-zero, then the inverse of${\mathbf {Q}}$exists and satisfies

$$\begin{aligned} {\mathbf {Q}}^{-1}=\left( \begin{array}{ccccc} k_{11} {\mathbf {W}}^{-1} & k_{12} {\mathbf {W}}^{-1} & \cdots & k_{1n} {\mathbf {W}}^{-1} & k_{1} {\mathbf {I}} \\ k_{21} {\mathbf {W}}^{-1} & k_{22} {\mathbf {W}}^{-1} & \cdots & k_{2n} {\mathbf {W}}^{-1} & k_{2} {\mathbf {I}} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ k_{n1} {\mathbf {W}}^{-1} & k_{n2} {\mathbf {W}}^{-1} & \cdots & k_{nn} {\mathbf {W}}^{-1} & k_{n} {\mathbf {I}} \\ l_{1} {\mathbf {I}}& l_{2} {\mathbf {I}}& \cdots & l_{n} {\mathbf {I}}& c {\mathbf {W}} \end{array} \right) _{k(n+1)\times k(n+1)}, \end{aligned}$$

(23)

where the$k_{ij}$’s, $k_i$’s,$l_i'$s and c are constants, such that$\sum _{i=1}^n k_{ij}(=\sum _{j=1}^n k_{ij})=0$for all j’s (and i’s),$\sum _{i=1}^n k_i=1$and$\sum _{i=1}^n l_i=1.$

Note that the $k_{ij}$’s, $k_i$’s and the $l_i$’s also change with n. However, for notational simplicity we suppress the dependence of n in the $k_{ij}$’s, $k_i$’s and the $l_i$’s.

Proof of Lemma 1.1

The proof is based on the following block matrix inversion formula

$$\begin{aligned} \left( \begin{array}{cc} {\mathbf {A}} & {\mathbf {B}} \\ {\mathbf {C}} & {\mathbf {D}} \end{array} \right) ^{-1}= \left( \begin{array}{cc} {\mathbf {A}}^{-1}+ {\mathbf {A}}^{-1} {\mathbf {B}} ( {\mathbf {D}}- {\mathbf {C}} {\mathbf {A}}^{-1} {\mathbf {B}})^{-1} {\mathbf {C}} {\mathbf {A}}^{-1}& - {\mathbf {A}}^{-1} {\mathbf {B}} ( {\mathbf {D}}- {\mathbf {C}} {\mathbf {A}}^{-1} {\mathbf {B}})^{-1}\\ -( {\mathbf {D}}- {\mathbf {C}} {\mathbf {A}}^{-1} {\mathbf {B}})^{-1} {\mathbf {C}} {\mathbf {A}}^{-1} & ( {\mathbf {D}}- {\mathbf {C}} {\mathbf {A}}^{-1} {\mathbf {B}})^{-1} \end{array} \right) , \end{aligned}$$

(24)

where ${\mathbf {A}}$ and ${\mathbf {D}}$ are square matrices allowed to be of different size. Let

the elements of ${\varvec{\Sigma }}^{-1}$ be denoted by

$$\begin{aligned} {\varvec{\Sigma }}^{-1}=\left( \begin{array}{cccc} \alpha _{11}& \alpha _{12} & \cdots & \alpha _{1n}\\ \alpha _{21}& \alpha _{22} & \cdots & \alpha _{2n}\\ \vdots & \vdots & \ddots & \vdots \\ \alpha _{n1} & \alpha _{n2} & \cdots & \alpha _{nn} \end{array} \right) _{n\times n}, \end{aligned}$$

and further let $\alpha _{\bullet j}=\sum _{i=1}^n \alpha _{ij}$, $\alpha _{i \bullet }=\sum _{j=1}^n \alpha _{ij}$ and $\alpha _{\bullet \bullet }=\sum _{i=1}^n \sum _{j=1}^n \alpha _{ij}$. Then, by (24), together with the fact that $({\varvec{\Sigma }} \otimes {\mathbf {W}})^{-1}={\varvec{\Sigma }}^{-1} \otimes {\mathbf {W}}^{-1}$, straightforward calculations confirm that

$$\begin{aligned} ( {\mathbf {D}}- {\mathbf {C}} {\mathbf {A}}^{-1} {\mathbf {B}})^{-1} = \frac{1}{\alpha _{\bullet \bullet }} {\mathbf {W}}, \end{aligned}$$

(25)

$$\begin{aligned} - {\mathbf {A}}^{-1} {\mathbf {B}} ( {\mathbf {D}}- {\mathbf {C}} {\mathbf {A}}^{-1} {\mathbf {B}})^{-1} = \left( \begin{array}{c} \frac{\alpha _{1 \bullet }}{\alpha _{\bullet \bullet }} {\mathbf {I}}\\ \vdots \\ \frac{\alpha _{n \bullet }}{\alpha _{\bullet \bullet }} {\mathbf {I}} \end{array} \right) , \end{aligned}$$

(26)

$$\begin{aligned} -( {\mathbf {D}}- {\mathbf {C}} {\mathbf {A}}^{-1} {\mathbf {B}})^{-1} {\mathbf {C}} {\mathbf {A}}^{-1} = \left( \begin{array}{ccc} \frac{\alpha _{\bullet 1}}{\alpha _{\bullet \bullet }} {\mathbf {I}}&\cdots& \frac{\alpha _{\bullet n}}{\alpha _{\bullet \bullet }} {\mathbf {I}} \end{array} \right) , \end{aligned}$$

(27)

and

$$\begin{aligned}& {\mathbf {A}}^{-1}+ {\mathbf {A}}^{-1} {\mathbf {B}} \left( {\mathbf {D}}- {\mathbf {C}} {\mathbf {A}}^{-1} {\mathbf {B}}\right)^{-1} {\mathbf {C}} {\mathbf {A}}^{-1} \\&\quad =\left( \begin{array}{cccc} \left(\alpha _{11}- \frac{\alpha _{\bullet 1} \alpha _{1 \bullet } }{\alpha _{\bullet \bullet }}\right) {\mathbf {W}}^{-1} & \left(\alpha _{12}- \frac{\alpha _{\bullet 2} \alpha _{1 \bullet } }{\alpha _{\bullet \bullet }}\right) {\mathbf {W}}^{-1}& \cdots & \left(\alpha _{1n}- \frac{\alpha _{\bullet n} \alpha _{1 \bullet } }{\alpha _{\bullet \bullet }}\right) {\mathbf {W}}^{-1}\\ \left(\alpha _{21}- \frac{\alpha _{\bullet 1} \alpha _{2 \bullet } }{\alpha _{\bullet \bullet }}\right) {\mathbf {W}}^{-1} & \left(\alpha _{22} - \frac{\alpha _{\bullet 2} \alpha _{2 \bullet } }{\alpha _{\bullet \bullet }}\right) {\mathbf {W}}^{-1}& \cdots & \left(\alpha _{2n}- \frac{\alpha _{\bullet n} \alpha _{2 \bullet } }{\alpha _{\bullet \bullet }}\right) {\mathbf {W}}^{-1}\\ \vdots & \vdots & \ddots & \vdots \\ \left(\alpha _{n1}- \frac{\alpha _{\bullet 1} \alpha _{n \bullet } }{\alpha _{\bullet \bullet }}\right) {\mathbf {W}}^{-1} & \left(\alpha _{n2}- \frac{\alpha _{\bullet 2} \alpha _{n \bullet } }{\alpha _{\bullet \bullet }}\right) {\mathbf {W}}^{-1} & \cdots & \left(\alpha _{nn}- \frac{\alpha _{\bullet n} \alpha _{n \bullet } }{\alpha _{\bullet \bullet }}\right) {\mathbf {W}}^{-1} \end{array} \right) . \end{aligned}$$

(28)

Combining (25)–(28), we have that ${\mathbf {Q}}^{-1}$ is of the same form as in (23) with $k_{ij}=\alpha _{ij}-\frac{\alpha _{\bullet j}\alpha _{i \bullet }}{\alpha _{\bullet \bullet }}$, $k_i=\frac{\alpha _{i \bullet }}{\alpha _{\bullet \bullet }}$ and $l_i=\frac{\alpha _{\bullet i}}{\alpha _{\bullet \bullet }}$. In addition, it is easy to verify that

$$\begin{aligned} \sum _{i=1}^n k_i& = \sum _{i=1}^n \frac{\alpha _{i \bullet }}{\alpha _{\bullet \bullet }} =1, \\ \sum _{i=1} k_{ij}& = \sum _{i=1} \left(\alpha _{ij}-\frac{\alpha _{\bullet j}\alpha _{i \bullet }}{\alpha _{\bullet \bullet }}\right)=\alpha _{\bullet j} - \frac{\alpha _{\bullet j}\alpha _{\bullet \bullet }}{\alpha _{\bullet \bullet }}=0, \end{aligned}$$

for all $j=1,\ldots,n$. Similarly it follows that $\sum _{i=1}^n l_i=1$ and $\sum _{j=1}^n k_{ij}=0$ for all $i=1,\ldots,n$, which completes the proof. $\square$

Proof of Proposition 3.1

Under the assumptions of Proposition 3.1 we here show that the coefficients of the functional kriging weights (9) of PWFK, which are obtained by minimizing (3) subject to the unbiasedness constraint of the predictor ($\sum _{i=1}^n \lambda _i(t)=1$, for all $t\in T$), yield weights that are constant over time, i.e., $\lambda _i(t)= {\mathbf {b}}_i^{\intercal } {\mathbf {B}}_{\lambda }(t)=\lambda _i$, $i=1,\ldots,n$. Giraldo et al. (2010) showed that the solution of the PWFK optimization problem is given by the solution to the system

$$\begin{aligned} {\mathbf {Q}} \varvec{\beta }= {\mathbf {J}} \implies \varvec{\beta }= {\mathbf {Q}}^{-1} {\mathbf {J}} \end{aligned}$$

(29)

where

$$\begin{aligned} {\mathbf {Q}} = \begin{pmatrix} {\mathbf {Q}}_1 &{} {\mathbf {Q}}_{12} &{} \cdots &{} {\mathbf {Q}}_{1n}&{}{\mathbf {I}} \\ {\mathbf {Q}}_{21} &{} {\mathbf {Q}}_{2} &{} \cdots &{} {\mathbf {Q}}_{2n}&{}{\mathbf {I}} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{}\vdots \\ {\mathbf {Q}}_{n1} &{} {\mathbf {Q}}_{n2} &{} \cdots &{} {\mathbf {Q}}_{n}&{}{\mathbf {I}} \\ {\mathbf {I}}&{}{\mathbf {I}}&{}\cdots &{}{\mathbf {I}}&{}{\mathbf {0}} \end{pmatrix}, \varvec{\beta }=\begin{pmatrix} {\mathbf {b}}_1 \\ {\mathbf {b}}_2\\ \vdots \\ {\mathbf {b}}_n\\ {\mathbf {m}} \end{pmatrix}, {\mathbf {J}}=\begin{pmatrix} \mathbf {J_1}\\ \mathbf {J_2}\\ \vdots \\ \mathbf {J_n}\\ {\mathbf {c}} \end{pmatrix},\\ \end{aligned}$$

$$\begin{aligned} {\mathbf {Q}}_i=\int _{T} {\mathbf {B}}_{\lambda }(t) Var[\mathbf {\chi }_{s_i}(t)] {\mathbf {B}}_{\lambda }^{\intercal }(t)\,dt, \end{aligned}$$

(30)

$$\begin{aligned} {\mathbf {Q}}_{ij}=\int _{T} {\mathbf {B}}_{\lambda }(t) Cov[\chi _{s_i}(t),\chi _{s_j}(t)] {\mathbf {B}}_{\lambda }^{\intercal }(t)\,dt, \end{aligned}$$

(31)

$$\begin{aligned} {\mathbf {J}}_i=\int _{T} {\mathbf {B}}_{\lambda }(t) Cov[\chi _{s_0}(t),\chi _{s_i}(t)] \,dt, \end{aligned}$$

(32)

for $i,j=1,\ldots,n$, ${\mathbf {m}}^{\intercal }=(m_1,\ldots,m_K)$ are the K Lagrangian multipliers and ${\mathbf {c}}$ is an unbiasedness constraint vector satisfying ${\mathbf {c}}^{\intercal } {\mathbf {B}}_{\lambda }(t)$=1.

From (11) we have that $Var[\mathbf {\chi }_{s_i}(t)]=w^2(t)\sigma _{ii}$ and $Cov[\chi _{s_i}(t),\chi _{s_j}(t)]=w^2(t)\sigma _{ij}$ for all $i,j=0,1, \ldots , n$. The expressions in (30) and (31) can thus be expressed as ${\mathbf {Q}}_i=\sigma _{ii} {\mathbf {W}}$ and ${\mathbf {Q}}_{ij}=\sigma _{ij} {\mathbf {W}}$ for $i,j=1,\ldots,n$, where ${\mathbf {W}}=\int _{T} w^2(t) {\mathbf {B}}_{\lambda }(t) {\mathbf {B}}_{\lambda }^{\intercal }(t)\,dt$, and hence, the matrix ${\mathbf {Q}}$ is of the form (22). By the assumptions in Proposition 3.1 and from Lemma 1.1 it follows that ${\mathbf {Q}}^{-1}$ is of the form (23). Computing the solution $\varvec{\beta }= {\mathbf {Q}}^{-1} {\mathbf {J}}$ yields that the ${\mathbf {b}}_i$’s are of the form

$$\begin{aligned} {\mathbf {b}}_i=\sum _{j=1}^n k_{ij} {\mathbf {W}}^{-1} {\mathbf {J}}_j+k_i {\mathbf {c}}, i=1,\ldots,n, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} {\mathbf {W}}( {\mathbf {b}}_i-k_i {\mathbf {c}})=\sum _{j=1}^n k_{ij} {\mathbf {J}}_j, i=1,\ldots,n. \end{aligned}$$

(33)

Thus, using (32) together with the expression for ${\mathbf {W}}$ we may express (33) as

$$\begin{aligned} \int _{T} w^2(t) {\mathbf {B}}_{\lambda }(t) {\mathbf {B}}_{\lambda }^{\intercal }(t) ( {\mathbf {b}}_i-k_i {\mathbf {c}})\,dt=\sum _{j=1}^n k_{ij} \sigma _{oj} \int _{T} w^2(t) {\mathbf {B}}_{\lambda }(t)\,dt \end{aligned}$$

or equivalently,

$$\begin{aligned} \int _{T} w^2(t) {\mathbf {B}}_{\lambda }(t) {\mathbf {B}}_{\lambda }^{\intercal }(t)\left ( {\mathbf {b}}_i-\left(k_i+\sum _{j=1}^n k_{ij}\sigma _{oj}\right) {\mathbf {c}}\right)\,dt= {\mathbf {0}}, i=1,\ldots,n. \end{aligned}$$

In the last expression we used the fact that ${\mathbf {B}}_{\lambda }^{\intercal }(t) {\mathbf {c}}$ equals 1 for all values of $t\in T$ (the unbiasedness constraint). It can now be seen that the above equation holds if ${\mathbf {b}}_i$ equals $(k_i+\sum _{j=1}^n k_{ij}\sigma _{0j}) {\mathbf {c}}$ and from the assumption of ${\mathbf {Q}}^{-1}$’s existence we also have that this solution is the only one. Thus, the weights satisfy

$$\begin{aligned} \lambda _i(t)= {\mathbf {b}}^{\intercal }_i {\mathbf {B}}_{\lambda }(t)= \left(k_i+\sum _{j=1}^n k_{ij}\sigma _{0j}\right) {\mathbf {c}}^{\intercal } {\mathbf {B}}_{\lambda }(t)=k_i+\sum _{j=1}^n k_{ij}\sigma _{0j}=\lambda _i, \end{aligned}$$

for all values of $t\in T$ and $i=1,\ldots,n$, and consequently, the PWFK predictor coincides with the OKFD predictor. $\square$

Appendix 2: Tables of the simulation study

Tables 6, 7, 8 and 9 contain information about the prediction performance in terms of mean squared prediction errors (MSPEs) for the cases 1–18 for small and large sample sizes with and without a deterministic trend, respectively. The smallest overall MSPE for each case is highlighted in bold. The numbers in parentheses represent the average computational time in seconds over the corresponding estimated models and replications. The last column shows p values from two-sided paired t tests comparing the overall MSPEs between the OKFD and the Sp.T. separable models.

Table 6 Simulated cases 1–9 (and 1*–9*) without (and with) a deterministic time trend considering small sample sizes

Table 7 Simulated cases 1–9 (and 1*–9*) without (and with) a deterministic time trend considering large sample sizes

Table 8 Simulated cases 10–18 (and 10*–18*) without (and with) a deterministic time trend considering small sample sizes

Table 9 Simulated cases 10–18 (and 10*–18*) without (and with) a deterministic time trend considering large sample sizes

Tables 10 and 11 contain information about the number of basis functions used in the OKFD models concerning the stationary (corresponding to isotropic Sp.T. processes with a separable and non-separable covariance function) and non-stationary cases and the three different sample sizes. The (p) cubic B-splines were constructed based on $p-4$ equally distributed interior knots on the interval [0, 1].

Table 10 Stationary

Table 11 Non-stationary

Table 12 Prediction performance in terms of mean squared prediction errors (MSPEs) for the cases 19–24 using small sample sizes