A unique value function for an optimal control problem of irrigation water intake from a reservoir harvesting flash floods

Abstract

Operation of reservoirs is a fundamental issue in water resource management. We herein investigate well-posedness of an optimal control problem for irrigation water intake from a reservoir in an irrigation scheme, the water dynamics of which is modeled with stochastic differential equations. A prototype irrigation scheme is being developed in an arid region to harvest flash floods as a source of water. The Hamilton–Jacobi–Bellman (HJB) equation governing the value function is analyzed in the framework of viscosity solutions. The uniqueness of the value function, which is a viscosity solution to the HJB equation, is demonstrated with a mathematical proof of a comparison theorem. It is also shown that there exists such a viscosity solution. Then, an approximate value function is obtained as a numerical solution to the HJB equation. The optimal control strategy derived from the approximate value function is summarized in terms of rule curves to be presented to the operator of the irrigation scheme.

1 Introduction

A stock-and-flow structure is a key concept in economics as well as in water resource management. Stocks of water in reservoirs, such as dams, aquifers, lakes, ponds, and tanks, regulate flows of water, which are intrinsically uneven and uncertain (Borgomeo et al. 2014; Zhang and Babovic 2011). Stochastic processes and control theories have been applied to water resource management problems in both the design and operation stages (Leroux and Martin 2016; Cui and Schreider 2009; Zhao et al. 2014; Pelak and Porporato 2016; Basinger et al. 2010). An extreme case is being studied in a harsh environment, where a small reservoir is constructed to collect ephemeral water flows from flash floods in order to fully irrigate perennial plants, as shown in Fig. 1 (Unami et al. 2015). The structure harvesting flash floods consists of a gutter cutting across a 16 m wide valley bottom and a conveyance channel of 60 m long to guide the water to the reservoir. The conveyance channel is equipped with a spillway to release excess backwater from the reservoir. Operation of the reservoir involves an optimal control problem considering the inherently stochastic occurrence of flash floods, while the operator can make decisions on the intake flow rate from the reservoir for irrigation. The entire irrigation scheme, which consists of a reservoir with flash flood harvesting facilities and a command area of plant cultivation, is so small that the decision maker has perfect information. The water dynamics in the irrigation scheme is modeled as a set of stochastic differential equations (SDEs) representing the water balance in the reservoir as well as the uncertain occurrence and intensity of flash floods and droughts. The performance index to be minimized is the expected deficiency of water in the future. In the present paper, we attempt to establish well-posedness for such an optimal control problem with mathematical rigor, which is lacking in earlier practical papers on relevant topics (Unami et al. 2013, 2015; Sharifi et al. 2016).

Fig. 1

Panoramic view of irrigation scheme with reservoir for harvesting flash floods

In the context of dynamics programming, the Hamilton–Jacobi–Bellman (HJB) equation governs the value function from which an optimal control strategy is derived for a time-continuous problem. The versatility of the HJB equation is evident as its industrial applications are so vast, covering the fields of population dynamics (Guo and Sun 2005), financial engineering (Junca 2012; Leach et al. 2007; Bo et al. 2013), aircraft flight mechanics (Almgren and Tourin 2015), climate risk assessment (Chaumont et al. 2006), and energy systems (Sieniutycz 2009, 2012, 2015). The notion of viscosity solutions is a powerful vehicle for approaching the HJB equation, which is nonlinear and degenerate in most cases, and comparison theorems are fundamental in discussing uniqueness and stability of solutions (Fleming and Soner 2006; Kawohl and Kutev 2007; Ishii 1987; Ishii and Lions 1990; Crandall and Lions 1983). Peron’s method is a standard means of constructing viscosity solutions (Crandall et al. 1992). However, the HJB equation derived from the optimal control problem considered herein encounters some difficulties. The comparison theorems known thus far are not applicable because of irregular conditions imposed when the reservoir is empty or full. Therefore, special auxiliary functions are sought to establish a comparison theorem, which guarantees the uniqueness of a continuous viscosity solution to the HJB equation with a relaxed Hamiltonian. Another theorem is also proven to show the existence of the viscosity solution as well as to justify a numerical approach, embedding a space of weak solutions into the space of viscosity solutions, in a manner analogous to a previous study dealing with one-dimensional stationary Hamilton–Jacobi equations of first order (Guermond and Popov 2008).

An approximate value function obtained as a numerical solution to the HJB equation yields the optimal control strategy in the real world. Concurrent use of the finite difference and finite element methods is a promising discretization technique for nonlinear and degenerate partial differential operators. The optimal control strategy is the maximizer of a characteristic function depending on the value function. Assuming that the control strategy derived from the approximate value function is optimal, it is summarized in terms of rule curves for reservoir operation (Senga 1991; Khan et al. 2012; Moghaddasi et al. 2013), and a simplified chart is presented to the operator for actual implementation. This is an innovative demonstration test in the prototype irrigation scheme based on a rigorous mathematical foundation.

As usual, the notations $C$, $C^{1}$, $C^{2}$, and $C^{\infty }$ shall be used for the sets of continuous and continuously differentiable functions.

2 Formulation of the optimal control problem

A stochastic model is developed for water dynamics in the irrigation scheme. Then, an optimal control problem is formulated with a performance index to be minimized, in order to deduce the optimal control strategy for irrigation water intake from the reservoir harvesting flash floods.

2.1 Stochastic model for water dynamics

The dynamics of the storage volume $X_{t}$ of the reservoir at time $t$ is governed by the water balance equation

$$ {\text{d}}X_{t} = \left( {Q_{\text{in}} - Q_{\text{out}} - u} \right){\text{d}}t $$

(1)

where $Q_{\text{in}}$ is the inflow rate of the harvested flash flood, which is equal to the runoff discharge of the flash flood after subtracting the rate of overflow from the spillway, $Q_{\text{out}}$ is the outflow rate due to evaporation and seepage, and $u$ is the intake flow rate as a control variable constrained in a set $U$ of admissible controls. A virtual variable $Y_{t}$ referred to as the water flow index is considered to model the dynamics of $Q_{\text{in}}$ and $Q_{\text{out}}$. The one-dimensional Langevin equation is assumed to govern $Y_{t}$ as

$$ {\text{d}}Y_{t} = - rY_{t} {\text{d}}t + \sqrt {2D} {\text{d}}B_{t} $$

(2)

where $r$ is a reversion coefficient, $D$ is a diffusion coefficient, and $B_{t}$ is the standard Brownian motion (Øksendal 2007). The advantages of using this virtual model (2) are capability in comprehensively representing the stochastic flow rate dynamics of flash floods as well as the occurrence of dry spells. A non-decreasing function $Q_{\text{in}} (y)$ is assumed to define the relationship between $Y_{t}$ and $Q_{\text{in}}$, while $X_{t}$ and $Y_{t}$ determine $Q_{\text{out}}$ with another function $Q_{\text{out}} (x,y)$. The storage volume $X_{t}$ of the reservoir is assumed to almost surely not exceed its capacity $V$, because of the well-functioning spillway. It is also trivial that $X_{t}$ cannot decrease when it is equal to 0. Consequently, the domain of $X_{t}$ is restricted to the closed interval $\left[ {0,V} \right]$, as is common in most reservoir operation problems. Consequently, (1) is rewritten as

$$ {\text{d}}X_{t} = a\left( {X_{t} ,Y_{t} ,u} \right){\text{d}}t $$

(3)

with

$$ a\left( {x,y,u} \right) = \left\{ {\begin{array}{*{20}l} {0 \wedge \left( {Q_{\text{in}} \left( y \right) - Q_{\text{out}} \left( {x,y} \right) - u} \right)} \hfill & {{\text{if}}\;x = V} \hfill \\ {Q_{\text{in}} \left( y \right) - Q_{\text{out}} \left( {x,y} \right) - u} \hfill & {{\text{if}}\;0 < x < V} \hfill \\ {0 \vee \left( {Q_{\text{in}} \left( y \right) - Q_{\text{out}} \left( {x,y} \right) - u} \right)} \hfill & {{\text{if}}\;x = 0} \hfill \\ \end{array} } \right. $$

(4)

where $\wedge$ and $\vee$ represent the minimum and the maximum, respectively. A target flow rate $Q_{\text{trg}}$ of irrigation water as a function of the time $t$ is set within the maximum capacity of the intake facility, e.g., a pump. Depending on the feasibility of intake from the reservoir, the admissible set $U$ is prescribed as

$$ U = \left\{ {\begin{array}{*{20}l} {\left\{ {0,Q_{\text{trg}} } \right\}} \hfill & {{\text{if}}\;X_{t} > 0{\text{ or }}Q_{\text{trg}} \le Q_{\text{in}} - Q_{\text{out}} } \hfill \\ {\left\{ 0 \right\}} \hfill & {{\text{if}}\;X_{t} = 0{\text{ and }}Q_{\text{trg}} > Q_{\text{in}} - Q_{\text{out}} } \hfill \\ \end{array} } \right.. $$

(5)

2.2 Performance index and HJB equation

The current time $s$ is assumed to be in an irrigation period $\left[ {0,T} \right)$ ($T < \infty$). The performance index $J^{u} (s,x,y)$ at time $t = s$ with storage volume $X_{s} = x$ and water flow index $Y_{s} = y$ is defined as

$$ J^{u} \left( {s,x,y} \right) = {\text{E}}^{s,x,y} \left[ {\int_{s}^{T} {f\left( {t,u\left( {t,X_{t} ,Y_{t} } \right),Y_{t} } \right)} {\kern 1pt} {\text{d}}t + V - X_{T} } \right] $$

(6)

where $\text{E}^{s,x,y}$ represents the expectation with respect to the probability law of the stochastic processes starting at point $\left( {s,x,y} \right)$, and $f$ is a bounded non-negative penalty function evaluating the departure of the actual intake flow rate $u$ from the target $Q_{\text{trg}}$. The value $X_{T}$ at the end of the irrigation period is the bequest to be maximized. The choice of $u$ is optimized to attain the infimum of $J^{u} \left( {s,x,y} \right)$. It is assumed that $u$ is a Markov control, the choice of which at time $t$ depends only on the current values of $X_{t}$ and $Y_{t}$. The infimum $\Phi = \Phi \left( {s,x,y} \right)$ of $J^{u} \left( {s,x,y} \right)$ exists because $f \ge 0$ and $0 \le V - X_{T} \le V$, and is referred to as the value function. The control $u^{*}$ attaining $\Phi$ is referred to as the optimal control. Therefore,

$$ \Phi \left( {s,x,y} \right) = J^{{u^{*} }} \left( {s,x,y} \right) = {\text{E}}^{s,x,y} \left[ {\int_{s}^{T} {f\left( {t,u^{*} \left( {t,X_{t} ,Y_{t} } \right),Y} \right)} {\kern 1pt} {\text{d}}t + V - X_{T} } \right]. $$

(7)

As mentioned in Chapters IV and V of Fleming and Soner (2006) including the verification theorem, the HJB equation

$$ \frac{\partial \Phi }{\partial s} + a\left( {x,y,u^{*} } \right)\frac{\partial \Phi }{\partial x} - ry\frac{\partial \Phi }{\partial y} + D\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} + f\left( {s,u^{*} ,y} \right) = \mathop {\inf }\limits_{u \in U} \left\{ {\frac{\partial \Phi }{\partial s} + a\left( {x,y,u} \right)\frac{\partial \Phi }{\partial x} - ry\frac{\partial \Phi }{\partial y} + D\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} + f\left( {s,u,y} \right)} \right\} = 0 $$

(8)

governs the value function $\Phi$ and the optimal control $u^{*}$ for $\left( {s,x,y} \right)$ in the set $G = \left[ {0,T} \right) \times \left( {0,V} \right) \times {\mathbb{R}}$, with the terminal condition

$$ \Phi (T,x,y) = V - x. $$

(9)

No boundary condition is imposed in the $x$-direction, because of the special treatment specified in (4). That value function $\Phi$ should be understood as a viscosity solution to the HJB Eq. (8), which is degenerating. The optimal control $u^{*}$ at any point in $G$ is obtained as

$$ u^{*} = \mathop {\arg \hbox{max} }\limits_{u \in U} \psi (u) $$

(10)

where $\psi$ is the characteristic function defined by

$$ \psi (u) = \psi (u;t,x,y,\Phi ) = u\frac{\partial \Phi }{\partial x} - f(t,u,y). $$

(11)

Then, the HJB equation (8) is rewritten as

$$ \frac{\partial \Phi }{\partial s} + \Delta Q\frac{\partial \Phi }{\partial x} - ry\frac{\partial \Phi }{\partial y} + D\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} - \psi (u^{*} ) = 0 $$

(12)

where

$$ \Delta Q = \left\{ {\begin{array}{*{20}l} {u^{*} \wedge \left( {Q_{\text{in}} - Q_{\text{out}} } \right)} \hfill & {{\text{if}}\;x = V} \hfill \\ {\left( {Q_{\text{in}} - Q_{\text{out}} } \right)} \hfill & {{\text{if}}\;0 < x < V} \hfill \\ {u^{*} \vee \left( {Q_{\text{in}} - Q_{\text{out}} } \right)} \hfill & {{\text{if}}\;x = 0} \hfill \\ \end{array} } \right.. $$

(13)

A penalty function is chosen as

$$ f(t,u,y) = \left\{ {\begin{array}{*{20}l} {\gamma (y)} \hfill & {{\text{if}}\;u \ne Q_{\text{trg}} (t)} \hfill \\ 0 \hfill & {{\text{if}}\;u = Q_{\text{trg}} (t)} \hfill \\ \end{array} } \right. $$

(14)

where $\gamma$ is a positive bounded weight depending on the water flow index $y$, which is assumed here to be

$$ \gamma = \frac{{Q_{\text{trg}} }}{{1 + \exp \left( {y - K} \right)}} $$

(15)

where $K$ is a model parameter, which will be determined from physical data observed in the real world (Sect. 5). For a feasible operational flow rate $Q_{\text{p}}$ of the intake facility, the irrigation period $\left[ {0,T} \right)$ is divided into $N + 1$ non-irrigation hours $I_{2i} = \left[ {t_{2i} ,t_{2i + 1} } \right)$ and $N$ irrigating hours $I_{2i + 1} = \left[ {t_{2i + 1} ,t_{2i + 2} } \right)$, where $Q_{\text{trg}} = 0$ and $Q_{\text{trg}} = Q_{\text{p}}$, respectively, so that $\left[ {0,T} \right) = \left[ {t_{0} ,t_{2N + 1} } \right) = \mathop \cup \limits_{k = 0}^{2N} I_{k}$. This partition of the entire irrigation period into a sequence of time intervals reduces the original problem into a sequence of the HJB equations with Hamiltonians independent of time. Under the above-mentioned conditions, it is easy to verify the boundedness of $\Phi$:

Remark 1

For any $s \in \left[ {0,T} \right)$,

$$ 0 \le \Phi \le \left( {T - s} \right)\hbox{max} \left( {Q_{\text{p}} } \right) + V. $$

(16)

When $Q_{\text{trg}} = Q_{\text{p}}$, (10) and (11) are reduced to

$$ u^{*} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if }}Q_{\text{p}} \frac{\partial \Phi }{\partial x} < - \gamma } \hfill \\ {\forall u \in U} \hfill & {{\text{if}}\;Q_{\text{p}} \frac{\partial \Phi }{\partial x} = - \gamma } \hfill \\ {Q_{\text{p}} } \hfill & {{\text{if}}\;Q_{\text{p}} \frac{\partial \Phi }{\partial x} > - \gamma } \hfill \\ \end{array} } \right. $$

(17)

and

$$ \psi = Q_{\text{p}} \frac{\partial \Phi }{\partial x} \vee - \gamma . $$

(18)

Otherwise, these two equations are reduced to

$$ u^{*} = 0 $$

(19)

and

$$ \psi = - \gamma . $$

(20)

The optimal control $u^{*}$ may not be unique, as in (17). However, eliminating $u^{*}$ reduces the HJB Eq. (12) with (18) and (20) to obtain

$$ \left\{ {\begin{array}{*{20}l} {\frac{\partial \Phi }{\partial s} + \left( {0 \wedge \left( {Q_{\text{in}} - Q_{\text{out}} } \right)} \right)\frac{\partial \Phi }{\partial x} - ry\frac{\partial \Phi }{\partial y} + D\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} + \gamma = 0} \hfill & {{\text{if }}Q_{\text{p}} \frac{\partial \Phi }{\partial x} \le - \gamma } \hfill \\ {\frac{\partial \Phi }{\partial s} + \left( {0 \wedge \left( {Q_{\text{in}} - Q_{\text{out}} - Q_{\text{p}} } \right)} \right)\frac{\partial \Phi }{\partial x} - ry\frac{\partial \Phi }{\partial y} + D\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} = 0} \hfill & {{\text{if }}Q_{\text{p}} \frac{\partial \Phi }{\partial x} \ge - \gamma } \hfill \\ \end{array} } \right.\quad {\text{if }}x = V, $$

(21)

$$ \left\{ {\begin{array}{*{20}l} {\frac{\partial \Phi }{\partial s} + \left( {Q_{\text{in}} - Q_{\text{out}} } \right)\frac{\partial \Phi }{\partial x} - ry\frac{\partial \Phi }{\partial y} + D\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} + \gamma = 0} \hfill & {{\text{if }}Q_{\text{p}} \frac{\partial \Phi }{\partial x} \le - \gamma } \hfill \\ {\frac{\partial \Phi }{\partial s} + \left( {Q_{\text{in}} - Q_{\text{out}} - Q_{\text{p}} } \right)\frac{\partial \Phi }{\partial x} - ry\frac{\partial \Phi }{\partial y} + D\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} = 0} \hfill & {{\text{if }}Q_{\text{p}} \frac{\partial \Phi }{\partial x} \ge - \gamma } \hfill \\ \end{array} } \right.\quad {\text{if }}0 < x < V, $$

(22)

and

$$ \left\{ {\begin{array}{*{20}l} {\frac{\partial \Phi }{\partial s} + \left( {0 \vee \left( {Q_{\text{in}} - Q_{\text{out}} } \right)} \right)\frac{\partial \Phi }{\partial x} - ry\frac{\partial \Phi }{\partial y} + D\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} + \gamma = 0} \hfill & {{\text{if }}Q_{\text{p}} \frac{\partial \Phi }{\partial x} \le - \gamma } \hfill \\ {\frac{\partial \Phi }{\partial s} + \left( {0 \vee \left( {Q_{\text{in}} - Q_{\text{out}} - Q_{\text{p}} } \right)} \right)\frac{\partial \Phi }{\partial x} - ry\frac{\partial \Phi }{\partial y} + D\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} = 0} \hfill & {{\text{if }}Q_{\text{p}} \frac{\partial \Phi }{\partial x} \ge - \gamma } \hfill \\ \end{array} } \right.\quad {\text{if }}x = 0. $$

(23)

3 Uniqueness of viscosity solution to the HJB equation

For each non-negative integer $k \le 2N$, the temporal variable is inverted as

$$ \tau = t_{k + 1} - s \in \left( {0,t_{k + 1} - t_{k} } \right], $$

(24)

and the value function $\Phi = \Phi \left( {\tau ,x,y} \right)$ is defined on the set $G_{k} = \left( {0,t_{k + 1} - t_{k} } \right] \times \left[ {0,V} \right] \times {\mathbb{R}}$. Then, the HJB equations (21), (22), and (23) is further rewritten as

$$ \frac{\partial \Phi }{\partial \tau } + H\left( {\tau ,{\mathbf{x}},\Phi ,\nabla \Phi ,\nabla \otimes \nabla \Phi } \right) = 0 $$

(25)

where ${\mathbf{x}} = \left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right)$, and $H$ is the Hamiltonian defined as

$$ H\left( {\tau ,{\mathbf{x}},\psi ,{\mathbf{p}},M} \right) = H\left( {\tau ,{\mathbf{x}},{\mathbf{p}},M} \right) = \hat{H}\left( {\tau ,x,y,p_{x} } \right) + ryp_{y} - D\mu_{yy} $$

(26)

with

$$ \hat{H}\left( {\tau ,x,y,p_{x} } \right) = \left\{ {\begin{array}{*{20}l} { - \alpha \left( {x,y,0} \right)p_{x} - \gamma } \hfill & {{\text{if }}Q_{\text{p}} p_{x} + \gamma \le 0} \hfill \\ { - \alpha \left( {x,y,Q_{\text{p}} } \right)p_{x} } \hfill & {{\text{if }}Q_{\text{p}} p_{x} + \gamma \ge 0} \hfill \\ \end{array} } \right. $$

(27)

and

$$ \alpha \left( {x,y,Q} \right) = \left\{ {\begin{array}{*{20}l} {0 \wedge \left( {Q_{\text{in}} \left( y \right) - Q_{\text{out}} \left( {x,y} \right) - Q} \right)} \hfill & {{\text{if }}x = V} \hfill \\ {Q_{\text{in}} \left( y \right) - Q_{\text{out}} \left( {x,y} \right) - Q} \hfill & {{\text{if }}0 < x < V} \hfill \\ {0 \vee \left( {Q_{\text{in}} \left( y \right) - Q_{\text{out}} \left( {x,y} \right) - Q} \right)} \hfill & {{\text{if }}x = 0} \hfill \\ \end{array} } \right. $$

(28)

where ${\mathbf{p}} = \left( {\begin{array}{*{20}c} {p_{x} } \\ {p_{y} } \\ \end{array} } \right)$ and $M = \left( {\begin{array}{*{20}c} {\mu_{xx} } & {\mu_{xy} } \\ {\mu_{yx} } & {\mu_{yy} } \\ \end{array} } \right)$. However, the discontinuity appearing in (28) when $x = 0$ and $x = V$ hinders the comparison theorem, which holds if the function $\alpha \left( {x,y,Q} \right)$ is relaxed as

$$ \alpha_{\eta } \left( {x,y,Q} \right) = \left\{ {\begin{array}{*{20}l} {\frac{V - x}{\eta }\alpha \left( {V - \eta ,y,Q} \right) + \left( {1 - \frac{V - x}{\eta }} \right)\alpha \left( {V,y,Q} \right)} \hfill & {{\text{if }}x \ge V - \eta } \hfill \\ {\alpha \left( {x,y,Q} \right)} \hfill & {{\text{if }}x = \eta < x < V - \eta } \hfill \\ {\left( {1 - \frac{x}{\eta }} \right)\alpha \left( {0,y,Q} \right) + \frac{x}{\eta }\alpha \left( {\eta ,y,Q} \right)} \hfill & {{\text{if }}x \le \eta } \hfill \\ \end{array} } \right. $$

(29)

where $\eta$ is a small positive relaxation parameter, so that $\alpha_{\eta } \left( {x,y,Q} \right)$ uniformly approaches $\alpha \left( {x,y,Q} \right)$ as $\eta \to 0$. Henceforth, this $\alpha_{\eta } \left( {x,y,Q} \right)$ will be used in (27) instead of $\alpha \left( {x,y,Q} \right)$. The definitions of $a\left( {x,y,u} \right)$ and $\Delta Q$ will be accordingly revised as $a_{\eta } \left( {x,y,u} \right)$ and $\Delta Q_{\eta }$ in (4) and (13), respectively. The assertion of Remark 1 is still valid for the relaxed case.

Remark 2

$\hat{H}\left( {\tau ,x,y,p_{x} } \right)$ with the relaxed (29) is Lipschitz continuous in each $I_{k}$ with respect to $\tau$, $x$, and $y$.

Now, we move on to viscosity solution to the relaxed HJB equation. A real-valued function $\Phi$ defined on a set $E$ is called upper semi-continuous, if for any $\left( {\tau ,{\mathbf{x}}} \right) \in E \subset {\mathbb{R}}^{3}$ and any $\varepsilon > 0$ there exists $\delta$ such that $\Phi \left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) < \Phi \left( {\tau ,{\mathbf{x}}} \right) + \varepsilon$ for all $\left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) \in B_{\delta } \left( {\tau ,{\mathbf{x}}} \right) \cap E$, where $B_{\delta } \left( {\tau ,{\mathbf{x}}} \right)$ represents the $\delta$-neighborhood of $\left( {\tau ,{\mathbf{x}}} \right)$. Similarly, it is called lower semi-continuous in the case where the inequality is replaced by $\Phi \left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) > \Phi \left( {\tau ,{\mathbf{x}}} \right) - \varepsilon$. Let $USC\left( E \right)$ and $LSC\left( E \right)$ denote the sets of all upper and lower semi-continuous functions defined on $E$, respectively. The upper and lower semi-continuous envelopes $\Phi^{U}$ and $\Phi^{L}$ of a real-valued function $\Phi$ on $G_{k}$ are defined as

$$ \Phi^{U} \left( {\tau ,{\mathbf{x}}} \right) = \mathop {\lim \sup }\limits_{{\left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) \to \left( {\tau ,{\mathbf{x}}} \right)}} \Phi \left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) $$

(30)

and

$$ \Phi^{L} \left( {\tau ,{\mathbf{x}}} \right) = \mathop {\lim \inf }\limits_{{\left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) \to \left( {\tau ,{\mathbf{x}}} \right)}} \Phi \left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right), $$

(31)

respectively. Note that $\Phi^{L} \in USC\left( {\bar{G}_{k} } \right)$ and $\Phi^{L} \in LSC\left( {\bar{G}_{k} } \right)$. For $\Phi^{U} \in USC\left( {\bar{G}_{k} } \right)$, being a viscosity sub-solution to (25) implies that

$$ \frac{\partial w}{\partial \tau } + H\left( {\tau ,{\mathbf{x}},w,\nabla w,\nabla \otimes \nabla w} \right) \le 0\quad {\text{at}}\;\left( {\hat{\tau },{\hat{\mathbf{x}}}} \right) \in G_{k} $$

(32)

for any test function $w \in C^{2} \left( {G_{k} } \right)$, such that

$$ w \ge \Phi^{U} \quad {\text{in}}\;\bar{G}_{k} ,\quad w = \Phi^{U} \quad {\text{at}}\;\left( {\hat{\tau },{\hat{\mathbf{x}}}} \right). $$

(33)

For $\Phi^{L} \in LSC\left( {\bar{G}_{k} } \right)$, being a viscosity super-solution to (25) implies that

$$ \frac{\partial w}{\partial \tau } + H\left( {\tau ,{\mathbf{x}},w,\nabla w,\nabla \otimes \nabla w} \right) \ge 0\quad {\text{at}}\;\left( {\hat{\tau },{\hat{\mathbf{x}}}} \right) \in G_{k} $$

(34)

for any test function $w \in C^{2} \left( {G_{k} } \right)$, such that

$$ w \le \Phi^{L} \quad {\text{in}}\;\bar{G}_{k} ,\quad w = \Phi^{L} \quad {\text{at}}\;\left( {\hat{\tau },{\hat{\mathbf{x}}}} \right). $$

(35)

If $\Phi^{U}$ is a viscosity sub-solution and $\Phi^{L}$ is a viscosity super-solution, then $\Phi$ is called a viscosity solution.

We firstly discuss the continuity of viscosity solutions, which are value functions of the optimal control problem, at $\tau = 0$.

Theorem 1

Suppose that $\Phi_{v}$ is a bounded viscosity solution to (25) with (29) and that $\Phi_{v}^{U} \left( {0,{\mathbf{x}}} \right) = \Phi_{v}^{L} \left( {0,{\mathbf{x}}} \right)$ for ${\mathbf{x}} \in \left[ {0,V} \right] \times {\mathbb{R}}$. If $\Phi_{v} \left( {0,{\mathbf{x}}} \right) = \Phi_{v}^{U} \left( {0,{\mathbf{x}}} \right) = \Phi_{v}^{L} \left( {0,{\mathbf{x}}} \right)$ as a function of ${\mathbf{x}}$ is continuous in $\left[ {0,V} \right] \times {\mathbb{R}}$, then

$$ \mathop {\lim }\limits_{{\left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) \to \left( {0,{\mathbf{x}}} \right)}} \left| {\Phi_{v} \left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) - \Phi_{v} \left( {0,{\mathbf{x}}} \right)} \right| = 0. $$

(36)

Proof

For $\tau^{\prime} \in \left[ {0,t_{k + 1} - t_{k} } \right]$ and ${\mathbf{x^{\prime}}} \in \left[ {0,V} \right] \times {\mathbb{R}}$, it holds that

$$ \Phi_{v} \left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) \le {\text{E}}^{{t_{k + 1} - \tau^{\prime},{\mathbf{x^{\prime}}}}} \left[ {\int_{{t_{k + 1} - \tau^{\prime}}}^{{t_{k + 1} }} {f\left( {t,u,Y^{\prime}_{t} } \right)} {\kern 1pt} {\text{d}}t + \Phi_{v} \left( {0,{\mathbf{X^{\prime}}}\left( {0,u} \right)} \right)} \right] $$

(37)

with

$$ {\mathbf{X^{\prime}}}\left( {\tau ,u} \right) = \left( {\begin{array}{*{20}c} {X^{\prime}_{{t_{k + 1} - \tau }} } \\ {Y^{\prime}_{{t_{k + 1} - \tau }} } \\ \end{array} } \right) = {\mathbf{x^{\prime}}} + \int_{{t_{k + 1} - \tau^{\prime}}}^{{t_{k + 1} - \tau }} {\left( {\begin{array}{*{20}c} {a_{\eta } \left( {X_{t} ,Y_{t} ,u} \right)} \\ { - rY_{t} } \\ \end{array} } \right)} {\kern 1pt} {\text{d}}t + \int_{{t_{k + 1} - \tau^{\prime}}}^{{t_{k + 1} - \tau }} {\left( {\begin{array}{*{20}c} 0 \\ {\sqrt {2D} } \\ \end{array} } \right)} {\kern 1pt} {\text{d}}B_{t} $$

(38)

for any admissible $u$, because $\Phi_{v}$ is a value function of the optimal control problem. For any $\varepsilon > 0$, there exists an admissible $\tilde{u}$ such that

$$ \Phi_{v} \left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) + \varepsilon > {\text{E}}^{{t_{k + 1} - \tau^{\prime},{\mathbf{x^{\prime}}}}} \left[ {\int_{{t_{k + 1} - \tau^{\prime}}}^{{t_{k + 1} }} {f\left( {t,\tilde{u},Y^{\prime}_{t} } \right)} {\kern 1pt} {\text{d}}t + \Phi_{v} \left( {0,{\mathbf{X^{\prime}}}\left( {0,\tilde{u}} \right)} \right)} \right]. $$

(39)

With the chosen penalty function (14), the first part of the expectation in the right hand side of (39) is evaluated as

$$ {\text{E}}^{{t_{k + 1} - \tau^{\prime},{\mathbf{x^{\prime}}}}} \left[ {\int_{{t_{k + 1} - \tau^{\prime}}}^{{t_{k + 1} }} {f\left( {t,\tilde{u},Y^{\prime}_{t} } \right)} {\kern 1pt} {\text{d}}t} \right] \le Q_{\text{trg}} \tau^{\prime}, $$

(40)

and then subtracting $\Phi_{v} \left( {0,{\mathbf{x}}} \right)$ from the inequalities (37) and (39) leads to

$$ \begin{aligned} \left| {\Phi_{v} \left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) - \Phi_{v} \left( {0,{\mathbf{x}}} \right)} \right| & \le \left| {{\text{E}}^{{t_{k + 1} - \tau^{\prime},{\mathbf{x^{\prime}}}}} \left[ {\int_{{t_{k + 1} - \tau^{\prime}}}^{{t_{k + 1} }} {f\left( {t,\tilde{u},Y^{\prime}_{t} } \right)} {\kern 1pt} {\text{d}}t +\, \Phi_{v} \left( {0,{\mathbf{X^{\prime}}}\left( {0,\tilde{u}} \right)} \right) - \Phi_{v} \left( {0,{\mathbf{x}}} \right)} \right]} \right| \\ & \le Q_{\text{trg}} \tau^{\prime} + \left| {{\text{E}}^{{t_{k + 1} - \tau^{\prime},{\mathbf{x^{\prime}}}}} \left[ {\Phi_{v} \left( {0,{\mathbf{X^{\prime}}}\left( {0,\tilde{u}} \right)} \right) - \Phi_{v} \left( {0,{\mathbf{x}}} \right)} \right]} \right| \\ & \le Q_{\text{trg}} \tau^{\prime} + {\text{E}}^{{t_{k + 1} - \tau^{\prime},{\mathbf{x^{\prime}}}}} \left[ {\left| {\Phi_{v} \left( {0,{\mathbf{X^{\prime}}}\left( {0,\tilde{u}} \right)} \right) - \Phi_{v} \left( {0,{\mathbf{x}}} \right)} \right|} \right] \\ \end{aligned} $$

(41)

for any ${\mathbf{x}} \in \left[ {0,V} \right] \times {\mathbb{R}}$. By the definition (38)

$$ \mathop {\lim }\limits_{{\left( {\tau^{\prime},{\mathbf{x^{\prime}}}} \right) \to \left( {0,{\mathbf{x}}} \right)}} \left| {\Phi_{v} \left( {0,{\mathbf{X^{\prime}}}\left( {0,\tilde{u}} \right)} \right) - \Phi_{v} \left( {0,{\mathbf{x}}} \right)} \right| = 0 $$

(42)

and therefore (36) holds. □

The following comparison theorem coupled with Theorem 1 proves the uniqueness of viscosity solutions of (25) with (29).

Theorem 2

Suppose that $\Phi_{1} \in USC\left( {\bar{G}_{k} } \right)$ is a bounded viscosity sub-solution to (25) with (29) and that $\Phi_{2} \in LSC\left( {\bar{G}_{k} } \right)$ is a bounded viscosity super-solution to (25) with (29). Then,

$$ \mathop {\sup }\limits_{{\left( {\tau ,{\mathbf{x}}} \right) \in \bar{G}_{k} }} \left( {\Phi_{1} \left( {\tau ,{\mathbf{x}}} \right) - \Phi_{2} \left( {\tau ,{\mathbf{x}}} \right)} \right) = \mathop {\sup }\limits_{{{\varvec{\upxi}} \in \left[ {0,V} \right] \times {\mathbb{R}}}} \left( {\Phi_{1} \left( {0,{\varvec{\upxi}}} \right) - \Phi_{2} \left( {0,{\varvec{\upxi}}} \right)} \right). $$

(43)

Proof

We opt for proof by contradiction in two stages. Firstly, an auxiliary function $\Psi$ is defined as

$$ \Psi \left( {\tau ,{\mathbf{x}},\sigma ,{\varvec{\upxi}}} \right) = \Phi_{1} \left( {\tau ,{\mathbf{x}}} \right) - \Phi_{2} \left( {\sigma ,{\varvec{\upxi}}} \right) - \frac{1}{2\delta }\left| {\tau - \sigma } \right|^{2} - \frac{1}{2\varepsilon }\left\| {{\mathbf{x}} - {\varvec{\upxi}}} \right\|^{2} - \varphi \left( \sigma \right) $$

(44)

where ${\varvec{\upxi}} = \left( {\begin{array}{*{20}c} \xi \\ \zeta \\ \end{array} } \right)$, and $\varphi \left( \tau \right) \in C^{\infty } \left( {\left[ {0,t_{k + 1} - t_{k} } \right]} \right)$ is a function satisfying $\varphi \left( \tau \right) \ge 0$ and $\varphi \left( \tau \right) = 0$ if $\tau = 0$. Two points $\left( {\bar{\tau },{\bar{\mathbf{x}}}} \right)$ and $\left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right)$ of $\bar{G}_{k}$ are assumed to maximize $\Psi$ as

$$ \Psi \left( {\bar{\tau },{\bar{\mathbf{x}}},\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) = \mathop {\sup }\limits_{{\left( {\tau ,{\mathbf{x}}} \right),\left( {\sigma ,{\varvec{\upxi}}} \right) \in \bar{G}_{k} }} \Psi \left( {\tau ,{\mathbf{x}},\sigma ,{\varvec{\upxi}}} \right). $$

(45)

Then, the inequality

$$ \begin{aligned} \Phi_{1} \left( {\bar{\tau },{\bar{\mathbf{x}}}} \right) - \Phi_{2} \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) - \frac{1}{2\delta }\left| {\bar{\tau } - \bar{\sigma }} \right|^{2} - \frac{1}{2\varepsilon }\left\| {{\bar{\mathbf{x}}} - {\bar{\mathbf{\xi }}}} \right\|^{2} = \Psi \left( {\bar{\tau },{\bar{\mathbf{x}}},\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) + \varphi \left( {\bar{\sigma }} \right) \hfill \\ \ge \Psi \left( {\bar{\sigma },{\bar{\mathbf{\xi }}},\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) = \Phi_{1} \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) - \Phi_{2} \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) \hfill \\ \end{aligned} $$

(46)

leads to evaluations

$$ \left| {\bar{\tau } - \bar{\sigma }} \right| \le \sqrt {K_{1} \delta } {\text{ and }}\left\| {{\bar{\mathbf{x}}} - {\bar{\mathbf{\xi }}}} \right\| \le \sqrt {K_{1} \varepsilon } $$

(47)

where $K_{1}$ is a non-negative constant given by

$$ K_{1} = 4\mathop {\hbox{max} }\limits_{{\left( {\tau ,{\mathbf{x}}} \right) \in \bar{G}_{k} }} \left( {\left| {\Phi_{1} \left( {\tau ,{\mathbf{x}}} \right)} \right|,\left| {\Phi_{2} \left( {\tau ,{\mathbf{x}}} \right)} \right|} \right) < + \infty . $$

(48)

Assume that $\bar{\tau } > 0$ and $\bar{\sigma } > 0$. We set a smooth function $v\left( {\tau ,{\mathbf{x}}} \right)$ as

$$ v\left( {\tau ,{\mathbf{x}}} \right) = \frac{1}{2\delta }\left| {\tau - \bar{\sigma }} \right|^{2} + \frac{1}{2\varepsilon }\left\| {{\mathbf{x}} - {\bar{\mathbf{\xi }}}} \right\|^{2} $$

(49)

which turns out to be a test function for a viscosity sub-solution because

$$ \Phi_{1} \left( {\tau ,{\mathbf{x}}} \right) - v\left( {\tau ,{\mathbf{x}}} \right) = \Psi \left( {\tau ,{\mathbf{x}},\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) + \Phi_{2} \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) + \varphi \left( {\bar{\sigma }} \right) $$

(50)

and therefore

$$ \left( {\bar{\tau },{\bar{\mathbf{x}}}} \right) \in \arg \mathop {\hbox{max} }\limits_{{\left( {\tau ,{\mathbf{x}}} \right) \in G_{k} }} \left\{ {\Phi_{1} \left( {\tau ,{\mathbf{x}}} \right) - v\left( {\tau ,{\mathbf{x}}} \right)} \right\}. $$

(51)

This implies that

$$ \frac{\partial v}{\partial \tau } + H\left( {\tau ,{\mathbf{x}},\nabla v,\nabla \otimes \nabla v} \right) = \frac{1}{\delta }\left( {\tau - \bar{\sigma }} \right) + H\left( {\tau ,{\mathbf{x}},\frac{1}{\varepsilon }\left( {{\mathbf{x}} - {\bar{\mathbf{\xi }}}} \right),\frac{1}{\varepsilon }I} \right) = \frac{1}{\delta }\left( {\tau - \bar{\sigma }} \right) + \hat{H}\left( {\tau ,{\mathbf{x}},\frac{1}{\varepsilon }\left( {{\mathbf{x}} - {\bar{\mathbf{\xi }}}} \right)} \right) + ry\left( {\frac{1}{\varepsilon }\left( {y - \bar{\zeta }} \right)} \right) - \frac{D}{\varepsilon } \le 0\quad {\text{at}}\;\left( {\bar{\tau },{\bar{\mathbf{x}}}} \right). $$

(52)

An eligible function $\varphi \left( \tau \right)$ is chosen here as

$$ \varphi \left( \tau \right) = \frac{1}{2}\beta \tau^{2} + \frac{2D}{\varepsilon }\tau $$

(53)

with $\beta > 0$, to set another smooth function $\hat{v}\left( {\tau ,{\mathbf{x}}} \right)$ as

$$ \hat{v}\left( {\sigma ,{\varvec{\upxi}}} \right) = - \left( {\frac{1}{2\delta }\left| {\bar{\tau } - \sigma } \right|^{2} + \frac{1}{2\varepsilon }\left\| {{\bar{\mathbf{x}}} - {\varvec{\upxi}}} \right\|^{2} + \varphi \left( \sigma \right)} \right) $$

(54)

which turns out to be a test function for a viscosity super-solution because

$$ \Phi_{2} \left( {\sigma ,{\varvec{\upxi}}} \right) - \hat{v}\left( {\sigma ,{\varvec{\upxi}}} \right) = - \Psi \left( {\bar{\tau },{\bar{\mathbf{x}}},\sigma ,{\varvec{\upxi}}} \right) + \Phi_{1} \left( {\bar{\tau },{\bar{\mathbf{x}}}} \right) $$

(55)

and therefore

$$ \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) \in \arg \mathop {\hbox{min} }\limits_{{\left( {\tau ,{\mathbf{x}}} \right) \in G_{k} }} \left\{ {\Phi_{2} \left( {\sigma ,{\varvec{\upxi}}} \right) - \hat{v}\left( {\sigma ,{\varvec{\upxi}}} \right)} \right\}. $$

(56)

This implies that

$$ \frac{{\partial \hat{v}}}{\partial \sigma } + H\left( {\sigma ,{\varvec{\upxi}},\nabla \hat{v},\nabla \otimes \nabla \hat{v}} \right) = - \beta \sigma - \frac{2D}{\varepsilon } + \frac{1}{\delta }\left( {\bar{\tau } - \sigma } \right) + H\left( {\sigma ,{\varvec{\upxi}},\frac{1}{\varepsilon }\left( {{\bar{\mathbf{x}}} - {\varvec{\upxi}}} \right), - \frac{1}{\varepsilon }I} \right) = - \beta \sigma - \frac{2D}{\varepsilon } + \frac{1}{\delta }\left( {\bar{\tau } - \sigma } \right) + \hat{H}\left( {\sigma ,{\varvec{\upxi}},\frac{1}{\varepsilon }\left( {{\bar{\mathbf{x}}} - {\varvec{\upxi}}} \right)} \right) + r\zeta \left( {\frac{1}{\varepsilon }\left( {\bar{y} - \zeta } \right)} \right) + \frac{D}{\varepsilon } \ge 0\quad {\text{at}}\;\left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right). $$

(57)

Comparing (52) and (57) yields

$$ \beta \bar{\sigma } + \frac{1}{\varepsilon }r\left( {\bar{y} - \bar{\zeta }} \right)^{2} \le \hat{H}\left( {\bar{\sigma },{\bar{\mathbf{\xi }}},\frac{1}{\varepsilon }\left( {{\bar{\mathbf{x}}} - {\bar{\mathbf{\xi }}}} \right)} \right) - \hat{H}\left( {\bar{\tau },{\bar{\mathbf{x}}},\frac{1}{\varepsilon }\left( {{\bar{\mathbf{x}}} - {\bar{\mathbf{\xi }}}} \right)} \right). $$

(58)

The left-hand side of (58) remains positive for any positive $\beta$, $\delta$, and $\varepsilon$, while its right-hand side approaches to zero as $\delta ,\varepsilon \to + 0$ because $\hat{H}$ is continuous, to yield a contradiction. Therefore, $\bar{\tau } = 0$ or $\bar{\sigma } = 0$ or both.

Now, we prove

$$ \mathop {\sup }\limits_{{\left( {\tau ,{\mathbf{x}}} \right) \in \bar{G}_{k} }} \left( {\Phi_{1} \left( {\tau ,{\mathbf{x}}} \right) - \Phi_{2} \left( {\tau ,{\mathbf{x}}} \right)} \right) \le \mathop {\sup }\limits_{{{\varvec{\upxi}} \in \left[ {0,V} \right] \times {\mathbb{R}}}} \left( {\Phi_{1} \left( {0,{\varvec{\upxi}}} \right) - \Phi_{2} \left( {0,{\varvec{\upxi}}} \right)} \right). $$

(59)

Assume that (59) is not true. Then, there exists a point $\left( {\tau_{M} ,{\mathbf{x}}_{M} } \right) \in G_{k}$ such that

$$ \Phi_{1} \left( {\tau_{M} ,{\mathbf{x}}_{M} } \right) - \Phi_{2} \left( {\tau_{M} ,{\mathbf{x}}_{M} } \right) = \mathop {\sup }\limits_{{\left( {\tau ,{\mathbf{x}}} \right) \in G_{k} }} \left( {\Phi_{1} \left( {\tau ,{\mathbf{x}}} \right) - \Phi_{2} \left( {\tau ,{\mathbf{x}}} \right)} \right) > \mathop {\sup }\limits_{{{\varvec{\upxi}} \in \left[ {0,V} \right] \times {\mathbb{R}}}} \left( {\Phi_{1} \left( {0,{\varvec{\upxi}}} \right) - \Phi_{2} \left( {0,{\varvec{\upxi}}} \right)} \right), $$

(60)

while one of the inequalities

$$ \left\{ {\begin{array}{*{20}c} {\Phi_{1} \left( {\bar{\tau },{\bar{\mathbf{x}}}} \right) - \Phi_{2} \left( {\bar{\tau },{\bar{\mathbf{x}}}} \right) \le \mathop {\sup }\limits_{{{\mathbf{x}} \in \left[ {0,V} \right] \times {\mathbb{R}}}} \left( {\Phi_{1} \left( {0,{\mathbf{x}}} \right) - \Phi_{2} \left( {0,{\mathbf{x}}} \right)} \right)} & {{\text{if }}\bar{\tau } = 0} \\ {\Phi_{1} \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) - \Phi_{2} \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) \le \mathop {\sup }\limits_{{{\varvec{\upxi}} \in \left[ {0,V} \right] \times {\mathbb{R}}}} \left( {\Phi_{1} \left( {0,{\varvec{\upxi}}} \right) - \Phi_{2} \left( {0,{\varvec{\upxi}}} \right)} \right)} & {{\text{if }}\bar{\sigma } = 0} \\ \end{array} } \right. $$

(61)

holds. By the evaluations (47), it is possible to choose $\varepsilon$ and $\delta$ such that $\left| {\bar{\tau } - \bar{\sigma }} \right| + \left\| {{\bar{\mathbf{x}}} - {\bar{\mathbf{\xi }}}} \right\| \le \rho$ for any $\rho > 0$. Then, considering the properties of upper and lower semi-continuous functions, $\rho$ is chosen so that

$$ \left\{ {\begin{array}{*{20}c} {\Phi_{2} \left( {\bar{\tau },{\bar{\mathbf{x}}}} \right) - \Phi_{2} \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) < \varepsilon_{0} } & {{\text{if }}\bar{\tau } = 0} \\ {\Phi_{1} \left( {\bar{\tau },{\bar{\mathbf{x}}}} \right) - \Phi_{1} \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) < \varepsilon_{0} } & {{\text{if }}\bar{\sigma } = 0} \\ \end{array} } \right. $$

(62)

for any $\varepsilon_{0} > 0$. Adding (62) to (61) results in

$$ \Phi_{1} \left( {\bar{\tau },{\bar{\mathbf{x}}}} \right) - \Phi_{2} \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) \le \mathop {\sup }\limits_{{{\varvec{\upxi}} \in \left[ {0,V} \right] \times {\mathbb{R}}}} \left( {\Phi_{1} \left( {0,{\varvec{\upxi}}} \right) - \Phi_{2} \left( {0,{\varvec{\upxi}}} \right)} \right) + \varepsilon_{0} $$

(63)

to obtain

$$ \begin{aligned} \Psi \left( {\bar{\tau },{\bar{\mathbf{x}}},\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) & = \Phi_{1} \left( {\bar{\tau },{\bar{\mathbf{x}}}} \right) - \Phi_{2} \left( {\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) - \frac{1}{2\delta }\left| {\bar{\tau } - \bar{\sigma }} \right|^{2} - \frac{1}{2\varepsilon }\left\| {{\bar{\mathbf{x}}} - {\bar{\mathbf{\xi }}}} \right\|^{2} - \varphi \left( {\bar{\sigma }} \right) \\ & \le \mathop {\sup }\limits_{{{\varvec{\upxi}} \in \left[ {0,V} \right] \times {\mathbb{R}}}} \left( {\Phi_{1} \left( {0,{\varvec{\upxi}}} \right) - \Phi_{2} \left( {0,{\varvec{\upxi}}} \right)} \right) + \varepsilon_{0} - \frac{1}{2\delta }\left| {\bar{\tau } - \bar{\sigma }} \right|^{2} - \frac{1}{2\varepsilon }\left\| {{\bar{\mathbf{x}}} - {\bar{\mathbf{\xi }}}} \right\|^{2} - \varphi \left( {\bar{\sigma }} \right) \\ & < \mathop {\sup }\limits_{{\left( {\tau ,{\mathbf{x}}} \right) \in G_{k} }} \left( {\Phi_{1} \left( {\tau ,{\mathbf{x}}} \right) - \Phi_{2} \left( {\tau ,{\mathbf{x}}} \right)} \right) + \varepsilon_{0} . \\ \end{aligned} $$

(64)

On the other hand,

$$ \begin{aligned} \Psi \left( {\tau_{M} ,{\mathbf{x}}_{M} ,\tau_{M} ,{\mathbf{x}}_{M} } \right) & = \Phi_{1} \left( {\tau_{M} ,{\mathbf{x}}_{M} } \right) - \Phi_{2} \left( {\tau_{M} ,{\mathbf{x}}_{M} } \right) - \varphi \left( {\tau_{M} } \right) \\ & = \mathop {\sup }\limits_{{\left( {\tau ,{\mathbf{x}}} \right) \in G_{k} }} \left( {\Phi_{1} \left( {\tau ,{\mathbf{x}}} \right) - \Phi_{2} \left( {\tau ,{\mathbf{x}}} \right)} \right) - \varphi \left( {\tau_{M} } \right). \\ \end{aligned} $$

(65)

Combining (64) and (65) results in

$$ \Psi \left( {\bar{\tau },{\bar{\mathbf{x}}},\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) < \mathop {\sup }\limits_{{\left( {\tau ,{\mathbf{x}}} \right) \in G_{k} }} \left( {\Phi_{1} \left( {\tau ,{\mathbf{x}}} \right) - \Phi_{2} \left( {\tau ,{\mathbf{x}}} \right)} \right) + \varepsilon_{0} = \Psi \left( {\tau_{M} ,{\mathbf{x}}_{M} ,\tau_{M} ,{\mathbf{x}}_{M} } \right) + \varphi \left( {\tau_{M} } \right) + \varepsilon_{0} . $$

(66)

Another choice of $\varphi \left( \tau \right)$ as

$$ \varphi \left( \tau \right) = \frac{1}{2}\beta \tau^{2} $$

(67)

with $\beta > 0$ is also eligible and leads to

$$ \Psi \left( {\bar{\tau },{\bar{\mathbf{x}}},\bar{\sigma },{\bar{\mathbf{\xi }}}} \right) < \Psi \left( {\tau_{M} ,{\mathbf{x}}_{M} ,\tau_{M} ,{\mathbf{x}}_{M} } \right) $$

(68)

as $\beta ,\varepsilon_{0} \to + 0$. However, (68) contradicts (45) and thus (59) is true. Consequently, we reach to (43). □

Remark 3

If there is a viscosity solution to (25) with (29) satisfying a specified continuous initial condition in the sense of Theorem 1, then its uniqueness and continuity are direct consequences of Theorem 2.

4 Existence of viscosity solution to the HJB equation

A weak solution to the HJB equation (25) with (29) from a specified initial condition is considered in order to show the existence of a viscosity solution as well as to provide a framework for approximate numerical solution.

Transformation of the independent variable $y$ to $z$ with $z = \tan^{ - 1} \left( {\sqrt {\frac{r}{2D}} y} \right)$ makes the domain bounded. Indeed, $G_{k}$ is mapped to $G_{k}^{*} = \left( {0,t_{k + 1} - t_{k} } \right] \times \bar{\Omega }_{x} \times \Omega_{z}$, where $\Omega_{x} = \left( {0,V} \right)$ and $\Omega_{z} = \left( { - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2},{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}} \right)$. Let $\Omega_{\tau }$ denote $\left( {0,t_{k + 1} - t_{k} } \right)$. Then, the HJB equation (25) is formally transformed into

$$ \frac{\partial \Phi }{\partial \tau } + \hat{H}\left( {\tau ,x,\sqrt {\frac{2D}{r}} \tan z,\frac{\partial \Phi }{\partial x}} \right) + r\sin z\cos z\left( {1 + \cos^{2} z} \right)\frac{\partial \Phi }{\partial z} - \frac{r}{2}\cos^{4} z\frac{{\partial^{2} \Phi }}{{\partial z^{2} }} = 0, $$

(69)

but $\Phi$ at each $\tau \in \left( {0,t_{k + 1} - t_{k} } \right]$ shall be sought in the function space $H_{xz}^{1}$, which is completed with the norm

$$ \left\| \Phi \right\|_{{H_{xz}^{1} }} = \int_{{\Omega_{z} }} {\left\| \Phi \right\|_{{H^{1} \left( {\Omega_{x} } \right)}} {\text{d}}z} + \int_{{\Omega_{x} }} {\left\| \Phi \right\|_{{H^{1} \left( {\Omega_{z} } \right)}} {\text{d}}x} $$

(70)

where

$$ \left\| \Phi \right\|_{{H^{1} \left( {\Omega_{*} } \right)}} = \sqrt {\int_{{\Omega_{*} }} {\left( {\Phi^{2} + \left| {\frac{\partial \Phi }{\partial *}} \right|^{2} } \right){\text{d*}}} } $$

(71)

for $* = x$ or $z$, to satisfy the weak form

$$ \frac{\text{d}}{{{\text{d}}\tau }}\int_{{\Omega_{x} }} {\hat{w}_{x} \int_{{\Omega_{z} }} {\hat{w}_{z} \Phi {\text{d}}z} {\text{d}}x} = - \int_{{\Omega_{x} }} {\hat{w}_{x} \int_{{\Omega_{z} }} {\left( {\left( {r\hat{w}_{z} \sin^{3} z\cos z + \frac{r}{2}\cos^{4} z\frac{{\partial \hat{w}_{z} }}{\partial z}} \right)\frac{\partial \Phi }{\partial z}{ + }\hat{w}_{z} \hat{H}\left( {\tau ,x,\sqrt {\frac{2D}{r}} \tan z,\frac{\partial \Phi }{\partial x}} \right)} \right){\text{d}}z} {\text{d}}x} $$

(72)

for any weights $\hat{w}_{x} \in H^{1} \left( {\Omega_{x} } \right)$ and $\hat{w}_{z} \in H^{1} \left( {\Omega_{z} } \right)$, where $H^{1} \left( {\Omega_{*} } \right)$ is the Sobolev space equipped with the norm (71). For $* = \tau$ or $x$ or $z$, it is known that there are embeddings $H^{1} \left( {\Omega_{*} } \right) \to C_{B} \left( {\Omega_{*} } \right)$ and $H^{1} \left( {\Omega_{*} } \right) \to C\left( {\bar{\Omega }_{*} } \right)$, where $C_{B} \left( {\Omega_{*} } \right)$ is the set of all bounded continuous functions on a domain $\Omega_{*}$, and $C\left( {\bar{\Omega }_{*} } \right)$ is the set of all bounded uniformly continuous functions on a domain $\Omega_{*}$. Both of $C_{B} \left( {\Omega_{*} } \right)$ and $C\left( {\bar{\Omega }_{*} } \right)$ are Banach spaces equipped with the uniform norm, and $C\left( {\bar{\Omega }_{*} } \right)$ is a closed subspace of $C_{B} \left( {\Omega_{*} } \right)$ (Adams and Fournier 2003). Let $C_{B} \left( {G_{k}^{*} } \right)$ denote the set of all bounded continuous functions on $G_{k}^{*}$, which is a Banach space equipped with the uniform norm $\left\| \Phi \right\|_{\infty } = \mathop {\sup }\limits_{{\left( {\tau ,x,z} \right) \in G_{k}^{*} }} \left| \Phi \right|$. Consider the function $g$ of $\hat{w}_{x}$, $\hat{w}_{z}$, and $\Phi_{(\kappa )}$ with time increment $\delta \tau$ as

$$ g\left( {\hat{w}_{x} ,\hat{w}_{z} ,\Phi_{(\kappa )} } \right) = \int_{{\Omega_{x} }} {\hat{w}_{x} \int_{{\Omega_{z} }} {\hat{w}_{z} \Phi_{(\kappa )} {\text{d}}z} {\text{d}}x} - \delta \tau \int_{{\Omega_{x} }} {\hat{w}_{x} \int_{{\Omega_{z} }} {F\left( {\hat{w}_{z} ,\Phi_{(\kappa )} } \right){\text{d}}z} {\text{d}}x} $$

(73)

where

$$ F\left( {\hat{w}_{z} ,\Phi } \right) = \left( {r\hat{w}_{z} \sin^{3} z\cos z + \frac{r}{2}\cos^{4} z\frac{{\partial \hat{w}_{z} }}{\partial z}} \right)\frac{\partial \Phi }{\partial z}{ + }\hat{w}_{z} \hat{H}\left( {\tau ,x,\sqrt {\frac{2D}{r}} \tan z,\frac{\partial \Phi }{\partial x}} \right). $$

(74)

For fixed $\hat{w}_{z}$ and $\Phi_{(\kappa )}$, $g$ is a continuous linear functional on $H^{1} \left( {\Omega_{x} } \right)$. For fixed $\hat{w}_{x}$ and $\Phi_{(\kappa )}$, $g$ is a continuous linear functional on $H^{1} \left( {\Omega_{z} } \right)$. Applying the Riesz representation theorem (Adams and Fournier 2003) twice, $g$ is identified with another function $\Phi_{(\kappa + 1)} \in H_{xz}^{1}$. Starting from an initial value $\Phi_{(0)}$, iterations $\left\{ {\Phi_{(\kappa )} } \right\}_{\kappa = 1,2,3 \ldots }$ with $\delta \tau = {\tau \mathord{\left/ {\vphantom {\tau {N_{\tau } }}} \right. \kern-0pt} {N_{\tau } }}$ and $N_{\tau } \ge 1$ yield the Riemann sum

$$ \int_{{\Omega_{x} }} {\hat{w}_{x} \int_{{\Omega_{z} }} {\hat{w}_{z} \Phi_{{(N_{\tau } )}} {\text{d}}z} {\text{d}}x} = \int_{{\Omega_{x} }} {\hat{w}_{x} \int_{{\Omega_{z} }} {\hat{w}_{z} \Phi_{(0)} {\text{d}}z} {\text{d}}x} - \tau \frac{1}{{N_{\tau } }}\sum\limits_{l = 0}^{{N_{\tau } - 1}} {\int_{{\Omega_{x} }} {\hat{w}_{x} \int_{{\Omega_{z} }} {F\left( {\hat{w}_{z} ,\Phi_{(l)} } \right){\text{d}}z} {\text{d}}x} } . $$

(75)

Equation (75) approaches

$$ \int_{{\Omega_{x} }} {\hat{w}_{x} \int_{{\Omega_{z} }} {\hat{w}_{z} \Phi {\text{d}}z} {\text{d}}x} = \int_{{\Omega_{x} }} {\hat{w}_{x} \int_{{\Omega_{z} }} {\hat{w}_{z} \Phi_{(0)} {\text{d}}z} {\text{d}}x} - \tau \int_{{\Omega_{x} }} {\hat{w}_{x} \int_{{\Omega_{z} }} {F\left( {\hat{w}_{z} ,\Phi } \right){\text{d}}z} {\text{d}}x} $$

(76)

as $N_{\tau }$ approaches $+ \infty$, which is consistent with (72).

Remark 4

There exists at least one solution $\Phi_{w} = \Phi_{w} \left( {\tau ,x,z} \right)$ to the initial value problem (72) with an initial value $\Phi_{(0)} \in H_{xz}^{1}$. Here, $\Phi_{w} \in H_{xz}^{1}$ for any $\tau \in \left( {0,t_{k + 1} - t_{k} } \right]$ and $\Phi_{w} \in C_{B} \left( {\Omega_{\tau } } \right)$ for any $\left( {x,z} \right) \in \bar{\Omega }_{x} \times \Omega_{z}$, implying that $\Phi_{w} \in C_{B} \left( {G_{k}^{*} } \right)$.

The following theorem asserts that the above-mentioned weak solution accords with the viscosity solution to (25).

Theorem 3

Suppose that $\Phi_{v} = \Phi_{v} \left( {\tau ,{\mathbf{x}}} \right) = \Phi_{v} \left( {\tau ,x,y} \right)$ is a bounded viscosity solution to (25) with (29) satisfying the initial condition $\Phi_{v} \left( {0,{\mathbf{x}}} \right) = \Phi_{v} \left( {0,x,y} \right) = \Phi_{\left( 0 \right)} \left( {x,\tan^{ - 1} \left( {\sqrt {\frac{r}{2D}y} } \right)} \right)$ for any $\left( {x,z} \right) \in \bar{\Omega }_{x} \times \Omega_{z}$ and that $\Phi_{w} = \Phi_{w} \left( {\tau ,x,z} \right)$ is a weak solution to (72) with (29) satisfying the same initial condition. Then,

$$ \Phi_{v} \left( {\tau ,x,y} \right) = \Phi_{w} \left( {\tau ,x,\tan^{ - 1} \left( {\sqrt {\frac{r}{2D}y} } \right)} \right) $$

(77)

in $G_{k}$.

Proof

Let $\Phi_{v}^{U}$ and $\Phi_{v}^{L}$ be the upper and lower semi-continuous envelopes of $\Phi_{v}$, respectively. Namely, $\Phi_{v}^{U}$ and $\Phi_{v}^{L}$ are the viscosity sub-solution and the viscosity super-solution, respectively. From Theorem 1,

$$ \Phi_{v}^{U} \left( {0,{\mathbf{x}}} \right) = \Phi_{v}^{L} \left( {0,{\mathbf{x}}} \right) = \Phi_{v} \left( {0,{\mathbf{x}}} \right) \in C_{B} \left( {\left[ {0,V} \right] \times {\mathbb{R}}} \right) $$

(78)

where $C_{B} \left( {\left[ {0,V} \right] \times {\mathbb{R}}} \right)$ is the set of all bounded continuous functions on $\left[ {0,V} \right] \times {\mathbb{R}}$. There exists a sequence $\left\{ {\Phi^{\left( n \right)} \left( {\tau ,x,z} \right)} \right\} \subset C^{1} \left( {G_{k}^{*} } \right) \cap C^{2} \left( {\Omega_{z} } \right)$ converging to $\Phi_{w}$. Namely, for any $\varepsilon > 0$, there exists a natural number $N_{1}$ such that

$$ \left\| {\Phi_{w} \left( {\tau ,x,z} \right) - \Phi^{\left( n \right)} \left( {\tau ,x,z} \right)} \right\|_{{H_{xz}^{1} }} < \varepsilon $$

(79)

for any $n > N_{1}$ at all $\tau \in \left( {0,t_{k + 1} - t_{k} } \right]$. Because of the embeddings $H^{1} \left( {\Omega_{x} } \right) \to C\left( {\bar{\Omega }_{x} } \right)$ and $H^{1} \left( {\Omega_{z} } \right) \to C_{B} \left( {\Omega_{z} } \right)$, there exists another natural number $N_{2}$, such that

$$ \left\| {\Phi_{w} \left( {\tau ,x,z} \right) - \Phi^{\left( n \right)} \left( {\tau ,x,z} \right)} \right\|_{\infty } < \varepsilon $$

(80)

for any $n > N_{2}$ at all $\tau \in \left( {0,t_{k + 1} - t_{k} } \right]$. Consequently, $\left\{ {\Phi^{\left( n \right)} \left( {\tau ,x,z} \right)} \right\}$ becomes a Cauchy sequence converging to a limit $\Phi_{c} \left( {\tau ,x,z} \right)$ in $C_{B} \left( {G_{k}^{*} } \right)$, and thus $\Phi_{w} \left( {\tau ,x,z} \right) = \Phi_{c} \left( {\tau ,x,z} \right)$ in $G_{k}^{*}$. Furthermore, for any $\delta > 0$, there exists a natural number $N_{3}$ such that

$$ \left| {\frac{{\partial \Phi^{\left( n \right)} }}{\partial \tau } + H\left( {\tau ,x,\sqrt {\frac{2D}{r}} \tan z,\Phi^{\left( n \right)} ,\nabla \Phi^{\left( n \right)} ,\nabla \otimes \nabla \Phi^{\left( n \right)} } \right)} \right| < \delta $$

(81)

for any $n > N_{3}$ in $G_{k}^{*}$. For each $n$, let $\delta_{i}^{\left( n \right)}$ ($i = 1,2$) be real numbers such that

$$ \delta_{1}^{\left( n \right)} = \inf \left\{ {\delta \ge 0\left| {\delta \sqrt \tau > \Phi_{v}^{U} \left( {\tau ,x,\sqrt {\frac{2D}{r}} \tan z} \right) - \Phi^{\left( n \right)} \left( {\tau ,x,z} \right)} \right.} \right\} $$

(82)

and

$$ \delta_{2}^{\left( n \right)} = \sup \left\{ {\delta \le 0\left| {\delta \sqrt \tau < \Phi_{v}^{L} \left( {\tau ,x,\sqrt {\frac{2D}{r}} \tan z} \right) - \Phi^{\left( n \right)} \left( {\tau ,x,z} \right)} \right.} \right\}. $$

(83)

Then, test functions $w_{i}^{\left( n \right)}$ are chosen as

$$ w_{i}^{\left( n \right)} = w_{i}^{\left( n \right)} \left( {\tau ,x,y} \right) = \Phi^{\left( n \right)} \left( {\tau ,x,\tan^{ - 1} \left( {\sqrt {\frac{r}{2D}y} } \right)} \right) + \delta_{i}^{\left( n \right)} \sqrt \tau $$

(84)

so that

$$ w_{1}^{\left( n \right)} \ge \Phi_{v}^{U} \quad {\text{in}}\;\bar{G}_{k} ,\quad w_{1}^{\left( n \right)} = \Phi_{v}^{U} \quad {\text{at}}\;\left( {\hat{\tau }_{1} ,{\hat{\mathbf{x}}}_{1} } \right) $$

(85)

and

$$ w_{2}^{\left( n \right)} \le \Phi_{v}^{L} \quad {\text{in}}\;\bar{G}_{k} ,\quad w_{2}^{\left( n \right)} = \Phi_{v}^{L} \quad {\text{at}}\;\left( {\hat{\tau }_{2} ,{\hat{\mathbf{x}}}_{2} } \right) $$

(86)

for some $\left( {\hat{\tau }_{i} ,{\hat{\mathbf{x}}}_{i} } \right) \in G_{k}$. This implies that $w_{i}^{\left( n \right)}$ are indeed eligible for test functions of viscosity sub-solution $\Phi_{v}^{U}$ and viscosity super-solution $\Phi_{v}^{L}$, resulting in

$$ \frac{{\partial w_{1}^{\left( n \right)} }}{\partial \tau } + H\left( {\hat{\tau }_{1} ,{\hat{\mathbf{x}}}_{1} ,w_{1}^{\left( n \right)} ,\nabla w_{1}^{\left( n \right)} ,\nabla \otimes \nabla w_{1}^{\left( n \right)} } \right) = \frac{{\partial \Phi^{(n)} }}{\partial \tau } + H\left( {\hat{\tau }_{1} ,{\hat{\mathbf{x}}}_{1} ,\Phi^{(n)} ,\nabla \Phi^{(n)} ,\nabla \otimes \nabla \Phi^{(n)} } \right) + \frac{{\delta_{1}^{\left( n \right)} }}{\sqrt \tau } \le 0 $$

(87)

and

$$ \frac{{\partial w_{2}^{\left( n \right)} }}{\partial \tau } + H\left( {\hat{\tau }_{2} ,{\hat{\mathbf{x}}}_{2} ,w_{2}^{\left( n \right)} ,\nabla w_{2}^{\left( n \right)} ,\nabla \otimes \nabla w_{2}^{\left( n \right)} } \right) = \frac{{\partial \Phi^{(n)} }}{\partial \tau } + H\left( {\hat{\tau }_{2} ,{\hat{\mathbf{x}}}_{2} ,\Phi^{(n)} ,\nabla \Phi^{(n)} ,\nabla \otimes \nabla \Phi^{(n)} } \right) + \frac{{\delta_{2}^{\left( n \right)} }}{\sqrt \tau } \ge 0 $$

(88)

at respective $\left( {\hat{\tau }_{i} ,{\hat{\mathbf{x}}}_{i} } \right)$. In order to satisfy (87) and (88), $\delta_{i}^{\left( n \right)}$ must approach zero as $n \to \infty$, because of (81). Finally, we obtain

$$ \Phi_{v}^{U} \left( {\tau ,x,y} \right) = \Phi_{v}^{L} \left( {\tau ,x,y} \right) = \Phi_{c} \left( {\tau ,x,\tan^{ - 1} \left( {\sqrt {\frac{r}{2D}} y} \right)} \right) $$

(89)

in $G_{k}$, and thus (77). □

5 Application with numerical demonstration

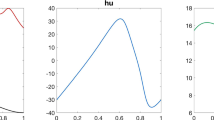
A prototype irrigation scheme including a reservoir for harvesting flash floods is being developed at the Agricultural Research Station of Mutah University, located in the Lisan Peninsula of the Dead Sea near the town of Ghor al Mazrah in Jordan. The model parameters are determined from the physical dimensions of the structures as well as from hydro-meteorological observation conducted from September 27th, 2014 through September 22nd, 2016. Indeed, the reservoir consists of two sections: a 300 m³ section enclosed in a greenhouse, and a 700 m³ section, the surface of which is exposed to open air. Once a flash flood is harvested in the open section, the water is immediately transferred to the closed section if there is room. Therefore, the sections are regarded collectively as a single reservoir of V = 1000 m³ with $Q_{\text{out}} \left( {x,y} \right)$ varying in the $x$-direction. The irrigation period $\left[ {0,T} \right)$ is set as 5.2560 × 10⁵ min of a non-leap year from May 1st through April 30th. No flash flood is expected during the months from May through October. The period from 08:00 a.m. through 08:12 a.m. is prescribed as the irrigation hours for every day throughout the irrigation period. Without loss of generality, the diffusion coefficient $D$ is assumed to be unity. In the two consecutive winter rainy seasons of 2014–2015 and 2015–2016 included in the observation period, there were 16 events of flash floods (10 events in 2014–2015 season and 6 events in 2015–2016 season), out of which 8 events (3 events in 2014–2015 season and 5 events in 2015–2016 season) yielded substantial harvesting. The model parameter $K$ represents the supremum of $y$, where there is no inflow of flash flood to the reservoir, and its value is estimated to be 2.4165. The most likely value of the reversion coefficient in terms of the compatible transition probability density function is 0.0011421 per minute. The functions $Q_{\text{in}} \left( y \right)$ and $Q_{\text{out}} \left( {x,y} \right)$ are determined as shown in Fig. 2. The blue line in the figure indicates $Q_{\text{in}}$ in the unit of m³/min during the wet months from November through April, identified from statistical analysis of the observed data as

$$ Q_{\text{in}} \left( y \right) = \left\{ {\begin{array}{*{20}l} {60.000} \hfill & {{\text{if 5}}8.181 < y} \hfill \\ {18.305\log y - 14.3833} \hfill & {{\text{if }}3.7700 < y \le 58.181} \hfill \\ {27.641y - 94.299} \hfill & {{\text{if }}3.6000 < y \le 3.7700} \hfill \\ {3.6107\left( {y - K} \right)^{2.1767} } \hfill & {{\text{if }}K < y \le 3.6000} \hfill \\ {0.0000} \hfill & {{\text{if }}y \le K} \hfill \\ \end{array} } \right., $$

(90)

while $Q_{\text{in}} \equiv 0$ during the dry months from May to October. Seepage is negligible because of plastic sheets covering the bottom of the reservoir, and the closed section is free from evaporation. Evaporation from the water surface of the open section is estimated at ${{10} \mathord{\left/ {\vphantom {{10} {\left( {1 + \exp \left( {y - K} \right)} \right)}}} \right. \kern-0pt} {\left( {1 + \exp \left( {y - K} \right)} \right)}}$ mm/day., which is multiplied by the water surface area depending on $x$ to yield $Q_{\text{out}} \left( {x,y} \right)$. Note that there is no significant difference in observed evaporation between the wet and dry months.

Fig. 2

Prescribed inflow discharge $Q_{\text{in}} \left( y \right)$ and outflow discharge $Q_{\text{out}} \left( {x,y} \right)$ according to observed data

To approximately solve the HJB equation (72) with (29) from a specified initial condition and then to derive the optimal control strategy, a computational procedure is developed as follows. The z-domain $\Omega_{z}$ is divided into $n_{z}$ sub-domains of equal length $\Delta z = {\pi \mathord{\left/ {\vphantom {\pi {n_{z} }}} \right. \kern-0pt} {n_{z} }}$. The x-domain $\Omega_{x}$ is also divided into $n_{x}$ sub-domains of equal length $\Delta x = {V \mathord{\left/ {\vphantom {V {n_{x} }}} \right. \kern-0pt} {n_{x} }}$, and the unknown $\Phi$ is attributed to each node $\left\{ {x = i\Delta x,z = k\Delta z} \right\}$ as $\Phi_{i,k}$. For discretization in the z-direction, the finite element scheme developed by Unami et al. (2015) is applied to the weak form (72). For discretization in the x-direction, the first-order upwind finite difference scheme is used. The mesh size $\Delta x$ is regarded as the relaxation parameter $\eta$. Then, the system of ordinary differential equations resulting from those discretization schemes is numerically solved in the $\tau$-direction using the Runge–Kutta method with a constant time step $\Delta \tau$ to update the value of each $\Phi_{i,k}$. The optimal control strategy $u^{*}$ is derived from the computed $\Phi_{i,k}$, according to (10). A computational run with $n_{x} = 100$, $n_{x} = 120$, and $\Delta \tau = {1 \mathord{\left/ {\vphantom {1 {60}}} \right. \kern-0pt} {60}}$ minutes was completed within nine days and four hours using the supercomputer system of the Academic Center for Computing and Media Studies, Kyoto University. Distribution of computed optimal control $u^{*}$ is delineated in Figs. 3, 4, 5, 6 and 7 for the irrigation hours of representative days, which are May 1st (Day 0), July 31st (Day 91), October 30th (Day 182), January 29th (Day 273), and April 30th (Day 364). The boundary between two adjacent cells of $u^{*} = 0$ and $u^{*} = Q_{\text{p}}$ in the $x$-$y$ domain for each $\tau \in \left[ {0,t_{2i + 2} - t_{2i + 1} } \right)$ is marked as a segment in a different color at each time stage of 1-min intervals. If there is a surface of $x_{\theta }$ such that

$$ u^{*} = \left\{ {\begin{array}{*{20}c} {Q_{\text{p}} } & {{\text{if }}x > x_{\theta } } \\ 0 & {{\text{if }}x < x_{\theta } } \\ \end{array} } \right. $$

(91)

in the $\tau$–$y$ domain, the surface is referred to as a rule curve. Possibly due to the coarse discretization, oscillations in the delineated segments appear slightly in Figs. 3, 4, 5 and 6 and more visibly near $y = - \infty$ in Fig. 7. However, practically significant rule curves can be extracted. The rule curves are mostly monotonically increasing with respect to $y$, and, throughout the irrigation period, water should not be withdrawn from the reservoir under sufficiently wet conditions. The restriction on intake is strictest on Day 0 and is then relaxed as time evolves. Rule curves vanish after Day 182 under dry conditions.

Fig. 3

Distribution of computed optimal control $u^{*}$ during irrigation hours on May 1st (Day 0)

Fig. 4

Distribution of computed optimal control $u^{*}$ during irrigation hours on July 31st (Day 91)

Fig. 5

Distribution of computed optimal control $u^{*}$ during irrigation hours on October 30th (Day 182)

Fig. 6

Distribution of computed optimal control $u^{*}$ during irrigation hours on January 29th (Day 273)

Fig. 7

Distribution of computed optimal control $u^{*}$ during irrigation hours on April 30th (Day 364)

The chart for the rule curves actually presented to the operator, which includes only three cases of water flow index $y = \pm 3.2935 = \pm 1.3629K = \sqrt {{{2D} \mathord{\left/ {\vphantom {{2D} r}} \right. \kern-0pt} r}} \tan \left( { \pm {\pi \mathord{\left/ {\vphantom {\pi {40}}} \right. \kern-0pt} {40}}} \right)$ and $y = 0$, is shown in Fig. 8. The operator has also been told that irrigation should not be performed during flash floods. On the other hand, the rule curve for $y = - 3.2935$ should be applied under much drier conditions.

Fig. 8

Rule curves presented to operator of irrigation scheme

6 Conclusions

A prototype irrigation scheme with a reservoir for harvesting flash floods motivated the mathematical analysis of the present paper. A water dynamics model was constructed based on practically acceptable assumptions, and the model parameters were determined from the observed data.

The optimal control problem formulated for the model was shown to have a unique value function, which solves the HJB equation in the viscosity sense. In other words, it was successfully demonstrated that the optimal control problem was well-posed. Skillful use of the properties of viscosity sub-solutions and viscosity super-solutions, as well as the choices of auxiliary functions, played key roles in the proofs of the non-trivial theorems. The innovative construction method for the weak solution rationalized the numerical approximation of the value function. The comparison theorem, Theorem 2, is independent of Theorem 1 and is applicable to discontinuous viscosity solutions in general.

The rule curves for operation of the reservoir were numerically derived, suggesting that the optimal control is also unique. This is another remarkable outcome of the present study, because optimal control in a deterministic reservoir operation problem may be not unique, but may be arbitrary. Field verification of the optimal control strategy is being initiated in the real world, cultivating a perennial plant species Phoenix dactylifera in the irrigated command area.