Space time evolution of sand bed topography and associated flow turbulence: experiments with statistical analysis

Abstract

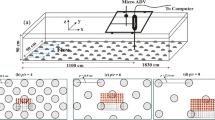
A series of flume experiments were conducted with varying the flow discharges at the Fluvial Mechanics Laboratory of Indian Statistical Institute (Kolkata) to understand the co-evolution patterns of generating bed forms and the corresponding flow turbulence. Instantaneous bed elevations and velocity components were recorded continuously for sufficient time using high resolution instruments, such as, Ultrasonic Ranging System and acoustic Doppler velocimeter, at some spatial location over the deformed bed for each flow discharge. Increase in mean bed elevations and bed-slopes was found to be increased in discharge. Heavy-tailed nature of the probability density functions of magnitude of bed elevation increments, magnitude of single continuous bed elevation increments and instantaneous Reynolds shear stresses along three planes were analyzed using Pareto and truncated Pareto distributions. The spectral analysis of bed elevations revealed that the slope of log–log linearity increased with increase in flow discharge. Wavelet cross-correlations depicted strong dependence of bed form evolution on the corresponding instantaneous Reynolds shear stress along xz-plane. A Gram–Charlier type of distribution was used to estimate the probability density function of fluctuating velocity components, instantaneous Reynolds shear stresses along three planes and the joint probability density functions of the fluctuating velocity components, which showed good fit with the experimental data.

Appendix

1.1 Exceedance probability

At a particular location, the change in bed elevation is defined here by,

$$\begin{aligned} \Delta z(t) = z(t+\Delta t) - z(t) \end{aligned}$$

(1)

where z(t) denotes the bed height at time t at that location and $\Delta t$ is the temporal resolution (here $\Delta t$ = 0.25 s).

This equation leads to three cases for the surface evolution process—positive values of $\Delta z(t)$ (>0) correspond to deposition events ($D_i$), negative values of $\Delta z(t)$ (<0) define erosion events ($E_i$) and $\Delta z(t) = 0$ denotes inactivity at that time and at that location (Ganti et al. 2011; Singh et al. 2011, 2012). Further, considering the time scale of the events viz. deposition, erosion and inactivity as discussed, we define a continuous period during which neither deposition nor erosion takes place at that location, is denoted as the period of inactivity, $\tau _i$. Similarly, time durations of continuous deposition [uninterrupted $\Delta z(t)>0$] and continuous erosion events [uninterrupted $\Delta z(t)<0$] are denoted as $\tau _d$ and $\tau _e$ respectively. Furthermore, the magnitudes of a single depositional event ($D_e$) or an erosional event ($E_e$) are defined as,

$$\begin{aligned} D_e = \sum _{i=1}^{\tau _d} {D_i} \end{aligned}$$

(2)

and

$$\begin{aligned} E_e = \sum _{i=1}^{\tau _e} {E_i} \end{aligned}$$

(3)

1.2 Pareto and truncated-Pareto distribution: parameterizing the heavy-tail

In this section, we want to characterize the exceedance probability of both erosional ($E_i$) and depositional ($D_i$) magnitudes. A common distribution with a power law decay is a Pareto distribution. The probability density function of a Pareto distribution is given by,

$$\begin{aligned} f(x) = \alpha \frac{\gamma ^\alpha }{x^{\alpha + 1}} \end{aligned}$$

(4)

where $\alpha$ is the tail index, $\gamma$ is the minimum possible value of the random variable x and the density is defined for $x \ge \gamma$. The probability of exceedance of a Pareto distribution is expressed as,

$$\begin{aligned} P(X > x) = {\bigg (\frac{\gamma }{x}\bigg )}^\alpha \end{aligned}$$

(5)

Pareto distribution assigns a finite probability for the occurrence of very large magnitude events with no upper limits. But in natural systems, physical mechanisms govern the evolution of the system and impose upper bounds (Bruno et al. 2004; Zhang et al. 2007) that truncates the tail of the distribution. The truncated Pareto distribution is therefore a more appropriate choice for estimating the tail behavior. The probability density function of the truncated Pareto distribution is given by,

$$\begin{aligned} f(x) = \frac{\alpha \gamma ^\alpha x^{-\alpha - 1}}{1 - {(\gamma /\nu )}^\alpha } \end{aligned}$$

(6)

and its probability of exceedance is given by,

$$\begin{aligned} P(X > x) = \frac{\gamma ^\alpha (x^{-\alpha } - \nu ^{-\alpha })}{1 - {(\gamma /\nu )}^\alpha } \end{aligned}$$

(7)

where $\nu$ is the truncation parameter or the upper bound on the random variable x, $\alpha>$ 0 is the tail index and $\gamma$ is the lower bound on the random variable X.

Clauset et al. (2009) proposed a maximum likelihood estimation (MLE) method to estimate the parameters $\alpha$ and $\gamma$ of the Pareto distribution. Aban et al. (2006) proposed a MLE method to estimate the parameters of the truncated Pareto distribution. This estimation involves the conditional MLE based on the $(r + 1)$ largest-order statistics representing only the portion of the tail where the truncated Pareto approximation holds. Consider $X_1$, $X_2$, … $X_n$ denote an array of random samples and let $X_{(1)} \ge X_{(2)} \ge$ ⋯ $\ge X_{(n)}$ denote its order statistics, where $X_{(r)}$ is the r-th largest observation. Then the conditional MLE for the parameters of the truncated Pareto distribution based on the (r + 1) largest-order statistics is given by $\nu = X_{(1)}$, $\gamma = r^{\frac{1}{\alpha }}(X_{(r + 1)}){[n - (n - r){(X_{(r + 1)}/X_{(1)})}^\alpha ]}^{-1/\alpha }$ and $\alpha$ is obtained by solving

$$\begin{aligned} \frac{r}{\alpha } + \frac{r{(X_{(r + 1)}/X_{(1)})}^\alpha \ln (X_{(r + 1)}/X_{(1)})}{1 - {(X_{(r + 1)}/X_{(1)})}^\alpha } - \sum _{i=1}^{r} [\ln X_{(i)} - \ln X_{(r + 1)}] = 0 \end{aligned}$$

(8)

Aban et al. (2006) proposed an asymptotic level-q test ($0< q < 1$) which rejects the null hypothesis $H_0 : \nu = \infty$ (for Pareto distribution) if and only if $X_{(1)} < {[nC / (-\ln q)]}^{1/\alpha }$, where $C = \gamma ^\alpha$. The corresponding p-value is given by $p = e^{(-n C {X_{(1)}}^{-\alpha })}$. In practice, they proposed the use of the Hill’s estimator (Hill 1975):

$$\begin{aligned} \alpha _H = {\bigg [r^{-1} \sum _{i=1}^{r}\big \{\ln X_{(i)} - \ln X_{(r+1)}\big \}\bigg ]}^{-1} \end{aligned}$$

(9)

and

$$\begin{aligned} C = \frac{r}{n}{(X_{(r + 1)})}^{\alpha _H} \end{aligned}$$

(10)

to estimate the parameters C and $\alpha$. A small value of $p < 0.1$ (as suggested by Clauset et al. 2009) would indicate that the Pareto distribution does not provide a good fit to the data. A detailed descriptions about the complete proofs and the parameter estimation method of Pareto and truncated Pareto distribution of a distribution exhibiting power law tail can be found in the work by Aban et al. (2006) and Ganti et al. (2011).

1.3 Wavelet transform

In contrast to the Fourier transform, the wavelet transform uses base functions (wavelets) that have smooth ends per second (Lau and Weng 1995; Mackenzie 2002). Wavelets are small packets of waves; they are defined by a specific frequency and decay towards either end. Since the wavelet functions are compact, the wavelet coefficients only measure the variations around a small region of the data array. The “localized” nature of the wavelet transform allows to easily pick out features in the data, by accurately measuring the energy distribution across a range of scales. The localization also means that a wavelet coefficient at a point is not affected by the coefficients of another point in a signal, which enables this procedure to remove noises of all different scales from a signal. In this context wavelets are preferred for this study to the ‘classical’ spectral analysis in the frequency domain. Mathematically, a wavelet transformation decomposes a signal f(t) into elementary functions $\psi _{a,b}(t)$ derived from a mother wavelet $\psi (t)$ by dilation and translation,

$$\begin{aligned} \psi _{a,b}(t) = \frac{1}{(a)^{1/2}}\psi \bigg (\frac{t-b}{a}\bigg ) \end{aligned}$$

(11)

where a is a scaling parameter (dilation) that sets the frequency represented by the wavelet and b determines the time center (translation) of the wavelet (Lau and Weng 1995; Debnath 2002). The Continuous Wavelet Transform (CWT), W (wavelet coefficients), of the signal f(t) about the mother wavelet $\psi (t)$ is defined as the convolution integral,

$$\begin{aligned} W(a,b) = \frac{1}{(a)^{1/2}} \int \psi ^*\bigg (\frac{t-b}{a}\bigg ) f(t) dt \end{aligned}$$

(12)

where the scale and time center are still determined by the parameters a and b of the wavelet. Again, the wavelet cross-covariance (WCC) between two signals $f_1(t)$ and $f_2(t)$ is defined as:

$$\begin{aligned} WCC_{f_1, f_2}(a,\Delta t) = \int _{- \infty }^{+ \infty } W_{f_1}(a, b)W_{f_2}(a, b + \Delta t)db \end{aligned}$$

(13)

where $W_{f_1}(a, b)$ and $W_{f_2}(a, b + \Delta t)$ are the wavelet coefficients of two signal $f_1(t)$ and $f_2(t)$ respectively with scale a and locations b and $b + \Delta t)$.

For this study, we used Mexican hat wavelet as the mother wavelet for the computation of wavelet coefficients of bed elevations at a range of scales, which is defined as,

$$\begin{aligned} \psi (t) = (1-t^2)e^{-t^2/2} \end{aligned}$$

(14)

This is the basic form of the wavelet from which dilated and translated versions are derived and used in the wavelet transform. The Mexican hat is, in fact, the second derivative of the Gaussian function e$^{-t^2/2}$: that is, with unit variance but without the usual 1/$\sqrt{2\pi }$ normalization factor. Mexican hat is better at identifying single maxima and minima than other mother wavelets. The relative contribution of the signal energy contained at a specific a scale and b location is given by the two-dimensional wavelet energy density function,

$$\begin{aligned} E(a,b) = |W(a,b)|^2 \end{aligned}$$

(15)

A plot of E(a,b) is known as a scalogram (analogous to the spectogram in Fourier transform). The relative contribution to the total energy contained within the signal at a specific scale a, known as the wavelet power spectrum, is obtained by integrating over all locations b:

$$\begin{aligned} WS(a) = \int |W(a,b)|^2 db \end{aligned}$$

(16)

We can readily convert the scale dependent wavelet energy spectrum of the signal WS(a), to a frequency dependent wavelet energy spectrum $WS_w(f)$ in order to compare directly with the Fourier energy spectrum of the signal. To do this, we have to convert the wavelet scale a to a characteristic frequency of the wavelet. We use one of the most commonly used characteristic frequencies used in practice, i.e. the passband center of the wavelet’s power spectrum. Knowing the facts that the spectral components are inversely proportional to the dilation, i.e. f $\propto$ 1 / a and the passband center frequency of the mother wavelet is defined as $f_c$, hence the characteristic frequency associated with a wavelet of arbitrary scale a is given by

$$\begin{aligned} f = f_c/a \end{aligned}$$

(17)

where the passband center of the mother wavelet $f_c$ becomes a scaling constant and f is the representative or characteristic frequency for the wavelet at scale a. For the Mexican hat mother wavelet, $f_c$ is equal to $\sqrt{(5/2)}/2\pi$.

1.4 Gram–Charlier joint probability distribution

In order to estimate the joint probability density functions of velocity signals using the cumulant discard method (Nakagawa and Nezu 1977), the velocity fluctuations in each three directions ($u^\prime$, $v^\prime$ and $w^\prime$) are normalized by their respective standard deviations (r.m.s. values), and hence we obtain $\hat{u} = u^\prime /\sqrt{\overline{{u^\prime }^2}}$, $\hat{v} = v^\prime /\sqrt{\overline{{v^\prime }^2}}$ and $\hat{w} = w^\prime /\sqrt{\overline{{w^\prime }^2}}$. Considering the joint probability density function of $\hat{u}$ and $\hat{v}$ as $p(\hat{u}, \hat{v})$ and its characteristic function as $\psi (\alpha , \beta )$ with the moment of $\overline{\hat{u}^s \hat{v}^t}$ by $m_{st}$ and the corresponding cumulant $q_{st}$, the characteristic function $\psi (\alpha , \beta )$ is defined as,

$$\begin{aligned} \psi (\alpha , \beta ) = \int _{- \infty }^{+ \infty } \int _{- \infty }^{+ \infty } e^{i(\hat{u} \alpha + \hat{v} \beta )} p(\hat{u}, \hat{v}) d\hat{u} d\hat{v} \end{aligned}$$

(18)

Here $m_{st}$ and $q_{st}$ correspond to the coefficients in Taylor series expansions of $\psi (\alpha , \beta )$ and $\ln \psi (\alpha , \beta )$. Hence the relations between the moments and the cumulants are successively obtained. Through an inverse transformation of Eq. 18 in which the terms of $\psi (\alpha , \beta )$ less than fourth order are taken into account, $p(\hat{u}, \hat{v})$ can be written as,

$$\begin{aligned} p(\hat{u}, \hat{v}) = \frac{1}{2\pi } \int _{- \infty }^{+ \infty } \int _{- \infty }^{+ \infty } e^{-i(\hat{u} \alpha + \hat{v} \beta )} \psi (\alpha , \beta ) d\alpha d\beta \end{aligned}$$

(19)

Here $p(\hat{u}, \hat{v})$ is the joint density function of $\hat{u}$ and $\hat{v}$ which have zero means and unit variances. Further expanding the joint density function $p(\hat{u}, \hat{v})$ as a series of derivatives of the standard bivariate normal density function G$(\hat{u}, \hat{v})$ we get,

$$\begin{aligned} p(\hat{u}, \hat{v}) \equiv G(\hat{u}, \hat{v})\bigg [1 + \sum _{s + t = 3}^{4} \frac{q_{st}}{s!t!} H_{st}(\hat{u}, \hat{v})\bigg ] \end{aligned}$$

(20)

where $G(\hat{u}, \hat{v})$ is the bivariate normal density function, defined as

$$\begin{aligned} G(\hat{u}, \hat{v}) = \frac{1}{2\pi {(1 - R^2)}^{1/2}}e^{-\frac{{\hat{u}}^2 + 2R\hat{u} \hat{v} + {\hat{v}}^2}{2(1 - R^2)}} \end{aligned}$$

(21)

and $H_{st}(\hat{u}, \hat{v})$ is a Hermite polynomial in two variables of order $(s + t)$. Equation 20 represents a special form of joint probability density distribution of Gram–Charlier type. Similarly, estimation of $p(\hat{v}, \hat{w})$ and $p(\hat{u}, \hat{w})$ can be done using the respective bivariate normal density functions and Hermite polynomials.

The probability density functions of $\hat{u}$ are derived to be

$$\begin{aligned} p(\hat{u}) = G(\hat{u})\left[1 + \frac{Sk}{6}({\hat{u}}^3 - 3\hat{u}) + \frac{(Ku - 3)}{24}({\hat{u}}^4 - 6{\hat{u}}^2 + 3)\right] \end{aligned}$$

(22)

where $Sk \equiv$ Coefficient of skewness of $\hat{u} \equiv q_{30}$ and $Ku \equiv$ Coefficient of kurtosis of $\hat{u} \equiv (q_{40} + 3)$ and $G(\hat{u})$ is the standard normal density function. Similarly, estimation of $p(\hat{v})$ and $p(\hat{w})$ can be done.

Again, normalizing the instantaneous Reynolds shear stress $\tau _n (=\frac{u^\prime v^\prime }{\overline{u^\prime v^\prime }} = - \frac{\hat{u} \hat{v}}{R})$ and using the change of variables, probability density function of $\tau _n$, i.e. $p_{\tau _n}(\tau _n)$ is given by,

$$\begin{aligned} p_{\tau _n}(\tau _n)&= {} \int _{- \infty }^{+ \infty } \frac{R}{|\hat{u}|} p(\hat{u}, - R\tau _n/\hat{u})d\hat{u} \nonumber \\&= {} \frac{R}{\pi {(1 - R^2)}^{1/2}}e^{\frac{R^2 \tau _n}{1 - R^2}} \int _{0}^{+ \infty }e^{-\frac{{\hat{u}}^2 + R^2{(\tau _n/\hat{u})}^2}{2(1 - R^2)}} \nonumber \\&\quad\times\left [1 + \sum _{s + t = 3}^{4} \frac{q_{st}}{s!t!}\frac{1}{2}\big \{H_{st}(\hat{u}, - R\tau _n/\hat{u}) + H_{st}(-\hat{u}, R\tau _n/\hat{u})\big \}\right ]\frac{d\hat{u}}{\hat{u}} \end{aligned}$$

(23)

where $R = - (\frac{\overline{u^\prime v^\prime }}{\sigma _u \sigma _v})$ is the correlation coefficient. After some rigorous calculations, Nakagawa and Nezu (1977) estimated the probability density function of normalized shear stress to be,

$$\begin{aligned} p_{\tau _n}(\tau _n) = \frac{R}{\pi } e^{R\xi }\frac{K_0(|\xi |)}{{(1 - R^2)}^{1/2}} \end{aligned}$$

(24)

where $\xi = \frac{R\tau _n}{(1 - R^2)}$ and $K_0$ is the zero-th order modified Bessel function of second kind. For more details about the rigorous mathematics, the reader is referred to Nakagawa and Nezu (1977) and Maity and Mazumder (2014).