Abstract
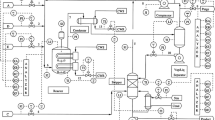
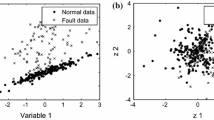
Multivariate statistical methods for online process monitoring have been widely applied to chemical, biological, and engineered systems. While methods based on principal component analysis (PCA) are popular, more recently kernel PCA (KPCA) and locally linear embedding (LLE) have been utilized to better model nonlinear process data. Additionally, various forms of dynamic and adaptive monitoring schemes have been proposed to address time-varying features in these processes. In this analysis, we extend a common simulation study in order to account for autocorrelation and nonstationarity in process data and comprehensively compare the monitoring performances of static, dynamic, adaptive, and adaptive–dynamic versions of PCA, KPCA, and LLE. Furthermore, we evaluate a nonparametric method to set thresholds for monitoring statistics and compare results with the standard parametric approaches. We then apply these methods to real-world data collected from a decentralized wastewater treatment system during normal and abnormal operations. From the simulation study, adaptive–dynamic versions of all three methods generally improve results when the process is autocorrelated and nonstationary. In the case study, adaptive–dynamic versions of PCA, KPCA, and LLE all flag a strong system fault, but nonparametric thresholds considerably reduce the number of false alarms for all three methods under normal operating conditions.







Similar content being viewed by others
References
Banadda N, Nhapi I, Kimwaga R (2011) A review of modeling approaches in activated sludge systems. Afr J Environ Sci Technol 5:397–408
Belkin M, Niyogi P (2003) Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput 15:1373–1396
Chen Q, Wynne RJ, Goulding P, Sandoz D (2000) The application of principal component analysis and kernel density estimation to enhance process monitoring. Control Eng Pract 8:531–543
Cheng C, Chiu MS (2005) Nonlinear process monitoring using JITL-PCA. Chemom Intell Lab Syst 76:1–13
Cheng CY, Hsu CC, Chen MC (2010) Adaptive kernel principal component analysis (KPCA) for monitoring small disturbances of nonlinear processes. Ind Eng Chem Res 49:2254–2262
Chetouani Y (2008) A neural network approach for the real-time detection of faults. Stoch Environ Res Risk Assess 22:339–349
Cho JH, Lee JM, Choi SW, Lee D, Lee IB (2005) Fault identification for process monitoring using kernel principal component analysis. Chem Eng Sci 60:279–288
Choi SW, Lee IB (2004) Nonlinear dynamic process monitoring based on dynamic kernel PCA. Chem Eng Sci 59:5897–5908
Choi SW, Lee C, Lee JM, Park JH, Lee IB (2005) Fault detection and identification of nonlinear processes based on kernel PCA. Chemom Intell Lab Syst 75:55–67
Chouaib C, Mohamed-Faouzi H, Messaoud D (2013) Adaptive kernel principal component analysis for nonlinear dynamic process monitoring. In: 2013 9th Asian Control Conference (ASCC). IEEE, Istanbul, Turkey
Dong D, McAvoy TJ (1996) Batch tracking via nonlinear principal component analysis. AIChE J 42:2199–2208
Downs JJ, Vogel EF (1993) A plant-wide industrial process control problem. Comput Chem Eng 17:245–255
García-Díaz CJ (2011) Monitoring and forecasting nitrate concentration in the groundwater using statistical process control and time series analysis: a case study. Stoch Environ Res Risk Assess 25:331–339
Ge Z, Yang C, Song Z (2009) Improved kernel PCA-based monitoring approach for nonlinear processes. Chem Eng Sci 64:2245–2255
Gikas P, Tchobanoglous G (2009) The role of satellite and decentralized strategies in water resources management. J Environ Manag 90:144–152
Ham J, Lee DD, Mika S, Sch\(\ddot{\text{o}}\)lkopf B (2004) A kernel view of the dimensionality reduction of manifolds. In: Proceedings of the Twenty-First International Conference on Machine Learning. ACM, New York, USA, p 47
Hart JD (1996) Some automated methods of smoothing time-dependent data. J Nonparametr Stat 6:115–142
Haykin S (1999) Neural Networks. Prentice-Hall, Englewood Cliffs
Hiden HG, Willis MJ, Tham MT, Montague GA (1999) Non-linear principal components analysis using genetic programming. Comput Chem Eng 23:413–425
Jackson JE, Mudholkar GS (1979) Control procedures for residuals associated with principal component analysis. Technometrics 21:341–349
Jones MC, Marron JS, Sheather SJ (1996) A brief survey of bandwidth selection for density estimation. J Am Stat Assoc 91:401–407
Kayo O (2006) Locally linear embedding algorithm: extensions and applications. Universitatis Ouluensis, Oulu. http://herkules.oulu.fi/isbn9514280415/isbn9514280415.pdf. Accessed 18 March 2014
Khediri IB, Limam M, Weihs C (2011) Variable window adaptive kernel principal component analysis for nonlinear nonstationary process monitoring. Comput Ind Eng 61:437–446
Kramer MA (1991) Nonlinear principal component analysis using autoassociative neural networks. AIChE J 37:233–243
Kruger U, Zhou Y, Irwin GW (2004) Improved principal component monitoring of large-scale processes. J Process Control 14:879–888
Kruger U, Antory D, Hahn J, Irwin GW, McCullough G (2005) Introduction of a nonlinearity measure for principal component models. Comput Chem Eng 29:2355–2362
Ku W, Storer RH, Georgakis C (1995) Disturbance detection and isolation by dynamic principal component analysis. Chemom Intell Lab Syst 30:179–196
Lee JM, Yoo CK, Choi SW, Vanrolleghem PA, Lee IB (2004a) Nonlinear process monitoring using kernel principal component analysis. Chem Eng Sci 59:223–234
Lee JM, Yoo CK, Lee IB (2004b) Statistical process monitoring with independent component analysis. J Process Control 14:467–485
Leverenz HL, Asano A (2011) Wastewater reclamation and reuse system. Treatise Water Sci 4:63–71
Liu X, Kruger U, Littler T, Xie L, Wang S (2009) Moving window kernel PCA for adaptive monitoring of nonlinear processes. Chemom Intell Lab Syst 96:132–143
Maulud A, Wang D, Romagnoli JA (2006) A multi-scale orthogonal nonlinear strategy for multivariate statistical process monitoring. J Process Control 16:671–683
Miao A, Song Z, Ge Z, Zhou L, Wen Q (2013) Nonlinear fault detection based on locally linear embedding. J Control Theory Appl 11:615–622
Mina J, Verde C (2007) Fault detection for large scale systems using Dynamic Principal Components Analysis with adaptation. Int J Comput Commun Control 2:185–194
Mjalli FS, Al-Asheh S, Alfadala HE (2007) Use of artificial neural network black-box modeling for the prediction of wastewater treatment plants performance. J Environ Manag 83:329–338
Nguyen VH, Golinval JC (2010) Fault detection based on kernel principal component analysis. Eng Struct 32:3683–3691
Parneet P (2013) Comparing and contrasting traditional membrane bioreactor models with novel ones based on time series analysis. Membranes 3:16–23
Rato T, Reis M (2013) Defining the structure of DPCA models and its impact on process monitoring and prediction activities. Chemom Intell Lab Syst 125:74–86
Roweis ST, Saul LK (2000) Nonlinear dimensionality reduction by locally linear embedding. Science 290:2323–2326
Russell EL, Chiang LH, Braatz RD (2000) Fault detection in industrial processes using canonical variate analysis and dynamic principal component analysis. Chemom Intell Lab Syst 51:81–93
Schölkopf B, Smola A, Müller KB (1998) Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput 10:1299–1319
Sheather SJ (2009) A modern approach to regression with R, vol 58. Springer, New York
Sheather SJ, Jones MC (1991) A reliable data-based bandwidth selection method for kernel density estimation. J R Stat Soc B 53:683–690
Sköld M (2001) A bias correction for cross-validation bandwidth selection when a kernel estimate is based on dependent data. J Time Ser Anal 22:493–503
Tenenbaum JB, De Silva V, Langford JC (2000) A global geometric framework for nonlinear dimensionality reduction. Science 290:2319–2323
van Sprang ENM, Ramaker HJ, Westerhuis JA, Gurden SP, Smilde AK (2002) Critical evaluation of approaches for on-line batch process monitoring. Chem Eng Sci 57:3979–3991
Vuono D, Henkel J, Benecke J, Cath TY, Reid T, Johnson L, Drewes JE (2013) Flexible hybrid membrane treatment systems for tailored nutrient management: a new paradigm in urban wastewater treatment. J Membr Sci 446:34–41
Westerhuis JA, Gurden SP, Smilde AK (2000) Generalized contribution plots in multivariate statistical process monitoring. Chemom Intell Lab Syst 51:95–114
Wold S, Esbensen K, Geladi P (1987) Principal component analysis. Chemom Intell Lab Syst 2:37–52
Woodall WH, Montgomery DC (2014) Some current directions in the theory and application of statistical process monitoring. J Qual Technol 46:78–94
Zeng Y, Zhang Z, Kusiak A, Tang F, Wei X (2016) Optimizing wastewater pumping system with data-driven models and a greedy electromagnetism-like algorithm. Stoch Environ Res Risk Assess 30:1263–1275
Zhang W, Liu X, Qi R, Jiang Y (2013) Improved locally linear embedding based method for nonlinear system fault detection. Int J Adv Comput Technol 5:515–523
Zhao S, Xu Y (2005) Multivariate statistical process monitoring using robust nonlinear principal component analysis. Tsinghua Sci Technol 10:582–586
Zheng Y, Zhang L (2013) Fault diagnosis of wet flue gas desulphurization system based on KPCA. In: The 19th International Conference on Industrial Engineering and Engineering Management. Springer, Berlin
Acknowledgments
This work was partially supported by the National Science Foundation under Cooperative Agreement EEC-1028969 (ERC/ReNUWIt) and by the State of Colorado through the Higher Education Competitive Research Authority. The authors would like to thank two anonymous referees whose comments and suggestions have improved the content and presentation of this work.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Kazor, K., Holloway, R.W., Cath, T.Y. et al. Comparison of linear and nonlinear dimension reduction techniques for automated process monitoring of a decentralized wastewater treatment facility. Stoch Environ Res Risk Assess 30, 1527–1544 (2016). https://doi.org/10.1007/s00477-016-1246-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-016-1246-2