An adaptive response surface method for continuous Bayesian model calibration

Abstract

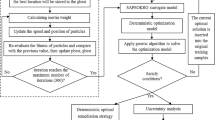
Non-linear numerical models of the injection phase of a carbon sequestration (CS) project are computationally demanding. Thus, the computational cost of the calibration of these models using sampling-based solutions can be formidable. The Bayesian adaptive response surface method (BARSM)—an adaptive response surface method (RSM)—is developed to mitigate the cost of sampling-based, continuous calibration of CS models. It is demonstrated that the adaptive scheme has a negligible effect on accuracy, while providing a significant increase in efficiency. In the BARSM, a meta-model replaces the computationally costly full model during the majority of the calibration cycles. In the remaining cycles, the full model is used and samples of these cycles are utilized for adaptively updating the meta-model. The idea behind the BARSM is to take advantage of the fact that sampling-based calibration algorithms typically tend to sample more frequently from areas with a larger posterior density than from areas with a smaller posterior density. This behavior of the sampling-based calibration algorithms is used to adaptively update the meta-model and to make it more accurate where it is most likely to be evaluated. The BARSM is integrated with Unscented Importance Sampling (UIS) (Sarkarfarshi and Gracie, Stoch Env Res Risk Assess 29: 975–993, 2015), which is an efficient Bayesian calibration algorithm. A synthesized case of supercritical CO₂ injection in a heterogeneous saline aquifer is used to assess the performance of the BARSM and to compare it with a classical non-adaptive RSM approach and Bayesian calibration method UIS without using RSM. The BARSM is shown to reduce the computational cost compared to non-adaptive Bayesian calibration by 87 %, with negligible effect on accuracy. It is demonstrated that the error of the meta-model fitted using the BARSM, when samples are drawn from the posterior parameter distribution, is negligible and smaller than the monitoring error.

Appendix 1: Unscented importance sampling (UIS)

Importance Sampling (IS) (Marshall 1956) is a method for generating samples from a probability distribution, denoted by $\pi \left( \varvec{m} \right)$ here, which is not easy to sample from and is available at least up to a normalizing constant. In IS, samples, denoted by $\hat{\varvec{m}}_{i}$ (i = 1 to N _s ) here, are drawn from a proposal distribution, denoted by $q(\varvec{m})$, which is close to $\pi \left( \varvec{m} \right)$ and is easy to sample from. Next, the samples are weighted to remove the bias,

$$ W_{i} = \frac{{w_{i} }}{{\mathop \sum \nolimits_{i = 1}^{N} w_{i} }} i = 1 \ldots N_{s} $$

(15)

where W _i is the normalized weight for the ith sample and w _i is un-normalized weight for the ith sample obtained by $w_{i} = \pi (\hat{\varvec{m}}_{i} )/q(\hat{\varvec{m}}_{i} )$. Statistics of $\pi \left( \varvec{m} \right)$ can be approximated by statistics of the weighted samples.

IS can be utilized for sampling from the posterior distribution of uncertain parameters of a system in presence of random error with mean of zero, $\varvec{\varepsilon}$, between the system behaviour model, $\varvec{g}\left( \varvec{m} \right)$, and system behaviour measurements (monitoring data), $\varvec{d}_{obs}^{{}}$. If $\pi_{\varepsilon } \left(\varvec{\varepsilon}\right)$ denotes the probability distribution of $\varvec{\varepsilon}$, $\pi^{0} \left( \varvec{m} \right)$ denotes the prior distribution of $\varvec{m}$ and c denotes the normalizing constant in the Bayes’ formula, un-normalized weights of the samples of the posterior distribution of m are obtained by

$$ w_{i} = c^{ - 1} \frac{{\pi_{\varepsilon } \left( {\varvec{d}_{obs} - \varvec{g}\left( {\hat{\varvec{m}}_{i} } \right)} \right)\pi^{0} \left( {\hat{\varvec{m}}_{i} } \right)}}{{q\left( {\hat{\varvec{m}}_{i} } \right)}}; \quad i = 1 \ldots N_{s} $$

(16)

When normalizing the weights, the normalizing constant is cancelled out from numerator and denominator in Eq. (16). Thus, normalizing constant in the Bayes formula (which is the problematic part in obtaining posterior distribution) does not need to be known in Bayesian IS.

A proposal distribution which is close to the true posterior is the key factor for efficient IS (Smith et al. 1997). Unscented Importance Sampling (UIS) (Sarkarfarshi and Gracie 2015) is an efficient method for obtaining a proposal distributions close to the true posterior distribution in continuous Bayesian IS. The benefits of UIS are computational efficiency and not making any assumptions about the model type nor probability distributions (prior, likelihood and posterior).

Now we briefly describe UIS formulation. Assume continuous Bayesian update of parameters of a system denoted by $\varvec{m}$ where the system model at time t _n is denoted by $\varvec{g}\left( {t_{n} ,\varvec{m}} \right)$ and monitoring data at time t _n is donted by $\varvec{d}_{obs}^{n}$. Assume the discrepancy between the model and monitoring data, denoted by $\varvec{\varepsilon}$, is a random variable with probability distribution of $\pi_{\varepsilon } (\varvec{\varepsilon})$. The posterior distribution of model parameters at time t _n is denoted by $\pi^{n} (\varvec{m})$ and $\pi (\varvec{m})$ denotes the prior distribution before calibration.

At time t _n , monitoring data $\varvec{d}_{obs}^{n}$ is obtained and we want to sample from $\pi^{n} (\varvec{m})$ accounting for all monitoring data up to time t _n . UIS at each time or cycle consists of two steps, as described in the following.

• 1. UKF step: in the UKF step, the true posterior is approximated by a Gaussian distribution using measurement update stage of Unscented Kalman Filter (UKF) (Julier and Uhlmann 1996). A full description of UKF can be found in the former reference. The UKF stage of UIS can be formulated as follows.

  • 1.1 Use $\pi_{b}^{n} \left( \varvec{m} \right) = N\left( {\varvec{\mu}_{m}^{n - 1} ,{\mathbf{C}}_{m}^{n - 1} } \right)$ as the prior distribution, where:

    • 1.1.1 $\varvec{\mu}_{m}^{n - 1} = \mathop \sum \limits_{i = 1}^{{N_{s} }} W_{i}^{n - 1} \hat{\varvec{m}}_{i}^{n - 1}$ and ${\mathbf{C}}_{m}^{n - 1} = \mathop \sum \limits_{i = 1}^{{N_{s} }} W_{i}^{n - 1} \left( {\hat{\varvec{m}}_{i}^{n - 1} -\varvec{\mu}_{b}^{n} } \right)\left( {\hat{\varvec{m}}_{i}^{n - 1} -\varvec{\mu}_{b}^{n} } \right)^{T}$ from the previous cycle, when n > 1

    • 1.1.2 $\varvec{\mu}_{m}^{n - 1}$ and ${\mathbf{C}}_{m}^{n - 1}$ are mean and covariance of $\pi^{0} \left( \varvec{m} \right)$ when n = 1

  • 1.2 Select the Sigma points ($\varvec{\chi}_{i}$) and corresponding weights (ϑ _i ) in the UKF algorithm:

    $$ \varvec{\chi}_{0} =\varvec{\mu}_{m}^{n - 1} $$
    $$ - 1 < \vartheta_{0} < 1 $$
    $$ \varvec{\chi}_{i} =\varvec{\mu}_{m}^{n - 1} \pm \left( {\sqrt {\frac{{N_{m} }}{{1 - \vartheta_{0} }}{\mathbf{C}}_{m}^{n - 1} } } \right)_{i} +\, \left( { i = 1, \ldots ,N_{m} } \right) - ( i = N_{m} + 1, \ldots ,2N_{m} ) $$

    where $\left( {\sqrt {\frac{{N_{m} }}{{1 - \vartheta_{0} }}{\mathbf{C}}_{m}^{n - 1} } } \right)_{i}$ is the ith row or column of the square root of $\sqrt {\frac{{N_{m} }}{{1 - \vartheta_{0} }}{\mathbf{C}}_{m}^{n - 1} }$ obtained by Cholesky decomposition.

    $$ \vartheta_{i} = \frac{{1 - \vartheta_{0} }}{{2N_{s} }}; \quad i = 1,2, \ldots ,2N_{s} $$

    where N _m is the number of uncertain parameters, i.e., dimension of the parameter vector $\varvec{m}$.

  • 1.3 Obtain propagated Sigma points through system model by ${\varvec{\Upsilon}}_{i} = \varvec{g}\left( {t_{n} ,\varvec{\chi}_{i} } \right)$.

  • 1.4 Obtain Sigma point and propagated sigma point statistics as follows:

    $$ \varvec{\mu}_{\chi } = \mathop \sum \limits_{i = 0}^{{2N_{m} }} \vartheta_{i}\varvec{\chi}_{i} ; \varvec{\mu}_{\varUpsilon } = \mathop \sum \limits_{i = 0}^{{2N_{m} }} \vartheta_{i} {\varvec{\Upsilon}}_{i} $$
    $$ {\mathbf{C}}_{\varUpsilon } = \mathop \sum \limits_{i = 0}^{{2N_{m} }} \vartheta_{i} \left[ {\varUpsilon_{i} -\varvec{\mu}_{\varUpsilon } } \right]^{T} \left[ {\varUpsilon_{i} -\varvec{\mu}_{\varUpsilon } } \right] ; {\mathbf{C}}_{\chi ,\varUpsilon } = \mathop \sum \limits_{i = 0}^{{2N_{m} }} \vartheta_{i} \left[ {\varvec{\chi}_{i} -\varvec{\mu}_{\chi } } \right]^{T} \left[ {\varUpsilon_{i} -\varvec{\mu}_{\varUpsilon } } \right] $$

    where $\varvec{\mu}_{\chi }$ is the mean of the Sigma points, $\varvec{\mu}_{\varUpsilon }$ is the mean of the propagated Sigma points, ${\mathbf{C}}_{\varvec{\Upsilon}}$ is the covariance of the propagated Sigma points and ${\mathbf{C}}_{\chi,\,\varvec{\Upsilon}}$ is the covariance between $\varvec{\chi}$ and ${\varvec{\Upsilon}}$.

  • 1.5 Obtain Gaussian posterior of UKF step with a mean of $\varvec{\mu}_{m}^{n} =\varvec{\chi}_{0} + \varvec{K}\left( {\varvec{d}_{obs}^{n} -\varvec{\mu}_{\varUpsilon } } \right)$ and a covariance of ${\mathbf{C}}_{m}^{n} = {\mathbf{C}}_{m}^{n - 1} - \varvec{K}\left( {{\mathbf{C}}_{\varUpsilon } + {\mathbf{C}}_{\varepsilon } } \right)\varvec{K}^{T}$ where $\varvec{K}$ is the Kalman gain and is obtained by $\varvec{K} = {\mathbf{C}}_{\chi ,\varUpsilon } \left( {{\mathbf{C}}_{\varUpsilon } + {\mathbf{C}}_{\varepsilon } } \right)^{ - 1}$ and C _ɛ is covariance of $\pi_{\varepsilon } (\varvec{\varepsilon})$.

• 2. IS step: in the IS step, the Gaussian approximation of the posterior from the UKF step is used as the proposal distribution of IS.

  • 2.1 Use posterior of UKF step as the proposal distribution denoted by $q^{n} \left( \varvec{m} \right)$

  • 2.2 Sample from $q^{n} \left( \varvec{m} \right)$ until desired number of samples is obtained. $\hat{\varvec{m}}_{i}^{n}$ denotes sample i at cycle n.

  • 2.3 Obtain un-normalized weights by $w_{i}^{n} = \pi^{0} (\hat{\varvec{m}}_{i}^{n} )/q^{n} \left( {\hat{\varvec{m}}_{i}^{n} } \right)\mathop \prod \limits_{l = 1}^{n} \pi_{{\varepsilon_{obs} }} \left( {\varvec{d}_{obs}^{l} - g\left( {t_{n} ,\hat{\varvec{m}}_{i}^{n} } \right)} \right)$

  • 2.4 Normalize weights to obtain the importance weights at cycle n, denoted by W ⁿ _i .

This algorithm is repeated when new monitoring data is obtained. The two stage scheme described above ensures that the proposal distribution is close to the true posterior at all calibration cycles and thus, increases the accuracy and computational efficiency of the IS. Moreover, no assumption is made on the type of the system model (e.g. linearity) or type of the prior, posterior and likelihood (e.g. being Gaussian). A more comprehensive description of UIS along with several case studies can be found in (Sarkarfarshi and Gracie 2015).