Equifinality of formal (DREAM) and informal (GLUE) Bayesian approaches in hydrologic modeling?

Abstract

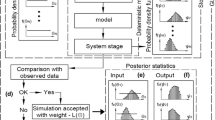
In recent years, a strong debate has emerged in the hydrologic literature regarding what constitutes an appropriate framework for uncertainty estimation. Particularly, there is strong disagreement whether an uncertainty framework should have its roots within a proper statistical (Bayesian) context, or whether such a framework should be based on a different philosophy and implement informal measures and weaker inference to summarize parameter and predictive distributions. In this paper, we compare a formal Bayesian approach using Markov Chain Monte Carlo (MCMC) with generalized likelihood uncertainty estimation (GLUE) for assessing uncertainty in conceptual watershed modeling. Our formal Bayesian approach is implemented using the recently developed differential evolution adaptive metropolis (DREAM) MCMC scheme with a likelihood function that explicitly considers model structural, input and parameter uncertainty. Our results demonstrate that DREAM and GLUE can generate very similar estimates of total streamflow uncertainty. This suggests that formal and informal Bayesian approaches have more common ground than the hydrologic literature and ongoing debate might suggest. The main advantage of formal approaches is, however, that they attempt to disentangle the effect of forcing, parameter and model structural error on total predictive uncertainty. This is key to improving hydrologic theory and to better understand and predict the flow of water through catchments.

Appendix

1.1 Calculation of predictive uncertainty from MCMC simulation

Assume that for each MCMC draw x ^j the distribution of each model outcome y _i , i = 1,...,n is F and that F(c) = Pr(y < c|x ^j) can be calculated exactly for any value of c. For example, from the MCMC runs using Eq. 9 and AR-1 normally distributed model and measurement error as in Eq. 6, F is a Student distribution t _v (μ, σ²) with v = n, $\mu = f({\bf x}^{j},{\hat{\phi}})$ and σ² = s ²/(1−ρ²) with s ² in Eq. 14. Now Pr(y < c) can be estimated from the J MCMC draws using the average of Pr(y < c|x ^j). To estimate a 100α% percentile we thus need to find c such that:

$$ \frac{1}{J}\sum_{j=1}^{J} Pr(y < c|{{\mathbf{x}}}^{j}) = \alpha $$

(16)

This can be done numerically by a root-finding algorithm. A 95% confidence interval is constructed by calculating the 2.5 and 97.5% percentile, respectively.