Abstract
More than three years after its appearance in Haiti, cholera has already caused more than 8,500 deaths and 695,000 infections and it is feared to become endemic. However, no clear evidence of a stable environmental reservoir of pathogenic Vibrio cholerae, the infective agent of the disease, has emerged so far, suggesting the possibility that the transmission cycle of the disease is being maintained by bacteria freshly shed by infected individuals. Should this be the case, cholera could in principle be eradicated from Haiti. Here, we develop a framework for the estimation of the probability of extinction of the epidemic based on current information on epidemiological dynamics and health-care practice. Cholera spreading is modeled by an individual-based spatially-explicit stochastic model that accounts for the dynamics of susceptible, infected and recovered individuals hosted in different local communities connected through hydrologic and human mobility networks. Our results indicate that the probability that the epidemic goes extinct before the end of 2016 is of the order of 1 %. This low probability of extinction highlights the need for more targeted and effective interventions to possibly stop cholera in Haiti.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The largest cholera epidemic ever recorded during the current pandemic wave is striking Haiti. At the end of October 2010, 10 months after a catastrophic earthquake, a violent cholera outbreak flared up in the valley of the Artibonite, the main river system of the country, most likely triggered by the importation of a toxigenic Vibrio cholerae strain (Chin et al. 2011; Piarroux et al. 2011; Hendriksen and al. 2011; Frerichs et al. 2012). The epidemic spread to the whole Haitian territory in less than two months. As of December 31, 2013, the Ministry of Public Health and Population reported more than 695,000 cases and an average cumulative attack rate of 6.9 %. With more than 8,500 deaths, the resulting cumulative case fatality rate is 1.2 %, an unusually high figure for a cholera epidemic, likely attributable, among other causes, to the unpreparedness of the Haitian health infrastructure to deal with such an emergency, in particular after the earthquake (Barzilay et al. 2013).
Cholera is an acute diarrheal disease that is transmitted through the ingestion of water or food contaminated with V. cholerae. The bacterium colonizes the human intestine but it can also survive outside the human host in the aquatic environment. Moreover V. cholerae can be a natural member of the aquatic microbial community in certain regions of the world where cholera is endemic (Colwell 1996; Lipp et al. 2002; Islam et al. 2004). Laboratory tests confirmed that V. cholerae can thrive in freshwater (Vital et al. 2007). A few studies in Haiti have screened environmental samples for toxigenic V. cholerae. One such study, conducted in the final months of 2010, when the epidemic was peaking, found the strain in only 5 samples out of 18 (Hill et al. 2011). Two other environmental studies were staged after the peak of the epidemic. The first attested the detection of toxigenic V. cholerae in 3 out of 179 samples (Alam et al. 2014), while the other found none (Baron et al. 2013). The absence of clear evidence of an established environmental community of toxigenic V. cholerae, supported by detailed field investigations, led some authors to conclude that the transmission cycle of the disease is being maintained by bacteria freshly shed by infected individuals (Rebaudet et al. 2013) and thus that the disease could possibly be eradicated. In particular, it was suggested that the dry season, when the disease is in a lull phase, represents a window of opportunity for targeted efforts to stop cholera transmission.
In this context, we develop a framework for the estimation of the probability that the variability of the dry season, together with the inherent demographic stochasticity of the disease transmission, lead to the extinction of the epidemic outbreak. In our analysis we assume that an environmental reservoir of V. cholerae cannot self-sustain indefinitely without inputs form infected individuals. The alternative hypothesis of a self-sustained reservoir of V. cholerae will be also discussed.
The dramatic outcome of the Haiti epidemic promoted the development of a number of mathematical models of cholera transmission (Bertuzzo et al. 2011; Andrews and Basu 2011; Tuite et al. 2011; Chao et al. 2011; Rinaldo et al. 2012; Gatto et al. 2012; Eisenberg et al. 2013; Mukandavire et al. 2013) in an effort to provide key insights into the course of the ongoing epidemic, potentially aiding real-time emergency management in allocating health care resources and evaluating the effects of alternative intervention strategies. The development and the application of these models were made possible by the immediate release of epidemiological records, and by the continuous advance of satellite estimates of environmental variables and georeferenced data-sets (Griffith and Christakos 2007; Jutla et al. 2013a, b). The various modeling approaches differ in assumptions, spatial resolution and degrees of spatial coupling, but they all address the coupled dynamics of susceptibles, infected individuals and bacterial concentrations in a spatially explicit setting of local human communities. Most of the models approximate the number of infected and susceptible individuals with continuous variables, an assumption often made in mathematical epidemiology when the number of individuals in each class is large enough to neglect the demographic stochasticity emerging from the intrinsic discrete nature of individual processes. Continuous models are computationally efficient and therefore suitable to be calibrated by contrasting simulations and epidemiological records. A notable exception is the agent-based model proposed by Chao et al. (2011), which, however, was not calibrated against data but relied on parameter values taken from literature. Other possible approaches to model stochasticity in disease transmission are the use of Langevin-type differential equations (Azaele et al. 2010; Mukandavire et al. 2013) or of spatiotemporal random fields which account for multiple sources of uncertainty (Angulo et al. 2012, 2013).
Continuous epidemic models are not suitable for the case at hand. In fact, they do not admit disease extinction in a finite time (Bartlett 1957). Moreover, demographic stochasticity is expected to play an important role during the lull phases when the number of infected individuals is small. We therefore develop a novel individual-based spatially-explicit stochastic model that accounts for the dynamics of susceptible, infected and recovered individuals hosted in different local communities connected through hydrologic and human mobility networks. The model also accounts for enhanced cholera transmission mediated by rainfall (Rinaldo et al. 2012), a critical factor for the seasonality of the epidemic cycle (Eisenberg et al. 2013; Gaudart et al. 2013). Moreover, we model the possible effect of the progressive decrease of population exposure to cholera due to intervention strategies (e.g. distribution of safe water and information campaigns) and increased population awareness of cholera transmission risk factors (de Rochars et al. 2011).
From an operational viewpoint, the deterministic counterpart of the stochastic model is used to calibrate the parameters in conditions in which differences between the two formulations are immaterial. To that end, fitting is performed on the first phase of the epidemic, when the number of infected individuals is deemed sufficiently large for the continuous approximation to apply. The stochastic model is then run with parameter sets sampled from the posterior distribution obtained in the calibration phase. We project the future evolution of the epidemic forcing the model with stochastically generated rainfall scenarios and we estimate the probability of extinction.
The paper is organized as follows. Section 2 details the spatially explicit model of cholera transmission in its deterministic and stochastic formulations. In Sect. 3 we illustrate the application to the Haiti epidemic case study. Results are presented in Sect. 4. A discussion Sect. 5 closes the paper.
2 Spatially explicit cholera model
The theoretical framework adopted builds on previous spatially explicit epidemiological models (Bertuzzo et al. 2008, 2010; Mari et al. 2012a, b) which have also been applied to the Haiti cholera epidemic (Bertuzzo et al. 2011; Rinaldo et al. 2012). The model subdivides the total population into \(n\) human communities spatially distributed within a domain that embeds both the human mobility and the hydrological networks. Two main improvements are introduced: first, we differentiate the role played by symptomatic and asymptomatic infected individuals in the environmental contamination; and second, we model the decrease of exposure to cholera due to intervention strategies and increased population awareness. In this section, we first describe the population-based, continuous deterministic model and then we derive its individual-based discrete stochastic counterpart.
2.1 Deterministic formulation
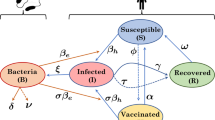
Let \(S_i(t)\), \(I_i(t)\) and \(R_i(t)\) be the local abundances of susceptible, symptomatic infected and recovered individuals at time \(t\) in each node \(i\) of the network, and let \(B_i(t)\) be the environmental concentration of V. cholerae at site \(i\) (Fig. 1). Cholera transmission dynamics can be described by the following set of coupled differential equations:
The population of each node is assumed to be at demographic equilibrium, with \(\mu \) being the human mortality rate, \(H_i\) the population size of the local community and \(\mu H_i\) a constant recruitment rate. The demographic structure of the population is neglected because of the lack of information on how epidemiological parameters vary with age. The force of infection \(F_i(t)\), which represents the rate at which susceptible individuals become infected due to contact with contaminated water, is expressed as:
The parameter \(\beta _i(t)\) represents the maximum exposure rate, which can change in time and space due to increasing population awareness as the epidemic unfolds (see below). The fraction \(B_{i}/(K+B_{i})\) is the probability of becoming infected due to the exposure to a concentration \(B_i\) of V. cholerae, \(K\) being the half-saturation constant (Codeço 2001). Because of human mobility, a susceptible individual residing at node \(i\) can, while travelling, be exposed to pathogens in the destination community \(j\). This is modeled assuming that the force of infection in a given node depends on the local concentration \(B_i\) for a fraction (\(1-m\)) of the susceptible hosts and on the concentration \(B_j\) of the surrounding communities for the remaining fraction \(m\). The parameter \(m\) represents the community-level probability that individuals travel outside their node and is assumed, in this formulation, to be node-independent. The concentrations \(B_j\) are weighted according to the probabilities \(Q_{ij}\) that an individual living in node \(i\) would reach \(j\) as a destination. We model human mobility through a gravity model (Erlander and Stewart 1990). Accordingly, connection probabilities are defined as
where the attractiveness factor of node \(j\) depends on its population size, while the deterrence factor is assumed to be dependent on the distance \(d_{ij}\) between the two communities and represented by an exponential kernel (with shape factor \(D\)). A fraction \(\sigma \) of infected individuals develops symptoms thus entering the \(I_i\) class. Symptomatic infected individuals recover at a rate \(\gamma \), or die due to cholera or other causes at rates \(\alpha \) or \(\mu \), respectively. Asymptomatic infected individuals shed V. cholerae at a much lower rate [around 1,000 times, (Kaper et al. 1995; Nelson et al. 2009)] than symptomatic ones and recover much more rapidly [in around one day instead of five according to Nelson et al. (2009)]. It is thus reasonable to assume that their role in the environmental contamination is negligible with respect to that of symptomatic individuals. However, it is crucial to account for asymptomatic infections because these individuals are temporarily immune and thus contribute to the depletion of the pool of susceptibles, affecting also the rate of occurrence of symptomatic infections. Mathematically, this translates into a flux of asymptomatic infected \((1-\sigma )F_i(t)S_i\) that enters the recovered compartment \(R_i(t)\) directly. The fraction \(\sigma \) of infections that produce symptoms is likely dependent on the dose of bacteria ingested. However, due to the lack of detailed information and for the sake of simplicity it is here assumed to be constant. Recovered individuals lose their immunity and return to the susceptible compartment at a rate \(\rho \) or die at a rate \(\mu \). Symptomatic infected individuals are assume to be non-mobile, therefore they contribute only to the local environmental concentration of V. cholerae at a rate \(p/W_i\), where \(p\) is the rate at which bacteria excreted by one infected individual reach and contaminate the local water reservoir of volume \(W_i\) [assumed to be proportional to population size, i.e. \(W_i=c H_i\) as in Rinaldo et al. (2012)]. It is assumed that the death rate of V. cholerae in the environment exceeds the birth rate thus resulting in the net mortality rate \(\mu _B\). Bacteria undergo also hydrologic dispersal at a rate \(l\): pathogens can travel from node \(i\) to \(j\) with probability \(P_{ij}\). We assume \(P_{ij} = 1\) if \(j\) is the downstream nearest neighbor of node \(i\) and zero otherwise. In order to express the worsening of sanitation conditions caused by rainfall-induced runoff, which causes additional loads of pathogens to enter the water reservoir due to the overflow of latrines and washout of open-air defecation sites (Gaudart et al. 2013), the contamination rate \(p\) is increased by the rainfall intensity \(J_i(t)\) via a coefficient \(\phi \) (Rinaldo et al. 2012; Righetto et al. 2013).
Disease incidence (i.e. number of new reported cases per unit of time, the quantity usually reported in epidemiological records) can be derived by computing the cumulative reported cases \(C_i(t)\) solving
and differentiating \(C_i(t)\) in time.
As anticipated before, we assume that the exposure rate \(\beta _i(t)\) can decrease as the population awareness of the cholera transmission risk factors increases and the intervention strategies unfold. From a mathematical standpoint, we assume that the local exposure decreases proportionally to the local cumulative attack rate \(C_i/H_i\) through an exponential function:
where \(\beta _0\) is the exposure at the beginning of the epidemic and the parameter \(\psi \) controls the rate at which \(\beta _i(t)\) decreases. The formulation used in Eq. 6 assumes that the awareness of the population increases more in regions hit more severely by the epidemic. This assumption is aimed at mimicking the fact that the health response of the Haiti government and of the partner agencies was targeted to the most-at-risk and plagued communities (de Rochars et al. 2011). Moreover, it is likely that the probability that a person changes her/his behaviour (e.g. the use of treated water, soap, latrines, etc.) in response to an information campaign is higher in communities with higher incidence, where the dramatic effects of the disease are evident.
Schematic representation of the modeling framework. For a detailed description, see Sect. 2.1
2.2 Stochastic formulation
In the stochastic formulation of the model, the population of each node is assumed to be made up of identical individuals classified according to their epidemiological status. Accordingly, the numbers of susceptible, symptomatic infected and recovered individuals hosted in node \(i\) at time \(t\) are discrete stochastic variables denoted as \(\mathcal {S}_i(t)\), \(\mathcal {I}_i(t)\) and \(\mathcal {R}_i(t)\), respectively. Calligraphic letters are used to differentiate stochastic variables from their deterministic counterparts. Concentration of V. cholerae at site \(i\), \(\mathcal {B}_i(t)\), is modeled as a continuous stochastic variable instead, as the number of bacteria is expected to be large enough to allow a continuous representation. Time is also a continuous variable. The state of the system is described by the vector (\(\varvec{\mathcal {S}}\),\(\varvec{\mathcal {I}}\),\(\varvec{\mathcal {R}}\),\(\varvec{\mathcal {B}}\)), where \(\varvec{\mathcal {S}}=(\mathcal {S}_1,\mathcal {S}_2,\ldots ,\mathcal {S}_n)^T\) and the other vectors are defined analogously.
All events involving human individuals (births, deaths and changes of epidemiological status) are treated as stochastic events that occur at rates that depend on the state of the system. Possible events are:
-
1.
birth;
-
2.
death of a susceptible individual;
-
3.
symptomatic infection;
-
4.
death of a symptomatic infected individual for causes other than cholera;
-
5.
cholera-induced death of a symptomatic infected individual;
-
6.
recovery of a symptomatic infected individual;
-
7.
asymptomatic infection;
-
8.
death of a recovered individual;
-
9.
immunity loss of a recovered individual.
Table 1 lists the rates \(\nu _i^k\) at which the generic event \(k\) occurs in node \(i\) and the corresponding state transitions of the system. Analogously to the deterministic approach (Eq. 5), the force of infection is defined as
Note that we do not model individual trips to specific destinations as in agent-based approaches (e.g. Chao et al. 2011), yet human mobility is accounted for by the force of infection (e.g. Xia et al. 2004). The equation that describes the dynamic of the concentration of V. cholerae \(\mathcal {B}_i(t)\) is obtained by substituting deterministic variables with their stochastic counterparts in Eq. (4).
The stochastic model outlined above is too complex to derive an analytical solution for the probability distributions of the state variables (or their moments). To investigate the properties of the system, we therefore resort to a Monte Carlo approach and simulate many different trajectories (realizations) of the process with a stochastic simulator algorithm (SSA, Gillespie 1977). The SSA assumes that event occurrence is a Poisson process whose rate \(\nu \) is defined by summing the rates of occurrence of all possible events:
At every time \(t\), \(\nu \) represents the rate at which the next event is expected to occur. Therefore, the inter-arrival time between two subsequent events is an exponentially distributed random variable with mean \(1/\nu \) (Gillespie 1977). The type of event that will occur is randomly selected among all possible events. Specifically, the probability of selecting event \(k\) in node \(i\) is equal to \(\nu _i^k/\nu \). The state of the system is then updated according to the randomly selected event. The SSA is iterated until the expiration of the simulation horizon.
3 Case study: Haiti cholera epidemic
3.1 Model set-up and data
To derive the computational domain, the Haitian territory (Fig. 2a) is subdivided into watersheds on the basis of hydrologic divides. Human communities are then defined as the population hosted within each watershed. Hydrologic divides can be inferred from drainage directions extracted from digital terrain models [DTM, see e.g. Tarboton (1997)]. We use the DTM provided by the US Geological Survey (USGS, available online at http://seamless.usgs.gov) which has a grid resolution of \(100\) m and a precision of \(\pm 0.5\) m in the elevation field. The first step consists in the determination of the unique steepest-descent flow-path from each pixel to the sea outlet. It is then possible to delineate the river basins, defined as the set of pixels that drain into the same point of the coastline. As this leads to a very heterogeneous basin size distribution, the larger basins have to be split into smaller units according to catchment divides, whereas the coastal (smaller) watersheds are aggregated to match the size of inland watersheds. The use of hydrologically-defined subunits allows to identify the unique hydrological connection from every node to the downstream one (or to the ocean for coastal watersheds) directly. These communities can thus be hierarchically organized within a river network, with the hydrologic connectivity matrix \(\mathbf P \) following directly. Following this procedure, the Haitian territory is subdivided into 365 hydrological subunits with an average extent of 76 km\(^2\) (Fig. 2b).
The population hosted in each hydrologic unit is estimated by using a remotely sensed map of population distribution provided by the Oak Ridge National Laboratory O.R.N.L. (2011). The spatial resolution is \(30 \times 30\) arc-seconds which represent, at that latitude, cells of about 1 km\(^2\) (Fig. 2c). Within hydrologic units, the population is assumed to be perfectly mixed. Distances \(d_{ij}\) among communities are computed using the road network provided by the OpenStreetMap contributors (available on-line at http://www.openstreetmap.org, Fig. 2d). Specifically, we compute the shortest distance along the road network between the centroids of the population distribution of each community.
Daily satellite rainfall estimates \(J_i(t)\) for each community have been computed starting from data collected by the NASA-JAXA’s Tropical Rainfall Measuring Mission (TRMM_3B42 precipitation estimates, see http://trmm.gsfc.nasa.gov/ for details). Rainfall data are spatially distributed with a resolution of 0.25° of latitude and longitude. Precipitation fields are first downscaled to the DTM resolution with nearest neighbor interpolation and then averaged over the watershed area to obtain a representative value for the whole community.
Epidemiological records are provided by the Haitian Ministry of Public Health and Population (available on-line at http://mspp.gouv.ht) and consist of a daily count of the total new reported cases of cholera in the ten Haitian departments (Fig. 2a).
3.2 Model calibration
We use the deterministic formulation presented in Sect. 2.1 to calibrate the model parameters. Specifically, we use the first phase of the epidemic, from November 2010 to the end of 2012, as training set. During this period the number of infected individuals is large and can thus be reasonably approximated with a continuous variable. This hypothesis will be later verified. Simulations of the deterministic formulation are much faster (\(\mathcal {O}\) (\(10^3\)) times) than the stochastic ones, thus allowing the use of efficient iterative calibration schemes. Some of the model parameters can be reliably estimated based on literature values, and epidemiological and demographic records (see Table 2 for an overview). The remaining parameters have been calibrated. By introducing the dimensionless bacterial concentrations \(B_i^*=B_i/K\) it is possible to group three model parameters (namely the rate \(p\) at which bacteria excreted by one infected individual reach and contaminate the local water reservoir, the per capita volume of water reservoir \(c\) and the half-saturation constant \(K\)) into a single ratio \(\theta =p/(cK)\), which is one of the calibrated parameters. The ratio \(\theta \) epitomizes all the parameters related to contamination and sanitation—the higher \(\theta \) the worse the sanitation conditions and the resulting contamination of the environment.
As initial conditions for model simulations we assume that, as of October 20 (\(t=0\)), the values of \(I_i(0)\) match the reported cases detailed in Piarroux et al. (2011). Also, \(B_i(0)\) is assumed to be in equilibrium with the local number of infected cases, i.e. \(B_i^*(0)= \theta I_i(0)/ (H_i \mu _B)\). Moreover, we impose that the whole population is susceptible at the beginning of the epidemic, i.e. \(S_i(0)=H_i-I_i(0)\), because of the lack of any pre-existing immunity (Enserink 2010; Walton and Ivers 2011; Sack 2011; Piarroux et al. 2011).
The calibration approach is based on Markov Chain Monte Carlo (MCMC) sampling. Specifically, we use the DREAM algorithm [Differential Evolution Adaptive Metropolis available online at http://jasper.eng.uci.edu/software.html] (ter Braak and Vrugt 2008), an efficient implementation of MCMC that runs multiple different chains simultaneously to ensure global exploration of the parameter space, and adaptively tunes the scale and orientation of the jumping distribution using Differential Evolution (Storn and Price 1997) and a Metropolis–Hastings update step (Metropolis et al. 1953; Hastings 1970). We adopt the DREAM\(_{\small {ZS}}\) variant of the DREAM algorithm (Vrugt et al. 2009). The algorithm is initialized with broad flat prior distributions (see Table 2) for parameter values and is allowed to run up to convergence (\(\mathcal {O}(10^5)\) iterations). The goodness of each single simulation is computed as the residual sum of squares (RSS) between weekly reported cholera cases in each of the Haitian departments (Fig. 2a) as recorded in the epidemiological data-set and simulated by the model.
3.3 Probability of extinction
To estimate the probability of extinction of the epidemic, we simulate several realizations of the stochastic formulation of the model from October 20, 2010 to December 31, 2017. To project the trajectory of the epidemic in the future, we also need to project rainfall scenarios. They are generated starting from the observed daily fields of precipitation estimates (15-years data-set, 1998–2012). Each month (say, a May) of the rainfall time-series used to force the model from January 2013 to December 2017 is obtained by randomly selecting (with replacement) among all the corresponding months (all the Mays) available. As a result, each sequence of generated rainfall is a standard bootstrapping of the observed data. This procedure allows to generate realistically space–time correlated rainfall fields.
Differently from a standard stochastic SIR model, the absence of infected individuals (\(\varvec{\mathcal {I}}=0\)) is not an absorbing state of the system. In fact, the presence of bacteria that can survive outside the human host may allow for new infections even in absence of other infected individuals. We therefore classify a trajectory as extinct when, from that time on, no new infections are observed in the simulated time span.
Summarizing, to estimate the probability of extinction (i) we sample a parameter set from the posterior distribution obtained in the calibration phase; (ii) we generate a rainfall scenario; and (iii) we simulate the epidemic using the stochastic formulation of the model. The previous points are iterated for \(10^4\) times and the relative proportion of trajectories that go extinct is recorded.
4 Results
Results of the calibration procedure are reported in Table 2. The corresponding fit is illustrated in Fig. 3. We show results aggregated at the country level; notice, however, that the calibration is performed by simultaneously fitting data at a higher spatial resolution—the departmental level shown in Fig. 2a (1,130 data points, \(RSS=2.41 \times 10^8\), Nash-Sutcliffe index \( = 0.79\)). The model shows an overall good agreement with the data, capturing the timing and the magnitude of the peaks correctly. In particular the model grasps the response to heavy rainfall events which promote a seasonal recrudescence of the epidemic. However, the model underestimates the peak of reported cases in spring 2012.
Calibration results indicate a likely lifetime of bacteria in the environment of about 1 month. Similar values have previously been obtained through calibration for the same case study (Tuite et al. 2011) or assumed in modeling studies (Hartley et al. 2006; Andrews and Basu 2011; Chao et al. 2011) based on clinical evidence (Tudor and Strati 1977; Kaper et al. 1995). The fitted value of the symptomatic ratio is close to the qualitative estimate of the World Health Organization (WHO 2010) according to which only 25 % of infected individuals reportedly show symptoms and among these just around 20 % develop profuse diarrhoea requiring medical attention. The immunity loss rate deserves some further considerations. The calibrated value corresponds to an average immunity duration of less than 1 year, which is somewhat shorter than the multi-year estimates usually reported in the literature (Koelle et al. 2005; WHO 2010). Notice, however, that these estimates refer to the duration of the immunity conferred by symptomatic infections, while in our framework \(1/\rho \) refers to the average immunity duration resulting from both symptomatic and asymptomatic infections. The latter are indeed expected to confer shorter protection [e.g. few months according to King et al. (2008)].
To disentangle the impact of each parameter on the dynamics of the epidemic outbreak, we have performed a sensitivity analysis of the model outcomes with respect to variations of the parameter values. In particular, we allow the parameters to vary (\(\pm 20\,\%\) variation with respect to the best-fit parameter set) one by one through repeated model runs. We then compute the variations of simulated total cholera incidence in the calibration phase with respect to the best-fit simulation (Fig. 3c).
Figure 4 shows the projection of the future course of the epidemic obtained using the stochastic formulation of the model forced by the generated rainfall scenarios. Data on incidence during 2013, which became available after the implementation of the model, are also reported for comparison with the model forecast. Projected future patterns show that the annual epidemic cycle is expected to show a lull phase during the dry winter months, followed by an increased incidence caused by spring rainfalls. The epidemic is expected to peak each year during autumn rainfalls. This yearly cycle is progressively attenuated by the decreasing population exposure. On average, the exposure rate is estimated to be reduced by 20, 50 and 55 % at the end of 2010, 2011 and 2012, respectively. At the end of the simulated period, the exposure rate is, on average, approximatively 30 % of its pre-epidemic value. The median incidence values simulated by the deterministic and stochastic formulations of the model during the calibration phase are almost indistinguishable (Figs. 3 and 4, comparison not shown for brevity), supporting the initial hypothesis that during the calibration phase the population of infected individuals is large enough to neglect demographic stochasticity and to approximate state variables with continuous variables. Finally, Fig. 4c shows that the probability that the epidemic goes extinct before the end of 2016 and 2017 is approximately 1 and 7 %, respectively.
We also performed a sensitivity analysis to assess the impact of each parameter on the future trajectory of the epidemic. In particular, we repeated the estimation of the probability of extinction varying, after the calibration horizon (December 31, 2012), each parameter one at a time (\(\pm 20\,\%\)). Figure 5 shows how the probability that the epidemic goes extinct before the end 2017 changes for each parameter variation.
5 Discussion
In this paper, a framework for the estimation of the probability of extinction of large cholera outbreaks has been presented and applied to the Haiti epidemic. Before discussing the actual estimates, which are not exempt from uncertainties and limitations as we shall analyze in this section, we want to highlight the strengths of the method proposed. We use a combination of deterministic and stochastic approaches trying to keep the advantages of both while avoiding their drawbacks. Specifically, the deterministic framework allows for an efficient and reliable calibration of the model parameters. The stochastic framework allows to evaluate the probability of extinction of the epidemic exploring the variability induced by parameter uncertainty, demographic stochasticity and rainfall fluctuations.
Calibration of the continuous deterministic model. a Time series of mean daily rainfall averaged over the Haitian territory. b New weekly cases as reported in the epidemiological records (gray circles) and simulated by the model (blue line). The blue shaded area shows the 5th–95th percentile bounds of the uncertainty related to parameter estimation. c Effects of parameter variations. Shown are variations of total cholera incidence during the calibration phase (October 2010–December 2012) produced by \(\pm 20\,\%\) variations of the parameters. Shaded or open bars represent, respectively, positive or negative variations of the relevant parameters
The results presented in Figs. 3 and 4 show that the model is able to reproduce complex spatio-temporal patterns with a so-far unseen level of detail, at least for the Haiti cholera epidemic. The sensitivity analysis (Fig. 3c) shows that the model results in the calibration phase are robust with respect to parameter variations. Indeed, variations of the model outputs are comparable to (or smaller than) the parameter variations. It is interesting to note the role of hydrologic transport. A positive variation of the rate \(l\) increases the rate at which bacteria are flushed away and lost into the ocean, thus reducing disease incidence. The analysis also shows that the total incidence is not particularly sensitive to variations of the parameters controlling human mobility (\(m\) and \(D\)). This can be explained by the fact that human mobility plays a crucial role at the onset of an outbreak when the infection invades disease-free regions [as shown by Bertuzzo et al. (2011), Rinaldo et al. (2012), Gatto et al. (2012)]; whereas it may becomes less important looking at longer time horizons (27 months in this case) when the disease has already invaded the whole country and epidemic dynamics are mostly controlled by local factors.
The comparison with the incidence data of 2013 (Fig. 4b), which were not used for calibration, provides the most compelling test for the predictive ability of the model. The pattern that actually occurred (a lull phase during winter followed by a slow increase during summer that finally peaks in autumn) was satisfactorily anticipated by our model forecast.
Projection of the future course of the epidemic obtained using the individual-based stochastic model. a Recorded rainfall patterns (gray bars) and median (green line) and 5th–95th percentile bounds (green shaded area) of the generated rainfall scenarios. b New weekly cholera cases as reported in the epidemiological records (gray and red circles) and simulated by the model. The green line and the green shaded area represent the median and the 5th–95th percentile bounds of the simulated trajectories, respectively. c Probability that the epidemic goes extinct before a certain time horizon (black line). The gray shaded area represents the 5th–95th percentile of the uncertainty estimated through a standard bootstrapping (random sampling with replacement) of the simulated trajectories
The results presented in this work strongly support the use of mathematical models for real-time prediction of the evolution of a cholera outbreak. Yet shortcomings remain. For instance, the model underestimates the epidemic peak in spring 2012. Analyzing the epidemiological records in more detail, one can notice that this peak was mostly localized in the capital Port-au-Prince. The comparative mismatch could be caused by an erroneous estimation of rainfall intensity. Indeed, satellite-based estimates of precipitation represent a precious alternative to traditional ground measurements, especially in developing countries where the gauge network is scarce or absent. However, they are not exempt from limitations, especially when looking at very local features (Huffman et al. 2007). Another possible source of such mismatch could be a local outbreak caused by environmental or social factors not directly (or not entirely) linked to rainfall, and therefore not accounted for in the model. This is also supported by the fact that a similar peak was not observed in spring 2013 and the model correctly predicts this feature (Fig. 4b). The analysis of epidemiological reports at the communal level [which are recorded but not yet available to the scientific community, see e.g. Barzilay et al. (2013), Gaudart et al. (2013)] perspectively represents a possible way to reduce structural errors of the model. Such data could shed light on specific transmission processes that become blurred when zooming out at the departmental level.
Effects of parameter variations on the probability that the epidemic goes extinct before the end of 2017. The black vertical line refers to the estimated probability (7 %). Bars show the variations produced by \(\pm 20\,\%\) variations of the parameters. Shaded or open bars represent, respectively, positive or negative variations of the relevant parameters
The sensitivity analysis illustrated in Fig. 5 expectedly reveals that the rate at which the exposure to the risk of cholera decreases as the epidemic unfolds (controlled by the parameter \(\psi \)) is the most important factor for the extinction of the epidemic. According to the calibrated parameters, exposure to cholera was reduced by 20 % at the end of 2010, the time of the main peak of the outbreak, and it is projected to be, on average, 30 % of its pre-epidemic value by the end of 2017. Notice that this estimate should not be interpreted as that the 70 % of the population will no longer be at risk, but rather that the rate at which individuals are exposed to the risk of disease transmission will decrease by 70 % due to the increased population awareness of the modes of cholera transmission. It is difficult to judge if these figures are realistic. The only study that investigates how the behaviour of the population has changed due to the epidemic dates back to the end of 2010 (de Rochars et al. 2011) and reports that household water treatment increased from 30 to 74 % on average. These figures suggest that the population was quite responsive to the campaigns for hygiene promotion set up by the Haiti government and its partner agencies. Moreover, the gradual return of the internally displaced people to their original households (Bengtsson et al. 2011) should generally improve the sanitation conditions. However, the expectation of a progressively decreasing exposure also in the future is far from being certainly matched. In fact, while the Ministry of Health is struggling to find funds for a long-term plan to eliminate cholera through investments in water and sanitation, many non-governmental organizations, which are preciously supporting local health facilities, are pulling out facing the donors’ fatigue (Adams 2013). Moreover it is possible that the gained awareness has a finite memory and could possibly wane if people are not continuously exposed to the risk of cholera. To have a better vision of the spectrum of possible future scenarios we have also repeated the analysis assuming that the exposure will no longer decrease after the calibration horizon—end of 2012. Under this assumption, no extinct trajectories are observed. This analysis highlights how the probability of extinction is very sensitive to this crucial, yet uncertain, parameter.
The results of the sensitivity analysis illustrated in Fig. 5 can also be interpreted to infer the effect of interventions aimed at improving the sanitary conditions on the extinction probability. Extensive constructions of sewage systems and latrines leading to an overall reduction of the contamination rate \(\theta \) of 20 % could increase the probability of eradicating the disease before 2018 up to 36 %. Likewise, an improvement of safe water distribution that can reduce the baseline risk of exposure to contaminated water \(\beta _0\) by 20 %, would result in a 34 % probability of extinction of the outbreak in the same time horizon. Less intuitive is the fact that also an increment of 20 % of the exposure \(\beta _0\) would results in an increased probability of extinction (Fig. 5). This counterintuitive effect derives directly from our simplified assumptions on the development of awareness. Higher exposure increases incidence (see Fig. 3c) which, in turn, increases awareness (Eq. 6), thus leading to a higher probability of extinction. Given the simplified modeling of awareness and the abovementioned uncertainties related to its future development, increasing the exposure to cholera is obviously not a recommended measure to eradicate the disease. The same effect can also be observed for other parameters that exacerbate cholera incidence, namely \(\sigma \), \(\theta \), \(\phi \) and \(m\). On the contrary, reductions of V. cholerae net mortality \(\mu _B\) or hydrologic transport rate \(l\) worsen the disease burden (see Fig. 3c) but reduce the extinction probability. Parameters controlling human mobility (\(m\) and \(D\)) are confirmed to be the least sensitive also for the probability of extinction.
Despite all the uncertainties, our estimates indicate that the extinction of the epidemic in Haiti is a rather unlikely event. This result quantitatively confirms field experts’ feelings that cholera “hasn’t burned itself out” and “won’t just go away” (Adams 2013). In our modeling framework, new infections are promoted by bacteria shed by other infected individuals; no other sources of contamination are considered. However, should clear evidence of an established environmental reservoir of pathogenic V. cholerae that can persist even in the absence of infected individuals (for instance in the estuarine environment) emerge, our estimates should be reconsidered. Including a self-sustained reservoir of V. cholerae in our framework would lead to an endemic dynamics without any possibility of a permanent extinction of the disease. More extensive and targeted environmental field studies to detect reservoirs of bacteria and to identify transmission pathways are therefore called for.
Understanding disease transmission during the lull phases that characterize the dry season is of crucial importance to understand extinction dynamics. However, the particular case definition used by the national cholera surveillance system (Barzilay et al. 2013), which differs from the standard adopted by WHO, could actually lead to on overestimation of the cholera burden during these phases. In fact, Haitian reports also include children under the age of 5, who are excluded by WHO standards because of the high prevalence of acute diarrhea caused by infections other than cholera in this age group. Diarrhea in adults is also likely to be reported as cholera independently of its actual origins because laboratory confirmation could not be performed for every single patient due to the huge number of cases. Rebaudet et al. (2013) estimated a background noise of diarrhea cases not related to cholera of about 250 cases per week. This noise source is not relevant when analyzing outbreak peaks, but it may become important during lull phases. For instance, this value accounts for almost 40 % of the cases reported during February 2012. These simple observations reveal the importance of targeted field epidemiological studies in the epidemic foci to estimate the actual cholera burden, possibly through extensive laboratory confirmations. Lull phases of the epidemic during the dry season are windows of opportunity to fight cholera (Rebaudet et al. 2013). Improving our understanding of the transmission dynamics during these periods would help design specific intervention strategies whose effects can be estimated by the proposed modeling framework. A real-time assessment not only of the future course of an outbreak but also of the effects of alternative intervention strategies is, in our opinion, the next important development that modern mathematical epidemiology should focus on in order to become an essential tool for emergency management.
References
Adams P (2013) Cholera in Haiti takes a turn for the worse. Lancet 381(9874):1264
Alam M, Weppelmann T, Weber C, Johnson J, Rashid M, Birch C, Brumback B, de Rochars V, Ali A (2014) Monitoring water sources for environmental reservoirs of toxigenic Vibrio cholerae O1 Haiti. Emerg Infect Dis 20(3):356–363
Andrews J, Basu S (2011) Transmission dynamics and control of cholera in Haiti: an epidemic model. Lancet 377:1248–1252
Angulo J, Yu HL, Langousis A, Madrid A, Christakos G (2012) Modeling of space–time infectious disease spread under conditions of uncertainty. Int J Geogr Inf Sci 26(10):1751–1772
Angulo J, Yu HL, Langousis A, Kolovos A, Wang J, Madrid A, Christakos G (2013) Spatiotemporal infectious disease modeling: A BME-SIR approach. PLoS One 8(9):e72168
Azaele S, Maritan A, Bertuzzo E, Rodriguez-Iturbe I, Rinaldo A (2010) Stochastic dynamics of cholera epidemics. Phys Rev E 81(5):051901
Baron S, Lesne J, Moore S, Rossignol E, Rebaudet S, Gazin P, Barrais R, Magloire R, Boncy J, Piarroux R (2013) No evidence of significant levels of toxigenic V. cholerae O1 in the Haitian aquatic environment during the 2012 rainy season. PLoS Curr. doi:10.1371/currents.outbreaks.7735b392bdcb749baf5812d2096d331e
Bartlett M (1957) Measles periodicity and community size. J R Stat Soc Ser A 120(1):48–70
Barzilay E, Schaad N, Magloire R, Mung K, Boncy J, Dahourou G, Mintz E, Steenland M, Vertefeuille J, Tappero J (2013) Cholera surveillance during the Haiti epidemic: the first 2 years. N Engl J Med 368(7):599–609
Bengtsson L, Lu X, Thorson A, Garfield R, von Schreeb J (2011) Improved response to disasters and outbreaks by tracking population movements with mobile phone network data: a post-earthquake geospatial study in Haiti. PLoS Med 8:e1001083
Bertuzzo E, Azaele S, Maritan A, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2008) On the space–time evolution of a cholera epidemic. Water Resour Res 44:W01424
Bertuzzo E, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2010) On spatially explicit models of cholera epidemics. J R Soc Interface 7:321–333
Bertuzzo E, Mari L, Righetto L, Gatto M, Casagrandi R, Rodriguez-Iturbe I, Rinaldo A (2011) Prediction of the spatial evolution and effects of control measures for the unfolding Haiti cholera outbreak. Geophys Res Lett 38:L06403
Chao DL, Halloran ME, Longini IM Jr (2011) Vaccination strategies for epidemic cholera in Haiti with implications for the developing world. Proc Natl Acad Sci USA 108(17):7081–7085
Chin C et al (2011) The origin of the Haitian cholera outbreak strain. N Engl J Med 364:33–42
CIA (2009) CIA’s world factbook. https://www.cia.gov/library/publications/the-world-factbook/index.html
Codeço C (2001) Endemic and epidemic dynamics of cholera: the role of the aquatic reservoir. BMC Infect Dis 1:1
Colwell R (1996) Global climate and infectious disease: the cholera paradigm. Science 274:2025–2031
de Rochars V, Tipret J, Patrick M, Jacobson L, Barbour K, Berendes D, Bensyl D, Frazier C, Domercant J, Archer R, Roels T, Tappero J, Handzel T (2011) Knowledge, attitudes, and practices related to treatment and prevention of cholera, Haiti, 2010. Emerg Infect Dis 17(11):2158–2161
Eisenberg M, Kujbida G, Tuite A, Fisman D, Tien J (2013) Examining rainfall and cholera dynamics in Haiti using statistical and dynamic modeling approaches. Epidemics 5(4):197–207
Enserink M (2010) Infectious diseases: Haiti’s outbreak is latest in cholera’s new global assault. Science 330:738–739
Erlander S, Stewart NF (1990) The gravity model in transportation analysis: theory and extensions. VSP Books, Zeist
Frerichs RR, Keim PS, Barrais R, Piarroux R (2012) Nepalese origin of cholera epidemic in Haiti. Clin Microbiol Infect 18(6):E158–E163
Gatto M, Mari L, Bertuzzo E, Casagrandi R, Righetto L, Rodriguez-Iturbe I, Rinaldo A (2012) Generalized reproduction numbers and the prediction of patterns in waterborne disease. Proc Natl Acad Sci USA 109(48):19703–19708
Gaudart J, Rebaudet S, Barrais R, Boncy J, Faucher B, Piarroux M, Magloire R, Thimothe G, Piarroux R (2013) Spatio-temporal dynamics of cholera during the first year of the epidemic in Haiti. PLoS Negl Trop Dis 7(4):e2145
Gillespie D (1977) Exact stochastic simulation of coupled chemical reactions. J Phys Chem 81:2340–2361
Griffith D, Christakos G (2007) Medical geography as a science of interdisciplinary knowledge synthesis under conditions of uncertainty. Stoch Environ Res Risk Assess 21(5):459–460
Hartley D, Morris J, Smith DL (2006) Hyperinfectivity: A critical element in the ability of V. cholerae to cause epidemics? PLoS Med 3:63–69
Hastings WK (1970) Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57:97–109
Hendriksen R et al (2011) Population genetics of Vibrio cholerae from Nepal in 2010: evidence on the origin of the Haitian outbreak. MBio 2:e00157
Hill VR, Cohen N, Kahler AM, Jones JL, Bopp CA, Marano N, Tarr CL, Garrett NM, Boncy J, Henry A, Gomez GA, Wellman M, Curtis M, Freeman MM, Turnsek M, Benner RA Jr, Dahourou G, Espey D, DePaola A, Tappero JW, Handzel T, Tauxe RV (2011) Toxigenic Vibrio cholerae O1 in water and seafood, Haiti. Emerg Infect Dis 17(11):2147–2150
Huffman GJ, Adler RF, Bolvin DT, Gu G, Nelkin EJ, Bowman KP, Hong Y, Stocker EF, Wolff DB (2007) The TRMM multisatellite precipitation analysis (TMPA): quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J Hydrometeorol 8(1):38–55
Islam M, Mahmuda S, Morshed M, Bakht H, Khan M, Sack R, Sack D (2004) Role of cyanobacteria in the persistence of Vibrio cholerae O139 in saline microcosms. Can J Microbiol 50:127–131
Jutla A, Akanda A, Huq A, Faruque A, Colwell R, Islam S (2013a) A water marker monitored by satellites to predict seasonal endemic cholera. Remote Sens Lett 4(8):822–831
Jutla A, Akanda A, Islam S (2013b) A framework for predicting endemic cholera using satellite derived environmental determinants. Environ Model Softw 47:148–158
Kaper JB, Morris JG, Levine MM (1995) Cholera. Clin Microbiol Rev 8:48–86
King A, Ionides E, Pascual M, Bouma M (2008) Inapparent infections and cholera dynamics. Nature 454:877–880
Koelle K, Rodo X, Pascual M, Yunus M, Mustafa G (2005) Refractory periods and climate forcing in cholera dynamics. Nature 436:696–700
Lipp E, Huq A, Colwell R (2002) Effects of global climate on infectious disease: the cholera model. Clin Microbiol Rev 15(4):757–770
Mari L, Bertuzzo E, Righetto L, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2012a) On the role of human mobility in the spread of cholera epidemics: towards an epidemiological movement ecology. Ecohydrology 5:531–540
Mari L, Bertuzzo E, Righetto L, Gatto M, Casagrandi R, Rodriguez-Iturbe I, Rinaldo A (2012b) Modelling cholera epidemics: the role of waterways, human mobility and sanitation. J R Soc Interface 9:376–388
Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E (1953) Equations of state calculations by fast computing machines. J Chem Phys 21:1087–1092
Mukandavire Z, Smith DL, Morris JG Jr (2013) Cholera in Haiti: reproductive numbers and vaccination coverage estimates. Nat Sci Rep 3:997
Nelson EJ, Harris JB, Calderwood SB, Camilli A (2009) Cholera transmission: the host, pathogen and bacteriophage dynamic. Nat Rev Microbiol 7:693–702
ORNL (2011) Haiti population data. http://www.ornl.gov/sci/landscan/index.shtml. Oak Ridge National Laboratory
Piarroux R, Barrais R, Faucher B, Haus R, Piarroux M, Gaudart J, Magloire R, Raoult D (2011) Understanding the cholera epidemic, Haiti. Emerg Infect Dis 17:1161–1168
Rebaudet S, Gazin P, Barrais R, Moore S, Rossignol E, Barthelemy N, Gaudart J, Boncy J, Magloire R, Piarroux R (2013) The dry season in Haiti: a window of opportunity to eliminate cholera. PLoS Curr 1
Righetto L, Bertuzzo E, Mari L, Schild E, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2013) Rainfall mediations in the spreading of epidemic cholera. Adv Water Resour 60:34–46
Rinaldo A, Bertuzzo E, Mari L, Righetto L, Blokesch M, Gatto M, Casagrandi R, Murray M, Vesenbeckh S, Rodriguez-Iturbe I (2012) Reassessment of the 2010–2011 Haiti cholera outbreak and rainfall-driven multiseason projections. Proc Natl Acad Sci USA 109(17):6602–6607
Sack D (2011) How many cholera deaths can be averted in Haiti? Lancet 377:1214–1216
Storn R, Price K (1997) Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim 11:341–359
Tarboton D (1997) A new method for the determination of flow directions and contributing areas in grid digital elevation models. Water Resour Res 33:309–319
ter Braak CJF, Vrugt JA (2008) Differential evolution Markov Chain with snooker updater and fewer chains. Stat Comput 18:435–446
Tudor V, Strati I (1977) Smallpox: cholera. Abacus Press, Tunbridge Wells
Tuite A, Tien J, Eisenberg M, Earn D, Ma J, Fisman D (2011) Cholera epidemic in Haiti, 2010: using a transmission model to explain spatial spread of disease and identify optimal control interventions. Ann Intern Med 154:593–601
Vital M, Fchslin H, Hammes F, Egli T (2007) Growth of Vibrio cholerae O1 Ogawa Eltor in freshwater. Microbiology 153(7):1993–2001
Vrugt JA, ter Braak CJF, Diks CGH, Robinson BA, Hyman JM, Higdon D (2009) Accelerating Markov Chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int J Nonlinear Sci Numer Simul 10:271–288
Walton D, Ivers L (2011) Responding to cholera in post-earthquake Haiti. N Engl J Med 364:3–5
WHO (2010) Prevention and control of cholera outbreaks: WHO policy and recommendations. Technical report World Health Organization, Regional Office for the Eastern Mediterranean
Xia Y, Bjørnstad ON, Grenfell BT (2004) Measles metapopulation dynamics: a gravity model for epidemiological coupling and dynamics. Am Nat 164:267–281
Acknowledgments
E. Bertuzzo, L. Mari and A.Rinaldo acknowledge the support provided by the European Research Council (ERC) advanced Grant program through the project “River networks as ecological corridors for species, populations and waterborne disease” (RINEC 227612). E. Bertuzzo, F. Finger and A. Rinaldo acknowledge the support from the Swiss National Science Foundation (SNF/FNS) project “Dynamics and controls of large-scale cholera outbreaks” (DYCHO CR23I2 _138104).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Bertuzzo, E., Finger, F., Mari, L. et al. On the probability of extinction of the Haiti cholera epidemic. Stoch Environ Res Risk Assess 30, 2043–2055 (2016). https://doi.org/10.1007/s00477-014-0906-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-014-0906-3