Skip to main content
SpringerLink
Log in

The comparison of sensitivity analysis of hydrological uncertainty estimates by GLUE and Bayesian method under the impact of precipitation errors

  • Original Paper
  • Published:
Stochastic Environmental Research and Risk Assessment Aims and scope Submit manuscript

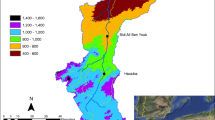
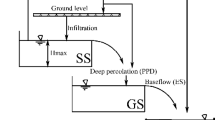
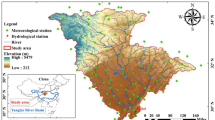
Abstract

The input uncertainty is as significant as model error, which affects the parameter estimation, yields bias and misleading results. This study performed a comprehensive comparison and evaluation of uncertainty estimates according to the impact of precipitation errors by GLUE and Bayesian methods using the Metropolis Hasting algorithm in a validated conceptual hydrological model (WASMOD). It aims to explain the sensitivity and differences between the GLUE and Bayesian method applied to hydrological model under precipitation errors with constant multiplier parameter and random multiplier parameter. The 95 % confidence interval of monthly discharge in low flow, medium flow and high flow were selected for comparison. Four indices, i.e. the average relative interval length, the percentage of observations bracketed by the confidence interval, the percentage of observations bracketed by the unit confidence interval and the continuous rank probability score (CRPS) were used in this study for sensitivity analysis under model input error via GLUE and Bayesian methods. It was found that (1) the posterior distributions derived by the Bayesian method are narrower and sharper than those obtained by the GLUE under precipitation errors, but the differences are quite small; (2) Bayesian method performs more sensitive in uncertainty estimates of discharge than GLUE according to the impact of precipitation errors; (3) GLUE and Bayesian methods are more sensitive in uncertainty estimate of high flow than the other flows by the impact of precipitation errors; and (4) under the impact of precipitation, the results of CRPS for low and medium flows are quite stable from both GLUE and Bayesian method while it is sensitive for high flow by Bayesian method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Ajami NK, Duan Q, Sorooshian S (2007) An integrated hydrologic Bayesian multimodel combination framework: confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour Res 43(1):W01403

    Article  Google Scholar 

  • Alvisi S, Creaco E, Franchini M (2012) Crisp discharge forecasts and grey uncertainty bands using data-driven models. Hydrol Res 43(5):589–602

    Article  Google Scholar 

  • Bernardo JM, Smith AF (1994) Bayesian theory. Wiley, Chichester

    Book  Google Scholar 

  • Beven KJ, Binley A (1992) Future of distributed models: model calibration and uncertainty prediction. Hydrol Process 6(3):279–298

    Article  Google Scholar 

  • Beven KJ, Freer J (2001) Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J Hydrol 249(1–4):11–29

    Article  Google Scholar 

  • Blasone RS, Madsen H, Rosbjerg D (2008a) Uncertainty assessment of integrated distributed hydrological models using GLUE with Markov chain Monte Carlo sampling. J Hydrol 353(1–2):18–32

    Article  Google Scholar 

  • Blasone RS et al (2008b) Generalized likelihood uncertainty estimation (GLUE) using adaptive Markov Chain Monte Carlo sampling. Adv Water Resour 31(4):630–648

    Article  Google Scholar 

  • Carlos MJ, Bera AK (1980) Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Econ Lett 6(3):255–259

    Article  Google Scholar 

  • Chib S, Greenberg E (1995) Understanding the Metropolis–Hastings algorithm. Am Stat 49:327–335

    Google Scholar 

  • Duan Q, Ajami NK, Gao X, Sorooshian S (2007) Multi-model ensemble hydrologic prediction using Bayesian model averaging. Adv Water Resour 30(5):1371–1386

    Article  Google Scholar 

  • Engeland K, Gottschalk L (2002) Bayesian estimation of parameters in a regional hydrological model. Hydrol Earth Syst Sci 6(5):883–898

    Article  Google Scholar 

  • Engeland K, Xu CY, Gottschalk L (2005) Assessing uncertainties in a conceptual water balance model using Bayesian methodology. Hydrol Sci J 50(1):45–63

    Article  Google Scholar 

  • Engeland K, Renard B, Steinsland I, Kolberg S (2010) Evaluation of statistical models for forecast errors from the HBV model. J Hydrol 384(1–2):142–155

    Article  Google Scholar 

  • Freer J, Beven K, Ambroise B (1996) Bayesian estimation of uncertainty in runoff prediction and the value of data: an application of the GLUE approach. Water Resour Res 32(7):2161–2174

    Article  Google Scholar 

  • Gelman A, Rubin DB (1992) Inference from iterative simulation using multiple sequences. Stat Sci 7:457–472

    Article  Google Scholar 

  • Hastings WK (1970) Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57(1):97–109

    Article  Google Scholar 

  • Hersbach H (2000) Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather Forecast 15(5):559–570

    Article  Google Scholar 

  • Jin X, Xu C-Y, Zhang Q, Singh VP (2010) Parameter and modeling uncertainty simulated by GLUE and a formal Bayesian method for a conceptual hydrological model. J Hydrol 383(3–4):147–155

    Article  Google Scholar 

  • Kavetski D, Franks S, Kuczera G (2002) Confronting input uncertainty in environmental modelling. In: Gupta HV, Sorooshian S, Rousseau AN, Turcotte R (eds) Calibration of watershed models. AGU Water Science and Applications Series. AGU, Washington, pp 49–68

    Google Scholar 

  • Kavetski D, Kuczera G, Franks SW (2006a) Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory. Water Resour Res 42(3):W03407

    Google Scholar 

  • Kavetski D, Kuczera G, Franks SW (2006b) Bayesian analysis of input uncertainty in hydrological modeling: 2.Application. Water Resour Res 42(3):W03407

    Google Scholar 

  • Kizza M, Guerrero J-L, Rodhe A, Xu C-Y, Ntale HK (2013) Modelling catchment inflows into Lake Victoria: regionalisation of the parameters of a conceptual water balance model. Hydrol Res. doi:10.2166/nh.2012.152

  • Krzysztofowicz R (1999) Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resour Res 35(9):2739–2750

    Article  Google Scholar 

  • Kuczera G, Parent E (1998) Monte Carlo assessment of parameter uncertainty in conceptual catchment models: the Metropolis algorithm. J Hydrol 211(1–4):69–85

    Article  Google Scholar 

  • Li L, Xia J, Xu C-Y, Chu J, Wang R (2009) Analyse the sources of equifinality in hydrological model using GLUE methodology. Hydroinformatics in Hydrology, Hydrogeology and Water Resources. In: Proceedings of Symposium JS.4 at the Joint IAHS & IAH Convention, Hyderabad, India, September 2009. IAHS Publications, vol. 331, pp. 130–138

  • Li L, Xia J, Xu C-Y, Singh VP (2010) Evaluation of the subjective factors of the GLUE method and comparison with the formal Bayesian method in uncertainty assessment of hydrological models. J Hydrol 390(3–4):210–221

    Article  Google Scholar 

  • Li L, Xu C-Y, Xia J, Engeland K, Reggiani P (2011) Uncertainty estimates by Bayesian method with likelihood of AR (1) plus Normal model and AR (1) plus multi-normal model in different time-scales hydrological models. J Hydrol 406(1–2):54–65

    Article  Google Scholar 

  • Li L, Xu C-Y, Engeland K (2013a) Development and comparison in uncertainty assessment based Bayesian modularization method in hydrological modeling. J Hydrol 486:384–394

    Article  Google Scholar 

  • Li L, Ngongondo CS, Xu C-Y, Gong L (2013b) Comparison of the global TRMM and WFD precipitation datasets in driving a large-scale hydrological model in Southern Africa. Hydrol Res. doi:10.2166/nh.2012.175

  • Lilliefors HW (1967) On the Kolmogorov–Smirnov test for normality with mean and variance unknown. J Am Stat Assoc 62(318):399–402

    Article  Google Scholar 

  • Liu Z, Martina MLV, Todini E (2005) Flood forecasting using a fully distributed model: application of the TOPKAPI model to the Upper Xixian Catchment. Hydrol Earth Syst Sci 9(4):347–364

    Article  Google Scholar 

  • Marshall L, Nott D, Sharma A (2007) Towards dynamic catchment modelling: a Bayesian hierarchical mixtures of experts framework. Hydrol Process 21(7):847–861

    Article  Google Scholar 

  • Montanari A (2007) What do we mean by ‘uncertainty’? The need for a consistent wording about uncertainty assessment in hydrology. Hydrol Process 21:841–845

    Article  Google Scholar 

  • Refsgaard JC, Storm B (1996) Construction, calibration and validation of hydrological models. Distrib Hydrol Model 22:41–54

    Article  Google Scholar 

  • Refsgaard JC, Van der Sluijs JP, Brown J, Van der Keur P (2006) A framework for dealing with uncertainty due to model structure error. Adv Water Resour 29(11):1586–1597

    Article  Google Scholar 

  • Ren ZH, Wang GL, Zou FL, Zhang HZ (2003) The research of precipitation of precipitation measurement errors in China. Acta Meteorol Sin 61(5):621–627

    Google Scholar 

  • Renard B, Kavetski D, Thyer M, Kuczera G, Franks S (2009) Understanding predictive uncertainty in hydrologic modeling: the challenge of identifying input and structural errors. Water Resour Res 46:W05521

    Google Scholar 

  • Shen Z, Chen L, Chen T (2013) The influence of parameter distribution uncertainty on hydrological and sediment modeling: a case study of SWAT model applied to the Daning watershed of the Three Gorges Reservoir Region, China. Stoch Environ Res Risk Assess 27(1):235–251

    Article  Google Scholar 

  • Smith P, Beven KJ, Tawn JA (2008) Informal likelihood measures in model assessment: theoretic development and investigation. Adv Water Resour 31(8):1087–1100

    Article  Google Scholar 

  • Thiemann M, Trosset M, Gupta H, Sorooshian S (2001) Bayesian recursive parameter estimation for hydrologic models. Water Resour Res 37(10):2521–2535

    Article  Google Scholar 

  • Tsai Frank T-C (2010) Bayesian model averaging assessment on groundwater management under model structure uncertainty. Stoch Environ Res Risk Assess 24(6):845–861

    Article  Google Scholar 

  • Vogel RM, Stedinger JR, Batchelder R, Lee SU (2008) Appraisal of the generalized likelihood uncertainty estimation (GLUE) Method. American Society of Civil Engineers, Reston

    Google Scholar 

  • Vrugt JA, Gupta HV, Bouten W, Sorooshian S (2003a) A shuffled complex evolution metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour Res 39(8):1201

    Google Scholar 

  • Vrugt JA, Gupta HV, Bouten W, Sorooshian S (2003b) A shuffled complex evolution metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour Res 39(8):1201

    Google Scholar 

  • Vrugt JA, ter Braak CJF, Gupta HV, Robinson BA (2009) Equifinality of formal (DREAM) and informal (GLUE) bayesian approaches in hydrologic modeling? Stoch Environ Res Risk Assess 23(7):1011–1026

    Article  Google Scholar 

  • Wang G (2005) Theory and method of distributed time-variant gain model. Institute of Geographic Sciences and Natural Resources Research, CAS. Beijing, Ph.D (in Chinese)

  • Wang G, Xia J, Chen J (2009) Quantification of effects of climate variations and human activities on runoff by a monthly water balance model: a case study of the Chaobai River basin in northern China. Water Resour Res 45(7):W00A11

    Google Scholar 

  • Wolff M, Isaksen K, Brækkan R, Alfnes E, Petersen-Øverleir A, Ruud E (2013) Measurements of wind-induced loss of solid precipitation: description of a Norwegian field study. Hydrol Res 44(1):35–43. doi:10.2166/nh.2012.166

    Article  Google Scholar 

  • Xiong L, Wan M, Wei X, O’Connor KM (2009) Indices for assessing the prediction bounds of hydrological models and application by generalized likelihood uncertainty estimation. Hydrol Sci J 54(5):852–871

    Article  Google Scholar 

  • Xu C-Y (2002) WASMOD—the water and snow balance MODelling system. In: Singh VP, Frevert DK (eds) Mathematical models of small watershed hydrology and applications. Water Resources Publications, LLC, Chelsea, pp 555–590

    Google Scholar 

  • Yang J, Reichert P, Abbaspour KC (2007a) Bayesian uncertainty analysis in distributed hydrologic modeling: a case study in the Thur River basin (Switzerland). Water Resour Res 43(10):W10401

    Article  Google Scholar 

  • Yang J, Reichert P, Abbaspour KC, Yang H (2007b) Hydrological modelling of the Chaohe Basin in China: statistical model formulation and Bayesian inference. J Hydrol 340(3–4):167–182

    Article  Google Scholar 

  • Yang J, Reichert P, Abbaspour KC, Xia J, Yang H (2008) Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J Hydrol 358(1–2):1–23

    Article  Google Scholar 

Download references

Acknowledgments

This study was supported by the Research Council of Norway, Research Project-JOINTINDNOR 203867, Department of Science and Technology, Govt. of India, Project 190159/V10 (SoCoCA) and Project NORINDIA 806793. The second author was also supported by Program of Introducing Talents of Discipline to Universities—the 111 Project of Hohai University.

Author information

Authors and Affiliations

  1. Uni Climate, Uni Research, Bergen, Norway

    Lu Li

  2. Bjerknes Centre for Climate Research, Bergen, Norway

    Lu Li

  3. Department of Geosciences, University of Oslo, Oslo, Norway

    Chong-Yu Xu

  4. Department of Earth Sciences, Uppsala University, Uppsala, Sweden

    Chong-Yu Xu

Authors
  1. Lu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chong-Yu Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lu Li.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, L., Xu, CY. The comparison of sensitivity analysis of hydrological uncertainty estimates by GLUE and Bayesian method under the impact of precipitation errors. Stoch Environ Res Risk Assess 28, 491–504 (2014). https://doi.org/10.1007/s00477-013-0767-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00477-013-0767-1

Keywords

Search

Navigation