Skip to main content
SpringerLink
Log in

Inference for the truncated exponential distribution

  • Original Paper
  • Published:
Stochastic Environmental Research and Risk Assessment Aims and scope Submit manuscript

Abstract

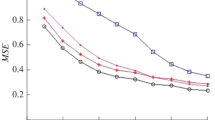
The constructed estimator is introduced for the right truncation point of the truncated exponential distribution. The new estimator is most efficient in important ranges of truncation points for finite sample sizes. The introduced inverse mean squared error clearly indicates the good behaviour of the new estimator. The estimation of the scaling parameter is considered in all discussions and computations. The methods and models of the extreme value theory are not appropriate to estimate the truncation point because they work only in the case of very large sample sizes. Furthermore, a procedure for a first goodness-of-fit test is introduced. All this has been researched by extensive Monte Carlo simulations for different truncation points and sample sizes. Finally, the new inference methods are applied at the end for the random distribution of wildfire sizes and earthquake magnitudes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Bayrak Y, Öztürk S, Cinar H, Koravos GC, Tsapanos TM (2008) Regional variation of the ω–upper bound magnitude of GIII distribution in and around Turkey: Tectonic implications for earthquake hazards. Pure Appl Geophys 165:1367–1390

    Article  Google Scholar 

  • Beauval C, Scotti O (2004) Quantifying sensitivities of PSHA for France to earthquake catalog uncertainties, truncation of ground-motion bariability, and magnitude limits. Bull Seismol Soc Am 94:1579–1594

    Article  Google Scholar 

  • Beg MA (1982) Optimal Tests and Estimators for Truncated Exponential Families. Metrika 29:103–113

    Article  Google Scholar 

  • Beirlant J, Goegebeur Y, Segers J, Teugels J (2004a) Statistics of extremes—theory and application. Wiley series in probability and statistics. John Wiley, Chichester

    Book  Google Scholar 

  • Beirlant J, Goegebeur Y, Segers J, Teugels J (2004b) Statistics of extremes—theory and application. http://lstat.kuleuven.be/Wiley/. Accessed date Dec 2009

  • Christopeit N (1994) Estimating parameters of an extreme value distribution by the method of moments. J Stat Plan Inference 41:173–186

    Article  Google Scholar 

  • Cooke P (1979) Statistical inference for bounds for random variables. Biometrika 66:367–374

    Article  Google Scholar 

  • Cosentino P, Ficarra V, Luzio D (1977) Truncated exponential frequency—magnitude relationship in earthquake statistics. Bull Seismol Soc Am 67:1615–1623

    Google Scholar 

  • Cumming SG (2001) A parametric model of the fire-size distribution. Can J For Res 31:1297–1303

    Article  Google Scholar 

  • Dargahi-Nourbary GR (1983) A procedure for the estimation of the upper bound for earthquake magnitudes. Phys Earth Planet Inter 33:91–93

    Article  Google Scholar 

  • de Haan L, Ferreira A (2006) Extreme value theory—an introduction, Springer series in operations research and financial engineering. Soringer, USA

    Google Scholar 

  • Deemer WL, Votaw DF (1955) Estimation of parameters of truncated or censored exponential distributions. Ann Math Stat 26:498–504

    Article  Google Scholar 

  • Dixit UJ, Nasiri PN (2006) Estimation of parameters of a right truncated exponential distribution. Stat Pap 49:225–236

    Article  Google Scholar 

  • Greenwood JA, Landwehr JM, Matalas NC, Wallis JR (1979) Probability weighted moments: definition and relation to parameters of several distributions expressible in inverse form. Water Resour Res 15:1049–1054

    Article  Google Scholar 

  • Gutenberg B, Richter CF (1941) Seismicity of the earth. Geol Soc Am Spec Pap 34:1–131

    Google Scholar 

  • Gutenberg B, Richter CF (1954) Seismicity of the earth and associated phenomena, 2nd edn. Princeton University Press, Princeton

    Google Scholar 

  • Hanks TC, Kanamori H (1979) A moment magnitude scale. J Geophys Res 84:2348–2350

    Article  Google Scholar 

  • Hannon PM, Dahiya RC (1999) Estimation of parameters for the truncated exponential distribution. Commun Stat Theory Methods 28:2591–2612

    Article  Google Scholar 

  • Hosking JRM, Wallis JR (1987) Parameter and quantil estimation for the generalized Pareto distribution. Technometrics 27:251–261

    Article  Google Scholar 

  • Hosking JRM, Wallis JR, Wood EF (1985) Estimation of the generalized extreme-value distribution by the method of probability-weighted moments. Technometrics 29:339–349

    Article  Google Scholar 

  • Kijko A (1983) A modified form of the first Gumbel distribution: model for the occurrence of large earthquakes, part II: estimation of parameters. Acta Geophysica 31:27–39

    Google Scholar 

  • Kijko A (2004) Estimation of the maximum earthquake magnitude mmax. Pure Appl Geophys 161:1655–1681

    Article  Google Scholar 

  • Kijko A, Graham G (1998) Parametric-historic procedure for probabilistic seismic hazard analysis part I: estimation of maximum regional magnitude mmax. Pure Appl Geophys 152:413–442

    Article  Google Scholar 

  • Leadbetter MR, Lindgren G, Rootzén H (1983) Extremes and related properties of random sequences and processes. Springer, New York

    Book  Google Scholar 

  • Mueller S (2010) The influence of maximum magnitude on seismic-hazard estimates in the Central and Eastern United States. Bul Seismol Soc Am 100:699–711

    Article  Google Scholar 

  • Nordquist JN (1945) Theory of largest values applied to earthquake magnitudes. Trans Am Geophs Union 26:29–31

    Google Scholar 

  • Page R (1968) Aftershocks and micro aftershocks of the great Alaska earthquake of 1964. Bul Seismol Soc Am 58:1131–1168

    Google Scholar 

  • Pisarenko VF (1991) Statistical evaluation of maximum possible earthquake. Phys Solid Earth 27:757–763

    Google Scholar 

  • Pisarenko VF, Lyubushin AA, Lysenko VB, Golubeva TV (1996) Statistical estimation of seismic hazard parameters: maximum possible magnitude and related parameters. Bul Seismol Soc Am 86:691–700

    Google Scholar 

  • Pisarenko VF, Sornette A, Sornette D, Rodkin M (2008) New approach to the characterization of Mmax and of the tail of the distribution of earthquake magnitudes. Pure Appl Geophys 165:847–888

    Article  Google Scholar 

  • Quenouille MH (1956) Notes on bias in estimation. Biometrika 43:353–360

    Google Scholar 

  • Raschke M (2009) The biased transformation and its application in Goodness-of-fit test for the gamma and beta distribution. Commun Stat Comput Simul 9:1870–1890

    Article  Google Scholar 

  • Raschke M (2010) Empirical behaviour of tests for the beta distribution and their application in environmental research. Stoch Environ Res Risk Assess. doi:10.1007/s00477-010-0410-3

  • Réyni A (1953) On the theory of order statistics. Acta Mathematica Academiae Scientarium Hungaricae 4:191–232

    Article  Google Scholar 

  • Robson DS, Whitlock JH (1964) Estimation of a truncation point. Biometrica 5(1):33–39

    Google Scholar 

  • Sheikha AK, Boahb JK, Younasa M (1989) Truncated extreme value model for pipeline reliability. Reliab Eng Syst Saf 25:1–14

    Article  Google Scholar 

  • Stephens MA (1986) Tests based on the EDF statistics. In: D’Agostino RB, Stephens MA (eds) Goodness-of-fit techniques. Marcel Dekker, New York

    Google Scholar 

  • Sukhatme PV (1937) Tests of significance for samples of χ2-population with two degrees of freedom. Ann Eugen 8:52–56

    Article  Google Scholar 

  • Tate RF (1959) Unbiased estimation: function of location and scale parameters. Ann Math Statist 30:331–366

    Article  Google Scholar 

  • Tuncel M, Yegulap M, Kuo JT (1974) Statistical prediction of the occurrence of maximum magnitude earthquakes. Bul Seismol Soc Am 64:393–414

    Google Scholar 

Download references

Acknowledgement

The author thanks S.G. Cumming for providing wildfire data.

Author information

Authors and Affiliations

  1. Gustav-Freytag-Str. 24, Leipzig, Germany

    Mathias Raschke

Authors
  1. Mathias Raschke
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mathias Raschke.

Appendix

Appendix

See Tables 2, 3, 4, 5, 6 7, 8 and 9.

Table 2 Bias and MSE of \( \hat{\theta}\) for sample size n = 20
Full size table
Table 3 Bias and MSE of \( \hat{T} \) for sample size n = 20
Full size table
Table 4 Bias and MSE of \( \hat{\theta}\) for sample size n = 100
Full size table
Table 5 Bias and MSE of \( \hat{T} \) for sample size n = 100
Full size table
Table 6 Inverse Bias and inverse MSE of T for sample size n = 20
Full size table
Table 7 Inverse Bias and inverse MSE of T for sample size n = 100
Full size table
Table 8 Ratio of rejections with the Anderson–Darling test for the exponential distribution for sample size n = 20 and different levels of significance α
Full size table
Table 9 Ratio of rejections with the Anderson–Darling test for the exponential distribution for sample size n = 100 and different levels of significance α
Full size table

Rights and permissions

Reprints and permissions

About this article

Cite this article

Raschke, M. Inference for the truncated exponential distribution. Stoch Environ Res Risk Assess 26, 127–138 (2012). https://doi.org/10.1007/s00477-011-0458-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00477-011-0458-8

Keywords

Search

Navigation