Regression Estimator for the Tail Index

Abstract

Estimating the tail index parameter is one of the primal objectives in extreme value theory. For heavy-tailed distributions the Hill estimator is the most popular way to estimate this parameter. Several recent publications’ aim was to improve the Hill estimator, using different methods, for example the bootstrap, or the Kolmogorov–Smirnov metric. These methods are asymptotically consistent, but for tail index $\xi >0.5$ the estimations fail to approach the theoretical value for realistic sample sizes. In this paper, we introduce new empirical methods, which combine the advantages of the Kolmogorov–Smirnov approach and the bootstrap. We demonstrate that our estimators are able to estimate large tail index parameters well and might also be useful for relatively small sample sizes. As an application, we consider the classic Danish fire data set and the most destructive natural disasters in Europe.

1 Introduction

In many applications of probability theory and statistics the most important problem of research is to estimate the high quantiles of a distribution, for example solvency margin calculations for risky investments or estimating the loss caused by a natural disaster, which may be observed once within a given time period (e.g. 100 years). These type of problems could be solved using tools provided by extreme value theory, summarized by [10, 16].

In the 1920’s [17] described the limit behaviour of the maximum of i.i.d. samples, which is the basis of many applications of extreme value theory. Later another approach emerged, where the extremal model is based on the values over a high threshold. Its theoretical background was developed by [1, 28], the statistical applications by [9], among others—summarized by [25]. Both approaches depend on the tail behaviour of the underlying distribution, which can be measured by the tail index.

Theoretical results for estimating the tail index were proved by [2, 8, 13] and others. Hill [24] constructed an estimator for the tail index parameter, using the k largest values of the ordered sample. Although finding the optimal number of the used sample elements is still a challenge, Hill’s estimator remained popular as [11, 14] introduced theoretical methods to calculate the optimal sample fraction. The work of [3, 23] opened the way for numerous methods to find the optimal threshold using bootstrap simulations (introduced by [15]) such as the double bootstrap method by [6], improved by [29], and other resampling-based algorithms by [18,19,20, 23]. The Kolmogorov–Smirnov method was developed by [7], this does not need simulations.

Hill’s estimator is asymptotically consistent for both threshold selection methods, however simulations show that for some sample distributions we need more than $10{,}000$ observations for a reasonably accurate estimation. In contrast to the previous methods we present a new algorithm that skips the direct threshold selection for the sample and calculates the tail index estimation via the tail indices of simulated bootstrap subsamples. In this way it results in acceptable estimators for moderate size samples, like $n \in (200, 2000)$ too.

In this paper, after a short mathematical overview of extreme value theory in Sect. 1.1, we present the Hill estimator (Sect. 2) with possible ways finding the optimal k. Additionally, we analyse the theoretical background of Kolmogorov–Smirnov method and present an approximating algorithm to make double boostrap method faster. In Sect. 3 we present a new algorithm for estimating the tail index parameter. The steps of calculation can be seen in Sect. 3.1. In a simulation study, we compare the methods (Sects. 3.2, 3.3), present a model selection scheme (Sect. 3.4) and use them on real life datasets (Sect. 4).

1.1 Mathematical Overview

Let $X_1, X_2, \ldots , X_n, \ldots$ be independent and identically distributed (i.i.d) random variables with distribution function F, and let $M_n=\max (X_1,X_2, \ldots , X_n)$. If there exist sequences $a_n >0$ and $b_n \in {\mathbb{R}}$ such that

$$\begin{aligned} {\mathbb{P}}\bigg (\frac{M_n-b_n}{a_n}<x\bigg )\rightarrow G^{*}(x) \end{aligned}$$

as $n \rightarrow \infty$ and $G^{*}$ is a non-degenerate distribution function, then it is said that F is in the maximum domain of attraction of $G^{*}$. The Fisher–Tippet theorem [17] claims that the limit distribution $G^*$ is the standardized extreme value distribution:

$$\begin{aligned} G^{*}_{\xi }(x)={\left\{ \begin{array}{ll} \exp \left\{ -(1+\xi x)^{-\frac{1}{\xi }}\right\} , &{} \text {if}\quad \xi \ne 0, \\ \exp \{-e^{-x}\}, &{} \text {if}\quad \xi = 0, \end{array}\right. } \end{aligned}$$

(1)

where $1+\xi x >0$ holds. The parameter $\xi$ is called the tail index of the distribution.

In real life applications, a three-parametric family (including location and scale parameters) is used, called generalized extreme value distribution (GEV). For every GEV distribution G there exist real numbers $a > 0$ and b, such that $G^{*}(x)=G(ax+b)$ for every x. The tail index parameter is invariant under such linear transformations.

Another approach to the investigation of the tail behaviour is the peaks over threshold (POT) model of [1, 28], where the extremal model is based on the values over a threshold u. Let $x_F$ be the right endpoint of the distribution F (finite or infinite). If the distribution of the standardized excesses over the threshold has a limit, that must be the generalized Pareto distribution:

$$\begin{aligned} {\mathbb{P}}\bigg (\frac{X-u}{\sigma _u}<x|X>u\bigg ) \rightarrow F_{\xi }(x),\quad \text {if}\quad u \rightarrow x_F, \end{aligned}$$

where

$$\begin{aligned} F_{\xi }(x)={\left\{ \begin{array}{ll} 1-(1+\xi x)^{-\frac{1}{\xi }}, &{} \text {if}\quad \xi \ne 0, \\ 1-e^x, &{} \text {if}\quad \xi = 0. \end{array}\right. } \end{aligned}$$

(2)

The two models result in the same parameter $\xi$ in Eqs. (1) and (2) for any given initial distribution F, for which the limit exists.

An $\ell (x)$ function is called slowly varying if $\lim _{t\rightarrow \infty }\ell (tx)/\ell (t)=1$ for every $x>0$. A sufficient condition for the limit theorems above, in case of positive tail index parameter (this implies $x_F=\infty$) is that

$$\begin{aligned} 1-F(x) \sim x^{-\frac{1}{\xi }}\ell (x),\quad \text {if}\quad x\rightarrow \infty . \end{aligned}$$

Finding a suitable function $\ell (x)$ and calculating the parameters of the limiting distribution of extremes is only feasible for special known distributions. In case of real life problems finding $\ell (x)$ is unrealistic, therefore estimating parameter $\xi$ is in the main focus.

2 Methods for Defining the Threshold in Hill Estimator

For a tail index $\xi >0$ Hill [24] proposed an estimator: let $X_1,X_2, \ldots , X_n$ be a sample from a distribution function F and $X_1^*\le X_2^*\le \cdots \le X_n^*$ the order statistic. The Hill estimator for the tail index is

$$\begin{aligned} {\hat{\xi }}=\frac{1}{k}\sum _{i=1}^{k} \log X_{n-i+1}^*-\log X_{n-k}^*. \end{aligned}$$

Similarly to the POT model, the Hill estimator also uses the largest values of the sample. The threshold is defined as the $(k+1)$th largest observation.

The Hill estimator strongly depends on the choice of k. It is important to mention that by the work of [26], ${\hat{\xi }}$ is a consistent estimator for the tail index only if $k \rightarrow \infty \text { and } k/n \rightarrow 0$ as $n \rightarrow \infty$. Using a too small k leads to large variance; however, for a too large k, the estimator is likely to be biased. Therefore, proposing a method for choosing the optimal k for the Hill estimator has been in the focus of research since its publication, see, e.g. [6, 7, 19, 20, 22] and others.

2.1 Double Bootstrap

One of the most accurate estimators, the double bootstrap method was introduced by [6] and improved by [29]. One can find a proposed k by minimizing the asymptotic mean squared error of Hill estimator. Define

$$\begin{aligned} M^{(i)}(n,k)=\frac{1}{k}\sum _{j=1}^{k} \left( \log X_{n-j+1}^*-\log X_{n-k}^*\right) ^{i}. \end{aligned}$$

For $i=1$ one can observe, that the ${\hat{\xi }}=M^{(1)}(n,k)$ is the Hill estimation. Let us define $M(n,k)=M^{(2)}(n,k)-2(M^{(1)}(n,k))^2$ and $k_2$ as the optimal threshold for M(n, k). Since

$$\begin{aligned} \frac{k_2}{k_1} \sim \left( 1-\frac{1}{\rho }\right) ^{1/(1-2\rho )} \end{aligned}$$

(3)

as proved by [6], where $\rho$ is a regularity parameter (which can be estimated in a consistent way), it is possible to estimate $k_2$ and $\rho$ instead of $k_1$. The double bootstrap method consists of the following steps:

• Choose $\varepsilon \in (0,1/2),$ and set $m_1=[n^{1-\varepsilon }]$ to ensure consistency as $n \rightarrow \infty$. Estimate $E(M(m_1,r)^2|X_1,X_2,\ldots ,X_n)$ by drawing $m_1$ size bootstrap samples from the empirical distribution function $F_n$ and minimize it in r. Denote the minimum by $r_1$.

• Set $m_2=[m_1^{2}/n]$ and minimize $E(M(m_2,r)^2|X_1,X_2,\ldots ,X_n)$ the same way as in the first step, denote the minimum by $r_2$.

• Estimate the regularity parameter $\rho$, which is important for the further calculations, by ${\hat{\rho }}=\log (r_1)/(-2\log (m_1)+2\log (r_1))$.

• Now one can estimate the optimal k using the approximation (3) by

  $$\begin{aligned} {\hat{k}}=\frac{r_1^{2}}{r_2}\bigg (1-\frac{1}{{\hat{\rho }}}\bigg )^{1/(2{\hat{\rho }}-1)}. \end{aligned}$$

The Hill estimator based on the double bootstrap method provides appropriate tail index estimate for $\xi >0$, but usually results in a long computation time because of the needed high number of bootstrap simulations. For smaller sample sizes the acceptable range is limited to $\xi >0.5$, as one can see the poor simulation results of [7] for lower tail indices.

2.2 Hall’s Methodology for Optimal k-Selection

In recent years many methods have arisen from the influence of [23] which use bootstrap samples to estimate the tail index parameter or improve the results of previous estimators. One of these methods appeared first in [18] and was concretized by [19], which paper also corrected the k selection, as follows.

Let $X_1,X_2,\ldots ,X_n$ be the sample. First, one must fix an initial $k_{\mathrm{aux}}$ threshold (usually $k_{\mathrm{aux}}=2\sqrt{n}$), an estimator $\gamma ^{(1)}(k)$ for $1/\xi$ (i.e. Hill with k as the threshold), and $n_1=n^{\varepsilon }$, $n_2=n_1^2/n$ subsample sizes, where n is the sample size, $\varepsilon \in (0.5,1)$ is arbitrary (usually $\varepsilon =0.85$ is used). The steps of the algorithm are the following:

• 1. Compute $\gamma ^{(1)}(k)$ for every $k=1,2,\ldots ,n-1$.

• 2. Simulate bootstrap samples of size $n_1$ and $n_2$, B times. Calculate

  $$\begin{aligned} t_{n_{i},l}(k)=\gamma ^{(1)}_{n_i,l}(k)-\gamma ^{(1)}(k_{\mathrm{aux}}), \end{aligned}$$

  for every k, where $\gamma ^{(1)}_{n_i,l}(k)$ is the estimate by using $n_i$-element ($i=1,2$) bootstrap samples, $l=1,2,\ldots ,B$ and k as threshold.

• 3. Let $k_0(n_i)=\arg \min _{n_1,n_2\in 1,2,\ldots ,n-1}\frac{1}{B}\sum _{l=1}^{B}\big (t_{n_{i},l}(k)\big )^2$.

• 4. As a corrected threshold one may use $k_0=\frac{(k_0(n_1))^2}{k_0(n_2)}$ if $k_0\in (1,n-1)$.

• 5. That way the corrected estimate for the tail index is $1/\gamma (k_0)$.

This algorithm can be really effective, however it has the same disadvantage as the double bootstrap method, namely finding $k_0(n_i)$ requires the calculations to be repeated for every k which takes approximately as long time as calculating the optimal $r_1,r_2$ in the double bootstrap method.

2.2.1 Acceleration Algorithm

For both the double bootstrap and Hall’s method, the computational time could be a crucial problem. Minimizing among a large interval of possible k or $t_{n_i}$ values needs a lot of calculations and especially the bootstrap simulations increase the needed time. These problems could lead us to use possibly less simulations, or execute the minimization over a smaller set.

We experienced that the absolute error of estimate is high by using small and large k values, while it is smaller in the neighbourhood of the optimum. The error function in k was usually smooth and showed a “U shaped” line (similar property was already mentioned by [19]). This motivates an approximation algorithm to find the minimal error value, instead of scanning all of the numbers $k= 1,\ldots ,n$, which takes unnecessary long simulation time. We propose the following step by step approximation algorithm:

• 1. Calculate the mean squared error only for $k=c\cdot \sqrt{n}$$(c\in \mathbb{Z^+})$ and execute the minimization among them. Denote the minimum by $m_a$.

• 2. Focus on the minimum $m_a$ and its $2\cdot \sqrt{n}$ wide surroundings and fix an integer b. Now minimize among the numbers $m_a \pm c\cdot b$$(c\in \mathbb{Z^+})$ in the examined region. Denote the minimum by $m_b$.

• 3. Continue the calculation in the $2\cdot b$ wide neighbourhood of $m_b$ and minimize among these values.

This way, one can find the global optimum for $k_0,r_1,r_2$ in double bootstrap and Hall’s method in most of the cases. However, sometimes the algorithm stops in a local optimum. Therefore, using the acceleration algorithm we trade-off some accuracy of estimation for faster computation time. In fact, as $n\rightarrow \infty$, the error rate decreases, since finding the optimal k is not crucial for the estimator—an adequate k results in similar estimate. In addition, the steps can be modified, to focus better on the potential optimal k values, making the calculation even faster.

In Table 1 one can see the comparison of Hall and accelerated Hall method. The mean of absolute error is similar for 200–1000 size samples, while the computation time is strongly in favour of accelerated method.

The acceleration algorithm can provide even better results in some cases (e.g. Table 1, $n=200$), however it is caused by the uncertainty of bootstrap simulations—original method may stop in a wrong value, while accelerated finds the right one. Using more bootstrap simulations this paradox diminishes.

Table 1 Comparison of accelerated and classical Hall method for Fréchet distribution with tail index 1

2.3 Kolmogorov–Smirnov Distance Metric

Another approach for tail index estimation was suggested by [7] which minimizes the distance between the tail of the empirical distribution function and the fitted Pareto distribution with the estimated tail index parameter. For the minimization the Kolmogorov–Smirnov distance of the quantiles can be used. Assume that the distribution of the sample is in the maximum domain of attraction of a GEV distribution which implies that the distribution function can be written in the following form:

$$\begin{aligned} F(x)=1-C x^{-\frac{1}{\xi }}+o\left( x^{-\frac{1}{\xi }}\right) . \end{aligned}$$

Rearranging this equation the value of x can be approximated by

$$\begin{aligned} x=\left( \frac{P(X>x)}{C}\right) ^{-\xi }. \end{aligned}$$

One can construct a quantile function by using this approximation. The probability $P(X > x)$ can be replaced by the observed relative frequency j/n, and $\xi$ may be estimated using the Hill estimator for a k, moreover C can be approximated by $\frac{k}{n}(X_{n-k+1}^{*})^{1/\xi }$ as the highest observations follow a Pareto distribution in the limit. These substitutions result in an estimator for the quantiles as a function of j and k.

$$\begin{aligned} q(j,k)=\left( \frac{k}{j}\left( X^{*}_{n-k+1}\right) ^{1/{\hat{\xi }}}\right) ^{{\hat{\xi }}}. \end{aligned}$$

This quantile estimator was first proposed by [31] as a maximum likelihood estimator using only the k upper ordered statistics.

In this procedure, the optimal k for the Hill estimator is chosen as the k, which minimizes the Kolmogorov–Smirnov distance between the empirical and the calculated quantiles

$$\begin{aligned} {\hat{k}}=\arg \min _k \left[ \sup _{j \in 1,\ldots ,T}|X_{n-j}^{*}-q(j,k)|\right] , \end{aligned}$$

where T sets the fitting threshold (we call it KS threshold). Choosing T is almost arbitrary because for heavy tailed distributions the largest differences always appear for the highest quantiles. We applied the rule of choosing $T=\max (50,\sqrt{n})$. The advantages of the Kolmogorov–Smirnov method are that it is easy to programme and its computation time is short. As [7] mentioned, it is the best performing known method if $0< \xi <0.5$ and by our experience, it also works well for small sample sizes. However, for distributions with tail index $\xi >0.5$ this technique results in highly biased estimates.

2.3.1 Asymptotics of Kolmogorov–Smirnov Method

Although the Kolmogorov–Smirnov method has a straightforward algorithm, its theoretical background and asymptotic behaviour is not presented yet. In Theorem 1 we state that under some conditions the Kolmogorov–Smirnov technique results in underestimates for the tail index. Moreover, the simulations show that the estimation is approximating the real tail index parameter if the number of observation increases. To the proof of the properties of the estimator we need the following lemma:

Lemma 1

If $k \rightarrow \infty$, then $\frac{1}{k}\log \left( \prod _{j=1}^{k}\frac{k}{j}\right) \rightarrow 1$.

Proof

For $k \rightarrow \infty$ by using the Stirling formula we have

$$\begin{aligned} \frac{1}{k}\log \left( \prod _{j=1}^{k}\frac{k}{j}\right)= & {} \frac{1}{k}\log \left( \frac{k^k}{k!}\right) \sim \frac{1}{k}\log \left( \frac{k^k}{\sqrt{2 \pi k}\frac{k^k}{e^k}}\right) \\= & {} \frac{1}{k}\log \left( \frac{e^k}{\sqrt{2 \pi k}}\right) =\frac{1}{k}\left( \log (e^{k})-\log (\sqrt{2\pi k})\right) \\= & {} 1-\frac{1}{k}\log (\sqrt{2\pi k})\rightarrow 1. \end{aligned}$$

$\square$

Theorem 1

Assume that $F(x)=1-C x^{-\frac{1}{\xi }}+o\left( x^{-\frac{1}{\xi }}\right)$, (i.e. the distribution is in the maximum domain of attraction of an extreme value distribution). The Hill estimator using the Kolmogorov–Smirnov k-selection technique has a negative bias as $n \rightarrow \infty$, $k\rightarrow \infty$, while $k/n\rightarrow 0$.

Proof

Let $X_1,X_2, \ldots , X_n$ be our sample, and let $X_1^{*},X_2^{*}, \ldots , X_n^{*}$ be the ordered sample. Let

$$\begin{aligned} q_{n}(j,k)=\left( \frac{k}{j}(X^{*}_{n-k+1})^{1/\xi }\right) ^{\xi } \end{aligned}$$

(4)

be a quantile estimator for ${\mathbb{E}}(X_{n-j+1}^{*})$, similarly to [7]. It is asymptotically unbiased as it is a maximum likelihood estimator for a given quantile by [31].

Under the given conditions $X_n^*,X_{n-1}^*\ldots ,X_{n-k}^*$ can be considered as a $k+1$ size ordered sample from a Pareto distribution with unknown parameters (see [25]). Therefore, a Glivenko–Cantelli type theorem for quantiles provides that $q_n(j,k)$ is a consistent estimator for the $(k+1-j)/(k+1)$ quantile of the unknown Pareto distribution which can also be approximated by $X_{n-j+1}^*$. Namely, for every $\varepsilon > 0$ there is an M such that if $k>M$ (and $n\gg M$) then the Kolmogorov–Smirnov distance between $q_n(j,k)$ and $X_{n-j+1}^*$ will be less than $\varepsilon$.

Choose k according to the Kolmogorov–Smirnov method (2.3) to ensure the approximation of quantile estimation and let ${\hat{\xi }}$ be the Hill estimate using k if $n>k>M$.

$$\begin{aligned} {\mathbb{E}}(\hat{\xi }) & = {\mathbb{E}}\left( {\frac{1}{k}\sum\limits_{{j = 1}}^{k} {\left( {\log \left( {X_{{n - j + 1}}^{*} } \right) - \log \left( {X_{{n - k}}^{*} } \right)} \right)} } \right) \\ & = \frac{1}{k}\sum\limits_{{j = 1}}^{k} {\mathbb{E}} \left( {\log \left( {\frac{{X_{{n - j + 1}}^{*} }}{{X_{{n - k}}^{*} }}} \right)} \right) \\ &\le \frac{1}{k}\sum\limits_{{j = 1}}^{k} {\log } {\mathbb{E}}\left( {\frac{{X_{{n - j + 1}}^{*} }}{{X_{{n - k}}^{*} }}} \right)\quad {\text{by using Jensen's inequality}} \\ & \sim \frac{1}{k}\sum\limits_{{j = 1}}^{k} {\log } \left( {\frac{{q_{n} (j,k)}}{{q_{n} (k + 1,k)}}} \right)\quad {\text{approximation by using }}(4) \\ & = \frac{1}{k}\sum\limits_{{j = 1}}^{k} {\log } \left( {\left( {\frac{{\frac{k}{j}\left( {X_{{n - k + 1}}^{*} } \right)^{{1/\xi }} }}{{\frac{k}{{k + 1}}\left( {X_{{n - k + 1}}^{*} } \right)^{{1/\xi }} }}} \right)^{\xi } } \right) \\ & = \frac{1}{k}\sum\limits_{{j = 1}}^{k} {\log } \left( {\left( {\frac{{k/j}}{{k/(k + 1)}}} \right)^{\xi } } \right) \\ & = \frac{\xi }{k}\sum\limits_{{j = 1}}^{k} {\log } \left( {\frac{{k/j}}{{k/(k + 1)}}} \right) \\ & = \xi \cdot \left( {\frac{1}{k}\log \left( {\prod\limits_{{j = 1}}^{k} {\frac{k}{j}} } \right)} \right) - \frac{\xi }{k}\left( {\log \left( {\prod\limits_{{j = 1}}^{k} {\frac{k}{{k + 1}}} } \right)} \right) \\ & = \xi \cdot \left( {\frac{1}{k}\log \left( {\prod\limits_{{j = 1}}^{k} {\frac{k}{j}} } \right)} \right) - \xi \left( {\log \left( {\frac{k}{{k + 1}}} \right)} \right) \to \xi + 0 \\ \end{aligned}$$

$\square$

Conjecture 1

Using the conditions of Theorem 1 the Hill estimator using the Kolmogorov–Smirnov k-selection technique shows asymptotically unbiased behaviour.

The consistency of the Hill estimator is well-known as $n \rightarrow \infty$, $k\rightarrow \infty$ and $k/n\rightarrow 0$. (see, e.g. [16]). The estimator is expected to behave regularly, implying the $L_1$ convergence. As an empirical observation by Monte Carlo simulations from standard generalized Pareto distribution (with $\xi =1$), we could observe, that for an increasing sequence k the ratio between the two sides of Jensen’s inequality in the proof of Theorem 1 tends to 1 (see Table 2). Similarly, in the approximation by quantile estimation the ratio of the two sides tends to 1 when $k\rightarrow \infty$ and $n\rightarrow \infty$ holds (see Table 3). These observations suggest that the Kolmogorov–Smirnov method results in asymptotically unbiased estimation for the tail index, under the conditions $k\rightarrow \infty$, $k/n\rightarrow 0$ and $n\rightarrow \infty$.

Table 2 Ratio of the two sides of the Jensen’s inequality, for different sample sizes and different k indices

Table 3 Ratio of the two sides of quantile estimate approximation, for different sample sizes and different k indices

However $k \rightarrow \infty$ is not an evident condition and even if it is realized we cannot say anything about the speed of convergence. This could lead to biased tail index estimate using the Kolmogorov–Smirnov method, especially if $\xi$ is large. For moderate size samples, this bias is estimated in Table 9, and it is always negative in accordance to Theorem 1.

As [7] presented, the Kolmogorov–Smirnov method provides acceptable estimators for moderate size samples if $\xi <0.5$, but for tail index $\xi \ge 0.5$ more than 10,000 size samples might be needed for proper estimates. In most real-life applications such a large sample size is not available, therefore in cases of distributions with infinite variance the estimator may have a significant bias.

In the previous paragraphs we have dealt with two important properties of Kolmogorov–Smirnov method: consistency (originated from Hill estimators consistency) and negative bias for finite samples. These properties motivates us to perform a simulation study, in order to estimate the bias of Hill estimator based on the Kolmogorov–Smirnov method using numerous initial distributions, sample sizes and theoretical tail indices. This will lead us to our new tail index estimator.

2.3.2 Finite Sample Properties of Kolmogorov–Smirnov Method

In this section, we show that Kolmogorov–Smirnov method has the following properties:

• The distribution of ${\hat{\xi }}$ is similar for each parent distribution

• Independence of sample size in the interval $n\in (200,10{,}000)$

• The bias is linear in $\xi$

First, we simulated 500 size i.i.d. samples from Fréchet, GPD, stable and Student distributions with fixed tail index parameter $\xi$. The estimates were calculated 30,000 times for each $\xi$. We experienced, that in accordance to the empirical distribution of ${\hat{\xi }}$ is similar, GEV-like for each parent distribution as one can see in Fig. 1. It would be beneficial to characterize the empirical distribution more precisely, since the best fitting GEV distribution is still rejected by the goodness of fit tests (chi square test after discretization, $p<10^{-16}$, which may be caused by the large sample size). Despite, the empirical distribution and the best fitted GEV distribution are in relation, thus the parameters of the GEV distribution (estimated by maximum likelihood) might characterize the empirical distribution well.

Fig. 1

Empirical density functions of Kolmogorov–Smirnov estimates for tail index $\xi =1$ based on 1000 size samples using 5000 simulations. The samples are originated from different heavy tailed distributions. The best fitted GEV distribution is similar to the empirical distributions of the estimates ($\hbox{parameters: shape}=-0.04$, $\hbox{location}=0.704$, $\hbox{scale}=0.273$)

Second, we simulated from 200 to 10,000 sized samples. We fitted GEV distribution to tail index estimates of 1000 Monte Carlo simulations. We experienced, that the GEV parameters and expectation of the tail index were similar, regardless of the sample size – see Table 4. We do not have results for larger samples, since double bootstrap and Hall method are much more effective in this case, due to their asymptotic properties. We can state that, for $\xi \in (0.5,4)$ the distribution of the Kolmogorov–Smirnov estimators does not depend on the sample size if $200<n<10{,}000$.

Table 4 The mean of the Kolmogorov–Smirnov estimates and the parameters of the fitted GEV distribution for KS estimates

Finally, we wanted to determine the bias of Kolmogorov–Smirnov method for $\xi \in (0.5,4)$. Therefore, we simulated 500 size samples from Fréchet distribution with various $\xi$ parameters. We calculated the average of estimated $\xi$ and the location parameter of the best fitted GEV distribution based on 30,000 simulations. As one can see in Fig. 2, the average and GEV parameters are in linear relation with the true $\xi$ parameter. Therefore, correcting the estimator by a linear transformation we can improve the Kolmogorov–Smirnov method. When $\xi >4$, we can not receive reasonable results, so the correction could not help (but these distributions do not have any practical relevance).

Fig. 2

Linear regression for the true tail index using mean and EVD parameters. Average of Kolmogorov–Smirnov estimates were calculated using 500 size Fréchet samples and 30,000 simulations

3 The Proposed New Estimator

Based on the finite sample properties of the Kolmogorov–Smirnov method, we constructed a new, empirical estimator, that corrects the potential bias. As we experienced in Sect. 2.3.2, the Kolmogorov–Smirnov method neither depends, on the type of the sampling distribution, nor on the size of the sample for the investigated cases, therefore a linear transformation can correct the bias. Based on the Monte Carlo simulation we fitted a linear regression model to the average of estimated $\xi$, GEV parameters and sample size against the theoretical $\xi$. We experienced that:

• Both the mean of the estimates and the location parameter of the fitted GEV were in strong correlation with $\xi$, thus two regression models are feasible for bias correction:

  One of the potential models is ${\hat{\xi }}=-0.119+1.603\cdot \mu _f$, where $\mu _f$ is the location parameter of the best fitted GEV model to the KS estimates. The other potential model is ${\hat{\xi }} ^*=-0.1181+1.3301\cdot {\xi } ^*$, where ${\xi } ^*$ is the mean of simulated KS estimates.

• Despite the assumed independence, the sample size was a significant factor. However, the coefficient was too small ($p=0.017$, $\hbox{coef}=-0.0000046$) to have important addition for small sample sizes so we omitted it.

• The covariance matrix of the fitted GEV parameters was analysed to choose the important factors. The eigenvalues (0.666, 0.0005, 0.00006) and the eigenvector of largest eigenvalue $(0.89,0.45,-0.09)$ suggests, that only the first two variables, i.e. the location and the scale parameter might have effect on ${\hat{\xi }}$. However, using both parameters in a linear regression model, only the location parameter shows significant effect $(p=0.0003)$.

However, for applying the correction models, we need to know the distribution of the Hill estimates on the sample. As [5] pointed out, m out of n bootstrap is a feasible way to estimate the distribution of a point estimator in the extreme-value setup. Therefore, the new bias corrected algorithm consists of a bootstrap simulation, and a transformation based on linear regression.

It is important to mention, that the method works best for $\xi \in (0.5,4)$ and for sample sizes between 200 and 10,000. Outside this region the statements above might not hold, thus the regression coefficients may be different.

Now, we present a step-by-step algorithm for the bias correcting method, we call this model regression estimator:

3.1 Algorithm

Let ${\underline{X}}=X_1,X_2,\ldots ,X_n$ be independent and identically distributed observations.

• 1. Fix $\varepsilon \in (0.5,1)$ (we use $\varepsilon =0.85$) and $m=n^{\varepsilon }$ to ensure the asymptotic properties of m out of n bootstrap [4, 5].

• 2. Simulate ${\underline{X}}_i$ bootstrap sample of size m from ${\underline{X}}$. Repeat it M times. Calculate the Hill estimate of each ${\underline{X}}_i$ using Kolmogorov–Smirnov method, denote the tail index estimate by $\xi _i$. The $\xi _1,\xi _2,\ldots ,\xi _M$ tail index estimates form an empirical distribution for the real $\xi$.

• 3. Denote $\xi ^*=(\sum _{j=1}^{M}{\xi _j})/{M}$ the average of Kolmogorov–Smirnov estimates—as a value, that is closely related to the tail index of ${\underline{X}}$. Let ${\hat{\xi }} ^*=-0.1181+1.3301\cdot {\xi } ^*$. We call this method mean based regression estimator (MRE).

• 4. Fit a generalized extreme value distribution to the $\xi _1,\xi _2,\ldots ,\xi _M$ estimates and denote the parameters as $(\mu _f,\sigma _f,\xi _f)$.

  Let ${\hat{\xi }}=-0.119+1.603\cdot \mu _f$. We call this method fitted regression estimator (FRE).

3.2 Simulations

The properties of the regression estimators were tested for simulated data from Pareto, Fréchet, Student and symmetric stable parent distributions. We also tested the estimator on a mixed distribution—the lower 80% consist of an exponential core, while the upper 20% is a Pareto tail. We set the tail index parameter to the same $\xi \in (0.2,4)$ value in each distribution for the samples of size 200, 1000 and 4000. For the simulation study we used the built-in rgpd (package: fExtremes), rfrechet (package: VGAM), rt and rstable (package: stabledist) functions of the R programming language. We compared the average of the estimated tail index values by FRE. Subsequently we calculated the average absolute error from the theoretical $\xi$. Using $m=n^{0.85}$, the subsample sizes were 90, 355 and 1153. We set a suitable KS threshold (maximal number of ordered statistic for KS method) to $\min (50,\sqrt{m})$. The results of the simulation can be seen in Table 8. The most important observations:

• For $\xi <0.5$ the error rate is higher than the optimal, while for $\xi >2$ one can see slight underestimation of the real tail index (except for the mixed distribution).

• For $\xi \in (0.5,2)$ the estimator seems to work properly.

• We can say generally that higher sample size results in more accurate estimate for every distribution and tail index.

• Symmetric stable distribution with $\xi =0.5$ is a special case: it is not in the domain of attraction of the Fréchet distribution, so extreme value model can not work on it. However it was an interesting question if the regression estimator works outside the domain of attraction or not—the answer is no.

Generally, we can say, that FRE works well for $\xi \in (0.2,4)$, but its best region is $\xi \in (0.5,2)$ for every type of parent distribution with proper extremal behaviour. We experienced similar properties for MRE too (Figs. 2, 3 and 4; Table 9).

3.3 Comparison of the Methods

In this section, we compare the effectiveness of Kolmogorov–Smirnov (2.3), double bootstrap (2.1) and Hall’s method (2.2) with accelerated algorithm to the two types of regression estimators. We try to decide which one is the most efficient on the average, absolute error and the computational time of estimation. We include different parent distributions (namely, Fréchet, symmetric stable, generalized Pareto, and Student) with varying tail indices and sample sizes.

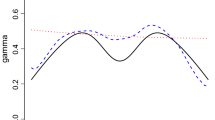
First, we present the average of absolute error of different methods using 200 size samples from the Student distribution with $\xi \in (0.1,1.5)$. The results in Fig. 3 imply that Kolmogorov–Smirnov method has the smallest error for $\xi <0.5$, while in the $\xi \in (0.5,1.5)$ region FRE and MRE seems to be the best. For larger $\xi$ double bootstrap starts to outperform the regression estimators. For 500 size samples the optimal range for MRE and FRE lies around $\xi =0.5$, while smaller tail indices can be estimated well with Kolmogorov–Smirnov method. For larger $\xi$ values Hall’s and double bootstrap method are better options for the estimation.

Second, we analysed the effect of sample size on the estimates. We fixed $\xi =0.7$, as a tail index value, where regression estimation works well. We present the average absolute error using different size samples for the methods in Fig. 4. The four parent distributions were analysed separately. We may conclude, that regression estimators seem to be the best for $n<200$. In case of Student distribution FRE has the smallest error for $n<500$, while for GPD the regression estimators have no competitors if $n<800$. Double bootstrap and Hall method start to behave better for larger sizes. Concluding the figure, for high tail indices the best method depends on the sample size and distribution, FRE and MRE are the best for smaller samples.

Finally, for $\xi \in (0.333,2)$ the mean of estimates, absolute error and computational time are presented in Table 9 for 200, 500 and 1000 sizes samples using different methods. The parent distribution is Fréchet, and the averages were calculated after 500 simulations. We can say, that for smaller sample sizes usually FRE or MRE has the best estimate and smallest error. For $n=1000$ double bootstrap starts to be better and Hall’s method also outperforms the regression estimator. Kolmogorov–Smirnov method is the fastest in every cases, but works properly only for $\xi <0.5$. Computational times of FRE and MRE methods are also competitive with the other accelerated algorithms.

Fig. 3

Average absolute error of methods for 200 and 500 size samples from Student ($1/\xi ,0$) distribution with varying tail index. Averages are based on 1000 simulations in each case. Subsample size, value of $\varepsilon$ were set as it was presented in the description of each method

Fig. 4

Average absolute error of methods for Fréchet, GPD, Student and symmetric stable distributions under 0.7 tail index and varying sample sizes. Location and scale parameters were standardized for every distribution. Averages are based on 1000 simulations. Subsample size, value of $\varepsilon$ were set as it was presented in the description of each method

We can conclude, that our new estimation method provides the best estimates among the examined options if the tail index is between 0.5 and 1.5. For small (less than 200) sized samples it always seems to be the best, but for moderate (200–500) it is preferred in case of Student or GPD—like parent distribution. However, for larger $\xi$ and different type of parent distribution the optimal region may be wider.

Some remarks:

• The effectiveness of FRE and MRE comes from the property that the methods are not sensitive with respect to the sample size. Therefore, the advantage can disappear if $n>1000$ due to consistency of other methods.

• Unlike for other examined methods, the distribution of FRE and MRE can be approximated by a normal distribution. One can see a comparison with double bootstrap in Fig. 5. Therefore, confidence interval calculations are easier.

• If $\xi \in (0.5,4)$, the errors of the FRE and MRE estimators are not sensitive to the underlying distribution, unlike the double bootstrap or Hall method. This property results in different optimality regions, thus for different distributions the double bootstrap and Hall method needs different sample sizes to outperform the regression estimators.

Fig. 5

QQ plots for case $\xi =2$ with FRE and double bootstrap to sample sizes of 500 and 1000. We have got p-values of 0.32 and 0.05 by the Anderson–Darling test for FRE, but for double bootstrap both p-values were less than 0.0001

3.4 Model Selecting Scheme

The results of Sect. 3.3 suggest, that different methods are optimal for different types of samples. Therefore, a model selecting scheme is beneficial for real life applications. For getting preliminary information about the sample we need to fit different distributions and calculate $\xi$ in a fast, but maybe not reliable way. This is formulated in the model selection algorithm as follows:

• 1. Estimate the tail index using the Kolmogorov–Smirnov method (2.3). If the estimated ${\hat{\xi }}$ is smaller than 0.45, then the true tail index is likely smaller than 0.5, therefore usually the Kolmogorov–Smirnov is the best working method (according to [7] and simulations).

• 2. If $1.22<{\hat{\xi }}$, then it is likely that for the true tail index $1.5<\xi$ holds (see Fig. 2 in Sect. 3), thus the double bootstrap method or Hall’s method gives the best estimates (Fig. 3).

• 3. If $0.45<{\hat{\xi }}<1.22$ and the sample size is less than 200, then it is likely that for the true tail index $0.5<\xi <1.5$ holds, thus the small sample implies that the FRE or MRE method gives the best estimate.

• 4. If $0.45<{\hat{\xi }}<1.22$, and the sample size is between 200 and 500, then the best fitting distribution determine the model. If GPD or the Student distribution fits the best, then usually FRE or MRE method gives the best estimate. On the other hand, if Fréchet or stable distribution fits the best, then usually double bootstrap or Hall method gives the best estimate.

• 5. For larger samples it is not clear which method is the best. As $n\rightarrow \infty$ the above rules loose their values, all the methods start to work well, and the best working method depends on the sample distribution.

4 Applications to Real Data

4.1 Danish Fire Losses

The Danish fire losses is a well known open dataset, which is available in an R package [27]. Previous discussions were published, e.g. by [12, 30]. The dataset contains 2167 fire losses, which occurred between 1980 and 1990. The true tail index parameter is between 0.5 and 1 by multiple estimators, therefore large sample size implies point no. 5 of the model selection scheme. It is not clear which method results in the best estimate, however the large sample size strongly supports the asymptotic double bootstrap and Hall method.

We estimated the tail index parameter by using the presented models, namely: double bootstrap, Kolmogorov–Smirnov and Hall’s method. Additionally, we fitted Pareto distribution for the data. As one can see in Table 5, all of the estimators results in $0.5<{\hat{\xi }}<0.75$ values, therefore the model selection might not have a big significance. It is important to mention, that MRE and FRE results in the smallest estimates. This might be caused by the fact, that we used $n^{0.85}=685$ subsample size, which is too large for such a big sample. However, we used the same method for regression estimator to subsample selection as the other estimators, it might not be optimal for m out of n bootstrap [4].

Table 5 Tail index estimation on Danish fire losses data using different methods

To check if we can improve regression estimates we considered smaller bootstrap subsample sizes, namely ones from the interval (50, 300). We calculated the tail index of the dataset with 10,000 bootstrap samples for different subsample sizes. The results can be seen in Table 6. By using 50–100 subsample size, we receive the values of most accurate methods. It might be a future task, to optimize $\epsilon$ based on the sample size, thus making the regression estimator more accurate for larger samples.

Table 6 MRE and FRE estimates for Danish fire losses data using different subsample sizes

4.2 European Natural Disaster Damages

As a second example, we analysed the damages of the most destructive storms and temperature related natural disasters of the past 50 years in Europe. The data originated from [21] database. First, we need to prepare the data for the tail index analysis. We summed up the damages occurring in different countries and days for each disaster. With these modifications the dataset contains 403 observations.

In the analysis we applied the presented tail index estimators. One can see in Table 7, that the estimates differ in a wide range, which can be explained by the small sample size and strange distribution—extremes are quite large, but more of them occurred in the observation period. The KS estimate is larger than 0.45, which suggests that the true tail index value is likely to be larger than 0.5. Since the sample size is also in the optimal range of regression estimator MRE or FRE can result in the best estimate for the data. One can see the histogram of data and the best fitted extreme value distribution using the estimated tail index in Fig. 6. The tail behaviour is best captured by the MRE, therefore regression estimates could result in the best high quantile estimates.

Table 7 Tail index estimation on European extreme natural disasters data using different methods

Fig. 6

Histogram of European disasters and best fitted GEV model using tail estimates of different methods. Location and scale parameters were estimated by maximum likelihood

For further analysis, one might have a look at the time dependent structure of the data. Climate change could have an effect on the severity of storms and heat waves, which can turn up as a positive trend among the observations. Therefore, using time dependent models might improve the effectiveness of the other estimators.

5 Conclusion

Our new regression method (Sect. 3) provides an alternative to estimate the tail index for heavy-tailed distributions. We have shown its merits by the parameter estimation of known distributions, and presented that our method is also useful for real life data. The computation time is similar to the double bootstrap method. However as our algorithm also applies bootstrap techniques, one can use less bootstrap samples to lower the computation time further if needed—at the expense of the estimations’ accuracy, or conversely.

Our simulations showed in agreement to [7] that the best estimation is the Hill estimation based on the Kolmogorov–Smirnov method (Sect. 2.3), if the $\xi$ parameter is less than 0.5. If the sample size is small $(n<200)$, FRE and MRE have the best properties in most cases. For moderate $(200<n<500)$ sample sizes and $0.5< \xi < 1.5$, the best working algorithm depends on the distribution of the sample. If it is GPD or Student-like, then usually the FRE and MRE can result in the best estimates. Otherwise using double bootstrap (2.1) or Hall method is suggested. If the size is more than 500, then in general the double bootstrap or Hall method could result in more accurate estimation. This model selection algorithm could be extended by comparing more methods or by more types of initial distributions.

Our regression estimation has two types (FRE and MRE), using the mean of the bootstrap samples or using the location parameter of the best fitted GEV distribution. Our experiments did not indicate which one is the more precise, therefore we suggest using both in a real life analysis. Further research could find the answer for this question.

Appendix

See Tables 8 and 9.

Table 8 Average FRE tail index estimations for 200, 1000 and 4000 size samples, by using 500 Monte Carlo simulations, while the bootstrap sample size is $m =n^{0.85}$

Table 9 Multiple tail index estimator for Fréchet distribution tested for different tail indices