Introduction

Allometric scaling relationships of the form Y = aX b are widely used in the analysis of tree structure. They can be used as models themselves, or as components of larger models. In practical situations, the purpose is often to obtain shortcut formulas for estimating hard-to-measure variables by using data from those that can be quantified more easily. For example, allometries allow the estimation of tree mass (Johansson 2007) or leaf area (Ford and Vose 2007) from stem diameter measurements.

The scaling relationships are often viewed as static relationships in which both the scaling exponent (b) and the normalization constant (a) obtain empirical values that are fixed within a single set of data. The procedure has been used as almost a standard (Henry and Aarssen 1999), and this partially stems from the convention of examining theoretical predictions of the value of the scaling exponent statistically (White et al. 2007). However, the theoretical values have been suggested as being poor at predicting the environmental or phylogenetic variability that seems to characterise empirical data (McKechnie et al. 2006; Duncan et al. 2007; Jeyasingh 2007; White et al. 2007).

There have been only a few attempts to give a mechanistic explanation for the statistical variability although both the scaling exponent and the normalization constant may have an interpretation based on biological processes (Kozłowski et al. 2003; Etienne et al. 2006; Mäkelä and Valentine 2006; Chown et al. 2007; Enquist et al. 2007; Price et al. 2007). As an alternative, some process-based models use conditional values of a and b, or additional variables to modify the values of a and b, instead of attempting to give a direct interpretation of the values of a and b by themselves (Duursma et al. 2007; Holdo 2007).

The use of static relationships in process-based tree models, and to some extent in statistical tests of theoretical values, can be misleading if the variability and its potential causes are not considered. For example, the scaling between woody mass and foliage mass seems to be strongly linked to the crown ratio of trees (Mäkelä and Valentine 2006). Crown ratio together with other crown parameters are, in turn, influenced by the amount of competition in the neighbourhood (Ilomäki et al. 2003; Kantola and Mäkelä 2004). Thus, the predictions are likely to be somehow biased, if a model uses any static scaling relationship that is directly or indirectly linked to crown ratio to predict stem properties in competing trees. In general, it appears that within constrained limits both scaling exponents and normalisation constants are strongly linked to the morphological and physiological traits of branching networks in plants (Enquist et al. 2007; Price et al. 2007). Hence, they can be modified by any factor that influences the formation of those networks, such as competition.

In this study, we used a field trial to demonstrate how the scaling relationships in trees can be modified by competitive processes, and how these processes can be incorporated into the scaling relationships to improve the information content of the scaling equations. We investigated the relationship between stem diameter and tree height, as well as between basal diameter of a branch and both the number of leaves and branch length. The study operates at the scale of ecological interactions by investigating the potential effect of neighbouring trees on the scaling of target trees. We operated with statistical models, and hence do not attempt to translate these ecological effects into physiological or molecular process-based models that would mechanistically explain the scaling relationships. For simplicity, we restricted our demonstrative analyses with the assumption of constant scaling exponents.

Material and methods

Scaling data

The scaling data were measured at study plots where silver birch (Betula pendula Roth) was growing in mixtures together with Scots pine (Pinus sylvestris L.), black alder [Alnus glutinosa (L.) Gaertner], Siberian larch (Larix sibirica Ledeb.), or other individuals of silver birch. The study trees were individual silver birches selected on the basis of having mainly one tree species surrounding each of them, in order to distinguish the influence of different species.

Study sites were experimentally established or otherwise planted as mixed stands representing Myrtillus forest site types, and mostly consisted of up to 50 m × 50 m plots where silver birch was abundant together with at least one of the other tree species studied. Pubescent birch (B. pubescens Ehrh.) was also frequently found, and some individuals of Norway spruce [Picea abies (L.) Karsten] were typically present in the undergrowth. The number of silver birch individuals selected for the study was 73 growing in 12 study sites with a median shortest site-to-site distance of 15 km along a southwest–northeast transect between the latitudes 60°N and 63°N, and longitudes 21°E and 29°E, in the boreal forest zone in Finland.

The neighbour trees were defined as trees that were either touching or had the potential of touching the study tree crown by growing their current branches straight through an open space within a 5-m radius cylinder centred at the stem base of the study tree. This definition emphasised the potential effect of crown interactions between neighbours. The neighbour species, in turn, was defined as the one with the sum of diameters at breast height being over half of the total sum of the breast height diameters of all the neighbour trees. The mean of the sum of diameters for the main neighbour species was larger than 80%.

The design of the sampling scheme conformed to a fractional factorial design in which the study site and neighbour species were the classification variables. All the species combinations were not present at all sites, but the observed combinations were partially overlapping to facilitate the analysis of ecologically pertinent effects (Zaluski and Golaszewski 2006). The two competition indices and the height of the study trees were used as continuous variables. Tree height was included to obtain a control for potential differences in developmental stage even though height within individual sites was rather uniform (average coefficient of variation being 18%). Within each site, there were typically two or three trees measured per available species combination (two to four combinations per site) and the size and age of both the study trees and their neighbouring trees was as uniform as possible. Across all the sites, the age of the study trees varied from 4 to 30 years.

Three different scaling relationships predicted in the literature were studied. The first was the relation between the basal diameter of the stem (D) and tree height (H), which has been suggested to scale as H ∝ D 2/3 (e.g. Niklas and Spatz 2004). The second was the relation between branch radius (r) and number of leaves (L) suggested to scale as L ∝ r 2 (West et al. 1999). The third was the relation between branch radius and branch length (l) as l ∝ r 2/3 (West et al. 1999).

The height of each tree was measured after felling. Basal diameter at about 20 cm above the ground was measured at two perpendicular directions and the mean of these values was used. For each branch in the study trees, branch diameter was measured with a calliper to obtain branch radius, and branch length was estimated by measuring a straight line from the base of the branch to the most distant shoot of the same branch. Leaf number was estimated for each sample of at least two branches per tree by counting the number of leaf-producing shoots (hereafter shoot number). Shoot number gives a good estimate of leaf number because the majority of foliage in birch is located in short shoots that usually bear two leaves.

The influence of the neighbouring trees was characterised by two competition indices (CI1 and CI6) that had the best explanatory power (lowest AIC, see Comparing three methods to estimate scaling parameters) to explain the allometric and other structural characteristics of silver birch in the present data (Vehanen and Kaitaniemi, unpublished results). The indices were selected from among the group of indices used by Rouvinen and Kuuluvainen (1997) to study crown competition:

$$ {\text{CI}}_{{\text{1}}} = {\sum\limits_{j = 1}^n {\arctan {\left[ {D_{j} /L_{{ij}} } \right]}} } $$
(1)
$$ {\text{CI}}_{6} = {\sum\limits_{j = 1}^n {\arctan {\left[ {{\left( {H_{j} - 0.8H_{i} } \right)}/L_{{ij}} } \right]}} },\quad H_{j} > 0.8H_{i} $$
(2)

where i denotes study tree, j neighbouring tree and n is the number of competitors in a radius of 5 m from the study tree. CI1 is the sum of angles of sectors where the width of a sector is the diameter (D) of neighbour tree at the breast height and the length of the sector (L) is the distance between the stem bases of the study tree and the neighbour tree. CI1 also acts as a substitute for the actual size of neighbours, because it correlated with the sum of breast height diameters of the neighbour trees (r = 0.89, N = 73).

CI6 indicates the sum of angles of sectors between the study tree and a neighbour tree. The height of one sector (H) is the height of a neighbour tree above 80% of the study tree height, and the length of the sector is the distance between the study tree and a neighbour tree. CI1 and CI6 describe different aspects of competition because their correlation was only moderate (r = 0.42).

Comparing three methods to estimate scaling parameters

We used three different approaches to determine the values of the parameters in the studied scaling relationships. Tree-specific values were used because it is conventional to calculate average values of the size variables for each independent observational unit in an allometric analysis (Niklas 1994). For branch length, we used the tree-specific averages of branch radius and branch length. For shoot number, we used tree-specific averages of the radius and shoot number of the sample branches.

The first approach was “traditional” and both the normalisation constant and the scaling exponent were allowed to obtain their empirical values as determined by fitting an allometric scaling function to the data (Proc NLIN, SAS Institute Inc., Cary, NC, USA). In the second approach, we set the scaling exponents to their theoretical values and used nonlinear regression (Proc NLIN) to determine the value of the normalisation constant alone. Because the purpose of the models was predicting the scaling relationships, it was not necessary to account for measurement error in the scaling variables (Warton et al. 2006).

The third approach was a multistep procedure where the normalisation coefficients were first calculated individually for each tree or each branch using the theoretical exponents. The tree-specific averages of these coefficients were then subjected to an analysis by which the effect of neighbouring species on their value was examined. The explanatory variables in the analyses were: study site, neighbour species, the two competition indices, and the height of the study trees. Study tree height was used to account for the potential effects of developmental stage. Interactions among these variables were also examined (excluding study site). The analyses were conducted using the SAS procedure GENMOD, which can be also used for continuous data (Orelien 2001). GENMOD uses maximum likelihood estimation that is suitable for unbalanced data, although with some uncertainty for small samples (Everitt and Pickles 2004). However, this was not a critical issue because GENMOD was used primarily as a tool for model selection and the actual statistical significance of the parameter values was only meant to point towards potentially important explanatory factors, i.e., not used for formal hypothesis testing.

Model selection based on Akaike’s Information Criterion (AIC, Akaike 1973) was used to identify the most efficient set of explanatory variables for predicting the values of the normalisation constants. AIC simultaneously maximizes the model fit and minimizes the number of parameters such that the model with the lowest value of AIC is judged the best. AIC of a candidate model i is calculated as AIC i  = −2 log L i  + 2V i , where L i is the maximum likelihood of the model i, and V i is the number of parameters estimated from the data for the model i. In this study, the final models with the lowest AIC were used to calculate the value of normalisation constant in the three scaling relationships examined.

The fit between the observed values and the values predicted by the different scaling relationships estimated with the three approaches was compared using both the coefficient of determination (r 2) and AIC value. AIC was used to control the possibility that changes in the model fit could be a simple consequence of the increased number of parameters due to the use of submodels to predict the value of the normalisation constant.

Results

Neighbouring trees had a clear effect on the value of the normalisation constant in all three scaling relationships. The model that best predicted the normalisation constant in the relationship between basal diameter and tree height included study site (χ 211  = 83.8, P < 0.0001), neighbouring species (χ 23  = 10.0, P = 0.02) and the interaction neighbouring species by CI6 (χ 24  = 22.9, P = 0.0001). The best model for the relationship between branch radius and shoot number included the effect of neighbouring species (χ 23  = 8.1, P = 0.04) and the interaction of neighbouring species with both CI1 (χ 24  = 21.5, P = 0.0003) and CI6 (χ 24  = 9.6, P = 0.05). In the relationship between branch radius and branch length, the best model included study site (χ 29  = 11.7, P = 0.23, branch length data missing for one site), neighbouring species (χ 23  = 16.7, P = 0.0008), and the interaction CI6 by neighbouring species (χ 24  = 9.7, P = 0.05).

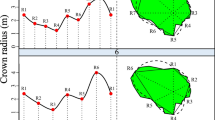
The three approaches for estimating scaling parameters produced clearly different outcomes (Fig. 1). Using the model-predicted normalisation constant with a fixed scaling exponent improved the fit of the scaling equation for tree height by 10% (r 2 = 0.95) compared with either of the two alternative scaling equations (r 2 = 0.84–0.85). The improvement was also true, if the penalty due to the number of parameters behind the value of normalisation constant was taken into account (the value of AIC decreased with ΔAIC < −25). For shoot number, the fit of the two scaling equations with empirical normalisation constant and with either empirical or constant scaling exponent was the same (r 2 = 0.47), but the fit was improved by 8% when model-predicted normalisation constant was used with a fixed exponent (r 2 = 0.55). However, the use of AIC suggested a penalty due to the number of parameters compared with the alternative scaling equations (AIC increased with ΔAIC > 15). For branch length, the use of model-predicted normalisation constant with constant exponent improved the fit by 4% (r 2 = 0.83) compared with the equation with empirical normalisation constant and constant exponent (r 2 = 0.79), and by 6% compared with the purely empirical equation (r 2 = 0.77). Again, AIC suggested penalty due to the number of parameters (ΔAIC > 28).

Fig. 1
figure 1

The fit of different scaling equations of the form Y = aX b in three different scaling relationships in silver birch (Betula pendula). Black dots denote observed values, black lines the fit of equations where a theoretical scaling exponent (b) was used, dashed lines the fit of equations where both normalisation constant (a) and b were determined empirically, and white dots are values predicted by equations where a submodel was used to predict a whereas a theoretical value was used for b

Full size image

Discussion

The fit between the data and three different scaling models was consistently improved by including the effect of competitive ecological interactions in separate submodels that predicted the value of the normalisation constant in the scaling equations. This is consistent with the concept that ecological factors can directly influence the value of the normalisation constant. Competition, for example, presumably affects photosynthetic rate (Robinson et al. 2001) that has been suggested to be an integral component of many normalisation constants in plant allometries (Enquist et al. 2007). Our analyses suggest a procedure of how these effects can be incorporated into statistical models.

Although the use of AIC suggested a penalty for the number of parameters in the submodels and that the improvement was true in only one of the three cases, it must be noted that large part of the penalty was caused by the use of site-specific parameters for up to 12 study sites. Obviously study site is not a good parameter, if more generic applications for the models are sought. Study site was only retained to show the potential for identifying the factor(s) underlying its unspecified effect. The effects of study site and neighbouring species could probably be replaced by a more specific mechanism such as light interception or soil mediated factors.

In general, the balance between the number of parameters and the fit of a model is a more complex issue than using just a simple statistical criterion to make decisions (Haefner 1996). If it is possible to gain a consistent 8% increase in the fit of an economically important model by adding just few parameters that are cheap to measure, then it surely is worth the effort, even though a statistical criterion suggests the opposite. For example, an extensive set of equations have been created to predict a number of tree traits that are allometrically scaled, and are used for various economically important purposes covering different aspects of forest mensuration. These include: carbon cycling, nutrient cycling, validation of process-based forest models, forest and greenhouse gas inventories etc. (Zianis et al. 2005). These equations operate with ground-measured variables describing just single target trees. They often include complex polynomial terms where tree height (H), stem diameter (D) or both are included in various combinations with additional parameters and exponents. However, it is known that competition modifies stem proportions, such as slenderness index (D/H) (Ilomäki et al. 2003). Thus it appears likely that the inclusion of neighbourhood effects could be used as an alternative for such complex terms where both H and D contribute. In remote sensing, for instance, a problem is that the estimates of stem properties have remained poorer than in ground measurements (Korpela and Tokola 2006). By using remotely sensed data to calculate competition indices and by including the tree heights and crown dimensions of both the target trees and their neighbours into equations that translate remotely sensed data into stem properties, it might be possible to improve the fit of estimates to correspond with ground measurements.

The improvement of model fit relied on the use of fixed scaling exponents, which is a feature that might be controversial as there is continuous disagreement on the constancy of the scaling exponents (Chown et al. 2007; White et al. 2007). However, our results and comparable studies suggest that much of the inconsistency might be a statistical artefact, and relate to the variation of the value of the normalisation constant (Kaitaniemi 2004). Even if there remains disagreement, it will be possible to experiment with alternative values of the scaling exponent and choose a combination that gives the best fit for a model that also includes an interpretation of the value of the normalisation constant. Fixing exponents can increase the predictive power of allometries when there is variability in normalization constants. This variability can be accounted for by measuring additional ecological factors at the level of the individual. Fitting both exponents and normalizations at the level of the individual (Mäkelä and Valentine 2006; Price et al. 2007), and accounting for relationships between these parameters and ecological factors, could even further increase the predictive power of allometries. However, because of the strong interdependence between the two parameter values (Lumer 1939), one of the scaling parameters may have to be set to a predetermined value before the value of the other can be accurately estimated using merely statistical fit.