1 Introduction

Modelling the mechanical behaviour of periodic composites with engineered microstructures has gained importance in recent decades due to their use in advanced engineering applications. Effectively capturing complex microstructural properties intrinct to composite materials is a main challenge. Even though direct numerical simulations (DNSs) provide a robust methodology for handling this complexity and gaining an understanding of material behaviour at the microscale, it is important to acknowledge that this approach comes with extensive computational effort. In contrast, homogenisation methods enable a more computationally efficient means to model the mechanical and physical behaviour of microstructures in composites.

Fig. 1
figure 1

A schematic illustration of the dynamic computational homogenisation method

Full size image

Computational homogenisation has become prominent as an effective tool within multiscale methods by modelling the complex mechanical behaviour of materials at different scales [1, 2]. The computational homogenisation method has not replaced other homogenisation methods, but it is clearly becoming a fundamental tool for modelling the mechanics of complex materials. Namely, the computational homogenisation method gives direct solutions compared to other homogenisation methods, so there is no need to formulate constitutive equations at the macroscale [3]. As long as the behaviour of the material constituents at the microscale is well-defined, the outcomes obtained with the computational homogenisation method converge as the RVE size increases, aligning closely with the solution acquired through the DNS. Compared to analytical and numerical homogenisation, the computational homogenisation method involves solving a boundary value problem at both the macro and microscales. The macroscopic solutions are used as input for a set of microscopic boundary value problems, while the microscopic solutions are used as input for the macroscopic boundary problem at the macroscopic integration points. This generates the cycle illustrated in Fig. 1 for the computational homogenisation method. The microscopic boundary value problem is assigned to each macroscopic integration point obtained using a finite element discretisation [4]. Even though the form of nested boundary value problems causes an increase in computational effort, the computational homogenisation method accelerated by parallel computations is still faster than the direct numerical simulation method [1, 5].

The computational homogenisation method has been extensively applied to quasi-static problems in various material types, including periodic composites [6, 7], polycrystalline materials [8], porous materials [9] and cellular materials [10]. However, Geers et al. [11] have addressed the challenges encountered in the computational homogenisation method. These include developing effective boundary value problems at both micro and macro scales, tackling dynamic cases that incorporate micro-inertia effects and wave propagation, and developing upscaling features that take into account spatial-temporal and kinematic factors. Notably, the use of this method in materials with complex microstructures has resulted in emerging extensions of the computational homogenisation technique to overcome these challenges. These extensions have facilitated a more comprehensive understanding of the mechanical behaviour of materials, particularly microstructural features. For instance, one extension is the dynamic computational homogenisation algorithm as presented in Pham et al. [12] to analyse metamaterials under dynamic excitation. These authors extended the Hill-Mandel principle to include macroscopic stress from the static contribution, but also macroscopic linear momentum from the dynamic contribution. In addition to the work of strain, the algorithm integrates the work of acceleration into the variation of work performed on both scales, leading to the Hill-Mandel condition in dynamics. Besides, Van Nuland et al. [13] have been performed the dynamic computational homogenisation on a nonlinear resonant acoustic metamaterial by transferring macroscopic constitutive tangents obtained from the Newton–Raphson method. The dynamic computational homogenisation method extended with the Newton-Raphson method was applied to a nonlinear metamaterial with rubber-coated inclusions, resulting in good estimation of band gap characteristics [13]. Furthermore, the boundary value problems have been analysed within frequency domain to investigate the behaviour of heterogeneous materials under dynamic loading at different frequencies [14].

The classic computational homogenisation method contains two (or possibly more) coupled and nested boundary value problems in which a macroscopic analysis is coupled with a microscopic analysis in defining the constitutive behaviour [15]. Namely, the macroscopic constitutive behaviour is adopted by the solution of the associated microstructural problem implemented over typically a representative volume element (RVE) through successive transitions between macro and microscales. Scale transitions enable exchanging information, which includes the macroscopic kinematic relations establishing the microstructural problem and averaging relations in accordance with energy conservation between the scales. The transition of kinematic relations from macroscopic to microscopic scales is defined as downscaling. Conversely, the transition of averaging relations in the opposite direction is defined as upscaling.

Scale transitions are performed in accordance with the principle of separation of scales on which the computational homogenisation method is based. In cases where the characteristics of a microscopic wave amplify due to consecutive wave reflections and refractions, wave dispersion emerges at the macroscale [16]. However, this interaction between micro and macroscales impedes the complete adoption of the separation of scales. Consequently, the classic computational homogenisation approach might not be applicable for transient problems (e.g. locally resonant acoustic metamaterials) [17]. To address this limitation, an extension of the computational homogenisation method with additional scale separation assumptions is used for periodic composites with dynamic kinematic and averaging relations to account for these micro-inertia effects [12, 18, 19]. Even though the development of dynamic transition relations achieves the problems emerging from the size of microstructures, the concept of separation of scales in computational homogenisation methods is not fully addressed for the transient problems [17].

A computational homogenisation method is developed using finite element discretisation in space and time integration, where the separation of both length and time scales is adopted. A macrostructure is spatially and temporally coupled with the RVE encapsulating the characteristics of a microstructure for scale transition relations between the two scales. The separation of scales principle enhances scale transitions across the scales. As a purpose of this work, a separation of time scale is presented to overcome the deficiencies in scale transitions emerging from the microstructure in dynamics. The recent findings indicate that accurate estimation of macroscopic material properties in dynamics requires a larger RVE size with a longer time period on the microscale [20]. Furthermore, the improvement in the convergence of the macroscopic material properties with the time averaging presented by the previous work [20] leads to adopting the separation of time scales in the dynamic computational homogenisation method. This approach to time averaging has also been used successfully in the context of numerical homogenisation of a visco-elastic material [21].

In this paper, the scale transitions strategy is reformulated by the simultaneous separation of length and time scales. The concept of the separation of length and time scales involves breaking down a complex material into multiple levels, with each scale capturing different characteristics of the material behaviour in both spatial and temporal dimensions. Consequently, the microstructure is separated with the associated macrostructure regarding space and time discretisation on the microscale. In the framework of multiscale (or multirate) time integration as introduced by Hodge [22], the resolution of macro and microscales in both space and time yields results similar to fully resolving microscales. Instead of relying solely on the separation of length scales, the simultaneous separations of length and time scales provide significant computational savings [23]. The proposed work exploits the benefits of simultaneous separations of length and time scales by increasing the RVE size as well as the time period on the microscale to obtain satisfactory accuracy in the macroscopic response of a material. Notably, the effects of separation of length and time scales in a dynamic computational homogenisation framework are studied for various material properties and validated against the direct numerical solution results. As such, the present paper extends the upscaling findings of the previous work [20] to a computational homogenisation framework that involves upscaling as well as downscaling.

The structure of the article is as follows. Whereas Sect. 2 gives an overview of the dynamic computational homogenisation framework and contains a novel approach to temporal coupling. Related scale transitions, including a novel downscaling procedure, are also formulated and constructed in this Section. The numerical implementation of this methodology is detailed in Sect. 3, followed by the demonstration of its effectiveness in Sect. 4. Concluding remarks and contributions of this research are then presented in Sect. 5.

2 Dynamic computational homogenisation setting

The computational homogenisation method establishes stress–strain \(\sigma _{\text{ M }}-\varepsilon _{\text{ M }}\) and momentum-velocity \(p_{\text{ M }}-{\dot{u}}_{\text{ M }}\) relations between the microscale and macroscale by averaging the response of the RVEs according to the Hill-Mandel principle to estimate the macroscopic response of periodic composites. This leads to coupling boundary value problems on the two scales. The solution of these nested boundary value problems is coupled by scale transition relations as regards energy consistency between these scales. The macroscopic constitutive behaviour is provided by the solution of the microscopic response instead of an analytical constitutive model so that there is no need to make any constitutive assumption on the macroscale. Briefly, the computational homogenisation method schematised in Fig. 1 consists of three main steps:

  • Solution of a macroscopic boundary value problem

  • Transfer of solutions between macro and microstructure models

  • Solution of a microscopic boundary value problem.

For simplicity and to illustrate the concepts, a very well-known problem is considered. At the macroscale, the bar is subjected to a constant load F at its right end and constrained at its left end. At the microscale, the bar consists of periodic unit cells of length \(\ell \). The macroscopic material properties are homogenised by the response of the RVE. At the microscale, the material of first laminate component is defined by Young’s modulus \(E_1\) and mass density \(\rho _1\), while for the second laminate component, the material properties are denoted as \(E_2\) and \(\rho _2\). The size of laminate components are determined depending on volume fractions, which are \(h_1\) and \(h_2\) for the first and second laminate components, respectively.

2.1 Scale separation

In the extended computational homogenisation methods, the scale transitions described in Sect. 2.4 contain spatial and temporal relations between the macro and microscales. In accordance with this strategy, an extended separation of scales principle is presented in this section not only the separation of length scales but also the separation of time scales.

2.1.1 Separation of length scales

In homogenisation methods, the principle of separation of length scales assumes that the size of the microstructure \(\ell \) is much smaller than the size of the macrostructure L [24] and the shortest wavelength of the macroscopic response for a given applied load \(\lambda _{\text{ M }}\) [11]:

$$\begin{aligned} \ell&\ll L \end{aligned}$$
(1)
$$\begin{aligned} \ell&\ll \lambda _{\text{ M }} \end{aligned}$$
(2)

In the case of transient problems, the size of the macrostructure L is no longer the sole, dominant macrostructural length scale. Its significance is reduced by the size of the macro-fluctuations \(\ell _{\text{ M }}\) tending to be considerably small compared to the size of the microstructure \(\ell \). To tackle these additional length scales, the long-wavelength approximation is assumed for the scale separations in homogenisation methods. The long-wavelength approximation states that the size of the microstructure \(\ell \) should be sufficiently smaller than the shortest wavelength of the microscopic response for a given applied load \(\lambda _{\text{ m }}\) [12]. In addition, the size of micro-fluctuations \(\ell _\mu \) due to the micro-inertia effects must be taken into account and must be smaller than the size of the microstructure \(\ell \) as follows

$$\begin{aligned}&\ell \ll \lambda _{\text{ m }} \end{aligned}$$
(3)
$$\begin{aligned}&\ell _\mu < \;\ell \ll \ell _{\text{ M }} \end{aligned}$$
(4)

Satisfaction of Expressions (1), (2), (4) and (3) ensures that the macroscopic response is independent of the size of the microstructure \(\ell \). In other words, the macroscopic strain \(\varepsilon _{\text{ M }}\) and macroscopic velocity \({\dot{u}}_{\text{ M }}\) are constant over the RVE so that these downscaling parameters can be applied as uniform loads on the boundary of the RVE. Expressions (4) and (3) become invalid when the scales are inseparable (e.g. larger micro-fluctuations \(\ell _\mu \), smaller macro-fluctuations \(\ell _{\text{ M }}\) and the wavelength of the microscopic response \(\lambda _{\text{ m }}\)) owing to the design requirements of periodic composites with tailored microstructures, which are

$$\begin{aligned}&\ell _\mu \le \;\ell \le \ell _{\text{ M }} \end{aligned}$$
(5)
$$\begin{aligned}&\ell \le \lambda _{\text{ m }} \end{aligned}$$
(6)

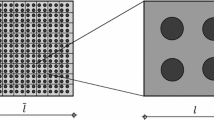
To obtain a convergent macroscopic response by dealing with inseparable scale inequalities, the spatial coupling between macro and microstructures is resolved by increasing the RVE size \(L_{\text{ m }}\). The spatial separation scheme between the two scales is presented in Fig. 2 for a one-dimensional periodically laminated bar. The size of the microstructure \(\ell \) is separated from the size of the macrostructure L by increasing the number of unit cells \(N_{\text{ uc }}\) at the microscale until obtaining the convergent macroscopic response. Therefore, at the microscale, the size of the RVE \(L_{\text{ m }}\) is directly linked with the size of the microstructure \(\ell \) and the number of unit cells \(N_{\text{ uc }}\).

As can be seen in Fig. 2, the size of microscopic unit cell \(\ell \) is kept the same and the length of the bar at the microscale increases with an increase in \(N_{\text{ uc }}\) until the macroscopic response becomes independent of the size of dynamic RVE \(L_{\text{ m }}\) is given by

$$\begin{aligned} L_{\text{ m }} = N_{\text{ uc }} \,\ell \end{aligned}$$
(7)

where \(L_{\text{ m }}\) and \(\ell \) are the size of the dynamic RVE and the size of microscopic unit cell, respectively.

Fig. 2
figure 2

Homogenised macrostructure separated spatially with laminated microstructure through macroscopic integration point

Full size image

2.1.2 Separation of time scales

The modelling of transient problems in the computational homogenisation method requires dynamic transition relations (i.e. momentum-velocity \(p_{\text{ M }}-{\dot{u}}_{\text{ M }}\) coupling) in addition to stress–strain \(\sigma _{\text{ M }}-\varepsilon _{\text{ M }}\) coupling. Thus, the shortest wavelength of the microscopic response \(\lambda _{\text{ m }}\), the size of the macro-fluctuations \(\ell _{\text{ M }}\) and the size of the micro-fluctuations \(\ell _\mu \) become significant according to the long-wavelength approximation. The importance of the principle of separation of length scales is that the convergent macroscopic response for transient problems can be obtained by increasing the RVE sizes. The principle of separation of time scales is formulated analogously to the principle of separation of length scales: it is assumed that the time window at which significant microstructural changes occur is much smaller than the time window at which significant macrostructural changes occur. In accordance with this, the principle of separation of time scales assumes that a convergent macroscopic response can also be obtained by longer time periods of the microscopic analysis so that a microscopic wave propagates during a large enough time window over the RVE to average the variations of the microscopic response (e.g. micro-fluctuations and micro-inertia effects). Thus, the temporal coupling between the macro and microscales is controlled by increasing the microstructure time window \(T_{\text{ m }}\).

In the extended computational homogenisation method proposed in this work, dynamic kinematic and averaging relations are not only coupled between the macro and microscales, but time integration parameters such as the microscopic simulation time \(t_{\text{ m }}^{\text{ f }}\) and the macroscopic time step \(\Delta t_{\text{ M }}\) are also coupled to build a temporal relation between the two scales as shown in Fig. 3. The microscopic simulation time \(t_{\text{ m }}^{\text{ f }}\) equals the macroscopic time step \(\Delta t_{\text{ M }}\) on the account of the temporal coupling between the microscopic and the associated macroscopic time integrations. To illustrate, downscaling parameters are transferred from the macroscale at the current macroscopic time \(t_{\text{ M }}^{\text{ n }}\) with the macroscopic time step \(\Delta t_{\text{ M }}\) used as the microscopic simulation time \(t_{\text{ m }}^{\text{ f }}\). After performing the microscopic analysis, upscaling parameters are transferred back to the macroscale at the next macroscopic time \(t_{\text{ M }}^{\text{ n+1 }}\).

As an alternative, similar to the separation of length scales, the microscopic time integration can also be performed independently from the macroscopic time integration to allow a large enough microscopic time window to include the variations of the microscopic response. The principle of the separation of time scales enables the macroscopic time step \(\Delta t_{\text{ M }}\) to be separated from the microscopic simulation time \(t_{\text{ m }}^{\text{ f }}\). The temporal coupling is presented in Fig. 4 between the two scales in order to ensure the macroscopic response not to be affected by the microscopic simulation time \(t_{\text{ m }}^{\text{ f }}\). A more relaxed relation is built depending on the time requiring the microscopic wave to propagate across the RVE \(t_{\text{ m }}^{\lambda }\). Therefore, the microstructure time window \(T_{\text{ m }}\) is directly linked with the microscopic time interval \(t_{\text{ m }}^{\lambda }\) to ensure the microscopic wave experience the variations in the RVE. Thus, the time window of the microscopic analysis \(T_{\text{ m }}\) is determined by the number of wave propagations \(N_{\text{ wp }}\) over the RVE as follows

$$\begin{aligned} T_{\text{ m }} = N_{\text{ wp }} \, t_{\text{ m }}^{\lambda } \end{aligned}$$
(8)

where \( t_{\text{ m }}^{\lambda }\) is the microscopic time interval. The number of wave propagations \(N_{\text{ wp }}\) increases to extend the microstructure time window \(T_{\text{ m }}\) until the macroscopic response is not affected by the variations of the microscopic response.

2.2 Macroscopic boundary value problem

To model the dynamic response of one-dimensional linear elastic laminated bar using computational homogenisation as depicted in Fig. 1, the macroscopic boundary value problem is formulated by the linear balance of momentum with the body forces as follows

$$\begin{aligned} \frac{\partial }{\partial x}\, \sigma _{\text{ M }} - {\dot{p}}_{\text{ M }} = f_{\text{ ext }} \end{aligned}$$
(9)

where \(\sigma _{\text{ M }}\) and \({\dot{p}}_{\text{ M }}\) are the macroscopic stress and the macroscopic momentum rate, respectively.

The macroscopic relations linking \({\dot{u}}_{\text{ M }}\) and \(\varepsilon _{\text{ M }}\) with \(p_{\text{ M }}\) and \(\sigma _{\text{ M }}\), respectively, are required at the macroscale to solve the macroscopic boundary problem defined by Eq. (9). In the computational homogenisation method, there is no need to assume a constitutive model at the macroscale since the macroscopic constitutive relations are determined by averaging the results of a microscale boundary value problem. The averaged microscopic quantities are transferred to the macroscale through associated macroscopic integration points. The averaged microscopic stress and momentum are embedded as residual forces in the macroscopic boundary value problem through the upscaling procedure. Consequently, the effects of heterogeneity explicitly defined at the microscale are introduced to the constitutive behaviour adopted as homogeneous at the macroscale.

Fig. 3
figure 3

Homogenised macrostructure linked temporally with laminated microstructure through macroscopic integration point

Full size image
Fig. 4
figure 4

Homogenised macrostructure separated temporally from laminated microstructure

Full size image

2.3 Microscopic boundary value problem

As representative model of the macrostructure, a one-dimensional periodically laminated microstructural boundary value problem over an RVE is considered for a microstructure assigned to each macroscopic integration point shown in Fig. 2. The constitutive behaviour of the macrostructure is obtained from the results of the microstructural boundary value problems. The RVE size and the microstructure time window for the microstructural boundary value problem should be taken large enough not to affect the macroscopic response significantly. For transient problems, the RVE size in dynamics is typically larger than one unit cell of periodic composites and the microstructure time window is longer than the macroscopic time step \(\Delta t_{\text{ M }}\) [20]. Accordingly, the separation of length and time scales procedures explained in Sects. 2.1.1 and 2.1.2 are performed to determine the RVE size \(L_{\text{ m }}\) and the microstructure time window \(T_{\text{ m }}\) for the microscopic boundary value problem. At the microscale, the selected RVE is solved by the balance of linear momentum with the absence of body forces

$$\begin{aligned} \frac{\partial }{\partial x}\, \sigma _{\text{ m }} - {\dot{p}}_{\text{ m }} = 0 \end{aligned}$$
(10)

where \(\sigma _{\text{ m }}\) is the microscopic stress and \(p_{\text{ m }}\) is the microscopic linear momentum. In order to solve the microstructural boundary value problems, the constitutive relations at the microscale are defined by constitutive laws, which accounts for heterogeneity in the RVE. Following earlier findings [7, 25, 26], it has been established that periodic boundary conditions offer advantages for modelling the RVE behaviour. Particularly, Yağmuroğlu et al. [20] highlighted specific benefits associated with imposing periodic boundary conditions on the RVE under dynamic loading conditions as compared to Dirichlet conditions. In the context of non-periodic RVE boundaries, Tamsen and Balzani [27] have introduced the concept of extended microscopic boundary conditions. Initial and boundary conditions are applied to the RVE through the dynamic kinematic relations via the downscaling procedure described in Sect. 2.4.1. The macroscopic kinematic quantities (the macroscopic strain \(\varepsilon _{\text{ M }}\) and velocity \({\dot{u}}_{\text{ M }}\)) are transferred through the macroscopic integration point to the microscale as a prescribed boundary condition.

2.4 Kinematics of the scale transitions

In the computational homogenisation method, the dynamic scale transitions construct spatial and temporal relations between the macro and microscales based on conservation of mass, momentum and energy [12, 28]. The downscaling and upscaling procedures are linked with the separation of length and time scales. Namely, the dynamic scale transitions occur at the microstructure time window \(T_{\text{ m }}\) determined by the principle of the separation of time scales. In addition, dynamic scale transitions are performed over the RVE following the principle of the separation of length scales. In this section, we expand on how the principle of the separation of length and time scales is related to the downscaling and upscaling procedures.

2.4.1 Downscaling

The solution of the macroscopic boundary value problem provides the macroscopic strain \(\varepsilon _{\text{ M }}\) and velocity \({\dot{u}}_{\text{ M }}\) as downscaling parameters for the RVE. The downscaling parameters are formulated as periodic boundary conditions for the RVE. The downscaling parameters are used to obtain microscopic momentum from the macroscopic velocity \({\dot{u}}_{\text{ M }}\) as well as microscopic stress from the macroscopic strain \(\varepsilon _{\text{ M }}\). For these purposes, the prescribed boundary condition of the RVE is formulated using Taylor series so that microscopic displacement \(u_{\text{ m }}\) and velocity \({\dot{u}}_{\text{ m }}\) can be related to the macroscopic strain \(\varepsilon _{\text{ M }}\) and the macroscopic velocity \({\dot{u}}_{\text{ M }}\) as

$$\begin{aligned} u_{\text{ m }}(x,t)=u_{\text{ M }}+\frac{\partial u_{\text{ M }}}{\partial x} \, \Delta x_{\text{ M }}+\frac{\partial u_{\text{ M }}}{\partial t} \, \Delta t_{\text{ M }} \end{aligned}$$
(11)

where \(\Delta x_{\text{ M }}\) is the size of a macroscopic unit cell and \(\Delta t_{\text{ m }}\) is the macroscopic time step when the dynamic kinematic relations are coupled at the macro and microscales. Rewriting Eq. (11) based on the principle of separation of length and time scales explained in Sects. (2.1.1) and (2.1.2) gives

$$\begin{aligned} u_{\text{ m }}=u_{\text{ M }}+\frac{\partial u_{\text{ M }}}{\partial x} \, L_{\text{ m }} +\frac{\partial u_{\text{ M }}}{\partial t} \, T_{\text{ m }} \end{aligned}$$
(12)

where \(L_{\text{ m }}\) and \(T_{\text{ m }}\) are the size of the RVE and the microscopic time window of the microscopic analysis, respectively.

2.4.2 Upscaling

After solving the microscopic boundary value problem, the averaged microscopic stress \( \langle \sigma _{\text{ m }}\rangle _{\text{ x }}\) and the averaged microscopic momentum \(\langle p_{\text{ m }}\rangle _{\text{ x }}\) parameters are transferred to the macro level as upscaling parameters. According to the Hill-Mandel averaging, the microscopic stress and the microscopic momentum are averaged as follows

$$\begin{aligned} \langle \sigma _{\text{ m }}\rangle _{\text{ x }}= & {} \frac{1}{L_{\text{ m }}} \int \limits _0^{L_{\text{ m }}}\sigma _{\text{ m }} \, \textrm{d}x \end{aligned}$$
(13)
$$\begin{aligned} \langle p_{\text{ m }}\rangle _{\text{ x }}= & {} \frac{1}{L_{\text{ m }}}\int \limits _0^{L_{\text{ m }}} p_{\text{ m }} \, \textrm{d}x \end{aligned}$$
(14)

where \(\sigma _{\text{ m }}\) and \(p_{\text{ m }}\) are microscopic stress and momentum, and \(L_{\text{ m }}\) is the RVE size. For each micro time step, the averaged stress \(\langle \sigma _{\text{ m }}\rangle _{\text{ x }}\) and the averaged momentum \(\langle p_{\text{ m }}\rangle _{\text{ x }}\) values are calculated. These intermediate averaging equations (13) and (14) are not employed independently at the microscale; rather, they are presented for conceptual clarity. Once the microscopic time window \(T_{\text{ m }}\) selected based on the separation of time scales procedure is completed at the microscale, the values at the end of the simulation \(t_{\text{ m }}^f\) are transferred as residual forces to the macroscale.

$$\begin{aligned} \sigma _{\text{ M }}= & {} \langle \sigma _{\text{ m }}(t_{\text{ m }}^f)\rangle _{\text{ x }} \end{aligned}$$
(15)
$$\begin{aligned} p_{\text{ M }}= & {} \langle p_{\text{ m }}(t_{\text{ m }}^f)\rangle _{\text{ x }} \end{aligned}$$
(16)

3 Numerical model implementation

3.1 Macroscopic equation of motion in a linear problem

In order to solve the macroscopic boundary value problem, Eq. (9) is implemented in a finite element discretisation with the implicit time integration scheme. The constant average acceleration is adopted as a variant of Newmark time integration methods, which enables the average of the microscopic stress \( \langle \sigma _{\text{ m }}\rangle _{\text{ x }}\) and momentum \(\langle p_{\text{ m }}\rangle _{\text{ x }}\) to be embedded into the macroscopic boundary value problem as residual forces. Hence, the weak form of Eq. (9) is expressed as

$$\begin{aligned} \int \! N^{\text{ T }} \rho N\,\textrm{d}x\, \ddot{u}_{\text{ M }}^{t+\Delta t} = \int \! N^{\text{ T }}t_{\text{ M }} \,\textrm{d}x\, u_{\text{ M }}^{t+\Delta t} - \int \! B^{\text{ T }}EB \,\textrm{d}x\, u_{\text{ M }}^{t+\Delta t} \end{aligned}$$
(17)

where N and B contain interpolation functions and their derivatives, respectively. The macroscopic displacement \(u_{\text{ M }}^{t+\Delta t}\) and acceleration \(\ddot{u}_{\text{ M }}^{t+\Delta t}\) can be computed as \(u_{\text{ M }}^t+\Delta u_{\text{ M }}\) and \(\ddot{u}_{\text{ M }}^t + \Delta \ddot{u}_{\text{ M }} \) to place the average of the microscopic stress and momentum in Eq (17). Incorporating the macroscopic displacement \(\Delta u_{\text{ M }}\) and acceleration \(\Delta \ddot{u}_{\text{ M }}\) increments into Eq (17) leads to

$$\begin{aligned} \int \! N^{\text{ T }} \rho N\,\textrm{d}x\, (\ddot{u}_{\text{ M }}^t+\Delta \ddot{u}_{\text{ M }})&= \int \! N^{\text{ T }}t_{\text{ M }} \,\textrm{d}x\, u_{\text{ M }}^{t+\Delta t} \nonumber \\&\quad - \int \! B^{\text{ T }}EB \,\textrm{d}x\,\textrm{d}x\, (u_{\text{ M }}^t+ \Delta u_{\text{ M }}) \end{aligned}$$
(18)

The macroscopic acceleration increment \(\Delta \ddot{u}_{\text{ M }}\) is replaced by the Newmark equation using the constant average acceleration method; hence, Eq. (18) is rewritten as

$$\begin{aligned}&\int \! N^{\text{ T }} \rho N\,\textrm{d}x\, \ddot{u}_{\text{ M }}^t \nonumber \\&\qquad + \int \! N^{\text{ T }} \rho N\,\textrm{d}x \bigg [\frac{4}{\Delta t^2} \Big (\Delta u_{\text{ M }} - {\dot{u}}_{\text{ M }}^t \Delta t -\frac{1}{4}\ddot{u}_{\text{ M }}^t\Delta t^2 \Big ) \bigg ] \nonumber \\&\quad = \int \! N^{\text{ T }}t_{\text{ M }} \,\textrm{d}x\, u_{\text{ M }}^{t+\Delta t} - \int \! B^{\text{ T }}EB \,\textrm{d}x\, (u_{\text{ M }}^t+ \Delta u_{\text{ M }}) \end{aligned}$$
(19)

Reorganising Eq. (19) for the solution of the macroscopic displacement increment \(\Delta u_{\text{ M }}\) results in

$$\begin{aligned}&\bigg [ \frac{4}{\Delta t^2} \int \! N^{\text{ T }} \rho N\,\textrm{d}x + \int \! B^{\text{ T }}EB \,\textrm{d}x \bigg ] \Delta u_{\text{ M }} \nonumber \\&\quad = \int \! N^{\text{ T }}t_{\text{ M }} \,\textrm{d}x\, u_{\text{ M }}^{t+\Delta t} - \int \! B^{\text{ T }}EB \,\textrm{d}x\, u_{\text{ M }}^t \nonumber \\&\qquad + \frac{4}{\Delta t}\int \! N^{\text{ T }} \rho N\,\textrm{d}x \, {\dot{u}}_{\text{ M }}^t + \int \! N^{\text{ T }} \rho N\,\textrm{d}x \, \ddot{u}_{\text{ M }}^t \end{aligned}$$
(20)

The right hand side of Eq. (20) is assigned as a residual force \(f_{\text{ M }}^{\text{ res }}\) at the macroscale. The macroscopic residual force is updated by the average of the microscopic stress \( \langle \sigma _{\text{ m }}\rangle _{\text{ x }}\) and momentum \(\langle p_{\text{ m }}\rangle _{\text{ x }}\) for each current macroscopic time \(t_{\text{ M }}^{\text{ n }}\), given by

$$\begin{aligned} f_{\text{ M }}^{\text{ res }} = f_{\text{ ext }} - f_{\text{ M }}^t(\sigma ) + f_{\text{ M }}^t(p) + f_{\text{ M }}^t({\dot{p}}) \end{aligned}$$
(21)

where \(f_{\text{ M }}^t(\sigma )\), \(f_{\text{ M }}^t(p)\) and \(f_{\text{ M }}^t({\dot{p}})\) are the static, momentum and momentum rate residual forces, respectively. Replacing \(f_{\text{ M }}^t(\sigma )\), \(f_{\text{ M }}^t(p)\) and \(f_{\text{ M }}^t({\dot{p}})\) in Eq. (21) with the average of the microscopic stress \( \langle \sigma _{\text{ m }}\rangle _{\text{ x }}\) and momentum \(\langle p_{\text{ m }}\rangle _{\text{ x }}\) then leads to the following equations

$$\begin{aligned} f^t_{\text{ M }}(\sigma )= & {} \int \! B^{\text{ T }} \langle \sigma _{\text{ m }}\rangle _{\text{ x }}^t = \int \! B^{\text{ T }} \sigma _{\text{ M }}^t \, \textrm{d}x \end{aligned}$$
(22)
$$\begin{aligned} f^t_{\text{ M }}(p)= & {} \int \! N^{\text{ T }} \langle p_{\text{ m }}\rangle _{\text{ x }}^t = \int \! N^{\text{ T }} p_{\text{ M }}^t\, \textrm{d}x \end{aligned}$$
(23)
$$\begin{aligned} f_{\text{ M }}^t({\dot{p}})= & {} \int \! N^{\text{ T }} \langle {\dot{p}}_{\text{ m }}\rangle _{\text{ x }}^t = \int \! N^{\text{ T }} {\dot{p}}_{\text{ M }}^t\,\textrm{d}x \end{aligned}$$
(24)

where \(\langle {\dot{p}}_{\text{ m }}\rangle _{\text{ x }}^t\) is the average of the microscopic momentum rate. As the microscopic stress \(\sigma _{\text{ m }}\) gives better accuracy than the microscopic momentum rate \({\dot{p}}_{\text{ m }}\) due to the increased oscillations that emerge when derivatives are taken, the average of the microscopic momentum rate is replaced by the average of the microscopic stress depending on Eq. (10), i.e.

$$\begin{aligned} f_{\text{ M }}^t({\dot{p}}) = f^t_{\text{ M }}(\sigma ) \end{aligned}$$
(25)

In the context of the dynamic computational homogenisation method addressing the macrostructural boundary value problem, a standard finite element discretisation is employed typically with implicit time integration methods. On the other hand, it is noteworthy that explicit time integration methods have demonstrated considerable efficacy, particularly in addressing highly accelerated problems [18].

3.2 Microscopic equation of motion in linear problem

In order to solve the microscopic boundary value problem, Eq. (10) is implemented in a finite element discretisation with implicit and explicit time integration schemes. The constant average acceleration variant of the Newmark scheme is adopted for the implicit time integration, whereas the central difference scheme is used for the explicit time integration. The left and right edge of the RVE are constrained by the downscaling parameters applied as periodic boundary conditions. The microscopic displacement \(u_{\text{ m }}^t\) and velocity \({\dot{u}}_{\text{ m }}^t\) at the current microscopic time step \(t_{\text{ m }}^{\text{ n }}\) are imposed on the prescribed nodes of the RVE as follows

$$\begin{aligned} u_{\text{ p }}^t = u_{\text{ M }} + \varepsilon _{\text{ M }}\, L_{\text{ m }} + {\dot{u}}_{\text{ M }} t_{\text{ m }}^{\text{ n }} \end{aligned}$$
(26)

where the nth microscopic time step \(t_{\text{ m }}^{\text{ n }}\) is given by \(t_{\text{ m }}^{\text{ n }} = n \Delta t _{\text{ m }}\). The microscopic time window is given by \(T_{\text{ m }} = N \Delta t_{\text{ m }}\), where N is the total number of microscopic steps. The macroscopic velocity \({\dot{u}}_{\text{ M }}\) is linearly increased over the microscopic time window \(T_{\text{ m }}\). Equation (10) is derived for the time integration schemes in the next Sections to obtain the residual forces with respect to the microscopic displacement \(u_{\text{ m }}^t\) and velocity \({\dot{u}}_{\text{ m }}^t\).

3.2.1 The constant average acceleration scheme

The strong form of Eq. (10) in the constant average acceleration scheme is given by

$$\begin{aligned} \int \! N^{\text{ T }} \rho N\,\textrm{d}x\, \ddot{u}_{\text{ m }}^{t+\Delta t} + \int \! B^{\text{ T }}EB \,\textrm{d}x\, u_{\text{ m }}^{t+\Delta t} = 0 \end{aligned}$$
(27)

The microscopic displacement \(u_{\text{ m }}^{t+\Delta t}\) and acceleration \(\ddot{u}_{\text{ m }}^{t+\Delta t}\) can be written as \(u_{\text{ m }}^t+\Delta u_{\text{ m }}\) and \(\ddot{u}_{\text{ m }}^t + \Delta \ddot{u}_{\text{ m }} \) to replace the microscopic displacement \(u_{\text{ p }}^t \) and velocity \( {\dot{u}}_{\text{ p }}^t\) of the prescribed nodes. Incorporating the microscopic displacement \(\Delta u_{\text{ m }}\) and acceleration \(\Delta \ddot{u}_{\text{ m }}\) increments into in Eq. (27) leads to

$$\begin{aligned} \int \! N^{\text{ T }} \rho N\,\textrm{d}x\, (\ddot{u}_{\text{ m }}^t+\Delta \ddot{u}_{\text{ m }}) + \int \! B^{\text{ T }}EB \,\textrm{d}x\, (u_{\text{ m }}^t+\Delta u_{\text{ m }})= 0 \end{aligned}$$
(28)

The microscopic acceleration increment \(\Delta \ddot{u}_{\text{ m }}\) is replaced by the Newmark equation based on an displacement expansion in the constant average acceleration scheme; hence, Eq. (28) is rewritten as

$$\begin{aligned}&\int \! B^{\text{ T }}EB \,\textrm{d}x\, (u_{\text{ m }}^t+ \Delta u_{\text{ m }}) + \int \! N^{\text{ T }} \rho N\,\textrm{d}x\, \ddot{u}_{\text{ m }}^t \nonumber \\&\quad \quad + \int \! N^{\text{ T }} \rho N\,\textrm{d}x \bigg [\frac{4}{\Delta t^2} \Big (\Delta u_{\text{ m }} - {\dot{u}}_{\text{ m }}^t \Delta t -\frac{1}{4}\ddot{u}_{\text{ m }}^t\Delta t^2 \Big ) \bigg ] = 0 \end{aligned}$$
(29)

Reorganising Eq. (29) for the solution of the microscopic displacement increment \(\Delta u_{\text{ m }}\) results in

$$\begin{aligned}&\bigg [ \int \! B^{\text{ T }}EB \,\textrm{d}x + \frac{4}{\Delta t^2} \int \! N^{\text{ T }} \rho N\,\textrm{d}x \bigg ] \Delta u_{\text{ m }} \nonumber \\&\quad = - \int \! B^{\text{ T }}EB \,\textrm{d}x\, u_{\text{ m }}^t \nonumber \\&\quad \quad + \frac{4}{\Delta t}\int \! N^{\text{ T }} \rho N\,\textrm{d}x \, {\dot{u}}_{\text{ m }}^t + \int \! N^{\text{ T }} \rho N\,\textrm{d}x \, \ddot{u}_{\text{ m }}^t \end{aligned}$$
(30)

The right hand side of Eq. (30) is assigned as a residual force \(f_{\text{ m }}^{\text{ res }}\) at the microscale. The microscopic residual force is imposed by the microscopic displacement \(u_{\text{ p }}^t \) and velocity \( {\dot{u}}_{\text{ p }}^t\) of the prescribed nodes for each current microscopic time \(t_{\text{ m }}^{\text{ n }}\), given by

$$\begin{aligned} f_{\text{ m }}^{\text{ res }} = - f_{\text{ m }}^\sigma (u_{\text{ m }}) + f_{\text{ m }}^p({\dot{u}}_{\text{ m }}) + f_{\text{ m }}^{{\dot{p}}}(\ddot{u}_{\text{ m }}) = 0 \end{aligned}$$
(31)

3.2.2 The central difference scheme

The strong form of Eq. (10) in the central difference scheme is given by

$$\begin{aligned} \int \! N^{\text{ T }} \rho N\,\textrm{d}x\, \ddot{u}_{\text{ m }}^t + \int \! B^{\text{ T }}EB \,\textrm{d}x\, u_{\text{ m }}^t = 0 \end{aligned}$$
(32)

Both terms of the left hand side of Eq. (32) are assigned as a residual force \(f_{\text{ m }}^{\text{ res }}\) for the central difference scheme at the microscale. The microscopic residual force is imposed by the microscopic displacement \(u_{\text{ p }}^t \) of the prescribed nodes for each current microscopic time \(t_{\text{ m }}^{\text{ n }}\), given by

$$\begin{aligned} f_{\text{ m }}^{\text{ res }} = - f_{\text{ m }}^\sigma (u_{\text{ m }}) - f_{\text{ m }}^{{\dot{p}}}(\ddot{u}_{\text{ m }}) = 0 \end{aligned}$$
(33)

Comparing implicit and explicit time integrations, the microscopic residual force in the constant average acceleration scheme can be expressed in terms of the prescribed displacement \(u_{\text{ p }}^t\) and velocity \({\dot{u}}_{\text{ p }}^t\), while the microscopic residual force in the central difference method is only defined by the prescribed displacement \(u_{\text{ p }}^t\). Examples of using time integration methods are discussed in Sect. 4.4

3.3 Computational homogenisation solution algorithm

The procedure of dynamic computational homogenisation method is schematised in Fig. 5 which can be concisely described by the following steps.

The macrostructural boundary value problem is defined at the macroscale by using a finite element scheme. The macrostructure is discretised in space and time. The boundary condition is imposed on the macrostructure, together with the external load in compliance with spatial and temporal discretisations. A microstructural boundary value problem (BVP) over the RVE is assigned to each macroscopic integration point. At the microscale, the RVE is determined according to the separation of length and time scales explained in Sects. 2.1.1 and 2.1.2.

In order to obtain the inital constitutive material model, an artificial initial macroscopic strain \(\varepsilon _{\text{0M }}=1\) is applied as the prescribed boundary condition of the RVE at the initial macro time step \(t_{\text{0M }}\). This forms the static microstructural BVP at the microscale. The solution of the microstructural BVP provides the average of the microscopic stress \(\langle \sigma _{\text{ m }}\rangle _{\text{ x }}\) to calculate the macrosopic Young’s modulus \(E_{\text{ M }}\). The macroscopic mass density \(\rho _{\text{ M }}\) is simply obtained by the equation of the rule of mixture \(\rho _{\text{ M }}=\sum _{k=1}^K \alpha _{\text{ k }}\rho _{\text{ k }}\). The initial macroscopic material properties are transferred back to the macroscale. With the initial estimates for the Young’s modulus and the mass density, an estimate for the wave speed can be determined which in turn aids the selection of a suitable time averaging window.

At the macroscale, the global stiffness and mass matrices are assembled using the initial macroscopic material properties. The macroscopic time integration is carried out to solve the macrostructural BVP for each macroscopic time increment \(\Delta t_{\text{ M }}\). The solution of the macrostructural BVP provides the macroscopic acceleration \(\ddot{u}_{\text{ M }}\), velocity \({\dot{u}}_{\text{ M }}\) and displacement \(u_{\text{ M }}\). For each macroscopic integration point, the macroscopic strain \(\varepsilon _{\text{ M }}\) and velocity \({\dot{u}}_{\text{ M }}\) are imposed as the prescribed boundary condition of its associated RVE through the downscaling procedure explained in Sect. 2.4.1.

The microscopic time integration is carried out to solve the microstructural BVP for each microscopic time increment \(\Delta t_{\text{ m }}\). When the microstructural analysis is completed, the solution of the microstructural BVP provides the microscopic acceleration \(\ddot{u}_{\text{ m }}^f\), velocity \({\dot{u}}_{\text{ m }}^f\) and displacement \(u_{\text{ m }}^f\) at the end of the microscopic analysis \(t_{\text{ m }}^{\text{ f }}\). As per the upscaling procedure explained in Sect. 2.4.2, the macroscopic velocity \({\dot{u}}_{\text{ m }}^f\) and displacement \(u_{\text{ m }}^f\) are spatially integrated to obtain the microscopic averaged stress \(\langle \sigma _{\text{ m }}\rangle _{\text{ x }}\) and momentum \(\langle p_{\text{ m }}\rangle _{\text{ x }}\) (i.e. the macroscopic stress \(\sigma _{\text{ M }}\) and momentum \(p_{\text{ M }}\)). The microscopic averaged stress \(\langle \sigma _{\text{ m }}\rangle _{\text{ x }}\) and momentum \(\langle p_{\text{ m }}\rangle _{\text{ x }}\) are embedded as the residual force into the macroscopic BVP for the next macroscopic time step \(t_{\text{ M }}^{n+1}\), thereby one loop of the dynamic computational homogenization is completed.

When the macroscopic time integration is completed, the macroscopic response of the periodic composite for the given applied load is obtained for each macroscopic time increment \(\Delta t_{\text{ M }}\). In case better accuracy in the macroscopic response is required, the choice of the RVE, examples of which are given in the next Section, can be updated depending on the separation of length and time scales.

Fig. 5
figure 5

Computational flowchart of dynamic computational homogenisation scheme

Full size image

4 Numerical results

In this section, a one-dimensional linear elastic laminate bar is modelled using the dynamic computational homogenisation procedure explained in Sects. 3.3 to assess the effects of \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\) at the microscale. The bar is clamped on the left end and a constant load \(F=10\) N is applied at the right end throughout the simulation. For the macroscopic boundary value problem, linear finite elements are used with the Newmark time discretisation. This investigation is conducted using a fixed-length macrostructure of 1 m, discretized into four elements, while a macroscopic time step of 1 s is employed for a simulation duration of 5 s. On the other hand, for microscopic boundary value problems, both the constant average acceleration scheme and the central difference method are implemented. The critical time step size \(t_{\text{ crit }}=0.0625\) s is used in the central difference method for reasons of stability as well as accuracy. Furthermore, certainly, the spatial and temporal coupling is assumed for all analyses below. Specifically, when applying the spatial coupling exclusively, the microstructure size is adjusted according to the number of unit cells, with each unit cell having a length of 0.0625 m. Conversely, in cases where the temporal coupling is exclusively applied, the microstructure size remains fixed at 0.25 m, while the microscopic simulation time varies accordingly.

The results of the multiscale problem are compared with those obtained by direct numerical simulations (DNS) to verify the accuracy of the multiscale model. In direct numerical simulations, the one-dimensional laminate bar is only analysed on the heterogeneous microscale. For all numerical examples, the error estimation formula is given by

$$\begin{aligned} e = \frac{|x_{\text{ CH }}-x_{\text{ DNS }}|}{|x_{\text{ DNS }}|} \cdot 100 \% \end{aligned}$$
(34)

where \(x_{\text{ CH }}\) and \(x_{\text{ DNS }}\) are values obtained from the results of computational homogenisation and direct numerical simulations, respectively. The comparison of macroscopic displacements and velocities against those obtained with DNS allows one to assess the accuracy of the local response of the multiscale model. In order to compare the global response of the multiscale model, averaged strain and kinetic energies containing microscopic stress and momentum can be formulated as follows

$$\begin{aligned} {\mathscr {U}}= & {} \frac{1}{2} u_{\text{ M }}^{\text{ T }}K_{\text{ M }}u_{\text{ M }} = \frac{1}{2} \int \! \varepsilon _{\text{ M }}^{\text{ T }}\langle \sigma _{\text{ m }}\rangle _{\text{ x }}^t \, \textrm{d}x \end{aligned}$$
(35)
$$\begin{aligned} {\mathscr {K}}= & {} \frac{1}{2}{\dot{u}}^{\text{ T }} M_{\text{ M }} {\dot{u}} =\frac{1}{2} \int \! {\dot{u}}^{\text{ T }} N^{\text{ T }} \langle p_{\text{ m }}\rangle _{\text{ x }}^t \, \textrm{d}x \end{aligned}$$
(36)

where \({\mathscr {U}}\) and \({\mathscr {K}}\) are strain and kinetic energies, respectively. \(\langle \sigma _{\text{ m }}\rangle _x^t\) and \(\langle p_{\text{ m }}\rangle _x^t\) are upscaling quantities comprising microscopic material constitutive relations.

4.1 Effect of number of unit cells

As a first examination of the influence of \(N_{\text{ uc }}\), the strain and kinetic energies of a one-dimensional linear elastic laminated bar are investigated. Strain and kinetic energies are appropriate quantities to evaluate the impact of an increase in the number of unit cells on the global effectiveness of the multiscale model. In this analysis, the strain and kinetic energies obtained by the DNS are compared with those obtained by the dynamic computational homogenisation method.

As shown in Fig. 6, an increase in the number of unit cells \(N_{\text{ uc }}\) results in better estimation of the multiscale strain energy, while the multiscale kinetic energy does not show the same trend. The multiscale acceleration and displacement values presented in Fig. 7 have good correlations with those obtained by the DNS with time at higher values of \(N_{\text{ uc }}\). On the other hand, the multiscale velocity values remain lower than the velocity values obtained by the DNS so that the momentum internal force \(f^{\text{ p }}_{\text{ M }}\) causes a huge error in the multiscale kinetic energy.

Fig. 6
figure 6

Effect of the number of unit cells on strain and kinetic energies against the reference solution obtained by the DNS

Full size image

In addition to evaluating the effect of the number of unit cells on the dynamic response of 1D bar system, macroscopic displacements and velocities at the local scale are also assessed using the dynamic computational homogenisation method. As has been depicted in Fig. 7, despite showing a consistent trend in both macroscopic results, a higher number of unit cells gives better estimations of the macroscopic displacement and velocity compared to those results obtained from the DNS. Particularly, when \(N_{\text{ uc }} = 8\) (green line), errors in macroscopic displacement and velocity at \(t_{\text{ m }} = 5\) s, are obtained as 5.44% and 13.41%, respectively.

Fig. 7
figure 7

Macroscopic displacement-time (left) and velocity-time (right) curves for \(N_{\text{ wp }}=8\) and various \(N_{\text{ uc }}\) together with the reference solution obtained by the DNS

Full size image

4.2 Effect of number of wave propagations

In contrast with \(N_{\text{ uc }}\) analysis, the number of wave propagations (i.e. the number of times the wave front travels through the entire microscopic sample, indicated with \(N_{\text{ wp }}\),) is increased while eight unit cells are used throughout this analysis. For each number of wave propagations the results obtained from the dynamic computational homogenisation are compared with the results obtained by the DNS. At higher values of \(N_{\text{ wp }}\) displayed in Fig. 8, the kinetic energy converges perfectly. Although the error in strain energy tend to decrease with an increase in \(N_{\text{ wp }}\), higher \(N_{\text{ uc }}\) provides better results for strain energy. When \(N_{\text{ wp }}\) increases, longer averaged stress profiles can be obtained on the micro-level. As a upscaling parameter, the averaged stress at the end of the micro simulation time is transferred to the macro-level. The micro simulation time is critical to be determined since a microscopic wave is required to reach at the end of the microscopic bar to contain all microscopic characteristics for multiscale analyses. When the spatial and temporal links are performed between macro and microstructures, the results of macroscopic stress and momentum are not accurate. As long as the numerical parameters such as minimum wave propagation time and critical time step are satisfied, higher number of wave propagations gives better estimates for averaged stress and momentum. Therefore, this also proves the importance of \(N_{\text{ wp }}\) on multiscale results obtained by the dynamic computational homogenisation method.

Fig. 8
figure 8

Effect of the number of wave propagations on strain \({\mathscr {U}}\) and kinetic energies \({\mathscr {K}}\) against the reference solution obtained by the DNS

Full size image

The local responses of macroscopic boundary value problem is also observed. In Fig. 9, higher number of wave propagation results in a good approximation of macroscopic displacement and velocity compared to the DNS results. In particular, when \(N_{\text{ wp }}=8\) (green line), the errors in macroscopic displacement and velocity at \(t_{\text{ m }} = 5\) s are 2.97% and 6.85%, respectively. Additionally, a slight change in \(N_{\text{ wp }}\) leads to a great amount of reduction in displacement and velocity errors, as shown in Fig. 9.

Fig. 9
figure 9

Macroscopic displacement-time (left) and velocity-time (right) curves at the value of \(N_{\text{ uc }}=8\) for various \(N_{\text{ wp }}\) values with the reference solution obtained by the DNS

Full size image

4.3 Combination of number of unit cells and number of wave propagations

Building upon the findings presented in Reference [20], the advantages of \(N_{\text{ uc }}\) for accurately calculating the strain energy and \(N_{\text{ wp }}\) for accurately calculating the kinetic energy are combined. Therefore, to achieve the highest level of accuracy in both strain and kinetic energy calculations, the superior effectiveness of an simultaneous increase in \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\) is evaluated by comparing to their individual components. As demonstrated in Sects. 4.1 and 4.2, the closest satisfactory results of the dynamic response of 1D bar are accomplished by applying eight unit cells and eight wave propagations, which are considered the minimum starting values for all analyses. As shown in Fig. 10, for the strain and kinetic energy, the combination of \(N_{\text{ uc }}=64\) and \(N_{\text{ wp }}=64\) gives minimum error at 10.5% and 0.6%, respectively. For any point in Fig. 10, the simultaneous increase of \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\) results in higher accuracies than separate increases of either \(N_{\text{ uc }}\) or \(N_{\text{ wp }}\).

Fig. 10
figure 10

Comparison of different \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\) combinations with regards to strain energy (left) and kinetic energy (right)

Full size image

4.4 Time integration algorithms for microstructure

Instead of implicit time integration on the microscale, explicit time integration can also be used for the microscopic boundary value problem. The central difference method, which is conditionally stable depending on the critical time step \(\Delta t_{\text{ crit }}\), is used to discretise the microstructural response in time. For reasons of stability, the microscopic time step \(\Delta t_{\text{ m }}\) used in the developed algorithm is required to be not larger than the critical time step on the microscale.

Firstly, we illustrate the dynamic response of the bar, focusing on macroscopic displacements and velocities in Fig. 11 under the conditions where \(N_{uc}=8\) and \(N_{wp}=8\). This comparison serves to evaluate the influence of the central difference method and the constant average method on the averaged response of the RVE in contrast to the DNS solutions. Even though the results obtained with both methods are coincident with those provided by the DNS, the central difference method shows better agreement with the DNS compared to the constant average method.

Fig. 11
figure 11

Comparisons of implicit and explicit model with the reference solution obtained by the DNS regarding macroscopic displacement-time (left) and velocity-time (right) curves at the values of \(N_{\text{ uc }}=8\) and \(N_{\text{ uc }}=8\)

Full size image

As presented in Fig. 12, at higher values of \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\), both strain and kinetic energies result in lower error estimations. Specifically, the errors in strain energy, when employing various time integration methods, range from 30% to 32%, while those in kinetic energy fall within the range of 0.03% to 3%. Notably, while the error in both energies tends to diminish with the implicit time integration method as \(N_{uc}\) and \(N_{wp}\) increase, a more consistent trend is observed in the errors associated with the explicit time integration method. These results confirm that both explicit and implicit time integration schemes can be used on the microscale, with the choice left to the preference of the user.

Fig. 12
figure 12

Influence of explicit and implicit time integration methods on strain energy (left) and kinetic energy (right) while simultaneously increasing in \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\). Error estimations in strain (left) and kinetic (right) energies are computed based on the DNS solutions

Full size image

4.5 Different impedance contrasts

The simultaneous increase of \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\) presented in Sect. 4.3 is considered the best effective estimation tool for overall properties. Therefore, the effect of this combination on the contrast in mechanical impedance of materials is investigated in this section. The material properties of the microscopic structure such as Young’s modulus E and mass density \(\rho \) are arranged in accordance with a user-defined impedance contrast factor \(z= \sqrt{E\rho }\), yet the wave speeds of each material \(c=\sqrt{E/\rho }\) are aimed to remain unchanged.

To begin with, the local displacement responses at the mid-point of the bar are shown in Fig. 13 for various impedance contrasts from low to moderate. The simultaneous increase in \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\) provides good estimations for all impedance contrast factors compared to the DNS solutions. In addition, there is a consistent trend for different impedance contrast factors and their error estimation. When the impedance contrast factor is low (e.g. \(z_{\text{ m }}=1.2\)), the local error estimation reaches the lowest value of 0.5%. With the moderately high impedance contrast factor (e.g. \(z_{\text{ m }}=2\)), the local error estimation is approximately 10.8%.

Fig. 13
figure 13

Influence of \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\) on macroscopic displacements at the mid-point of the bar for various impedance contrast factors. Error estimations in macroscopic displacements are computed based on the DNS solutions

Full size image

Moreover, the effectiveness of simultaneous increase in \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\) is also observed on the global response of the bar based on the strain and kinetic energies. As depicted in Fig. 14, errors in the strain energy at \(N_{\text{ uc }}=64\) and \(N_{\text{ wp }}=64\) are concentrated around 6–10% for all impedance contrast factors. On the other hand, as expected, the prediction of this model becomes less accurate for higher impedance contrast values (e.g. \(z_{\text{ m }}=2\)). While the error in kinetic energy for low impedance contrast (e.g. \(z_{\text{ m }}=1.2\)) is 0.6%, the one for moderately high impedance contrast (e.g. \(z_{\text{ m }}=2\)) is 29.7%.

Fig. 14
figure 14

Global influences of \(N_{\text{ uc }}\) and \(N_{\text{ wp }}\) on strain energy (left) and kinetic energy (right) for various impedance contrast factors. Error estimations in macroscopic displacements are computed based on the DNS solutions

Full size image

5 Conclusions

In this work, a spatial and temporal separation procedure is integrated into the dynamic computational homogenisation method to obtain improved estimation of elastodynamic response for multiscale periodic composites. A simultaneous separation of length and time scales between macro and microstructures is introduced to capture transient interactions and micro-inertia effects emerged from wave dispersion. The proposed model contains upscaling and downscaling formulations within the dynamic computational homogenisation framework that establish scale interactions between the macro and microscales for spatial-temporal separation.

In order to investigate the effectiveness of the proposed work, linear dynamic analyses are carried out for a one-dimensional laminate bar with several levels of impedance contrast. Results of the analyses are validated by comparing against the direct finite element solutions. From the global response perspective, it is observed that increasing the number of unit cells significantly reduces the error in strain energy, while increasing the number of wave propagations significantly reduces the error in kinetic energy. To combine advantages of increases in the numbers of unit cells and wave propagations, these two parameters are simultaneously controlled to obtain better convergence of macroscopic response in dynamics. Significantly, the simultaneous increases in both parameters lead to achieving higher accuracy compared to increasing each parameter individually. From the local response perspective, the macroscopic displacement and velocity results obtained by higher numbers of unit cells and wave propagation converge quickly to those results obtained through the DNS. Additionally, the effect of these simultaneous increases is evaluated for various impedance contrasts of material properties at the microscale. Despite achieving considerable improvement in the convergence of macroscopic response, the model becomes less accurate when high impedance contrasts exist in the material properties. Despite this progress, achieving closer convergence to DNS outcomes remains an ongoing focus for future iterations. Further enhancements toward reaching DNS accuracy constitute an imperative area for future research.